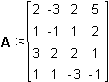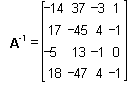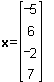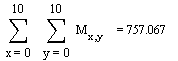1 Mathematical Models
!Jong; Graaf

T.M. de Jong, R.P. de Graaf

1.1 De oorsprong.......................................................... 2

1.2 Het wiskundige model is geen werkelijkheid. 2

1.3 Wiskunde is een taal............................................. 3

1.4 Nummeren.............................................................. 3

1.5 Tellen........................................................................ 3

1.6 Combinatorics........................................................ 3

1.7 Variatiebeperking.................................................. 5

1.8 Program of a site................................................... 5

1.9 Binary legends........................................................ 6

1.10 Additional legend units......................................... 6

1.11 Het medium............................................................. 6

1.12 Resolution and tolerance..................................... 7

1.13 Size systems.......................................................... 8

1.14 Geometry............................................................... 11

1.15 Graphs.................................................................... 11

1.16 Networks............................................................... 14

1.17 Probability.............................................................. 14

1.18 Linear Programming (LP)................................... 16

1.19 Matrix calculation................................................. 18

1.20 De Simplexmethode............................................ 18

1.21 Functies................................................................. 20

1.22 Fractals................................................................... 20

1.23 Differentiëren....................................................... 21

1.24 Integreren............................................................. 22

1.25 Differentiaalvergelijkingen................................. 24

1.26 Systems modelling............................................. 25

Een wiskundeprogramma voor de faculteit Bouwkunde TUD dat in de jaren '90 enkele jaren door de faculteit Wiskunde werd verzorgd, vond weinig aansluiting bij de bouwkundedocenten, hun voorbeelden en referenties. De studenten begrepen dan ook niet waar het goed voor was, ondervonden meer belemmering dan stimulans bij het ontwerpen en vermeden het bij de integrale toets waarin andere vakken het cijfer konden herstellen. De ontwerp-praktijk kan immers met enkele aanvullingen op de middelbare-schoolwiskunde uitstekend uit de voeten. De concrete vormproductie wint het nog altijd van de abstracte wiskundige omweg via coördinaatgewijze vormbeschrijving, zelfs al worden fractale vormen gegenereerd. De wiskundige en ontwerper Alexander heeft met zijn 'Notes on the syntheses of form'^[a] minder school gemaakt dan met zijn 'Pattern language'^[b]. De mechanische en bouwfysische rest wordt gedaan door gespecialiseerde adviesbureaus en computers nadat er eerst een schetsontwerp is geleverd. Geen van de oudere ontwerpers herinnert zich meer iets van de inhoud van het wiskunde-onderwijs dat zij zelf genoten in de jaren '60 en '70 toen dat op de Faculteit verplicht was, omdat zij er door de praktijk nooit meer aan herinnerd werden.

Van de samengestelde bouwkundediktaten, meetkunde, graphentheorie, transformaties en symmetrieën, matrixrekenen en lineair optimaliseren, statistiek, differentiaal- en integraalrekenen die in de jaren '90 in eenvoudige vorm werden geïntroduceerd met het probleemgestuurd onderwijs (PGO), vindt men anno 2000 alleen de laatste nog in de bookshop van de faculteit. Dit laatste relict is te danken aan de vasthoudenheid van de sector bouwfysica. Matrixrekenen wordt bij de optimaliseringsoefeningen in de latere jaren bouwmanagement uit de middelbare schoolwiskunde opgehaald. Men mist daarbij de verloren onderbouw in het eerste jaar. Met de langzame doorwerking van gemakkelijke computertoepassingen zoals spreadsheets en CAD (pixel- en vectorrepresentaties van vorm) bij het ontwerpen groeit echter een nieuwe belangstelling. Programma's als Excel, MathCad of MathLab vergemakkelijken het experimenteren met wiskundige formules als nooit tevoren. Wellicht moet uit deze wiskundige ingrediënten die ook door Broadbent^[c] als relevant voor het bouwkundige ontwerp worden onderschreven, een nieuwe wiskunde voor de bouwkunde worden samengesteld. De bouwkunde zelf en de civiele techniek staan immers historisch aan de wieg van de wiskunde. Dit hoofdstuk heeft niet de pretentie aan de wieg van een nieuwe bouw-wiskunde te staan, daartoe ontbreken de auteurs als stedebouwkundigen de nodige kwalificaties. Het geeft echter een zeer globaal overzicht van in het bouwkundige ontwerp toepasbare wiskundevormen met verwijzingen. en verbindt deze met een nieuw element als uitgangspunt: de combinatoriek. Wie zijn middelbare-schoolwiskunde wil ophalen^[d] of een beeldend overzicht van vrijwel de gehele wiskunde wil krijgen^[e] wordt naar betreffende publicaties verwezen. Hier wordt vooral gestimuleerd om te experimenteren met Excel. Toch geldt nog steeds het antwoord van Euclides, gericht aan een koning die vroeg of er geen eenvoudiger manier was om geometrie te leren dan zijn 'Elementen'^[f]: 'Er is geen koninklijke weg tot de geometrie'.

1.1 De oorsprong

Wiskunde is een taal, ontwikkeld om locaties, grootten (geometrie), aantallen (aritmetiek)^[g] en ontwikkelingen daarin uit waarnemingen (metingen en tellingen) te beschrijven, te bewerken en op grond daarvan nieuwe waarnemingen te voorspellen. Zo werd bij de stichting van steden in de Griekse kolonies tot 500vC. een vierkant van 50x50 plethra (ca. 1500x1500m) met behulp van een diagonaal van 70 plethra uitgezet om rechte hoeken te krijgen. Pythagoras (580-500vC) of één van zijn leerlingen gaf vervolgens het bekende bewijs dat de verhouding iets méér dan 7/5 moest zijn omdat 25+25 iets meer is dan 49. Hier werd uit de geometrie het aritmetische besef geboren dat er reële_getallen R zijn (zoals wortel 2 of de daaruit afgeleide reële lengte van de diagonaal) die niet door simpele deling (rationaal, Q) van natuurlijke_getallen (N, 1,2,3,…) kunnen worden verkregen De geometrie (letterlijk landmeetkunde) heeft zijn eerste beschreven ontwikkeling te danken aan de jaarlijkse overstromingen van de Nijl. In het oude Egypte wisten overstromingen de grenzen van landeigendommen uit, zodat deze elk jaar landmeetkundig opnieuw moesten worden vastgesteld uit bakens in het niet-overstroomde gebied. De aritmetiek heeft belangrijke wortels in de Foenicische handel. De Griek Euclides (ca. 300 vC.) verzamelde de toenmalige kennis van beide in zijn boek 'Elementen', tot in de 20^ste eeuw via de arabische wereld de basis van al het meetkunde-onderwijs. Euclides maakte gebruik van vroegere teksten, maar leidde de stellingen van de meetkunde voor het eerst door logische bewijsvoering af uit 5 axioma's^[h]. Daarmee werd een proces voltooid waarin de wiskunde werd losgemaakt uit de empirische praktijk van het meten en tellen aan voorbeelden.

1.2 Het wiskundige model is geen werkelijkheid

De wiskunde kan sindsdien evenals de logica zonder waarneming van invoergrootheden (niet-empirisch, a_priori) nieuwe inzichten samenstellen (synthetische_oordelen). Zij worden bij logisch bewijs ook zonder waarneming van uitvoergrootheden wetenschappelijk als nieuw inzicht aanvaard. De filosoof Kant (1724-1804) brak zich het hoofd hoe dat überhaupt mogelijk is: 'synthetische oordelen a priori'^[i]. Een empirisch-wetenschappelijke theorie constateert immers altijd, dat bij een onafhankelijke waarneming uit een verzameling X, een corresponderend afhankelijke waarneming uit een verzameling Y volgt. Als de elementen van X en Y beide in een corresponderend oplopende volgorde kunnen worden gezet, zodat zij de variabelen x en y vormen, kan men niet-gedane waarnemingen interpoleren en bij gelijkblijvende (niet in het model opgenomen) omstandigheden (ceteris paribus) naar de toekomst extrapoleren. Een wetmatigheid van hun correspondentie wordt beschouwd als werking tussen beide: y(x). Er zijn waarschijnlijke (causale ) en mogelijke (voorwaardelijke) werkingen. Als bijvoorbeeld de omvang van de bevolking (x) stijgt, stijgt het aantal gebouwen (y) volgens de werking y(x). Hoe groter het aantal waarnemingen (n), deste overtuigender is die theorie. Als je met honderd jaar tijdreeksen^[j] (n = 100) kunt aantonen dat tussen beide een werking te definiëren valt, overtuigt dat meer, dan een enkele correspondentie in het afgelopen jaar (n = 1). De onderzoeker kan bij grotere aantallen onafhankelijke invoerwaarnemingen een wiskundige werking y = f(x), bijvoorbeeld y=½x zoeken die dezelfde resultaten produceert als de afhankelijke waarnemingen (modelleren). Daarbij hoeft alleen de in- en output, en niet de modelmatig gebruikte wiskundige werkingen, een waarneembare relatie met de werkelijkheid te vertonen. Zodra andere feiten worden waargenomen dan de voorspelde, wordt de empirische theorie verworpen en niet noodzakelijk het wiskundige betoog dat daarin een rol speelde, al wordt dat wel eens met elkaar verward. Als de voorspellingen uitkomen wordt het wiskundig werkende model vervolgens weer vaak als 'ontdekte' werkelijkheid gezien ('God rekent altijd'^[k]). Dit is echter niet nodig om een theorie te aanvaarden (tot het tegendeel bewezen is): verschillende (wiskundige of werkelijke) werkingen kunnen immers hetzelfde resultaat opleveren.

1.3 Wiskunde is een taal

Evenals in het dagelijks taalgebruik, worden ook in de logica en wiskunde begrippen (uitdrukkingen, expressies) gebruikt en tot een model (uitspraken, zinnen, volzinsfuncties^[l], werkingen, functies) samengesteld met operatoren (werkwoorden, voegwoorden). De logica benut van deze operatoren vooral de voegwoorden (bijvoorbeeld als P dan Q), de wiskunde de werkwoorden (functies zoals optellen, sommeren). De logische afleidingen in de wiskunde hebben meestal de logische taalvorm: 'als werking P dan werking Q'. Het dagelijks taalgebruik kan echter unieke voorstellingen benoemen. Deze eerste naamgevingfunctie van de gewone taal heeft het karakter van een overéénkomst. Pas wanneer de voorstelling opnieuw wordt waargenomen is er een grond om te gaan tellen. Wat zich herhaalt leent zich voor de wiskunde. Naamgeving uit de omgangstaal is (veelal onuitgesproken) voorondersteld bij elke wiskundige operationalisering. Wiskunde kan niet worden gebruikt bij unieke_voorstellingen. Als een steen een kilo weegt, wegen twee stenen alleen twee kilo wanneer zijn 'gelijk' zijn. Deze gelijkheid (hier in grootte en materiaal) kan alleen met gewone woorden worden overééngekomen. Het verdelen van ongelijke stenen in gelijke brokstukken (het omzetten van grootten in aantallen, analyse) kan unica voor tellen toegankelijk maken, en vervolgens voor wiskundige operaties op de telling. Het is echter de vraag of dat altijd kan (Salomonsoordeel: twee keer een half kind is geen kind meer). Er kan bij analyse in andere kenmerken een samenhang verloren gaan die de essentie van het bouwkundig object raakt en bij synthese tot een andere grootte-orde (optellen) verloren is. De schaalparadox kan parten spelen bij het in steeds kleinere delen verdelen van een voorwerp om daaruit vervolgens met optellende bewerkingen weer een geheel van andere grootte-orde samen te stellen of te voorspellen (infinitesimaalrekening, differentiaal- en integraalrekening). De andere, daarbij (in een bepaalde conext) verloren kenmerken kan men vervolgens weer in de formules proberen mee te nemen (validiteit vergroten, zie …), maar dit verlegt het probleem.

1.4 Nummeren

Nummeren vooronderstelt alleen een verschil van plaats, geen gelijkheid van aard. Ik kan de totaal verschillende voorwerpen in mijn kamer nummeren (of letteren) om later te kunnen zien of ik iets mis, maar ik kan op deze nummering geen wiskundige bewerkingen toepassen. Toch zijn zij wiskundig van groot belang omdat geordend verschil van plaats (volgorde) in de getallenleer cruciaal is^[m]. Het nummer fungeert als label, als naam, als idendificatie (identificatienummer, ID-nummer, of index_i bij variabelen) dat verwisselen, overslaan en dubbeltellen kan voorkomen. Men kan met nummers dus niet rekenen, al is 'nummeren' wel stilzwijgend voorondersteld bij 'tellen'. De volgorde van nummers heeft in principe geen andere betekenis dan dat hij hetzelfde blijft, ookal verwisselen de genummerde objecten vervolgens van plaats. Het nummer stabiliseert verschillen van plaats die men ooit als op een foto heeft geconstateerd. Toch krijgt de volgorde waarin men nummert in de praktijk vaak een betekenis (bijvoorbeeld de volgorde van binnenkomst), waardoor daaruit toch conclusies kunnen worden getrokken. Hoewel men vaak de neiging heeft met het oog daarop enige logica in een nummering aan te brengen (categorisering), loopt deze vroeg of laat vast, terwijl de nummering gaten of tekort aan ruimte oploopt. Bij de huidige informatieverwerkingsmogelijkheden, is het dan bijvoorbeeld ook beter in een spreadsheet als database naast de kolom met volgordelijke identificatienummers (altijd los van de verschuivende rij- en kolomnummers aanmaken!) nieuwe kolommen te openen om categorieën te onderscheiden waarop men wil kunnen sorteren. Voor de wiskunde is van belang dat men invoer- en uitvoergetallen kan nummeren, indexeren, indentificeren en in vaste volgorde en combinatie uit een database kan halen. Het nummer is de drager van het verschil van plaats in een database. Een betrouwbare database is drager van verschillen van aard en plaats in de werkelijkheid (niet die aard en plaats zelf). Opdat een identificatiecode altijd naar hetzelfde object moet blijven verwijzen dient het gedurende het bestaan van dat object invariant te zijn. Bovendien mag het geen inhoudelijke betekenis hebben, zoals bijvoorbeeld een postcode huisnummer combinatie. Deze wijzigt namelijk bij verhuizing van het bijbehorende “object”.

1.5 Tellen

Waarnemingen kunnen alleen wiskundig worden uitgedrukt als zij meer dan één keer (in een vergelijkbare context) voorkomen en in enig opzicht als 'gelijk' in een verzameling kunnen worden ondergebracht. Pas dan kan men ze tellen. Deze gelijkheidsvooronderstelling van de verzamelingenleer en de wiskunde wordt wel eens vergeten of al te gemakkelijk door analyse opgelost. Zo kan een terrein 1000m² door telling meten, maar elke m2 heeft in tal van opzichten een andere waarde die de gevonden oppervlakte op zichzelf (zonder weging) betekenisloos maakt. De gelijkheidvooronderstelling kan leiden tot zinloze wiskundige toepassingen wanneer de beschreven verzameling qua context of object te heterogeen is voor enige weging. Zo kan ik het aantal voorwerpen in mijn kamer tellen, maar enige wiskundige operatie op dit aantal alléén, leidt niet tot bruikbare conclusies. Sommige voorwerpen zijn groot, andere klein, sommige hier waardevol, andere niet of elders niet. Ik kan uit het aantal misschien het aantal handelingen bij verhuizing afleiden, maar deze handelingen zullen weer verschillen met de aard van de voorwerpen. Ik kan wel zeggen: 'Als iets weggooi, dan heb ik minder te verhuizen'. Als ik met dat argument een verhuisdoos weggooi, dan heb ik wel minder te verhuizen, maar dit heeft geen relatie meer met de (zonder verhuisdoos grotere) inspanning van het verhuizen die wellicht aanleiding voor het argument was. Wiskundige modellering zou ons hier misleiden, en vergt een logische context.

Eén of andere gelijkheid_van_aard is dus al voorondersteld bij het tellen. Daarbij is echter merkwaardig genoeg ook een verschil voorondersteld: ik mag bij het tellen immers niet twee keer 'hetzelfde' voorwerp aanwijzen (dubbeltelling). De aangewezen voorwerpen moeten verschillen! Welk identiteitsverschil dit precies is, laten we hier in het midden^[n], we noemen het gemakshalve 'verschil_van_plaats', al dekt dit bijvoorbeeld niet direct de problemen bij het tellen van beweeglijke objecten zoals vlinders op een struik die beurtelings elkaars plaats innemen. Een getal of variabele vooronderstelt dus gelijkheid van aard en verschil van plaats ookal is die plaats niet altijd dezelfde.

1.6 Combinatorics

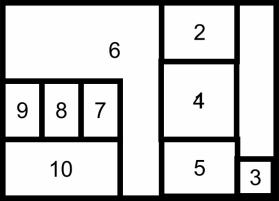
The designer faced by a white sheet of paper or a blank screen, is asked to indicate on it difference in place (instance_of_spread; form) and in kind (colour). The differences_in_kind are contained in a range to be generated (the 'legend', in its original connotation) which is spread in k units of colour (e.g. the program) over n niches (appropriate fields, for instance on the grounds of the site); the_differences_in_place.

n = 9 k=3, scheme

n = 100 k=32, rough draft

n = 256 k=78, Windows-icon

A program, approx. 1/3 of the site, spread over the ground in 3 resolutions.

How many different instances of spread can be generated in total? In mathematics the branch of combinatorics deals with that kind of 'arrangements' in finite sets and with counting the possibilities of arrangement under suitable conditions[o].

If a range of k = 3 colours is available for colouring n = 3 fields, 3³ = 27 variations apply. In this way the colours red, white and blue combined with three fields yield 27 distinct flags.

More generally: V(n,k) = n^k (variations_with_repetition). With as many colours as niches the expression reads nⁿ.

aaa	aba	aca	baa	bba	bca	caa	cba	cca
aab	abb	acb	bab	bbb	bcb	cab	cbb	ccb
aac	abc	acc	bac	bbc	bcc	cac	cbc	ccc
V(3,3) = 3^3 = 27 variations

Among them, however, there are many cases in which colours have been repeated or omitted. True 'tricolores' are but few. The first condition to be added amounts to the presence of all three colours. Colour one has 3 positions available; for the second 2 remain; and for the third 1. This limits the number of cases to 3 x 2 x 1 = 6, abbreviated to 3!, so-called permutations. More generally, one may write: P(n) = n! (permutations_without_repetition).

niches n	evenveel verschillende kleuren als niches
1	a
2	ab		ba
3	abc	acb	bac	bca	cab	cba
P(n) = n! : 1, 2 en 6 permutations

4	abcd abdc adbc dabc	acbd acdb adcb dacb	bacd badc bdac dbac	bcad bcda bdca dbca	cabd cadb cdab dcab	cbad cbda cdba dcba
P(4) = 4! = 24 permutations

1.7 Variatiebeperking

Permutations restrict the ultimate number of variations: 3!, is less than 3³; n! rises less fast than nⁿ, but faster than, for instance n^n/2, when only half the amount of niches is used for the number of colours ‘Factorials limit the largest powers’. Yet, permutations do increase fast enough to lead to a 'combinatorial explosion' on higher values for n:

Combinatorial explosions

Hoe uit al die mogelijkheden te kiezen? Dit is voor velen in het leven en in het ontwerpen een cruciale vraag. In feite is er bij zoveel mogelijkheden geen sprake meer van een bewuste keuze, zodat men zich bij de beperking van resterende, nog altijd onoverzienbare mogelijkheden door het toeval, de emotie van het moment, door modegevoeligheid of door routine laat leiden. Deelder^[p] zegt: 'Binnen de perken zijn de mogelijkheden even groot als daarbuiten'. Als je de resolutie maar verkleint. Hoewel de wiskunde over het algemeen wordt benut om enkelvoudige uitkomsten te krijgen, waarbij andere mogelijkheden tot ergernis van de ontwerper buiten beschouwing blijven, kan deze discipline ook benut worden om binnen exact geformuleerde, maar overigens vrij variërende voorwaarden (bijvoorbeeld een maatsysteem van 30x30x30cm^[q]) de overgebleven mogelijkheden te beperken en te kunnen overzien. De takken van voor de bouwkunde relevante wiskunde worden hier dan ook beschouwd als het formuleren van zulke beperkingen op het totale aantal combinatorische mogelijkheden. Maatsystemen zijn wiskundige reeksen die de afmetingen van componenten tot handzame maten beperken. De meetkunde beperkt zich tot aanéénsluitende (contigue) spreidingstoestanden (vormen) zoals lijnen, oppervlakken, inhouden, die met een minimum aan informatie tot hun contouren, met enkele punten te beschrijven zijn. De grafentheorie beperkt zich tot de verbindingen (lijnen met of zonder richting) tussen deze punten, ongeacht hun werkelijke positie. De topologie formuleert bij variabele posities transformaties van vormen, zodat de ene vorm met een formule in de andere kan worden omgezet. Deze discipline is echter te ingewikkeld om in dit bestek aan de orde te stellen. Kansrekening en haar toepassing in de statistiek beperkt zich tot het optreden van welgedefinieerde gebeurtenissen, bijvoorbeeld het optreden van één of meer gevallen tussen de mogelijke gevallen in een gegeven ruimte of tijd. Optimalisaties door lineair_programmeren met behulp van matrixrekenen, formuleren de overblijvende exact beperkte mogelijkheden als 'oplossingsruimte'. Naast deze wiskundige beperkingen zijn er tal van intuïtieve beperkingen, waardoor mogelijkheden buiten beschouwing blijven. Als men bijvoorbeeld in de afbeeldingen op blz. Fout! Bladwijzer niet gedefinieerd. e.v. het beeldtype van een deur in een wand herkent, moet de basis van de deur (het programma k) in het onderste deel van de wand (de aanwezige ruimte n) liggen, tenzij men er een trapje bij tekent.

1.8 Program of a site

With variations (n^k) and factorials or permutations (n!) alone it is impossible to determine the number of cases when a particular colour has to be present in a predictable amount (a quantitative 'program' per colour). With a program for an available space n, where one colour (for instance black) has always to be present at least k times P(n,k) = n!/k! possibilities exist (permutations_with_repetition). The k! of the ratio restricts the explosive effect of n! at higher values of n, except of course, if it equals 1. That applies in the first column of the figure below; if k = 1 (so K! = 1) it has no effect on the ratio; the number of permutations P remains, as in the previous example with letters, 4! = 24. At k = 2 (k! = 2) and k = 3 (k! = 6) the number is restricted.

P(4,1) = 4!/1! = 24	P(4,2) = 4!/2! = 12	P(4,3) = 4!/3! = 4
Permutations in 4 niches, with at least k = {1,2,3} black elements combined with other hues.

The larger the program k of one colour (in this case black) with regard to the total space available, the less possibilities remain for other colours to generate cases. Evidently, k, the number of colours surfaces to be distributed may not exceed the space n available.

The formula presupposes that the niches remaining will be filled with as many different colours. They generate the additional cases, not requiring attention from a programmatic point of view.

1.9 Binary legends

If not only the program k, but also the remainder n - k is combined into one colour, no other colours remain to generate additional cases. A permutation with two colours, k₁ and k₂ equals the formula n! / k₁!k₂! The possible arrangements of program k1 and the remainder k2 develops into n! / k!(n-k)! (Newtons_binomium)[r].

Within both surfaces, sequencing is now irrelevant in which the niches are filled in with one colour. The only consideration of importance left is the number of different instances in which one quantity k is allotted to n possibilities without a role for its own sequencing. This entity plays a leading part in statistics. Factor k then is the number of possibilities of an event, n - k its complement of possibly not happening that event. So, not only possibilities in space apply: n may also reflect time. A little counter-intuitively the common expression is 'combinations'; and one simplifies the formula P (n, k₁, k₂ ) = n! / k₁! k₂! to C (n,k) = n! / k! (n - k)! ; or shorter still , 'n over k'.

(combinations_without_repetition).

C(4,1)	C(4,2)	C(4,3)
1x2x3x4/ ((1x)(1x2x3)) = 4	1x2x3x4/ ((1x2)(1x2)) = 6	1x2x3x4/ ((1x2x3)(1)) = 4
abbb,babb,bbab,bbba	aabb,abab,abba,baab,baba,bbaa	aaab, aaba, abaa, baaa
Combinations in 4 niches of 2 colours

1.10 Additional legend units

The number of elements of the program (legends units, colours, letters) may be raised above 2; within the limits of n, of course.

This enables the calculation of the numbers of cases belonging to a specified program on a location. If one wants to allocate for instance 4 programmatic elements to n fields, there are

P(n,k₁,k₂,k₃,k₄) = n!/k₁!k₂!k₃!k₄! design possibilities. The total of the colour surfaces k₁+k₂+ … desired is again not allowed again to exceed, of course, the surface available in total n. With a computer program such as Excel one can calculate, for instance, that the possibilities of allocating 4 types of usage of 25m² each to an area of one are 100m2 [s]. Without fail, one will experience the highest level of freedom of design if a one-colour program occupies half the site available (k1 = k2); a sound reason to plea with the principal for as much open space as space built.

At higher resolutions as shown in the diagrams of page 3 even the number of black-white combinations rises again explosively C(9,3) = 84, C(100,32) = 140 000 000 000 000 000 000 000 000 (1,4E+26 for short in Excel).

The black-white possibilities of the Windows-icon shown (16pixels x 16pixels = 256pixels), amounts at 78 pixels C(256,78) already to 1,2149E+67 images. Excel calculates this with the command = COMBIN(256,78).

If one studies, for instance, 5625 locations of 1 km² in the colours 'built' (815) and 'open' (4818), approximately 10¹⁰⁰⁸ urban cases exist for the 'Randstad' area in the Netherlands. The average PC can't deal with this. Excel digests in this case at great pains k=156.

1.11 Het medium

Een pen, potlood of viltstift tekent punten en lijnen die een minimale oppervlakte innemen, overeenkomend met de dikte van het materiaal. Oppervlakken kunnen dan worden weergegeven door het oppervlak te vullen met zulke lijnen. Dat is in feite arceren. Een beeldscherm bouwt het beeld op uit kleine oppervlakken (beeldpunten, pixels) die aanééngesloten lijnen of oppervlakken kunnen suggereren. Dit lijkt op het kusthistorische verschil tussen de Florentijnse (lijngeoriënteerde) en Venetiaanse (puntgeoriënteerde) designa. Een normaal scherm telt 1024x768 pixels. Een pixel-georiënteerd programma (paint- of photoprogramma) voorziet slechts in het kleuren van deze beeldpunten zoals bij schilderen. Overschrijft men een ‘lijn’ of ‘oppervlak’, dan kan men dat niet anders herstellen dan door het opnieuw in de oude kleur vullen van de overschreven pixels. Voorgrond en achtergrond worden meestal niet in lagen onderscheiden die men één voor één of in combinatie zichtbaar kan maken. Een computertekenprogramma (vectorprogramma, drawprogramma of CAD) vat alleen de essentiële punten van een tekening samen in een matrix van coördinaten en vertaalt de tekening in pixels zodra hij wordt opgeroepen. De tussenliggende pixels worden bij opslag niet onthouden, zodat de opslag minder geheugen vergt dan een pixelbeeld. Bij vergoting van de tekening of detail past de resolutie zich automatisch aan, zodat de lijnen altijd scherp blijven. In een wiskundeprogramma ^[t] kan dit als grafiek gesimuleerd worden. In onderstaande grafiek is op de vertikale as de eerste rij van de matrix uitgezet, op de horizontale as de tweede rij.

een object als wiskundige grafiek

Met de herhaling van het eerste coördinatenpaar (3,0) in de laatste kolom (vector) van de matrix is de figuur gesloten en inkleurbaar. Het wiskundeprogramma vergt bij het maken van een grafiek ook de opgave van het aantal kolommen m dat in de grafiek moet worden weergegeven. Een vector is een matrix met één kolom (of rij) die in het platte vlak slechts twee getallen nodig heeft als hij vanuit de oorsprong wordt gedefinieerd. In onderstaande figuur zijn 3 vectoren a, b en b-a getekend. Zij illustreren de rekenregels die bij de toegepaste mechanica goed van pas komen.

lijnstukken met vectoren definiëren

Het lijnstuk AB wordt door de coördinaten van de vectoren a en b weergegeven, de tussenliggende punten worden berekend door een coëfficiënt l tussen 0 en 1 een reeks waarden te geven in de formule l(b-a)+a. Zo levert l=0,5 het tussenliggende punt D(2,3). Hoe meer waarden men laat berekenen, deste groter wordt de resolutie van de lijn AB.

			l =0,5
a	b	b-a	l(b-a)	l(b-a)+a
1	3	2	1	2
4	2	-2	-1	3

1.12 Resolution and tolerance

The number of possibilities is already drastically reduced during the initial stage of the design by the coarseness or, in reverse, the resolution of the drawing. That is something differing from the scale of a drawing. The position of a deliberately coarsely sketched line must be judged according to commonly understood conventions within certain margins. The size of such a margin surrounding a drawn point we call 'grain'. We call the radius of the circle inscribed in the drawing as a whole 'frame', and their ratio 'the resolving_capability’, or 'resolution' ^[u].

A video display unit of 1024 x 768 pixels has accordingly a resolution of approximately 0,1 %. A sketch with linear grain of roughly 10 % of the frame is known as a loose_sketch. It is used in a concept, a type or a schema. It is only at ± 3 % that one refers to it as a 'sketched_design'. A 'design' has hardly a larger resolution than 1%, a 'building design' - the original 'blue-print' - doesn't exceed 0,1 %. It is only at this level that such things as detail in woodwork of a door in a wall are displayed. If the frame of the sketched design is 30 x 30 cm (for instance with an oblong A3 with margins for notes and remarks) the surfaces and lines of the sketched design should not be interpreted more narrowly than to 3% x 30 cm » 1 cm from the core of the dots, lines or contours. This is an admissible variance to both sides and, by the same token, half the tolerance of a drawing with a resolution of 3%.

Often a sketched design is for this reason produced with a felt-tipped 'pen'; with the same order of magnitude as the tolerance of the drawing.

Subsequently, the tolerance of 2 cm in the sketched design, represents, drawn on a scale of 1 : 10, in reality 20 cm. Only at a building design level 1 : 10 on the same A3 format (± 0,1 %), the tolerance in the drawing equals 0,1 % x 300 mm x 2 = 0,6 mm; thus in reality 6 mm. That doesn't suffice to draw adjacent and connected parts in, say, the woodwork of a door. For this reason, the precise lengths should be stated explicitly in the building design, the 'blue-print'.

De deur moet iets kleiner zijn dan de binnenmaat van het kozijn om te kunnen passen (passing). Bovendien maakt een timmerman of machine deuren en kozijnen in serieproductie altijd iets te groot of te klein en de steller hangt ze iets te hoog of te laag in het kozijn. De grenzen die men daaraan stelt (productietolerantie) moeten worden berekend door afweging van de prijs van de precisie en de prestatie van de deur als afsluiting. Dat vergt kansberekeningen en optimaliseringstechniek.

Als een deur in een extreem geval 1mm groter is, het bijbehorende kozijn 1mm kleiner en de ophanging 1mm hoger dan op grond van passing voorgeschreven is, is de totale afwijking 3 mm. In het andere extreme geval is de deur 1mm kleiner, het kozijn 1mm groter en de ophanging 1mm lager dan voorgeschreven, zodat een enkele keer bovenaan de deur een kier van 3mm verschijnt. Als de toegestane productietolerantie bijvoorbeeld 6mm is, dan zijn dit in de praktijk aanvaardbare afwijkingen. Het heeft dan geen zin maten in de tekening met een grotere precisie weer te geven.

	te grote kozijnen
te kleine deuren		te grote deuren
	te kleine kozijnen
V(2,4)

Hiermee is ook het wiskundig gebruik van cijfers achter de komma voor de bouwkunde en de techniek in het algemeen principieel aan banden gelegd. Men mag niet meer denken in getallen die een punt op de getallenlijn vertegenwoordigen: zij vertegenwoordigen een afstand, traject, een marge, een bandbreedte op die lijn en worden slechts genoemd naar het aangenomen midden daarvan (nominale_maat). De nominale maat geven wij aan in de bestektekening, maar het is absoluut zeker dat deze maat nooit geleverd zal worden. Lijngrafieken moeten dan ook altijd als staafdiagrammen worden voorgesteld met klassen, klassebreedten en klassegrenzen.

1.13 Size systems

A restriction to multiples of 30 cm (little less than a foot), partitioned into 10 modular units of 3 x 10 cm is a well-known bridle to sizes in construction of buildings. A grid like that is used to localize foundations, columns and walls without design efforts. A grid may have a different size in any one of the three dimensions. A preceding analysis of usage may yield an appropriate size of the grid for a specific function. The distinct multiples of the size of the grid yield distinct functional possibilities. In the preceding paragraphs a grid is implicitly used.

However there are also sequences of increasing, decreasing (diminishing) numbers, or numbers converging to one value or divergent numbers forming by addition a mathematical series (sum-array).

Een rekenkundige_reeks heeft een beginterm a, een reden v, en een lengte n. De termen, hun verschil en som lopen rechtlijnig op. De reeks is dan gegeven door de rij van termen en de som s_n = a + (a+v) + … +(a+(n-1)v) = n(2a + (n-1)v)/2. Er zijn ook rekenkundige rijen van hogere orde.

Bij een meetkundige rij is de reden r een vermenigvuldigingsfactor, zodat het quotiënt van twee opeenvolgende termen constant is, hun verschil kan op- en aflopen. De reeks is dan gegeven door de rij van termen en de som s_n = a + ar + … + ar^n-1 = a(rⁿ-1)/(r-1). Als de reden een positieve of negatieve fractie van 1 is, dan convergeert de rij naar a/(1-e).

starting term	reason	length	array	sum
a	v	n	a + v(n-1)	n(2a + v(n-1))/2
10	20	1	10	10
		2	30	40
		3	50	90
		4	70	160
		5	90	250
Arithmetical sequence (series)

			array	sum at | r | <> 1
a	r	n	a * r^n-1	a(r^n-1)/(r-1)
10	2	1	10	10
		2	20	30
		3	40	70
		4	80	150
		5	160	310
				limit on | r | < 1
				a/(1-r)
Geometrical sequence (series)

Een voorbeeld van een rekenkundige reeks in de bouwkunde zijn stramienen. De reden v is de stramienmaat, de beginterm a de constructiedikte van een buiten. De waarde van de n-de term geeft de plaats van een muur aan. Een ander voorbeeld betreft een gebouw met één schuine gevel, zoals het KPN-gebouw van Renzo Piano in Rotterdam. De schuine gevel begint op de eerste verdieping. De beginterm a staat hierbij voor de vaste oppervlakte per verdieping, de reden v voor de oppervlakte winst per verdieping. De n-de term geeft de oppervlakte van de n-de verdieping aan. De som van de termen de totale oppervlakte van verdiepingen aan de schuine gevel.

Toepassingen van meetkundige reeksen vindt men in de financiële sector, zoals samengesteld interest en annuiteïten.

Een inleg van 1000 € tegen 5% rente levert na 1 jaar 1000 * 1.05 = 1050 € op. Na twee jaar is dat 1050 * 1.05 = 1102.50 € of wel 1000 * 1.05 * 1.05 is 1000 * 1.05²

Algemeen na n jaar is een bedrag van K₀ aangegroeid tot K_n = K₀ * (1+r/100)ⁿ , een meetkundige reeks. Indien ieder jaar een bedrag vqn 1000 € wordt ingelegd dan kan na n jaren een bedrag van 1000 * (1.05ⁿ – 1) / (1.05 – 1) € worden opgenomen, gelijk de som van een meetkundige reeks. Ook de hypothecaire aflossing is een meetkundige reeks.

Een ander voorbeeld van een meetkundige reeks is de gegeneraliseerde definitie van de gulden snelde regel: Verdeel een lijnstuk met lengte L in een n-tal lijnstukken met lengte m₀ ... m_n-1 zodanig dat m_i > m_i+1 en m_i / m_i+1 (i=0 .. n-2) constant en gelijk aan L / m₀ is Deze constante wordt aangegeven met het symbol f_n, naar de griekse beeldhouwer Phidias, die de regel gebruikte voor n=2. De lengte van m₀ is gelijk aan L / f_n , die van m₁ aan m₀ / f_n ofwel L / f_n²

De som van de lijnstukken is gelijk aan L waaruit volgt dat å 1/ f_nⁱ gelijk moet zijn aan 1.

Ook bij de ervaring van geluid speelt de meetkundige reeks een rol. Een geluidstoename van 10 dB wordt twee keer zo luid ervaren, een toename van 20 dB vier keer zo luid.

(zie Lootsma, F.A. , Multi-Criteria Decision Analysis via ratio an difference judgement, Delft University of Technology, Delft,1999)

A sequence well-known from architecture is Fibonacci's sequence: a new term equals the sum of the previous terms. The ratio between two adjacent terms converges to the 'golden_rule': the smaller number (minor m) has a fixed ratio to the larger one (Magior M); and this one, again, to the sum of both, like follows: m : M = M : (m + M).

De eenvoudig te berekenen reeks van Fibonacci kan men bij verschillende getallen beginnen. Begint men bij 10 (kolom B), dan volgt een goed bruikbare bouwkundige reeks. In kolom D ziet men de reeks lange tijd gelijk oplopen met die van de gulden snede.. Ook de reeks van de gulden snede kan men op een willekeurig punt laten beginnen, maar dan moet men naar boven een andere, (reciproke) formule gebruiken dan naar beneden. Sinds de klassieke oudheid is men gefascineerd door zijn schoonheid. Er werden tal van pogingen in het werk gesteld om haar in de natuur en het menselijk lichaam te herkennen. Le_Corbusier nam tot 1947 de menselijke lengte van 1,75m als uitgangspunt. Daarna ontwikkelde hij een rode reeks met 6 Engelse voet (1,8288m) als uitgangspunt. Vervolgens begon hij bij 2,16m, de reikwijdte van een mens met naar boven uitgestrekte hand.

	A	B	C	D	E
	Fibonacci				Gulden snede
				0,1
1				0,1	0,1
2			0,3	0,2	0,2
3			0,3	0,3	0,3
4	1		0,6	0,5	0,5
5	1		0,9	0,8	0,8
6	2		1,5	1,3	1,3
7	3		2,4	2,1	2,1
8	5		3,9	3,4	3,4
9	8		6,3	5,5	5,6
10	13	10	10,2	8,9	9,0
11	21	10	16,5	14,4	14,6
12	34	20	26,7	23,3	23,6
13	55	30	43,2	37,7	38,2
14	89	50	69,9	61,0	61,8
15	144	80	113,1	98,7	100,0
16	233	130	183,0	159,7	161,8
17	377	210	296,1	258,4	261,8
18	610	340	479,1	418,1	423,6
19	987	550	775,2	676,5	685,4
20	1597	890	1254,3	1094,6	1109,0
21	2584	1440	2029,5	1771,1	1794,4
22	4181	2330	3283,8	2865,7	2903,4
23	6765	3770	5313,3	4636,8	4697,9
24	10946	6100	8597,1	7502,5	7601,3
25	17711	9870	13910,4	12139,3	12299,2
	Berekeningen in Excel
	X6		X15/((1+WORTEL(5))/2)
	X7				X15
	X7+X6		(1+WORTEL(5))/2*X15

	E	D	E	F	G	H
	Gulden snede
		Le Corbusier
1	0,1	tot 1947	Rode rij			Blauwe rij
2	0,2	0,2	0,2			0,3
3	0,3	0,3	0,4			0,4
4	0,5	0,5	0,6			0,7
5	0,8	0,9	0,9			1,1
6	1,3	1,4	1,5			1,8
7	2,1	2,3	2,4			3,0
8	3,4	3,7	3,9			4,8
9	5,6	6,0	6,3			7,8
10	9,0	9,8	10,2			12,6
11	14,6	15,8	16,5	Modulor		20,4
12	23,6	25,5	26,7	27		33,0
13	38,2	41,3	43,2	43		53,4
14	61,8	66,8	69,9	70	86	86,3
15	100,0	108,2	113,0	113	140	139,7
16	161,8	175,0	182,9	183	226	226,0
17	261,8	283,2	295,9			365,7
18	423,6	458,2	478,8			591,7
19	685,4	741,3	774,7			957,4
20	1109,0	1199,5	1253,5			1549,0
21	1794,4	1940,8	2028,2			2506,4
22	2903,4	3140,2	3281,6			4055,4
23	4697,9	5081,0	5309,8			6561,8
24	7601,3	8221,3	8591,5			10617,2
25	12299,2	13302,3	13901,3			17179,0
	X15/((1+WORTEL(5))/2)
	X15
	(1+WORTEL(5))/2*X15

De rode en blauwe reeks hadden voor bouwkundige toepassing te grote stappen tussen de termen, zodat hij ze combineerde en afrondde in de Modulor. Tal van andere pogingen zijn gedaan om de mogelijkheden van het ontwerp met maatreeksen overzichtelijk en in ontwerpbeslissingen met een vooronderstelde ingebouwde schoonheid hanteerbaar te maken^[v].

1.14 Geometry

It is impossible to imagine a door distributed in tiny slits across a wall. Geometry[w] restricts itself to contingent instances of spread that can be enveloped by a few points, distances and directions. This presupposition of continuousness lowers the amount of combinatorial possibilities dramatically. The extent to which this geometrical point of view restricts the combinatorial explosion, is the subject of combinatorial_geometry: it studies distributions of surfaces and the way these are packed. However, the often implicit requirement that points in one plane should lie contingently within one, two or three dimensions is more obvious and self-evident in the case of a door, than in the one of a city. That is the reason why urban design is interested in non-contingent instances of spread.

The possibilities are restricted geometrically, following the often implicit presupposition of rectangularity. Particularly an efficient way of production suggests this presupposition. When one limits oneself in geometry to enclosed surfaces or enclosed spaces and masses, three simple shapes may be imagined in a flat plane: the square, the isoscalar triangle and the circle. They have been drawn in the following diagram, believe it or not, with an equally sized area (program). Their circumferences are roughly proportioned like 8 : 9 : 7. But why are they so extraordinarily simple, that they, in addition or subtraction (see….), survive as geometrical archetypes in construction?

Minimal number of directions in one loop	Minimal number of changes of direction in one loop	Minimal variation of changes of direction in one loop
simple shapes

Their simplicity may be explained by the minima added in words to the diagram. This gives at the same time a technical motivation for application. A minimal number of directions is for production - e.g. sawing and size management - an effective restriction. It influences directly the product's price. A minimal number of directional changes (nodes) is constructively effective (also from a viewpoint of stiffness of form). A minimal variation in directional changes(one without interruption, smooth) is effective with motions in usage; when one keeps the steering wheel of a car in the same position, sooner or later a circle is described.

Our intuition meets its demasque, by keeping the area equal: the triangle wins out. This visual illusion may be used for spaces needing particularly spatial power. A second famed example of geometry's capacity to lead to counter-intuitive conclusions is the seeming difference in surface between the centre and the periphery as Tummers[x] emphasizes. In the diagram below they equal one another.

Apparent difference in surface between centre and periphery

Functions characterized by the importance of interconnectedness at all sides - like greenery, parks - tend to be better localized centrally, while differently structured functions (e.g. buildings) are better placed peripherally.

Er zijn tal van handboeken op het gebied van de meetkunde, zodat wij niet nader ingaan op de vormbeperkende mogelijkheden van deze discipline^[y].

1.15 Graphs

When one notes in a figure only the number of intersections (nodes) and the number of mutual connections per intersection (valence, degree of the node) we deal with a graph.

Een graaf (graph) G is een verzameling knooppunten (nodes, points, vertices) en een verzameling lijnen, takken (branches, arcs, links, edges) geheten, die sommige knooppuntparen met elkaar verbinden. Een tak tussen node i en node j wordt genoteerd als arc (i,j), kortweg arc_ij.

Lengte, positie en vorm van de knooppunten en takken hebben hierbij geen betekenis. (In de bouwkunde kan de relatieve positie van de knooppunten t.o.v. elkaar veelal wel een betekenis hebben)

Amongst many figures corresponding types may be discerned wherein neither length nor area play a role (e.g. designing structure, not yet form and size). This enables the study of formal, technical and programmatical properties in space and time even before the sizes of the space or the duration in time are known.

A cube may serve as an example. It has 8 nodes. Each of them has 3 connections. This fixes the number of connecting lines (branches) : 8 X 3/2 = 12. For each connecting branch occupies 2 of the 8 x 3 connections in total.

	input		output
figure	nodes	connections per intersection (valence, degree)	branches = nodes x valence/2	planes = branches - nodes+ 2	connections = branches x 2	boundaries = branches x 2	boundaries per plane (valence) = boundaries / planes
tetrahedron	4	3	6	4	12	12	3
cube	8	3	12	6	24	24	4
octahedron	6	4	12	8	24	24	3
K3,3	6	3	9	5	18	18	3,6
K5	5	4	10	7	20	20	2,9

Following the formula of Euler, the number of planes = number of branches - number of nodes + 2. As soon as the planes (still without dimensions) come into the picture, we deal with a map. By the same token it suffices to count in a figure the intersections and their valences in order to be able to calculate the number of branches and planes in the map.

The regular solids can be represented in a plane by a graph.

tetrahedron	cube	octahedron
Regular solids as a graph

Based on this, terminology of graph theory is readily explained. These are single_graphs: there are no cycles arriving at the same node as the one of departure; or multiple_connections between two nodes.

Furthermore they are regular: in each node the number of connections per graph is equal.

The tetrahedron has a complete_graph (K) unlike the other two, where possible connections - the diagonals - fail.

The graph of the cube clearly demonstrates that the outer area should be in calculated in order to count 6 planes. It is as if the cube is 'cut open' in one plane, in order to 'ex-plane' it on the page. It is immaterial which plane serves as outer plane. Graph theory doesn't distinguish yet between inside and outside.

Grafentheorie maakt nog geen onderscheid tussen binnen en buiten.

The graphs of the tetrahedron and the cube are 'planar': the flatland doesn't feature crossings without intersection. The diagram below shows to the left an 'isomorph_graph' for the octahedron where the number of nodes equals the number of valences.

Vergelijk de graaf van de octaëder met die op blz. Fout! Bladwijzer niet gedefinieerd..

octahedron	K5	K3, 3

The branch between nodes 6 and 1 of the octahedron may be 'contracted' in such a fashion, that one node remains, where all other branches end previously ending in 6 and 1, with whom they were 'inciding' or 'incident' in the parlance.

If a graph yields to contraction to K5 or K 3,3, it can be proven that it is non_planar. Architectonically this is especially important: by the same token no blueprint can exist that relates all the relationships as recorded in the graph.

4 rooms	diagonal	K4

In de eerste twee figuren zijn nog niet alle kamers met elkaar verbonden.

According to K4, each of the four rooms, may be linked by 3 openings mutually amongst themselves. The left shows the solution with two openings where one may circulate, the corresponding graph has also been drawn (a circuit). The middle demonstrates a solution where two of the four rooms have 3 doors. A 'dual_map' must be drawn in order to solve the complete graph. To do that, K4 is made isomorphically planar, and the planes renamed to intersection. The outer area of the graph is also involved.

isomorphic K4	dual K4	a solution

The branches of the dual map are now no connections anymore, but separations in the blueprint to be constructed perpendicular to the connections. From a fundamental point of view, no solution exists in flatland for 5 rooms, each sharing one door with all other rooms (K5) : no planar graph could be drawn of K5.

By regarding each space as a node between other spaces, programmatic requirements can be verified as to their feasibility along the lines of graph theory.

Suppose, that the relation-density between rooms in a dwelling, results in the following relational scheme:

1	hall
		1
2	front room		1
				1
3	water closet		1
		2
4	living room				1
		2
5	kitchen		2
		2
6	garden
		1
7	bedroom 1		1
		1		1
8	bathroom				1
		1
9	bedroom 2		1
10	bedroom3

At 10 rooms, combinatorial speaking 10!/2! 8! = 45 relations exist (K10). They can never be established directly:

K10	planar selection

Yet, the selection of the relational scheme can be made planar, therefore it has a solution. With its high valence in the scheme of dwelling, the garden (6) is crucial. If this node, or the living room (4), is removed, a 'non-conjunctive' graph originates. Following that, it may be decided to give rooms 6 to 10 a separate floor; or even its own floor. If a node allows this freedom, it is termed a 'separational_node' . The minimal number of nodes n that can be taken away with the incident branches in order to make them non-conjunctive makes the graph 'n-conjunctive'. It is an important measure of cohesion in a system.

In de volgende figuur is een mogelijke realisatie gegeven:

Mogelijke plattegrond van de planaire selectie

Een kaart van het rijkswegennet van ons land is een voorbeeld van een netwerk. Iedere tak stelt een wegvak voor, iedere knoop een kruispunt of verkeersplein. Door de takken te voorzien van hun lengte kan de gebruiker eenvoudig de afstand tussen zijn punt van herkomst en bestemming bepalen. Indien de vervoerstromen over het netwerk en hun intensiteit bekend zijn kan eenvoudig de verkeersbelasting op iedere tak worden bepaald Zo’n netwerk kan ook de verkeersafwikkeling binnen een gebouw voorstellen, waarbij de takken gangen, trappen en liften voorstellen Bepaald kan dan bijvoorbeeld worden hoeveel studenten zich tijdens een collegewissel waar door het gebouw verplaatsen, op basis waarvan de dimensionering van de gangen etc. kan worden bepaald.

Ook de organisatiestructuur van een bedrijf kan in een netwerk worden afgebeeld Indien bij het ontwerp van een nieuw bedrijfpand die structuur in het pand moet terugkomen kan dit netwerk een uitgangspuntvormen; er valt uit af te leiden welke afdelingen direct met elkaar betrokken zijn en dat in het nieuwe pand ook fysiek willen zijn.

Met netwerken is het dus mogelijk de istructuur van gebouw of wijk te beschrijven, zonder het gehele gebouw of de gehele wijk te beschrijven.

1.16 Networks

A graph with on its branches a weight (stream, flow) of any type (time, distance) is called a network [z]. If this flow displays a direction as well, the network is termed a directed_graph. A path is a sequence connecting branches with a direction and a flow. A network is a cyclical_network, if a node connects with itself via a path. The length of the path is determined by the sum of the weight of the paths concerned. The length of the shortest path between two nodes may be determined by following, step by step, a sequence of calculating rules, the shortest-path_algorithm [aa]. An algorithm in this vein is in existence for the longest path, the 'critical-path_method'. This method is used in 'network planning' in order to determine, within a project, the earliest and latest moments of starting and finalizing each and any activity of the project; and, consequently the minimal duration of the project [bb]. In this the nodes represent the activities, the branches the relation between the activities [cc]. The start of an activity (successor) is determined by the time of finalization of all preceding activities (predecessors). With regard to the network planning, it is feasible to monitor the progress of (complex) projects; as well as to survey the consequences of retardation of activities. However, the problems caused by retardation are not to be solved. In order to achieve such a solution one has to employ other techniques; like linear programming (LP).

1.17 Probability

An event is a set of results A[dd] from a space_of_results W [ee] (a set much larger) that might have yielded different results as well. The chance of an event of A well-defined instances taking on ''what had been possible'' W is - expressed in numbers - A/W. Often it isn't easy to get an idea of what would have been possible; certainly when W has subsets dependent on A, for the event may influence the remaining possibilities.

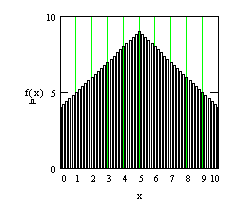
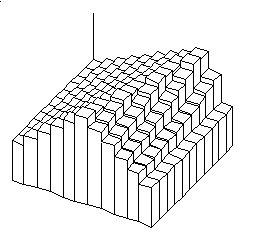
Het aantal mogelijkheden om een vlak te vullen met 100 gebouwen van 0 tot 9 verdiepingen is bijvoorbeeld 100¹⁰. Twee van die mogelijke gebeurtenissen zijn hieronder getekend: wild en geordend wonen. De kans dat bij een maximum hoogte van 9 verdiepingen één van beide precies gerealiseerd wordt is twee (somregel) op 100¹⁰.

Wild en geordend wonen

Bij dit wilde_wonen^[ff] is de bouwhoogte volkomen aan het toeval overgelaten^[gg]. Het gevolg is, dat bij 100 gevallen de gemiddelde bouwhoogte het midden tussen 0 en 9 al nauwkeurig benadert (4,5). Het voorbeeld van geordend wonen met gemiddeld 2,2 verdiepingen ligt verder van het gemiddelde dan dat van het wilde wonen en is dus als categorie minder ‘waarschijnlijk’ ook al zijn alle 100¹⁰ uitkomsten op zichzelf even waarschijnlijk. In onderstaande matrix zijn de hoogten uit bovenstaande linker figuur van het wilde wonen weergegeven.

kolommen rijen	1	2	3	4	5	6	7	8	9	10	gemiddelde per rij
1	5	0	6	1	6	2	1	8	7	6	4,2
2	1	5	7	2	8	5	3	1	4	7	4,3
3	3	3	3	7	4	5	3	1	5	1	3,5
4	2	3	6	5	4	0	0	9	7	8	4,4
5	1	6	6	1	5	7	3	4	2	0	3,5
6	0	9	5	6	8	9	2	3	6	4	5,2
7	1	6	7	6	2	1	5	4	6	4	4,2
8	5	3	0	8	5	0	6	3	5	8	4,3
9	3	8	1	9	0	3	8	4	6	9	5,1
10	2	7	9	5	8	7	6	8	1	9	6,2
Gemiddeld voor het totaal:											4,5

Er is als het ware honderd keer gegooid met een dobbelsteen die 10 uitkomsten tussen 0 en 9 kan geven. De rijen vormen telkens een steekproef van 10 'worpen' uit 100. Zo'n deelgebeurtenis in de eerste rij gebouwen kan al 10¹⁰ (10 000 000 000) gemiddelden opleveren waaronder slechts 10! = 3 628 800 verschillende gemiddelden (minder dan 0,4%!). Als je daaruit alleen al de 10 gemiddelden bekijkt die uit de hele getallen (0 .. 9) bestaan waaruit zij worden samengesteld, dan moet je constateren dat voor 4 en 5 de meeste (9!/4!5!=126) combinaties bestaan.

rijen												gemiddelde per rij
9!/0!9!=	1	0	0	0	0	0	0	0	0	0	0	0
9!/1!8!=	9	combinaties voor een gemiddelde										1
9!/2!7!=	36	combinaties voor een gemiddelde										2
9!/3!6!=	84	combinaties voor een gemiddelde										3
9!/4!5!=	126	combinaties voor een gemiddelde										4
9!/5!4!=	126	combinaties voor een gemiddelde										5
9!/6!3!=	84	combinaties voor een gemiddelde										6
9!/7!2!=	36	combinaties voor een gemiddelde										7
9!/8!1!=	9	combinaties voor een gemiddelde										8
9!/9!0!=	1	9	9	9	9	9	9	9	9	9	9	9
Gemiddeld voor het totaal:												4,5
Mogelijkheden om uit de 10 getallen van 0 tot 9 een gemiddelde samen te stellen

Om tot elk ander gemiddelde te komen zijn er minder combinaties voorhanden. Voor een uitkomst van gemiddeld 0 of 9 bestaat bijvoorbeeld slechts één denkbare combinatie (de onwaarschijnlijke gebeurtenissen van 10 nullen, onbebouwd of 10 negens, maximaal bebouwd). De gemiddelden verdichten zich tussen 4 en 5. Bovenstaande combinatiemogelijkeden representeren dan ook de kansdichtheid. In de betreffende kolom tekent zich dan ook al Gausskromme af.

Dat geldt natuurlijk ook voor de kolommen. In onderstaande tabel zijn gemiddelde, mediaan en modus van de kolommen cumulatief weergegeven door steeds meer kolommen in de beschouwing te betrekken.

n =	10	20	30	40	50	60	70	80	90	100
gemiddelde	2,3	3,6	4,1	4,3	4,4	4,4	4,3	4,3	4,4	4,5
mediaan	2,0	3,0	4,0	5,0	5,0	5,0	5,0	4,5	5,0	5,0
modus	1,0	3,0	3,0	5,0	5,0	5,0	5,0	5,0	5,0	5,0

Hoe meer worpen, hoe dichter het gemiddelde bij de 4,5 komt. Dat geldt echter nog niet voor de mediaan (evenveel uitkomsten lager als hoger) en nog minder voor de modus (de hoogste uitkomst). Hun afwijkingen van het gemiddelde duiden op asymmetrische, scheve_verdelingen.

Meer uitkomsten stabiliseren het gemiddelde

Het gemiddelde reduceert de variatie van een groot aantal getallen tot één getal. De variatie zelf wordt weer zeer gedeeltelijk recht gedaan met de 'standaardafwijking' s. Ongeveer 2/3 van de gevallen wijkt gewoonlijk minder van het gemiddelde af dan deze standaardafwijking. Ongeveer 95% ligt binnen 2 x s uit het gemiddelde (95%_waarschijnlijkheidsgebied). Deze maat s heeft alleen zin voor gevallen die zich door combinatiemogelijkheden rondom een gemiddelde verdichten. Dat is bijvoorbeeld niet het geval bij de honderd individuele gevallen in bovenstaand voorbeeld. Zij hebben ieder evenveel kans op 0, 1, 2, 3, 4, 5, 6, 7, 8 of 9 verdiepingen. De op grond daarvan wiskundig berekende 'standaardafwijking' aan weerskanten van 4,5 zou ongeveer 5 verdiepingen bedragen. Binnen die zinloos brede marge vallen álle uitkomsten, en dus niet slechts 2/3. De 10 kolomgemiddelden concentreren zich echter wél bij het totale gemiddelde. Gemiddelde waarden als 4 en 5 konden immers uit méér combinaties van individuele verdiepingshoogten worden samengesteld dan extremen zoals 0 of 9. Beschouwen we de spreiding van déze 10 meer gehoorzame uitkomsten, dan is de standaardafwijking te berekenen uit de som van de uitkomsten (uitkomstensom) en de som van hun kwadraten (kwadratensom):

kolomnummer	1	2	3	4	5	6	7	8	9	10	som
uitkomsten (gemiddelden)	2,3	5,0	5,0	5,0	5,0	3,9	3,7	4,5	4,9	5,6	44,9
kwadraten	5	25	25	25	25	15	14	20	24	31	209,8
Standaardafwijking s =WORTEL((kwadratensom-uitkomstensom^2/n)/n) n=10											0,91

De standaardafwijking is hier s = WORTEL((kwadratensom-uitkomstensom^2/n)/n) = 0,91^[hh]. Gemiddelde m en standaardafwijking s kunnen gebruikt worden om de gebeurtenis in een staafgrafiek te vergelijken met een overeenkomstige normale_verdeling(m,s) van de kansdichtheid die bij zeer veel gebeurtenissen wordt benaderd. Deze verdeling representeert bij een gegeven m en s het totaal van waarschijnlijke mogelijkheden W tegen de achtergrond waarvan de gebeurtenis A één uitkomst is.

Ter weerszijden van het gemiddelde zijn om de s (0,91 verdiepingen) vijf klassegrenzen onderscheiden met 0 en 9 als extremen. Het aantal gevallen tussen 4,5 en 5,4 verdiepingen is boven verwachting.

verdeling		0		0		1			0			2			6			1			0			0		0		gevallen
tussen de	^		^		^		^			^			^			^			^			^			^		^ om de
klassegrenzen		0,0		0,9		1,8			2,7			3,6			4,5			5,4			6,3			7,2		8,1		9,0		0,91
normaal:								2			14			34			34			14			2						% kans

Met zulke klassegrenzen kan direkt worden afgelezen in hoeverre deze uitkomsten te verwachten waren op grond van een normale verdeling van kansen. Het geval van een kolomgemiddelde van slechts 2,3 verdiepingen (in de linker kolom van het wilde wonen-gebied) is tamelijk ver van het totale gemiddelde. Elk gemiddeld aantal verdiepingen onder 2,7 of boven 6,3 ligt buiten het 95% waarschijnlijkheidsgebied (14 + 34 + 34 + 14 = 96).

De gebruikelijke fout van beleidvoerders en statistici is nu, zulke gevallen te verwaarlozen of zelfs als uitgangspunt voor normstelling te hanteren. De ontwerper is daarentegen gespecialiseerd in onwaarschijnlijke mogelijkheden, zij het in een context die door waarschijnlijkheden wordt geregeerd.

1.18 Linear Programming (LP)

Gesteld dat we op een locatie van 14000 m² binnen 16 maanden zoveel mogelijk willen investeren in woningbouw (W eenheden) en voorzieningen (V eenheden)^[ii]:

asked: number of units	mln Dfl investment	1000 m^2surface	months building time
	per unit
D	5	2	1
F	8	1	2
maximally	Z	14	16

What to build? In other words: what are F, D en Z? The objective (Z maximal) implies to make 5D + 8F as large as possible (maximize it) under the following boundary_conditions:

Max! Z=	5	D	+	8	F	maximize this investing Z within
	2	D	+	1	F	£	14	x1000 m^2 surface and
	1	D	+	2	F	£	16	months, while
					F	³	0	f and d are not negative
		D				³	0

Oplossingsruimte

All points (combinations of D and F) within the solution_space satisfy all constraints not all fulfil the requirement of optimisation of a maximal Z. When no facilities were to be built (F=0) the surface restriction 2W+1V £ 14, determining the maximal value of Z is restrictive, resulting in D = 7 dwelling units to be built in 1D + 2F = 7 months. The investment will be 5D + 8F = 35 mln. If we were to build no dwellings (D = 0), the maximal duration of building holds sway, realizing 8 units of facilities within 16 months. The maximum investment Z would be 64 mln. This is not yet maximal. Considering only the surface constraint, F = 14 units of facilities could be built on the site resulting in an investment of 112 mln, but that would take too much time: 28 months.

Now we want to know for which point within the solution space the investment, represented by the function 5D + 8F, is maximal.

In the origin (D=0, F=0) the investment will be zero, so Z = 0. Moving the line to D > 0 and/or F > 0 will increase Z. We will find the solution after moving this line as far as possible from the origin without leaving the solution space. In this case this point (4,6) The investment will be 5 * 4 + 8 * 6 = 68. The lines through this point define the solution. The boundary conditions are then called 'effective'. Removing or changing one of the boundary conditions will amount to changing the solution. When there are for some reason 15.5 months available, we can realize 4.2 dwelling-units and 5.7 facility-units. If a feasible solution has been found, the solution will always find itself in a corner point (intersection of two lines); unless the object function (objective) is parallel to the boundary condition determining the solution.

This simple example shows already how sensitive optimalisations are vis-à-vis their context (two weeks less building-time results in a different solution) and how important it is to re-adjust continuously the boundary conditions, which are quickly considered stable or to vary them experimentally in sensitivity-analyses with regard to different perspectives, changing contexts. This requires tireless calculation in order to be able to react to changing conditions. If boundary conditions like that are within one's own sphere of influence they may also be considered as objectives. This way the choice of what is called an end or a mean gets a different perspective and becomes in another context arbitrary.

Often designers manage to annihilate boundary conditions deemed stable: all of a sudden different objectives become interesting. This sensitivity with regard to context, only increases if more boundary conditions or objectives are taken into account; for instance, the valuation of occupants of facilities (e.g. 3) in contrast to dwellings (5) : then maximize 3F + 5D, while keeping, for example, the budget constant. The space of solution gets now 5 rather than 4 corners, which might be optimal in one way or another.

With a problem with n variables and n restrictions, the corner-points number m+n / m!n!

In case of a dainty LP problem with 50 variables and 50 restrictions some 10 ²⁹ equations

should be solved; and that is even for the fastest computer a time-consuming task. Luckily it is not necessary to study all corner points. Proceeding from an initial solution obeying all conditions (and admitted or feasible solution) many corner-points less have to be investigated in order to find a solution; approximately m+n. The procedure to follow is known as the Simplex method, that finds in a finite number of steps an eventual solution. With this

the inequalities are transformed into equalities by adding 'slack_variables' before the unequal sign:

2D + 1F £ 14	becomes	2X1 + 1X2 + X3 = 14
1D + 2F £ 16		1X1 + 2X2 + X4 = 16

This way unknown variables have been added. With two of them, like F and D, optimalisation can still be visualized on a piece of paper. If more than two dimensions of decision are to be made variable, one is restricted to the outcome of an abstract sequence of arithmetical operations like the Simplex method, a method that employs matrix calculation [jj].

Matrix A can also be used for calculation of the area and number of times needed to realize any combination of nunber of dwelling-units and number of facility-units. If we want to know how may units can be realized within a given area and time, we have to solve the problem x = A^-1 b. In real-life the number of variables and constraint are not equal. neither it’s necessary to comsume all available amount of space or time. So inequalities will be introduced. The result is that the number of solutions may be infinite. Therefore the linear objective-function has been added. among all solution find that one that result in a minimum or maximum value of the objective function as shown in 1.18.

1.19 Matrix calculation

Take a system of equations, for instance:

2x₁ -3x₂+2x₃+5x₄=3

1x₁ -1x₂+1x₃+2x₄=1

3x₁+2x₂+2x₃+1x₄=0

1x₁+1x₂ -3x₃ -1x₄=0

Usually the coefficients, the unknown_variables and the results are symbolically summarized as Ax = b. In this A, x and b represent numbers concatenated in lists (matrices) or columns (vectors) [kk], in this case

In this way the sum of the products 2x₁ - 3x₂ + 2x₃ + 5x₄ equals the first number of b (b₁ = 3), the next one 1x - 1x₂ + 1x₃ + 2x₄ equals b₂ = 1, et cetera. This shows how matrix multiplication of each row of A with the column vector x works. In the imagination the column must be toppled in order to match each a with its own x. In order to calculate such a sum of products at all, the number of columns should be equal, of course, to the number of rows of x. Considering that the number of rows of A conversely is not equal to the number of columns of row vector x, vector multiplication xA is impossible here: in matrix calculation Ax is not the same thing as xA. One cannot divide matrices and vectors [ll], but often it is possible to calculate an inverse matrix A^-1, so that one may write Ax = b as x = A^-1b [mm]. By that, one can not only determine n unknown variables in n equations by substitution, much writing and miscalculations, but also by applying the Gauss-Jordan method; or in the case of more solutions b by the (inverse matrix)

The point of contact of the two equations of paragraph Fout! Verwijzingsbron niet gevonden., may be determined easily both graphically and by substitution, but in the matrix guise the solution would look like this:

The essential operations, with regard to the solving of a system of equations by means of the Gauss-Jordan method are:

· multiplying all coefficients of one row with an identical factor adding a multiple of a row to a (different) row.

These operations are also essentially important with regard to the Simplex algorithm, to be discussed next.

1.20 De Simplexmethode

Het Simplex-algorithme is in feite zeer simpel en bestaat uit twee fasen:

Fase 1: Zoek een startoplossing die aan alle beperkingen voldoet. Zo’n oplossing heet een toegelaten oplossing.

Fase 2:Zolang de oplossing niet optimaal is: verbeter de oplossing een blijf daarbij aan alle beperkingen voldoen.

Het algorithme zal worden toegelicht aan de hand van een probleem met uitsluitend *-beperkingen De oorsprong is dan een toegelaten start-oplossing zodat Fase 1 kan worden overgeslagen. ^[nn] Als voorbeeld dient de opgave uit paragraaf Fout! Verwijzingsbron niet gevonden., blz. Fout! Bladwijzer niet gedefinieerd.. Allereerst worden de ongelijkheden herschreven als gelijkheden met restvariabelen:

i

ai,s0

Z

ai,1

X1

ai,2

X2

ai,3

X3

ai,4

X4

b

0

1

Z

+

-8

X1

+

-5

X2

+

0

X3

+

0

X4

=

0

1

0

Z

+

1

X1

+

2

X2

+

1

X3

+

0

X4

=

14

2

0

Z

+

2

X1

+

1

X2

+

0

X3

+

1

X4

=

14

De cruciale gegevens zijn hieronder samengevat in een ‘Simplextableau’.

Simplextableau 1

m	Con	Bas	Z	W	V	opp	tijd	b
n			0	1	2	3	4
0	Z		1	-8	-5	0	0	0
1	Opp	3	0	1	2	1	0	14
2	Tijd	4	0	2	1	0	1	16

De rijen zijn genummerd als i = 0…2, de kolommen j=0..4. Rij 0 stelt de doelfunctie voor, rijen 1 en 2 de beperkingen. Kolom 0 hoort bij de Z waarde, kolommen 1 en 2 bij de ‘echte’ variabelen, woningen en voorzieningen, kolommen 3 en 4 bij de restvariabelen van de beperkingen. Kolom b bevat de waarden van de in kolom Bas genoemde basisvariabelen (die tezamen de basis vormen); in dit geval zijn dat initiëel de restvariabelen. De waarde van de niet in deze kolom genoemde (niet-basis) variabelen bedraagt 0.

Vervolgens zal getracht worden deze initiële oplossing te verbeteren door herhaald uitwisselen van een te introduceren niet-basis-variabele tegen een te verwijderen basis-variabele.

Stap 1: Optimaliteitstest

Zijn alle elementen binnen rij Z / 0 dan is de bij dit tableau behorende basisoplossing optimaal. Bevat rij Z negatieve waarden selecteer de kolom k met de meest negatieve waarde, i.c. kolom 1, variabele W. Deze kolom wordt spil- of pivotkolom genoemd. De betreffende niet-basis-variabele wordt nu in de basis geïntroduceerd.

Stap 2: Selectie te verwijderen basis-variabele

Bepaal de maximale waarde die deze variabele aan kan nemen op voorwaarde dat aan alle beperkingen voldaan blijft. Selecteer de rij r waarvoor de quotiënt van de waarde b_r en a_rk, met a_rk groter dan nul, minimaal is. Deze rij wordt de spil- of pivotrij, element a_rk de spil of pivot, i.c. a_2,1 met waarde 2. De bij die rij horende basisvariabele (kolom Bas) wordt nu uit de basis verwijderd

Stap 3

Transformeer pivotkolom in eenheidsvector met op de plaats van de pivot een 1:
vermenigvuldig de pivotrij met 1 / pivot (normaliseren pivotrij):

rij
2	0	2	1	0	1	8	maal 0.5
	0	1	0.5	0	0.5	4

Trek nu een zodanig veelvoud van de pivotrij van de overige rijen af, dat telkens de pivotkolom 0 (a_ik) wordt. Ga daarna terug naar stap 1.

rij
0	0	-8	-5	0	0	0
trek af	0	-8	-4	0	-4	-64	maal -8
	0	0	-1	0	4	64
1	0	1	2	1	0	14
trek af	0	1	0.5	0	0.5	8	maal 1
	0	0	1.5	1	-0.5	6

Het tableau heeft nu de volgende vorm gekregen:

Simplextableau 2

m	Con	Var	Z	W	V	opp	tijd	b
n			0	1	2	3	4
0	Z		1	0	-1	0	4	64
1	Opp	3	0	0	1.5	1	-0.5	6
2	Tijd	1	0	1	0.5	0	0.5	8

Daar rij 0 nog steeds negatieve elementen bevat is de gevonden oplossing nog niet optimaal. De stappen 1 tot en met 3 worden nogmaals uitgevoerd. De te introduceren variabele is nu 2, de te verwijderen variabele de slack (3) van de oppervlakte beperking (rij 1).

De pivotrij wordt nu

rij
1	0	0	1.5	1	-0.5	6	maal 0.67
	0	0	1	0.67	-0.33	4

De overige rijen worden:

rij
0	0	0	-1	0	4	64
trek af	0	0	-1	-0.7	0.33	-4	maal 1
	0	0	0	0.67	3.67	68
2	0	1	0.5	0	0.5	8
trek af	0	0	0.5	0.33	-0.17	2	maal 0.5
	0	1	0	-0.33	0.67	6

Het tableau wordt nu:

Simplextableau 3

m	Con	Var	Z	W	V	opp	tijd	b
n			0	1	2	3	4
0	Z		1	0	0	0.67	3.67	68
1	Opp	2	0	0	1	0.67	-0.33	4
2	Tijd	1	0	1	0	-0.33	0.67	6

Rij nul bevat nu geen negatieve elementen meer zodat de gevonden oplossing optimaal is. De gevonden oplossing is gelijk aan de eerder gevonden grafische oplossing (woningen 6, voorzieningen 4, investeringen 68).

1.21 Functies

In colloquial speech sentences are formulated in which a subject x operates on an object y. The verb in the sentence describes this operation. In logic a sentence like that, telescopes in a 'fullsentence_function' y(x): 'y as operation of x' . In the same way mathematical formulae can be made which translate an input x (argument, original) according to a well-defined operation (function, representation_instruction, e.g. 'square') into an outcome y (output, function_value, image, depiction, e.g. the square). The outcome is represented as an operation of x: y = f (x) ; e.g. y = x². The value of the independent variable x is chosen from a set of values X (the domain), the definitional range of the function.

Each value from this set corresponds to only one outcome from a set Y (range, co-domain, function_value_field) with possible values of y. With a given input the outcome is therefore certain [oo]. That is the reason why a function value x in a graph never runs back, like in the graph of a circle. There are just decreasing, increasing or unchanging values of y in the direction of x in the graph, allowing in one way unmistakable differentiation (rating growth) and integration (summing form x₁ to x₂). Because of this function, it is the ideal mathematical means to describe causal_relationships. Each cause has one consequence, of course, but the same consequence may have different causes. If the sun starts shining, the building warms up, but the heat in a building may also result from the function of a heating system.

However when cases should be studied in which one architectural design can have different effects, workings, functions according to circumstances, each effect should be modelled as a separate function.

Functions like that are alternately activated by steering_functions according to circumstances. Since these functions change with the context, this context should be introduced as a set 'exogenous_varables' and be included as parameters (for instance coefficients) in the functions. These exogenous variables to be introduced may be modelled next in a wider context as output of other functions. It results in a dynamic_system of functions and magnitudes.

Een computerprogramma voor wiskundige bewerkingen zoals Matlab moet dan worden uitgebreid met een modelleerprogramma zoals Simulink of Stella.

1.22 Fractals

Fractals zijn wiskundige figuren, die zelfgelijkvormigheid vertonen.

Een hoofdmotief keert in ieder detail terug.

Zij zijn het resultaat van eigenlijk vrij eenvoudige formules, maar deze vele malen herhaald berekend (bijvoorbeeld 100.000 maal).

Praktisch is men genoodzaakt, bij het gebruik van de computer, in verband met het oplossend vermogen van het beeldscherm (bij voorkeur een kleurenscherm van goede kwaliteit), de berekeningen na enkele ronden af te breken.

Door een kunstgreep is het mogelijk op een détail "in te zoomen", d.w.z. een detail vergroot af te beelden, simpel door een kleiner goed gekozen "window " in te voeren. Men kan dan het resultaat van meer ronden (détails van een hogere orde) zichtbaar maken. Als regel ziet men dan in de détails het hoofdmotief terug. Bij een niet al te krachtige computer, wordt men in dit uitvergroten beperkt door zowel de geheugen-capacitiet, als door de rekentijd, die dan nodig is.

Professioneel onderzoek op het terrein van de Fractals, wordt gedaan in een aantal instituten, die daartoe de beschikking hebben over zeer krachtige snelle computers en beeldschermen van grote afmetingen en met zeer grote aantallen beeldpunten.

(Amsterdam; Bremen Dld.; Atlanta, Georgia, USA).

In hoofdzaak kan men fractals naar hun voortbrengingsprincipe in 5 soorten onderscheiden;

· Herhaalde vertakking (boomfractals);

· vervanging ("kronkels", "draaikrommen");

· transformatie (bladertakken);

· JULIA- en CANTOR- verzamelingen, berustend op de formule: z' = z² + C.

En als bijzonder type:

· de MANDELBROT- verzameling.

Bij herhaalde vertakking onstaan fraaie structuren, gebaseerd op een drie-ster, een H, interne driehoeken (zeef van Sierpinski), tweesprong, 5-ster resp. 7-ster. Er is analogie met biologische structuren, zoals een scheefgewaaide boom, een bloedvatenstelsel, een longstructuur.

Bij herhaalde vervanging wordt een recht lijnstuk - - - vervangen door bijvoorbeeld

- ^ -, of /\, of een meander. Zo onstaan "kronkels ", draakkrommen, krommen genoemd naar hun ontdekkers, zoals Levy, Minkovski, Koch, etc. Bij deze laatste is er een analogie met een kustlijn, hetgeen kan helpen bij het bepalen van de lengte van een kustlijn en van andere grillige contouren.

Bij herhaalde tranformatie (verplaatsing, verdraaiing, vervorming inclusief verkleining), onstaan figuren die bladeren, of takken met bladeren kunnen voorstellen. Bij toepassing van een groot aantal van zulke geschikt gekozen transformaties, kunnen beelden van niet bestaande bossen, niet bestaande landschappen met bergen en fjorden en zelfs een menselijk gelaat worden gegenereerd.

Het lukt zelfs een beeld van een reëel object te "fractaliseren", d.w.z., van een voldoende aantal transformatie-formules telkens de 6 parameters zodanig te bepalen, dat ze dat beeld met grote nauwkeurigheid opleveren. Verdere ontwikkeling van deze techniek is van zeer groot belang voor het overseinen van beelden, die dan immers door slechts een klein aantal getallen volledig zijn bepaald.

Bij herhaalde toepassing van een formule, zoals z' = z² + C, (waarin z en C z.g. complexe getallen zijn, die kunnen worden voorgesteld door een punt {x, y} resp. {A, B} in het complexe vlak en waarmee dus een nieuw punt z wordt berekend als de som van (de oude) z-kwadraat en de constante C), onstaan spiralen die in elkaar krimpen of expanderen afhankelijk van de start-waarde van z.

Bij bepaalde start-waarden voor z, onstaan grensgevallen en dat levert dan "krommen" met een bizarre vorm; een JULIA-verzameling.

Soms is het een samenhangende kromme, soms bestaat de kromme uit een aantal losse delen (niet-samenhangend), afhankelijk van de waarde van C.

De verzameling van de punten C (A, B) vormt een MANDELBROT-verzameling. Laat men de computer een tekening maken van alle punten C die een samenhangende JULIA-verzameling kunnen opleveren, dan ontstaat een uiterst interessante figuur, die verrassenderwijs ook een fractal-karakter vertoont.

Bij het inzoomen op delen van die figuur, ontdekt men zeer complexe en uiterst boeiende deelstructuren, waar telkens weer in détails de hoofdmotieven tevoorschijn komen.

Ten opzichte van de andere besproken fractals is de MANDELBROT-fractal van een hogere hiërarchie.

1.23 Differentiëren

Uit het verschil van twee gelijkmatig in ruimte of tijd opéénvolgende waarden in een rij, kan men de verandering op een bepaald moment of ter plaatse afleiden. Ook deze afgeleide verschillen kan men op een rij zetten. Als alle ‘gaten’ tussen twee opéénvolgende waarden in een rij worden gevuld (Cauchy-rij, bijvoorbeeld de rij waarden van een een continue_functie y), spreekt men niet meer van ‘verschil’ D (dit is immers tot nul genaderd), maar van differentiaal d. Deelt men het tot nul genaderde waardeverschil dy door de inmiddels eveneens tot nul genaderde afstand in ruimte of tijd dx tussen beide waarden, dan spreekt men van een differentiaalquotiënt dy/dx.

In de grafiek van een functie staat dit quotiënt voor de helling op een bepaalde plaats of moment. Ook voor de helling van een autoweg wordt de verhouding tussen hoogte en lengte (in procenten) weergegeven. Bij de afgeleide functie naderen echter beide tot nul zodat ze slechts betrekking hebben op één punt van een lijn inplaats van op een traject. Het quotiënt y' = dy/dx, is positief bij stijging, negatief bij daling (zie bijgaande figuur).

Er bestaan tal van regels om van een gegeven functie voor alle waarden tegelijk een afgeleide_functie te formuleren. Deze afleidingen kunnen sinds Leibniz en Newton grotendeels bewezen worden, maar men hoeft dat bewijs strikt genomen niet te kennen om de regels te kunnen gebruiken. Het is echter de vraag of zonder enig bewijs in de Euclidische traditie het bij een opleiding beoogde wiskundig inzicht gebaat is. Dit inzicht is echter ook niet gebaat bij begriploos toepassen van deze uit het hoofd geleerde regels. Daarom is het wél goed, dat men de regels zelf tegenwoordig niet meer uit het hoofd hoeft te leren. Computerprogramma’s zoals Mathcad, Matlab, Mathematica of Maple passen deze regels automatisch en foutloos toe, zodat alle aandacht kan worden geconcentreerd op het uitwendig gedrag van de functies en hun afgeleiden.

In bijgaande tabel kan men zien dat men minima, maxima en buigpunten kan vinden door de afgeleide y'=0 te stellen of de afgeleide van de afgeleide y''=0, en vervolgens bijbehorende x uit te rekenen. Men kan daarna met die x bijbehorende y berekenen. Dit is vooral van belang bij optimaliseringsvraagstukken. Als men echter van een bepaalde functie y bijvoorbeeld alleen weet dat hij toenemend stijgt, dan kan men omgekeerd zoeken naar een formule voor y waarvoor zoals y' als y'' positief is. Voor deze omgekeerde weg (integratie) bestaan eveneens tal van rekenregels.

1.24 Integreren

Gesteld, dat men van een kap met twee schilden voorlopig alleen de te overkappen breedte, bijvoorbeeld b=10m, de linker- en rechter goothoogte gh1=gh2=4, de nokhoogte nh1=nh2=9 en de nokpositie np=0.5b vaststelt. Dan is de helling van de dakvlakken daarvan afhankelijk.

In Mathcad ziet de berekening er als volgt uit:

Breedte en nokpositie van een kap

Dakschild Links Dakschild Rechts

De dakhellingen zijn nu:

De wiskundige formule die de loop van het linker dakschild tussen x=0 (linker goot) en x=np (nok) beschrijft, is h1x, vermeerderd met de goothoogte. Het rechter dakschild heeft echter dalende helling h2 en dus een andere formule tussen nok x=np tot de rechter goot (x=b). Mathcad kan beide formules tot een discontinue functie f(x) samenvatten met een ‘if’-statement: ‘als x<np, dan f(x)=gh1+h1x, anders f(x)=nh+h2(x-np)’. Dit wordt als volgt genoterd:

Gevelfunctie:

_{Oppervlakte van de kopgevel:}

De over de breedte bepaalde integraal geeft de oppervlakte van de kopgevel.

Wanneer men nu de diepte y=0..10 in de beschouwing betrekt, kan men deze oppervlakte nog eens over y integreren om de inhoud te krijgen.

Gesteld, dat de nokpositie met de diepte y varieert volgens een willekeurige formule np(y), dan variëren de dakhellingen h1(y) en h2(y) ook met de diepte y:

De gevelfunctie wordt nu een gebouwfunctie met met twee variabelen f(x,y). In de gevelfunctie hoeft men voor de constante np slechts de variabele np(y) in te vullen en hetzelfde te doen voor h1 en h2:

Wanneer men voor x en y discrete waarden van 0 tot 10 invult, kan men de waarden opslaan in een 10x10 matrix M_x,y=f1(x,y).

Deze kan als volgt zichtbaar gemaakt worden:

Sommeert men de waarden over rijen en kolommen in de matrix, dan krijgt men een eerste benadering van de inhoud, het dubbel integreren van de functie f1(x,y) over x en y geeft uiteraard een meer exacte berekening.

Dit is natuurlijk vooral gemakkelijk, wanneer men vloeiende dakvormen kiest, bijvoorbeeld:

Oppervlakte van de voorgevel:

Differentiaal- en integraalrekenen kan begrepen worden aan de hand van ruimtelijke vraagstukken, maar vindt vooral toepassing bij analyse van processen. Daarbij wordt de differentiaal dx vaak met de notatie dt aangeduid en de groei (of krimp) op een bepaald tijdstip met .

Een bekend voorbeeld is de toenemende snelheid waarmee een lichaam van een variabele helling afrolt, zoals een regendruppel van bovenstaande kap. In de bouwkunde zijn het voornamelijk berekeningen voor klimaatbeheersing die van differentiaal- en integraalrekening gebruik maken.

1.25 Differentiaalvergelijkingen

Bevolkingsgroei biedt een voorbeeld van groei die zelf kan groeien, soms constant (k) met de omvang van de bevolking P(t) zelf:

Men kan dit constateren zonder al een formule voor P(t) te kennen. Een dergelijke vergelijking waarin een onbekende functie samen met één of meer van haar afgeleiden voorkomt, noemt men een differentiaalvergelijking. Ook de gewone omgangstaal kent primitieve differentiaalvergelijkingen, bijvoorbeeld: ‘Als de bevolking vermeerdert, wordt ook de bevolkingsgroei evenredig groter.’

Het oplossen van een differentiaalvergelijking bestaat nu uit het vinden van formules voor de onbekende functie. Als we bijvoorbeeld in bovenstaande vergelijking voor P(t) e^kt invullen, dan klopt de differentiaalvergelijking nog steeds, omdat de afgeleide van e^kt gelijk is^[pp] aan ke^kt:

Eén oplossing voor de differentiaalvergelijking is dus P(t)=e^kt, maar dit hoeft niet de enige oplossing te zijn. Veelal is er een familie van oplossingen. We hadden bijvoorbeeld ook Ce^kt kunnen invullen, want de afgeleide daarvan is Cke^kt, zodat ook daarvoor de differentiaalvergelijking klopt. Onderstaande oplossingen zijn dus slechts enkele van een oneindig aantal mogelijke oplossingen voor bijvoorbeeld k=2:

Om te weten welke formule uit deze familie de juiste is, moeten we de uitkomst op enig tijdstip, bijvoorbeeld t=0 (beginwaarde) kennen. Gesteld dat we weten dat de bevolking in het begin 2 mensen telde, dan kunnen we C berekenen uit Ce^kt=2. Aangezien e⁰=1, geldt voor elke k: C=2. C is in deze familie van vergelijkingen altijd de beginwaarde. Daaruit volgt als enig juiste formule: P(t)=2e^kt. Dit zou echter betekenen dat er, als ieder mens gemiddeld na 25 jaar (een generatie) 2 kinderen zou krijgen, na 2000 jaar (80 generaties) 2,418 x 10²⁴ kinderen zouden zijn. Als de bevolking van Nederland in het jaar 0 één echtpaar zou hebben gehad, moet men k op 0,199 stellen om op de huidige 16mln inwoners te komen. De complicatie dat dat niet allemaal kinderen zijn verwaarlozen we hier ^[qq].

Al in deze vereenvoudigde vorm blijkt dat de hypothese van constant van de bevolking afhankelijke groei die in onze differentiaalvergelijking gehanteerd werd niet juist kan zijn. Er zijn grenzen aan de groei die door de draagkracht van het milieu gesteld worden. Dit blijkt uit populaties van tal van andere soorten dan de mens en de werkelijke loop van de bevolking vanaf 1750 in miljoenen inwoners.

De exponentiële groei gaat alleen bij een relatief kleine bevolking op. Bij het naderen van de grenzen G die onder andere door het grondgebied gesteld worden, vlakt de groei af. We kunnen aan de differentiaalvergelijking een term toevoegen die dit bewerkstelligt:

Als P(t) klein is t.o.v. G, nadert de term tussen haakjes 1, zodat onze oorspronkelijke hypothese blijft opgaan, in het andere geval wordt de groei 0 of zelfs negatief. Logistische curves zoals de volgende voldoen hieraan:

De functie is een variant van de derde functie die als voorbeeld in paragraaf Fout! Verwijzingsbron niet gevonden. op blz. Fout! Bladwijzer niet gedefinieerd. genoemd werd.

Differentiaalvergelijkingen worden gebruikt om vanuit een hypothese families van functies te genereren, waaruit gekozen kan worden op grond van bekende beginwaarden.

1.26 Systems modelling

Any system has a border; beyond it exogenous variables serve as input for the first functions, they meet within the system. The output of these functions serves on its turn as an input for subsequent functions, sometimes operating in parallel

The system as a whole, delivers in the end an output of tables, images, animations or commands in a process of production.

If a system is modelled on a computer, it is a program that just like a text processing program awaits input and eventually a command to execute (e.g. the command 'print').

A programming_language like Basic, Pascal, C or Java, contains, except mathematical functions, a host of control functions, like 'print' , and control statements like 'do…while', 'if …then… else'.

De ‘als … dan …’-functie, zoals toegepast in de 'gevelfunctie' op blz.Fout! Bladwijzer niet gedefinieerd. is een goed voorbeeld om te begrijpen hoe bij de invoer in een systeem en in de loop van het proces naar gelang de omstandigheden kan worden beoordeeld welke volgende functie de binnenkomende grootheid moet bewerken en aan welke volgende functie het resultaat als invoer moet worden doorgegeven.

---

[a] Alexander, Christopher (1971) Notes on the syntheses of form, Harvard University Press, Cambridge, Massachussetts.

[b] Alexander, Christopher (…) Apattern language, …

[c] Broadbent, Geoffrey (1988) Design in architecture: architecture and the human sciences, David Fulton Publishers Ltd., ISBN 047110583X of 1853460591 (paperback)

[d] Kervel, E. van (1990) Prisma van de wiskunde 2000 wiskundige begrippen van A tot Z verklaard, Uitgeverij het Spectrum BV, Utrecht

[e] Reinhadt, Fritz; Soeder, Heinrich (1977) Atlas van de wiskunde, Bosch & Keuning NV, Baarn, ISBN 9024669561

[f] Een complete interactieve versie van de 'Elementen', een 'bijbel' voor de geometrie, is te vinden op het internet: http://aleph0.clarku.edu/~djoyce/java/elements/elements.html. Op deze site en haar links wordt betoogd dat het verlaten van de Euclidische methode in het onderwijs ten gunste van een afleiding uit de verzamelingentheorie het logisch afleiden van conclusies uit axioma's via stellingen naar nieuwe stellingen verwaarloost. De site is interessant door de mogelijkheid meetkundige schema's te wijzigen. Hierdoor blijkt duidelijk het werkingskarakter van wiskundige stellingen en formules.

[g] Een onderscheid dat door de Griekse wiskundige Proclus werd gemaakt.

[h] De niet-Euclidische meetkunde verwerpt één of meer van deze axioma's.

[i] Kant, Immanuel (1787) Critic der reinen Vernunft, Zweyte hun und wieder verbesserte Auflage, Riga, Johann Friedrich Hartknoch. Het programma van dit onderzoek is vooral helder samengevat in het voorwoord op deze uitgave. Een korte inleiding op Kant: Uwe Schultz (1992) Kant Immanuel, Tirion, Baarn.

[j] Een bekende publicatie van het CBS

[k] 'Ho Theos aei geometrei', luidde een bekende Griekse uitspraak

[l] Zie …

[m] Russell, …

[n] Frege, Gottlob (1884, 1981) De grondslagen der aritmetica, een logisch-mathematisch onderzoek van het getalbegrip, Het Wereldvenster, Bussum. Dit probleem wordt in paragraaf 34 tot 54 beschreven en blijkt niet zo eenvoudig als het lijkt.

[o] Formulation derived from Reinhardt; Soeder (1977) p. 463.

[p] J.A. Deelder (1991) Euforismen, De Bezige Bij, Amsterdam.

[q] Een voorbeeld van een maatsysteem met gelijke maten is overigens ook aan de orde bij de keuze de keuze van een resolutie.

[r] In case 0!, 0! = 1

[s] This can be done with the formula =FACT(100)/(FACT(25)*FACT(25)*FACT(25)*FACT(25))

[t] Hier is het programma Mathcad gebruikt.

[u] Met resolutie wordt gewoonlijk de diameter van de korrel bedoeld, hier gebruiken we de term als verhoudingsmaat.

[v] G. Kruijtzer (1998) Ruimte en getal, Architectura & Natura

[w] Berger. M (1977) Geometry I en II (New York) Springer Verlag and Aarts (2000), A.Verweij (1991) Meetkunde voor Bouwkunde (Delft) TUDelft(TWI)

[x] Tummers, L.J.M.; Tummers-Zuurmond, J.M. (1997) Het land in de stad. De stedebouw van de grote agglomeratie (Bussum) Uitgeverij Thoth

[y] Berger. M (1977) Geometry I en II, Springer Verlag, New York; Aarts (2000) …, A.Verweij (1991) Meetkunde voor Bouwkunde, TUDelft(TWI)

[z] With a 'network' usually a directed network is implied.

[aa] Amongst others, used in programmes like Route Planner, to calculate the shortest path from A to B.

[bb] For instance: in order to calculate the time required to realize a building or site.

[cc] This form of representation is known as an AON-network: Activity On Node.

Initially only AOA-networks were used with the activities on the arrows (Activity On Arrow. In that case the flow on the arrows represent the temporal duration.

[dd] This latin capital is properly chosen, iin view of its form-equivalence with the stream that ‘comes out’ of an urn.

[ee] This greek capital is properly chosen, iin view of its form-equivalence with the urn, proverbial in statistical textbooeks, turned upside-down and producing arbitrarily red and white marbles.

[ff] De term is afkomstig van Carel Weeber (1998), Het wilde wonen, …. Daarbij worden wel bouwhoogte-beperkende regels voorondersteld.

[gg] In Excel te simuleren met =INTEGER(10*ASELECT()). 100 van deze afgeronde randomcijfers in een vierkant kunnen in de afgebeelde grafiek met functietoets F9 tot leven gebracht worden.

[hh] s := √ ( (S x2 - S x S x / n ) / n )

[ii] Gehanteerde conventie : namen van onbekende variabelen in hoofletters, namen van bekende met kleine letters. Bij vermenigvuldiging bekende voor onbekende, dus: a * X

[jj] Further reading:: Hillier, F.S. ; Lieberman, G.J. (1973) Operations Research, holden-day (Stanford) Stanford University ISBN 0=8162-3856-1

[kk] X is a column vector, XT the same sequence as a row vector

[ll] Horssen, W.T. van,; Burgh, A.H.P. van der (1985) Inleiding Matrixrekening en Lineaire Optimalisering (Utrecht) Epsilon Uitgaven, describe in which cases that is possible.

[mm] For instance in Exel A-1 is calculated by the function {=MINVERSE(A2:D5)} and x by {=MMULT(F2:I5;K2:K5)} if you indicate a field of 4 x 4, call the function, select the necessary inputfields A-1 and b and close with crtl-shift.

[nn] Het algorithme voor fase 1 is met een kleine toevoeging gelijk aan dat van fase 2

[oo] In the reverse however, an outcome may be produced by different values of the input.

[pp] Dit is de reden dat men constanten graag als macht van het getal e=2,718 voorstelt: de afgeleide van ekt (kekt) is gemakkelijker te berekenen dan de afgeleide van Kt (Kt x ln(K)).

[qq] Zie daarvoor de Jong (1997) Populatie en habitat (Delft) Faculteit Bouwkunde TUDelft