4.1 Water
balance.................................................................................................................. 2
4.1.1 Evaporation
and precipitation............................................................................................ 2
4.1.2 Runoff............................................................................................................................ 3
4.1.3 References
to Water balance........................................................................................... 4
4.2 River
drainage................................................................................................................... 6
4.2.1 River
morphology............................................................................................................. 6
4.2.2 Q by
measurement........................................................................................................ 11
4.2.3 Q on
different water heights in the same profile................................................................. 11
4.2.4 Calculating
Q with rounghness........................................................................................ 11
4.2.5 Using
drainage data....................................................................................................... 14
4.2.6 Probability
of extreme discharges................................................................................... 17
4.2.7 Level and
discharge regulators........................................................................................ 19
4.2.8 References
to river drainage............................................................................................ 20
4.3 Water
reservoirs.......................................................................................................... 22
4.3.1 Terminology.................................................................................................................. 22
4.3.2 Water
delivery............................................................................................................... 23
4.3.3 Capacity
calculation...................................................................................................... 23
4.3.4 Avoiding
floodings by reservoirs....................................................................................... 24
4.3.5 Water
management and hygiene..................................................................................... 25
4.3.6 Maps
concerning local water management....................................................................... 26
4.3.7 References
to Water reservoirs....................................................................................... 27
4.4 Polders............................................................................................................................. 28
4.4.1 Need of
drainage and flood control................................................................................... 28
4.4.2 Artificial
drainage........................................................................................................... 29
4.4.3 Polders......................................................................................................................... 31
4.4.4 Drainage
and use.......................................................................................................... 32
4.4.5 Weirs,
sluices and locks................................................................................................ 33
4.4.6 Coastal
protection......................................................................................................... 35
4.4.7 References
to Polders.................................................................................................... 36
4.5 Networks
and crossings.............................................................................................. 37
4.5.1 Networks...................................................................................................................... 37
4.5.2 Crossings..................................................................................................................... 38
4.5.3 Bridges......................................................................................................................... 40
4.5.4 Harbours
P.M................................................................................................................ 42
4.5.5 References
to Networks and crossings............................................................................ 42
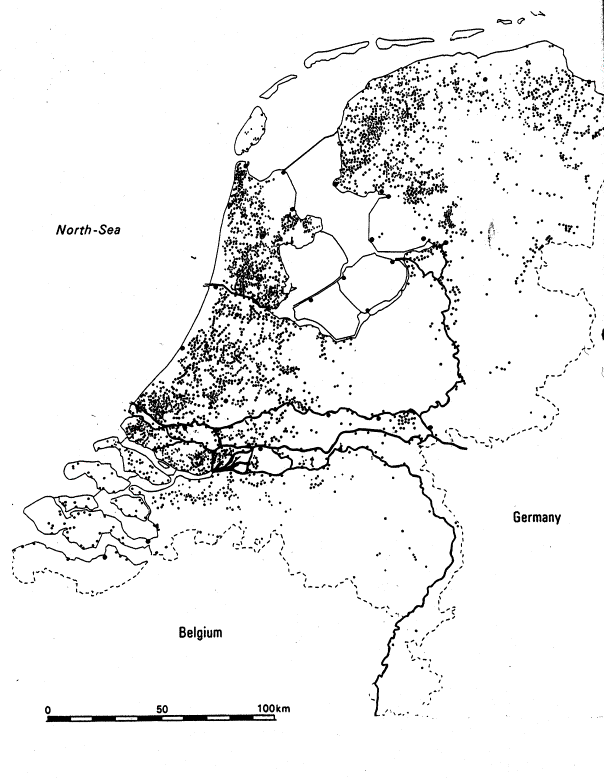
The surface of the Earth is ample half a billion km2 and there is 1.39 billion km3
water. So, if water was equally
dispersed the Earth would be fully covered by a 2.7km deep ocean (Fig. 1). The 48m upper layer would be ice. However, 29% is
land. It contains 3% of all existing water, but 2/3 is frozen.
If all ice would
melt by gobal warming sea level would raise 66m.
|
1000
km3
|
salt
|
fresh
|
total
|
m3/m2
|
mm
|
|
atmosphere
|
|
12,9
|
12,9
|
0,025
|
25
|
|
sea
|
1 338 000
|
|
1 338 000
|
2 624
|
2 624 021
|
|
land, from which
|
12 957
|
35 004
|
47 960
|
94
|
94 057
|
|
snow and ice
|
|
24 364
|
24 364
|
48
|
47 782
|
|
subterranean
|
12 870
|
10 530
|
23 400
|
46
|
45 891
|
|
lakes
|
85,4
|
91
|
176,4
|
0,346
|
346
|
|
soil moisture
|
|
16,5
|
16,5
|
0,032
|
32
|
|
swamps
|
|
2,1
|
2,1
|
0,004
|
4
|
|
life
|
1,1
|
|
1,1
|
0,002
|
2
|
|
total
|
1 350 957
|
35 004
|
1 385 960
|
2 718
|
2 718 079
|
|
|
|
Fig. 1
Total amount of water on Earth
|
|
|
Fortunately the sun
still adds snow to the poles.
You can evaporate 1m3 water by 2.26GJ,
2.26GWs, 630kWh or 72Wa (say 72 m3 natural gas). The Earth’s surface
receives 81 PW from sun. So the sun could evaporate 1.1 million km3
per year.
Actually less then
half is evaporated in unsaturated air only (Fig. 2). It falls down discharging its solar heat in the same time as soon as the
air becomes saturated in cooler areas by condensation (precipitation). That is nearly 1m3/m2
or 1m and more precise 957mm (Fig. 2).
|
|
evaporation
|
precipitation
|
runoff
|
evaporation
|
precipitation
|
runoff
|
|
|
1000 km3/a
|
mm/a
|
|
sea
|
419
|
382
|
|
1157
|
1055
|
|
|
land
|
69
|
106
|
37
|
467
|
717
|
250
|
|
total
|
488
|
488
|
|
957
|
957
|
|
|
|
|
Fig. 2
Yearly gobal evaporation, precipitation and runoff
|
|
|
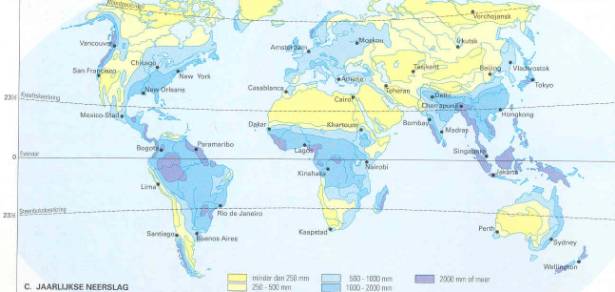
Areas like deserts receive less then 200mm, areas like tropical rain forests more then 2 000mm average per year (Fig. 3).
|
|
|
Wolters-Noordhof (2001) page 181
|
|
Fig. 3 Global distribution of precipitation
|
|
|
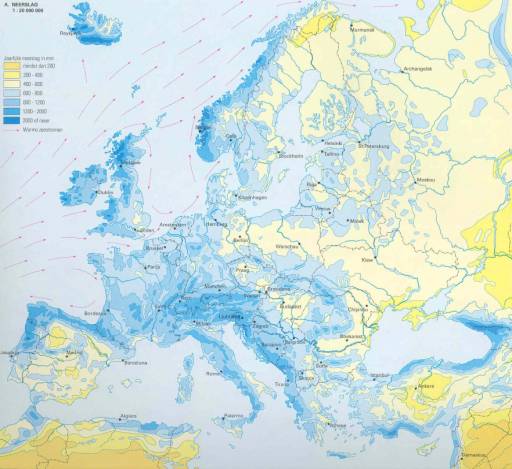
Europe has the same extremes (Fig. 4).
|
|
|
Wolters-Noordhof (2001) page 61
|
|
Fig. 4 European distribution of
precipitation
|
|
|
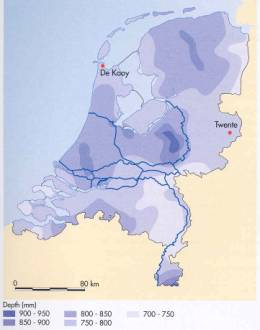
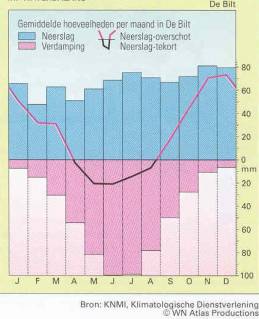
The Netherlands receive from 700mm in East Brabant
until 900mm in central Veluwe (Fig.
5), but there have been years of 400mm and 1200mm.
|
|
|
|
Huisman, Cramer et al. (1998) page 18
|
Wolters-Noordhof (2001) page 53
|
|
Fig. 5 Distribution of precipitation in The
Netherlands
|
Fig. 6
Precipitation minus evaporation in The Netherlands
|
|
|
|
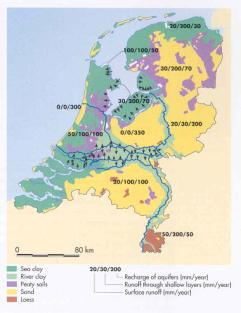
When precipitation exceeds evaporation as soon as lakes and subterranean aquifers have
been filled up water runs off subterranean or along brooks and rivers (Fig. 8 and Fig. 9).
|

|
|
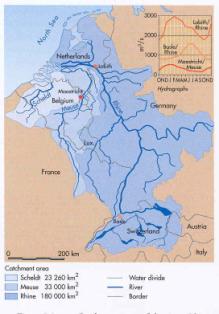
Harrison and Harrison (2001)
|
|
Fig. 7 European river system
|
|
|
The Netherlands receive runoff from catchment areas of rivers Rhine (entering The Netherlands in Lobith), Meuse and
Scheldt (Fig. 7).
|
|
|
|
Huisman, Cramer et al. (1998) page 21
|
Huisman, Cramer et al. (1998) page 13
|
|
Fig. 8 Major soil types and average annual
runoff in The Netherlands
|
Fig. 9 Received runoff in The Netherlands
|
|
|
|
The river Rhine has a catchment area of 180 000km2 characterised
by 1 775mm precipitation minus 1 392mm evaporation average per year in that area until Lobith. So, 383mm, 69km3/year
or at average 2000m3/sec water runs off and comes in at Lobith. Snow and ice in mountains level out
season fluctuations of rivers storing precitipation in winter, releasing it in
summer. Nevertheless, in February at its normal annual maximum it is 8km3
or 3000m3/sec causing water level 10m NAP at Lobith. But in 1995 17m NAP and
13 000m3/sec is measured at Lobith.
Jong (1995) collected weeks of frontpage news about
floodings retrievable in the Chair library. Evacuation of 50 000
inhabitants was ordered by Royal Commissioner of Gelderland Terlouw when floodings threatened Betuwe area behind Lobith in 1995.
Afterwards, the threat of floodings caused plans to inundate polders
preventively in case of emergency, but a polder of 1km2 x 1m =
1 000 000m3 would have stored water for 77 seconds only.
So, retention in Rhine basin have to increase, bottoms deepened or dikes along rivers have to be heightened. But which height is enough?
Harrison, H.
M. and N. Harrison (2001) Schiereiland Europa. De hooggelegen
gebieden (Berlijn) Reschke & Steffens.
Huisman, P.,
W. Cramer, et al., Eds. (1998) Water in the Netherlands NHV-special
(Delft) NHV, Netherlands Hydrological Society NUGI 672 ISBN 90-803565-2-2 URL Euro 20.
Jong, T. M.
d. (1995) Krantenknipsels watersnoodramp 1995 (Rotterdam) NRC.
Wolters-Noordhof,
Ed. (2001) De Grote Bosatlas 2002/2003 Tweeënvijfstigste editie + CD-Rom
(Groningen) WN Atlas Productions ISBN
90-01-12100-4.
The morphology of a river system and its discharge quantity Q depends on human impact, the proportion of subterranian and
surface runoff (Fig. 8), the character and load of transported eroded
material and the directions, velocities and quantities caused by slopes in the catchment
area.
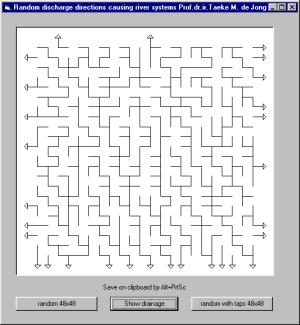
Fig. 10 shows a landscape with 24 x 24 squares (sloped
mountain areas or polders) with 4 possible drainage directions, producing converging trucated
river systems. Computer programme Jong (2003) ‘river(drainage.exe)’ (see www.bk.tudelf.nl/urbanism/team
publications 2003), made from the ‘random walk’ example of Leopold and Wolman cited by Zonneveld (1981), arouses such
random landscapes producing river systems. The image is built up in columns
from upper left to down below. The programme prevents convergent arrows and
smallest circuits by changing lowest arrow 90o into right or
downward if they occur. So, the runoff tends towards ‘South East’ as if the landscape has a main slope.
Watersheds become visible separating catchment areas. Why do they
concentrate into separate basins and converge into main streams? Draw them and
calculate the discharge Q for some outputs taking European precipitation and
evaporation values into account. Suppose surfaces and altitudes, draw the
altitude lines and estimate velocities.
|

|
|
|
|
Zonneveld (1981)
|
|
Fig. 10
Directions of drainage in a landscape
|
Fig. 11
Surface streams caused by Fig.
10
|
|
|
|
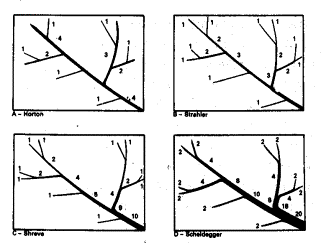
You can divide a river system in different truncation orders from source to output. Fig.
12 shows
four methods. Strahler (above right) concerns small source brooks without tributaries
above as first order. Streams collecting water form first order are second
order rivers and so on. Try to divide Fig.
11 in such
orders.
|
|
|
|
Zonneveld (1981) page 179
|
After
Zonneveld (1981) page 183
|
|
Fig. 12
Four methods to distinguish ‘orders’
|
Fig. 13
Average number and length of orders in ‘random walk rivers’
|
|
|
|
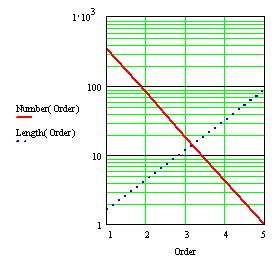
Leopold and
Wolman calculated random walk rivers have 4.4 upstream branchings of
lower Strahler order at average. In practice it varies between 2 and 5. This
‘bifurcation ratio’ plays a rôle in traffic as
well, though street patterns and artificial drainage systems in flat lands are not like a tree but like a lattice (compare Alexander (1966))[1].
If there are 20km streets per km2, you can best raise some 7km of
them into the order of neighbourhood roads and transform 2km into district
ways. So, the optimal proportion between the density of ways and sideways in a lattice seems to be approximately a factor three according to
Nes and Zijpp (2000).
Suppose a metropolis of 30km radius has 60 x 60 = 3600km2 surface with
2km/km2 district ways processing 1000 motor vehicles per hour. There should be 7200km
district ways in a grid of average 1x1km. To calculate density from the grid
mesh bordered by 4km district roads, you have to count them half
because they serve adjacent meshes as well. Many of them would be overloaded by
through traffic when you would not raise 1/3 of them into city highways (2400km in a grid of 3x3km, 0.67km/km2) with a capacity
of 3000 mv/h and less exits. However, on their turn they would be overloaded.
So, this argument produces a semi logaritmic range of orders (Fig. 14).
|
|
km nominal mesh
|
km/metropolis
|
km/km2 inclusive density
|
exclusive
|
mv/h
|
|
district roads
|
1
|
72000
|
2,00
|
1,33
|
1000
|
|
city highways
|
3
|
24000
|
0,67
|
0,47
|
3000
|
|
local highways
|
10
|
7200
|
0,20
|
0,13
|
10000
|
|
regional highways
|
30
|
2400
|
0,07
|
0,05
|
30000
|
|
national highways
|
100
|
720
|
0,02
|
0,02
|
100000
|
|
and so on
|
|
|
nearly 3.00
|
2.00
|
total
|
|
|
|
|
|
|
|
|
Fig. 14
Theoretical orders of urban traffic infrastructure
|
|
|
|
|
|
|
|
The total density of ways is 2km/km2. One third of them we have transformed into
highways of several orders. So, the density of ways includes the highways.
Exclusing highways, there are 1.33km/km2 small district ways left.
If we would like to reduce the amount of exits of local highways to save
velocity, we have to disconnect district ways into dead ends. If we like to
connect them mutually with extra parallel service roads along side the city
highway we need the inclusive density at least.
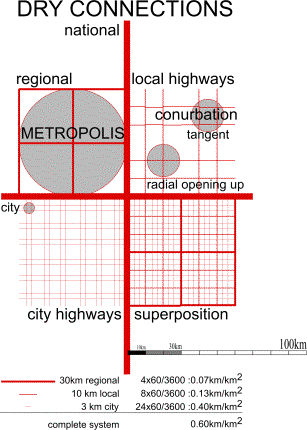
If we try to draw a system of highways in a square of 60x60km (Fig.
15) we
firstly draw a grid of 10x10km. There are 14 local highways of 60km, but 6 of
them we transform into a higher order. So, their exclusive density is
8x60/3600=0.13 indeed (Fig.
14). However,
we can not fill 10km space between local highways with 3.3 city highways. So we
choose 3 highways lowering the inclusive density from 0.67 into 0.60km/km2.
This causes a raise of exclusive district way density from 1.33 into 1.40, but
on this scale we can not draw them anyhow.
|
|
|
|
|
|
Fig. 15 Orders of dry and wet connections in
a lattice
|
|
|
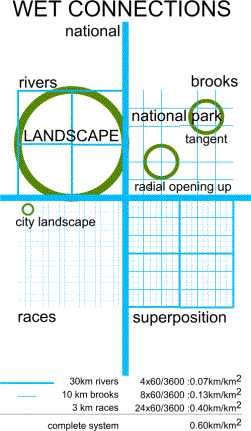
For wet connections the same applies when we call city
highways races, local highways brooks and regional highways rivers. The
bifurcation ratio of brooks before meeting a river within these regular latices
seems to be 20 (Fig. 16 left).
However, 4 boundary sections could be used as a mirror axis (dash dotted lines)
subsequently counting half. The same density could be reached with a
bifurcation ratio 2 and 5 orders (Fig.
16 right).
|

|
|
|
Feather like
|
Tree like
|
|
density
|
29 sections
|
29 sections
|
|
bifurcation ratio
|
18
|
2
|
|
number of ‘orders’
|
2
|
5
|
|
|
|
|
|
Fig. 16
Feather and tree -like connection patterns
|
|
|
In the squares of Fig.
15 tree
like connection patterns seem to require a little higher density and consequenly
higher costs when restricted to bifurcation ratio 2.
If somebody can design a lower density within this boundary conditions I will
publish it next time. On the other hand, tree like opening up every point of
the area makes many variants and diversity of locations possible when you have more space to lay out (Fig. 17).
|
|
|
|
Feather like
|
Tree like
|
|
density
|
96 sections
|
98 sections
|
|
bifurcation ratio
|
18
|
2
|
|
number of ‘orders’
|
2
|
6 or 9
|
|
|
|
|
|
Fig. 17
Feather and tree like connection patterns opening up a square
|
|
|
Perhaps opening up a 9 x 9 square in a tree-like way with
bifurcation ratio 3 could reach the same or even lower densities and consequently
lower costs. Try it. Does it result in less nodes and
longer sections? The number and characteristics of nodes and the length of
sections are important for spatial quality. Which rôle does the length of
individual sections L play instead of total length per order in Fig. 13?
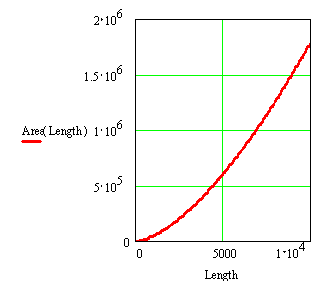
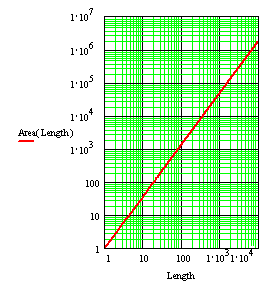
The average
length L of a random walk river section is related to its catchment area A by L(A)=A0.64. If length L is given the inverse
produces the catchment area, A(L)=L1.563 (Fig. 18 and Fig. 19).
|
|
|
|
|
|
|
Fig. 18
Catchment area related to the length of a river section
|
Fig. 19
Logaritmic representation of Fig.
18
|
|
|
|
Check Fig. 11 by counting the corresponding squares
in Fig. 10 of a
specified order and its length. Compare your measurements with Fig. 19 and Fig. 13.
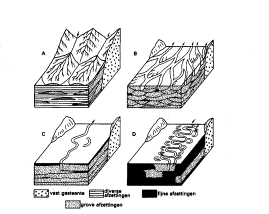
The sections of a river have different morphologies dependent
on the coarse-grainedness of transported material and the character of its
banks Fig. 20. Near
glaciers rough
material is laid down in talus. So the water takes diverse and changing
courses. Lower sections still bear rough material wearing out the outside parts
of a bend into meanders, because rough material laid
down there in the same time becomes a water barrier until heavy showers force a
break through Fig. 21 and Fig. 22.
|
|
|
|
From
Allan cited by Zonneveld (1981) page 148
|
From Hoppe cited by Zonneveld (1981) page 149
|
|
Fig. 20
Forms of deposit
|
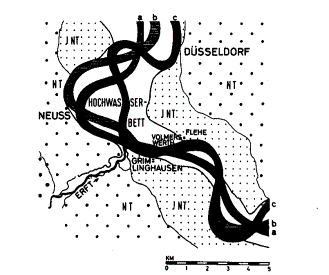
Fig. 21
Move of Rhine near Neuss from Roman times (a) via Middle Ages (b) until
recently
|
|
|
|
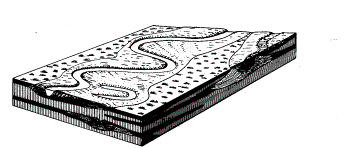
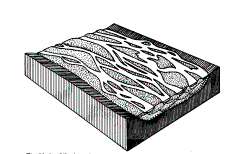
In low lands finer deposits raise the bed in calm periods forcing water to wear away easier
courses producing a twining river landscape with temporary islands.
|
|
|
|
Zonneveld (1981) page 143
|
Zonneveld (1981) page 144
|
|
Fig. 22
Meandering river with historical deposits
|
Fig. 23 Twining river
|
|
|
|
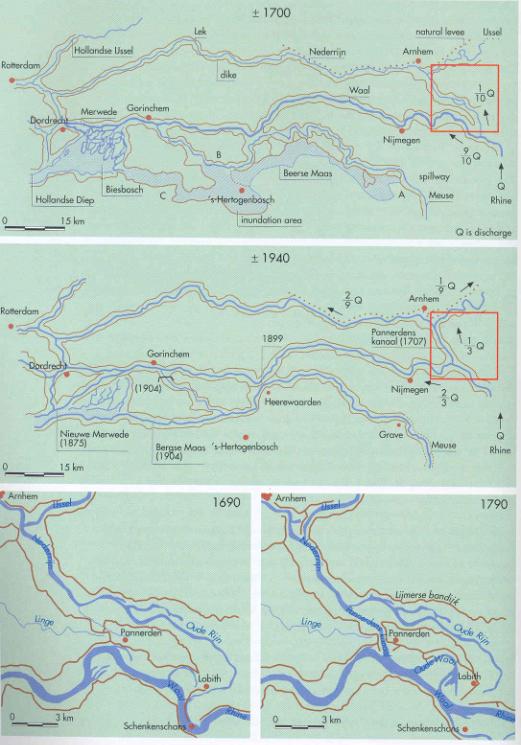
The Rhine area behind Lobith is an example of both processes (Fig. 24).
From
Lobith Rhine distributes water via Waal, Lower Rhine and IJssel in historically changing proportions.
|
|
|
Huisman, Cramer et al. (1998) page 38
|
|
Fig. 24 Historical distribution of Rhine
water from Lobith
|
|
|
|
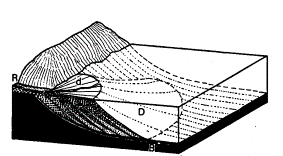
|
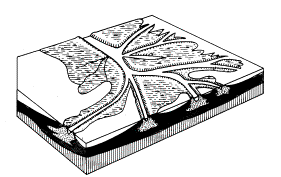
|
|
Escher 1948 cited by Zonneveld (1981) page 160
|
Zonneveld (1981)page 161
|
|
Fig. 25 Delta development with
river (R), top-sets (d) and fore-sets (D)
|
Fig. 26 Mississippi delta
|
|
|
|
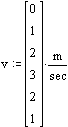
The velocity v of water can be measured on different
vertical lines h with mutual distance b in a cross section of a river (Fig. 27). You
can multiply v x b x h and summon the outcomes in cross section A to get Q = S(v*b*h).
|
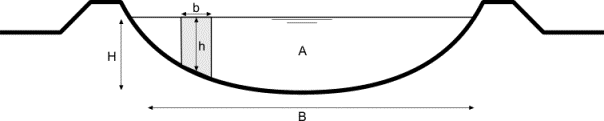
|
|
Akker and Boomgaard (2001)
|
|
Fig. 27
Profile of a river
|
|
|
For example: asked the river
drainage Q (Fig. 29),
given hi, bi and vi from profile subdivisions
(Fig. 28).
|
|
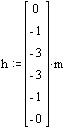
|
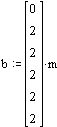
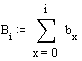
|
|
|
height
h
|
width
b
coordinate
B
|
velocity
v
|
|
|
|
Fig. 28
Data from profile
|
|
|
|
|
|
|
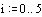
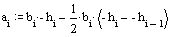
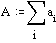
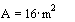
|
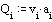
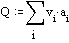
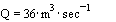
|
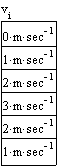
|

|

|
|
profile subdivisions
|
drainage per subdivision
|
velocity
|
surface
|
drainage
|
|
|
|
Fig. 29
Drainage (profile subdivisions and velocities)
|
|
|
H varies,
but you can measure it easily. Then you can calculate drainage Q(H) by a
formula characteristic for the profile concerned. However, periods of high
drainage Q or regular floodings in winter change profile and formula. Comparing
measurements like in paragraph 1.2.2 on different water heights you find a curve often
looking like a parabola, approached by Q = a*Hb or H=(Q/a)1/b
(Fig. 30). Parameters ‘a’ and ‘b’
characterise the profile.
|
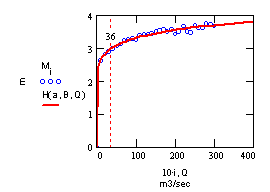
|
|
|
|
Akker and Boomgaard (2001)}.}.
|
|
Fig. 30 ‘Measurements’ Mi and
Q(a,B,H)
= a*HB or the inverse
H(a,B,Q)= (Q/a)1/B to get H on the y-axis
|
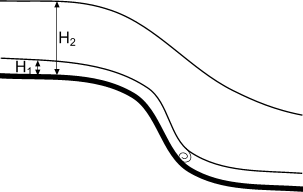
Fig. 31
Change of boundary condition downstream; a ‘drowning’
waterfall
|
|
|
|
Measurements
deviate from the formula because velocity varies. When measuremens can not be
simulated by a smooth curve, probably boundary conditions downstream change by
high water levels. Then you have to make two graphs, one until the point of
change, one for the higher values. When for example a waterfall downstream
suddenly ‘drowns’ at increasing water levels (Fig.
31) the slope of the curve can change by sudden increase
of velocity. When Q=0 at H0 ¹
0, for instance when we
want to express H0 related to a reverence surface like NAP, we need
a correction like Q = a(H-H0)b.
You can find constants a and b by the least
squares method provided by Excel using graphs. Put measurements of height and
drainage calculated according to Fig.
30 in two columns. Make a point graph and select it.
Choose ‘add trend’ in ‘graph’ from the main Excel window above,
|
|

|
|
|
|
choose power,
|
click both lowest,
|
click axis,
|
choose logarithmic,
|
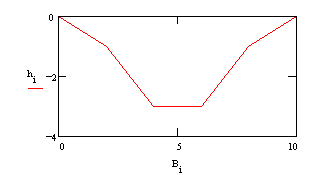
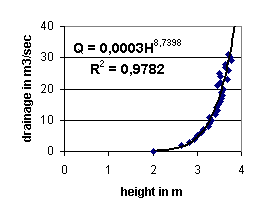
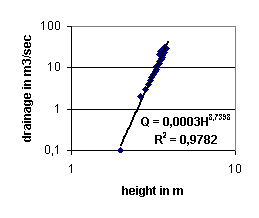
and you produce graphs like Fig. 32 and Fig. 33 with power regression line and formula.
With R2 near to 1 you have a reliable formula. In Fig. 32 we used ‘measurements’ of Fig. 30 putting
the independently variable measurements on the x-axis this time to find
a=0.0003 and b=8.7398.
|
|
|
|
|
|
|
Fig. 32 ‘Measurements’ Mi and Q(a,b,H) = a*Hb
|
Fig. 33
Logarithmic representation of Fig. 32
|
|
|
|
The
logarithmic representation log Q = log a + b log (H-H0) produces a
straight line easy to extrapolate to other heights and drainages. But be
careful, there could be jumps in velocity by downstream events. If you have
made graphs before and after the jump because measuremens could not be
simulated by a smooth curve, each interval in Fig.
33 has different slopes representing different
behaviour.
Just like
wind, water slows down by roughness of the bed. The cross length of roughness in a
wet profile P (Natte Omtrek) is calculated by summing
hypothenuses of triangles according to Pythagoras characterised by the square
root of (bi)2+(hi‑hi‑1)2
(see Fig. 27 and Fig.
35).
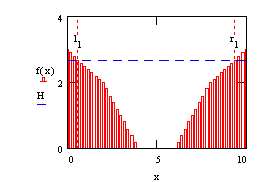
Considering
the profile as a function H=f(x) we can read the waterlevel H from accompanying left border x1=l and right border x2=r
as values from f(x) (Fig. 34). The cross length of roughness P (Natte Omtrek) and
the surface of the wet cross section A are both calculated as a function of H (Fig. 35).
|

|
Cross
length by Pythagoras:
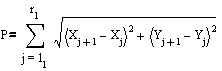
Surface wet
cross section:
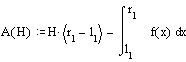 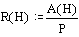
|
|
|
|
|
Fig. 34
Profile as a function
|
Fig. 35
Calculating wet cross section A and cross length of
roughness P (NatteOmtrek)
|
|
|
|
When we
divide the surface of the wet cross section A of a stream by this cross length of roughness P we get a measure
indicating what part of the flowing water is hindered by roughness called
‘hydrolic radius’ R = A/P in metres.
Method
Chézy
The average
velocity of water v = Q/A in m/sec is dependent on this radius R, the roughness
C it meets, and the slope of the river as drop of waterline s, in short
v(C,R,s).
According
to Chézy v(C,R,s)=CÖRs m/sec, and Q = Av = ACÖRs m3/sec. Calculating C
is the problem.
Method
Strickler-Manning
Instead of v=CÖRs, Strickler-Manning used 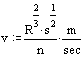 with roughness n token from Fig.
36.
with roughness n token from Fig.
36.
|
Characteristics of bottom and slopes
|
n
|
|
|
from
|
until
|
|
Concrete
|
0.010
|
0.013
|
|
Gravel
bed
|
0.020
|
0.030
|
|
Natural
streams:
|
|
|
|
Well
maintained, straight
|
0.025
|
0.030
|
|
Well
maintained, winding
|
0.035
|
0.040
|
|
Winding
with vegetation
|
0.040
|
0.050
|
|
Stones
and vegetation
|
0.050
|
0.060
|
|
River
forelands:
|
|
|
|
Meadow
|
0.035
|
|
Agriculture
|
0.040
|
|
Shrubs
|
0.050
|
|
Tight
shrubs
|
0.070
|
|
Tight forest
|
0.100
|
|
Akker and Boomgaard (2001)
|
|
Fig. 36
Indication of roughness values n according to
Strickler-Manning
|
|
|
Method
Stevens
Instead of v=CÖRs Stevens used v=cÖR considering
Chézy’s CÖs as a constant c to be
calculated from local measurements. So, Q = Av = cAÖR m3/sec and c is calcuated by c=(AÖR)/Q. When we measure H and Q several times (H1,
H2 …Hk and Q1, Q2 … Qk),
we can show different values of A(H)ÖR(H) resulting
from Fig.
35 as a straight line in a graph (Fig. 37). We can add the corresponding values of Q we found
earlier in the same graph reated to A(H)ÖR(H). When we read today on our inspection walk a new water
level H1 on the sounding rod of the profile concerned we can interpolate H1
between earlier measurements of H and read horizontally an estimated Q1 between
the earlier corresponding values of Q to read Q from graph.
|

|
|
|
|
Fig. 37 Graph used according to Stevens with ‘measurements’ of Fig. 32
|
|
|
However,
from these ‘measurements’ c appears to be not very constant, but the graph
remains a practical way to estimate Q from H.
Once you collected drainage data throughout a year you can put
them in a hydrograph (afvoer-verlooplijn).
|
|
|
|
Akker and Boomgaard (2001)}.}.
|
Akker and Boomgaard (2001)}.}.
|
|
Fig. 38 River with continuous base
discharge
|
Fig. 39 River with periodical base
discharge
|
|
|
|
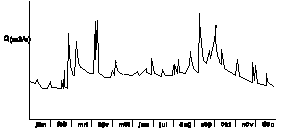
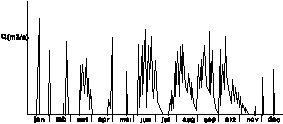
Fig. 38 shows peaks caused by periods of much precipitation and fast discharge. Fig. 39 shows the behaviour of a season bound river, periodically dry.
A
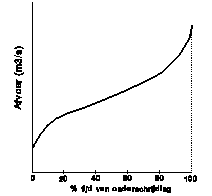
duration line (Fig. 40) shows frequency of discharges
arranged from minimum to maximum. The x‑axis shows how long river discharges are less then indicated on y-axis. The river characterised in Fig. 40 never falls dry: 0% of time it has
less discharge then indicated on the y-axis left, but the maximum discharge is
indicated right: the whole period concerned it was less then that.
A duration line is not a probability curve to estimate discharge on a
certain day. After all, river discharges on subsequent days are not
independent, but strongly related in periods like seasons. Cumulated periodes
of low discharge may indicate measures to prevent shortages in use of water.
Cumulated periods of highest (peak) discharges determine measures concerning
maintenance, prevention of risks and design. The longer the included time
series, the more useful they are. Often they are not long enough to determine a
design frequency considering the life span of civil works.
|
|
|
|
Akker and Boomgaard (2001)
|
Akker and Boomgaard (2001)
|
|
Fig. 40 Duration line
|
Fig. 41 Dataset with peak discharges
|
|
|
|
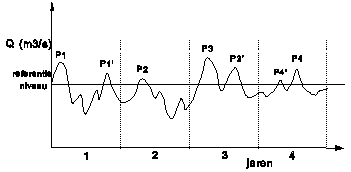
Drainage hydrology knows two data sets characterising peak discharges; annual maximum series indicating maxima only and partial duration series indicating peaks exceeding a reference level like the top of
summer dikes. Fig. 41 shows an
example of both. To make discharges statistically independent we use separate
‘river years’. P1 - P4 are an annual
maximum series of 4 river years. To make a partial duration series we
need P1', P3' and P4' as well. The lower the
reference level, the more peaks we take into consideration.
The peak discharge QT exceeded once in average T
years (‘return period’) is called ‘T-years
discharge’. Even if Q exceeds QT
once in average 10 years (T=10year) it can happen 2 years in succession. There
are large fluctuations round the average. Extreme values vary more per year
then per 10 year. For T>10 we can use extreme values of highest and lowest
values known from the past. If there are no discharge data you can ask older
people or read markings of historical high water level former inhabitants left
behind. However they are not useful if river morphology (profile) and
subsequently Q(H) has changed by nature, artificial normalisation or raising
dikes.
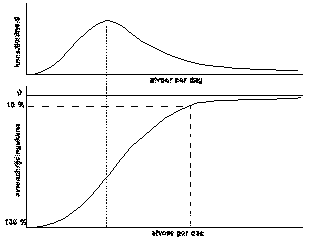
The probability of extreme values is called ‘extreme value
distribution’. It is described in
different ways, for instance like Gumbel type I for maxima, Weibull type III for minima, Log-Gumbel, Pearson or Log-Pearson type III distribution.
In 1941
Gumbel described an extreme value distribution, successful in
hydrological applications since then. The Gumbel I distribution is often used
for maximum discharges. It
supposes independent observations of extreme values X1, X2,
X3...Xn (for example successive year maxima) to be
exponentially distributed. Then P’, the cumulative probability discharge will
be equal to or smaller then earlier observations learned (Q£X) is approximated by
P’ = exp(-exp(-y)) and the reverse y = -ln(-ln(P’)). The
complementary probability P = 1 ‑ P’ discharge Q
will exceed an observation (Q>X) is 1/T and the reverse
P’ = 1 – P = 1 – 1/T. So, the ‘reduced
variable’ y = -ln(-ln(1 – 1/T)).
When we
arrange the measurements from maximum m=1 until minimum m=N (the number of
years we were measuring), return period T = (N+1)/m (‘plotting
position’) and P = m/(N+1).
To resume: 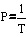 ,
, 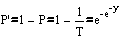 . So, we can make a graph
. So, we can make a graph 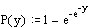 expressing
P in y.
expressing
P in y.
But we can also express T in y and
make a graph 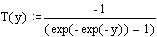 (Fig. 42).
(Fig. 42).
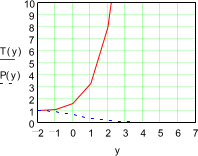
Fig. 42 shows return period once a year (T) has probability 1
(P), once in two years has probability 0.5 or 50%. Both are expressed in y. To
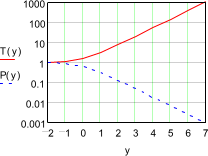
see once in 1000 years we should represent the vertical axis logaritmically (Fig. 43). The Gumbel I distribution becomes a straight line
when we stretch out T and P properly around their common value 1. Then T and P
look proportional to y. In that case we can put them on the horizontal axis
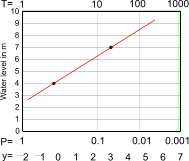
alongside y to get so called ‘Gumbel paper’ (Fig.
44). The vertical axis now is free to give water level H
a place. When we know how many times every observed water level occurred last
years, we can calculate the return time T, put the observation on Gumbel paper
and read immediately the probability P of that observation without calculating
reduced variate y. Many observa-tions give a cloud of points. We can draw a
straight line though that cloud and estimate which water level could occur in
1000 years or the reverse formulate a risk and read the desired height of dikes!
|
|
|
|
|
|
|
|
|
Fig. 42 T(y) and P(y)
|
Fig. 43
Fig. 42 Logaritmically
|
Fig. 44 Gumbel I paper
|
|
|
|
|
The
horizontal axis of Fig. 44 is ‘Gumbel distributed’. You can distribute the vertical
axis logarithmically if there is much sprawl in the cloud of observations. Some
observations could deviate too much to be reliable. They could be observed
wrongly, calculated, put on paper or even emerge by copying.
|
|
|
Akker
and Boomgaard (2001)}.}.
|
|
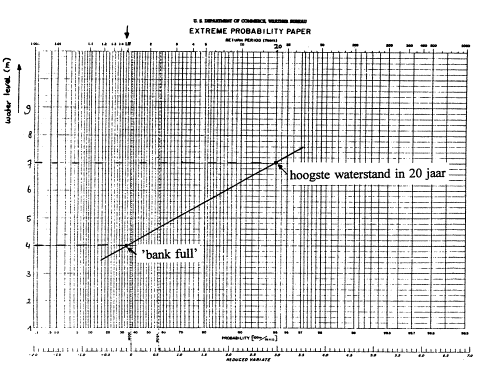
Fig. 45
Estimating an extreme value graph missing data
|
|
|
To analyse
extreme minimal discharges you can use ‘log – Gumbel III distribution’ with
plotting position T=(N+0.5)/(m-0.25) so, P=(m-0.25)/(N+0.5).
When you
have no properly measured discharge data one should rely on information about water levels in the past. For
one point in the graph you can assume ‘bank full level’ once in 1.5 year (Fig. 45). This corresponds to usual height of dikes or
raisings along the banks. A next point in the graph could be obtained from
markings by the inhabitants (for example the highest level in the past 20
years).
|
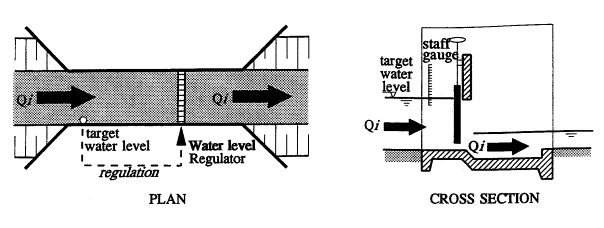
|
|
Ankum (2003) page 156
|
|
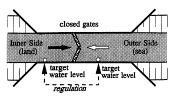
Fig.
46 Level regulator with
level as target
|
|
|
|
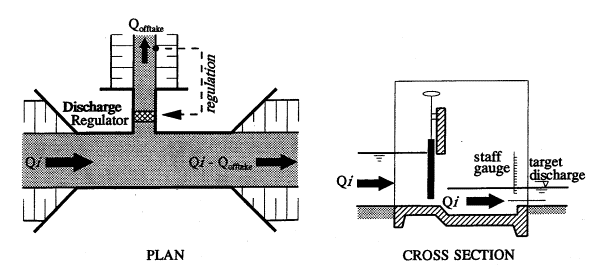
|
|
Ankum (2003) page 156
|
|
Fig. 47 Discharge regulator with
discharge as target
|
|
|
|
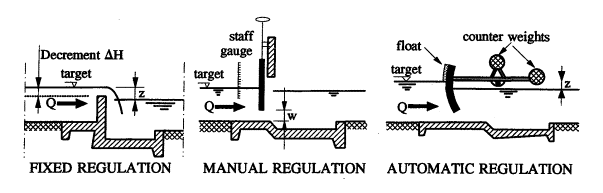
|
|
Ankum
(2003) page 167
|
|
Fig. 48 ‘Manners’ of regulation
|
|
|
The fixed regulators are called weirs (stuwen), manual or automatic
regulators are called gates (schuiven).
Akker, C. v. d. and M. E. Boomgaard (2001)
Hydrologie (Delft) DUT Faculteit Civiele Techniek en Geowetenschappen.
Alexander, C. (1966) A city is
not a tree (London) [s.n.].
Ankum, P. v. (2003) Polders en
Hoogwaterbeheer. Polders,
Drainage and Flood Control (Delft) Delft University of Technology, Fac. Civiele Techniek en Geowetenschappen,
Sectie Land- en Waterbeheer: 310.
Huisman, P., W. Cramer, et al., Eds. (1998) Water in the Netherlands
NHV-special (Delft) NHV, Netherlands Hydrological Society NUGI 672 ISBN 90-803565-2-2 URL Euro 20.
Jong, T. M. d. (2003) Riverdrainage.exe
(Zoetermeer) MESO.
Nes, R. v. and N. J. v. d. Zijpp
(2000) Scale-factor 3 for hierarchical road networks: a natural phenomenon?
(Delft) Trail Research School Delft University of Technology.
Zonneveld, J. I. S. (1981) Vormen in
het Landschap. Hoofdlijnen van de geomorfologie (Utrecht / Antwerpen)
Uitgeverij Het Spectrum ISBN
90-274-6209-7.
Snow and
ice in mountains are most important forms of water storage. They level out season fluctuations
of rivers like Rhine storing precitipation in winter, releasing it in summer
when we need it most. At lower scale water reservoirs buffer fluctuations in runoff for water supply in dry periods,
provide 23% of world electricity production and avoid downstream floodings (retention). Retention in Rhine Basin has great impact on runoff reaching Lobith (Fig. 49).
|
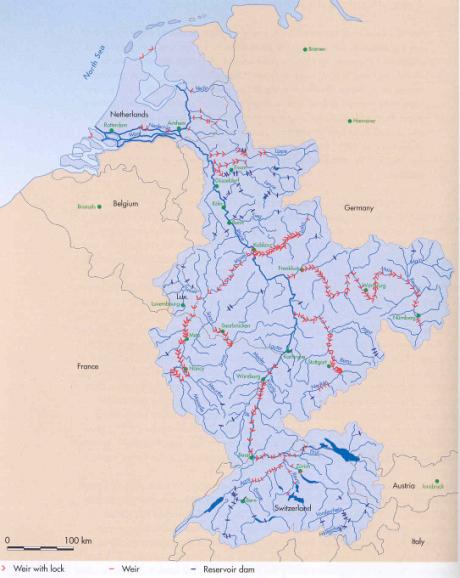
|
|
Huisman, Cramer et al. (1998)
|
|
Fig. 49
Retention in Rhine basin
|
|
|
Within the
Netherlands water is stored in shallow reservoirs. Afsluitdijk and Detawerken created large reservoirs for watermanagement in The Netherlands.
They are primarily meant for safety, but serve more purposes. For example, the
Northern Delta basin serves fresh water supply and stop the inward push of salt
water. Rhine water now can be used for water demand around IJsselmeer and makes river IJssel navigable. IJsselmeer stores remaider of precipitation in winter
to meet the demand of agriculture in summer. Summer and winter water level in
the IJsselmeer is regulated by weirs in Afsluitdijk. Outlet waterways around
polders (boezem) serve as reservoirs as well.
Polders themselves have regulated water levels (polderpeil) as negative reservoirs with inlets
and outlets on boezem waters.
A water
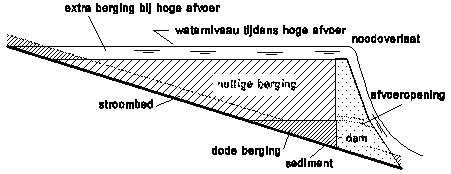
reservoir has ‘useful storage’ (nuttige berging) S and ‘dead storage’ (dode berging) below discharge opening (Fig. 50).
The height
and width of a possible emergency overflow determines maximum capacity. Surface
A is largest there, so the extra (effective) storage slowing down high upstream
discharge avoiding floodings downstream can be substantial, be it not useful
for other purposes (Fig. 50).
The storage
of original river bed (dotted line in Fig.
50) is hardly part of effective storage, but nearly
fully part of artificial useful storage.
|
|
|
Akker
and Boomgaard (2001)
|
|
Fig. 50
Terminology of reservoirs (example with barrage).
|
|
|
When
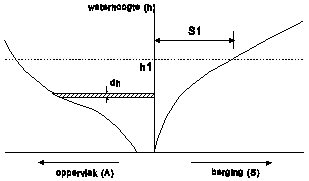
surface A varies with height h storage S is not proportional to height. By
measuring surfaces on different heights A(h) you get an area-elevation curve (Fig. 51). The storage on any height S(h) (capacity curve) is
the sum of these layers or integral 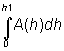 .
.
|
|
|
Akker and Boomgaard (2001)
|
|
Fig. 51 A(h) and S(h)
|
|
|
Fig. 51 left below shows dead storage,
important to avoid fish mortality, ecological damage and stench. It
makes sedimentation possible without loss of useful storage.
The time
you can deliver a desired capacity (yield) can vary from days (distribution
reservoir with small storage) to years (large storage reservoir), dependent on instream. The
maximum yield during a normative dry period is called ‘save yield’. There is
always a possibility of dryer periods then normative. So, determining save
yield requires a probability approach.
The maximum
water delivery equals instream plus accepted decrease of useful storage minus
often substantial evaporation and leakage. Increasing fluctuation of instream
increases the necessity of useful storage; constant instream would make storage
superfluous.
The choice
of reservoir capacity depends on both desired delivery capacity and accepted
risk of incidental non delivery. Irrigation systems can stand larger risks (for example 20% of time delivery below design capacity) then much
more sensible urban water supply systems
You can simulate the working of a reservoir (‘operation study’) based on runoff data of daily
(small reservoirs), monthly (normal) or yearly (very large reservoirs)
intervals in the existing river. Do not restrict to ‘critical periods’ of low runoff. Long term runoff
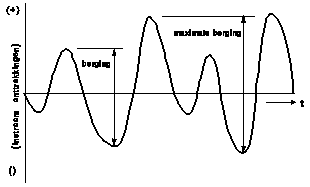
series give a better reliability comparison of different capacities. Fig. 55 shows the cumulative sum of input
minus output (inclusive evaporation and leakage). The graph is divided in
intervals running from a peak to the next higher peak to start with the first
peak. For every interval the difference between the first peak and its lowest
level determines the required storage capacity of that interval. The highest
value obtained this way is the required reservoir capacity.
|
|
|
Akker
and Boomgaard (2001)
|
|
Fig.
52 Determining necessary storage capacity
|
|
|
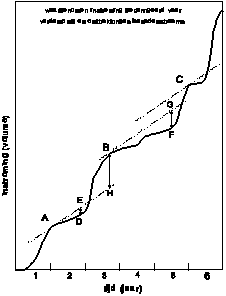
In 1883
Rippl introduced the ‘Rippl diagram’ (Fig.
53) summing input minus evaporation and leakage into an
increasing line. The slope is proportional to the net input. Constant water
demand is represented by straight lines. You can move them until they touch the
ultimate points of the summing curve (A, B and C; in these points the
increasing useful storage changes into decrease). Exactly where the straight
line behind such a point crosses the curved one the reservoire is full again.
The maximum vertical distance between demand line and summing curve FG is the
required capacity. The vertical distance between two successive demand lines
(BH) is discharged by emergency overfow.
|
|
|
|
|
Akker
and Boomgaard (2001)
|
|
Fig. 53 Rippl diagram
|
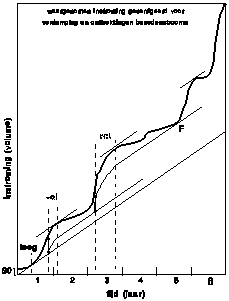
Fig. 54
Exploitation
of a reservoir
|
|
|
|
If demand
is not constant it becomes a curved line, but the analysis remains the same. In
that case you can move the demand line vertically only to keep time of supply
and demand the same.
A summing
curve can be used to determine water delivery at given capacity as well. Then
demand lines should be moved to a vertical distance not larger then that given
capacity and crossing the summing curve somewhere later otherwise the reservoir
will never be filed up again. The slope of the demand lines represents maximum
delivery in the period concerned.
Fig. 54 shows the exploitation of a
reservoir in a given period starting with a storage S0 in the
beginning of the first year. After some months the content decreases up to 0,
but a large input fills the reservoir completely. The arrow has the same length
as FG from Fig.
53. From this moment until delivery is
larger than input water is discharged by emergency overflow. The vertical distance between
input and tota output does not change as long as the reservoir is full. Then a
period of decrease and increase follow until the reservoir is full again. Fig. 54 shows an empty reservoir in F because capacity was
calculated by the difference of supply and demand in this point.
To keep
summing curves manageable for ever increasing large amounts of water in periods
long enough to be reliable you can subtract an average discharge. Then the
reduced summing curve fluctuates around a horizontal line rising when input is
larger then average and descending when smaller.
Before deciding for a
capacity often more detailed studies about leakage as a function of water level
and evaporation as a function of surface are made related to one or more
periods with available data. Computer models can test the usefulness of
different strategies.
A reservoir can be used for more purposes at once, but used only to avoid
floodings downstream it is called a retention reservoir. To avoid floodings you have to
take longer periods of high input then incidental peaks into account. A
retention reservoir should be as empty as possible if you expect a high water
wave. In that case you open discharge openings as soon as possible before the
expected wave comes to increase storage capacity and to postpone emergency
overflow as long as possible. Risk = probability x consequence. To estimate the
risk a reservoir can not store runoff long enough you need to know probability
distributions of daily discharge (Fig.
55 above), regular output as a function of water level
in the reservoir, and other factors like consequences of unverifiable overflow.
|
Akker
and Boomgaard (2001)
|
|
Fig. 55 Probability distribution daily discharge and exceeding probability
|
|
|
Fig. 55 below shows the accumulated
probability distribution. The dotted line shows 10% probability a discharge on
vertical axis is exceeded. In practice much smaller probabilities are used, for
instance 0.1%. Simply stated it corresponds 0.1 x 365/100 = 0.365 day per year » once per 3 year if you take a day as unbroken period.
Construction of reservoirs has environmental impacts. It requires space at the expense of
original functions. Losses can not only be expressed in money. Landscape and
nature have emotional or intrisic value as well. Weighting advantages and
disadvantages is difficult, the more so because the intended function can not
be guaranteed for 100% and side effects can not be predicted. For example the
Assuan dam changed Nile delta substantially. Nile transports less slugdge. So, measurements
against erosion of coast became necessary. Irrigation alongside Nile increased,
but bilharzia disease dispersed in a large area as well.
The storage of water in the lower parts of The
Netherlands will require heavy surface claims. The 4th National Plan
of watermanagement policy V&W V&W (1998) (stressing environment), and its last
successor ‘Anders omgaan met water’ V&W (2000) (stressing security) mark a change from accent on a
clean to a secure environment, just as the 4th National Plan of
environmental policy VROM (2001) compared with its
predecessors[2]. Several
floodings in The Netherlands and elsewhere in Europe has focused the attention
on global warming and watermanagement.
The future problems and proposed solutions are summarized in the figures below[3].
Storage is a central item reducing risks of lowlands.
|
|
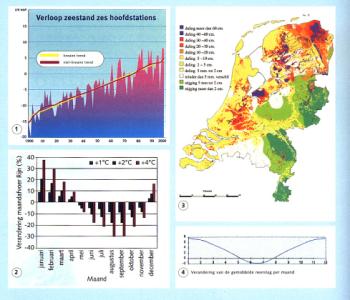
In Fig. 56 above most left, global warming,
in the figure right the ground descend of the western and northern part of the
Netherlands are shown.
Bottom most left, different scenarios of temperature
increase,
right of it, the expected increase of precipitation in winter and decilne in summer are shown.

|
|
V&W (2000)
|
|
|
Fig. 56
Expected problems
|
Fig.
57 Strategies: 1 care, 2
store, 3 drain
|
|
|
|
Water
management is recognisable everywhere in the lowlands.
|

|
|
Das (1993)
|
|
Fig. 58 Lowlands with spots of
recognisable water management
|
|
|
Civil
engineering offices are busy with many water management tasks (Fig. 59).
|

|
|

|

|
|
01 Water structuring
|
02 Saving water
|
03 Water supply and purificatien
|
04 Waste water management
|
|

|

|
|
|
|
05 Urban hydrology
|
06 Sewerage
|
07 Re-use of water
|
08 High tide management
|
|

|

|

|
|
|
09 Water management
|
10 Biological management
|
11 Wetlands
|
12 Water quality management
|
|

|

|

|
|
|
13 Bottom clearance
|
14 Law and organisation
|
15 Groundwater management
|
16 Natural purification
|
|
Das (1993)
|
|
Fig. 59 Water managemant tasks in
lowlands
|
|
|
|
|
|
The
Netherlands are covered by maps showing
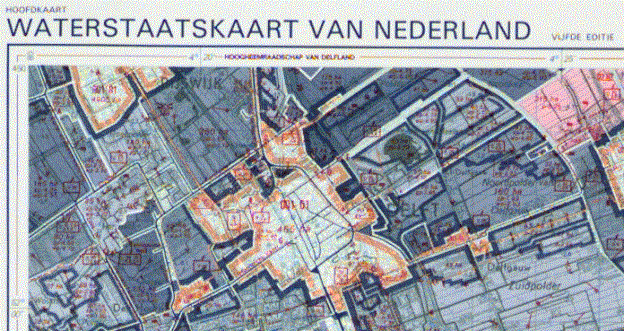
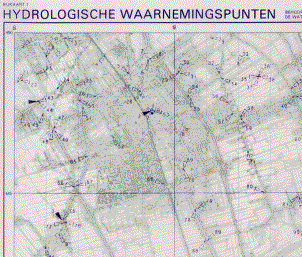
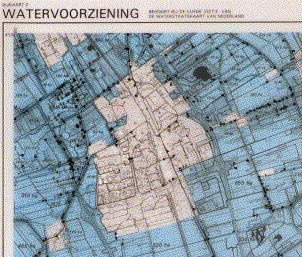
the compartments governing their own watermanagement (Waterschappen), and their drainage areas (Fig. 60 above). Overlays show hydrological
measure points (Fig. 60 below left) and the supply of surface water (Fig. 60 below right).
|
|
|
Rijkswaterstaat (1985)
|
|
|
|
|
Rijkswaterstaat
(1984)
|
Rijkswaterstaat
(1984)
|
|
Fig. 60 Hydrological maps of Delft and
environment.
|
|
|
On the first map you can find the names of compartments,
pumping-stations, windmills, sluices, locks, dams, culverts, water pipes.
Akker, C. v.
d. and M. E. Boomgaard (2001) Hydrologie (Delft) DUT Faculteit Civiele
Techniek en Geowetenschappen.
Das, R.
(1993) Integraal waterbeheer werken aan water (Deventer) Witteveen + Bosch.
Huisman, P.,
W. Cramer, et al., Eds. (1998)
Water in the Netherlands NHV-special (Delft) NHV, Netherlands
Hydrological Society NUGI 672 ISBN
90-803565-2-2 URL Euro 20.
Rijkswaterstaat
(1984) Hydrologische waarnemingspunten Rotterdam - Oost 37 (Delft) Meetkundige
Dienst.
Rijkswaterstaat
(1984) Watervoorziening Rotterdam - Oost 37 (Delft) Meetkundige Dienst.
Rijkswaterstaat
(1985) Waterstaatskaart van Nederland Rotterdam - Oost 37 (Delft) Meetkundige
Dienst.
V&W, M.
v. (1998) Waterkader Vierde Nota waterhuishouding. Verkorte versie (Den
Haag) Ministerie V&W.
V&W, M.
v. (2000) Anders omgaan met water. Waterbeleid in de 21e eeuw. (Den
Haag) Ministerie van Verkeer en Waterstaat.
VROM, M. v.
(2001) Een Wereld en een Wil. Werken aan duurzaamheid.Nationaal
Milieubeleidsplan 4 - samenvatting (Den Haag) Ministerie van
Volkshuisvesting, Ruimtelijke Ordening en Milieubeheer ISBN vrom 010294/h/09-01.
Urban areas
need dry crawl spaces to keep unhealthy moist out of the buildings but they
need wet foundations as long as they are made of wood. Let us say
groundwaterlevel (recognisable from open water in the area) should stay at
least 1m below ground level (Fig.
61, Fig.
62).
|

|

|
|
(Paul van Eijk)
|
|
|
Fig. 61
Flooding of a canal in Delft
|
Fig. 62 Deep canal in Utrecht
|
|
|
|
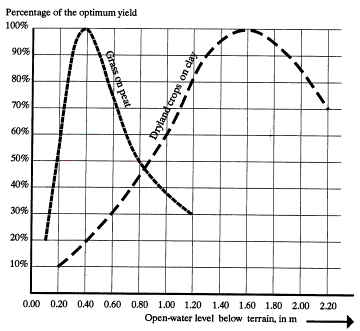
Grasslands may be wetter, dryland crops should be dryer then 1m below terrain (Fig. 63).
|
|
|
Ankum
(2003) page 53
|
|
Fig. 63 Crop yields for different open water levels
|
|
|
Lowlands
with drainage and flood control problems cover nearly 1mln km2 all
over the world (Fig. 64) and nearly half world population lives there because
of water shortage elsewhere (Rijkswaterstaat (1998;
Rijkswaterstaat (1998; Rijkswaterstaat (1998)).
|
x1000 km2
|
1 crop
|
2 crops
|
3 crops
|
Total
|
|
North
America
|
170
|
210
|
30
|
400
|
|
Centra
America
|
|
20
|
190
|
210
|
|
South
America
|
60
|
290
|
1210
|
1560
|
|
Europe
|
830
|
50
|
|
880
|
|
Africa
|
|
300
|
1620
|
1920
|
|
South Asia
|
10
|
460
|
580
|
1050
|
|
North and
Central Asia
|
1650
|
520
|
20
|
2190
|
|
South-East
Africa
|
|
|
530
|
530
|
|
Australia
|
|
310
|
120
|
430
|
|
|
|
|
|
9170
|
|
Ankum (2003), page 2
|
|
Fig. 64 Area of lowlands with drainage
and flood control problems
|
|
|
Inhabitated
or agricultural areas below high tide river or sea level (polders) have to be
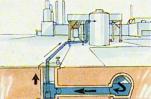
drained by one way sluices using sea tides or pumping stations (Fig. 65, Fig.
67), surrounded by belt canals (boezemkanalen), protected by dikes, made
accessible for shipping traffic by locks, internally drained by races (tochten), main ditches (weteringen), ditches (sloten), trenches (greppels), and pipe drains.
|
|
|
Ankum
(2003), page 78
|
|
Fig. 65 Pumping stations in The
Netherlands
|
|
|
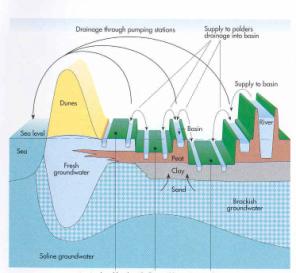
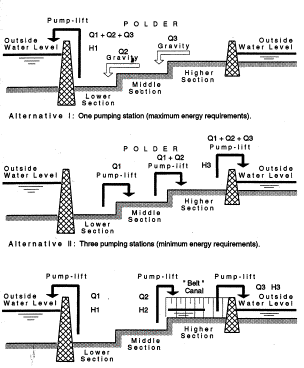
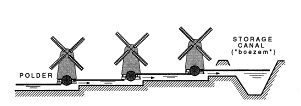
Pumping in polders with different altitudes can be done at
once from the deepest part using gravity or in compartiments separated by dikes
and weirs saving potential energy (Fig. 67).
|


|
|
|
|
|
|
Huisman, Cramer et al.
(1998) page 36 ; Veer (?)
|
Ankum (2003), page 76 and
55
|
|
Fig. 66 Lowland system
|
Fig. 67 Drainage by one to three pumping
stations, in earlier times by a ‘row of windmills’ (‘molengang’)
|
|
|
|
Water is
drained by one way sluices (Fig.
68) at low tide or pumped up via belts (boezems) into the river or the sea.
|
|
|
|
|
Ankum
(2003), page 68 and 38
|
|
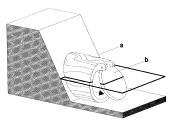
Fig. 68 The oldest one way sluice found
in The Netherlands and its modern principle
|
|
|
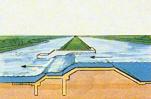
Fig. 69 shows the belt system of Delfland.
|
|
|
Ankum
(2003) page 62
|
|
Fig. 69 The belt (‘boezem’) system of
Delfland
|
|
|
One way
sluices lose purpose when average sea and river level raise and ground
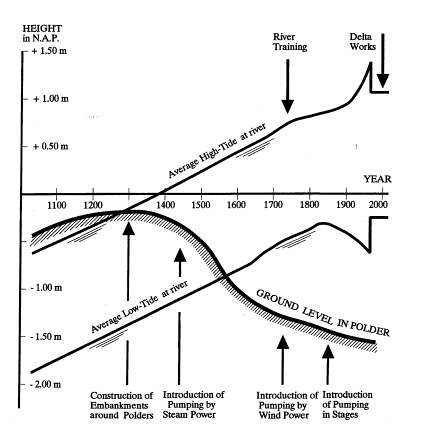
level drops mainly because of the subsidence of peat polders (Fig. 70). Drying peat oxidates and disappears.
|
|
|
Ankum
(2003) page 71
|
|
Fig. 70 Rising outside water levels and
dropping ground levels
|
|
|
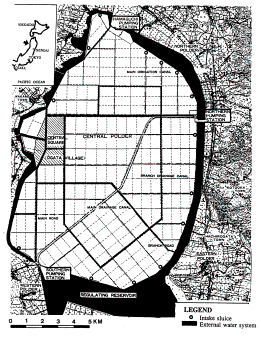
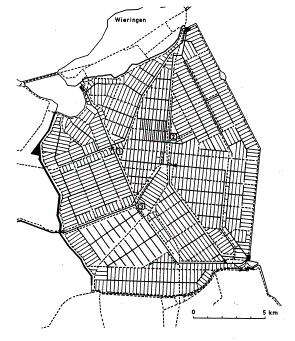
Polders are optimally drained by a regular pattern of ditches (Fig. 71, Fig.
72).
|
|
|
|
Ankum
(2003) page 42 and 82
|
|
Fig. 71
Hachiro Gata
Polder in Japan
|
Fig. 72 Wieringermeer polder (Kley 1969)
|
|
|
|
The
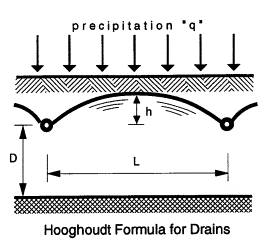
necessary distance L between smallest ditches or drain pipes is determined by precitipation q [m/24h], the maximally accepted
height h [m] of ground water above drainage basis between drains and by soil
characteristics.
|

|
|
|
Ankum
(2003) page 36
|
|
Fig. 73 Variables
determining distance L between trenches
|
Fig. 74 Variables
determining distance L between drain pipes
|
|
|
|
Soil is characterised by its permeability k [m/24h].
|
Type of soil
|
Permeability k in m/24h
|
|
gravel
|
>1000
|
|
coarse sand with gravel
|
100
|
1000
|
|
corse sand, frictured clay in new polders
|
10
|
100
|
|
middle fine sand
|
1
|
10
|
|
very fine sand
|
0.2
|
1
|
|
sandy clay
|
0.1
|
|
peat, heavy clay
|
0.01
|
|
un-ripened clay
|
0.00001
|
|
|
|
|
Fig. 75 Typical
permeability of soil types
|
|
|
|
A simple
formula is L=2Ö(2Kh/q).
If we accept h=0.4m and several times per year precipitation is 0.008m/24h,
supposing k=25m/24h the distance L between ditches is 100m. However, the
permeability differs per soil layer. To calculate such differences more precise
we need the Hooghoudt formula desribed by Ankum (2003) page 35.
However,
plot ditches are used as property boundaries and they determine agricultural
and urban practice. Any use has its own requirements for plot division. Systems
of plot division have to take dry infrastructure into account, combining different
network systems.
|
|
|
Ankum
(2003) page 59
|
|
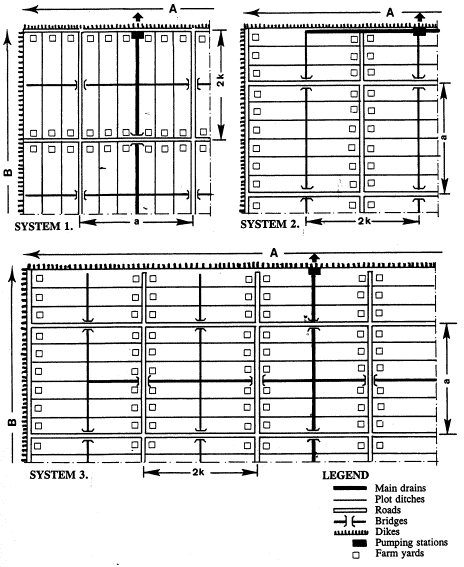
Fig. 76 Alternative systems of plot division in polders
|
|
|
We will elaborate that in 1.5
There are
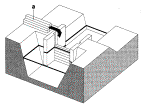
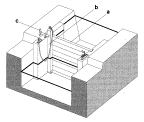
many types of water level regulators elaborated by Arends (1994) (Fig. 77, Fig.
78, Fig. 79).
|
|
|
|
|
|
Schotbalkstuw
|
Schotbalkstuw met
wegklapbare aanslagstijl
|
Naaldstuw
|
Automatische klepstuw
|
|
|
|
|
|
|
Dakstuw
|
Dubbele
Stoneyschuif
|
Wielschuif
rechtstreeks ondersteund door jukken
|
Wielschuif via
losse stijlen ondersteund door jukken
|
|
Arends
(1994)
|
|
|
|
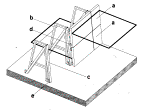
Fig. 77
Types of weirs
|
|
|
|
|
|
|
|
|
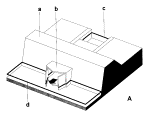
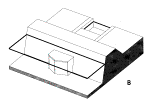
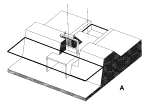
Uitwateringssluis
open
|
Uitwateringssluis
closed
|
Inlaatsluis open
|
Inlaatsluis closed
|
|
|
|
|
|
|
Irrigatiesluis
|
Ontlastsluis closed
|
Ontlastsluis flooded
|
Ontlastsluis open
|
|
|
|
|
|
|
Keersluis
|
Spuisluis
|
Inundatiesluis (military)
|
Damsluis
(military)
|
|
Arends (1994)
|
|
|
|
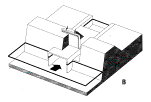
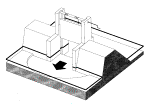
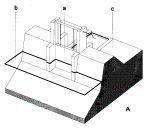
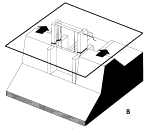
Fig. 78
Types of sluices
|
|
|
To allow
accessibility of shipping traffic you need locks at every transition of water level.
|
|
|
|
|
Schutsluis
|
|
|
|
|
|
Dubbelkerende
schutsluis
|
|
|
|
|
|
Gekoppelde sluis
|
Sluis met verbrede
kolk
|
Bajonetsluis
|
|
|
|
|
|
Tweelingsluis
|
Schachtsluis
|
Driewegsluis
|
|
Arends,
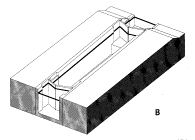
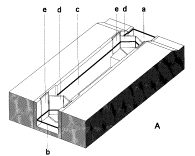
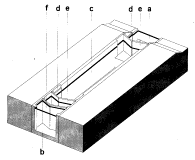
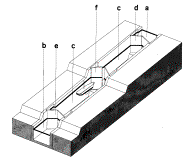
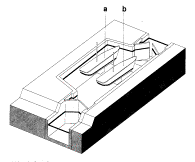
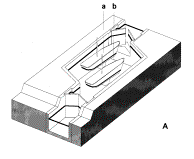
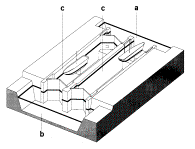
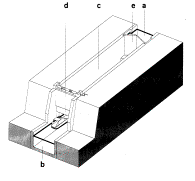
G.J.(1994) Sluizen en stuwen (Delft) DUP Rijksdienst voor de Monumentenzorg
|
|
|
|
Fig. 79
Types of locks
|
|
|
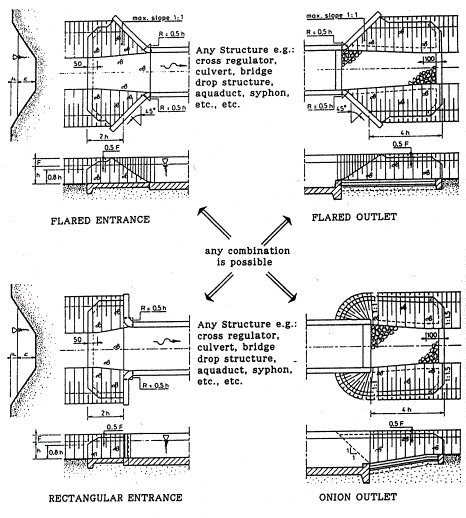
Any regulator, culvert, sluice, lock or bridge requires a structure with entrance and exit of water needing space
themselves (Fig. 80).
|
|
|
Ankum
(2003) page 164
|
|
|
|
Fig. 80 Samples of the ‘entrance’ and
‘exit’ of a structure
|
|
|
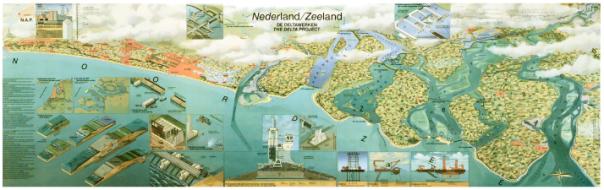
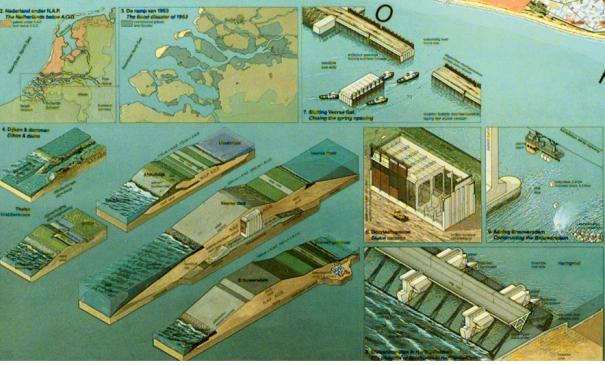
Floodings in 1953 caused the Delta Project, the greatest coastal protection
project of The Netherlands, (Fig.
81) showing many modern constructions.
|
|
|
|
|
Hettema
and Hormeijer (1986)
|
|
Fig. 81
Delta project
|
|
|
Ankum, P. v.
(2003) Polders en Hoogwaterbeheer. Polders, Drainage and Flood Control (Delft) Delft University of
Technology, Fac. Civiele Techniek en Geowetenschappen, Sectie Land- en
Waterbeheer: 310.
Arends, G. J.
(1994) Sluizen en stuwen. De ontwikkeling van de sluis- en stuwbouw in
Nederland tot 1940 (Delft) Delftse Universitaire Pers / Rijksdienst voor de
Monumentenzorg ISBN 90-6275-700-6.
Hettema, T.
and P. Hormeijer (1986) Nederland/Zeeland (Amsterdam) Euro-Book Productions.
Huisman, P.,
W. Cramer, et al., Eds. (1998)
Water in the Netherlands NHV-special (Delft) NHV, Netherlands
Hydrological Society NUGI 672 ISBN
90-803565-2-2 URL Euro 20.
Rijkswaterstaat (1998) "Delta's
of the World. 200th anniversary of Rijkswaterstaat" Land + Water 11
Rijkswaterstaat (1998) Summary
and Conclusions (SDD '98) International conference at the occasion of 200
year Directorate-General for Public Works and Water Management, Conference
(Location) Delft University Press.
Rijkswaterstaat (1998) Sustainable
Development of Deltas (SDD '98) Inetrnational conference at the occasion of
200 year Directorate-General for Public Works and Water Management, Conference
(Location) Delft University Press.
Veer, K. v.
d. (?) Nederland/Waterland (Amsterdam) Eurobook productions.
Although
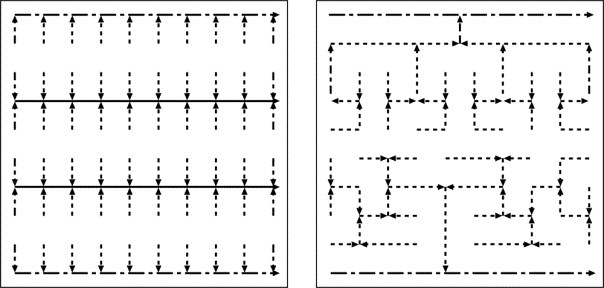
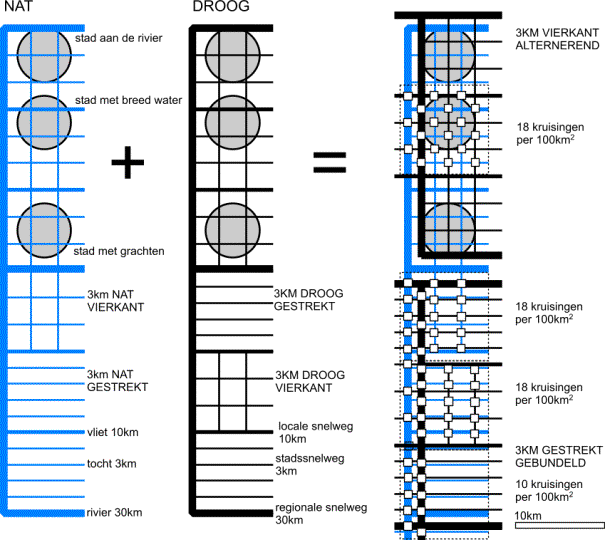
natural drainage follows a dendritic pattern, this is crossed by a predominantly
orthogonal system of dry channels with similar hierarchical orders. For various reasons, there is a
tendency for the artificial drainage of flat areas to be rectangular in shape. Because of this, the following considerations apply to
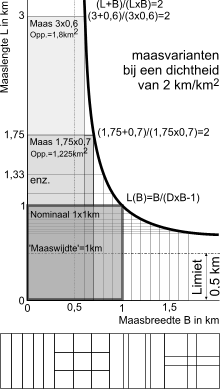
both wet and dry networks. Fig.
82 shows a sequence of relationships between mesh lengthand width.in rectangular meshes with a net
density of 2 km per km2.
|
|
|
|
|
Hildebrandt
and Tromba (1989)
|
|
Fig. 82
Length (L) and
width (W) of the mesh for a given net density of (D=2)
|
Fig. 83 The
formation of right angles
|
|
|
|
Length and
width of squares are 2/d.The same density also occurs in a pattern of
roads that go infinitely in one direction every 0.5 km. Thus, when the length
and width of the mesh 1/d = 0.5 km, the ratio between length and width is at
its limit. In that case, where the net density is 2 km per km2 there can be no
‘crossroads’ any
more.
This
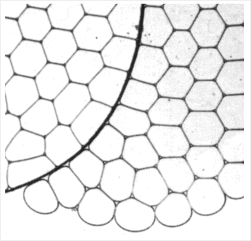
consideration only applies to an orthogonal system. The most efficient
enclosure is made by encircling the enclosed area with a minimum length of
road. As is well known, this is the circle, but in a continuous network, this
is approximated by a hexagonal system,. This minimal ratio between periphery
and area is demonstrated three dimensionally by very many natural phenomena
where preference is given to a minimal ratio between area and content.
A good example is a cluster of soap bubbles. A cluster of soap bubbles forced into a thin
layer produces a two-dimensional variant. The bubbles arrange themselves in
polygons with an average of six angles. If one then pulls a thread through
them, the nearest bubbles will re-arrange themselves again into an orthogonal
pattern (Fig. 52). Urban developments from radial to tangential can also be
interpreted against this background. The interlocal connections pull the radial
system straight, as it were. The additional demand for straight connections
over a distance longer than that between two side roads (called a ‘stretch’ here) introduces
rectangularity. Every deflection from the orthogonal system is then less
efficient.
This can be
clarified by engaging in a thought experiment: Imagine a rectangular framework
with hinged corners that is completely filled with marbles. If one re-shapes
this framework into an ever narrower parallelogram, then there will be space
for fewer and fewer marbles, so, in every case, the rectangular shape proves to
be optimal, in this respect.
|
|
|
|
|
Fig. 84 Styling wet connections, where the density
is translated into nominal orthogonal mesh widths.
|
|
|
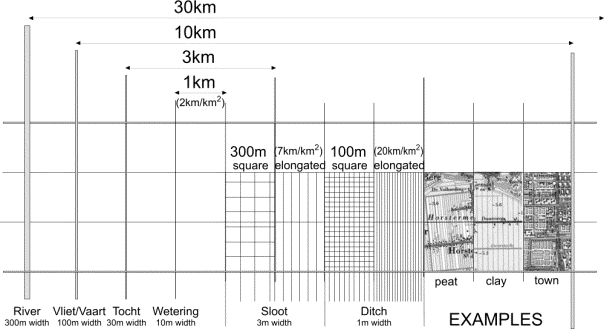
The density
in the pattern of drainage ditches shown on a topographical map, gives one a global picture of the
soil types of that area. There are no ditches on sandy soils, whereas a wide mesh of ditches is a characteristic of clay soils and a fine mesh, of peaty soils (for examples, see Fig.
84). For convenience, the breadth of each watercourse is
fixed here at 1% of the equilateral mesh width.
This
difference is caused mainly by different vertical percolation of water k expressed in metres per twenty-four hours. That percolation is
slow in peat and clay (for example 20m/24h at average in the low West Holocene
of the Netherlands) and fast in rough sand (350m/24h in the higher East
Pleistocene of the Netherlands or sand raised town areas). Density d of lowest order ditches or brooks depends further from once a year
maximum precitipation N in metres per twenty-four hours (for example 0.007 m/24h or
0.008m/24h) and the difference between ditch level and ground water level in
the area between ditches or brooks h (for example 0.4m). Then, d(k,N,h)=250Ö(2N/kh) km/km2 (Fig. 85)
|
|
Peat
|
Clay
|
Sand
|
|
Percolation
k [m/24h]
|
6
|
23
|
280
|
|
Precipitation
N [m/24h]
|
0.007
|
0.007
|
0.008
|
|
Waterlevel
between ditches h [m]
|
0.4
|
0.4
|
0.4
|
|
Network
density d [km/km2]
|
20
|
10
|
3
|
|
|
|
Fig. 85
Network density
caused mainly by soil characteristic of percolation
|
|
|
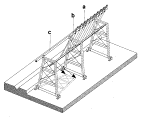
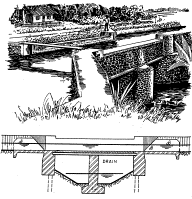
Mutually
crossings of waterways seldom separate their courses vertically (Fig. 86) as motorways do (Fig.
87).
|
|

|
|
Ankum (2003) page 160
|
Standaard and Elmar (?)
|
|
Fig. 86
Crossing of
separated waterways
|
Fig. 87
Crossings of
highways
|
|
|
|
More
often their water levels are separated by locks (Fig. 79) or become inaccessible for ships by weirs or
siphons.
However,
crossings between ways and waterways have to be separated vertically in full
function anyhow. And they often occur.
|
|
|
|
|
|
|
|
|
|
|
Fig.
88 Rivers, canals and brooks
|
Fig. 89 Superposition races
|
Fig.
90 Interference with highways
|
Fig.
91 Interference with highways and railways
|
|
|
|
|
|
When one
lays different networks over each other, an interference occurs that
defines the number of crossings, and, because of this, the level of
investment in civil engineering constructions (Fig. 92).
|
|
|
|
|
Fig. 92 Interference between wet and dry networks.
|
|
|
The
position of urban areas with respect to orders of magnitude of water and roads
dictates their character to a large extent. The elongation (stretching) of
networks reduces the need for engineering constructions when their meshes
lie in the same direction. If one bundles them together, this also helps to
prevent fragmentation. The aim of the ‘dual network
strategy’, on the other hand, is to position
water, as a ‘green network’, as far way as possible from the
roads (in an alternating manner). However, this has the effect of increasing fragmentation.
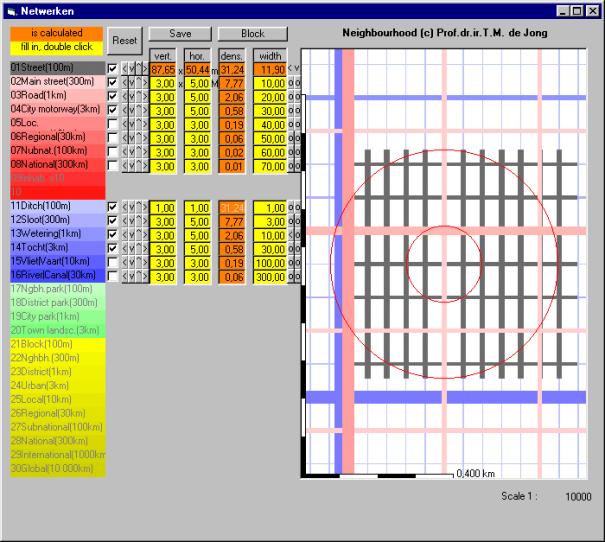
Fig. 93 shows how different dry and
wet networks in different orders cause crossings of different kinds.
|
|
|
|
Jong (2001)
|
|
Fig. 93 Interference of dry and wet
networks in different orders causing crossings of different kinds
|
|
|
|
Trenches
and ditches become drains or underneath roads culverts in the urban area, but
main ditches (3m wide), races (10m) and canals (30m) have to be crossed by bridges. From 9 different kinds of crossing
Fig. 93 counts 6 types (Fig.
94).
|
|
neigbourhood streets (10m wide)
|
district roads
(20m wide)
|
city highways
(30m wide)
|
|
main
ditches (10m wide)
|
2
|
|
1
|
|
races
(30m wide)
|
3
|
1
|
|
|
canals
(100m wide)
|
2
|
|
1
|
|
|
|
|
|
|
Fig. 94 Five types of crossings supposed
in Fig. 93
|
|
|
|
|
|
Especially
when the canal is a belt canal with a higher level then the other waterways many complications
arise. Extra space is needed for weirs, dikes and sluices, perhaps even locks
and many slopes not useful for building. The slope the city highway gets from
crossing the high belt canal could force to make a tunnel instead of a bridge.
Anyhow, several expensive bridges will be necessary and some of them will be
dropped from the budget, causing traffic dilemmas elsewhere.
|

|
|
|
|
Fig. 95 Neighbourhood street crossing
canal and railroad in Utrecht
|
|
|
The
slope behind the bridge in Fig.
95 is not steep enough to get a tunnel under the railway
high enough for public transport (2.60m is too low).
|
based on pressure
|
or
|
draw
|
|

|

|
|
|
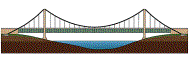
arch bridge (boogbrug)
approach ramp(aanbrug)
thrust (horizontale druk)
deck (rijvloer)
trussed arch with upper and lower chord (vakwerkboog boog met boven- en onderrrand)
abutment (landhoofd)
|
beam bridge (balk- of liggerbrug)
abutment (landhoofd)
overpass, underpass (bovenkruising, onderdoorgang)
deck (brugdek)
continuous beam (doorgaande ligger)
pier (pijler)
parapet (leuning)
|
suspension
bridge (hangbrug)
anchorage
block (ankerblok)
suspension cable (hangkabel)
suspender (hanger)
deck (rijvloer)
center span (middenoverspanning)
tower (toren)
side span (zijoverspanning)
abutment (landhoofd)
|
|
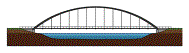
|

|

|
|
trough arch bridge (boogbrug met laaggelegen rijvloer)
|
multiple span beam bridge (balk- of liggerbrug met meer overspanningen)
|
fan cable stayed bridge (waaiertuibrug)
cable stay anchorage (tuiverankering)
|
|

|

|

|
|
half-through arch bridge (boogbrug met
tussengelegen rijvloer)
|
viaduct
|
harp cable stayed bridge (harptuibrug)
|
|

|

|
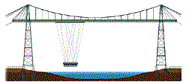
|
|
deck arch bridge (boogbrug met hooggelegen rijvloer)
|
cantilever bridge (kraagliggerbrug, cantileverbrug)
suspended span (zwevend brugdeel)
cantilever span (uitkragende zijoverspanning)
|
transporter bridge (zweefbrug)
trolley (wagen)
platform (platform)
|
|

|
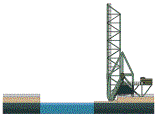
|
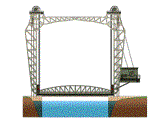
|
|
fixed two-hinged three-hinged arch (ingeklemde, tweescharnier~,
driescharnierboog)
|
single-leaf bascule bridge (enkele basculebrug)
counterweight (contragewicht)
|
lift bridge (hefbrug)
guiding tower (heftoren)
lift span (val)
|
|

|

|

|
|
portal bridge (schoorbrug)
portal frame (portaal)
pier (pijler)
|
double-leaf bascule bridge (dubbele
basculebrug)
|
floating bridge (pontonbrug)
manrope (mantouw)
pontoon (ponton)
|
|
|
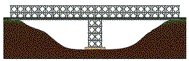
|

|
|
|
Bailey bridge (baileybrug)
|
swing
bridge (draaibrug)
|
|
Standaard
and Elmar (?)
|
|
Fig.
96 Names of Bridges and their components
|
|
|
These types
of bridges could be made of steel, concrete or wood. Depending on the material
they have a different maximum span (fig. 97).
|
english name
|
dutch name
|
span in m.
|
notes
|
|
|
multiple span
beam bridge
|
balk- liggerbrug
met meer overspanningen
|
unlimited
|
|
|
|
viaduct
|
viaduct
|
unlimited
|
old-fashioned
|
|
|
ferry bridge
|
pontbrug
|
unlimited
|
|
|
|
suspension bridge
|
hangbrug
|
2000
|
wind-sensitive
|
|
|
fan cable stayed
bridge
|
waaiertuibrug
|
1000
|
wind-sensitive
|
|
|
harp cable stayed
bridge
|
harptuibrug
|
1000
|
wind-sensitive
|
|
|
cantilever bridge
|
kraagliggerbrug,
Gerberligger
|
550
|
|
|
|
arch bridge
|
boogbrug
|
500
|
steel
|
|
|
trough arch
bridge
|
boogbrug met
laaggelegen rijvloer
|
500
|
? with draw
connection
|
|
|
fixed two-hinged
three-hinged arch
|
ingeklemde,
tweeschanier-, driescharnierboog
|
500
|
? with draw
connection
|
|
|
half-through arch
bridge
|
boogbrug met
tussengelegen rijvloer
|
500
|
?
|
|
|
deck arch bridge
|
boogbrug met
hooggelegen rijvloer
|
500
|
?
|
|
|
beam bridge
|
balk- of
liggerbrug
|
250
|
steel truss,
framework
|
|
|
arch bridge
|
boogbrug
|
200
|
stiffened bars
|
|
|
floating bridge
|
pontonbrug
|
200
|
military
|
movable
|
|
lift bridge
|
hefbrug
|
150
|
old-fashioned
|
movable
|
|
portal bridge
|
schoorbrug
|
150
|
between supports
with tube beam
|
|
|
beam bridge
|
balk- of
liggerbrug
|
100
|
steel concrete
|
|
|
beam bridge
|
balk- of
liggerbrug
|
100
|
concrete tube
beam
|
|
|
transporter
bridge
|
zweefbrug,
transbordeur.
|
100
|
? old fashioned
1895-1920; 2 in europe left
|
movable
|
|
double-leaf bascule bridge
|
dubbele basculebrug
|
100
|
|
movable
|
|
swing bridge
|
draaibrug
|
60
|
even as aquaduct
|
movable
|
|
arch bridge
|
boogbrug
|
50
|
hout
|
|
|
single-leaf
bascule bridge
|
enkele
basculebrug
|
50
|
|
movable
|
|
portal bridge
|
schoorbrug
|
40
|
? concrete
|
|
|
beam bridge
|
plaatliggerbrug
|
30
|
or wider with
large construction height
|
|
|
beam bridge
|
balk- of
liggerbrug
|
30
|
|
|
|
strauszbridge
|
ophaalbrug
|
25
|
|
movable
|
|
beam bridge
|
balk- of
liggerbrug
|
20
|
2m wood truss,
framework
|
|
|
beam bridge
|
spoorverkeer
staal
|
15
|
small
construction height
|
|
|
ship bridge
|
schipbrug
|
10
|
? te doesburg
|
movable
|
|
beam bridge
|
balk- of
liggerbrug
|
10
|
wood
|
|
|
raft bridge
|
vlotbrug
|
10
|
? floating from
under approach ramp
|
movable
|
|
crane bridge
|
kraanbrug
|
10
|
old-fashioned
|
movable
|
|
roll bridge
|
rolbrug
|
8
|
one example 67m
|
movable
|
|
clap bridge
|
klapbrug
|
8
|
without
counterweight
|
movable
|
|
|
valbrug
|
5
|
old-fashioned
(castles)
|
movable
|
|
|
oorgatbrug
|
1
|
for mast only,
old-fashioned (hindeloopen)
|
movable
|
|
Bailey bridge
|
Baileybrug
|
|
military
|
|
|
Jong (1996; Jong (1996)
|
|
fig. 97 Maximum span of different
bridges
|
|
|
|
|
|
|
The construction height below deck is often limiting factor.
Ankum, P. v.
(2003) Polders en Hoogwaterbeheer. Polders, Drainage and Flood Control (Delft) Delft University of
Technology, Fac. Civiele Techniek en Geowetenschappen, Sectie Land- en
Waterbeheer: 310.
Hildebrandt,
S. and A. Tromba (1989) Architectuur in de natuur, de weg naar de optimale
vorm (Maastricht/Brussel) Wetenschappelijke Bibliotheek Natuur en
Techniek ISBN 90 70157 81 0.
Jong, H. d.
(1996) Handboek Civiele Kunstwerken (losbladig 3 mappen) (Den Haag)
TenHagen Stam ISBN 90-70011-18-2.
Jong, H. d.
(1996) Video 'Beweegbare stalen bruggen' Handboek Civiele Kunstwerken
(Den Haag) tenHagen&Stam bv. Afd. Klantenservice Lezersmarkt.
Jong, T. M.
d. (2001) Standaardverkaveling 11.exe.
Standaard, M.
and m. Elmar (?) Beeldwoordenboek Zo heet dat Standaard Multimedia;
Elmar multimedia.
[1] Why are
street patterns and artificial drainage systems in flat lands not like a tree
but like a lattice?
[2] The 4th
National Plan of Watermanagement Policy [V&W, 1998c #829], and its last successor
‘Anders omgaan met water’[V&W, 2 000b #832] mark a change from accent, just
as the 4th National Plan of Environmental
Policy [VROM, 2 001a #839] compared with its
predecessors. Which change of accent is that?
[3] Which future
problems in watermanagement and proposed solutions have a great impact on
landuse in the Netherlands? Which solutions are proposed in the 4th
National Plan of Watermanagement Policy [V&W, 1998c #829], and its last successor
‘Anders omgaan met water’[V&W, 2 000b #832]?


























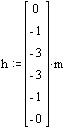
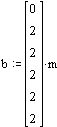












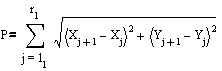
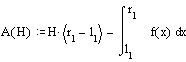
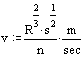




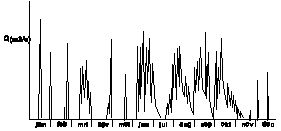











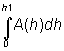 .
.