Sun wind water earth life
living; legends for design
COLOFON
Editor/author: T.M.
de Jong (ed.)
Authors: C.
van den Akker
D. de Bruin
M.J.
Moens-Gigengack
C.M. Steenbergen
M.W.M.
van den Toorn
Book production and design: T. M. de Jong
Cover and
frontispiece design: T. M.
de Jong
Published and
distributed by: Publicatiebureau
Bouwkunde
2008, Publicatiebureau Bouwkunde
Delft University of
Technology, Faculty of Architecture
P.O. Box 5043
2600 GA Delft
The Netherlands
Telephone: +31
15 27 84737
Telefax: +31
15 27 83030
Sun
wind water
earth life living; legends for design
Prof.dr.ir. T. M. de Jong
ed. 2009-08-18
Prof.dr.ir. C. van den
Akker
Ir.D. de Bruin
Drs. M.J. Moens
Prof.dr.ir. C.M.
Steenbergen
Ir. M.W.M. van den Toorn
AR2U070 Territory
http://team.bk.tudelft.nl publications 2009
Contents
Introduction.. 7
1 Sun, energy and plants.. 11
1.1 Energy. 12
1.2 Sun, light and shadow.. 35
1.3 Temperature, geography and and history. 50
1.4 Planting by man. 67
2 Wind, sound and noise.. 105
2.1 Global atmosphere. 106
2.2 National choice of location. 112
2.3 Regional choice of location. 121
2.4 Local measures. 128
2.5 District and neighbourhood variants. 140
2.6 Allotment of hectares. 148
2.7 Sound and noise. 154
3 Water, networks and crossings.. 163
3.1 Water balance. 165
3.2 Civil engineering in The Netherlands. 205
3.3 Water policy. 236
3.4 The second network: roads. 247
3.5 Other networks: cables and ducts. 288
4 Earth and site preparation.. 312
4.1 Introduction. 313
4.2 Earth sciences. 315
4.3 Engineering.. 338
4.4 Applications for designers. 348
5 Life, ecology and nature.. 352
5.1 Natural
History. 353
5.2 Diversity, scale and dispersion. 366
5.3 Ecologies. 392
5.4 Valuing Nature. 429
5.5 Managing Nature. 446
6 Living, human density and environment.. 457
6.1 Adaptation and Accommodation. 459
6.2 Habitat. 482
6.3 Density. 500
6.4 Economy. 524
6.5 Environment. 547
6.6 Soil pollution. 577
7 Legends for design.. 595
7.1 Mapping.. 596
7.2 Child perception. 622
7.3 Composition analysis. 629
7.4 Legends. 638
7.5 Scales of separation. 643
7.6 Boundaries of imagination. 659
Literature.. 671
Key words.. 686
Questions.. 711
‘Building
is cooperating with the Earth.’
Marguerite
Yourcenar.
Motivation
Activating senses
Sun, wind, water, earth and
life touch our living senses immediately, always, everywhere and without any
intervention of reason. They simply are there in their unmatched
variety, moving us, our moods, memories, imaginations, intentions and plans.
Mathematics next to senses
However, the designer transforming sun into light, air into space
and water into life, touches pure mathematics next to senses.
Mathematicians left alone destroy mathematics releasing it from senses, losing
their unmatched beauty and relief, losing their sense for design. To restore
that intimate relation, the most freeing part of our European cultural heritage
my great examples are Feynman’s
lectures on physics, D’Arcy Thomson’s
‘On Growth and Form’ and Minnaert’s
‘Natuurkunde van het vrije veld’ (‘Outdoor physics’). Minnaert elaborated the
missing step from feeling to estimating.
I am sitting in the sun. How
much energy do I receive, how much I send back into universe?
I am walking in wind. How
much pressure do I receive and how much power my muscles have to overcome? It
is the same pressure giving form to the sand I walk on or giving form and
movement to the birds above me! I am swimming in the oldest landscape of all
ages, the sea. How can I survive?
Re-constructing behaviours
No longer can I escape from
reasoning, from looking for a formula, a
behaviour that works. But this reasoning is next to senses and once I found a
formula I can leave the reasoning behind going back into senses and sense. The
formula takes its own path in my Excel sheet as a living thing. It ‘behaves’.
Look! Does it take the same path as the sun, predicting my shadow? Put a pencil
and a ruler in the sun. Measure, compare, lose or win your competition with the
real sun as Copernicus did.
Mathematics have no longer
much to do with boring calculations. Nowadays computers do the work, we do the
learning. They sharpen our reasoning and senses. We see larger contexts and
smaller details than ever before discovering scale. Discovering telescopic and
microscopic scale we find the multiple universe we live in, freeing us from
boredom forever, producing images no human can invent. We do not believe our
eyes and ears, we discover them. It challenges our imagination in strange
worlds no holiday can equal. Life math is a survival journey with excitement
and suspense.
Science as design
But do we understand
the sun? No, according to Kant (1976) we design a sun behaving like
the sun we feel and see from our position and scale of time and space we live
in. We never know for sure whether it will behave tomorrow in the same way as
our sheet does now. But we have made something that works here
and now.
‘Yes! It works.’ That is a
designer’s joy.
How to use this book
This book is not a reader.
It contains original texts by the authors from our school and one civil
engineer to understand how specialists think, supporting our profession as
urban designers.
Systematic encyclopaedia
It is ordered in an
systematic encyclopaedic style. It is accessible by its table of contents
(elaborated in more detail at the beginning of each chapter), and by a key word
list containing some 6000 key words at the end of the book, including other
authors we refer to. Full references to other authors are given in a reference
list, also to be found via the key word list. Direct references into
publications and websites to look up immediately as a result of reading are
given as foot notes (a) indicated by letters in the text and listed
at the bottom of the page. Questions for exercise are indicated as numbered end
notes (1) by numbers in the text listed at the end of the book (see
page 711).
However, these questions don not yet cover the whole content of the book.
A conditional sequence: physics
first
The chapter titles start as
the title of the book indicates: Sun, Wind, Water, Earth, Life, Living and
Legends for design. These subjects are ordered this way, because it is the
conditional sequence we experience them directly outdoor and gradually can
understand them best.
The sequence of the chapters
follows the range of abiotic, biotic and conceptual phenomena with apparently
increasing complexity. The simulation of these phenomena is firstly approached
by supposing a causal sequence (effect follows cause: c Ţ e) usual in physics. Even life, living and legends for design obey
the boundary conditions of physics. So,
we firstly try to simulate these phenomena by purely causal simulation.
After all, we can not imagine living systems (B) without an abiotic environment
(A), as we can not imagine conceptual systems (C) without a living environment
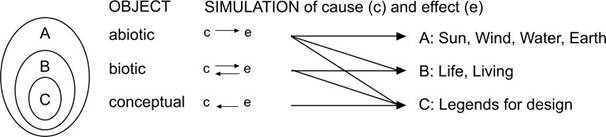
(B). Let us call that ‘ABC-model’ (see Fig. 1).
|
|
|
|
|
Fig. 1 Simulating reality by different
approaches according to the ‘ABC-model’
|
|
|
Biotic feed-backs included
However, biotic phenomena
(including humans) and some human artifacts seem to take the effects of earlier
behaviour into account, adapting next behaviour (‘empirical cycle’). A one way causal simulation of such a phenomenon should contain
its history from second to second including the evolutionary history of its
ancestors from the very beginning. It should not exclude details that might
have been crucial. That long description to predict behaviour would require too
many gradually changing cycles finally solving chicken-and-egg questions
typical for biology. But you can understand the pattern and process of an egg
in a shorter way if you suppose what will come out (for convenience, without
additional teleological assumptions). In that approach the effect also
‘precedes’ the cause (see Fig. 1). The
main ‘experience’ of a species is stored in its genes and in other chemical
substancies steering action, completed by increasing ‘experiences’ of a
specimen born in a specific context. We still do not understand much of all
feed-back loops in any organism. But, we can simplify the description of its
behaviour by drawing a black box and looking what is going in (input) and what
is coming out (output) in a determined period. That is called ‘systems
approach’. By a systems approach you design a model with the same input and
output as observed to predict behaviour. In the algorithm of such a model many
‘if … then …’ statements will appear connecting the possible branches of causal
behaviour in different circumstances. If the behaviour of the model is much the
same as observed we are inclined to suppose the model represents reality, which
is not the case.
Conceptual projection added
For our purpose, the most
satisfying description of the difference between humans compared to other
animals is their ability to represent a larger range of activities beforehand[c]. It is the very basis of making artifacts serving further purposes
(if I will do this first, then I can do that later) and the very basis of task
division (if you do this, I can do that). So, humans are supposed to simulate
internally a longer range of ‘causes’ (actions) and ‘effects’ before they come
into action (‘look before you leap’) than routinous animals. As soon as action
and utilising its effect are connected by an intermediate (interfunctional)
action, such as making an instrument, the whole range can be noted as an
algorithm. Designing is such an intermediate activity in a range of activities
‘planned’ beforehand. That kind of ‘conceptual’ behaviour completes many
unconscious components of behaviour stored in an organism as biotic routines.
That is why in this paper we leave out the supposed ‘cognitive’ part of human
behaviour as long as we can simulate (understand) it sufficiently by a black
box. But, there comes a time these biotic simulations do not fit reality any
more. Then, we have to add new suppositions about the ‘plan’ humans have in
mind before they act. Many ‘plans’ (earning a living, finding a partner, getting
children) look the same. But the question is, if these are really ‘plans’ or
simply the ‘conceptualisation’ of predictable biological inclinations
afterwards to justify them socially. What we can simulate by less suppositions
we will do (‘razor of Ockham’). Interpreting humans as mere animals clarifies
an increasing amount of behaviour[d]. But, there are still unpredictable behaviours apparently following
a ‘plan’. The question is, if we ever could predict that kind of behaviour. In
that case we have to give up our supposition of free will (supposed in
democracy) after all. In this paper we will not do so, because it is the core
of design to find unexpected possibilities (necessary in an ecological crisis).
If these possibilities could be expected it would be predictions, not designs.
In Fig. 1 is
expressed that conceptual projection can not be used to simulate abiotic and
biotic phenomena.
Levels of scale
A principle of ordering we
aimed for in any separate chapter is the level of scale. So, you can choose the
sub-chapter concerning the level of scale you focus on in your study. We have
tried to start every chapter on the highest level of scale. There are arguments
to start with the lowest level, most directly related to our senses, but we
chose the other way round, because lower levels of scale are better understood
knowing their context. This way, you may get a feeling for contextual factors
determining a particular environment and its mathematical modelling with
parameters stemming from that context. In design practice you can reason the
reverse way or both ways. But, to know how to design ‘throught the scales’ you
have to be aware of scales, the frame and grain of legend units, the scale
specific inferences and the danger of using conclusions from an ather scale.
Design related use
So, you do not have to read
everything before you can use it making inventories for design (like a local
atlas of thematic maps), while designing or reflecting on your designs.
Reflecting on your design work is what we ask in the assignments of the course
accompanying this book: how did you apply Sun in your earlier design work, what
could you have done, how do you apply Sun in your actual design work and what
could you do with it in the future? The same is asked for Wind, Water and so
on. A growing number of computer programs for experiments and calculations per
section is downloadable from http://team.bk.tudelft.nl publications 2008.
Non-disciplinary combinations like Sun, energy and plants
The chapter ‘Sun’ contains
sub-chapters on energy, entropy, temperature, light, the history of our
territory dependent on solar fluctuations, man-made plantation (written by
Prof.dr.ir.C.M. Steenbergen and Drs. M.J. Moens),
shadow and vision as well. These subjects are often related in design or better
comprehensible in the offered context. Perhaps in your design you can connect
things in another way than the usual scientific and specialist’s distinctions
of disciplines suggest. For the same reason we did not aim for a distinction
between natural and man-made phenomena in the sequence of chapters. It is
rather a conditional sequence of growing complexity in cycles of inductive
observing, deductive understanding and practical application. So, any chapter
is better understood knowing something about the subject of the preceding
chapter.
Wind, sound and noise
The chapter ‘Wind’ contains
sound and noise as well, because both are movements of air. These flows are
more complex than those of mere energy and light.
Water, networks and crossings
The chapter ‘Water’ is
primarily based on the lecture notes Prof.dr.ir. C. van den Akker offered us for use when he retired from the
Faculty of Civil engineering. Ir.D. de Bruin, drs. M.J. Moens and ir. M.W.M. van
den Toorn added many subjects relevant for design. However, it contains traffic
as well, based on the book of ir. B. Bach, because the combination of these different flows on the Earth’s
surface and their resulting networks are an important part of urban and
regional design. So, we did not primarily make a distinction between natural
and man-made networks. The comparison of their characteristics is interesting,
instructive, and may be a source of new design ideas.
Earth and site preparation
The chapter ‘Earth’,
primarily written by Drs. M.J. Moens and elaborated by ir. M.W.M. van
den Toorn , is
better understood if you know something about wind and water. The division of
its sub-chapters starts strictly with levels of scale, but then sub-chapters
follow about soil pollution and preparing a site for development.
Life, ecology and nature
The ecological chapter
‘Life’ supposes sun, wind, water and earth. These conditions are discussed
earlier in the book, so the chapter can focus on the distribution and abundance
of life itself. Biology is physics with numerous feed-back mechanisms, not te
be modelled so easily in a mathematical sense. However, it introduces
approaches of system-dynamics, demography, useful in human environments as
well. Life contains human life. So, this chapter tries to consider man as a
species between other species (syn-ecology), while the next chapter ‘Human
Living’ concentrates on human species only (aut-ecology). However, there are
sub-chapters on valuing and mananging nature by man in your plan, and on the
role of an urban ecologist.
The subject of this chapter
is not very familiar to designers. So, you can think it is not very relevant.
But in my opinion ecology, the science of distribution and abundance of
species, is the very core of urban and regional design. Design changes
predictable distributions. Local vegetaton and wild life clarifies much about
what designers feel as a mysterious ‘genius loci’. Ecology is a neglected
source of local identity. Evolution of life has something in common with design
thinking: its course of trial and error into diversity and order. The
evolutionary taxonomy of plants and animals, types of life, their distribution
and adapation into different environments, accommodating and modifying them,
give examples of the same problems any design task stands for. Your typological
repertoire of design solutions selects environments and the reverse different
environments select different types of design.
Living, human density and
environment
The chapter ‘Living’ shows
the history of human occupation in general and in The Netherlands in
particular. That piece of land in between France,
Belgium, Germany and Great Britain contains both lower
and higher grounds, combining many characteristics of its neighbours. Its delta
gives an impression of a development known from many densely populated lowlands
in the world, the spatial composition of ecological, technical, economic,
cultural and administrative components. A sub-chapter is devoted to urban
density on different levels of scale. The sub-chapter ‘Environment’ discusses
some consequences of living in high densities like environmental problems,
environmental norms, gains and losses.
Legends for design
The chapter ‘Legends for
design’ stimulates to consider these phenomena of urban physics as innovative
components, legend units, spatial types given form in a design composition. It
raises philosophical questions on unusual types, their suppositions,
combinations and consequences.
Simulators accompanying the book
Every chapter is accompanied
by Excel sheets programmed with Visual Basic Language to exercise mathematical
relations described in this book. These simulators show the hidden suppositions
of specialists in yellow sliders by which you can change the model and see the
results without own calculations. By doing so, you can ask the right questions
if specialists criticize your design with mathematical certainty. They often
show counter-intuitive results. If you do not believe them, then Excel allows
you to show the formulas en their relations to criticize their inference. That
will make you less vulnerable in the company of many specialists you will meet
in practice.
Contents...................................................................................................................................... 11
1.1 Energy............................................................................................................................... 12
1.1.1.... Physical
measures........................................................................................................... 12
1.1.2.... Entropy............................................................................................................................ 14
1.1.3.... Energetic
efficiency........................................................................................................... 19
1.1.4.... Global
energy................................................................................................................... 22
1.1.5.... National
energy................................................................................................................ 28
1.1.6.... Local energy
storage......................................................................................................... 33
1.2 Sun, light and shadow................................................................................................... 35
1.2.1.... Looking from
the universe (a, b
and latitude l)..................................................................... 35
1.2.2.... Looking from
the Sun (declination
d)................................................................................... 37
1.2.3.... Looking back
from Earth (azimuth and sunheight)................................................................ 38
1.2.4.... Appointments
about time on Earth..................................................................................... 41
1.2.5.... Calculating
sunlight periods............................................................................................... 43
1.2.6.... Shadow........................................................................................................................... 45
1.3 Temperature, geography and and history............................................................... 50
1.3.1.... Spatial
variation................................................................................................................ 50
1.3.2.... Long term
temporal variation.............................................................................................. 55
1.3.3.... Seasons and
common plants............................................................................................. 61
1.4 Planting by man............................................................................................................... 67
1.4.1.... Introduction...................................................................................................................... 67
1.4.2.... Planting and
Habitat.......................................................................................................... 83
1.4.3.... Tree
planting and the urban space...................................................................................... 90
1.4.4.... Hedges.......................................................................................................................... 101
The internationally accepted
SI system of units defines energy and power according to Newton by distance, time and mass as follows.
As long as a force ‘f’ causes an acceleration ‘a’, a distance ‘d’
is covered in a time interval ‘t’. Multiplying f by d produces the yielded
energy f · d, expressed in joules.
Energy per time interval t produces the performed power f · d / t expressed in watts (see Fig. 2).[1]
|
Velocity ‘v’ and acceleration
‘a’ suppose distance d and time interval t:
|
|
d (distance)
|
d
|
|
d
|
|
|
|
ľ
|
= v (velocity)
|
ľ
|
= a (acceleration)
|
|
t (time)
|
t
|
|
t2
|
|
|
Linear momentum ‘i’ and force ‘f’ suppose mass m, velocity v and
acceleration a:
|
|
|
d
|
|
d
|
|
|
m (mass)
|
ľ
|
m = i (momentum)[2]
|
ľ
|
m = ma = f (force)[3]
|
|
|
t
|
|
t2
|
|
|
|
times distance = energy ‘e’
|
divided by time = power ‘p’
|
|
|
d2
|
|
d2
|
|
|
ľ
|
m = e (energy)[4]
|
ľ
|
m = e/t = p (power)[5]
|
|
t2
|
|
t3
|
|
|
Energy is expressed in joules (J), power (energy per second) in watts
(W)[6]
|
|
|
J=kg*m2/sec2
|
W = J/sec
|
|
Old measures should be replaced as follows:
|
|
k= kilo(*103)
|
kWh = 3.6 MJ
|
kWh/year = 0.1142W
|
|
M= mega(*106)
|
kcal = 4.186 kJ
|
kcal/day = 0.0485W
|
|
G= giga(*109)
|
pk.h = 2.648 MJ
|
pk = hp = 735.5 W
|
|
T= tera(*1012)
|
ton TNT = 4.2 GJ
|
PJ/year = 31.7 MW
|
|
P= peta(*1015)[7]
|
MTOE = 41.87 PJ
|
J/sec = 1 W
|
|
E= exa(*1018)
|
kgfm = 9.81 J
|
|
|
|
BTU = 1.055 kJ
|
W (watt) could be read as watt*year/year.
|
|
|
watt*sec = 1 J
|
|
|
The equivalent of 1 m3 natural gas (aeq)[8], roughly 1 litre petrol[9], occasionally counts 1 watt*year:
|
|
Occasionally:
|
m3 aeq = 31.6 MJ and
|
aeq/year = 1 W, or
|
|
Wa = watt*year = 31.6 MJ
|
1 W = 1 watt*year/year
|
|
|
1 MJ = 0.0316888 Wa
1 GJ = 31.7 Wa
1 TJ = 31.7 kWa
1 PJ = 31.7 MWa
|
‘a’ from latin ‘annum’ (year)
Wa is watt during a year
‘k’ (kilo) means 1 000x
‘M’ (mega) means 1 000 000x
|
|
|
|
Fig. 2 Dimensions of energy
|
|
|
A happy coincidence
A year counts 365.24 · 24 · 60 · 60 = 31 556 926 seconds or 31.6 Msec,
since M means ‘·million’.
So, the power of 1 watt during a year: 1 watt·year =
31.6 MW·sec = 31.6 MJ =
1 Wa (‘a’ derived from latin ‘annum’, year), which is energy.
[10]
Occasionally the equivalent of 1 m3 natural gas (‘aeq’) or 1 litre petrol or 1 kg coal energy counts for approximately
31.6 MJ = 1 Wa energy as well.[11]
So: m3 natural gas (‘aeq’) ≈
watt·year = Wa (energy)
and m3 natural gas per year ≈ watt = W (power).
So, read ‘Wa’ and think ‘1
m3 natural gas’, ‘1 litre petrol’ or ‘1 kg coal’ (energy);
read ‘W’ and think ‘1
m3 natural gas per year’ (power);
read ‘kW’ and think ‘1000
m3 natural gas per year’ (power);
read ‘kWh’ and think ‘1000
m3 natural gas per year
during an hour’ (again energy).
Easy calculating
kilowatthours (kWh) and joules (J) by heart
Since there are 365.24 · 24 = 8 766 hours
in a year: 1 Wa (watt·year) =
8 766 watt·hour (Wh) or
8.766 kilowatt·hour (kWh), because ‘k’ means ‘·thousand’.
Since there are 31 556 926 seconds in a year: 1 Wa = 1watt·year = 31 556 926 Ws (J) or
31 557 kJ, 31.557 MJ or 0.031557 GJ, because k = ·1 000,
M = ·1 000 000 and
G = ·1 000 000 000.[12]
This Wa measure is not only
immediately interpretable as energy content of roughly 1 m3 natural
gas, 1 litre petrol or 1 kg coal, but via the average amount of hours per year
(8 766) it is also easily transferable by heart into electrical measures
as kWh and then via the number of seconds per hour (3 600) into the
standard energy measure W·s=J (joule).
Moreover, in building design and management the year average is
important and per year we may write this unit simply as W (watt). So, in
this chapter for power we will use the usual standard W, known from
lamps and other electric devices while for energy we will use Wa. If we
know the average use of power, energy costs
depend on the duration of use. So, we
do not pay power (in watts, joules per second), but we pay energy
(in joules, kilowatthours or wattyears): power x time.
Watts in everyday life
A quiet person uses approximately 100 W, that is during a
year the equivalent of 100 m3 natural gas. That power of 100 W is the same as the power of a candle or
pilot light or the amount of solar energy/m2 at our latitude. That is a lucky
coincidence as well. The power of solar light varies from 0 (at night) to 1000
W (at full sunlight in summer) around an average of approximately 100 W.
Burning a lamp of 100 W during a year takes 100 Wa as well,
but electric light is more expensive than a candle.[13] Crude oil is measured in barrels of 159 litres. So, if one
barrel costs € 80, a litre costs € 0.50. However, a litre petrol (1 Wa) from the petrol
station after refining and taxes costs more than € 1. Natural gas requires less
expensive refinary.
In the Netherlands 2008, 1 m3 natural gas (1Wa) costs
approximately € 0,70. However, an electric
Wa costs approximately € 1.80. That is more than 2
times as much. Why?
Conversion of fuel into a useful kind of energy
Electric energy is
usually expressed in ‘kWhe’ (‘e’ = electrical),
heat energy in ‘kWhth’ (‘th’ = thermal).
A kWhe electricity
is more expensive than a kWhth of heat by burning gas, petrol or
coal, because a power station can convert only approximately 38% from the
energy content of fossile fuels into electricity (efficiency h=0.38). The rest is
necessarily produced as heat, mainly dumped in the environment ‘cooling’ the
power station like any human at work also looses heat.[14] That heat content could be used for space heating, but the transport and
distribution of heat is often too expensive.
However, enterprises
demanding both heat (Q) and work (W) at the same spot, could gain a profit by
generating both locally (cogeneration, in Dutch ‘warmte-kracht-koppeling’ WKK).
Necessary heat loss
The necessary heat loss
is described by two main laws of thermodynamics: no energy gets lost by conversion (first law of thermodynamics), but it always degrades (second law of thermodynamics).
By any conversion only a part of the original energy can be utilised
by acculumation and direction
at one spot of application. The rest is dispersed as heat content Q
(many particles moving in many directions), to concentrate a minor useful part
W (work) on the spot where the work has to be done. The efficiency h of the conversion is W/(W+Q). In the case of electricity production
it is 38kWhe/100kWh or 38%. Once the work W is done, even the energy
of that work is transformed into heat. However, according to the first law of
thermodynamics both energy contents are not lost, they are degraded, dispersed,
less useful. However it could still be useful for other purposes.
For example, the
temperature of burning gas is ample 2000oC, much too warm for space
heating. If you would use the heat from burning fuels firstly for cooking, then
for heating rooms demanding a high temperature and at last for heating rooms
demaning a low temperature, the same heat content is used three times at the
same cost in a ‘cascade’. To organise that is a
challenge of design.
Exergy
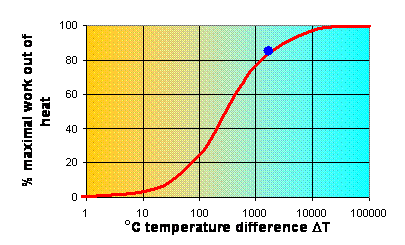
Theoretically any difference in
temperature can be used to extract some work, but the efficiency of a small
temperature difference DT is lower than that of a large temperature difference (see Fig. 3).
|
|
|
|
|
Fig. 3 The %maximum amount of work (W) retrievable from a temperature
difference DT
|
|
|
The amount of work you
can get out of heat (W/Q) per temperature difference available is called exergy. Apparently, chemical
energy like fossile fuels do have a higher ‘quality’ than work; work has a
higher quality than heat; high temperature heat has a higher quality than low
temperature heat.
So, using high quality
energy where low quality would be enough, leaves unused the opportunity to use
the same energy several times in a cascade of uses.
The ‘quality’ of energy
can be expressed in a single quantity. That quantity is called ‘entropy’.
The ‘quality’ of energy
The ‘quality’ of heat (Q) and work (W) is apparently different,
though both are ‘energy’.
In the same way high temperature (T) energy has a higher ‘quality’
than the same energy at low T.
Converting fossile fuels
into heat, the ‘state’ of energy changes. But how to describe that ‘state’ and
its ‘quality’? To introduce that ‘state’ in energy calculations the term
‘entropy’ S is invented by Clausius ca. 1855. In a preliminary approach one
could think S = Q/T, but it concerns change,
forcing us into differentials. It is often translated as ‘disorder’, but it is a
special kind of disorder as Boltzmann showed in 1877. What we often perceive as
‘order’, a regular dispersion in space, is
‘disorder’ in thermodynamics. Let us try to understand that kind of
thermodynamic disorder to avoid confusion of both kinds of ‘order’.
‘Disorder’ in thermodynamics
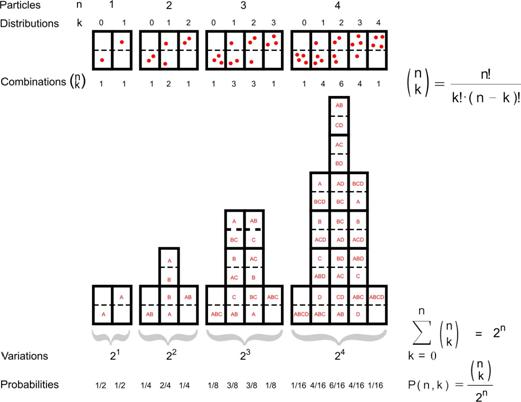
In Fig. 4 all possible
distributions of n = {1,2,3,4}
particles in two rooms are represented.
If you mark every individual
particle by A, B, C, D, you can count the possible combinations producing the same distribution k over the
rooms numbered as k = {0,1 …n).
|
|
|
|
|
Fig.
4 k Distributions of n particles in two rooms
|
|
|
|
|
|
|
|
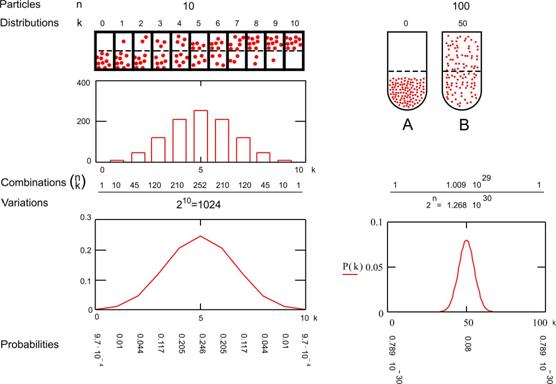
Fig. 5 The decreasing probability of
concentration with a growing number of
particles
|
|
|
The numbers n and k
determine the probability P(n,k) that this combination will occur.
Minimum and maximum values
of k represent the extreme concentrations in one room or the other.
The more particles there
are, the more combinations are possible and the more improbable will be the two
extreme cases of accumulation in one room. For example, if there are 10
particles, the probability of total sprawl is 252 possible combinations from
1024 (25%), but the probability of total accumulation in one room is 1 case
from 1024 (0.1% see Fig. 5, left).
Fig. 5 (A) shows the
least probable distribution of 100 particles in a cylinder, but state B is very
probable. These
probabilities can be calculated as approximately 1/13·1029 (A) and
1/13 (B).
So, if anything changes it
will most probably change from A into B instead of from B into A.
That asymmetry of process is
the core of thermodynamics.
From Fig. 5 you also can
learn that by an increasing number of particles most combinations accumulate
around the middle of k=0.5·n. If you would calculate the possible combinations
of 1000 particles the probability of sprawl (B) between k=495 and 505 (1% of n)
would be practically 1 (100%). The graph would show a vertical line rather than
a gaussian ‘bell’.
Difference of
entropy
Suppose now the content of
the cylinder is a mole of gas (that is approximately 6·1023
particles, Avogadro’s number n). Then the probability of state B approximates 1
(100%). The probability of state A is again 1/2n. That is nearly
zero, because the number 2n is extraordinary large: a 1 with more
than 1023 zeros. An ordinary computer can not calculate all
combinations of that number as done in Fig. 4. However, to
determine the entropy of state A we need the natural logarithm (the exponent to
‘e’ or 2.718) of that probability: ln1/2n or ln(2-n). And
ln(2-n) is easily written as -n·ln(2). That will save a lot of
calculation, because n will disappear in the definition of entropy by Boltzmann
using that probability:
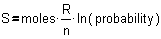
Fig. 6 The statistical definition of entropy by Boltzmann in 1877
In state A and B with n =
6·1023 particles, the number of moles is 1; n is Avogadro’s number.
R is a constant (gas
constant) we will explain later. So, entropy is related to probability by a constant! However,
Boltzmann chose the logarithm of probability, because if you want to know the
entropy of two sub systems (for example two moles), you would have to multiply
the combination of each sub system. If you take the logarithm first, than you
can simply add both.
In this case we can write
the increase of entropy from stage A into B as SB-SA:
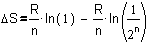
Fig.
7 The increase of entropy from accumulation in one room into sprawl
in two rooms
The probability of state B is very near 1, and the logarithm of 1 is
zero, so we can write:
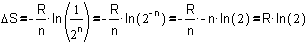
Fig.
8 Simplifying the formula of Fig. 7
So, the entropy of stage B is R·ln(2). The natural logarithm of 2 is
0.693, but what is R?
R is the gas constant per mole of gas:
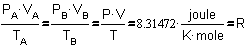
Fig. 9 Defining the gas constant R
In Fig. 9 P is the
pressure (force/m2) and V is the volume (m3). So, on
balance P·V is ‘force times distance’: energy (expressed in newton·m: joule). T
is the temperature in degrees of Kelvin (K).
In a mole of gas the proportion between that energy and temperature
in normal conditions appears to be the same: 8.31472 joule/K. That constant is named ‘gas constant’ R. So, that is
also valid for both stage A and B. Now we could calculate the increase of
entropy as R.ln(2) = 5.8 joule/K·mole.
However, in thermodynamics the ‘probability’ of a state contains
more than the distribution over two rooms. For example the reduced freedom of
movements of particles in liquids and solids. That is why we limit ourselves
here to complete freedom of movement (gas) to describe the states A and B.
Moreover, gas plays a dominant role in energy conversion any engineer is occupied with.
Change of entropy
If a mole of gas expands
from A to B, the heat content Q disperses over a doubled volume. So, the
temperature tends to drop and the system immediately starts to adapt to the
temperature of the environment. That causes an influx of extra heat energy DQ. So, in a slow
process T could be considered as constant and the pressure will halve to keep
also P·V constant at R·T (see Fig. 10).
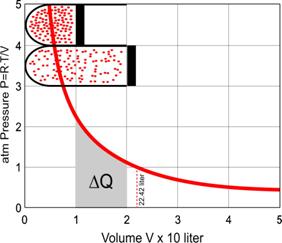
|
|
P·V = R·T (see Fig.
9), so P = R·T/V (see the graph left).
If at any moment Q :=
P·V, any small change dQ equals P·dV and a
larger change DQ from stage 1
into 2 is the sum of these small changes:
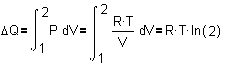
so, 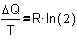 . Remember now
Fig. 8: . Remember now
Fig. 8: 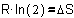
if 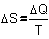 , then also , then also 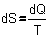 . So, . So,
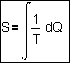
|
|
|
|
|
Fig.
10 Extending 1 mole of gas (22.42 liter
at 1 atmosphere) from 10 to 20 liter keeping T at 0oC or 273.26K.
|
|
|
|
The heat energy Q is equal
to P·V, but if it increases P itself is dependent on V.
So, every infinitely little
increase of V (dV) has to be multiplied by a smaller P. Summing these products
P·dV between V = 1 and V = 2 is symbolised by the first
‘definite integral’ sign in Fig. 10. However, that
formula can not be solved if we do not substitute P by R·T/V (see Fig. 9) in the next
formula. In that case the mathematicians found out that definite integral is
equal to R·T·ln(2).
Now we have a real quantity
for DQ, because
R·T·ln(2) = 1574 joule.
So, DQ/T = R·ln(2),
and R·ln(2) reminds us of Fig. 8: it is DS, the change
of entropy!
A few steps according to Fig. 7 takes us back to
the statistical definition of Boltzmann in Fig. 6, but now it is
related to heat content Q and temperature T, the variables used in any
engineering.
If DS = DQ/T, then also
dS = dQ/T and now we can write the famous integral of Clausius:
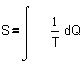
Fig. 11 The
thermodynamic definition of entropy
This formula shows that an
increasing heat content increases entropy, but a higher temperature decreases
it. If we now keep the heat content the same (closed system) and increase
volume, then accumulation, pressure and temperature decrease (Boyle-Gay Lussac, see Fig. 9), so entropy
will increase.
So, accumulation (storage,
difference between filled and empty) decreases entropy, increases order.
Design and the conception of order, specialists’ conceptions
The explanantion of entropy
above is extended, because of two reasons.
Firstly, while defending a
concept of order, arrangement in design, designers often refer to low
entropy and that is not always correct. Perceptual order could refer to a
regular dispersion of objects in space and just that means sprawl, entropy. In
thermodynamics an irregular dispersion with local accumulations has a lower
entropy (disorder) than complete sprawl. However, in fluids and solids
rectangular or hexagonal patterns with low entropy appear, due to molecular
forces. But in general, if the particles have freedom of movement, sprawl is much
more probable than accumulation.
It reminds us of the
avoidance of urban sprawl. Thermodynamically
accumulation is possible, but very improbable. So, if thermodynamics has
any lessons for designers: sprawl is not the task of design, if there is freedom
of movement, than it very probably happens without intention.
Secondly, energy and entropy
are basic concepts in any engineering. To understand specialists in their
reasoning and to be able to criticise them demands some insight by designers.
The impact of the industrial revolution, the accumulation
of population in cities can not be understood without understanding the
manipulation of sprawl on another level of scale as has happened in the
development of the internal-combustion engine. The internal-combustion engine
is extensively used in industry and traffic. So, I would like to proceed with
some explanation of that engine, the main application of sunlight stored in
fossile fuels in human society.
Forced
concentration
The (change of) force by
which a piston is pushed out of a cylinder is equal to the proportion of (change of)
energy and entropy Fig. 12. In a cylinder
engine, alternating states of dispersion are used to convert imported
disordered energy (heat) partly into directed movement. It is only possible by
exporting part of the heat in an even more dispersed form (cooling). The
necessary event of cooling makes an efficiency of 100% impossible and increases
entropy in a larger environmental system. The reverse, adding rotating energy
to this engine the principle that can be used for heating (heat pump) and cooling
(refrigerator).
|

|
|
|
|
Fig.
12 Carnot-engine
|
|
|
The proportion of the
applicable part from total energy content of a primary source is the efficiency of the conversion.[15] In Fig. 13 some conversion
efficiencies are represented.
|
Device or process
|
chemical->thermic
|
thermic->mechanisal
|
mechanical->electric
|
electric->mechanical
|
electric->radiation
|
electric->chemical
|
chemical->electric
|
radiation->electric
|
thermic->electric
|
efficiency
|
|
100%
|
|
electric dynamo
|
|
|
|
|
|
|
|
|
|
|
|
electric motor
|
|
|
|
|
|
|
|
|
|
|
|
90%
|
|
steam boiler
|
|
|
|
|
|
|
|
|
|
|
|
HR-boiler
|
|
|
|
|
|
|
|
|
|
|
|
80%
|
|
c.v.-boiler
|
|
|
|
|
|
|
|
|
|
|
|
electric battery
|
|
|
|
|
|
|
|
|
|
|
|
70%
|
|
fuel cell
|
|
|
|
|
|
|
|
|
|
|
|
60%
|
|
50%
|
|
steam turbine
|
|
|
|
|
|
|
|
|
|
|
|
40%
|
|
electric power station
|
|
|
|
|
|
|
|
|
|
|
|
gas turbine
|
|
|
|
|
|
|
|
|
|
|
|
30%
|
|
car engine
|
|
|
|
|
|
|
|
|
|
|
|
neon lamp
|
|
|
|
|
|
|
|
|
|
20%
|
|
solar cell
|
|
|
|
|
|
|
|
|
|
|
|
10%
|
|
thermocouple
|
|
|
|
|
|
|
|
|
|
|
|
0%
|
|
|
|
Fig. 13 Energy conversion efficiencies
|
|
|
Producing electric power
An electric power station converts primary fuel (mostly coal) into
electricity with approximately 38% efficiency. Fig. 13 shows that such
a power station combines 3 conversions with respecitive efficiencies of 90, 45
and 95%. Multiplication of these efficiencies produces 38% indeed.[16] The step from chemical into electrical power could also be made
directly by a fuel cell (brandstofcel), but the profit of a higher efficiency (60%) does not yet
counterbalance the costs.
The table shows the solar cell as well. The efficiency is between 10 and 20%
(theoretical maximum 30%). Assuming 100W sunlight per m2 Earth’s surface
average per year in The Netherlands (40 000 km2 land surface) we can
yield at least 10W/m2.
Domestic use of
solar energy
The average Dutch household uses approximately 375 wattyear/year or 375W
electricity.
In a first approach a household would need 37.5 m2 solar cells. However, a
washing machine needs also in periods without sunshine now and then 5000W. So,
for an autonomous system solar electricity has to be accumulated in batteries.
According to Fig. 13 such batteries
have 70% efficiency for charging and discharging or 0.7 x 0.7 = 50% for total
use. The needed surface for solar cells doubles in a second approach to at
least 75 m2 (37.5 m2 / (0.7 x 0.7)).
Changing into alternating current
However, most domestic devices do not work on direct current (D.C.) from solar cells or batteries, but on
alternating current (A.C.). The efficiency of conversion into
alternating current may increase the needed surface of solar cells into 100 m2
or 1000 W installed power. Suppose solar cells cost € 3,‑ per installed W, the investment to harvest your own
electricity will be € 3 000,‑. In the tropics it will be approximately a half.
Peak loads
Suppose, electricity from the grid amounts about € 0.70 per Wa. So, an average use of
approximately 375 W electricity approximately amounts to € 250 per year. In this example the
solar energy earn to repay time exclusive interest is already approximately
3000/250 per year = 12 year. Concerning peak loads it is better to cover only a
part of the needed domestic electricity by solar energy and deliver back the
rest to the electricity grid avoiding efficiency losses by
charging and discharging batteries. It decreases the earn to repay time.
The costs of solar cells compared to fossile fuel
The costs of solar cells decreased since 1972 a factor of approximately
100. Their efficiency and the costs of fossile fuels will increase. To pass the
economic efficiency of fossile fuels as well the price of solar cells has to
come down relatively little (Fig. 14). ‘Solar power
cost about $4 a watt in the early 2000s, but silicon shortages, which began in
2005, have pushed up prices to more than $4.80 per watt, according to Solarbuzz
… In a recent presentation, Bradford said that prices for solar panels could
drop by as much as 50 percent from 2006 to 2010.’
|

|
|
|
|
Fig.
14 Decreasing costs of solar cells and petrol, possibly developing according to p.
|
|
|
The efficiency of solar cells compared to plants
The efficiency of solar
cells is rather high compared with the performance of nature. Plants convert approximately 0.5 % of sunlight in
temporary biomass (sometimes 2%, but overall 0.02%), from which
ony a little part is converted for a longer time in fossile fuels. Biomass production
on land delivers maximally 1 W/m2 being an ecological disaster by
necessary homogeneity of species. In a first approach a human of 100 W would
need minimally 100 m2 land surface to stay alive. However, by all
efficiency losses and more ecologically responsible farming one could better
depart from 5 000 m2 (half a hectare).
There is more than
6 000 times as much solar power available as mankind and other organisms use.
The Earth after all has a radius of 6Mm
(6 378 km at the equator, 6 357 km at the poles) and therefore a profile
with approximately 128 Mm2 (p x 6 378 km x 6 378 km = 127 796 483 000 000
m2) capturing sunlight. The solar constant outside atmosphere measures 1 353 W/m2,
on the Earth’s surface reduced to approximately 47% by premature reflection (‑30%) or conversion in heat by
watercycle (‑21%) or wind (‑2%). The remainder (636 W x 127 796 483 000 000
m2 of profile surface unequally distributed
over the spherical surface) is available for profitable retardation by life or
man. However, 99.98% is directly converted into heat and radiated back to the
universe as useless infrared light. Only a small
part (-0.02%) is converted by other organisms in carbohydrates and since about
a billion years a very small part of that is stored more than a year as fossile
fuel.
|
|
|
Earth
|
The Netherlands
|
|
radius
|
Mm
|
6
|
|
|
|
profile
|
Mm2
|
128
|
|
|
|
spherical surface
|
Mm2
|
510
|
0,10
|
0,02%
|
|
|
|
|
|
|
|
solar constant
|
TW/Mm2
|
1353
|
832,99
|
61,57%
|
|
solar influx
|
TW
|
172259
|
33,83
|
0,02%
|
|
from which available
|
|
|
|
|
|
sun 47% or 100W/m2
|
TW
|
80962
|
10,00
|
0,01%
|
|
wind 2%
|
TW
|
3445
|
0,68
|
0,02%
|
|
fotosynthesis 0,02%
|
TW
|
34
|
0,01
|
0,02%
|
|
|
|
Fig.
15 Globally and nationally received solar power
|
|
|
The human use of energy
The actual energy use is negligible compared to the available solar
energy (Fig. 15 and Fig. 16).
|
|
|
Earth
|
The Netherlands
|
|
coal
|
TW
|
3
|
0,02
|
0,45%
|
|
oil
|
TW
|
4
|
0,03
|
0,77%
|
|
gas
|
TW
|
2
|
0,05
|
2,14%
|
|
electricity
|
TW
|
2
|
included in fossile
|
|
traditional biomass
|
TW
|
1
|
|
|
|
total
|
TW
|
13
|
0,10
|
0,73%
|
|
|
|
Fig. 16 Gobal and national energy use
|
|
|
Biological storage
The biological process of
storage produced an atmosphere livable for much more organisms than the
palaeozoic pioneers. Without life on earth the temperature would be 290oC
average instead of 13oC. Instead of nitrogen (78%) and oxigen (21%) there would be a warm blanket of 98%
carbon dioxide (now within a century increasing from 0.03% into 0.04%). By fastly oxidating the
stored carbon into atmospheric CO2 we bring the climate of Mars and heat death closer, unless increased growth
of algas in the oceans keep up with us.
Wind and biomass
Concerning Fig. 14, Fig. 15 and Fig. 16 making a plea
for using wind or biomass is strange. Calculations of an ecological
footprint based on surfaces of biomass necessary to
cover our energy use have ecologically dangerous suppositions. Large surfaces
of monocultures for energy supply like production forests
(efficiency 1%) or special crops (efficiency 2%) are ecological disasters.
Without concerning further
efficiency losses Dutch ecological footprint of 0.10 TW (Fig. 16) covered by
biomass would amount 10 times the surface of The Netherlands yielding 0.01 TW (Fig. 15). However,
covered by wind or solar energy it would amout
1/7 or 1/100. However, efficiency losses change these facors substantially (see
1.1.5).
How much fossil fuel is left
To compare energy stocks of
fossile fuels with powers (fluxes) expressed in terawatt in Fig. 15 and Fig. 16, Fig. 17 expresses them
in power available when burned up in one year (a = annum).
|
|
|
Earth
|
The Netherlands
|
|
coal
|
TWa
|
1137
|
0,65
|
0,06%
|
|
oil
|
TWa
|
169
|
0,03
|
0,02%
|
|
gas
|
TWa
|
133
|
1,60
|
1,20%
|
|
total
|
TWa
|
1439
|
2,28
|
0,16%
|
|
|
|
Fig.
17 Energy stock
|
|
|
By this estimated energy
stock the world community can keep up its energy use 110 years.[17]
However, the ecological
consequence is ongoing extinction of species that can not keep pace with climate change. Forests can not
move into the direction of the poles in time because they need thousands of
years to settle while others ‘jump from the earth’ flying for heat.
Fission of uranium
Fig. 16 shows an actual global energy use of 13 TWa. One TWa is 1 000 GWa.
One GWae can also be generated in a nuclear power station. Instead
of 2 000 000 000 kg coal, that requires 800 kg enriched uranium (U)
only. Dependent on the density in the
rock, substantial extraction marks can be left in the landscape. Storage and
transport of the raw material with uranium has to be protected against possible
misuse.
The conversion ino electricity occurs best in a fast breeder reactor.
Older fission cycles with and without retracing of plutonium (Pu) use so much
more uranium that the stocks will not be sufficient until 2050. The fast
breeder reactor recycles the used uranium with a little surplus of plutonium
(see Fig. 18). However, that requires higher temperatures than without recycling.
With non-braked ‘fast’
neutrons from the core of the reactor in the ‘casing’ or ‘mantle’ of
fissionable material non-fissionable heavy uranium (U238) is converted in
fissionable plutonium (Pu239), suitable for fuel in the same reactor.
Uranium stocks
Because the uranium stocks are estimated to be approximately 5 000
000 000kg, approximately 6 million GWa electricity could be extracted
(plus approximately two times as much rest heat). If you estimate the world
electricty use to be 1000 Gwe per year, then that use can be
sustained some 6 000 years with fast breeder reactors. Supposing an
all-electric society and a world energy use of 10 000 GWa, then the uranium
stocks are enough for 600 year.
|

|
|
|
|
Fig.
18 Nuclear fuel cycle of a
fast breeder reactor in 1000kg, producing 1 GWae
|
|
|
Impacts of radio activity on the human body
The released radio-active material radiates different kinds of ionizing
particles. Dependent on their energy (expressed in electronvolt, eV) they can
penetrate until different depths in the soft body tissues where they can cause
damage (see Fig. 19).
|
in millimetres
|
charged particles
|
non-charged particles
|
|
|
alfa
|
proton
|
beta
|
neutron
|
gamma
|
|
on 1 MeV
|
0.005
|
0.025
|
5
|
25
|
100
|
|
on 10 MeV
|
0.2
|
1.4
|
50
|
ca 100
|
310
|
|
|
|
Fig. 19 Halving depth of ionizing
radiation in body tissue
|
|
|
In the air similar distances apply. That means that approaching radio
active waste until some metres does not have to be dangereous. The real danger
starts by dispersion of radio-active particles in the air, water, soil and
food. Through that dispersion the sources of radiation can enter the body and
cause damage on a short distance of vulnerable organs.
The damage is determined by the quantity of the particles of Fig. 19, but also by the composition of the intake and the time they remain in
the body (biological halving time). The composition determines the radio active
halving time and the energy of different particles. The damage is different for
sex cells, lungs, bone forming tissue and/or red bone marrow.
Objections against nuclear enery conversion
Against nuclear energy social and political objections are raised
concerning:[18]
1.
possible misuse of plutonium (proliferation of nuclear weapons)
2.
risks in different parts of the cycle
3.
the long lasting dangers of dispersion of radio-active waste.
Possible misuse
In Fig.
18 some moments exist where ample 2 000kg of
plutonium have to be transported into the next production phase. At these
moments the plutonium can be stolen. If in the breeder conversion plant 12 kg
PuO2 is stolen, then 10 kg pure metal can be produced, the ‘critical
mass’ for an nuclear bomb. However, it is not easy to produce a nuclear bomb
from this material without very large investments.[19]
Risks during operation
In different parts of the cycle risky moments occur. Though the
formation of a ‘critical mass’ where enough neutrons are confined to cause a
spontaneous explosion is very improbable, non-nuclear causes like a failing
coolingsystem or ‘natrium burning’ can get a ‘nuclear tail’ if they cause a
concentration of fissionable material. Both can be caused by terrorist attacks
or war.
Liquid natrium is used as cooling medium in breeder reactors because
water would brake the necessary fast neutrons. Natrium reacts violently with
water and air (eventually with the fission material as well). So, the cooling
system sould not have any leakage. If the cooling system fails, then the fisson
material can melt forming a critical mass somewhere. A breeder reactor can
contain 5 000 000 kg of natrium and by its breeding mantle a
relatively large amount of fission material.
Waste
The danger of dispersion of
radio-active material does not only occur by
accidents. Radio active waste has to be isolated from the biosphere for
centuries to prevent entering the food chains. For any GWa electricity produced
the wastes are approximately:
1 000 kg of fission products
10 000 kg of highly active solid waste (in Dutch: HAVA)
20 000 kg of medium active solid waste (MAVA)
300 000 kg of low active solid waste (LAVA)
2 GWa of heat
Besides that, once in the 20 years dismantling of the plant has to be
taken into account. Many components will have become radio active, so they have
to be stored or reused for new plants.
Dispersion of radio-active material
If concentration of these wastes on a few places could be guaranteed for
many centuries, this relatively small stream of waste would be no problem. The
distance of impact of these radiations is so small, that you can live safely in
the neigbourhood of wastes from many centuries.
However, you cannot guarantee concentration for centuries. Even salt
domes can be affected by geological or climatic proceses. Blocks of concrete
can leake, storage places can be blown up by terrorist or military operations.
Dispersion through the air, water, soil, the food chain or the human
body is dangerous and impredictable. Comparison with other environmental risks
is difficult. If you take the accepted maximum concentrations in the air as a
starting point, you can calculate how much of air you need to reach an
acceptible concentration of the dispersed wastes. To make a volume like that
imaginable, you can express it as the radius of an imaginagy air dome reaching
the accepted concentration by complete dispersion. In that case very roughly
calculated recent nuclear waste of 1 GWa
requires 50km radius. One year old waste requires 40km, 10 years old waste 15km
and 100 years old waste 7km. However, from calculations like this you cannot
conclude that you are safe at any distance. In reality dust is not dispersed in
the form of a dome, but depending on the wind in an elongated area remaining
above the standards over very long distances.
Fission and fusion
If you would have a box with free neutrons and protons at your disposal,
you could put together atoms of increasing atomic weight. However, you would
have to press very hard to overcome the repelling forces between the nuclear
particles. Once you would have forced them together the attracting forces with a
shorther reach would take over the effort and press the particles together in
such a way that they have to loose mass producing energy. Until 56 particles (iron, Fe56)
you would make energy profit. Adding more particles increases the average
distance between the particles mobilising the repelling forces again. If you
would like to build furter than iron, then you would have to add energy.
However, that also means that heavier atoms like uranium can produce fission
energy as discussed above.
Bond energy
The added or released energy are called bond energy. The amount of
available bond energy is dependent from the number of particles in the atomic
nucleus (zie Fig. 20). For example, if you split the nuclei of 1000 kg of uranium (U235) or
even better plutonium (Pu239) into strontium (Sr96) and cesium (Cs137), Fig. 20 shows that you can yield several GWa’s. However, it is also clear that
if you put together 1000 kg of the hydrogen isotopes deuterium (D2) and tritium
(T3) into helium (He4), approximately ten times more GWa can be released.
|

|

|
|
|
|
|
Fig. 20 Bond energy of nuclei as a function of the
number of particles
|
Fig.
21 Progress of nuclear fusion as
expected in 1982
|
|
|
|
Nuclear fusion, the Sun on Earth
This ‘putting together’ is called nuclear fusion. That is more difficult
than it seems, because you could overcome the repelling forces only on 100 000
000 degrees kelvin if in the same time you could keep the hydrogen together in
sufficient density long enough (criterion of Lawson). The Sun does so by its
mass, isolated by vacuum, delivering its energy by radiation only. On Earth
until now, that only has succeeded in experiments with hydrogen bombs, each
ignited with a limited fission of uranium. Since long, the temperature under
controlled laboratory circumstances is no problem anymore. Already in 1960
higher temperatures have been reached. The real problem is, to reach the
Lawson-criterion together with these high temperatures. In that respect
impressive progress is made at the end of the 20th century
recapitulated in the "Lawson-diagram" of Fig. 21.
Thermonuclear power conversion
In 1982 it seemed probable that the first thermonuclear reactor (a
converter based on fusion) could deliver electricity before the end of the
century. But that fell short year after year. Immense budgets were and still
are spent to reach that phase. However, after reaching fusion in controlled
circumstances many technical problems have to be solved, but in the end
thermonuclear reactors will play an important role in energy supply. In the
initial phase of this technology lithium (to be bred from the very volatile and
radio active heavy isotope of hydrogen tritium) will be necessary (D+T
reactor). However, exclusive use of abundantly available and harmless deuterium
will be possible at last.
The stock of deuterium
One of 7000 hydrogen nuclei is a deuterium nucleus. If you estimate the
total amount of water on Earth at one billion km3, the stock of
deuterium is 30 000 Pg (1Pg is 1000 000 000 000 kg). This amount
is practically spoken inexhaustible. The end product is non radio active inert
helium. The radio active waste of a thermonuclear reactor merely consists of the
activated reactor wall after dismantlement. At average that will be
approximately 100 000 000 kg construction material. In the right composition
it will loose its radio activity in 10 years. Instead of storing it, you can
better use it to construct a new plant immediately. Connected to that,
thermonuclear plants can be built best in units of 1.5 GWe regularly
renewed by robots. So, we would need approximately 9000 plants to meet our
current global needs or 7 for the Dutch.
Risks of thermonuclear power
The risks of fission power
plants like for example the proliferation of plutonium, a "melting
down" with dispersion of radio active material are not present in
thermonuclear processes based on deuterium. Any attack will stop the process by
a fall-down of temperature. However, the use of the extremely volatile radio
active tritium in the initial phase is very dagerous. Plutonium is not a
necessary by-product as in any fission cycle, but you can use a fusion reactor
to breed plutonium if you really want to do so. Perhaps it is possible to make
existing radio active wastes from earlier fission harmless in the periphery of
the ‘fusion sun’.[20]
Energy scenarios
For the contribution of
different kinds of energy supply scenarios are made (Fig. 22).
|

|
|
|
|
Fig.
22 Energy scenarios
|
|
|
The small contribution solar
energy (even combined with nuclear power) and the great confidence in fossile
fuels and biomass are remarkable.
Use
According to CBS (2009) Dutch
energy use (see Fig. 23) approaches 100
GW (0,1 TW) from which approximately 10% finally electric: 10Gwe
(0.01TWe)[ee].[21]
|

|

|

|
|
|
|
|
|
Fig.
23 Development of Dutch energy use 1945-2008 ..
|
Fig. 23 .. of which used by power stations
2000-2008
|
Fig. 23 .. of which
used as electricity, heat and lost
|
|
|
|
|
Sun and wind energy
An ecological footprint of
1/7 of our surface on the basis of nearly 7 times as much wind as we need looks favourable, but how
efficiently can wind be harvested? How useful is the power of 680 GW blowing
over The Netherlands? The technical efficiency of wind turbines is maximally 40%, practically 20%. The energy
from wind principally cannot be harvested fully because the wind then would
stand still behind the turbine. At least 60% of the energy is necessary to
remove the air behind the turbine fast enough. Technical efficiency alone (R1)
increases the windbased footprint of 1/7 into more than ˝. But there are other
efficiencies (see Fig. 24) together
reducing the available wind energy from 680 GW available into maximally 20 GW
useful.
The Netherlands
full of windturbines only can afford 1/5 of the energy demand
Putting the Dutch coast from
Vlaanderen to Dollard full with a screen of turbines and behind it a second one
and so on until Zuid Limburg, these screens could not be filled by more than
80% with circular rotors (R2). In the surface of the screen some space has to
be left open between the rotors to avoid nonproductive turbulence of
counteracting rotors (R3). In a landscape of increasing roughness by wind
turbines the wind will choose a higher route. So, in proportion to the height
the screens need some distance to eachother (R4). The higher the wind turbine,
the higher the yield, but we will not harvest wind on heights where costs
outrun profits too much (R5). Decreasing height could be compensated partly by
increasing horizontal density (R6) though local objections difficult to be
estimated here can force to decrease horizontal density (R7).
|
R1 technical efficiency
|
0,20
|
R5 vertical limits
|
0,30
|
|
R2 filling reduction
|
0,80
|
R6 horizontal compensation
|
2,50
|
|
R3 side distance
|
0,25
|
R7 horizontal limits
|
P.M.
|
|
R4 foreland distance
|
0,85
|
PRODUCT TOTAL
|
0,03
|
|
|
|
Fig.
24 Reductions on theoretical wind potential.
|
|
|
By these efficiency
reductions the ecological footprint on basis of wind appears not to be 1/7, but
at least 5. For an ecological footprint on the basis of solar energy there are
only technical and horizontal limits. A comparable ecological footprint then is
1/10. In both cases efficiency losses should be added caused by storage,
conversion and transport, but these are equal for both within an all-electric
society.
Sun, wind or biomass?
The ecological footprint
based on biomass depends on location-bound soil characteristics and efficiency
losses for instance by conversion into electricity. A total efficiency of 1%
applied in the comparance of Fig. 25 is optimistic.[22]
|
|
|
|
W/m2
|
|
rounded
off total Dutch energy use
|
100
|
GW
|
1.00
|
|
rounded
off Dutch electricity use
|
10
|
GW
|
0.10
|
|
|
|
|
|
|
SUN
|
|
|
|
|
The
Nederlands receives
|
10000
|
GW
|
100
|
|
after
reduction by 0.1
|
1000
|
GW
|
10
|
|
required
surface
|
10%
|
|
|
|
|
|
|
|
|
BIOMASS
|
|
|
|
|
The
Nederlands receives
|
10000
|
GW
|
100
|
|
after
reduction by 0.01
|
100
|
GW
|
1
|
|
required
surface
|
100%
|
|
|
|
|
|
|
|
|
WIND
|
|
|
W/m2
|
|
over
The Nederlands blows at least
|
680
|
GW
|
6.80
|
|
after
reduction by 0.03
|
17
|
GW
|
0.17
|
|
required
surface
|
577%
|
|
|
|
|
|
Fig.
25 Comparing the yield of sun, biomass and wind
|
|
|
Costs
What are the costs? In Fig. 26 for wind, sun
and biomass the required surface is represented only. The environmental costs
are not yet stable. Environmental costs of new technologies are in the beginning
always higher than later on. For coal, uranium and heavy hydrogen the environmental costs are calculated, the
required surface is negligible.
|
|
total
|
|
per inh.
|
|
|
Current Dutch energy use
|
96
|
GW
|
5993
|
W
|
|
yielded by
|
|
|
|
|
|
solar cells
|
10
|
x 1000 km2
|
0,06
|
ha
|
|
wind
|
564
|
x 1000 km2
|
3,53
|
ha
|
|
biomass
|
96
|
x 1000 km2
|
0,60
|
ha
|
|
surface of The Nederlands inclusive Continental Plat
|
100
|
x 1000 km2
|
0,63
|
ha
|
|
Actual use electric
|
10
|
GW
|
652
|
W
|
|
remaining heat
|
26
|
GW
|
1630
|
W
|
|
yielded by
|
|
|
|
|
|
coal
|
20864
|
mln kg coal
|
1304
|
kg coal
|
|
waste
|
62592
|
mln kg CO2
|
3912
|
kg CO2
|
|
waste
|
835
|
mln kg SO2
|
52
|
kg SO2
|
|
waste
|
209
|
mln kg NOx
|
13
|
kg NOx
|
|
waste
|
1043
|
mln kg as
|
65
|
kg as
|
|
uranium
|
0.01
|
mln
kg uranium
|
0,001
|
kg uranium
|
|
waste
|
3.45
|
mln
kg radio-active
|
0,216
|
kg radio-active
|
|
heavy hydrogen (fusion)
|
0.01
|
mln
kg h.hydrogen
|
0,001
|
kg h.hydrogen
|
|
waste
|
0.01
|
mln kg helium
|
0,001
|
kg helium
|
|
|
|
Fig.
26 Environmental costs of energy use
|
|
|
The environmental costs of
oil and gas are less than those of coal, but concerning CO2-production comparable: the total production is
approximately 30kg per person per day! That makes clear we have to avoid the
use of fossile fuels.
The contribution of alternative sources
The contribution of non
fossile fuels is increased substantially (Fig. 27), but it is not
yet 1 from the yearly used 100 GW. The growth of 0,5% into 0,8% is mainly due
to the use of waste including biomass unused otherwise.
|

|

|
|
|
|
|
Fig.
27 Sustainable energy sources and nuclear power in the Netherlands 2007
|
Fig.
28 GW sustainable energy sources between 1990 en 2008gg
|
|
|
|
The growth of the
contribution of wind, heat pumps and sun (Fig. 28) is impressive
on itself, but responsible for approximately 0.1% of total energy use.
Stagnating decrease of solar cell costs
Why does solar energy develop so slowly while so much energy can be
gained? Solar cells are 100 times as cheap as 40 years ago. The stagnating
decrease in price of Fig. 14 would be due to
increasing silicium prices and efficiency improvements in peripheral equipment.
Just before passing the economic efficiency of fossile fuels these barriers
loom up. The oil industry has collected solar patents and studies that
question, in the mean time developing the technology to exploit the still large
stocks in oil sands (an ecological disaster). Scenarios still depart from a
small contribution of solar energy in 2030. The development of the steam engine lasted 40 years. Are the technological
barriers now larger? Any way, the consequences are larger than those of the
industrial revolution. Many people
will loose their jobs or investments, but use of energy, depletion of resources
and mobility would no longer be environmental problems. Only basic ecological
problems remain: from the 1.5 mln known species 100 000 are lost, 80% of the human
population is not healthy.
The capacity of electric
power stations in The Netherlands is approximately 15 GWe
(15 000 MWe), from which at average 10 GWe is
used (the rest is necessary to receive peak loads). These plants produce in the
same time approximately 15 GWth. From that heat only a part is used
by cogeneration. Electric power stations can not be switched off immediately.
Temporary overproduction is sold cheaper at night or into foreign countries
(for example to pump up water in storage reservoirs). Approximately 2% is generated
by nuclear power, 1% sustainable, the rest by fossile fuels (see Fig. 23).
|

|

|
|
|
|
|
Fig. 29 Power stations in The
Netherlands
|
Fig. 30 MW capacity per power
station of Fig.
29
|
|
|
|
The use of electricity takes
up only a small part of our total consumption of primary energy sources. The
Dutch energy balance as a whole is represented in the flow diagram of Fig. 31[T.M.1] .
|

|
|
|
|
Fig.
31 Energy flows through The Netherlands, 2000 (x PJ equalling
31.7 MWa)
|
|
|
A summary like Fig. 31 is made every year. Adding “winning” (extraction) and import
while subtracting export, “bunkers” (stocks) and “verliezen en verschillen”
(losses and differences), one has left “verbruikerssaldo” (balance of use). Subtracting from that
balance of use what power companies need themselves, one has left the quantity
customers can use. Losses on the way to the customer have to be subtracted to
find what really lands to the customer, the ‘finaal gebruik’ (final use).[23]
Energy slaves
Calculating back these
figures per inhabitant, expressing them into the individual human power during
a year (100 Wa), one gets a figure like the number of ‘energy slaves’ people have to their
disposal. The balance of use comes down to about 60 energy slaves per Dutch
(wo)man. Power companies need 11 of them to produce the rest. So, 46 remain for
final use. From these 46 energy slaves industry takes 19, transport 8 and 19
are needed for offices and dwellings. From these 19 natural gas delivers 13,
oil 3 and electricity 3 as well.
In 1982 the average
inhabitant had 11 energy slaves in his own home, 10 of them needed for heating.
At that time there were 2.8 inhabitants per dwelling. So, at average
approximately 3000 m3 natural gas per year was needed for heating a house.
The importance of storage
for alternative sources
Sustainable energy sources fluctuate per season or per 24 hour. That
is why their supply does not stay in line with demand. Therefore, energy
storage is of overriding importance
for succes of these sources, but also for mobile applications like cars.[24]
Different kinds of storage
In Fig. 32 some kinds of storage are summed up with their use of space and
efficiency. If you lift up 1000 kg water (1m3) 1 meter against
Earth’s gravity (9.81 m/sec2), you need 1000 kgf or 9810 newton
during 1 m and 9810 newton·meter is 9810 joule or 0.0003109 watt
during a year (Wa, see Fig. 2, page 12). Now you have got potential energy you can partly gain back as
electricity any time you want by letting the water flow down via a water
turbine and a dynamo. The efficiency is approximately 30%. So, you can gain
back maximally some 0.000095 Wa/m3 electricity. If you have a basin
of 1km2 where you can change the waterlevel 1m you can deliver 95 We during a year, 190 We
during half a year or 34722 We (0.00003472 GWe) during a
day. To deliver 1 GWe you need 1/ 0.00003472 km2 = 28800
km2 (see Fig. 32). That is nearly three-quarter of the Netherlands! A larger fall (of 10m for example) improves
both storage and efficiency of the turbine by increased speed of falling water.
|
|
Storage[25]
|
Efficiency
|
Surface for 1 GWe during
|
|
|
gross
|
(max.)
|
net
|
24 hours
|
half a year
|
|
|
Wa/m3
|
%
|
Wa/m3
|
km2
|
km2
|
|
Potential energy
|
|
|
|
|
|
|
water (fall = 1 m)
|
0,0003
|
x30%
|
=0,0001
|
28800
|
5259600
|
|
water (fall = 10 m)
|
0,003
|
x75%
|
=0,002
|
1152
|
210384
|
|
water (100 m)
|
0,03
|
x90%
|
=0,03
|
96
|
17532
|
|
50 atm. pressed air
|
1,3
|
x50%
|
=0,6
|
4
|
789
|
|
Kinetic energy
|
|
|
|
|
|
|
fly weel
|
32
|
x85%
|
=26,9
|
0,10
|
18,56
|
|
Chemical energy
|
|
|
|
|
|
|
natural gas
|
1
|
x80%
|
=0,8
|
3,42
|
625,00
|
|
lead battery
|
8
|
x80%
|
=6,3
|
0,43
|
78,89
|
|
hydrogen (liquid)
|
274
|
x40%
|
=109,5
|
0,03
|
4,57
|
|
petrol
|
1109
|
x40%
|
=443,6
|
0,01
|
1,13
|
|
Heat
|
|
|
|
|
|
|
water (70oC)
|
6
|
x40%
|
=2,5
|
1,08
|
197,24
|
|
rock (500oC)
|
32
|
x40%
|
=12,7
|
0,22
|
39,45
|
|
rock salts(850oC)
|
95
|
x40%
|
=38,0
|
0,07
|
13,15
|
|
|
|
Fig. 32 Storage
capacity (for conversion into electricity) from some systems
|
|
|
Land use
From the row ‘50 atm. pressed air’ on, the last column of Fig. 32 simply departs from a surface with a built height of 1m needed to
deliver 1 GWe (1 000 MWe) during 24 hours or half a year continuously. By doubling the
height of course you can halve the needed surface. Space for turbines and
dynamos is not yet included. Fossile fuel like petrol still stores energy most
efficiently.
However, in normal storage circumstances this surface is estimated
too large for two reasons. Firstly energy production by some differentiation of
sources never falls out completely. So you can partly avoid storage. Secondly,
the average time difference between production and consumption is smaller than
half a year or 24 hours. So, you need a smaller capacity. However, you have to
tune the capacity to peak loads and calculate a margin
dependent on the risks of non-delivery you want to take. These
impacts can be calculated as separate reductions of the required storage
The actual Dutch energy use amounts nearly 100 GW, partly converted
into electricity. So, you do not need 100x the given surface per GW to cover
this use from stock. After all, in the total figure losses of conversion from
fuel into electricity are already calculated in, and these are calculated in Fig. 32 as well.
The different axes of the Earth’s
rotation and orbit a=23,46o
The earth orbits around the
sun in 365.25 days at a distance of 147 to 152 million km. The radius of the earth is only maximally 6 378 km. So, the sunlight reaches any spot on earth by practically
parallel rays. The surface covering that practically circular orbit is called
the ecliptic surface. The polar axis of the Earth has always an angle a = 23,46o
with any perpendicular on that ecliptic surface.
The angle b between polar
axis and sunrays varies around 90o at average
On December 22nd
(Fig. 33) the angle b between polar
axis and the line from Sun into Earth within the ecliptic surface equals 90o + a. On March 21st
b = 90o,
on June 21st b = 90o - a and on
September 23rd again b = 90o. Arrows a in Fig. 33 show the only
latitudes where sunrays hit the Earth’s surface
perpendicular at December 22nd and June 21st. So, the sunlight reaches the earth
perpendicular only between plus or minus 23,46o latitude from the equator (tropics). Anywhere else
they hit the Earth’s surface slanting. At December 22nd the sunlight
(sunray b in Fig. 33) does not even
reach the northpole inside the arctic circle at 90o – 23,46o = 66, 54o
latitude (arctic night).
|

|
|
|
|
Fig.
33 The orbit of the earth around the sun
|
|
|
Sunlight reaching
the earth’s surface
The sunlight reaching the
earth’s atmosphere has a capacity of 1353 W/m2 (solar constant). Some 500 km
atmosphere reduces it by approximately 50%. So, any m2 of sunrays
reaching the surface of the Earth distributes say 677 W over its slanting
projection on the earth’s surface. Let us restrict ourselves in the next
section to the two moments per year the sunrays are perpendicular to the
Earth’s axis of rotation ( b = 90o on March 21st and on September 23rd).
Culmination g, the maximum angle of sunrays to
the local Earth’s SN surface
In Fig. 34 (left) the solar
capacity of 1m2 (677W) is distributed that way over the larger
surface SN (South-North). That 1 m2 capacity, divided by hypotenuse
surface SN, equals sin(g) = cos(l).
So, 1m2 Earth’s
surface in P (maximally turned to the Sun at solar noon) receives cos(l) x 677W.
|

|
|
|
|
Fig.
34 The maximally received solar capacity at latitude l;daily fluctuations
with the hour angle h.
|
|
|
Hour angle h reducing solar
capacity turning away from noon
However, by rotation of the
Earth noon-point P travels around our latitude in 24 hours. At any other point
of the cross-section the maximum capacity cos(l) x 677W at noon
is reduced again by turning away from the sun (see Fig. 34 right). At solar
midnight our location is turned away as much as possible from the sun (hour
angle h = 0o). At noon our location is exposed to
the sun as much as possible (hour angle h = 180o). So, at 6 o’clock solar time the
hour angle is 90o, at 18 o’clock 270o. Between these hours the maximum capacity cos(l) x 677W at noon
is reduced again by cos(h-180)
according to the hour of the day.
The average solar capacity given latitude l
The University
of Technology in Delft is positioned around 52o
latitude, a global parallel crossing the building for Electrotechnical and
Civil Engineering on its campus. The cosine of 52o is 0.616. So,
there the year average solar capacity at noon is 417 W per square meter
earth surface. Averaged again per 24 hours it is 417/p = 133 W (not
concerning Dutch weather conditions). This value is reached only as daily
average on March 21st or September 23rd. At other dates
it varies symmetrically around that average.
Average sunlight per day
On March 21st or September 23rd it happens 24 hours on the whole latitude l circle because
these days polar axis is perpendicular to the sunrays. That circle with radius r of latitude l (‘parallel’), seen from the Sun is a straight line with 2r
length. On both days the Sun continuously delivers cos(l)·677W
distributed over any m2 of that line. In 24 hours that capacity is
distributed over a larger circular surface length 2pr of the whole latitude circle. So, the 24hour average is that
capacity divided by p. We do not yet
have to calculate more cosinuses for every hour (Fig. 34 right) to
conclude that 24hour average. And March 21st or September 23rd
offer useful averages for the whole year as well.
The day period between
sunrise and sunset varies and throughout the year the sunlight
reaches the earth’s surface at noon by a varying maximum angle g (‘culmination’ related to the
Earth’ surface, not to be confused by declination d related to its polar axis, see Fig. 36). After all, seen from the sun the earth nods ‘yes’ (Fig. 35). Bending to left and right does not matter for locally received
sunrays.
|

|
|
|
|
Fig.
35 The yearly nodding earth with a parallel l=52o
seen from the sun
|
|
|
December 22nd the earth is maximally canted a = 23.46o
backwards related to the sunrays. At noon we receive: 677 · cos(52o +
a) = 170 W/m2.
Canting forward on June 21st we have to subtract a:
677 · cos(52o – a) = 595 W/m2. Inbetween we need a
variable ‘declination’ {d | +23.46o ≤ d ≤ –23.46o
} instead of a. In Fig. 36 declination d is positive in June, so now we
can write 677 · cos(l – d) W/m2
for any day at noon at any latitude. From Fig. 36 we can derive
visually: g + l - d = 90o or l - d = 90o
- g.
Declination d could be read
from Fig.
36 or calculated according to Voorden (1979) by d = 23.44 sin(360o x (284 +
Day) / 365). As ‘Day’ we fill in the number of days from January 1st,
for instance:
Mar21 = 31
+ 28.25 + 21 = 80.25
Jun21 = 31 + 28.25 + 31 + 30 + 31 + 21 = 172.25
Sep21 = 31
+ 28.25 + 31 + 30 + 31 + 30 + 31 + 31 + 21 = 264.25
Dec22 = 31
+ 28.25 + 31 + 30 + 31 + 30 + 31 + 31 + 21 + 31 + 30 + 22 = 356.25
The turning earth
But how is that capacity
distributed per hour? The earth turns 360o in 24 hours ousting the Old World by the New Word all the time. That is 15o
per hour, drawn in Fig. 35 (left) by 12
visible meridians of 15o.
The distribution on a
constant latitude l is not only
affected by a declination d varying day by
day but also by the hour angle h visibly varying every minute. From Fig. 37 we derive the
hour angle of sunset and sunrise: cos(hsunset)= h x cot(b)/r x cos(l), while h =
r·sin(l).
|

|

|
|
|
|
|
Fig.
37 Sunset and sunheight at noon varying with b and hour
angle h on one parallel circle.
|
Fig.
38 Looking back to the universe in the Autumn.
|
|
|
|
Within that formula, r plays
no rôle and cot(b) = tan (90o
– b) = tan(d), see Fig. 36.
So, we can write:
sunrise = acos(sin(l) x tan(d) / cos (l)) / 15o
and sunset = 24 hour - sunrise.
The turning sky
Now we can move our field of
vision down to earth looking back to the universe as Copernicus saw it, reconstructing the preceding model
from what he saw. Then we see any star moving daily in perfect circles around,
the Pole Star (Polaris) practically
standing still. So, we see the Great Bear and some ‘circumpolar’ constellations througout the year turning around Polaris (Fig. 38). Other
constellations disappear daily behind the horizon, be it seasonly at an other
moment of the day and therefore in some seasons by day not visible behind the
brightness of the Sun. Polaris is a star 1600 times more powerful than the Sun,
but on a distance of 300 light years. Occasionally it stands in our polar axis
apparently standing still that way, moving too little (1 degree) to take into
account.
The sun against the background of stellar constellations
The Sun makes its daily
circles shifting approximately 1 degree per day (the year circle of 360o
is called eclipse) against a more
stable remote background of 12 constellations (the Zodiac), according to
its yearly wave seen by a nodding Earth.
Turning ourselves 360o
we see a lamp on our desk describing a circle around us as well. Bowing our
head backward 23.46o while turning around we see the lamp low in our
field of vision. When we stay turning around and in the same time walk around
the lamp keeping our head in the same polar direction (slowly nodding forward
until we are half way and than again backward) we experience how we see the sun
during the year starting from December 22st. When we had a third eye
in our mouth we would have a complementary view from the southern hemisphere as
well.
Sun bows in a sky dome
Such circles we
can draw as sun bows in a sky dome using b as deviation
from the polar axis (Fig. 39).
|

|
|
|
|
Fig.
39 Sun bows 3D in a sky dome, map and cross section.
|
|
|
Projecting the sun bow on the earth’s surface
The circular parallel sun
bow divided in hours has to be projected as an ellipse on the Earth’s surface
(see Fig. 40). The hours in
the Azimuth angle then decrease in the direction of sunrise and
sunset.
|

|
|
The hour angle h
in
the parallel surface
|
projected
|
on the Earth’s surface.
|
|
Fig.
40 The hour angle transformed into Azimuth.
|
|
|
Some formulas
To transform the hours of
the parallel surface into hours on the Earth’s surface we can observe two
triangles perpendicular to the surface SouthZenithNorth (see Fig. 41) the first with
two equal sides SunM and MD (r sin b), the second with two equal sides
SunP and PD ( r) as well, and a common third side. The first triangle has an
angle SunMD=180o-h. So, we can use the cosine rule
two times to calculate the square of the third side SunD in both triangles and
angle SunPD = arc p. Spherical cosine rules applied on the spherical triangle
SunZenithD produce Sunheight and Azimuth as angles.
|

|

|

|
|
|
Spherical cosine rule:
cos a = cos b cos c+
sin b sin c cos A
|
|
|
Cosine rule:
a2 = b2
+ c2 - 2bc cos A
|
|
|
|
|
|
|
|
Fig.
41 Two isosceles triangles and a spherical one
|
|
|
|
|
However, Voorden (1979) in
his Appendix A and C (see Enclosure 2) derives by more difficult transformation
rules the usual and easier formulas:
Declination = 23.44o x sin(360o x
(284+Day)/365))
Sunheight=
asin(sin(Latitude)
sin(Declination(Day)) – cos(Latitude) cos(Declination(Day) cos(Hour x 15o)
Azimuth=
asin(cos(Declination(Day) sin(Hour x 15o))/cos(Sunheight(Latitude,
Day, Hour))
On a meridian 1o East of us (68 km on our
latitude) local solar time is already 4 minutes later. If we used the
solar time of our own location we could only make appointments with persons
living on the same meridian. So, we agreed to make zones East from Greenwich of ± 7.5o around
multiples of 15o (1026 km on our latitude), using the solar time of that
meridian. However, between the weekends closest to April 1st an
November 1st we save daylight in the evening by using summertime. By adding an hour around April 1st in the summer, 21.00h
seems 22.00h on our watch and it is unexpectedly light in the evening. So, to
find the solar time from our watch we have to subtract one hour in the summer
and the number of degrees of longitude x 4 minutes West of the agreed meridian.
In the Netherlands
we use the solar time of 15o East of Greenwich (time zone 1), but
live between 3o and 8o.
|

|
|
|
|
Fig. 42 Time zones
|
|
|
So, on the Faculty of
Architecture in Delft (4o 22.5’ easter longitude = 4.38o)
in winter we have to subtract 15 x 4 minutes from our watch time and add 4.38 x
4 minutes (-10.62o x 4 minutes = -48.48 minutes) to find an
approximate solar time. In summertime we have to subtract an extra hour.
Slowing down
traveling around the sun
In addition to these
corrections we have to add or subtract some minutes (time equalization E) amongst others due to differences in travel
speed (29.3 km/s in summer, 30.3 km/s in winter) around the Sun according to Fig. 43.
|
 
|
|

|
|
|
|
Fig. 43 Time equalization per day of the year
|
|
|
So, instead of the Hour we
read on our watch (WHour with minutes decimally added) in the formulas for
Sunheight and Azimuth we should fill in Sun Hour (SHour) from:
As Timezone we fill in 1, 2, 3 and so on with a maximum of
23. As Summertime we fill in daylight saving yes=1, no=0 and
E(Day) we read or calculate from Fig. 43.
Finally, atmospheric
refraction of 34’ and sun radius of 16’ (together nearly
1o) shows us sunrise nearly 4 minutes earlier and sunset 4 minutes
later, but by day this effect approaches to zero at noon.
Putting the formulas we
found in an Excel Sheet (download http://team.bk.tudelft.nl, publications 2007 Sun.xls), we can check them by observing
shadows.
|
Input
|
|
|
|
|
|
|
|
|
|
|
Date
|
|
Time
|
Latitude
|
Longitude
|
|
|
|
Date
|
Days
|
Hour
|
Minute
|
Degrees
|
Minute
|
Degrees
|
Minute
|
Timezone
|
Summertime
|
|
18-apr-03
|
108,25
|
11
|
45
|
52
|
0
|
4
|
30
|
1
|
yes
|
|
|
|
Fig. 44 Data needed
for solar calcuations
|
|
|
We need date, time, geographical
coordinates, the time zone and wether or not we have to take summer time into account. The Sheet brings them into a
decimal form and adds a time correction to calculate the hour angle in radians. Excel needs radians to calculate sine, cosine and
tangent.
|
Calculated
|
hour
|
h
|
m
|
deg
|
|
|
|
|
rad
|
|
Watch time
|
11,75
|
11
|
45
|
|
|
|
|
|
|
|
TimeCorrection
|
-1,69
|
-2,00
|
19
|
|
|
|
|
|
|
|
Sunhour
|
10,06
|
10
|
4
|
|
|
|
|
|
|
|
Hour angle
|
|
|
|
151
|
|
|
|
|
2,63
|
|
|
|
|
|
|
|
|
|
|
|
|
Timezone
|
1
|
|
|
|
|
|
|
|
|
|
Summertime
|
1
|
|
|
|
|
|
|
|
|
|
Latitude
|
|
|
|
52,00
|
|
|
|
|
0,91
|
|
Longitude
|
|
|
|
4,50
|
|
|
|
|
0,08
|
|
|
|
Fig. 45 Restating
data in dimensions needed
|
|
|
The sheet then calculates
the declination of the day and at what time on our watch we
can expect sunrise, culmination and sunset neglecting atmospheric influence from –4 to + 4 minutes. Finally the sheet
calculates Azimuth and Sunheight. Azimuth is
calculated from South, but a compass gives the number of degrees from North (180 –
Azimuth).
|
Calculated
|
hour
|
h
|
m
|
deg
|
|
|
|
|
rad
|
|
Declination
|
|
|
|
10,6
|
|
|
|
|
0,18
|
|
|
|
|
|
|
|
|
|
|
|
|
Watch Sunrise
|
6,77
|
6
|
46
|
|
|
|
|
|
|
|
Watch Culmination
|
13,69
|
13
|
41
|
|
|
|
|
|
|
|
Watch Sunset
|
20,61
|
20
|
37
|
|
|
|
|
|
|
|
Azimuth
|
|
|
|
40
|
|
|
|
|
0,70
|
|
On Compass
|
(180 - Azimuth)
|
|
140
|
|
|
|
|
|
|
Sunheight
|
|
|
|
42
|
|
|
|
|
0,74
|
|
Prediction
|
|

|
|
Height
|
10,00
|
|
Shadow
|
10,97
|
|
|
|
Fig. 46 Solar
calculations
|
|
|
The height of an object on
the Earth’s surface given, the sheet calculates the length of its shadow.
Measuring
sunheight
Now we can check these
results by putting a pencil in the sun. Measure its height, the length of its
shadow and Azimuth as the angle of its shadow with a North-South
line (using a map or reliable compass, not disrupted by iron in the
neighbourhood!) (Fig. 47).
|

|
|
|
|
Fig.
47 Fast indoor check of shadow.
|
|
|
Outdoors you can measure
angles copying, folding and cutting the paper instrument of Fig. 48 to get the
sunheight and the height of buildings. To measure
height of buildings you need a mirror or mirroring piece of glass. Measuring
Azimuth you need a compass or map as well.
|

|
|
|
|
Fig. 48 Cut and fold this paper instrument
|
|
|
Using the paper
instrument
|

|

|

|
|
|
|
Fig.
49 Measuring Azimuth, sunheight and building height outdoors
|
|
|
Fig. 49 shows a compass directed to the sun by adjustment to the
shadow line of a vertical object. It indicates 106o
from North, which is 74o from South (azimuth). Sunheight
appears to be 39o on the paper instrument. Turning the instrument 180o
partly covered by a piece of glass we read an angle of 40o (tangent
0.84) to the upper edge of the mirrored building. According to our distance
meter that building is at 8.37m distance. However,
when we measure it by tape measure it appears to be 10.30m, occasionally just
like the shadow . So, we do not trust the electronic divice. It apparently has
measured the tree closer by. The height of the building must be 10.30 x 0.84 = 8.65m above the table
surface from which we took the measurement (35cm above ground level). So, the
building should be 9m high. That could be right, because the building has 2
storeys (3 layers).
Check your measurement by calculation
Now we can fill in the
measurements (Fig.
50) and check its prediction.
|
date
|
09-06-03
|
dd-mm-yy
|
|
Watch time
|
10.15
|
hour.minute
|
|
Building height
|
9
|
metres
|
|
Shadow
|
10.30
|
metres
|
|
Azimuth
|
74
|
degrees
|
|
Sun height
|
39
|
degrees
|
|
Building height and Shadow would indicate (calculated):
|
|
Azimuth
|
74
|
1.29
|
|
|
degrees
|
radians
|
|
Sunheight
|
41
|
0.79
|
|
|
|
Fig.
50 Checking shadows
|
|
|
The sun height may be
measured a quarter earlier. Then it was calculated as 39o indeed.
The shadow was predicted to be 10.27m elsewhere in the sheet So, the
measurement agrees with the calculation rather well.
Around your house
Fig. 51 shows a plot
division of 19 dwellings taking shadow into account
(download http://team.bk.tudelft.nl publications 2003 standaardverkaveling.exe). All of them have the
same plot area of 120m2, but the Southern dwellings have narrow and
deep plots to make front gardens possible and make the back gardens accessible
for sunlight at some distance of the buiding. However, the Northern dwellings
with South gardens have shorter and wider plots and parking lots instead of
front gardens and public green. Eastern and western buiding blocks have no sun
in the street in the morning or evening but at noon they have. But at the back
they have a different character. Western blocks do have sun in the garden and living room in
the morning, Eastern blocks in the evening. Having breakfast or dinner in the sun attract (or create) people with
different life styles.
|

|

|
|
|
|
|
Fig. 51 Plot division taking shadow into account
|
Fig. 52 Avoiding shadow by
neigbours according to German regulations
|
|
|
|
The value of dwellings can
decrease when neigbours are not limited in building on their plots by regulation
removing sun from other gardens. So, many urban plans regulate building on private plots.
In the garden
Fig. 53 shows the length
of shadows on June 2nd from an object of 10m
height for every hour. Try other dates.
|

|

|
|
|
|
|
Fig.
53 Shadows throughout the day June 2nd
|
Fig.
54 A garden on June 2nd at 12 o’clock
|
|
|
|
At noon - 13h40min. -
shadows are smallest. Turning the figure with that point North we got some idea
(not precise, see Fig. 40!) of the shadows
to be expected throughout the day. The figure is symmetrical around that point
and the centre. It does not seem so because the graph rounds off on full hours,
sunrise is at 5h31min., sunset at 21h50min. and noon inbetween. So, we can put the figure on a map
of same scale with that orientaton and shift it on a line with given height to
get som idea of the shadow caused by a building block, a line of trees and so
on. East~ and westward shadows are symmetrical.[26]
Diversity of life
From an urbanistic point of
view shadow is important for climate and lightning of outdoor space, gardens
and public spaces. Fig. 54 shows a South
garden with two small trees at the southern border
(above) throwing shadow. The Northern part has sunlight all day and ants
clearly undermine the pavement there. There is a substantial damage on
pavements by ants in towns. However, the continuously shadowed
Southern part of the garden is more moisty and the pavement is filled by rough
moss. At the Eastern
and Western part of the circle inbetween the tiles (20x20cm) grass and flatter
kinds of moss find their optimum.
North and South
parts
In the sunny Northern side
sun loving plants like grape (Fig. 55 left) find their
optimum, in the Southern shadowed borders you find shadow loving plants like
ferns (Fig. 55 middle).
|

|

|

|
|
grapes
|
ferns
|
cars
|
|
Fig.
55 Full sun to grow grapes, filtered shadow for ferns and full
shadow for parking cars
|
|
|
|
|
On the other side of the
building (Fig. 55 right) there is
full shadow all day with high trees catching light in their crowns only and
slow growing compact shrubby vegetation in a little front garden. Such fully
shadowed spaces are suitable for parking lots. “Keep pavements
in the shadow” may be a sound rule.
The roof of public space
Trees filter sunlight by small openings projecting
images of the sun on the ground as Minnaert noted in the first article of his marvellous
book in three volumes on physics of the open air. You can see it best when an
eclipse of the sun is projected thousendfold on the
ground (Fig. 56). Most solar
images are connected to vague spots and sometimes the
openings in the foliage are too large to get clear images. Leaves of a
tree are composed differently into a so called leaf mozaic (Fig. 57).
That roof of public space is worth more attention. People love the
clairobscur of filtered light with local possibilities of choice for full
sun and full shadow meeting their moods. It challenges their eyes more than one
of the extremes continuously. Urban designers should be aware of the importance
of light and its diversity in cities. None of them ever makes a shadow plan, though any
painter knows that shadow makes the picture. The same goes for artificial city
light in the evening and at night. Dry engineers
calculate the minimum required amount of light for safety to disperse
streetlamps as equally (economically) as possible over
public space.
Fight for light
Nature’s diversity is
primarily based on competition for light. Some plants
grow as high as possible to outrun neighbours. Others are satisfied by less
light growing slower, using more years to reproduce. By very closed foliage some trees do not leave any light to plants on
the ground like spruces and beeches. They are the
trees of dark forests. Trees of light
forests are not stingy with light for plants growing below, like birches. They need
helpers there to get the right minerals from soil. So, trees are different in
light permeability (Fig. 58).
|

|

|

|

|
|
weeping willow (treurwilg)
|
poplar(populier)
|
alder(els)
|
lime(linde)
|
|

|

|

|

|
|
plane(plataan)
|
elm(iep)
|
|
|
|
|
|
|
Fig. 58 Light permeability of trees
|
|
|
|
|
|
Light
How do we measure such
differences? The power of visible radiation (the part of radiation we call ‘light’) produced by a
1/60 cm2 black body with the temperature of melting platina (2047oK)
under specified pressure in a specified angle (‘sr’, 8% of a sphere, see Fig. 59) is 1 candela (cd).[27] That equals 1/683 watt/sr. It is a measure characterising the power
of a source of light in its point of departure, not its dispersed impact
elsewhere, at any distance or surface. To quantify that amount of light we need an other unit, the lux. To calculate
the number of lux you receive at your desk, you have to take the distance to
the source into account, because that determines the dispersion of light power
per m2 of your desk. If you want 1 lux covering 1m2, you
need a power of 1 candela at 1m distance and that is called 1 lumen. The
surface increases with the square of the distance, so at 2 m distance you need
4 lumen and 14 candela (produced by a light bulb of less than 0.1 watt). To be
able to read you need much more.
The Sun produces 2·1028
candela, but the amount of light reaching the Earth is small. To calculate that
amount we have to divide the number of candelas of the Sun by some angle
covered by the Earth to get the number of lumens at that distance. What we
subsequently receive per m2 is lux (lumen/m2). The Earth
receives 7·1017
lumen. Devided by its cross (see Fig. 33) section that
would be approximately 5000 lux. That is too much to read a book.
Now, let us take a closer
look.
|

|
An angle covering 1
spherical m2 at 1m distance (radius) around the source is called a ‘spherical radius’ (‘sr’, ample 8% of a sphere, a
rotated angle of 65.541o).
A candela (cd) produces per sr a power
of 1 lumen (lm), at 0.5 sr
0.5 lm, dispersing that power according to the distance to source. So, cd =
lm/sr and lm = cd·sr.[28]
But how much power
actually reaches your book? The lightning power of 1 lm per m2 on
a specific location is 1 lux (lx). So, lx = cd·sr /m2.[29]
And you need 300 – 1500
lux to read a book. Lux is something we can measure easily by a lux meter. Fig. 60 shows how
shifting the lux meter 10cm can decrease lightning power from 2500 to 1100
lux.
|
|
|
|
Fig. 59 Candela, lumen, lux
|
|
|
Light on your desk
|

|

|

|
|
directly under
the lamp
|
at a small
distance
|
90o
turned laying flat
|
|
Fig. 60 Impacts of distance to source and direction of surface on
local lightning power
|
|
|
|
|
Turning the lux meter 90o
(Fig. 60) diminishes the
available power/m2 further to 300 lux. So, distance to source and
orientation of surface to light in the neighbourhood of the source
(here approximately 30cm) make much difference. On larger distance the impact
is less dramatic. Besides to this, the colour differences between the
photographs show the differences a camera can not compensate like our eyes do
by perception with brains near by.
To calculate which lamp you
need at a given distance to read a book, you can avoid candelas if you know the
lumen/watt efficiency of a lamp. A light bulb has 12 lm/W, low voltage halogen
20, a LED nowadays reaches 150. If you need 300 lux, that is 300 lm/m2
at 1m, but lumens are dispersered over a larger surface by the square of the
distance to the source, so you should divide the available lumens by the square
of the distance. So, at 2m you need 1200 lm. That is a light bulb of 100W, a
low voltage halogen of 60W or LEDs totalling 8W.
The Earth
Latitudinal differences
account for the largest global variations (from approx. -40°C to 30°C) in
average monthly temperatures (Fig. 61 and Fig. 62).
|

|

|
|
|
|
|
Fig. 61 Global winter temperatures
|
Fig. 62 Global summer temperatures
|
|
|
|
Europe
Latitudinal differences
account for most of the average monthly temperature variations in Europe,
but these are moderated by the sea from approx. -15°C to 25°C (Fig. 63 and Fig. 64).
|

|

|
|
|
|
|
Fig. 63 Winter temperatures in Europe
|
Fig. 64 Summer temperatures in Europe
|
|
|
|
The Netherlands
Latitudinal differences
account for most of the average monthly temperature variation in the Netherlands, but they are moderated
by the sea, especially in winter, from approx. 3°C to 17°C (Fig. 65 and Fig. 66).
|

|

|
|
|
|
|
Fig. 65 Winter temperatures in the Netherlands
|
Fig. 66 Year temperatures in the Netherlands
|
|
|
|
Heat islands
The study of urban heat islands (see Fig. 67) has become synonymous with the study of urban climate. Since the
increased urbanization and industrialization of the middle of the twentieth
century the intensity and the extent of the thermal anomalies has grown. The
urban heat island influences physiological comfort, cooling and heating
requirements, air circulation and precipitation.
|

|

|
|
|
|
|
Fig. 67 The urban heat island
|
Fig. 68 “Green finger parks” as a
contra form of radials in the city
|
|
|
|
The structure of the city itself
influences also the climatic conditions of the city through the density of the
buildings, the urban open space, the width of the streets, the crookedness of
the streets, the squares and the occurrence of parks and trees aligning streets
or squares. Wind velocity will not be discussed in this section.
What causes the urban heat
island?
What causes the differences in climatic conditions between an urban
area and the surrounding rural areas? The urban heat island is caused by the large heat capacity and the high
heat conductivity of urban building material. These facts prevent also a rapid
cooling of the urban environment after sunset. This balance causes all kind of
movements from the surroundings of a city to the city. The heat island is
also equally influenced by other factors such as: rapid runoff of precipitation
and as a result a lower amount of evapotranspiration. Through
all the buildings and metalled surface the city does not have left over a lot
of space where rain can infiltrate the soil. The rain will stream in the sewers and will be discharged immediately. The extra heat in the form of waste heat from urban and industrial
buildings the year round together with the heat from the air conditioning in
the summer deliver an equally important amount of heat to the city.
Contrast with rural areas
This is in great contrast with
the situation in rural areas, where the heat capacity is substantially lower.
The heat conductivity is also lower in the rural area. The extra heat delivery
by buildings and industry is also nearly negligible.
The differences between urban and
rural areas concerning heat capacity and conductivity and the other above
mentioned factors make it possible to draft an energy balance between these two
areas. This balance alters dependent on the situation such as summer-winter,
sunshine or rainfall.
The differences are responsible
for pressure differences in the atmosphere and cause equalization by a
streaming of air from an area with high air pressure towards an area with a low
air pressure. This means a streaming of air from the colder rural area towards
the warmer city or a wind blowing towards the city. The wind is relatively
cooler then the temperature in the city. The wind will have the Buys Ballot
deviation so it will have a deviation to the right on the northern hemisphere
and to the left on the southern hemisphere.
Differences in the built up
area
Of course there are heat
differences in the built up area. It will be obvious that the heat capacity and
the heat conductivity will be different for the various urban fabrics. They
will be influenced strongly by the cover and the shape of roofs i.e. tiles or
bitumen and flat or with inclination, metalled surfaces and parks in
combination with water bodies like lakes and canals. Especially the parks with
water bodies can have a positive influence on temperature. The temperature
there is lower than in the surrounding urban area. If a wind blowing in the
city from the rural area outside the built up area passes a large enough park the
temperature of the air will cool down. The form of the parks in the built up
area plays an important role. Since the air does not flow directly in a
straight stream from outside to the centre of a city but with a curve, a belt
of parks around the city will not be so effective as “green finger parks” in
the form of radials in the city (see Fig. 68).
Local variation
In the Netherlands,
on 3rd March 1976, the differences in local temperatures, within metres of each other, ranged from -2°C to 62°C (Fig.34)!
The air temperature at a height of 1 metre (Fig. 69) was 11.8°C.
|

|
|
|
|
Fig. 69 Surface
temperatures along a line perpendicular
to edge of a forest
|
|
|
Plants are long term
indicators of local climate and environment (sun, wind,
water, soil) while occasional measurements give a random indication of moments.
Plants receiving shadow
throughout the day in the growing seasons grow larger and narrower (etoilement) than the same species
receiving more sunlight. They look for light rising as high they can (see Fig. 70A).
|

|
|
|
|
Fig. 70 The influence
of variations in light
|
|
|
A plant can not grow if
the day is too short (see Fig. 70B above).
However, some species
are adapted in a way they grow better if the day is short (see Fig. 70B below).
The plant species listed below occur so widely that it is well worth
while getting to know them.
In the tables below, a number of plants are mentioned in the month
in which they can first be encountered in the Netherlands.
The distance to the sun
‘vibrates’ in periods of 100 000 years or less, causing ice ages and great differences in wind, water, earth
and life stored and named in layers of soil (Fig. 71).
|

|
|
|
|
Fig.
71 Temperature fluctuations in The Netherlands in the past 3 million
years
|
|
|
These impacts are readable from the
topographic history of The Netherlands (Fig. 72).[30]
|
 -200000 -200000
|

-150000
|

-75000
|

-40000
|

-10000
|
|

-5500
|

-4100
|

-3000
|

-2100
|

-1000
|
|

-200
|

600
|

1000 high tide
|

1000 low tide
|

1100
|
|

1300
|

1550
|

1675
|

1800
|

1850
|
|

1930
|

1960
|

1989
|
|
|
|
|
Fig. 72 De topographic history of
The Netherlands
|
|
|
The Dryas and
Alleröd Periods (from 10,000 years BC)
In the famous Lascaux caves, people have made images of mammoths and
long haired rhinos. These animals became extinct during the last Ice Age. In
Scandinavian countries this period is known as Weichsel and in the Alpine countries as Würm. A tundra plant
‘dryas octopetala’ grew in our part of Europe at that
time and gave its name to the last cold period of the Weichsel.
|

|
15 000 – 10 000 b.C. Older Dryas period

|
|
|
|
|
Fig. 73 The end of
the Weichsel ice age, the Dryas period
|
Fig. 74 Vegetation
during the Dryas period
|
|
10 000– 9 000 b.C. Alleröd period

[T.M. de3]
|
9 000 – 8 000
b.C.

[T.M. de4]
|
|
|
|
Fig. 75
Sub-divisions of the Dryas
|
|
|
The PreBoreal and Boreal Periods (from 8,000 BC)
In the warmer periods that
followed the Dryas, people learnt
how to hunt smaller animals using correspondingly smaller stone tools. The
Mesolithicum, the Middle
Stone Age, had already started,
and peat was also beginning to form due to the warmer
climate.
About 8,000 BC the oceans
began to rise again, because of the melting ice, and the North Sea filled with water again.In the Netherlands,
peat formation began late in the Boreal Period, after the cold extensions of the Dryas
and Pre-Boreal, and this
continued into the warm and humid Atlanticum. The rising sea
levels flooded western parts of the country.
|
Pre-Boreal (8,000 BC)
|
Early Boreal (7,000 BC)
|
|

|

|
|
|
|
Fig. 76 The
landscape of the Pre-Boreal and Early Boreal
|
|
|
Approximately 5,500 BC the
sea formed off-shore bars that during the ebb tide were blown higher, forming
dunes. In the Waddenzee, behind the dunes,
fine sand and silt were deposited, successively, on top of the peat base. The
silt became the ‘old’ or ‘blue’ marine clay of (the provinces of) Holland.
|

|

|
|
|
|
|
Fig. 77 The Boreal landscape. (from 5,500 BC)
|
|
|
Atlanticum (from approx.
4,000 BC)
While ever the sea continues
to rise, the coast and the peat advance. Approx. 3,000 BC the rise in sea level
began to slow down; the off-shore bars remained intact and these broadened out
seawards to form a strong coast.
A new row of dunes was laid
down in front of the old ones and the
peat that had grown on top of the blue marine clay, in so far as the sea had not
washed it away, was dug out later. Peat streams first became estuaries and then
reverted back to peat streams again. The sea cut into the Sub-Boreal peat
leaving channels in which fine sand was deposited. Subsequent drainage caused a
reversal in relief.
|
Atlanticum (4,100 BC).
|
Atlanticum (3,000 BC)
|
|

|

|

|
|
|
|
|
|
|
Fig. 78 The
landscape of the Atlanticum
|
|
|
|
|
|
|
|
|
Approx. 2,100 BC, rivers
carred fresh water into the lagoon behind the off-shore bars, causing
widespread peat formation
|

|

|
|
|
|
Fig. 79 The
Sub-Boreal landscape
|
|
|
Approx. 1,000 BC: The
stagnation of water from streams also causes hoogveen (i.e. peat formations above the water table) to develop on the lower
parts of sandy ground (e.g., the Peel and Drente).
Approx. 200 BC: peat erosion
also occurs along the shores of the Almere lake (Zuiderzee area), thereby
extending the lake.
|
Late Sub-Boreal, 1000 BC
|
Sub-Atlanticum, 200 BC
|
|

|

|

|
|
|
|
|
|
|
|
Fig. 80 The
Sub-Boreal landscape and Subatlanticum
|
|
|
|
|
|
|
|
Approx. 100 BC: The sea
attacked again and large areas of the laagveen (i.e. peat formations below the water table)
were washed away: this continued for centuries. Bloemers, Kooijmans et al. (1981) and Klok and Brenders (1981) describe Roman relics from this period in
The Netherlands like Corbulogracht (Fig. 82).
Approx. 600 AD: The sea
first broke through in the North to create the Waddenzee and the Zuiderzee.
|

|

|
|
|
|
|
Fig. 81 The
landscape of the Early Middle Ages, 600 AD
|
Fig. 82 Roman sites
|
|
|
|
Wetland and water
Few shoreline and water
plants flower before may.
|
|
wetand
|
water
|
|
|
May
|

|

|
|
|
|
yellow iris/yellow flag
(gele lis)
|
yellow water-lily
(gele plomp)
|
|
|
June
|

|

|
|
|
|
bulrush (lisdodde)
|
arrowhead (pijlkruid)
|
|
|
July
|

|

|
|
|
|
common reed (riet)
|
spiked
water-milfoil (aarvederkruid)
|
|
|
|
|
|
|
|
Fig. 83 Flowering
periods wetland and water
|
|
|
|
|
|
Disturbed and
ruderal grounds
If one comes across pioneer
vegetation in a certain season, then one can assume that the ground has been
recently disturbed. If one comes across plants that grow on rough ground
(ruderals), then one can assume that the soil was disturbed one or more years
previously.
There are few plants growing
on rough ground that flower before March.
|
|
pioneering-plant
|
ruderal
|
|
Jan
|

|

|
|
|
|
chickweed (vogelmuur)
|
groundsel (klein
kruiskruid)
|
|
|
Feb
|

|

|
|
|
|
common whitlowgrass (vroegeling)
|
coltsfoot (klein hoefblad)
|
|
|
March
|

|

|

|
|
|
shepherd’s-purse (herdertasje)
|
purple dead-nettle (paarse dovenetel)
|
giant
butterbur (groot hoefblad)
|
|
April
|

|

|

|
|
|
dandelion (paardebloem)
|
rape (koolzaad)
|
cow
parsley (fluitekruid)
|
|
May
|

|

|

|
|
|
greater plantain (grote weegbree)
|
oxe-eye daisy (margriet)
|
comfrey (smeerwortel)
|
|
June
|

|

|

|
|
|
biting stonecrop
(muurpeper)
|
persicaria/red shank (perzikkruid)
|
rosebay willowherb (wilgeroosje)
|
|
July
|
|
|

|
|
|
|
|
tansy (boerenwormkruid)
|
|
|
|
|
|
|
Fig. 84 Flowering times
pioneers and ruderals
|
|
|
|
|
|
There are few pioneering
plants that begin to flower after June.
Grassland and
forest
If one encounters woodland
vegetation, then the soil has remained undisturbed for a longer time.
|
|
grass land
|
wood/forest
|
|
Jan
|

|

|

|
|
|
daisy (madeliefje)
|
hazel (hazelaar)
|
snow
drop (sneeuwklokje)
|
|
Feb
|

|

|

|
|
|
lesser
celandine (speenkruid)
|
alder (zwarte els)
|
cornelian cherry (gele kornoelje)
|
|
March
|

|

|

|
|
|
ground ivy (hondsdraf)
|
silver birch (ruwe berk)
|
wood anenome (bosanemoon)
|
|
April
|

|

|

|
|
|
lady’s smock/ cuckooflower (pinksterbloem)
|
poplar (populier)
|
broom (brem)
|
|
May
|

|

|

|
|
|
meadow buttercup
(scherpe boterbloem)
|
common
oak (zomereik)
|
herb-robert (robertskruid)
|
|
June
|

|
|

|
|
|
tormentil (tormentil)
|
|
wild honeysuckle
(wilde kamperfoelie)
|
|
July
|

|
|

|
|
|
water mint (watermunt)
|
|
hop (hop)
|
|
|
|
|
|
|
Fig. 85 Flowering times on
grass land and in forest
|
|
|
|
|
|
Few trees flower after May.[31] [32]
Mowing Grasslands
Grassland plants indicate
frequent mowing, however, from
the nature of grassland vegetation and on the basis of the above table, one
should be cautious to mow in flowering periods if you do not want to disturb
animals like butterflies.[33]
|

|
|
|
|
Fig.
86 The effect of mowing on various species
|
|
|
Some species show a second
flowering period after mowing.
Mowing to remove minerals
On poor soils one encounters special plants in greater
diversity than on rich soils. There, they are pushed aside by very common
species like stinging nettle (brandnetel).
For more than 10 years
already there has been a mowing policy in Zoetermeer that is directed towards
ensuring that the food content of roadside vegetation is drastically reduced by
regularly removing biomass:
|

|
|
|
|
Fig. 87 Mowing management in Zoetermeer
|
|
|
Over a period of 10 years,
impoverishing the soil does not appear to lead to a large increase in the
number of species growing there. Obviously, more time is needed for this to
happen.
The key thing to remember when
designing and using planting elements is that you are dealing with living material.[34] Architects work with dead material; buildings are not living
organisms. Trees grow, and young trees have a form, different
from mature trees. They look different in winter and change under the influence
of climatic conditions. A plane tree, for example, has a pyramidal
form when young and then ‘sags’ when older. Trees attain their typical growth
form when they are 15 to 20 years old and keep it
until they are 80, but by then they will have acquired an individual
‘character’. Shrubs usually achieve their mature form after about
10 years. Perennials and roses reach maturity in just 2 to 3 years.
The following illustrations give
an impression of the wealth of effects that can be achieved with planting.
|
|
|
|
|
|
|

|

|

|

|

|
|

|

|

|

|

|
|

|

|

|

|

|
|
|
|
Fig. 88 Visual effects of planting
|
|
|
Conceptual framework
Introduction
The conceptual framework is a
language to express and convey planting effects. To describe a particular
effect we can draw from the themes and related visual forms described below.
The overall effect. Depends on the role of each theme.
Themes
The degree of screening[35]
Height is an important consideration
when deciding on planting elements. Their height determines how much of the
objects behind the planting can be seen. The degree to which they are hidden is
called the degree of screening.
The degree of transparency
The visibility of objects behind
the planting also depends on how much can be seen through the planting. This is
referred to as the degree of transparency.
The degree of uniformity
When looking at a planting
element we can examine the diversity of species in relation to the height of the composition to determine vertical variation in texture.
The degree of continuity
In the same way, the diversity
of species along the length of the planting element can be examined. The
horizontal variation in texture is important.
Structure[36]
The manner in which trees and
shrubs are placed to create a unified composition has a strong influence on the
other themes. Structure plays a major role in creating the overall
effect.
Edge profile
In urban areas planting elements
are usually narrow and consist, essentially, of two edges. The profile of these edges has
a major influence on the appearance of planting elements.
The degree of naturalness
The mood or atmosphere created depends to an important extent on
whether the composition has a formal, artificial appearance or an informal, ‘natural’ feel.
Characteristic Forms
Each theme can manifest itself
in different ways characteristic forms. These can be clearly indicated by
introducing terms for all the possible forms.
The degree of screening
|

|
|

|
|
Fig. 89 Edge: maximum planting height 0.5m
|
|
Fig. 90 Articulation: planting height between
0.5 and 1.5 m
|
|
|
|
|
|

|
|

|
|
Fig. 91 Partition: planting height between 2
and 5 m
|
|
Fig. 92 Screening: planting is higher
than 5 m
|
The
degree of transparency
|

|
|

|
|
Fig. 93 Wall: the planting blocks all vision
|
|
Fig. 94 Curtain: even, partial visibility
through the planting
|
|
|
|
|
|

|
|
|
|
Fig. 95 Window: opening in the planting
|
|
|
The degree of uniformity
|

|
|

|
|
Fig. 96 Even: no clear vertical variation in
texture
|
|
Fig. 97 Layered: clear vertical variation in
texture
|
The degree of continuity
|

|
|

|
|
Fig. 98 Constant: no horizontal differences in
texture
|
|
Fig. 99 Rhythm: differences in texture at
regular intervals
|
|
|
|
|
|

|
|
|
|
Fig. 100 Accentuation: random striking
differences in texture
|
|
|
Edge
profile
|

|
|

|
|
Fig. 101 Receding
|
|
Fig. 102 Upright
|
|
|
|
|
|

|
|
|
|
Fig. 103 Overhanging
|
|
|
Degree of naturalness
|

|
|

|
|
|
|
|
|
Fig. 104 Straight and ‘hard’: the planting has
straight contours and ‘hard’ boundaries
|
|
Fig. 105 Ragged and ‘soft’: the planting has
irregular contours and vague edges
|
Structure
|

|

|

|
|
Fig. 106 Trees
|
Fig. 107 Trees with occasional shrubs
|
Fig. 108 Shrubs with occasional trees
|
|
|
|
|
|

|

|

|
|
Fig. 109 Shrubs
|
Fig. 110 Trees with a shrub margin
|
Fig. 111 Trees with a shrub layer
|
Each of the characteristic forms
described above can be created using different design tools:
Edge
·
Native stock trimmed to form a
hedge
·
Low-growing non-native plants
Articulation
·
Native stock trimmed to form a
hedge
·
Smaller, non-native shrubs
Partition
·
Native shrubs with or without
trimmed edges
·
Larger
non-native shrubs
Screening
·
Tree planting, no crown raising
·
Tree planting with shrub layer;
the trees and shrubs must intertwine
Wall
·
Native species with a dense,
compact habit
·
Non-native evergreen species
·
Wide spacing and sufficient
thinning to allow full growth and the development of complete foliage cover
·
No crown thinning, branch reduction
or crown raising
·
Broad
plant bed
Curtain
·
Species with an open and loose
habit
·
Small distances between plants,
which encourages them to grow upwards
·
Crown thinning, branch
reduction and crown raising is possible
·
Narrow plant bed
Window
·
Native shrubs pruned to the
right height
·
Low, non-native shrubs
·
Widely spaced shrubs for full
growth and good foliage cover
·
Trees with upright crowns
·
Trees with raised crowns
Even
·
Large number of species,
individually mixed
·
Small number of species with
very similar textures
·
One species
Layered
·
A few layers with very
different textures
·
Each layer consists of one species
or a few species with very similar textures
Constant
·
In species-rich planting the
length of the planting element must be many times its height (minimum 100 m)
Rhythm
·
Striking individual trees or
shrubs planted at regular intervals
Accentuation
·
Striking individual trees or
shrubs at irregular intervals
Receding
·
Free growth along the edge
·
Shrub margin in front of tree
planting
Upright
·
Use of woodland planting as
hedge
·
Tree planting with low
branching crowns
Overhanging
·
Edge pruning in a margin of
trees and shrubs
·
Crown raising in an margin
containing only trees
Straight and hard
·
Pruning for shape
·
Straight, clearly defined edges
·
Rhythmic or striking
accentuation along the edge
·
A sharp silhouette
·
Layered
Ragged and soft
·
Vague, ill-defined edges;
abundant herbs in the edge
·
Individual mixing of striking
species
·
Ragged silhouette
The effect over time
Planting schemes can be grouped
according to the way they develop from the time of planting until they reach full maturity.
The first group consists of
planting schemes with a pronounced static character. Stated simply, the effect of
such planting schemes changes little over time, they just become higher and
fuller. These planting schemes are simple, containing just a few species which
each have a clear place and contribute to the overall long-term effect.
In contrast, the second group
consists of planting schemes with a distinctly dynamic character. A typical example is
traditional woodland planting schemes: species-rich, individually
mixed planting. The roles of the individual species constantly change, creating
a succession of visual effects over time.[37]
The final group of planting
schemes are those with a cyclical development. The visual effect is obtained
by periodic rigorous pruning back to restore the same visual effect.
Each of the planting groups
described above can be linked to a number of specific design techniques to choose from.
Static
planting
|
·
The structure of the planting
and the role played by each species in the visual effect is determined
beforehand.
·
The way the visual effect
will develop is clear from the start; specific maintenance work will need at certain times to achieve this
effect.
·
When the planting has reached
maturity the purpose of maintenance work is to maintain vitality and a tidy
appearance.
·
Radical rejuvenation measures
are delayed as long as possible.
·
The ‘nurse crop’ system cannot be used.
·
Use of long-lived species.
·
Rows of different species.
|

|
|
|
Fig. 112 Static planting technique
|
Dynamic
planting
|
·
Indicate the characteristic
forms that will determine the appearance of the planting (e.g.
transparency)The structure of the planting and the role of each species in creating the visual effect are not fixed
in advance. During the growth of the planting there are certain moments when
the designer and technical maintenance staff have to decide how the planting
scheme will continue to develop. The choice is influenced by the previous
visual forms.
·
The ‘nurse crop’ system can
be used.
·
Plants may be individually mixed.
·
Species with different life cycles
may be mixed together, although this makes maintenance more complex and
expensive. The most manageable system is to keep to the life cycle of the
main plants.
·
The plant bed must be at
least 50 m wide; any narrower and it is extremely difficult to manage the
visual effect. The planting will acquire a ragged appearance with, in places,
considerable differences in height, texture and transparency.
|

|
|
|
Fig. 113 Dynamic planting technique
|
Cyclical planting
·
The appearance of the planting
is fixed beforehand.
·
The desired appearance develops
too quickly but is repeated; the effect is dominated by periodically cutting
back to just above ground level.
·
The timing of pruning is based
on the fastest growers – depending on their rate of growth, once every three to
seven years.
·
The ‘nurse crop’ system cannot be used.
·
Only species amenable to hard
pruning can be used.
·
A wide range of species can be
used because species do not have the chance to suppress other species.
Both the nature of the plant
material and the environment in which it is planted
impose a number of limitations. If these limitations are not properly taken
into account in the design, the desired visual effect will not be achieved.
The range of influential factors
can be divided into two groups:[38]
·
The characteristics of the
plant material itself, called ‘iron laws’.
·
Environmental influences, in
this case the urban environment.
Introduction
The native species available for
planting differ widely in two respects:
·
Light requirement
·
Rate of growth
These differences drive two
processes that are always at work in woodland planting schemes:
·
The natural process of forming
open spaces in woodland
·
Process of species supressing
other species
Because these processes always
occur they are often called referred to as ‘iron laws’.
The natural process of forming open
spaces in woodland
Under natural conditions, herbs
are in time overgrown by shrubs, which in turn are eventually
shaded out by trees. The planting ‘hollows out’, as it were, from the middle.
Eventually, the middle of the planting area will consist mainly of trees;
shrubs can maintain themselves only along the edges. What develops is, in
effect, a natural woodland profile. This process repeats itself
when trees die and fall. In the open spaces where sunlight reaches the ground,
herbs spring up again, only to be overgrown by shrubs, etc.
|
|
|
|
This profile does not develop in artificial urban environments
because the plant beds are usually far too narrow. This means that in urban
areas ‘woodland planting’ based on this natural process
can only contain a segment of the natural profile of the woodland edge. There
are a number of possibilities:
|

|
|
|
|
|
|
Fig. 114 Woodland
profile
|
|
|
|
|
These are called ‘planting forms’ – in effect, no more than
combinations of trees and shrubs derived from the natural woodland edge.
|

|
|
|
|
|
|
Fig. 115 Planting forms
|
|
|
|
If the process is not the basis
of the design, a further option can be added to the list:
|
|
|
|
In such a planting scheme the
process must be continually checked, which requires intensive maintenance.
The appearance easily degrades if maintenance work is not carried out on
time.
|

|
|
|
|
|
|
Fig. 116 Tree layer with a shrub layer
|
|
|
|
Each of the planting forms has
specific planting and maintenance requirements. These are listed below.
Tree
layer
|
|
|
|
Dimensions:
·
minimum width of the plant
bed: 15 metres
·
in narrower compartments one
or two rows of nursery-grown standard trees
|

|
|
|
|
|
|
Fig. 117
Tree layer
|
|
|
|
Tree layer with occasional shrubs
|
|
|
|
In addition to the recommendations for the tree layer above:
·
the shrubs must tolerate
shade
·
the trees must cast as little
shade as possible
|

|
|
|
|
|
|
Fig. 118
the tree layer with occasional shrubs
|
|
|
|
Shrub planting
|
|
|
|
Giving each shrub less space encourages rapid vertical growth.
Constraining horizontal growth, though, usually reduces the robustness of
each individual shrub.
|

|
|
|
|
|
|
Fig. 119 Shrub planting
|
|
|
|
Shrub planting with occasional trees
|
|
|
|
|
·
the trees should cast little
shade
·
trees should be nursery-grown
standards planted at least 20 metres or more apart
the shrubs must grow more slowly than the trees
|

|
|
|
|
|
|
Fig. 120 Shrub planting with occasional trees
|
|
|
|
Tree planting with a shrub margin
|
|
|
|
The recommendations made for the tree layer and for shrub planting
apply here; tree planting with a shrub margin is actually these two forms
joined together. Again, some additional recommendations can be made:
|

|
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig. 121 Tree planting with a shrub margin
|
|
|
|
|
|
|
|
|
Dimensions
·
minimum width of the plant bed for a symmetrical profile: 25 metres
·
minimum width of the plant bed
for an asymmetrical profile: 20 metres
·
15 metres is sufficient width
for a row of nursery-grown standard trees and a row of nursery-grown shrubs
Plant selection and situation
·
sun-loving shrubs can only be planted on open south-facing sites
·
a continuous strip of shrubs on
north-facing edges is not possible: only a few dispersed shade-tolerant shrubs
will be able to survive
·
eastern and western edges
should be planted with shade-tolerant shrubs
|

|
|
|
|
Fig. 122 This is necessary to ensure
sufficient daylight penetration
|
Process of species suppression by
other species
The environment into which new
plants are put (bare soil) is ideal for pioneer species However, planting schemes
often involve planting pioneer species and climax speciesvvv in the same bed. The pioneer species thrive in
this environment and soon outgrow the climax species.
We can deal with this in different ways:
·
accept the suppression of
species
·
prevent the suppression of
species
Working against the suppression of species is not really possible.
Maintaining a rich mixture of pioneer and climax species ‘whatever the cost’
involves a considerable amount of work. The visual effect is highly vulnerable
to any delays in maintenance work.
Accepting the suppression of species
When some slow-growing species have only a temporary role to play in
the visual effect, the suppression of species presents no problems. When the planting is
still young these species can maintain themselves without difficulty and
enhance the appearance of the planting for a while. When the plants grow up
they are eventually suppressed and the fast growing species dominate.
|
|
|
|
|
This means that:
·
the appearance of the
planting changes quite a lot during its development, in a sequence of
intermediary forms
·
this planting type requires
relatively little maintenance
|

|

|
|
|
|
|
|
|
Fig. 123 Intitial
species
|
Fig. 124 suppressed
later
|
|
|
|
|
Preventing the suppression of
species
If a limited number (1 to 3)
of species with the same growth rate are planted none of them will be
suppressed.
This means that:
·
the appearance of the planting
changes little over time
·
such planting schemes require
relatively little maintenance During its development each species plays the
same role in the overall effect.
|

|

|
|
|
Fig. 125 Small number of
species
|
Fig. 126 not suppressed
later
|
|
|
|
|
|
Artificial succession
A totally different way of dealing with
different growth rates is to use the nurse crop system. Pioneer and climax species are planted together, the pioneers (the nurse
crop) protect the climax species when they are young. Once the pioneers have
fulfilled their function they are cut, allowing the climax species to develop
further.
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig. 127 Nurse crop
|
Fig. 128 removed
|
Fig. 129 leaves climax
species
|
|
|
|
|
This approach means:
·
the appearance of the planting
changes considerably and suddenly over time; in effect there are two stages, each
with its own appearance
·
this type of planting requires
a relatively high level of maintenance
·
the appearance degrades if
maintenance falls behind schedule
Introduction
Besides the influences of
the plants themselves, the influences of the physical environment surrounding
the planting also play a role: in this case, the urban
environment.
Data on a number of these
factors are available, for example on:
·
the soil (profile, mineral
composition, organic matter content)
·
water management regime
·
traffic engineering
requirements (sightlines)
·
mains services, cables and
pipes
·
building control (distance to
outer wall)
·
pollution (exhaust gases, road
salt)
·
gusts and downdraughts
A few important aspects are discussed below. These are:
·
the limited space
·
the limited amount of daylight
·
informal use (wear and tear)
Limited space
It is only really the width of a plant bed that sets firm
limitations on the use of woodland planting in urban areas. The plots in urban
areas are often too narrow. Native species in particular need plenty of
horizontal space to grow freely. Shrubs can easily achieve a diameter of 5
meters and the crowns of the biggest trees can be as much as 10 metres across
or more, given time.
The minimum width of a pant bed must be greater than the width of a
spreading shrub because after woodland planting has been thinned the margin
will never consist of a straight row of plants.
Minimum width of the plant bed
·
Shrubs in woodland planting require a plot at least 6 metres wide.
·
A woodland planting that
includes trees requires a plot at least 15 metres wide.
Plant beds narrower than 6 metres wide
·
Only suitable for woodland
planting if at a later stage the margins are continually cut back or pruned.
·
Straight row of nursery-grown
shrubs or trees.
·
The required width can then be
reduced to 5 metres. If the margins are also cut back the plot may be even
narrower.
·
Non-native species with a
narrower growth form.
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig. 130 Plant beds
narrower than 6 metres wide
|
|
|
|
|
Besides a sufficiently wide plant bed, a generous margin is needed
if plants are to grow freely and reach their full width.
Edges
On edges you should leave
space for later development.
|
|
|
|

|

|
|
|
|
|
Fig. 131 Leaving space
|
Fig. 132 for later
|
|
|
|
Another possibility is to plant up the whole plot and remove the
outside row at the first thinning.
|
|
|
|
|
|
An unplanted strip should be left along the margin of the plant bed.
This can be temporarily filled with grass, herbs or ground cover plants.
|

|

|

|
|
|
|
|
|
|
|
Fig. 133
Initial planting
|
Fig. 134
thinning
|
Fig. 135
for growth
|
|
|
|
|
|
|
|
|
|
|
|
|
The stems of the shrubs in the outside row should be no less than 2.5
metres from the edge of the plant bed
|

|
When trees are included in the planting they should be at least 5
metres from the edge of the plant bed.
|

|
|
|
|
|
|
|
|
|
|
Fig. 136
Shrub distance
|
|
Fig. 137
Tree distance
|
|
Planting patterns
|
A regular pattern of rows is the most preferred option for the
long narrow plots usually found in urban areas; it permits mechanised
planting and hoeing and systematic thinning.
|

|
|
An irregular pattern requires more complex maintenance and makes
the visual effect more difficult to control; in narrow plots the planting can
easily take on a patchy appearance.
|

|
|
Rows can either be planted to form a square or triangular grid; an important feature of the triangular pattern is that after the
first systematic thinning the remaining plants are equal distances apart,
which is highly beneficial for their subsequent development.
|

|
|

|
|
|
|
|
Fig. 138 Planting
patterns
|
|
|
Limited daylight penetration
The way the edges of the
planting develop is heavily influenced by the amount of light. Two aspects play
a role here:
|
|
|
|
The orientation of the
edge in relation to the sun.
The location of any nearby objects; other planting and buildings
often cut out a lot of light.
|

|
|
|
|
|
Fig. 139 Sunlight
orientation
|
|
|
|
We can deal with these effects in various ways:
·
Appreciate the positive aspects
of the differences between margins resulting from differences in daylight
penetration.
For example, the differences between a north-facing edge and a south-facing edge can be seen as a
special feature. On the shaded side you can look between the stems into the
planting; in the background the sunlight filters through the foliage on the other side in a soft green haze. On the
sunny side you look at a dense mat of foliage; a few small patches of the
darkness beyond are occasionally visible.
·
Give all edges the same profile through the careful choice of
species.
If the aim is to ensure a good edging with shrubs, species will have to be
planted along the eastern and western edges different from those along the
southern or northern edges.
·
Careful siting of plants in relation to nearby objects[39].
|
|
|
|

|

|
|
|
|
|
Fig. 140 Siting of
plants
|
|
|
|
-
Trees and shrubs can become
straggly and thin if the distance between the plant bed and a nearby object is
less than the height of that object.
-
Spreading, well formed trees
and shrubs and a dense margin can develop where the distance between the plant
bed and a nearby object is greater than the height of that object.
Informal use (wear and tear)
Plants in urban areas are exposed to heavy use. Paths
may be worn by people walking through planting elements and children may play
in them.
Such wear and tear can be resisted. This is often desirable for
planting elements in semi-public spaces, such as residential courts, where residents can exert
informal social control to prevent damage to planted areas. Narrower
strips of planting are particularly vulnerable and the survival of the whole
planting element could be at risk.
·
Preventing informal use
-
The first step is to locate the
planting element with sufficient care: study the walking routes and level of
use in general; maybe even cancel the planting altogether.
-
Plant species that are hard to
walk through, such as thorny bushes, but do not forget that
these can severely hamper maintenance work and are not suitable near schools or
playgrounds.
-
Another option is to add exotic
species to the woodland mix. These give the planting a
more graceful appearance which can evoke greater respect from the public, particularly if they feel
attached to the area.
Instead of preventing informal use there may be opportunities to make use of it.
This may be possible in planting with a clear public function in a more
anonymous location. In such places, informal use of planting elements can
enrich the functional value of the public domain. Moreover, planting areas in
public spaces are usually larger and so informal use is no threat to the
survival of the planting element as a whole. Plots accessible to the public
must be at least 25 to 30 metres wide (deep).
·
Accepting informal use
-
When managing a fait accompli, e.g. surfacing a short
cut worn through regular use, the special qualities (e.g. a certain sense of
secrecy) of cutting through the vegetation is destroyed.
-
Not replanting open spots in
the planting.
-
Use species that are resilient
to wear and tear.
-
Opportunities can be created,
for example by tipping a pile of sand in the planting area so that children can
make a mountain bike arena.
The suitability of planting
depends on climatological conditions (wind, light, seasons)[40] and physical conditions (soil, groundwater level, air and the space
available above and below ground). A different selection of plants is needed
behind the dunes along the coast than on a site in a fenland polder or on the
sandy soils of Noord-Brabant.
As a designer, you will at
first be tempted to base your choice of plants on spatial qualities to do with
dimension, form (habit), colour and structure. A further consideration is
whether the site is in a rural or an urban environment, where there are special
restrictions.
Whatever the scale at which
you are working, the final detailing is crucial. Financial resources will often
be an important consideration (particularly if planting or transplanting older
trees is involved).
Wind
Wind, usually from the sea,
is an important factor in the west and north of the Netherlands; frost in the east and
south. The effects of wind must be fully considered as it exerts considerable
pressure on twigs and branches (in leaf). In rural areas, the direction of the
prevailing wind can often be read from the shape of the trees.
Poplars grow rapidly and quickly make a spatial
impact, but are ‘not solid enough’. At about 40, branches tend to split and so
many trees are felled at around this age. Poplars are not the trees to plant if
you want them to be around in 100 years time, although they can live for a long
time. As solitaires, it may be worth the extra
work, but not for an avenue.
Unfortunately, many a good tree succumbs to our autumn storms; the
poorest specimens have by then lost their leaves, but those that still have a
good leaf cover are exposed to the full force of the wind.
But wind is not restricted to rural areas. The taller buildings
built in recent years create considerable ‘downdraughts’. In front of the Robeco
building in Rotterdam some trees have been planted to absorb these
downward gusts so that passing cyclists are not literally blown through the
air! Climatological conditions, therefore, do play a role in urban planting.
Light
Light pollution (albeit only at high levels) and salt (road salting in winter, fish stalls on the market) are
disastrous for trees. Light requirement and ‘drip damage’ are more important
factors affecting shrubs, and trees with dense crowns permit only a very little
undergrowth. The so-called ‘woodland planting’ (plots with trees and
shrubs) dating from the 1970s often cause problems now. The trees are large and
the undergrowth is dying off purely due to insufficient light. Of the original
large plots full of trees and shrubs, only the edges will eventually remain,
the planting being hollow under the tree canopy in the middle. If you want the
shrubs top remain, plant the trees far apart or choose trees with open crowns
that let a lot of light through. ‘Drip damage’ can be a significant problem;
some hedges (e.g. Yew) are very susceptible to
drip damage, other, like Beech or Sycamore, are unaffected.
Seasons
Planting should look attractive the whole year round. Some trees and
plants bloom in winter. Autumn colouration can also add variety.
Spring (flowering)[41]
·
trees: alder and willow (March); cherry and magnolia (april); apple, horse chestnut, hawthorn (may)
·
Shrubs: hamamelis, forsythia (March); currant, rhododendron (April); azalea (May)
·
bulbs/tubers:
·
early: (February/March):
snowdrop, crocus
·
late: (April/May): narcissus, tulip
·
trees: horse chestnut, catalpa (july); golden rain (June)
·
shrubs: hibiscus, hydrangea, roses and perennials
Autumn (colours)[43]
·
trees: sycamore, birch, hornbeam, sweet chestnut, hawthorn, honey-locust, oak
·
shrubs: whitebeam, currant, spindle
Winter
·
berries: hawthorn, privet, ornamental apple
·
evergreen shrubs: rhododendron, holly, viburnum
·
shrubs with berries: currant, whitebeam, ivy, privet, rose
Winter (flowering)[44]
·
tree: prunus subhirtella ‘autumnalis’ (flowers November/December and again in April)
|
|
|
|
`
|
|
|

|

|
|
Fig. 141 Lime (summer)
|
Fig. 142 Lime (winter)
|
|
|
|
Pysical conditions concern soil, groundwater, air and space for
roots.[45]
Soil
Roughly speaking, soil in
the Netherlands
can be classified into clay, peat and sandy soils (and all the intermediary
forms). Plants on sandy soils – often in windy locations – have adapted by
reducing the size of their leaves (e.g. sea buckthorn, juniper), by growing hairs on their
leaves (mullein) or by taking on light or
greyish colours.
Examples of coastal trees:[46]
·
alder
·
poplar
·
oak
·
willow
·
rowan
Because of their structure, clay and loamy soils retain water for a
long time. They are often cold in spring, and less oxygen is available than in
sandy soils.
Examples of trees on clay/loam soils:[47]
·
alder
·
horse chestnut
·
birch
·
cherry
Another important factor is the presence of calcium, which supports a different
type of vegetation; a base-poor dune vegetation contains different plants to
calcareous dune valley vegetation. Peaty areas are acid and always
moist; nutrient levels are a crucial factor. alder and rowan do well in nutrient-rich peat, birch in nutrient-poor peat. Well-known shrubs
suitable for acid soils are rhododendron and azalea. If they are planted in
other soil types, peat will always have to be added to the soil.[48]
The above also applies, in principle, in rural areas, where plants
still have a ‘feel’ for the soil. Clearly, in purely urban environments the
original soil is less important for plants, particularly trees.
|
|
|
|
Sea clay
River clay
Peat
Sandy soils
Loamy soils
|

|
|
|
Fig. 143 Soils of The Netherlands
|
|
|
|
Groundwater
If the water table is too high, few trees and shrubs will be able to survive. Tree roots will
develop poorly and not anchor the tree well in the ground; as a result they are
easily blown over. Of course, too little groundwater is not good, either; the
plants wilt.
Trees which can grow in wet conditions are: Alder, Birch, Poplar and
Willow. [49]
Trees that can grow in dry conditions are a few Maple species,
Birch, Hornbeam, Acacia and a few Poplar species. During the growing season
(May to August) tress take up large quantities of water from the soil.
In an urban environment, trees depend on a number of sources of
water:
·
Groundwater
·
Capillary water (‘sucked’ up from the groundwater through the
soil)
·
Pendular water (precipitation that clings to the surface of
particles in the aerated zone)
The demand for water in summer is greater than the amount of
pendular water. The extra is drawn from the groundwater; the water table falls
in summer, but it is replenished again in winter from rain and snow.
Much water in the city goes straight into the sewer; the more
‘porous’ the paving is the better this is for the trees. But the
water must remain for as long as possible in the pendular water zone. Humus is a valuable component in the soil because it
retains a lot of water.
The best situation is a water table that fluctuates around 1.25 m under the soil
surface (1.50 m in the summer and 1 m in the winter).[50] Under these conditions trees can become well established and firmly
anchored. If a tree cannot take up enough water, the roots go in search of
more. The root ball of a healthy tree reflects the size of the
crown.
|
|
|
|

|

|
|
1. Soil containing humus
2. Capillary zone
3. Water table
|
|
|
Fig. 144 Spring
|
Fig. 145 Autumn
|
|
|
|
|

|

|
|
|
|
|
Fig. 146 Groundwater
level approx. 1.25 m:Roots and branches: above ground = below ground
|
Fig. 147 Deep
groundwater level: roots ‘search out’ water
|
|
|
|
Air
Trees in built-up areas – except trees in parks and gardens – grow
in a habitat that simply cannot be compared with a site in a wood or open
landscape. The soil in the country is open (to air and water) and
fallen leaves provide a supply of nutrients. Conditions in urban areas are very
different. Paving requires well compacted soil; but trees need open soils. Air
is kept out by the closed road surface and compacted soil, which leaves almost
no pore volume for air to penetrate.
In open soils, about 50% of the volume is air; below 15% oxygen,
roots become stunted, at 11% oxygen they start to die. All paving seals the
surface of the soil and so open spaces – slotted flags or widely spaced paving
bricks – are essential. Trees cannot develop roots under asphalt surfaces (0% oxygen). The pressure and vibration caused
by heavy traffic further compacts the soil.
In ‘sinking’ areas (peat soils) in the West of the
Netherlands the paving has to be raised every so often, even up to 30
or more centimetres at a time. As a result, many trees receive too little oxygen and die. Oak and Beech always die, Lime trees grow a new layer of roots if the additional
soil layer is no deeper than 25 to 30 cm. Elms and Planes tolerate these conditions quite well.[51]
|
|
|
|
A. Sinkhole
B. Sawn kerb, min. length 500
C. Kerb type Cru 80
D. Tree grille Cruquius concrete blue limestone
colour 1200 x 1200 x 120
E. Air grate
F. Dark paving brick (size, 20x6.6x6)
G. Dark paving brick (Waal
size, 20x5x7)
|
 ` `
|
|
|
|
|
|
Fig. 148 Tree pit
|
|
|
|
Root corridor and tree pit
Urban trees cannot be viewed
in isolation from their environment; they are one of the factors that define
the public domain in the city. Street trees add to the quality of public spaces
and have a different effect in each place. When planting trees in urban areas
it is wise to design a strip for trees only, with no cars, cables and pipes or
street furniture: a ‘corridor’. This ‘plantpit’ can be finished with a 10
cm layer of sand, with paving on top (with no risk that the paving will sink
any faster than the surrounding area).[52]
If this is not possible, a tree pit of 2 x 2 x 1 m should be made
and filled with suitable tree soil. Tree soil is light soil, contains approx.
4% humus, is well aerated and well drained, retains water well and contains
sufficient nutrients. Where more air is required in the soil, perforated
drainage pipes can be used as ‘air pipes’ to ensure better aeration of the
soil.
In many places, though, hard road surfacing and numerous mains
services and cables leave no room for planting. In these situations the
minimum area required for a tree is 7.5 m on both sides (i.e. 15 m apart)
because otherwise they will have an even greater struggle for survival. The
more open the structure of the topsoil, the better this is for the tree.
It is important to choose a good tree grille. Square tree grilles are
often used in paved areas because these fit well into the pattern of most
paving materials. Cast iron or metal tree grilles are attractive, but
expensive. Accumulation of dirt and rubbish in the space between the grille and
the soil (approx. 10 cm) can be prevented by filling this space with Argex
pellets until right under the grille. These are light,
expanded clay granules (reddish brown) which considerably improve
aeration. Another attractive solution is to use gravel. A cheaper option is 30 x
30 cm slotted flags. In parking areas always ensure that the tree trunk is protected.
|
|
|
|
Cross-section
Pavement
Tree corridor
Road / main sewer
Pavement / cables and pipes
|

|
|
|
|
|
|
Fig. 149 Cross-section
|
Size, form, structure, colour
Size and form not only depend on climatological and physical
factors, but also have a major impact on the streetscape. In spatial terms, they may
or may not provide structure or accentuate the spatial composition (see Tree Structure Plan Amsterdam). Texture relates to the
shape, size and arrangement of the leaves and it is very important when
detailing to ensure compatibility with the materials used. Colour speaks for
itself. A significant fact is that light green tints have the effect of
expanding spaces, dark green and red-brown
make spaces seem smaller and can create a sombre
atmosphere. Copper-leaved trees are striking, particularly as solitaires, such
as copper beeches on farms (also sycamore/maple, apple, cherry, oak).
Choosing a tree
When choosing trees, consider the amount of space
above ground. If you meet the conditions discussed above (tree pit, soil, etc.)
there is a chance that the trees will grow to maturity and attain their full
size. Plane trees can easily have branches 10 m long, and so
they should be planted 12 m from buildings. If the pavement is not very wide,
choose a tree a size or two smaller or a tree with a columnar crown. If not,
the crown will soon grow up against wall and must either be pruned each year,
or the tree felled and another species planted.
Size classes of trees:[53]
·
Size class 1: 15 m and taller
·
Size class 2: to about 10 m
·
Size class 3: to about 5 m
Size 1 trees develop crowns at least 15 metres across. Large dense crowns
must be avoided in small streets, where trees with light open crowns are to be
preferred (e.g. Gleditsia/Honey Locust). For most residents the minimum
acceptable distance between crown and wall is about 2 metres. Obviously,
planting distances will bear some relation to the location of the doorways,
drives and passages along street frontages.
Planting distances
If trees are planted very
close to buildings, drastic measures are repeatedly needed to ensure enough
daylight penetration. Sometimes these measures
can be so drastic that the resulting remnant of the tree may no longer make a
positive contribution to the streetscape.
To plant trees that can develop freely with the minimum number of
complaints, you need to weigh up the following considerations:
·
The nature of the building
facade
·
The distance between the trees
and the building
·
The distance between the trees
·
The tree species
·
The pruning method
In real terms, this means that when planting new trees, minimum distances must
be adhered to. Greater distances should be used when planting trees with a
broad, dense crown, such as plane and horse chestnut.
Trees may only be planted at shorter distances than given in the
table:
·
When planting trees with a
columnar or thin crown
·
Along ‘blind’ walls
·
When special pruning methods are used, such as espalier, pyramid pruning
and pollarding
·
When only a few trees are
planted along a street frontage
Rows of trees let through very different amounts of daylight, depending on whether the
crowns of the trees join together (closed) or are spaced apart. This makes it
important to note the relevant planting distances for the various size classes.
Planting
As a rule trees are planted between 1 November and 15 April. They are then
resting and have the best chance of becoming established.
Standard sizes of trees for planting are:
·
14–16 cm girth (approx. 5 cm
diameter)
·
16–18 cm girth (approx. 6 cm
diameter)
·
18–20 cm girth (approx. 6.5 cm
diameter)
The price ratio for these sizes is 1:1.5:2.
Planting distances for rows of trees:
|
|
|
|
|
Size class
|
open row (spaces between
crowns)
|
closed row (crowns
touching)
|
|
size class 1
|
> 18 m
|
5–10 m
|
|
size class 2
|
> 12 m
|
5–8 m
|
|
size class 3
|
> 9 m
|
< 5 m
|
|
|
|
|
Minimum distance between the buildings and the centre of the stem[54]
|
|
|
|
size class
|
min. distance stem to
building
|
|
size class 1
|
6 m
|
|
size class 2
|
4 m
|
|
size class 3
|
3 m
|
|
|
|
In urban renewal areas where high levels of vandalism are expected it is better to plant fewer
larger trees rather than a larger number of thinner trees.
Transplanting
Trees with stems about 30 cm diameter can be transplanted; the larger the tree, the
more expensive the operation. Trees with bigger stems can be transplanted, but their chances of
survival are much smaller. Ensure that the root ball is as large as possible (min. 3 m across and
1–1.5 m deep). If you know well in advance that a tree will be transplanted the
roots can be cut when the tree is still standing, and new hair roots will grow
to form a neat compact root ball. This can be done is summer or winter.
The latest method is to soak the root ball in winter. This then
freezes to create a solid ball of soil and roots. The tree can then be lifted
out with a crane and transported by trailer to its new site. After planting
(good pit and tree soil, etc.) the tree should be pruned to restore the balance
between the root system and the crown. Prices depend on size, transport options
(disconnecting the overhead tram lines, transplanting at night, etc.) and
financing. Transporting a Horse Chestnut with a stem diameter of 45 cm over a
distance of 1 km (difficult journey, disconnection of tramlines and transport
by night) costs about € 10,000 per tree.
|
|
|
|
groundwater (grondwater)
compacted street sand (verdicht straatzand)
gravelbed (grindbed)
heavy clay (zware klei)
drainage (drainage)
Bicycle path (fietspad)
Parking places. (parkeerplaats)
Tree soil, compacted in two layers (bomengrond
verdicht in twee lagen)
Road (rijbaan)
Asphalt (asfalt)
Soakaway (zinkput)
Pipe between drain and soakaway (verbindingsdrain
tussen drain en zinkput)
|

|
|
|
(Source: Groen 1, 1994)
|
|
|
Fig. 150 Modern tree pit design for the trees in the
Plantagemiddenlaan, Amsterdam
|
|
|
|
Different visual effects can be reached applying loose groups and
solitaires, rows, rhythm, screens, walls or diferent canopies.[55]
Loose groups and solitaires
|
The plants are allowed to
grow in their natural form and are often used to create a contrast between a
‘hard’ architectural element and a loosely structured planting scheme. A
‘loose’ planting scheme can only be used when there is sufficient
space available. Solitary trees are, in effect, ‘green monuments’; they often stand in
special locations and have a striking form (e.g. a Lime tree in the village square).
|

|
|
|
|
|
|
Fig. 151 Loose groups
|
|
|
|
Rows
|
A planting scheme in which the distance between trees is so great
that the crowns cannot meet. Rows are often used for long,
regular street frontages. The free-standing trees provide some visual
articulation along the length of the street. In rows the specific
characteristics of the tree species are the key visual features: each crown
is clearly set off against the buildings.
|

|
|
|
|
|
|
Fig. 152 Rows
|
|
|
|
Rhythm
|
Comparable with a row, but
in this case the trees are planted in such a way that the visual articulation
they provide is integrated into the design structure of the built
environment. A rhythm may consist of solitaires. This planting pattern can be
a good solution for situations where there is not enough space for continuous
planting schemes. Instead, many trees can be planted on corners or other
regularly occurring sites where there is more room.
|

|
|
|
|
|
|
Fig. 153 Rythm
|
|
|
|
Screen
|
A screen is a transparent wall of trees through which the facades of the buildings
are more or less visible, depending on the viewpoint. A screen is best
created using species with an open crown in which the branches do not grow in
one main direction so that they easily flow together to form a visual whole.
Elms are good trees for creating a screen. Some
other species, if planted close together and with some extra pruning, can also
be used to create a screen effect. A problem, though, is that if the trees
are planted close together the transparent effect can easily be lost.
|

|
|
|
|
|
|
Fig. 154 Screen
|
|
|
|
Wall
|
A wall consists of multiple rows of trees planted
short distances apart so that the crowns grow into each other. If tree
species that develop dense crowns are used (e.g. Lime) it may even be possible
to plant just one row; the trees must then be no more than 8 m apart. In the summer
this planting scheme creates the effect of a ‘green wall’. It is important that
the trees form a continuous whole. If the planting distances are too great or
if too many trees are missing from the row, the wall effect is largely lost.
|

|
|
|
|
|
|
Fig. 155 Wall
|
Canopy
|
|
|
|
A canopy consists of multiple rows of trees short
distances apart and with intertwining crowns. The most suitable trees species
are those with a broad, fairly open crown. The canopy effect is largely lost
if the trees are planted too far apart to form a unified mass.
|

|
|
|
|
|
|
Fig. 156 Canpy
|
|
The choice of tree
species, pruning method and intensity of the maintenance regime are
determined partly by the street profile. The biggest problems arise in narrow
streets with trees that are too large. In narrow streets with pavements between 3 and 5 metres wide,
only trees with a narrow pyramidal or columnar crown should be planted. Trees
with a broad pyramidal crown or a definite spreading habit must be planted at
least 7 m from the nearest building.
|

|

|
|
|
|
|
Fig. 157. Columnar
or pyramidal crowns in narrow streets
|
|
|
|
|
Trees in size classes 2
and 3 are also suitable for planting in these situations. Fig. 158 shows a cross-section
through a narrow pyramidal tree in a narrow street. This tree requires a lot
of pruning:
Crown thinning: pruning
branches back to allow daylight penetration to the buildings
Possibly crown reduction:
shortening lateral branches to prevent them touching the buildings
In wider streets with
pavements at least 6 m wide it is possible to plant trees that have a more
spreading habit. The maintenance work required is comparable with that in
example A.
|

|
|
|
|
|
|
|
|
Fig.
158 Narrow columnar habit
|
|
|
|
|
|
|
Fig. 159 shows a tree with a columnar crown has been used.
These require less pruning: only crown raising and possibly a little
thinning. Unfortunately, few species have this habit. The well-known Populus nigra ‘Italia’ cannot be
planted in narrow streets because its very shallow roots push up the hard surfacing
(heave). This species requires a zone about 5 m across free of hard
surfacing.
|

|
|
|
|
|
|
Fig. 159 Pyramidal habit
|
|
|
|
|
Fig. 160 shows a tree planted near
a private garden. In these cases, medium-sized trees should be planted no
less than 5 m away from the edge of the garden. For trees with a spreading
habit, like Plane and Horse Chestnut, this distance may need
to be as much as 15 m.
This distance must be
adhered to prevent:
·
the tree blocking out all
light to the garden;
·
undue sucker growth in the
garden;
·
spreading branches.
In special cases, meetings
can be held with local residents/users about planting trees in or near
private gardens, but firm maintenance agreements will have to be made.
|

|
|
|
|
Fig.
160 Tree close to private garden
|
|
|
The sensitivity of certain species to climatological influences,
particularly when they get older, can pose considerable problems. The most
striking example is vulnerability to wind. Large, spreading branches
are highly dangerous and may lead to liability problems for the party
responsible for maintenance (usually the municipal council).
Besides the habitat of the trees, other essential factors in
achieving the desired visual effect are the choice of species and planting scheme. If, for example, a screen
of trees is to be planted in a street, the designer will have to decide whether
to use a slow-growing species at short distances apart or a fast-growing
species planted further apart. In narrow streets, however, fast-growing species
will soon cause problems and it is better not to use them.
There are three methods for achieving a reasonably good
planting(visual effect(time)) in a relatively short time:
- plant slower growing trees at short intervals;
- plant a mix of fast and slow growing species;
- plant semi-mature trees (more than 10 years old).
Re 1: Planting at short intervals quickly yields a reasonably good
visual effect. Short distances between trees are often necessary to obtain a
screen or wall effect. An advantage of planting trees close together is that the trees compete for light and
quickly grow upwards, giving an upright habit with straight stems. A
disadvantage is the extra pruning that is often required.
Re 2: Mixing species with different growth rates requires intensive
maintenance work which must be carried out promptly. It is only recommended for
planting in broad strips of vegetation (woodland planting). The advantage here
is that slow growers are ‘forced up’ by faster growing species. This only works
with some species: elms can be combined with poplars; oaks grow too slowly and are eventually shaded out.
Re 3: Another option is to plant semi-mature trees at their final
distances apart. Semi-mature trees, however, find it hard to adapt to their new
habitat and it takes a few years before they grow at their normal rate again.
Moreover, transplanting is an expensive business. An advantage of
container trees is that they can be planted easily and successfully at any
time, even outside the planting season. This makes these trees highly suitable
for use in special situations: rapid restoration of planting schemes in squares
or along an important road, or after accidents, etc. However, container trees are often slow to become established and can
be ‘overtaken’ by smaller, root-balled trees.
Planting distances
When deciding on the planting distances needed to achieve the desired visual effect
the following points should be considered:
- the final diameter of the crown of the tree
- height of the tree
- the habit of the tree (tree shape, height/width ratio, openness
of the crown)
- the root system
- shading of nearby buildings
- width of the road and path (for canopy effect)
- the relation between the final height of the tree and nearby
buildings
- the period needed to achieve the desired visual effect
A number of examples are presented to explain points 1, 2 and 3.
Road and street planting, seen from
the carriageway
Seen from the carriageway,
rows, screens, walls and canopies create increasingly enclosed effects.
|
Visual contact with the
wider environment. Trees planted at 20 to 30 m intervals form an open
row which permits a good view of the wider environment (trees of size class
1) (See Fig.
161).
|

|
|
|
|
|
|
Fig.
161 Screen/row
|
|
|
|
|
Greater delineation of the
road; a wall gives a stronger effect than a screen. Planting intervals should
be no greater than 10 m to allow the crowns to grow together. A careful
choice of species is necessary because not every species grows well in this
configuration (See Fig. 162).
|

|
|
|
|
|
|
Fig.
162 Wall
|
|
|
|
|
The vault: the trees have an
upright habit (with branches at an angle of 45 to 60 degrees). The crowns
just meet to form a very high ‘roof’. A narrow road planted with Elms creates this effect well (See Fig. 163).
|

|
|
|
|
|
|
Fig.
163 Canopy, vault
|
|
|
|
|
The flat canopy: mature broad pyramidal
trees or trees with overhanging branches give a flat, broad canopy. The
branches grow at an angle of 0 to 45 degrees. Trees that can be used to
create this effect are Oak, Horse Chestnut and Lime (See Fig.
164).
|

|
|
|
|
|
|
Fig.
164 Flat canopy
|
|
|
|
|
The cathedral effect: two rows on either side
of the road, the crowns of the inner rows are lifted higher than the outer
rows(See Fig.
165).
|

|
|
|
|
|
|
Fig.
165 rows are lifted higher than the outer rows
|
|
|
|
Planting distances have a considerable effect on the urban
environment according to the applied size class.[56]
Closed screen or wall
|

|
|
|
|
Fig. 166 Trees of size
class 1; planting distance 5–12 m; open under the crowns
|
|
|
|

|
|
|
|
Fig. 167 Trees of size
class 2; planting distance 3–8 m
|
|
|
|

|
|
|
|
Fig. 168 Trees of size
class 3; planting distance 2–4 m
|
|
|
Row
|

|
|
)
|
|
Fig. 169 Trees of size
class 1; planting distance 20–30 m
|
|
|
|

|
|
|
|
Fig. 170 Trees of size
class 2; planting distance 15–30 m
|
|
|
|

|
|
|
|
Fig. 171 Trees of size
class 3; planting distance 10–20 m
|
|
|
|
|
|
|
|
|

|

|

|

|
|
|
|
|
|
|
Fig. 172 Alder (els)
|
Fig. 173 Black Poplar
(populier)
|
Fig. 174 Ash (es)
|
Fig. 175 London Plane (plataan)
|
|
|
|
|
|
|
|
|
|
|
|

|

|

|

|
|
|
|
|
|
|
Fig. 176 Elm (iep)
|
Fig. 177 Common Oak /
Pedunculate Oak (eik)
|
Fig. 178 Downy/White
Birch (witte berk)
|
Fig. 179 Sycamore /
Great Maple (esdoorn)
|
|
|
|
|
|
|

|

|

|

|
|
|
|
|
|
|
Fig. 180 Locust Tree /
False Acacia (acacia)
|
Fig. 181 Common Lime
(linde)
|
Fig. 182 Common Beech
(beuk)
|
Fig. 183 Horse Chestnut
(kastanje)
|
|
|
|
|
|
|

|

|

|

|
|
|
|
|
|
|
Fig. 184 Weeping Willow (treurwilg)
|
Fig. 185 White Willow (schietwilg)
|
Fig. 186 Pollarded Willow (knotwilg)
|
Fig. 187 Weeping Ash
(treures)
|
|
|
|
|
|
There is a balance between
the amount of leaves and roots a tree has. If too much growth (above ground) is
cut away the tree will compensate for its shortage of leaves by throwing up
many new shoots. Pollarded trees such as Poplar and Willow must be pruned each year. Trained
trees/espaliers are grown for their architectural form. Examples are:
A nursery grown tree has been pruned in the nursery to obtain a
clear stem height of 2 m while its natural form is maintined. During the first
5 to 10 years the crown of the tree will require some light pruning. Trees
close to the edges of a road must have their lower branches remove to ensure
sufficient clearance for passing traffic.
Trees do not last forever,
so do not hesitate to remove old specimens with a limited life expectancy and
plant younger trees!
Crown raising
Trees planted along roads and paths should have their lower branches
removed. This crown raising (to a height of about 2.5 m) is started when
the trees are still young. Depending on the situation, a street tree will have
to undergo further crown raising over the years. In some cases up to as much as
7 m above ground level (species with hanging branches).
When raising a tree crown thought should be given to obtaining the
right balance between the length of the stem and the crown (2:3 or 1:2). It is
an unattractive sight for a tree of 14 m to have a clear stem height of 7 m. In
these cases it is better to go for an asymmetrical crown. In the example above the
tree may have its crown raised to 4 m on the pavement side, but up to 7 m. on
the side above the road. This gives the streetscape a much better appearance.
The rows of elms planted along canals are a good example of
asymmetrical crown raising. In some cases, pruning will still be necessary on
the side facing the buildings to ensure sufficient daylight penetration.
|
|
|
|
|
|
|

|

|

|

|

|
|
|
|
|
|
|
|
Fig. 188 crown raising
near building
|
Fig. 189 crown raising
along a canal
|
Fig. 190 partial crown
lifting
|
Fig. 191 crown raising
in grass
|
Fig. 192 crown raising
in a street
|
|
|
|
|
|
|
Crown raising heights
|
planting stock
|
2.5 m
|
|
residential streets
|
3 m
|
|
main roads
|
4.5 m
|
|
tram lanes
|
4.5 m
|
|
trees with hanging
branches
|
to 7 m
|
|
asymmetrical: housing side
asymmetrical: canal +
quayside
asymmetrical: canal +
grass
|
2.5 m
2.5 m
0–2.5 m
|
|
in grass
|
0–2.5 m
|
|
in ground cover
|
0–2.5 m
|
|
in low shrubs (to 1.5 m)
|
0–2.5 m
|
|
in medium-sized shrubs (to
2 m)
|
2.5 m
|
|
in tall shrubs (from 2 m)
|
2–7 m
|
Summary
The choice of plants depends
on:
1. The site and growing conditions
2. Growth characteristics
and habit of the planting material
3. The appearance of the
planting and the atmosphere it creates
4. Practical aspects
(function and goal)
5. Cost and available funds
|
|
|
|
1. Site and growing conditions
·
natural landscape
·
cultivated landscape
·
urban area
·
nature and character of the buildings (tall
buildings create windy conditions)
Growing
conditions
Soil type
·
Sand nutrient
rich
·
Peat nutrient
poor
·
Clay
o
calcareous / lime rich
o
non-calcareous / base poor
o
acid
o
good/poor structure
o
humus content
Groundwater
levels
·
high – wet
·
low – dry
·
water retaining capacity of the soil
Climatological
conditions
·
sheltered
·
exposed
·
coastal
·
urban area
·
industrial site
·
wind
·
frost
Light
requirement
·
open site / full sun
·
semi-shade
·
full shade
2. Growth characteristics and habit
Tree dimensions
·
Size class 1
·
Size class 2
·
Size class 3
Shrub dimensions
·
Evergreen – taller than 4 m
·
Deciduous 2–4
m
·
0.5–2 m
·
less than 0.5 m
Crown shape and
habit of trees
·
spherical
·
spreading
·
broad pyramidal
·
narrow pyramidal
·
columnar
·
weeping
Crown shape and
habit of shrubs
·
groundcover
·
spreading
·
upright
·
compact
·
overhanging
|
Texture
·
leaf shape
·
leaf size
o
large
o
medium
o
small
·
leaf arrangement
Leaf colour
·
light green – dark blue-green
·
light to dark brown
·
yellow
·
variegated
Blossom
·
flower colour
·
flowering season early
spring
·
spring
·
summer
·
autumn
·
fruit
·
autumn colour
·
bark
3. Appearance
Visual effect
·
ankle height
·
knee height
·
waist height
·
breast height
·
eye level
·
above eye level
Mutual relation
between elements
·
harmony
·
contrast
·
rhythm
·
decorative value
4. Practical aspects
·
winter hardness
·
vitality
·
disease resistance
·
abundant and/or long-lasting blossom
·
function in the plan
·
spatial layout
·
relation to buildings
·
relation to existing planting
·
client’s wishes
·
wind protection
·
shade
·
traffic guidance
·
noise reduction
·
enclosure
·
ground cover
5. Costs
·
purchase costs and required dimensions
·
intensity of maintenance
·
length of implementation period
·
available financial resources
|
Hedges divide the space where a fence or wall is undesirable. The primary function of a hedge
is always separation, most obviously to divide two uses, for example to divide
a private space (garden) from the public space. Hedges provide a natural
background for other plants; thorny hedges form an impenetrable barrier. Hedges
have an important spatial effect. They can be classified into those which
divide up the space in which they stand (‘free-standing’) and those that form
part of a larger mass immediately behind them.[57]
When the spatial impacts of hedges are examined more closely, it
seems obvious to classify them by height. According to their application, we
can then distinguish: edges (to approx 0.5 m high), partitions (0.5–1.5 m) and
full screens (more than 2 m high). Their respective applications are: as an
edge when used to mark out patterns or a composition of lines, as partitions
when their function is to resist or direct movement, and as a full screen to
visually seal off a space.
One spatial effect of hedges is to facilitate comprehension of the
scale of the space and the elements in it, because the hedge has a consistent
size (height) which serves as a reference on a human scale. Another spatial
effect is created if the hedge is quite long and forms a connecting element
that provides continuity. For this purpose hedges do not have to be trimmed; a
row of shrubs (a ‘loose hedge’) can also create this effect. Besides their
spatial effects, hedges may also, possess a number of intrinsic
characteristics.
Natural (loose) habits of shrubs can be tightened up by pruning to
form a hedge. These neater forms give hedges a more cultivated appearance, and
the hedge is a symbol of continuous human intervention in the natural process
of growth. A trimmed hedge can be used in two ways:
As a contrast with ‘looser’ forms in the surrounding area, or with a
less cultivated environment (e.g. a neat hedge around a farm, set in an
agricultural or quasi-natural landscape).
As a harmonising element; the regular ‘architectural’ shape of the
hedge harmonises with an architectural, usually urban, environment.
Hedges may have an ornamental
value, which cannot be seen in isolation from the above – the contribution
the hedge makes to the appearance of the wider environment. The characteristics
of hedges discussed above make them an ideal means to accentuate a prominent
location.
Hedges have two major disadvantages. First, they have to be pruned
regularly, in some cases two or three times a year. Second, they take up
considerable quantities of nutrients, which are then not available for any
plants near the hedge, making regular fertilisation necessary.
Hedges between the main road and
bicycle lane or footpath
These hedges are planted for
traffic safety reasons: they make crossing impossible and at
night they prevent glare from the headlights of oncoming traffic. These street
profiles are only found in post-war urban areas and non-urban areas. Trimmed
hedges require a lot of maintenance, though, and in these situations can easily
be replaced by untrimmed hedge/shrub planting if there is sufficient space, or,
in places where the safety function is not essential, by a normal verge.
Hedges along watercourses
(See Fig.
193)These are also planted for safety reasons, to keep
children away from the water. The hedge is a friendlier type of fence. The need for and value of
hedges in the neighbourhood should be determined. Such hedges do not remove the
danger altogether, but keep it at a distance and make it less threatening, but,
because of this very effect, can make the (unknown) danger much greater.
In addition to the functions mentioned above, these uses of hedges
can enhance appreciation of the scale of the space in which they stand.
Hedges as a visual screen to hide
(mainly) parked cars
(See Fig.
196)This
use of hedges is particularly dependent on the environment. They are suitable
for this purpose in an urban environment, but in other environments they can
easily be replaced by an untrimmed hedge or shrubs. It may even be worth
considering removing some taller plants; owners often want to see their parked cars
from the house.
Hedges as space-shaping elements
Hedges can create their own separate (sub)rhythm different in
character from the larger space they are part of. An example is a garden
surrounded by a hedge, possibly in a park, the regular form providing a
contrast that sets off the space. In this case the trimmed hedge is an
essential element. Should the situation within the hedges ‘not work’, it is
better first to see if another use of the space can improve the situation
before deciding to grub up any hedges. Hedges are planted around playgrounds and seating areas mainly for safety reasons
because they stop children running onto the road. Besides this strictly
functional aspect, hedges also provide ‘shelter’ and ‘security’ for the play
area. In other words, the hedge marks out a territory.
The same quality of ‘security’ or ‘cover’ is provided by hedges
surrounding a sitting area with benches. A trimmed edge is justified around
such areas if they form a contrast with the loose forms in the area and so
create their own place, or if the site is located within a paved area where the
use of hedges adds an architectural dimension and has a practical effect of
saving space (the ‘paved character’ relates to walls as well as horizontal
surfaces).
The hedge as linear element
A tall or medium-sized hedge can provide a background for roses, for
example, or a border. Removing such a hedge
often destroys the appearance of the border and is only advisable if the border
is of a sufficient size.
Hedges that form a pattern or
composition of lines
Very low hedges, which are essentially an edging, are found around
borders of roses or perennials. Often they are laid to give the border a less
dreary look when there is little to see in the border itself. This situation
has value only if two conditions are met:
The height of the hedge is in proportion with the planting material in
the border
The hedges themselves form a particular pattern that is interesting
enough when the roses of perennials have been pruned or cut down.
Use of these types of hedge is only justified in prominent places or
in situations where there is very little green. Moreover, their maintenance is
time-consuming in proportion to their length. Sometimes a compromise solution
is acceptable to reduce the length of such hedges.
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig.
193 Hedge along watercourse
|
Fig. 194 Contrast
|
Fig. 195 Hedge in open
space
|
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig.
196 Hedge bordering car park
|
Fig. 197 Harmony
|
Fig. 198 Hedge as part
of a mass
|
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig. 199 Hedge enclosing
a garden
|
Fig. 200 Partition
|
Fig. 201 Edges
|
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig. 202 Hedge round a
‘place’
|
Fig. 203 Hedge bordering
shrub bed
|
Fig. 204 Complete screen
|
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig. 205 Shelter for seating
|
Fig. 206 Edge
|
Fig. 207 Background to
border
|
|
|
|
|
|
|
Planting distance
|
Loose/regular
|
Growth rate
|
|
Evergreen hedges
|
|
|
|
|
box (buxus sempervirens)
|
5/m1
|
regular
|
|
|
holly (ilex aquifolium)
|
3 ŕ 4/m1
|
regular
|
|
|
common yew (taxus baccata)
|
3/m1
|
regular
|
|
|
holly (ilex aquifolium)
|
|
loose
|
|
|
privet (ligustrum ovalifolium)
size 40–60
|
3 ŕ 4/m1
|
regular
|
|
|
|
|
|
|
|
deciduous hedges
|
|
|
|
|
hornbeam (carpinus betulus)
|
4/m1
|
regular
|
|
|
beech (fagus silvatica)
|
3 ŕ 4/m1
|
regular
|
|
|
hawthorn (crategus monogyna)
|
|
loose
|
|
|
blackthorn (prunus spinose)
|
|
loose
|
|
|
rose – botanical roses
|
|
loose
|
|
|
|
|
|
|
|
Growth rate: number of
years until the plant reaches a height of 1.5 metres (depending on habitat,
soil type and maintenance)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig. 208 vertical
|
Fig. 209 rounded
|
Fig. 210 tapered
|
|
|
|
|
Contents.................................................................................................................................... 105
2.1 Global
atmosphere...................................................................................................... 106
2.1.1.... Air, its mass and density................................................................................................. 106
2.1.2.... Wind, its force and power................................................................................................ 106
2.1.3.... The atmosphere.............................................................................................................. 107
2.1.4.... Climate.......................................................................................................................... 108
2.1.5.... The urban impacts of wind............................................................................................... 109
2.1.6.... Measures, targeted impacts per level of scale.................................................................... 111
2.2 National
choice of location....................................................................................... 112
2.2.1.... National distribution of wind velocity.................................................................................. 112
2.2.2.... Closer specification of wind statistics................................................................................ 112
2.2.3.... The energy profit of wind turbines...................................................................................... 115
2.2.4.... Energy losses from buildings........................................................................................... 117
2.2.5.... Temperature impacts....................................................................................................... 118
2.2.6.... Comfort of outdoor space................................................................................................. 119
2.2.7.... Dispersion of air pollution................................................................................................. 120
2.2.8.... Summary national comparison......................................................................................... 120
2.3 Regional
choice of location...................................................................................... 121
2.3.1.... Roughness of surrounding grounds................................................................................... 122
2.3.2.... Impact of new urban area lose from or adjacent to town in case of
Westerly wind.................. 124
2.3.3.... Impact of new urban area lose or adjacent in case of Easterly wind..................................... 125
2.3.4.... Impacts on energy losses by ventilation behind the edge in the
interior of town..................... 126
2.3.5.... Highways, railways, green areas and forests..................................................................... 126
2.4 Local
measures............................................................................................................. 128
2.4.1.... Local shelter of residential areas...................................................................................... 128
2.4.2.... Increase of wind velocity by height.................................................................................... 129
2.4.3.... The form of a town........................................................................................................... 130
2.4.4.... Dispersion of urban area.................................................................................................. 135
2.4.5.... The form of town edge..................................................................................................... 136
2.4.6.... Wind directions, temperature and built form....................................................................... 138
2.5 District
and neighbourhood variants...................................................................... 140
2.5.1.... From calculable ‘rough surface’ into allotments in a wind tunnel.......................................... 140
2.5.2.... Wind tunnel experiments................................................................................................. 140
2.5.3.... Pressure differences between front and back façades......................................................... 142
2.5.4.... District lay out................................................................................................................ 143
2.5.5.... Neighbourhoods.............................................................................................................. 145
2.6 Allotment
of hectares................................................................................................ 148
2.6.1.... From wind tunnel experiments into methods of calculation.................................................. 148
2.6.2.... Impact of trees................................................................................................................ 150
2.6.3.... Comparing repeated allotments 100x100m........................................................................ 150
2.6.4.... Wind behaviour around high objects.................................................................................. 152
2.7 Sound
and noise............................................................................................................ 154
2.7.1.... Music............................................................................................................................ 154
2.7.2.... Power or intensity........................................................................................................... 156
2.7.3.... Sound and noise............................................................................................................. 159
2.7.4.... Birds.............................................................................................................................. 160
2.7.5.... Traffic noise.................................................................................................................... 161
Pull the closed end of a garden hose out of a bucket filled with
water and take it with you upstairs to the fifth floor. Above 10m, water is
replaced by vacuum like vapour (mercury has
vacuum above 76cm). Apparently, atmospheric air pressure on the bucket (1 bar,
100 000Pa, 100 000N/m2 or old fashioned: 0.987 atm,
10 197.162 kgf/m2)[58] can not push it higher. So,
the mass of approximately 500km air above 1m2 Earth’s surface should
equal approximately 10m3 water or 10 000kg.
Because the surface of the Earth is ample half a billion km2 there is ample 5 x 1018
kg air, less than a millionth of the Earth’s mass (6 x 1024kg). At
sea level density r of air is 1 290g/m3 [59] which equals 3 x 1025 particles (Fig. 213).
So, if your own cross section is
1m2, then in one second at a wind velocity of 1m/sec (3.6km/hr),
1m·1m2= 1m3 air (1.29kg) would hit you. Fortunately much
of this mass immediately starts flowing sideward around you (see chapter 2.6.4). Otherwise it would not ‘pass
by’ and a train of many m3 (many times 1Ľ kg) moving air in front of
you had to be resisted. But you are only changing its direction and velocity,
braking it by ‘negative acceleration’, which is felt as a force, because
force=mass·acceleration as we learned from Newton.
|

|

|
|
|
|
|
Fig. 211 Wind force (= air mass x velocity/sec)
Air mass = density x volume and air volume = height x width x
length. Because air length = velocity x sec, velocity occurs two times in the
formula for wind force, so force increases parabolically by square of
velocity.
|
Fig. 212 Wind velocity increasing by height
depending on roughness of foreland.
Wind load on a building has to be calculated on every layer of
height and summed up to total height. Sideward flow is neglected here
|
|
|
|
But, to keep calculations simple
we suppose you have to resist 1m3 of air per second, that is
1.29kg/s at 1m/s, which is a force of 1.29kg·m/s2 or 1.29N. It is
per m2, so you can also say a ‘pressure’ of 1.29N/m2 or
1.29 pascal (1.29Pa). In storm (10m/sec) it will increase to 129N/m2
(Fig. 211), because now 10m3
air or 12.9kg hits you in one second also with ten times higher velocity! To
get an impression: that force corresponds to the force produced by a child+bike
(30kg) hitting you cycling at 15km/hour.
So, to calculate the force or pressure (force/m2), you
have to take velocity two times into account. One time you need velocity
to calculate the air mass hitting you in one second and the second time you
need velocity to calculate acceleration (velocity per second) to
determine force because force=mass·acceleration.
So, wind force increases parabollically by square of wind velocity (see Fig. 211)[60]. However, these figures are valid on 1m height average, where ‘storm’ in grass land corresponds to 10m/sec (36km/hr) , but at 10m
and 20m height it corresponds to 24 and 26m/sec at the same time. The velocity
increases with the altitude first like a parabole, then logaritmically and at
last exponentially in the ‘boundary layer’ influenced by the ‘roughness’ of the
Earth (see Fig. 212).
Buildings are wider and heigher than
you are, taking up much more m2 surface. But you can not simply
multiply the surface by the force you have to resist on ground level to get the
force a building has to resist, firstly because the velocity increases by
height. You have to calculate the wind load on an building on every level and
sum all these force contributions up to total altitude (see Fig. 212). Download the Windvelocity(height) program with 8 pictures in the
same directory and it will estimate the force in layers of 1cm be it neglecting
sideward effects. The environment on the ground (roughness) has great influence, determining differing parameters you have to
use. Get a feeling how it works by changing wind velocity and roughness in the
program. It is a fast and rough approximation. To be more precise you should
calculate it at any spot by vector integration in 3 dimensions, including
sideward movements, decelerations and accelerations depending on the shape of
the building[61].
However, air density also decreases from 1290g/m3 at
ground level into 1g/m3 at 50km height (see Fig. 213)[62]. So, aeroplanes meet less resistance the higher they fly
(until 20km), but propellers and wings will work less effective as well. That
is why jet engines are used at higher altitudes with higher velocities.
|

|
|
|
|
|
Fig. 213 Pressure,
Density, Particles/m3(height)
A bar is 100000N/m2 or 100000Pa or approximately 1 atmosphere
1.E+03 in Excel means 103
|
|
|
|
The air temperature has three turningpoints according to the
altitude (see Fig. 214)[63].The smallest wave lengths
of ultraviolet sunlight entering the atmosphere from
500km altitude are directly absorbed heating the thin air more than 1000oC
until it equals heat loss by own radiation. That
influence reaches until approximately 100km altitude. Around 50km (mesosphere)
the rest of UV light is nearly fully captured by ozone heating the air until 20oC
at 50km with decreasing influence between 50 and 10km (stratosphere). On 10km
the atmosphere measures ‑ 50oC. However, the main stream
of visible and infrared light is not captured and heats up the Earth’s surface,
on its turn heating up the atmosphere by convection from below
until 10km (troposphere) or radiating it back to universe as invisible infrared
light, only captured by CO2.
|

|

|
|
|
|
|
Fig.
214 Air temperature(altitude)
|
Fig. 215 Air
temperature(log(altitude))
|
|
|
|
An air bubble heated by the Earth’s surface
climbs up in the troposphere expanding by decreasing environmental pressure.
The aquired heat content is dispersed in a larger volume. So, its temperature
decreases until it matches the environmental slower decreasing main temperature
and rising stops. Meanwhile from a specific temperature onward damp could condensate
to steam and ice resulting in cumulus clouds rising with drying air. They
show a flat bottom indicating a temperature boundary for condensation is passed[64]. By condensation solar heat
is released, giving the steaming air bubble an extra push upward.
|

|

|
|
|
|
Fig. 216 Cumulus clouds with flat
bottom
|
Fig. 217 Air bubble condensating
|
|
|
|
The Earth turns Eastward 360o in 24 hours. The equator is
40 000km long[65], as Napoleon ordered to
determine the length of a metre. So, at the equator we have a velocity of
1 670km/hour and we are 3g lighter than at the poles by centripetal force. That force has stretched the Earth’s radius 22km outward compared
with the radius toward poles when Earth was yet a turning droplet from a
sneezing sun. The same still happens to equatorial atmosphere: it is thicker
there than at the poles[66].
Equatorial air heated and saturated from moist by tropical
temperatures climbs fast and high (see Fig. 218). Shortages on the ground are supplied by ‘trade winds’ from South
East and North East[67]. Coming from North and
South they are not used to equatorial high speed Eastward. Seen from the ground
their inertia give them a Westward drift. But they are pulled along with rough
grounds. Then, once heated they climb higher than everywhere else on Earth,
because of centripetal forces. Moreover, environmental density and temperature
decrease slower here with so much competing air bubbles around, stimulated by
an extra push from condensation causing tropical showers below.
But they continue to loose heat by expansion and radiation into the
universe and reach the point they can not rise anymore because their
temperature matches the environment. Where to go? Pressed by their upward
pursuers they fly back high Northward and Southward getting colder and colder
by radiation as an outburned balloon. They land in a subtropic latitude slower
Eastward turning as if they came from South East causing subtropical high
pressure and cyclones in struggle with winds
departing direction South West into tropics as they did themselves in their
youth. They join them at last causing a horizontally rolling spiral movement at
larger scale between tropics and subtropical regions or they travel direction
pole participating in a second rolling movement as South-Western winds we know so well in The
Netherlands.
From the poles cold, heavy sinking air is swung by a turning Earth
in all directions as polar winds. Parallel whirlings drag eachother like
gearwheels in turning cells. Nobel prize winner and founder of chaos theory
Prigogine (1977) boiled water in a very
regular and stable pan like Bénard did in 1904 and saw regular cells emerging
as structured ‘order’ out of chaos. Something like that could happen on a very stable, regularly
heated Earth. But the Earth is turning and nodding (see Fig. 35), shaking its atmosphere like busdrivers their passengers. And it
has continents heating up faster than oceans, having
less water to evaporate. Disturbed by so much global and local causes
meteorologists never can predict the weather of next week because little events
have great consequences in the world of chaos like the proverbial butterfly
causing a tornado some years later elsewhere. What is cause? However, in the long term we find some regularities (three
‘rolling’ cells from equator to pole) in the sum of turbulences called wind.
Local velocity of wind affects:
- wind loads on buildings, plantation and objects in
streets and gardens.
- the energy use of
buildings;
- the potential profit of
wind turbines;
- the dispersion of air
pollution;
- the comfort of outdoor
space;
In Fig. 211 we already showed the parabolic course of impact 1.
In Fig. 219 up to Fig. 222 on the vertical axis estimates of the other impacts are represented
as a working of average wind velocity classes from 0,5 (0‑1) up to 19,5
(19-20) m/sec on the horizontal axis.
|

|

|
|
Fig. 219 Ventilation characteristic
Ventilation losses from
dwellings increase according to the velocity of wind particulary in non
airtight houses[68]. However, from 4 m/sec people close their windows. So, in this
interval more wind decreases ventilation losses.
|
Fig. 220 Powercharacteristic
The produced power of this
standard wind turbine increases up to 60 kW on a wind velocity of 16 m/sec.
Most wind turbines brake on higher velocities to avoid damage[69].
|
|

|

|
|
Fig. 221 Air dispersion characteristic
This tentative diagram represents air pollution disperses best by
storm, but that impact is already reached on moderate wind.
|
Fig. 222 Comfort characteristic
In this tentative diagram is supposed that a weak wind with an
average velocity of 1-3m/sec is
appreciated most.
|
|
|
|
Fig.
219 is used by Vermeulen (1986), point of departure in this chapter. In that time, high rise
buildings were much more airtight than
low rise buildings. That difference will be less today, but to show the impact of wind
on energy use of buildings the 1985 span is most illustrative and still
relevant. When after all, convection losses, losses by precipitation (drying up of buildings) neglected by Vermeulen and Jong (1985) would be calculated as
well, an equivalent and even stronger positive relation than for former low
rise buildings could be actual. An actual total energy loss characteristic
then, could have an other form, but the line of reasoning remains the same.
Minimisation of energy losses desires minimisation of wind
velocity anyway. The fourth impact requires rather optimisation (not too much,
but not too little as well). For higher velocities the aim is also minimisation
of wind velocity. However, the second an third impact on the contrary require
maximisation of local wind velocity. So, their aim is contrary to the first and
last impact. In this representation temperature influences (relevant for Fig. 219 and Fig.
222) are still neglected.
Local average wind velocity can be influenced by
environmental planning and design on national (r=100km), regional (r=30km) and
different local levels (r= {10, 3, 1, 0.3 en 0.1}km).
Measures on these levels are discussed in this chapter. They are not all
equally applicable. Sometimes they have a theoretical of experimental character
with little profit. Then they have a didactic value useful discussing next
values. If that occurs, the measures and their impacts are discussed in a
conditional sequence: any measure should be seen within boundary conditions of preceding
measures. So, one can not miss a paragraph: measures on a local level could be
understood only within boundary conditions of regional scale and these for
their part from those on national level.
Here sometimes fades the boundary between ‘measure’ and ‘given circumstances’. Is the current Dutch coast the consequence of human measures or
should one speak of ‘given circumstances’? A once performed measure then is a
given circumstance, a condition for subsequent measures. To keep this chapter clear and readable anything deviating from a
reference situation will be concerned als
‘measure’. Every time two states wil be compared: the reference and its
deviation by application of the ‘measure’ concerned. The impacts of that
measure are assessed. Though we wil try to formulate the ‘measures’ as context independent as possible the impact assessment remain
context sensitive.To be able to apply such measures in other circumstances
succesively added theoretical insights are
necessary.
The choice of reference in such a method of
‘experimental impact assessment’ is important. Choosing ‘the average Dutch outskirt, filled with
low-rise dwellings’ as a reference produces a rather practical image of
measures, be it not well applicable for inner cities and high-rise areas.
However, we are attached to raise some theoretical insight in aerodynamics. So, we will change references to show impacts that can not
be assessed in a standard reference. So, the reference sometimes will have a theoretical character like
‘a city in the sea’ or ‘a sea in the city’ to clarify impacts by extremes. In practice after all, a measure lies between these extremes. By
attention for extremes not only one specific measure is discussed, but a range
of measures with gradually changing impacts.
The measures discussed in this chapter can be taken on the level of
- national choice of
location (100km radius, page 106)
- regional choice of
location (30 km radius, page 112)
- arrangement of rural
areas, form of conurbations (10 km radius, page 124)
- local choice of
location (10 km radius, page 121)
- form of town and town edge (3 km radius, page 130)
- lay-out of districts and district quarters
(1 km radius, page 128)
- allotment of
neighbourhoods and neighbourhood quarters (300 m radius,
page 145)
·
allotment and urban details and ensembles divided in 4 hectares (100 m
radius, page 140)
·
buildings (radius 30m), and
·
the micro climate, important for humans, plants and animals (radius 10m).
The conditionality into two directions is self evident. To be able
to compare variants on one level a reference on any other level is presupposed.
That creates difficulties in comparing measures on different levels of scale,
because references have to change to reach more general insight in impacts.
Morover, for every several impact (on energy saving, energy
production, air pollution and comfort) other characteristics of wind are
relevant. For instance for energy saving windstatistics of the winter season
are relevant, for other impacts those of the whole year, eventually specified
per season. If not otherwise mentioned this chapter counts on wind statistics of the whole year.
What kind of difference does it make choosing a new housing estate
near Amsterdan or Eindhoven
concerning energy use, the possibility to extract energy from wind, the
dispersion of air pollution and the comfort of outdoor space?
To weigh different building locations concerning these impacts on a
national level a simple calculation of wind statistics per location is needed.
Here we give a description of such calculations.
On more than 50 locations in The Netherlands wind velocity is
regularly measured (Fig. 223).
|

|

|
|
Selection
from Wieringa, Rijkoort et al. (1983) page 28
|
Selection
from Wieringa, Rijkoort et al. (1983) page 84
|
|
Fig. 223 Wind stations in the
period 1945-1980
|
Fig. 224 Year average potential wind velocity[70]
.
|
|
|
|
Wind stations register gusts of more than 5 seconds duration.
All measurements are averaged for one hour resulting in the ‘hour average wind
velocity’[71]. From these hour averages a year average can be
calculated, the ‘year average wind velocity’[72]. Obstacles around the wind
station introduce a deviation by which these data are not immediately
applicable in neighbouring locations. The correction into a ‘standard ground
roughness 3’ (grass land) and a standard
height of 10 metre produces the
‘year average potential wind velocity’ given in Fig. 224. Using local ground data (roughness classes) from the year average potential wind velocity one can calculate back the
year average wind velocity of neighbouring locations on different heights.
However, in the year average wind velocity some data are lost
relevant for energy use, potential energy profit, dispersion of air pollution
and comfort of outdoor space as impact of different wind velocities.
Firstly we miss a specification of wind direction and a statistical
distribution into different wind velocities throughout the year. For that
purpose we still have to go back to the sources the ‘distributive frequency
division of the hour average wind
velocity per wind direction, reduced to 10 metre height above open ground’ per
wind station. In Fig. 225 this frequency division of wind station Schiphol in the years 1951 - 1976 is
given in numbers per 10 000 observations.
|
Velocity Class*
|
Still or variable
|
|
|
E**
|
|
|
S
|
|
|
W
|
|
|
N
|
TOTAL
|
|
m/sec
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
|
vk
|
w
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5
|
348
|
10
|
8
|
11
|
10
|
12
|
16
|
14
|
16
|
15
|
9
|
13
|
14
|
148
|
|
1,5
|
78
|
39
|
43
|
50
|
51
|
58
|
72
|
53
|
66
|
51
|
36
|
44
|
55
|
618
|
|
2,5
|
15
|
59
|
82
|
98
|
80
|
97
|
132
|
111
|
119
|
84
|
68
|
79
|
102
|
1111
|
|
3,5
|
2
|
88
|
118
|
133
|
94
|
118
|
155
|
160
|
125
|
106
|
84
|
94
|
107
|
1382
|
|
4,5
|
|
86
|
132
|
136
|
86
|
124
|
150
|
170
|
113
|
110
|
77
|
87
|
87
|
1358
|
|
5,5
|
|
82
|
110
|
101
|
55
|
86
|
121
|
157
|
113
|
112
|
74
|
76
|
71
|
1158
|
|
6,5
|
|
74
|
112
|
82
|
46
|
71
|
100
|
163
|
119
|
109
|
73
|
76
|
66
|
1091
|
|
7,5
|
|
46
|
88
|
52
|
22
|
47
|
73
|
113
|
123
|
98
|
58
|
62
|
42
|
824
|
|
8,5
|
|
38
|
59
|
29
|
8
|
27
|
51
|
92
|
90
|
77
|
48
|
37
|
26
|
582
|
|
9,5
|
|
21
|
44
|
17
|
5
|
17
|
32
|
68
|
84
|
59
|
40
|
29
|
15
|
431
|
|
10,5
|
|
13
|
29
|
14
|
3
|
10
|
21
|
52
|
70
|
45
|
30
|
17
|
7
|
311
|
|
11,5
|
|
8
|
14
|
6
|
1
|
4
|
13
|
32
|
53
|
32
|
19
|
10
|
4
|
196
|
|
12,5
|
|
4
|
8
|
3
|
|
2
|
8
|
25
|
45
|
26
|
14
|
7
|
3
|
145
|
|
13,5
|
|
1
|
3
|
1
|
|
1
|
4
|
15
|
30
|
17
|
7
|
4
|
2
|
85
|
|
14,5
|
|
1
|
2
|
1
|
|
|
1
|
8
|
20
|
9
|
4
|
3
|
|
49
|
|
15,5
|
|
|
1
|
|
|
|
1
|
6
|
12
|
6
|
3
|
1
|
|
30
|
|
16,5
|
|
|
|
|
|
|
|
3
|
8
|
4
|
3
|
1
|
|
19
|
|
17,5
|
|
|
|
|
|
|
|
2
|
8
|
4
|
2
|
|
|
16
|
|
18,5
|
|
|
|
|
|
|
|
2
|
5
|
3
|
1
|
|
|
11
|
|
19,5
|
|
|
|
|
|
|
|
1
|
2
|
1
|
1
|
|
|
5
|
|
20,5
|
|
|
|
|
|
|
|
|
2
|
1
|
|
|
|
3
|
|
21,5
|
|
|
|
|
|
|
|
|
1
|
1
|
|
|
|
2
|
|
22,5
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
1
|
|
TOTAL
|
443
|
570
|
853
|
734
|
461
|
674
|
950
|
1247
|
1225
|
970
|
651
|
640
|
601
|
10000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* Here the middle of the class ± 0,5 is mentioned only.
|
|
|
|
|
|
|
|
|
|
** Here the wind direction in ‘hours of the clock’ are given; 12 hour
indicates North.
|
|
'12 hour' contains all wind
directions between -10 en 10 degrees from North.
|
|
|
|
Vermeulen, Hoogeveen et al.
(1983) Enclosure 4.27
|
|
Fig. 225 Frequency division w of
wind velocity per class vk Schiphol 1951 until 1976 per 10 000.
|
|
|
Frequency divisions like Fig. 225 are available from every wind station mostly specified per summer
(may – october) and winter (november – april) half year and sometimes even per
month.
Calculating the average wind velocity in Schiphol from Fig. 225 as

fits in the velocity class 5 – 5.5 m/s of location Schiphol
indicated in Fig. 224.
In the last row of Fig. 225 all observations are specified by wind direction (Fig. 226).
|

|
|
|
|
Fig. 226 Compass card, per 10 000 observations
|
|
|
Because there are 10 000 observations, one can direcly read
from Fig. 226 that 12% of the wind in Schiphol comes from directions 7 and 8.
Together that is roughly 25% from South – West.
Fig. 227 shows Fig. 225 as a diagram of frequency divisions of wind velocity per class in
total and per direction.
The form of the graphs is higly similar to the mathematical graph of
a Weibull probability distribution[73] like

represented in Fig. 228 with C and a as form and scale parameters specific for every location (Fig. 229).
|
|
form
|
schale
|
% from direction (‘hours’ from
North, 0 is calm or variable):
|
|
|
|
|
|
|
|
E
|
|
|
S
|
|
|
W
|
|
|
N
|
|
|
C
|
a
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
Beek
|
2,01
|
0,042
|
2
|
7
|
9
|
7
|
3
|
4
|
10
|
20
|
17
|
8
|
4
|
4
|
4
|
|
Den Helder
|
2,00
|
0,014
|
1
|
6
|
7
|
8
|
6
|
5
|
10
|
13
|
12
|
10
|
8
|
8
|
7
|
|
Eelde
|
1,74
|
0,059
|
3
|
6
|
8
|
8
|
7
|
5
|
9
|
14
|
14
|
10
|
7
|
5
|
4
|
|
Eindhoven
|
1,86
|
0,052
|
8
|
7
|
8
|
5
|
6
|
6
|
7
|
13
|
16
|
9
|
6
|
5
|
4
|
|
Schiphol
|
1,86
|
0,032
|
4
|
6
|
9
|
7
|
5
|
7
|
10
|
12
|
12
|
10
|
7
|
6
|
6
|
|
Vlissingen
|
1,95
|
0,025
|
1
|
9
|
9
|
6
|
4
|
5
|
9
|
13
|
13
|
11
|
6
|
7
|
7
|
|
|
|
Fig. 229 Weibull parameters en contribution per wind direction for 6
stations.
|
|
|
By this formula with tables like Fig. 229 we can avoid long tables like Fig. 225 and calculate back a stepless distribution of wind velocities in 12
directions on any location with the roughness of grassland. That represents
local wind characteristics we need to connect to the impact characteristics
from page 110. Later on we will show how per direction local landscape
characteristics other than grassland are calculated in.
The number of observations of wind blowing with a given velocity and direction w(v,d) in Fig. 225 per number of observations 10 000 for many years in the past,
is equivalent to its probability P(v,d) for the future. P(v,d) is proportional
to the number of hours h(v,d) that kind of wind blowing from the total number
of hours in a year. So h(v,d) = 8 766 x P(v,d).
That number of hours determines the energy profit of wind turbines in an year.
For example, if you know the power a wind turbine delivers on every velocity
(power characteristic, see Fig. 220) you can find the profit by multiplying the number of expected
hours that velocity will occur in an environment of grass land (Fig. 230).
|
|
|
Westra and
Tossijn (1980), page 37
|
|
Fig. 230 The way of calculating energy profit of a wind turbine
|
|
|
Comparing national locations concerning the profit of wind turbines, direction of wind does not yet play the rôle it does concerning
energy losses in buildings or comfort of outdoor space. The turbine after all
can turn with the wind where buildings can not. On lower levels of scale we
have to make this calculation for every direction seperately reduced by its
specific roughness other than grass land.
However, this diagram of calculation can be used to estimate the
impact of national choice of location on energy use of buildings,
the comfort of outdoor space and the dispersion of air pollution as well. So,
we will elaborate it for the difference in energy profit of wind turbines in
the environment of Schiphol and Eindhoven.
In Fig.
231 left the velocity frequences per direction of wind from Fig. 225 and Fig.
227 are summarised into a total frequency division while
the contribution of every separate direction remains (cumulatively)
recognisable. Point of departure still is a standard height of 10 metres and a
ground roughness comparable to open grass land. On lower levels of scale we
will vary them as well.
Left in Fig. 231 the expected number of hours per verlocity is given. The power
characteristic of the wind turbine per velocity in the middle of Fig. 231 is equivalent to Fig. 220. Multiplying the number of hours of every subsequent velocity by
the corresponding power produces the energy profit right in Fig. 231.
Apparently the wind turbine delivers most energy on directions 6, 7,
8 and 9 ‘hour’. So in that directions we have to keep the site open. However
situating a wind turbine South East of town shields the turbine from an also
considerable contribution from North
West (1, 2 and 3 ‘hour’). So you can situate it
better somewhat above West of town.
Comparing national locations can be done more simple by a rule of
thumb for the energy profit of wind turbines with a height of 10m
surrounded by open grass land[74]:

E = total yearly
energy production in kWh/ m˛·year
vg = year average wind velocity
averaged per hour
O = surface of rotor
In Fig. 232 the energy profits presupposing a height of 10m in open grass land
near Schiphol and Eindhoven
are compared this way.
|
Schiphol:
|
2·5,4ł
= 315 kWh/ m˛
|
x 340 m˛ =
107 000 kWh
|
|
Eindhoven:
|
2·4,25ł
= 154 kWh/ m˛
|
x 340 m˛ =
522 000 kWh
|
|
|
|
Fig. 232 The energy profit of
wind turbines in Schiphol and Eindhoven
by rule of thumb
|
|
|
The total profit of a reference turbine of 340m2 of 10m height in
all directions surrounded by grass land is in the environment of Schiphol
approximately 100 000 kWh per year and in Eindhoven approximately 50 000 kWh.
We neglected amongst others height and wind direction
differentiating velocity and local roughness. Wind supply is reduced from
different directions, but most wind turbines are erected higher, reducing this
impact. In Fig. 233 is indicated how wind velocity in open grass land (the
international standard for local wind velocity measures) increases by height z.
We will discuss this factor more precisely in paragraph 2.4.2.
|

|

|
|
|
|
|
Fig. 233 Wind velocity factor for height
|
Fig. 234 Contribution per wind
direction 10m height
|
|
|
|
Because the energy profit of wind turbines increases proportional to
the third power of wind velocity (see rule of thumb on page 116) you can adapt the average wind velocity vg by this factor to the
third power. The wind velocity on 20m according to Fig. 233 is x 1,13 higher than on 10m. To the third power this factor
becomes 1,44. By this factor you can mulitply the profit on 10m to get the profit
on 20m (for Schiphol and Eindhoven
approximately 155 000 kWh and 75 000 kWh per year respectively). The absolute
differences of both locations increase, as well as the contributions of
different wind directions (Fig. 234).
The way of calculation in Fig. 230 can be applied to energy losses of buidings, the distribution of
air pollution and the comfort of outdoor space as well. In that case you do not
multiply the expected occurences of wind velocities by those in the power
characteristic of wind turbines, but by those of the respective other
characteristics mentioned on page 110.
Energy losses from buildings by wind not only consist of ventilation
losses, but we will neglect other ones (convention, precitipation) as less
important (see Vermeulen and Jong, 1985). For ventilation losses form dwellings we will restrict
ourselves to wind data form the heating season, not importantly differing from
better accessible data concerning the winter half year. The average wind
velocity in a winter half year is approximately 10% higher than throughout the
year (Fig. 235 and Fig. 236).
|

|

|

|

|
|
|
|
|
|
|
Fig. 235 Winter half year velocities Schiphol
|
Fig. 236 Winter half year
velocities Eindhoven
|
Fig. 237 Winter probabilities Schiphol
|
Fig. 238 Winter probabilities Eindhoven
|
|
|
|
|
|
The probability (number of hours) of wind from all directions is
approximately the same in winter as throughout the year for all directions (Fig. 237 and Fig. 238).
In Fig. 239, Fig. 219 is repeated: the ventilation characteristic of an average one
family low rise dwelling and an average more airtight one family high rise
appartment. In this graph the average occupant’s behaviour to open windows at
wind velocities lower than approximately 5 m/s is recognisable. This behaviour
sometimes makes wind suppressing measures decreasing wind velocity less than 5
m/sec useless.
As expected Fig. 240 shows low rise familiy dwellings lose more in Schiphol (6861 kWh)
than in Eindhoven
(5557 kWh, 1300 kWh less). However, high rise dwellings lose less in
Schiphol (2516 kWh) than in Eindhoven
(2626 kWh, 110 kWh more). In Eindhoven
with lower wind velocities people open up their windows more often and that
counts negative in high rise buildings.
On which side you can shelter a dwelling best: the side of the
coldest Easterly wind or the South-West side where most wind is coming from?
Answering this question requires input of temperature data. We choose an approach based on wind and temperature data Gids (1986) from wind station Eelde (with a wind characteristic
between that of Schiphol and Eindhoven).
We consider a period of the year between beginning December and the end of
February. This approach gives a weight factor spreading heat losses by
ventilation over 12 wind directions. Multiplied by the earlier mentioned figure
for total energy losses of two dwellings in Schiphol en Eindhoven this produces contributions per
wind direction as represented in Fig. 241 and Fig. 242.
|

|

|
|
|
|
|
Fig. 241 Ventilation losses weighting temperature per wind direction
Schiphol
|
Fig. 242 Ventilation losses
weighting temperature per wind direction Eindhoven
|
|
|
|
Sheltering on East (3 ”hour” or 90°) appears to be nearly as
effective as sheltering West South West (8 “hour” or 240°), though highest
velocities come from South West[75].
The same approach without temperature impacts, this time using the
tentative graph Fig. 222 reproduced in Fig. 243 would produce Fig. 244.
|

|

|
|
|
|
|
Fig. 243 Tentative comfort
characteristic
|
Fig. 244 Tentative appreciation comfort
|
|
|
|
In Fig. 244 the appreciation of every velocity is multiplied again by the
respective probable velocity per direction. For all directions together
Schiphol would get 11 000, Eindhoven
16 000 points. Schiphol would probably like shelter in directions with a Westerly component. Eindhoven
probably does not need any shelter but eventual complaints are most probably
caused by wind from North West
(10 or 11 ‘hour’)[76].
The higher the wind velocity the better air pollution is dispersed,
though increasing velocities have diminishing returns. This impact is
tentatively represented in Fig. 221 repeated in Fig. 243.
The impact having an overall positive relation to wind velocity, it
shows pronounced similarity with the compass chard of Fig. 226. In Schiphol air pollution is better dispersed. The
multiplication produces approximately 16 000 in Schiphol and 12 500
in Eindhoven.
Comparing Schiphol and Eindhoven
on these criteria with most reservations concering the tentative ones, Fig. 247 shows which location scores best[77].
|
CRITERION
|
WIND DIRECTION
|
1 2 3 4 5 6
|
7 8 9 10
|
11 12 TOT
|
|
1 minimise
|
ventilation loss
|
E E E E E E
|
E E E E
|
E E E
|
|
2 maximise
|
wind energy
|
S S S S S S
|
S S S S
|
S S S
|
|
3 maximise
|
dispersion of air pollution
|
S S S S S S
|
X E S S
|
S S S
|
|
4 optimise
|
outdoor space comfort
|
E E E E E E
|
E E E E
|
E
E E
|
|
|
|
|
|
|
|
S: Schiphol better E: Eindhoven
better X: No difference
|
|
|
|
Fig. 247 Comparison Schiphol and Eindhoven
on 4 criteria
|
|
|
Temperature impacts are neglected. The evaluation of dispersion of
air pollution is highly similar to the energy profit of wind turbines and the
evaluation of outdoor space comfort is similar to that of ventilation losses
from non airtight buildings. The difference for such buildings is substantial
(1 300 kWh/year in favour of Eindhoven), but in the case of airtight
buildings the much lower difference (110 kWh/year) is paradoxically in favour
of Schiphol by the behaviour of inhabitants (more closed windows). In the next
paragraphs we will restrict to energy profits of wind turbines and ventilation
loss in airthigt and non airtight buildings. In case of non airtight buildings
we can use the conclusions mostly for outdoor comfort as well and in case of
energy profits of wind turbines in the same time we can think of dispersion of
air pollution.
On a regional level you no longer can take grassland in all
directions as a standard of comparison. Wind is hampered by vegetation and
buildings. On a regional level we not yet see them individually, but roughly as
‘roughness’. New buildings are sheltered by vegetation or existing (sometimes
less air tight) buildings. However, they shelter other locations themselves.
So, locating new buildings sheltered is not always obvious, especially when
they are airtight. There are arguments to locate new buildings South West of
town as well (sheltering old less airtight ones, comfort of existing outdoor
space, dispersion of air pollution, possibilities to yield wind energy at
location).
In this paragraph we restrict ourselves to regions comparable to
Schiphol as far as wind statistics are concerned. We concentrate on roughness
of surrounding grounds. Due to the Weibull approach (Fig. 228) we do not need tables with all occuring velocities like Fig. 225. We can use the average velocity (like Fig. 235) and its probability (Fig. 237) per direction, summarized again in Fig. 248.
|
WIND DIRECTION :
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
TOT*
|
|
in degrees from
North :
|
30
|
60
|
90
|
120
|
150
|
180
|
210
|
240
|
270
|
300
|
330
|
0
|
|
|
|
|
|
E
|
|
|
S
|
|
|
W
|
|
|
N
|
|
|
whole year
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m/sec average
|
5,30
|
5,68
|
4,89
|
4,19
|
4,71
|
5,08
|
6,14
|
6,97
|
6,51
|
6,14
|
5,44
|
4,67
|
5,43
|
|
hours/ year
|
500
|
747
|
643
|
404
|
519
|
832
|
1074
|
1072
|
850
|
574
|
563
|
528
|
8766
|
|
*inclusive periods of calm or variable direction
|
|
|
|
Fig. 248 Potential wind velocities and their probabilities Schiphol
|
|
|
In this paragraph we consider wind velocities in winter to be 10%
the year average from Fig. 248 (important for calculating ventilation losses and comfort of
outdoor space). The probability from a specific direction we take equal to half
the values from Fig. 248.
In wind surveys classes of roughness are distinguished (Fig. 249
|
|
|
|
1
|

|
·
open sea
·
pond with free brush length of at least
1km
|
|
2
|

|
· land surface without obstacles or vegetation
o
shallow
o
beach
o
ice plain
o
snow landscape without trees
· pond with free brush length of approximately 1km
|
|
3
|

|
· flat land with shallow vegetation (grass) and isolated, rarefied obstacles:
o
air strip
o
grassland without trees
o
fallow fields
|
|
4
|

|
· farm land with regular low (<0,5 m) crops
· grassland with ditches on mutual distance less than 20 x their
width
· dispersed obstacles on mutual distance of more that 20 x their own
height:
o
low hedges
o
singuar row trees without
leaves
o
singular farms
|
|
|
|
|
|
5
|

|
H < 2 m:
· farm land with alternating high and low crops
· vineyards, maize fields
2m < H < 5m:
· low orchards
· influential obstacles with mutual distance 15 x their own height:
o
rows of trees with leaves
|
|
6
|

|
3m < H < 10m:
· groups of obstacles with a mutual distance of 10x their typical
height:
o
large farmsteads
o
parcels of forest
o
dispersed shrubs
o
young densely planted woods
o
orchards
|
|
7
|

|
10m < H < 15m:
· bottom regularly and fully covered by rather large obstacles with
mutual distance not larger than 2x their height:
o
regular forests
o
low rise buildings in
villages
o
suburbs
|
|
8
|

|
H > 10m
· centre of a large city with alternating high rise and low rise
buildings
· heavy forests with many irreguar open spaces
|
|
|
|
|
|
Fig. 249 Classes of roughness
|
|
|
|
|
The standard class supposed in wind data is class 3[78]. Wind characteristics on
locations surrounded by other classes of roughness are derived mathematically
from the data provided in class 3.
We wil now concentrate on a location of a residential area (class of
roughness 7) Leidscheveen between Zoetermeer and
Voorburg - Leidschendam[79]. The experimental question is, to compare wind climate without
Leidscheveen, with Leidscheveen and when Leidscheveen would have been built
adjacent to Zoetermeer (‘VoZo’). In paragraph 2.3.5 we will compare several arrangements of green and buildings
(roughness 6, 7 and 8) between Zoetermeer and Delft with or without a residential
area Rokkeveen adjacent to Zoetermeer.
|

|
|
Citydisc/Top.Dienst
|
|
Fig. 250 Study
area Den Haag – Zoetermeer – Delft
|
|
|
Fig. 251 shows a 30° cutout from ‘zero point’ in Zoetermeer direction West
(‘9 hour’). Fig. 252 shows the calculated average wind velocity on 20m height in the
reference. Below the graph the reference is styled as sequence of different
roughnesses. The numbers refer to the classes of roughness in Fig. 249. Such calculations utilise the parameters from the last two columns
of Fig. 249.
|

|

|

|

|
|
|
|
|
|
|
Fig. 251 Voorburg
-> Zoetermeer reference
|
Fig. 252 Average
wind velocity Fig. 251
|
Fig. 253 Voorburg with Leidscheveen lose
|
Fig. 254 Zoetermeer
with VoZo adjacent
|
|
|
|
|
|
Fig. 253 shows
Leidscheveen 1km lose from Voorburg. This urban area
with approximately 8 500 dwellings slows down wind on 20m height roughly
from 5 to 4 m/sec, but it has little impact on the built up area of Zoetermeer
3,5 km further on without obstacles inbetween. Fig. 254 shows an imaginary variant with VoZo adjacent to Zoetermeer. In Fig. 252 (reference) on zero point (right) an imaginary wind turbine has
10 530 kWh/year energy profit due to Westerly
wind only; equivalent energy losses from a non airtight dwelling are 750
kWh/year. In Fig. 253 they decrease by 760 and 20; in Fig. 254 by 3 010 and 170 kWh/year.
Fig. 255 to Fig. 258 show reference and experiments to clarify the impact in case of
Easterly wind on ‘zero point’ Voorburg. They are less realistic to remain
comparable with the previous experiment.
|

|

|

|

|
|
|
|
|
|
|
Fig. 255 Zoetermeer ->
Voorburg reference
|
Fig. 256 Average wind velocity Fig. 255
|
Fig. 257 Zoetermeer –> Voorburg with Leidscheveen
|
Fig. 258 Zoetermeer –> Voorburg variant
|
|
|
|
|
|
Fig. 256 immediately shows the lower average wind velocity from East
compared with West. So, the impact is less as well. On the new zero point an
imaginary wind turbine has 3070 kWh/year energy profit due to Easterly wind
only; equivalent energy losses from a non airtight dwelling are 460. In Fig. 257 they decrease by 1000 and 23 in Fig. 258 by 710 and 60 kWh/year.
Fig. 259 shows the impacts of regional alternatives behind the Westerly edge of Zoetermeer. They decrease fast within
100m. Fig. 260 shows the same behind the Easterly edge of Voorburg. They are
smaller because Westerly wind blows more often
and stronger (see page 117) and the foreland of Voorburg already had a higher roughness than
Zoetermeer, but lower temperatures neglected here could increase the impact.
|

|

|
|
|
|
|
Fig. 259 Impact Westerly wind on Zoetermeer
|
Fig. 260 Impact Easterly wind
Voorburg
|
|
|
|
So, the total impact on ventilation losses is small, though they
have some significance for comfort of outdoor space. That is why we pay not
much intention to calculating these impacts more precise now, but they are
point of departure and give insight for calculating measures on lower levels of
scale. Not only temperature could affect the outcome, but also impacts
perpendicular on the direction of wind. These ‘lateral impacts’ depend on the
total form of the conurbation. They will be studied closer in 2.4.3 page 130. Furtermore we have to realise that these calculations are based on
average roughnesses. Wide ways, open allotment and lay-out of the edge could
increase wind loads inside of town locally substantially. We should conclude
that in calculating the impact of measures on lower levels of scale the
regional lay-out adjacent to towns are most important. So, we have to examine
them in more detail.
Fig. 261 shows a 10km long cutout of 30o this time seen from zero
point Zoetermeer in wind direction '8 hour' to Delft. The largest zone is farm
land (roughness 4) increasing wind velocity up to 6.67 m/sec on the edge of
town Zoetermeer in Fig. 262.
|

|

|

|

|
|
|
|
|
|
|
Fig. 261 Delft -> Zoetermeer reference
|
Fig. 262 Average wind velocity in reference of Fig. 261
|
Fig. 263 Delft -> Zoetermeer simplified reference
|
Fig. 264 Delft -> Zoetermeer with Rokkeveen
|
|
|
|
|
|
Fig. 263 simplifies Fig. 262 by gathering Delft
and Delftse Hout as a zone with roughness 6. This simplification increases wind
velocity at the edge of town Zoetermeer from 6,67 m/sec in Fig. 262 to 6,74 m/sec in Fig. 263. Such differences at more than 5km distance apparently do not
matter much. So, Fig. 263 becomes our reference. In Fig. 264 Rokkeveen is added[80]. Though this residential
area has a great impact on the wind velocity profile, for the town edge of
Zoetermeer the impact is surprisingly less than we would expect because after
slowing down above Rokkeveen the wind accelerates within 500m very fast above
railways and highway A12 between Rokkeveen and existing Zoetermeer[81]. So, the impact of
Rokkeveen reduces wind velocity from 6,74 to 5,92 m/s, reducing ventilation
loss on the edge of town Zoetermeer by only 90 kWh/dwelling·year (1 m3 natural
gas).
In Fig. 265 before Rokkeveen a green structure replaces farm land (roughness 6
see page 122).
|

|

|

|

|
|
|
|
|
|
|
Fig. 265 Delft -> Zoetermeer with green structure
|
Fig. 266 Delft -> Zoetermeer 1km regular forest added
|
Fig. 267 Delft -> Zoetmeer 1km heavy forest added
|
Fig. 268 The same, with farm land instead of green structure
|
|
|
|
|
|
In Fig. 266 except this green structure 1km forest (roughness 7) is added as
well. Both cases do not make much difference on the old town edge. The impact
is more than undone by railways and highway. Wind velocity is compared to the
reference decreased from 6,74 to respectively 5,45 and 5,35 m/sec, but the
largest amount was already caused by Rokkeveen. At the old town edge
ventilation losses caused by this direction of wind are decreased by
approximately 150 kWh/dwelling·year and for adjacent directions something
comparable but smaller.
In Fig. 267 regular forest is replaced by heavy forest (roughness 8). Wind
velocity at the old town edge then decreases somewhat (5,25 m/sec), but not
significant though the wind profile changes substantially. The fast increase
above Rokkeveen is remarkable.
In Fig. 268 the impact of a lower roughess on larger distance is studied by
replacing Delft,
Delftse Hout and green structure by farm land. By these measures wind velocity
at the old town edge still increases from 5,25 to 5,71 m/sec.
2.4.1
Local shelter of residential areas
From Chapter 2.2 we learned that the impact
of relatively small linear open spaces as railways and highways perpendicular
on wind is substantial. Wind sheltering action has to be taken as close to the
residential area as possible. That is why we shift our attention some
kilometres into a cutout with its zero point in Rokkeveen itself (8 ‘hour’
South West see Fig. 250). This residential area is
not separated from its foreland by a highway or wide water. So, shelter can
adjoin immediately to residential area.
|

|

|

|

|
|
|
|
|
|
|
Fig.
269 Reference windvelocity
|
Fig. 270 Delft
-> Rokkeveen with 6km green structure
|
Fig.
271 Delft -> Rokkeveen with 1km regular forest
|
Fig.
272 Delft -> Rokkeveen with 1km heavy forest
|
|
|
|
|
|
In Fig. 269 we suppose above Delft a stable velocity of
less than 4 m/sec. Above 1km Delftse Hout it climbs up and stabilises on 4.5
m/sec in a few hundred metres. Then above 5 km farmland it starts to climb
up fast continuing to increase more slowly to 6,52 m/sec. Then above Rokkeveen
it slows down fastly to 4,61 m/sec and outside the graph slowly to
4.2 km/sec above above suburban built up area.
In Fig. 270 farmland is replaced by
green structure (rougness 6). Then wind velocity at the edge of Rokkeveen
decreases substantially from 6.52 to 4.73 m/sec. Energy loss per non airtight
dwelling per year as far as due to wind from this direction decreases 190 kWh
only (from 987 kWh to 797 kWh).
If the last km before
Rokkeveen would have been replaced by green structure only, velocity would
reduce to 5.23 m/sec. Ventilation loss would still reduce by 141 kWh.
Would 1km roughness higher
than 6 have more impact?
In Fig. 271 and Fig. 272 only the last km before
Rokkeveen farmland (roughness 4) is replaced by regular forest (roughness 7)
and heavy forest (roughness 8). From these thought experiments we conclude 1km
regular forest has approximately the same impact as 6km green structure.
However, 1km heavy forest with rather high trees (15m) reduces wind velocity
substantially to 2.90 m/sec at the edge of town. Energy loss per non airtight
dwelling per year as far as due to wind from this direction there decreases 324
kWh from 987 kWh to 663 kWh. However, above suburban built up area wind
velocity increases again fastly stabelising on approximately 4.2 m/sec.
Fig. 273 and Fig. 274 compare regional remote
(see 2.3.5) and locall adjacent (see
above) impacts.
|

|

|
|
|
|
|
Fig.
273 Impact regional layout
on Zoetermeer separated by railways and
highway
|
Fig.
274 Impact locally adjacent shelter on Rokkeveen
|
|
|
|
Representated impacts are
restriced to 1 of 12 wind directions. Figures may be multiplied by a factor 3
to 5 if more directions are sheltered. The impact is decreasing fastly up to
100m in the urban area.
Preceding calculations are
tacitly restricted to velocity differences in direction of wind itself
(x-direction) and not perpendicular on x (in witdth y and height z). In Fig. 233 we casually mentioned the
importance of velocity differences in height (z-direction), but then the view
restricted to a height of 10m (international standard measuring wind) and
passing chapter 2.2 to 20m (where wind is not
disturbed substantially by single buildings).
On differences in wind
velocity perpendicular to wind direction in witdh (lateral differences in wind
velocity) we did not say more than
mention them (2.3.4). Tacitly we supposed
styled roughesses and velocities to be continued endlessly perpendicular to the
surface of drawing.
However, on this level of
scale we can not maintain these simplifications. A separated built up area
(‘roughness island’) ondergoes substantial
impacts from wind parallel to its edges. Wind survey yielded experimental
results by which we can estimate these lateral impacts. However, that requires
some insight in increase of wind velocity by heigth.
To calculate wind velocity v
as a working of height z (v(z), wind profile, see Fig. 212, Fig. 276 and Fig. 277) we divide the atmosphere
from the largest height z=d3 where wind still is influenced by
Earth’s surface to the ground in tree layers:
90% ‘boundary layer’ from d3 to 0.1
x d3;
9% ‘wall layer’ from d2 = 0.1 x
d3 to d1 = 0.01 x d3;
1% ‘viscose layer’ from d1 to
ground level.
The wind velocity of these
layers can be approximated by three different formulas (Voorden 1982, Appendix
B):
(1) where d3 >
z > d2: v3(z) = vd3 · (z/d3)a;
(2) where d2 ł z ł d1: v2(z)
= (vd3 · 0.4 / (Sqr(25 + (ln(d3 / d0))2))
/ 0.4) · ln(z / d0) ;
(3) where d1 >
z > 0: v1(z) = v2(d1) · ((2 · z / d1)
- (z2 / d12)).
If we know velocity v at d3
(vd3) the exponential formula (1) produces a velocity for every z in
boundary layer below d3 supposed we know d3 and exponent a. Exponent a and d3
are parameters dependent on roughness, we can take them from Fig. 275. For the wall layer the
logaritmic formula (2) needs an other parameter d0
different for every roughness as well (Fig. 275). In an urban environment
with much local turbulence the lowest viscose layer has theoretical value only.
But for roughesses lower than 5 we can approximate wind velocities by parabolic
formula (3). Within formula (3), formula (2) is used
to calculate v2(d1).
|
Rough‑ness class
|
a
|
d3
|
d2
|
d1
|
d0
|
parameters used elsewhere
|
|
|
|
|
|
|
D(h)
|
b
|
|
|
m
|
m
|
m
|
m
|
|
|
|
|
1
|
0.104
|
250
|
25.0
|
2.50
|
0.0002
|
0
|
|
0.07
|
|
2
|
0.144
|
275
|
27.5
|
2.75
|
0.005
|
0
|
|
0.08
|
|
3
|
0.181
|
300
|
30.0
|
3.00
|
0.03
|
0
|
|
0.09
|
|
4
|
0.213
|
350
|
35.0
|
3.50
|
0.1
|
0
|
|
0.11
|
|
5
|
0.245
|
400
|
40.0
|
4.00
|
0.25
|
0.3
|
0.7
|
0.14
|
|
6
|
0.273
|
450
|
45.0
|
4.50
|
0.5
|
0.7
|
|
0.16
|
|
7
|
0.313
|
475
|
47.5
|
4.75
|
1
|
0.8
|
|
0.18
|
|
8
|
0.363
|
500
|
50.0
|
5.00
|
2
|
0.8
|
|
0.20
|
|
|
|
Fig.
275 parameters dependent from roughness in formulas used in wind
surveys.
|
|
|
If we do not know vd3,
but we know v10m or v20m, we can vary the upper scroll
bar of the computer programme Windvelocity(height), - downloadable from http://team.bk.tudelft.nl publications 2003 - to get the right profile.
|
|

|
|
|
Jong (2001)
|
|
Fig.
276 Exponential v3(z)
and Logaritmic v2(z) increase of wind velocity by height
|
Fig.
277 Logaritmic v2(z) and Parabolic
v1(z) increase of wind velocity by height
|
|
|
|
Fig. 278 shows the result of a wind
tunnel experiment described in Vermeulen
(1986). This experiment serves as a reference for thought experiments to
follow.
Above a roughness island like a town or forest in a smooth environment
discontinuities in wind velocity appear. The wind meets the edge of the
roughness island for the first time (x = 0) still having a regular velocity
profile like described on page 130. Above the roughness island
a specific velocity profile is estabished with lower velocities than the
surrounding smooth surface. However, on some height above the roughness island
the old profile remains. The height up to where the new profile establishes its
impact is called ‘internal boundary layer thickness (Di). The development of this
boundary layer is drawn by dots in Fig. 278. Behind the roughness isand
the old profile recovers up to a second boundary layer height. In the used
model x=300cm from the first change of roughness, the first boundary layer
height (D1) amounts 16,5 cm , the second (D2) 9,5 cm.
|

|

|
|
|
|
|
Fig.
278 Wind velocity profiles
in height
|
Fig.
279 Wind velocity profiles
in width
|
|
|
|
Fig. 278 shows wind profiles from
the beginning (x=0) above and behind (up to x=300) the roughness island in
cross section in case that island would extend endlessly perpendicular to the
surface of drawing. Fig. 279 shows wind profiles 3.9cm
above the roughness island in front view limited on two sides on a distance of
x={0, 50, 100, 150cm) from the front edge. At x = 0 wind still behaves
undisturbed like above a smooth surface. After 50cm above the rough surface
wind velocity has slowed down, but on both sides the velocity of the smooth
surface remains. Between both velocities a lateral transitional zone develops. In the experiment the width of the
transitional zone appears to be 1.2 times the internal boundary layer thickness
D1.
Fig. 278 shows, the thickness of the
internal boundary layer D1 is approximately 1/10 times the distance
to frontal edge x.
So, behind x=1000m (where D1
is approximately 100m) a transitional zone can penetrate the air above the
roughness island already 120m from the side edges. When the island is 240m
width the transitional zones meet eachother. So, the wind velocity from this
point on could increase by interacting lateral impacts to the back of the
island in spite of the underlying roughness.
For example, above an
elongated separated urban area with its narrow front to South, Southerly wind
not only slows down in its own direction, but produces on the Westerly and Easterly edges a side effect.
This increases wind velocity by interaction above the Northern part of the
area.
To examine this interaction
in more detail a windtunnel experiment on a narrow roughness island is carried out. Fig. 280 shows a map of the model
with hypotheses concerning the transition zone, and Fig. 281 a front view with the
result of measurements.
|

|

|
|
|
|
|
Fig. 280 Hypothetical interaction above an elongated roughness island.
|
Fig.
281 Measurements above an
elongated roughness island x=100cm.
|
|
|
|
Fig. 281 shows results of
measurement near the point where interaction hypothetically should begin
(x=100cm). Behind this point (shaded area in Fig. 280) wind velocity should
increase anew. Examining these results next deviantions draw attention:
1 wind velocity decreases more than expected (8,6 m/sec instead of
9,25 m/sec);
2 transition zone outside the roughness island is wider than 1,2 ·
D1 = 10,2 cm;
3 transition zone inside the roughness island is narrower than 10,2
cm.
We can explain these
deviations concerning the possibility wind swerves out meeting a narrow
roughness island (initial interaction). Fig. 282 represents this additional
supposition. As a result of the crooked flow and the material used in the
experiment in the very start wind meets a higher roughness than on
perpendicular flow. That may explain the first effect. The other effects are
caused by a slightly outward initial change of direction of the transition zone
as a whole.
|
|

|
|
|
|
|
Fig.
282 Supposed initial interaction
|
Fig.
283 Arithmatical approach of lateral interaction with and without
initial interaction
|
|
|
|
Fig. 283 shows how to calculate wind
velocity in transition zones. Starting points are undisturbed velocities above
smooth (vsmooth) and rough (vrough) surfaces and their
internal boundary layer thicknesses d3. The difference between both
velocities has to be bridged. Above the island already 65 % is bridged ,
the remaining 35 % is bridged above the smooth surface.
A wide roughness island has
no initial interaction. The difference is bridged symmetrically in a distance
of 1. 2·D1. A roughness island narrower than 200 x Z0 (roughess
length, not the length of the island) causes initial interaction. Wind velocity
difference is bridged over a much larger distance outside the island and above
the rough surface over a somewhat smaller distance. The island of Fig. 281 was 25 cm wide, 80
times the roughness length z0 = 0,3 cm, much less than 200. By
initial interaction 65 % was bridged above the island over a distance D1
(8,5 cm), the remaining 35 % over a distance 2·D1 (17 cm).
Returning to the thought
experiment of page 124 concerning Leidscheveen we
can put Fig. 253 on top of its background Fig. 252 as shown in Fig. 284.
|

|

|
|
|
|
|
Fig. 284 Westerly wind in and around Leidscheveen from Fig. 252 and Fig. 253
|
Fig. 285 Leidscheveen as a rougness island
|
|
|
|
Fig. 285 shows Leidscheveen styled
as a square of 2x2km.It has no intial interaction because it is wider than 200
times the rougness length Z0 = 1 belonging to class 7. So, the transition zone
will penetrate the built up area 1. 2· D1 m.
Fig. 286 and Fig. 287 are distorted details of Fig. 284 and Fig. 285.
Fig. 286 shows velocities outside
and above Leidscheveen in more detail. Below their difference is represented.
65 % of the difference is bridged above rough urban area (Fig. 286). That is the way you find
wind velocity on the edge inbetween the curves above. In the South East corner
of Leidscheveen wind velocity is increased up to 5 m/sec by lateral impacts,
while earlier calculations (Fig. 284) indicated there 3,7 m/sec.
This velocity is not reached on the East edge until 300 meter (1. 2·D1) from
the South edge (Fig. 287).
|
|

|
|
|
|
|
Fig.
286 Given (continues lines)
and calculated (dotted) wind velocities outside and above Leidscheveen as distorted detail from Fig. 284
|
Fig.
287 Transition zone penetrating from South in normal decrease of Westerly wind velocity above Leidscheveen as distorted
detail from Fig. 285
|
|
|
|
From Fig. 278 we learned D1
(the height where the undisturbed wind velocity meets the disturbed one) is
approximately 1/10 of x. So, we can approximate the distance from the South
edge (Fig. 283) 1.2 x D1
in Fig. 287 by drawing a straight line
into the South West corner of the island, but here it is calculated according
to a method by Vermeulen (1983). From Fig. 286 we know the velocity above
Leidscheveen without lateral effect at the East edge (3.7m/sec) and the
penetrating velocity in the South East corner (5m/sec). Inbetween the velocity
increases proportional (Fig. 283) to the distance from the
South edge. The velocities on the South edge we know from Fig. 286 as well. Connecting points
of equal wind velocity at the East an South edge we get ‘altitude’ lines of
equal wind velocity.
The below left quadrant of Fig. 288 is a copy from Fig. 287 mirrored 1km above and
extrapolated 4km into the East. Width (1km) and length (4km) are not
proportionally drawn. Now interaction appears behind the point where
1,2·D1-lines cross. According to Vermeulen (1986) the
‘altitude’ lines within the interaction area you can simply connect.
|
|

|
|
|
|
|
Fig.
288 Elongated island head in wind (length drawn shortened)
|
Fig.
289 Head and flank in wind (proportionally drawn)
|
|
|
|
Fig. 289 ‘head in wind’ shows the same model in
true proportions: an elongated island with ‘altitude lines’ 4, 4,5 en 5m/sec
adopted from Fig. 288. Wind velocity in heart
line primarily drops from 4.8 to 3.8m/sec, but then increases up to 5m/sec on
the East edge due to lateral impacts. Drawing the case ‘flank in wind’ the first left km from Fig. 288 is used only extrapolating
the middle parts. In that case the urban area is surprisingly exposed to lower
wind velocities because lateral impacts play practically no rôle. That
conclusion is controversial to the usual intuition that elongated urban areas
should be located with ‘head in wind’. ‘Flank in wind’ appears to be better
from a viewpoint of shelter. However, the question is how much this measure
yields. Fig. 290 compares them by a grid of
hectares.
Suppose there are 40
dwelling per hectare. From ventilation losses of non airtight dwellings due to Westerly wind we now can calculate the total difference.
|
Windvelocity
|
head
|
flank
|
Ventilatilion loss in kWh due to Westerly wind
|
|
m/sec
|
ha
|
ha
|
Per dwelling
|
Per ha.
|
Total head
|
Totaal flank
|
|
3,75
|
88
|
252
|
504
|
20160
|
1774080
|
5080320
|
|
4,00
|
98
|
90
|
521
|
20840
|
2042320
|
1875600
|
|
4,25
|
12
|
|
539
|
21560
|
258720
|
|
|
4,50
|
120
|
58
|
557
|
22280
|
2673600
|
1292240
|
|
4,75
|
34
|
|
577
|
23080
|
784720
|
|
|
5,00
|
48
|
|
597
|
23880
|
1146240
|
|
|
Totaal
|
400
|
400
|
|
|
8679680
|
8248160
|
|
|
|
Fig. 291 Difference in ventilatition
loss head and flank in wind
|
|
|
The difference due to
western wind amounts 8679680 – 8248160 = 431 520 kWh per year
(approximately 27 kWh average per dwelling). However, this amount can not be
charged as profit by giving an elongated urban area a turn by 90o.
On every orientation after all, the impact of at least four wind directions
have to be analysed. Then the profit is the difference in impact from two wind
directions head and two flank.
Is a non elongated (‘compact’) town better than a
whether or not favourably oriented elongated or dispersed one? This question
can not be answered for all cases because elongatedness is substantially
dependent from orientation. Anyway, for Westerly
wind in case of Leidscheveen the following is valid. Fig. 292 and Fig. 293 show three classes of wind
velocity on a hectare grid.
From the ventilation loss
per dwelling due to Westerly wind of 3,75, 4
en 4,50 m/sec we can calculate a difference (Fig. 294).
|
Windvelocity
|
Compact
|
Spread
|
Ventilationloss in kWh due to westerly wind
|
|
m/sec
|
ha
|
ha
|
per woning
|
per ha
|
totaal compact
|
totaal gespreid
|
|
3,75
|
250
|
160
|
504
|
20160
|
5040000
|
3225600
|
|
4,00
|
72
|
128
|
521
|
20840
|
1500480
|
2667520
|
|
4,50
|
78
|
112
|
557
|
22280
|
1737840
|
2495360
|
|
Totaal
|
400
|
|
|
|
8278320
|
8388480
|
|
|
|
Fig.
294 Difference in ventilation loss in compact and dispersed towns
|
|
|
The difference in favour of
building compact towns amounts 8388480 – 8278320 = 110 160 kWh per year only (approximately 7 kWh average per
dwelling). Velocity and probability of Western wind amounts a little above the
average. So, you can multiply this figure by approximately 10 to estimate the
total profit.
Comparison with elongated
forms is more difficult by orientation sensitivity. A fast method of
multiplying the profit of westerly wind does not make sense then. For every
several case the calculation has to be repeated for all 12 wind directions. We
will not elaborate that.
The intended profit of this paragraph
to be used in next paragraphs is insight in the importance of lateral wind
effects as such.
The acquired insights make
rough study of town edge design possible. By doing that in the same time we
reach the lowest level of scale roughness based calculations can be useful. On lower levels of scale the
average image of roughness is disturbed too much by local form variations essential
for urban design. However, they remain indispensable as input for predictions
on lower levels of scale. The next chapter will examine levels of district and
neigbourhood further by carefully designed wind tunnel experiments. They will
link up connections between urban design and wind behaviour in more detail.
However, on the level of
town edge design the roughness approach (grain approximately 100m radius) still
makes sense for rough conclusions. We restrict to the impacts of large gaps in
the city edge. They occur by large access roads with noise zones or green lobes
penetrating the city.
Fig. 295 shows a model of a small
town (approximately 50 duizend inwoners) with lobes like that.
|

|

|

|

|
|
|
|
|
|
|
Fig.
295 Small town with green lobes
|
Fig.
296 Wind velocity profile
cross section A
|
Fig.
297 Windvelocity profiel
doorsnede B
|
Fig.
298 Difference profile A en
B
|
|
|
|
|
|
Fig. 296 and Fig. 297 show the windvelocity
profiles of cross section A and B in case it would be Leidscheveen blown by
Western wind. Fig. 298 shows above the last 3000m
of both profiles projected on top of eachother. Below the difference between
both profiles is represented; 65% has to be bridged laterally above urban area
over a distance 1,2 · D1. This determines wind velocity on the edge.
From these data we estimate
again an average wind velocity per hectare.
Fig. 299 shows lobes penetrating
from four directions. In Fig. 300 the lobes are filled with
forest of the same roughness as the urban area keeping the urban surface equal.
From the ventilation losses
belonging to wind velocity 3,75, 4, 4,5 and 5m/sec due to westerly wind, Fig. 301 calculates the difference.
|
Windvelocity
|
Open
|
Closed
|
Ventilationloss in kWh due to westerly wind
|
|
m/sec
|
ha
|
ha
|
per dwelling
|
per ha
|
total open
|
total closed
|
|
2,75
|
154
|
305
|
504
|
20160
|
3104640
|
6148800
|
|
4,00
|
184
|
74
|
521
|
20840
|
3834560
|
1542160
|
|
4,50
|
106
|
82
|
557
|
22280
|
2361680
|
1826960
|
|
5,00
|
21
|
4
|
597
|
23880
|
501480
|
95520
|
|
Totaal
|
465
|
465
|
|
|
9802360
|
9613440
|
|
|
|
Fig.
301 Difference in ventilation loss by ‘open’ and ‘closed’ town edge
|
|
|
The difference is 9 802 360 –
9 613 440 = 188 920 kWh per year
(Approximately 10 kWh per dwelling). Multiplying Westerly
wind impact by 10 the total average profit is approximately 100 kWh x 1860
dwellings.
In chapter 2.2 we restricted our thought experiments to two wind directions and in
this chapter even to one (Westerly wind).
Assuming an average temperature for all wind directions we
reported virtual ventilation losses of non airtight, low rise buildings due to Westerly wind as an indicator. Their differences
clarified an impact of environmental roughness useful for other impacts as
well. We exclusively varied regional and local environment applying different
roughnesses, keeping the rest constant. Otherwise the impact of environmental
roughness on itself could not be clarified. It would be mixed up with other
causes (possible measures). To clarify other causes the reverse we have to keep environmental
rougness constant. If we take one layout of roughnesses in the environment –
the one we will use in next chapters for experiments in the wind tunnel (Fig. 306) – we can compare the contribution of every several wind direction
and their temperature properly (Fig. 302). We calculated energy losses by ventilation for every wind
direction in the same way we did above (column A and B) and for airtight
dwellings (column C and D).
|
|
|
|
without temperature
influence
|
|
temperature influence
|
|
with temperature
influence
|
|
|
|
|
non airtight
|
airtight
|
|
non airtight
|
airtight
|
|
non airtight
|
airtight
|
|
wind direction
|
|
A
|
B
|
C
|
D
|
|
E
|
F
|
|
A x E
|
B x E
|
C x F
|
D x F
|
|
'hours'
|
degrees
|
|
kWh
|
|
kWh
|
|
|
|
|
|
kWh
|
|
kWh
|
|
|
1
|
30
|
|
322
|
6%
|
154
|
6%
|
|
70%
|
66%
|
|
227
|
4%
|
101
|
4%
|
|
2
|
60
|
|
492
|
9%
|
228
|
9%
|
|
116%
|
111%
|
|
570
|
10%
|
254
|
10%
|
|
East 3
|
90
|
|
405
|
7%
|
201
|
8%
|
|
168%
|
151%
|
|
681
|
12%
|
304
|
12%
|
|
4
|
120
|
|
246
|
4%
|
129
|
5%
|
|
205%
|
174%
|
|
504
|
9%
|
225
|
9%
|
|
5
|
150
|
|
369
|
7%
|
186
|
8%
|
|
64%
|
57%
|
|
238
|
4%
|
106
|
4%
|
|
South 6
|
180
|
|
530
|
10%
|
259
|
10%
|
|
71%
|
65%
|
|
377
|
7%
|
168
|
7%
|
|
7
|
210
|
|
729
|
13%
|
232
|
9%
|
|
100%
|
141%
|
|
731
|
13%
|
326
|
13%
|
|
8
|
240
|
|
769
|
14%
|
315
|
13%
|
|
107%
|
116%
|
|
819
|
15%
|
365
|
15%
|
|
West 9
|
270
|
|
591
|
11%
|
253
|
10%
|
|
107%
|
111%
|
|
631
|
11%
|
281
|
11%
|
|
10
|
300
|
|
389
|
7%
|
172
|
7%
|
|
90%
|
91%
|
|
349
|
6%
|
156
|
6%
|
|
11
|
330
|
|
366
|
7%
|
173
|
7%
|
|
71%
|
67%
|
|
260
|
5%
|
116
|
5%
|
|
North 12
|
0
|
|
329
|
6%
|
167
|
7%
|
|
45%
|
40%
|
|
149
|
3%
|
67
|
3%
|
|
|
Total
|
|
5537
|
100%
|
2469
|
100%
|
|
|
|
|
5536
|
100%
|
2469
|
100%
|
|
|
|
Fig. 302 Contributions per wind
direction to total energy loss by ventilation
|
|
|
In the lowest row ‘Total’, column A shows we can multiply the loss
of Westerly wind by 10 to have an idea of
total loss from all directions indeed. The totals without temperature influence
are the same as those including temperature influence, because in columns A, B,
C and D we assumed an average temperature of all directions.
Columns E and G show tentative weight factors for temperature, based
on Visser (1986). Multiplying A, B, C and D by these factors produces
the necessary correction to get a better idea about the real losses per
direction. They are used in next chapters as well.
|

|

|
|
|
|
|
Fig. 303 Contributions per wind direction to total energy loss by
ventilation without temperature influence (A and C in Fig. 302)
|
Fig. 304 Tentative correction factors for temperature influence (E and
F in Fig. 302)
|
|
|
|
Fig. 303 and Fig. 304 show Easterly winds being
less probable but colder have a larger impact on energy losses by ventilation
than South Westerly winds. To understand why
Southerly winds contribute more in airtight buildings (Hoogbouw in Fig. 304) than in non airtight ones (Laagbouw) you have to
look at Fig.
219.
Changing location and size of a homogenuous undirected roughness, influences every external wind direction in the same way. However,
changing form on a lower level of scale introduces internal directions within
that field of roughness behaving differently even for one single external wind
direction. And design can vary form within form. This complication you can
imagine as 3 potter’s wheels turning around the same centre. If we consider 12
directions, there are 12 x 12 x 12 combinations (Fig. 305).
|

|

|
|
|
|
|
Fig. 305 Three levels of schale
where orientation has to be taken into account
|
Fig. 306 Supposed wind tunnel context by standard Northerly wind
|
|
|
|
The external wheel represents 12 local wind statistics (W1, W2, W3 …
concerning probability, velocity and temperature) as it applies outside and at
the edge of the urban fragment we consider. The second wheel represents the
considered fragment with its own arrow indicating North (b1). In this chapter the direction of
the allotment as a whole (b1, b2, b3 ...) is variable. The middle wheel
represents façades within the allotment having variable orientations (a1, a2, a3 ...), causing different ventilation
losses locally. In previous paragraphs a and b were neglected. Ventilation losses were averaged over all
directions of allotments and façades.
In this chapter a and b are varied by interpreting tests of 18
different allotments in the wind tunnel of Visser (1986) from 7 different angles (0o – 90o
by steps of 15o) with a standarised W and foreland roughness (Fig. 306). From these 7 measured angles, 4 (0o – 90o
by steps of 30o) appeared to be sufficient to draw conclusions about
all directions of allotment.
On the level of districts and neighbourhoods 4 configurations 1 x 1 km Jong (1986) - fully
elaborated in models 1:500 - are tested by Visser (1986). In each of the four models 30 x 2 measuring points were installed
at front and back side of different building blocks to measure pressure
differences (Fig. 307).
Right above in each configuration (Fig. 307) each time you find a quarter of a district centre. So, any
configuration could be thought mirrored twice around this centre into a full
district 2x2km consisting of 4 district quarters. Each configuration consists
of 9 neighbourhood quarters 300x300m (one central, 8 peripheral). Each
neighbourhood quarter consists of 9 ensemble
quarters (hectares 100x100m one
central, 8 peripheral). District roads are planted with trees;
neighbourhood and ensemble roads are not.
The configuration is outside blown along from
North to East (90o from North). At South and West side the configuration as a
district quarter is part of an imaginary district filled up with equal
roughness.
In this paragraph we study the differences between the four
configurations not trying to develop calculation models.
|

|

|

|
|

|
|

|
|
1 ‘Low rise at the edge’
|
|
2 ‘High rise at the edge’
|
|

|

|

|
|

|
|

|
|
3 ‘Edge green’
|
|
4 ‘Central green’
|
|
|
|
Fig. 307 District configurations
in wind tunnel with measuring points
indicated
|
|
|
Concerning the average result of all measuring points the
differences between the configurations are remarkably small. However, there are
substantial differences between locations within configurations. (Fig. 314and Fig. 317). Fig. 308 shows hectare allotments applied in the tested configurations.
|
In configuration
1 and 2
|
|

|

|

|
|
Vrije
sect. 30w/h 10m
|
Hoek1a 22w/ha
22m
|
Hof1 96 w/ha
15,5m
|
Hof4 53,3w/h 10m
|
|
In configuration
2
|

|
|
In configuration
3 and 4:
|

|
|
Lijn10 84w/ha 17m
|
Lijn12 53w/ha 10m
|
|
|
|
Fig. 308 Hectare allotments applied in the tested configurations
|
|
|
In paragraph 2.6.1 we study the results of 14 wind tunnel experiments by Visser (1986) on hectare level; 7 with green and 7 without. In these
experiments a number of theoretical repeating point, line, corner and courtyard
allotments 500x500m elaborated in models 1:250 are tested. The force these
allotments ondergo by standard wind is measured. From these tests TNO developed
a calculation method for allotments repeating in two dimensions. By this method
more types of allotment are calculated.
Ventilation loss of a dwelling not only depends on wind statistics
derived from year average wind velocity vg on z=10m height in the nearest wind
measuring station (vg(10), for example 5,4m/sec near Schiphol). It depends also
on the environment and orientation of the building block. On these more local
factors pressure differences between front and back façades follow determining
ventilation losses at last.
Pressure differences are proportional to driving
pressure of wind: 0,5 x r x vg(10)2. In this formula r (‘ro’) is the density of air.
Pressure differences between front and back façades determining ventilation are
measured in wind tunnel. Dividing such pressure differences by the local
driving pressure of wind produces a factor DCp(10) representing the resistance of an allotment independent from
wind velocity. The result of wind tunnel tests are expressed in DCp(10). Fig. 309 shows the relation between ventilation loss near Schiphol and DCp(10) in any wind direction Visser (1986). Airtight buildings in vg(10) lose less energy by
increasing pressure because inhabitants close windows they opened in less
pressure!
Inside urban areas energy yield of wind turbines is less relevant.
However, pressure difference is important as well for comfort of outdoor space,
dispersion of air pollution and wind loads. But we have measured ventilation
losses and will use it as an indicator.
|

|
|
|
|
|
|
Degrees from y-axis
|
|
|
Point
|
0
|
30
|
60
|
90
|
av.
|
|
1
|
0,00
|
0,18
|
0,32
|
0,32
|
0,21
|
|
2
|
0,10
|
0,16
|
0,07
|
0,04
|
0,09
|
|
3
|
0,10
|
0,02
|
0,10
|
0,02
|
0,06
|
|
4
|
0,02
|
0,14
|
0,24
|
0,05
|
0,11
|
|
5
|
0,12
|
0,08
|
0,11
|
0,11
|
0,11
|
|
6
|
0,34
|
0,38
|
0,02
|
0,04
|
0,20
|
|
7
|
0,34
|
0,26
|
0,10
|
0,04
|
0,19
|
|
8
|
0,08
|
0,05
|
0,12
|
0,16
|
0,10
|
|
9
|
0,35
|
0,28
|
0,11
|
0,05
|
0,20
|
|
10
|
0,10
|
0,00
|
0,10
|
0,12
|
0,08
|
|
11
|
0,11
|
0,12
|
0,02
|
0,05
|
0,08
|
|
12
|
0,10
|
0,19
|
0,24
|
0,19
|
0,18
|
|
13
|
0,01
|
0,10
|
0,12
|
0,01
|
0,06
|
|
14
|
0,18
|
0,08
|
0,04
|
0,05
|
0,09
|
|
15
|
0,02
|
0,13
|
0,25
|
0,38
|
0,20
|
|
16
|
0,10
|
0,19
|
0,14
|
0,13
|
0,14
|
|
17
|
0,02
|
0,12
|
0,22
|
0,30
|
0,17
|
|
18
|
0,18
|
0,11
|
0,01
|
0,16
|
0,12
|
|
19
|
0,19
|
0,16
|
0,01
|
0,06
|
0,11
|
|
20
|
0,02
|
0,08
|
0,19
|
0,07
|
0,09
|
|
21
|
0,04
|
0,10
|
0,14
|
0,01
|
0,07
|
|
22
|
0,00
|
0,16
|
0,12
|
0,16
|
0,11
|
|
23
|
0,38
|
0,36
|
0,30
|
0,13
|
0,29
|
|
24
|
0,14
|
0,32
|
0,35
|
0,35
|
0,29
|
|
25
|
0,17
|
0,06
|
0,28
|
0,24
|
0,19
|
|
26
|
0,53
|
0,28
|
0,05
|
0,12
|
0,25
|
|
27
|
0,23
|
0,20
|
0,04
|
0,22
|
0,17
|
|
28
|
0,34
|
0,03
|
0,22
|
0,48
|
0,27
|
|
29
|
0,13
|
0,08
|
0,07
|
0,05
|
0,08
|
|
30
|
0,06
|
0,01
|
0,08
|
0,02
|
0,04
|
|
31
|
0,08
|
0,07
|
0,02
|
0,10
|
0,07
|
|
32
|
0,05
|
0,07
|
0,16
|
0,30
|
0,15
|
|
Gem.
|
0,14
|
0,14
|
0,14
|
0,14
|
0,14
|
|
|
|
Visser (1986)
|
|
|
Fig. 310
DCp(10) in measure points of configuration 1 in 4 directions
|
|
|
|
Fig. 310 shows DCp(10) measured in every measure point of configuration 1 four times
while wind was blowing 0o to 90o from y-axis each time
turning the model 30o (any direction could be North).
Measuring points 23 and 24 (high rise at a crossing, see Fig. 307 conf. 1) suffer the largest pressure differences, 23 on 0o,
24 on 60o and 90o. This kind of details we study in
paragraph 2.5.5. This paragraph studies the averages in lowest row compared with
the averages of the other configurations.
The averages in lowest row of Fig. 310 seem to show the direction of wind does not matter but this is only
the case in configuration 1. It is explained best because half of the measured
blocks there are oriented perpendicular to the other half. So, the minimum
ventilation loss of one building block compensates the maximum of the other
one. Configuration 2 is less balanced that way and configurations 3 and 4 have
only one orientation of building blocks (Fig. 311).
|

|

|
|
|
|
|
Fig. 311 Average DCp(10) in
different configurations two times mirrored around the centre.
|
Fig. 312 Average ventilation loss of a non airtight dwelling in kWh per
allotment direction if standard Northerly wind would blow from all directions
|
|
|
|
Comparing the impact of locations and allotment directions we should use an equal
standard wind (here Northerly wind, representing approximately 2.69% of the
virtual total ventilation loss per allotment direction) for every allotment
direction (Fig. 312).The virtual total ventilation loss then is 100%. Fig. 313 shows averages multiplied into such a virtual total.In
configuration 1 it is 5 344kWh for non airtight dwellings. That is less
than we calculated by roughness 7 in Fig. 302 (5 536kWh in column A X E), and for airtight dwellings it is
more (3 266 kWh instead of 2 469 in column C x F). Perhaps the
roughness class of configurations is closer to 8 than class 7 we used in
paragraph 2.4.6 and supposed in Fig. 306.
|
|
Configuration 1
|
Configuration 2
|
Configuration 3
|
Configuration 4
|
|
|
calculated
|
|
|
|
|
|
|
|
|
|
|
roughness
|
average
|
virtual
|
average
|
virtual
|
average
|
virtual
|
average
|
virtual
|
|
|
100%
|
2,69%
|
100%
|
2,69%
|
100%
|
2,69%
|
100%
|
2,69%
|
100%
|
|
non airtight
|
5536
|
144
|
5344
|
141
|
5233
|
129
|
4787
|
131
|
4862
|
|
airtight
|
2469
|
88
|
3266
|
89
|
3303
|
|
|
|
|
|
DCp(10)
|
|
0,14
|
|
0,14
|
|
0,05
|
|
0,06
|
|
|
|
|
Fig. 313 Estimating average ventilation losses from 4 allotment
directions multiplied into a virtual total.
|
|
|
Average pressure difference in configuration 2 (high rise on the
edge) is the same (DCp(10)=0.14) as in configuration 1 (low rise on the edge). But there are differences per allotment direction. So, you
can not yet conclude both configurations should have the same ventilation loss.
Wind directions deliver different contributions and their reduction
depends on the North direction arrow of the allotment in the compass card of wind
directions. Because configuration 3 (edge green) and configuration 4
(central green) have lower pressure differences in all directions (Fig. 312) we can conclude they will have less ventilation loss than
configurations 1 and 2 indeed. However, the difference between a lay out with
green on the edge or within the centre is negligible!
Configuration 1 (low rise on the edge) has more ventilation losses
from non airtight low rise dwellings and less from airtight high rise ones than
configuration 2 (high rise on the edge). Fig. 309 shows airtight highrise has less ventilation loss by more wind
pressure. Inhabitants close their windows earlier.
Slant flow along (30o of 60o) causes in all
cases maximum loss (Fig. 311). Perhaps we should orientate allotments with two perpendicular directions
East or South West sheltering one of them best and the othe not at all. This
yields more than both half. We tested that hypothesis by calculating
perpendicular and slant flowing along for 12 North direction arrows but the
result disappointed because adjacent wind directions score high as well by
slant flow. They dim the aimed impact into a negligible result.
That is of course not the case in parallel blocked configurations 3
and 4.
So, measures on the level of district or neighbourhood have more local
than general impacts. Big local impacts level out in the district as a whole in
such a way that differences in its lay out become marginal.
We restrict ourselves to perpendicular flow with Northerly wind
character (2.7%) from 0o and 90o out of y-axis. In both
cases wind meets on 300m from town edge a 30m wide neighbourhood road and on
600m a 70m wide district road with trees.
A roughness approach (paragraph 2.4.6) would show decreasing loss until 100m from town edge stabilising
on approx. 150kWh for non airtigh low rise and for airtight high rise
increasing stabilising on 75 kWh. Fig. 314 shows wind tunnel results
elaborated into kWh (paragraph 2.4) from configurations 1 (low rise on the edge) and 2 (high rise on
the edge) as a working of distance to town edge.
|

|

|
|
configuration 1 (low rise on the edge)
|
configuration 2 (high rise on the edge)
|
|
|
|
Fig. 314 Ventilation losses of non
airtight low rise and iartight high rise dwellings by standard Northerly wind
(2.7% of virtual total) as a function of distance to town edge in
configurations 1 and 2
|
|
|
Wind tunnel experiments now specified to location give a clearer
distinction between low rise and high rise on the edge then leveled out over
the district. The largest low rise loss in configuration 1 appears in measure
point 15 (197kWh), a 15.5m high building located on a 15m wide road without
trees and a foreland of 10m high dwellings. The smallest appears in measure
point 13 (116kWh), a courtyard dwelling. The difference is approx. 80 or
virtually 3000kWh.
Fig. 317 shows the same figures as Fig. 314 for configuration 3 en 4
without high rise.
|
|
|
|
configuration 3 (green on the edge)
|
configuration 4 (central green)
|
|
|
|
Fig. 317 Ventilation losses of non airtight low rise dwellings by standard
Northerly wind (2.7% of virtual total) as a function of distance to town edge
in configurations 3 and 4
|
|
|
From the results of 14 wind
tunnel experiments on repeating theoretical point, line, corner and courtyard
allotments with and without green a calculation method is
developed Visser
(1987; Visser (1987) predicting average pressure
differences between front and back façades of dwellings DCp(z) (DCp on heigth z).
The reference height z is 2.5 times the average building height.
The calculation is
restricted to allotments with two main directions at most. For two
directions we have to determine the value of DCp
perpendiculary blown along by wind (DCp0).
Façades may bend 30o from main direction at most. Within that margin
measuring a second main direction is not necessary. The expected DCp per flow
direction is calculated for 100 x 100m allotment types in Fig. 319.
|

|

|

|

|

|

|
|
*Punt01 10m
|
*Punt02 10m
|
Punt03 10m
|
*Punt04 10m
|
Punt05 10m
|
*Punt06 10m
|
|

|

|

|

|

|

|
|
Punt07 15,5m
|
Punt08 15,5m
|
*Punt09 22m
|
Punt10 22m
|
Lijn01 10m
|
*Lijn02 10m
|
|

|

|

|

|

|

|
|
Lijn05 10m
|
Lijn06 10m
|
Lijn07 15,5m
|
*Lijn08 22m
|
Lijn09 22m
|
*Hoek01 22m
|
|

|

|

|

|

|

|
|
Hoek02 22m
|
*Hof01 15,5m
|
Hof02 10 en 15,5m
|
Hof03 10m
|
*Hof04 10m
|
*Hof05 15,5m
|
|
Visser
(1987; Visser (1987)
|
|
Fig. 319 Allotment
types 100x100m with different height Visser (1987) calculated DCp(z) for
|
|
|
Fig. 320 shows the result of these calculations.
|
|
height
|
vert.surf.
|
without green
|
with green 6m high
|
with green 10m high
|
|
|
m
|
F/O
|
N
|
+30
|
+60
|
+90
|
av.
|
N
|
+30
|
+60
|
+90
|
gem.
|
N
|
+30
|
+60
|
+90
|
av.
|
|
Punt01
|
10
|
0,24
|
0,14
|
0,13
|
0,09
|
0,00
|
0,09
|
0,13
|
0,12
|
0,09
|
0,00
|
0,09
|
0,12
|
0,11
|
0,08
|
0,00
|
0,08
|
|
Punt02
|
10
|
0,24
|
0,14
|
0,13
|
0,09
|
0,00
|
0,09
|
0,13
|
0,12
|
0,09
|
0,00
|
0,09
|
0,12
|
0,11
|
0,08
|
0,00
|
0,08
|
|
Punt03
|
10
|
0,24
|
0,19
|
0,17
|
0,13
|
0,00
|
0,12
|
0,18
|
0,17
|
0,12
|
0,00
|
0,12
|
0,12
|
0,19
|
0,11
|
0,00
|
0,11
|
|
Punt05
|
10
|
0,16
|
0,19
|
0,17
|
0,12
|
0,00
|
0,12
|
0,18
|
0,17
|
0,12
|
0,00
|
0,12
|
0,12
|
0,19
|
0,11
|
0,00
|
0,11
|
|
Punt06
|
10
|
0,30
|
0,14
|
0,13
|
0,10
|
0,00
|
0,09
|
0,14
|
0,13
|
0,09
|
0,00
|
0,09
|
0,13
|
0,12
|
0,08
|
0,00
|
0,08
|
|
Punt07
|
15,5
|
0,14
|
0,23
|
0,21
|
0,15
|
0,00
|
0,15
|
0,22
|
0,20
|
0,14
|
0,00
|
0,14
|
0,20
|
0,19
|
0,13
|
0,00
|
0,13
|
|
Punt08
|
15,5
|
0,21
|
0,16
|
0,15
|
0,11
|
0,00
|
0,11
|
0,16
|
0,14
|
0,10
|
0,00
|
0,10
|
0,14
|
0,13
|
0,03
|
0,00
|
0,08
|
|
Punt09
|
22
|
0,09
|
0,20
|
0,19
|
0,13
|
0,00
|
0,13
|
0,20
|
0,10
|
0,10
|
0,00
|
0,10
|
0,20
|
0,19
|
0,13
|
0,00
|
0,13
|
|
Punt10
|
22
|
0,18
|
0,19
|
0,18
|
0,13
|
0,00
|
0,13
|
0,19
|
0,18
|
0,10
|
0,00
|
0,12
|
0,18
|
0,12
|
0,12
|
0,00
|
0,11
|
|
Lijn01
|
10
|
0,24
|
0,21
|
0,19
|
0,14
|
0,00
|
0,14
|
0,20
|
0,18
|
0,13
|
0,00
|
0,13
|
0,18
|
0,12
|
0,12
|
0,00
|
0,11
|
|
Lijn02
|
10
|
0,24
|
0,21
|
0,19
|
0,14
|
0,00
|
0,14
|
0,20
|
0,19
|
0,13
|
0,00
|
0,13
|
0,18
|
0,17
|
0,12
|
0,00
|
0,12
|
|
Lijn05
|
10
|
0,32
|
0,14
|
0,13
|
0,03
|
0,00
|
0,08
|
0,13
|
0,12
|
0,08
|
0,00
|
0,08
|
0,12
|
0,11
|
0,09
|
0,00
|
0,08
|
|
Lijn06
|
15,5
|
0,25
|
0,20
|
0,19
|
0,13
|
0,00
|
0,13
|
0,19
|
0,18
|
0,10
|
0,00
|
0,12
|
0,18
|
0,16
|
0,12
|
0,00
|
0,12
|
|
Lijn07
|
11
|
0,18
|
0,28
|
0,26
|
0,18
|
0,00
|
0,18
|
0,27
|
0,24
|
0,18
|
0,00
|
0,17
|
0,24
|
0,22
|
0,16
|
0,00
|
0,16
|
|
Lijn08
|
22
|
0,35
|
0,12
|
0,11
|
0,08
|
0,00
|
0,08
|
0,12
|
0,11
|
0,08
|
0,00
|
0,08
|
0,11
|
0,10
|
0,07
|
0,00
|
0,07
|
|
Lijn09
|
22
|
0,35
|
0,12
|
0,11
|
0,08
|
0,00
|
0,08
|
0,12
|
0,11
|
0,08
|
0,00
|
0,08
|
0,11
|
0,10
|
0,07
|
0,00
|
0,07
|
|
Hoek01
|
22
|
0,18
|
0,28
|
0,26
|
0,18
|
0,00
|
0,18
|
0,28
|
0,26
|
0,18
|
0,00
|
0,18
|
0,27
|
0,24
|
0,19
|
0,00
|
0,18
|
|
Hoek02
|
22
|
0,35
|
0,28
|
0,26
|
0,18
|
0,00
|
0,18
|
0,28
|
0,26
|
0,18
|
0,00
|
0,18
|
0,27
|
0,24
|
0,18
|
0,00
|
0,17
|
|
Hof01
|
15,5
|
0,25
|
0,14
|
0,13
|
0,09
|
0,00
|
0,09
|
0,13
|
0,12
|
0,09
|
0,00
|
0,09
|
0,12
|
0,11
|
0,08
|
0,00
|
0,08
|
|
Hof01>
|
15,5
|
0,19
|
0,25
|
0,23
|
0,17
|
0,00
|
0,16
|
0,24
|
0,22
|
0,16
|
0,00
|
0,16
|
0,22
|
0,20
|
0,15
|
0,00
|
0,14
|
|
Hof02
|
10
|
0,16
|
0,22
|
0,20
|
0,14
|
0,00
|
0,14
|
0,21
|
0,19
|
0,14
|
0,00
|
0,14
|
0,19
|
0,18
|
0,17
|
0,00
|
0,14
|
|
Hof02>
|
15,5
|
0,19
|
0,25
|
0,23
|
0,17
|
0,00
|
0,16
|
0,24
|
0,20
|
0,16
|
0,00
|
0,15
|
0,22
|
0,20
|
0,15
|
0,00
|
0,14
|
|
Hof03
|
10
|
0,16
|
0,22
|
0,20
|
0,14
|
0,00
|
0,14
|
0,21
|
0,19
|
0,14
|
0,00
|
0,14
|
0,19
|
0,18
|
0,10
|
0,00
|
0,12
|
|
Hof03>
|
10
|
0,12
|
0,33
|
0,30
|
0,21
|
0,00
|
0,21
|
0,31
|
0,28
|
0,20
|
0,00
|
0,20
|
0,28
|
0,26
|
0,10
|
0,00
|
0,16
|
|
Hof04
|
10
|
0,24
|
0,26
|
0,24
|
0,17
|
0,00
|
0,17
|
0,25
|
0,23
|
0,16
|
0,00
|
0,16
|
0,23
|
0,21
|
0,15
|
0,00
|
0,15
|
|
Hof05
|
15,5
|
0,37
|
0,19
|
0,18
|
0,13
|
0,00
|
0,13
|
0,18
|
0,17
|
0,12
|
0,00
|
0,12
|
0,17
|
0,15
|
0,11
|
0,00
|
0,11
|
|
average
|
|
|
0,20
|
0,19
|
0,13
|
0,00
|
0,13
|
0,20
|
0,18
|
0,13
|
0,00
|
0,12
|
0,08
|
0.17
|
0,12
|
0,00
|
0,12
|
|
|
|
Fig. 320 DCp(z) for 4 flow along
directions in 23 allotment types (> second measurement perpendicular)
|
|
|
Hof01, Hof02 and Hof03 have
two main directions of front-back façades. So, DCp had to be
measured two times. Hoek01, Hoek04, Hof04 and Hof05 have two directions with
the same characteristics perpendicular. So, the same measurement can be used
the reverse (90o is 0o, 60o is 30o
and so on) for the perpendicular part. Averaging the impact of both directions
proportional to the number of dwellings you get numbers for corner and
courtyard allotments comparable with point and line alotments.
Then we have to take other
windstatistics than Northerly into account. The quarter we calculated is only
very exceptionally equal to a quarter of all ventilation losses as well. This
is for instance the case if that quarter (0o to 90o from
y-axis) coincides with wind directions West to North. For every other North
indicating arrow the calcuated quarter will contribute more or less than 25% of
the ventilation loss, dependent from the wind statistics exposed. This
contribution is calculated for 12 North indicating arrows and completed into a
100% virtual total loss. The supposition that a dwelling surrounded by
repeating allotments is equally sheltered into the other quarters
is better justified than in previous paragraphs.
Fig. 321 shows the
result of this calculation on the average of Fig. 320 itemized for
airtight high rise allotments and low rise ones supposed to be non airtight.
|
|
without green
|
with green 6m height
|
with green 10m height
|
|
main direction
|
|
30
|
60
|
90
|
virt.
|
|
30
|
60
|
90
|
virt.
|
|
30
|
60
|
90
|
virt.
|
|
average
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
low rise
|
162
|
249
|
599
|
507
|
5162
|
|
247
|
594
|
506
|
5130
|
|
244
|
585
|
505
|
5075
|
|
high rise
|
90
|
136
|
343
|
414
|
3343
|
90
|
136
|
343
|
414
|
3343
|
90
|
136
|
343
|
414
|
3347
|
|
|
|
Fig. 321 Ventilation loss as a consequence of standard Northerly wind.
|
|
|
The impact of 6m high
(young) trees is negigible. However, when for instance after
10 years trees reach a height of 10m there is some impact. However, locally the
impact may be substantial (page 146).
Fig. 322 and Fig. 323 show some
allotment types in seqeunce of virtual ventilation losses.
|
|
|
loss
|
height
|
density
|
distance
|
|
|
kWh/won
|
m
|
dwell./ha
|
m
|
|
Lijn05
|
4789
|
10
|
64
|
15
|
|
Punt01&02
|
4795
|
10
|
48
|
15
|
|
Punt06
|
4817
|
10
|
48
|
17
|
|
Punt08
|
4901
|
15
|
72
|
18
|
|
Hof01
|
4906
|
15
|
96
|
40
|
|
Punt05
|
4980
|
10
|
36
|
23
|
|
Punt03
|
4982
|
10
|
48
|
23
|
|
Lijn06
|
5008
|
15
|
64
|
40
|
|
Lijn01&02
|
5025
|
10
|
48
|
23
|
|
Punt07
|
5068
|
10
|
64
|
35
|
|
Hof02
|
5086
|
14
|
64
|
40
|
|
Hof03
|
5130
|
10
|
48
|
40
|
|
Lijn07
|
5187
|
11
|
64
|
40
|
|

|
|
|
|
|
Fig.
322 Allotment types in
sequence of loss
|
Fig. 323 Relation loss and block distance in m
|
|
|
|
Remarcably there is nearly
no relation with dwelling density. Lijn05 and
Lijn07 of equal dwelling density (64 dwellings in the hectare concerned) and
nearly the same height (10 and 11m respectively) have lowest and highest loss.
However, frontal density F/O (vertical surface F per horizontal surface
O) is determining (see Fig. 320 ) reasonably
related with distance between building blocks (drawn as polynome
regression in Fig. 323 ), but diverging
at higher distances.
Fig. 325 and Fig. 326 show the
results for point and line allotments on any orientation.
|

|

|
|
|
|
|
Fig.
325 Ventilation loss of point
allotments
|
Fig.
326 Ventilation loss of line allotments
|
|
|
|
Biggest loss is reached when
you orientate façades of point and line allotments 7 due West. Smallest loss is
reached by line allotments 5 or point allotments 1,2 and 6 orientated on North North West (330o). The virtual
difference is more than 1000kWh/dwelling.
Fig. 327 shows courtyard
allotments. Orientation
sensitivity levels out most in hof04 and hof05 because perpendicular blocks have
equal length. Higher blocks like hof01 and hof05 (15.5m high) lose less than
lower ones like hof03 and hof04 (10m).
|

|

|
|
|
|
|
Fig. 327 Ventilation loss of courtyard allotments
|
Fig. 328 Ventilation loss of high rise allotments
|
|
|
|
Fig. 328 shows losses of airtight high rise allotments
on a much smaller scale. Total variation is less than 100kWh. Inhabitant’s
behaviour causes maxima where low rise non airtight allotments showed minima.
Wind behaviour on smallest
scale is decribed more in detail by Voorden (1990).
From that publication we derive some conclusions only. The accidental physical
context and size or form of the objects cause unpredictable turbulences.
Without windtunnel experiments calculations do not produce much general
conclusions. However, scale models of free standing sharp edged buildings
higher than 15m above the environment in a frontal flow of wind in the wind
tunnel show some regularity in causing whirls windward and leeward recognisable on real
scale (Fig. 329).
|

|
|
|
|
Fig.
329 Whirls around a free standing building
|
|
|
Windward and leeward a
standing whirl arises causing unexpected wind directions on
ground level. Walking or cycling along windward of the building, but especially
through the wake area (zog-gebied) leeward you can experience sudden
and diametral changes in wind direction. Protecting yourself with an umbrella
against the wind from your left side you suddenly get wind from the right side.
Fig. 329 (below) shows
the same impact horizontally. The density of lines indicates wind velocity. At
ground level near the edges of the building (no entrances there!) and 1H to 2H leeward, that velocity
could be as high as at the top of the building. The whirls leeward are caused
by low pressure on that side; the wind ‘comes back’ to fill the gap caused by
high velocities at the edge pulling calm air with them. Openings in the
building at ground level may avoid whirls there, but yield new wind velocities
at ground level like Fig. 329 (below) now not
considered as a plan but as a cross section.
Permeable walls like applied at the entrance of the Faculty of
Architecture in Delft
or dense shrubs avoid pressure differences causing whirls.
They can slow down wind velocity at ground level and protect windy areas,
supposed they can resist high wind velocities themselves. Networks of small
wind turbines utilise local wind velocity, but they still have to be designed.
Movement of
air is measured as wind when it is moving into one direction longer
than 5 seconds (2.2.1). When it is flowing back in the
next 5 seconds it is not even counted in wind statistics. But if the wind is
blowing at average into one direction more than an hour we count it as wind and
we calculate the ‘hour average wind velocity’ we used in chapters above. Wind is
caused by slowly increasing temperature differences on the Earth’s surface
causing differences in air pressure. Sometimes these differences are leveled
out by wind in an hour, sometimes in weeks and seldom the air is flowing back
into the area it came from. If the air transported in a minute would flow back
in the next minute and the reverse like water on a beach we would call it
vibration. It would have a vibration time T of 60sec with a frequency f of 1/60 = 0.017
vibrations per second or 0.017Hz (hertz).
Vibrations
in the air from 16 vibrations per second (vibration time 0.063 sec) to
20 000 are accepted by our eardrums as sound. Vibrations slower than 16Hz are
called infrasonic, faster than 20 000 ultrasonic. You can not hear infrasonic vibrations in the air until 16Hz,
but you sometimes can feel them in your lungs Minnaert (1975). The frequences used in music are nearly competely covered by the 88 keys of
piano. It counts more than 7 octaves (Fig. 330) starting with 27.5Hz (the most
left key A1) and ending with 4186Hz (the most right key c5,
part of the 8th octave, not fully covered).
|
code
|
A1
|
A
|
a
|
a1
|
a2
|
a3
|
a4
|
a5
|
|
|
frequency
f
|
27.5
|
55
|
110
|
220
|
440
|
880
|
1760
|
3520
|
Hz
|
|
wave
length l
|
12.364
|
6.182
|
3.091
|
1.545
|
0.773
|
0.386
|
0.193
|
0.097
|
metres
|
|
f x l
|
340
|
340
|
340
|
340
|
340
|
340
|
340
|
340
|
m/sec
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 330 Starting notes of octaves on the piano
|
|
|
|
|
|
|
|
|
|
|
|
Any next
octave doubles the frequency. An octave is subdivided in 12 notes (named a, ais
or bes, b, c, cis or des, d, dis or es, e, f, fis or ges, g, gis). Because 21/12
= 1.0594630944, the frequency of any next key is a factor 1.0594630944
higher than the previous one. So you can calculate the frequency of any note (n=0…87) by f(n)=27.5 x 1.0594630944n
(Fig. 331).
|

|
|
McMahon and Tyler Bonner (1983), Dutch edition McMahon and Tayler Bonner (1987) page 98
|
|

|
|
Michels (1993) page 24
|
|
Fig. 331 The
span of music
|
|
|
The travel
speed of sound c in air is in normal conditions 340m/sec (in
steel 5064m/sec). And speed is the number of vibrations per second f times
their length l: c=f x l (Fig. 330). So, the wave length l of audible sound in air (l = c / f) varies between
340/20 000 = 21.25m and 340/16 = 0.017m.
Take a
drawing tube of L = 0.65m closed at one side
(width does not matter), drum on it and you hear primarily a sound of 130Hz,
which is musical note c with wave length 4 x 0.65 = 2.60m.
But it is mixed with a specific range of overtones (Fig. 332).
|

|

|

|

|
|
|
l0=4L/1=2.60m
|
l1=4L/3=0.867
|
l2=4L/5=0.52
|
|
|
f0=340/l0=131Hz
|
f1=340/l1=392Hz
|
f2=340/l2=654Hz
|
|
|
‘c’
|
‘g1’
|
‘cis2’
|
|
|
|
|
|
|
Fig. 332 Tones produced by a tube of 0.65m closed at one side.
|
|
|
|
|
|
The lines
drawn in the tube represent the position of particles in extreme phases as if
there were only some of them. The distance between the extreme phases (1-1,
2-2, 3-3 …) are different, represented in the sinuses below. The closed left
side of the tube forces a ‘node’ (line elongated into the sinus)
where particles stand still as centres of condensing and thinning, the open
side an ‘antinode’, where they move most, enjoying
the freedom of the end of the tube. So, possible wavelengths are restricted to l = 4/1, 4/3, 4/5 … x L and frequences to a
proportion of 1:3:5…. In tubes open (antinodes) or closed (nodes) at both sides
they are restricted to l = 2/1,
2/2, 2/3 … x L, supposed you do not force local antinodes by openings
(like a flute does). The frequences appear in a proportion
of 1:2:3…, just like strings fixed at two sides do. A voice with less than
9 overtones sounds dim, a voice with more than 14 overtones sounds shrill.
The primary
frequency of a string fs depends on length L, tension s and density r (1 290g/m3) according to fs = L/2 √ s/r. A string with given density and tension tuned by the right force
will give a lowest tone with wavelength 2 x L. Touching the string
softly (flageolet, causing a node there without losing
the lowest tone) half way you will hear a tone with wavelength L (one octave
higher) as well. Touching at one third you will hear a tone with wave length
2/3 x L as well, a combination called fifth (kwint, 2:3). Dividing further
you get fourths (kwart, 3:4), tierces (terts, 4:5) and so on.
Air
particles between nodes move very fast around their quiet position like a sinus
shown in Fig. 332 causing change in air density. Concentration causes increase of
temperature and heat loss. However the particles move fast enough to prevent
substantial energy loss by heat exchange (keeping the process reversible, adiabatic). The maximum divergence of
particles is called amplitude A. The power of a sound wave (called intensity ‘I’ and expressed in W/m2) depends
on that amplitude, but also on frequency f, air density (normally 1.290kg/m3), and travel speed (normally 340m/sec) according to
I = r x (2 x p x f x A)2 x c/2. So, in
normal r and c conditions power
depends on amplitude A and frequency f according to
I = 8658 x (f x A)2.
A speaking
voice produces 10-5 W. A globe with a
radius of 28cm has a surface of 1m2. So, at 28cm distance that voice
has a power of 10-5 W/m2. It is composed by adding
8658·(f x A)2 for every frequency and its accompanying amplitude in
the voice. But suppose it produces tone c only, without overtones (in reality
produced by electronic device only), then frequency is 131Hz, and amplitude A
should be 0.0000003m. A piano produces maximally 0.2W/m2 and if
it would be produced by tone c only the amplitude should be 0.0000367m. For an
exended symphony orchestra and a loudspeaker the figures would be 5W/m2
(A=0.0000183m) and 100W/m2 (A=0.00082m).
Fig. 334 shows the dependency of intensity I
on these particular amplitudes and on musical frequencies from 27.5 to 4000Hz).
The
logarithmical representation (Fig. 334) shows the range from soft to loud
better. Dividing the intensity by a standard of 10-12 W/m2
(comparing it with that standard) we get positive logarithms from 0 to 14 only,
starting with what is just audible. Multipying it by 10 we get a useful range
of decibells (dB) from 0 to 150 (Fig. 335).
Changing the frequency axis in a
logaritmical scale (Fig. 336) we get beautiful straight lines of
growing deciBells by increasing frequencies for every amplitude.
Fig. 337 is the same graph with the boundary
of what we think to hear.
|

|
|
Creemers,
Atteveld et al. (1983) page 186
|
|
Fig. 337 Pain boundary (above) and impression of sound.
|
|
|
At 1000Hz
our impression of sound could be approximated by deciBells. However,
on both sides of this centre we hear less from the actual pressure of lower and
higher tones on our eardrums. That can be dangerous. Lines of equal sound
impression more or less parallel to the boundary below connect the same levels
of sound impression (loudness) expressed in ‘foons’ in the same range of
deciBells at 103Hz. An often used rough correction is the audible
deciBell dB(A) (Fig. 338).
|

|
|
|
|
Fig. 338 Corrections on deciBells to get audible dB(A).
|
|
|
The
combined tones of an instrument make a sound. When we
complete the sinuses into l = 4 x 0.65m
and add the overtones of Fig. 332 with supposed smaller amplitudes
neglecting the higher overtones we get a representation of the sound of the
tube (Fig. 339).
|

|

|
|
|
|
|
Fig. 339 Combined complete sinuses of Fig.
332
|
Fig.
340 Fig. 339 added
|
|
|
|
However,
especially string instruments have to improve the contact with the air by
surfaces vibrating with the string to get a louder sound. These constructions
resonate with the own velocities, amplitudes and
frequencies of their material and form adding new wave lengths producing the
typical sound of the instrument. The amplitudes per frequency are called the
spectrum of the instrument (Fig. 341 and Fig. 342).
|

|

|
|
|
Michels (1993) page 16
|
|
Fig. 341 Supposed
amplitudes of the tube from Fig.
332
|
Fig. 342 Spectra of other instruments
|
|
|
|
There are
harmonious spectra with natural proportions of frequencies and chaotic spectra
called noise. When you are able to recognise the
composing sinuses by Fourier analysis or measurement you can calculate the power
of a spectrum summing all intensities per amplitude by integration to predict
power. But there are deciBell meters to do it afterwards.
Fig. 343 shows the spectrum of an electric
piano with little overtones for the tone ‘A’ in eight octaves with seconds on
the x-axis. Here we clearly see the doubling from 27.5,
55, 110, 220, … until 3520 kHz for pure tones. The tones of the piano fluctuate
around these averages.
|

|

|
|
|
|
|
Fig. 343 Spectrum of an electric piano
|
Fig. 344 Oscillogramme and spectrum of a bluetit
(pimpelmees)
|
|
|
|
Fig. 344 we see the spectrum of a
bluetit-song with frequencies reaching twice as high as our voice until 8 kHz. The
oscillogramme above shows the amplitude or power. Enlargement would show the
sinusoid waves. Their invisibly small wave-lengths determine the frequency
below. Fig. 345, Fig. 346 and Fig. 347 show the oscillogrammes and spectra
of three other birds often heard around your house. They show how
characteristic birds’ songs are. These songs are present in any city, but you
do’nt hear them any more and few will recognise them.
|

|

|

|
|
|
|
|
|
Fig. 345 Great tit (koolmees)
|
Fig. 346 House sparrow (huismus)
|
Fig. 347 Magpie (ekster)
|
|
|
|
|
These
spectra are made with the Raven Lite programme, free downloadable from http://www.birds.cornell.edu/brp/raven/Raven.html .
There are
many sources of noise in town. Traffic and aviation are the most important ones.
|
|
speed
|
quantity
|
emission
|
|
|
|
km/h
|
mv/h
|
dB(A)
|
|
|
light motor vehicles
|
50
|
300
|
69,48
|
|
|
middle heavy motor vehicles
|
50
|
50
|
72,90
|
|
|
heavy motor vehicles
|
50
|
50
|
77,70
|
|
|
motorcycles
|
50
|
100
|
75,21
|
|
|
Total
|
|
500
|
80,81
|
+
|
|
|
|
|
|
|
|
% truck traffic
|
10
|
%
|
|
|
|
road surface
|
|
|
|
|
|
Road surface correction
|
|
|
3,63
|
+
|
|
|
|
|
|
|
|
distance to crossing
|
100
|
m
|
|
|
|
Crossing correction
|
|
|
0,80
|
+
|
|
|
|
|
|
|
|
%reflection other side of road
|
75
|
%
|
|
|
|
Reflection correction
|
|
|
1,13
|
+
|
|
|
|
|
|
|
|
distance to source
|
10
|
m
|
|
|
|
Distance reduction
|
|
|
10,00
|
-
|
|
Air muffling reduction
|
|
|
0,20
|
-
|
|
|
|
|
|
|
|
height of observer
|
1,5
|
m
|
|
|
|
height of source
|
0
|
m
|
|
|
|
%soft ground to road axis
|
0
|
%
|
|
|
|
Ground reduction
|
|
|
0,00
|
-
|
|
Meteo reduction
|
|
|
0,57
|
-
|
|
|
|
|
|
|
|
Total
|
|
|
75,59
|
dB(A)
|
|
Jong (2003)
|
|
Fig. 348 Calculating traffic noise
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Traffic is a linear and fluctuating source. You can
predict the average intensity in dB(A) from 7 o’clock during 12 hours day or night
according to Volksgezondheid Volksgezondheid
en Milieuhygiene (1981), SRM1, see Fig. 348.
Backgrounds are discussed in Nijs
(1995) .
Download Jong, T.M. de (2003) TrafficNoise.xls
from http://team.bk.tudelft.nl publications 2003, say ‘yes’ to the
macro’s, fill in the yellow parts and try.
This calculation
is valid only if:
-
there are no noise protection screens or buildings;
-
there are no slopes;
-
the road is more or less straight;
-
some other conditions,
otherwise you should use SRM2.
Fig. 349 shows some indications for traffic
load you can use in designing stage.
|
Indication:
|
|
|
|
|
|
radius served urban area
|
traffic lanes
|
width
|
mv/h
|
|
30m
|
|
|
1
|
3m
|
2
|
|
100m
|
|
street
|
2
|
10m
|
20
|
|
300m
|
neighbourhood
|
street
|
2
|
20m
|
200
|
|
1km
|
district
|
road
|
2
|
30m
|
1000
|
|
3km
|
town
|
highway
|
4
|
40m
|
2000
|
|
10km
|
subregional
|
highway
|
8
|
50m
|
10000
|
|
30km
|
regional
|
highway
|
10
|
60m
|
16000
|
|
100km
|
subnational
|
highway
|
16
|
70m
|
24000
|
|
|
|
|
|
|
|
|
Fig. 349
Indications of traffic load
|
|
|
|
|
|
|
|
National
Law (see www.overheid.nl click Wet- en regelgeving, look for ‘geluidhinder’) demands in new
plans for urban area less than 50 dB(A) within 200m from streets with 1 or
2 traffic lanes or within 350m from roads and highways with more than 2 traffic
lanes causing that amount of noise. But Burgomaster and Aldermen can request
the Provincial Council on the basis of a noise survey to increase the norm to
55 dB(A). In special cases named in the Law it can be increased until
70 dB(A).
Comparable
norms are given for other souces like industy.
To
calculate noise from aeroplanes Kosten units (Ke) are used. They take into
account maximum level of noise per movement, number of movements per year and
time of the day.
3
Water, networks and crossings
Contents.................................................................................................................................... 163
3.1 Water
balance............................................................................................................... 165
3.1.1.... Earth............................................................................................................................. 165
3.1.2.... Evaporation and precipitation............................................................................................ 166
3.1.3.... Runoff............................................................................................................................ 168
3.1.4.... Static balance................................................................................................................ 173
3.1.5.... Movement ignoring resistance.......................................................................................... 174
3.1.6.... Resistance..................................................................................................................... 177
3.1.7.... Erosion and sedimentation............................................................................................... 183
3.1.8.... Hydraulic geometry of stream channels............................................................................. 185
3.1.9.... River morphology............................................................................................................ 186
3.1.10.. Simulating a simple drainage system................................................................................ 188
3.1.11.. Bifurcation or trunking in traffic networks........................................................................... 190
3.1.12.. Catchment area and river length....................................................................................... 192
3.1.13.. Local morphologies......................................................................................................... 193
3.1.14.. Measuring velocities to get Q........................................................................................... 197
3.1.15.. Discharge Q on different water heights.............................................................................. 199
3.1.16.. Interpolation of experimental data by using Excel............................................................... 199
3.1.17.. Calculating drainage Q with a rough profile........................................................................ 201
3.1.18.. Level and discharge regulators......................................................................................... 203
3.2 Civil
engineering in The Netherlands........................................................................ 205
3.2.1.... History........................................................................................................................... 205
3.2.2.... The distribution of water................................................................................................... 207
3.2.3.... The threat of floods.......................................................................................................... 208
3.2.4.... Risks of flooding............................................................................................................. 210
3.2.5.... Measures to avoid floods................................................................................................. 214
3.2.6.... Coastal protection........................................................................................................... 216
3.2.7.... The Delta project............................................................................................................. 217
3.2.8.... The central coast line...................................................................................................... 219
3.2.9.... The northern defence system........................................................................................... 220
3.2.10.. Polders.......................................................................................................................... 221
3.2.11.. Need of drainage and flood control.................................................................................... 221
3.2.12.. Artificial drainage............................................................................................................ 224
3.2.13.. Configuration and drainage patterns of polders................................................................... 228
3.2.14.. Drainage and use............................................................................................................ 229
3.2.15.. Weirs, sluices and locks................................................................................................. 230
3.2.16.. Water management tasks in the landscape....................................................................... 233
3.2.17.. Local water management maps........................................................................................ 234
3.3 Water
policy.................................................................................................................. 236
3.3.1.... Coordination of different administrative sectors................................................................... 236
3.3.2.... Water boards.................................................................................................................. 238
3.3.3.... Delfland Waterboard........................................................................................................ 239
3.3.4.... Spatial plans checked on their impact on water: ‘Watertoets’.............................................. 241
3.3.5.... Water management in spatial design................................................................................ 242
3.3.6.... Hydrologic cycle and water system.................................................................................. 243
3.3.7.... Water quality and management........................................................................................ 244
3.3.8.... Sustainability and water management............................................................................... 245
3.4 The
second network: roads....................................................................................... 247
3.4.1.... Names and scale............................................................................................................ 247
3.4.2.... Functional charge of networks.......................................................................................... 249
3.4.3.... Rectangularity forced by connections of a higher level........................................................ 249
3.4.4.... Superposition of levels..................................................................................................... 251
3.4.5.... Interference of different networks....................................................................................... 252
3.4.6.... Crossings....................................................................................................................... 253
3.4.7.... A traffic network.............................................................................................................. 262
3.4.8.... Measures....................................................................................................................... 262
3.4.9.... A residential street.......................................................................................................... 263
3.4.10.. Space for speed.............................................................................................................. 264
3.4.11.. Roads of a higher level..................................................................................................... 265
3.4.12.. Urban islands in a network............................................................................................... 265
3.4.13.. A neighbourhood............................................................................................................. 269
3.4.14.. A road hierarchy............................................................................................................. 270
3.4.15.. From a model back into a real city.................................................................................... 272
3.4.16.. Traffic surface................................................................................................................. 275
3.4.17.. Harbours P.M................................................................................................................. 287
3.5 Other
networks: cables and ducts......................................................................... 288
3.5.1.... The electricity network..................................................................................................... 292
3.5.2.... The gas network............................................................................................................. 293
3.5.3.... Water pipes.................................................................................................................... 294
3.5.4.... Pressure pipelines for sewage water................................................................................. 295
3.5.5.... The telephone network..................................................................................................... 295
3.5.6.... Radio and television transmitters...................................................................................... 296
3.5.7.... Network for the transport of raw materials.......................................................................... 297
3.5.8.... Tunnels.......................................................................................................................... 297
3.5.9.... Urban scale.................................................................................................................... 299
3.5.10.. The future....................................................................................................................... 309
In case all ice would melt
The surface of the Earth is approximately 510,000,000 km˛ large (see page 22) and there is 1 390 000 000 km3 water. So, if there were no differences in temperature or ground level and
water was equally dispersed over the Earth, the planet would be fully covered
by a 2.7km deep ocean (Fig. 350)[82]. The 48m upper layer would be ice.
However, there is
148 900 000 km2 land and 361 100 000 km2
water. So, 29% is land. It contains 3% of all existing water, and 2/3 of that
part is frozen. If all ice would melt by gobal warming sea level would
raise 66m. Water would submerge the most densily populated areas of the Earth.
Fortunately the sun still adds
snow to the poles.
The case of maximal
glaciation
On the other hand, during an age
of maximal glaciation the the amount of glacier ice would have been
three times larger as the present ice volume. The sea level would have been lowered as much as 140 meters. The continental shelves would have been exposed to the air so man
could live there.
The average height of the land is 823 m above sea level. We can calculate the
potential mechanical power of the system of the water streaming to the sea over
the land. Assuming that 37,000 kmł of runoff
water will flow downhill 9 TW (see Fig. 2 and also Fig. 16) would have been produced by the
runoff water.
The amounts of water
|
1000 km3
|
salt
|
fresh
|
total
|
m3/m2
|
mm
|
|
atmosphere
|
|
12,9
|
12,9
|
0,025
|
25
|
|
sea
|
1 338 000
|
|
1 338 000
|
2 624
|
2 624 021
|
|
land, from which
|
12 957
|
35 004
|
47 960
|
94
|
94 057
|
|
snow and ice
|
|
24 364
|
24 364
|
48
|
47 782
|
|
subterranean
|
12 870
|
10 530
|
23 400
|
46
|
45 891
|
|
lakes
|
85,4
|
91
|
176,4
|
0,346
|
346
|
|
soil moisture
|
|
16,5
|
16,5
|
0,032
|
32
|
|
swamps
|
|
2,1
|
2,1
|
0,004
|
4
|
|
life
|
1,1
|
|
1,1
|
0,002
|
2
|
|
total
|
1 350 957
|
35 004
|
1 385 960
|
2 718
|
2 718 079
|
|
|
|
Fig. 350 Total amount of water on Earth(see also Fout! Verwijzingsbron
niet gevonden.)
|
|
|
The amounts of water on the Earth are confined in reservoirs of
different size and form. In their order of importance these reservoirs are:
oceans, glaciers, groundwater, lakes and rivers, atmosphere and biomass (all
living matter man included). In actual fact 97% of all surface water is
confined in the oceans and most of the other 3% is fixed in glaciers. So,
little water is left over for the other reservoirs.
The cycle of water
|

|
|
Igor
A. Shiklomanov, State Hydrological Institute (SHI, St. Petersburg) and United
Nations Educational, Scientific and Cultural Organisation (UNESCO, Paris),
1999; Max Planck, Institute for Meteorology, Hambuirg, 1994, Freeze, Allen,
John, Cherry, Groundwater, Prentice-Hall: Englewood Cliffs NJ, 1979.
|
|
Fig. 351
The hydrological cycle
|
|
|
Continuously changing the state of water
The sun is the generator or motor of the changes in
the state of water. The sun will evaporate water of the oceans and other other
water reservoirs to the 100% water vapour saturation of the air. The saturation of the air with
water vapour is determined by the temperature. The higher the temperature the
more vapour the air can contain. The vapour is perceptible by the clouds in the air because of the always present
condensation nuclei .The wind will move the clouds from the oceans to the
continents and depending the temperature above the continents will happen nothing
(temperature ≥ temperature in the
cloud) or it will rain or snow (in both cases is the
temperature ≤
temperature in the cloud). Rain, hail and snow is called precipitation.
Energy needed for evaporation
You can evaporate 1m3 water by 2.26GJ, 2.26GWs, 630kWh or 72Wa
(say 72 m3 natural gas). The Earth’s surface receives 81 PW
from sun. So the sun could evaporate 1.1 million km3 per year.
Actually less than half is evaporated in unsaturated air only (Fig. 352). It falls down discharging its solar heat in the same time as soon as
the air becomes saturated in cooler areas by condensation (precipitation). That is nearly 1m3/m2 or 1m and more precise
957mm (Fig. 352).
|
|
evaporation
|
precipitation
|
runoff
|
evaporation
|
precipitation
|
runoff
|
|
|
1000 km3/a
|
mm/a
|
|
sea
|
419
|
382
|
|
1157
|
1055
|
|
|
land
|
69
|
106
|
37
|
467
|
717
|
250
|
|
total
|
488
|
488
|
|
957
|
957
|
|
|
|
|
Fig.
352 Yearly gobal evaporation, precipitation and runoff
|
|
|
Areas like deserts receive less than 200mm, areas like tropical
rain forests more than 2 000mm average per year (Fig. 353).
|

|
|
Wolters-Noordhof
(2001) page 181
|
|
Fig.
353 Global distribution of precipitation
|
|
|
Europe has the same extremes (Fig. 354).
|

|
|
|
|
Fig.
354 European distribution of precipitation (Wolters-Noordhof (2001)
page 61)
|
|
|
The Netherlands receives from 700mm in East Brabant to 900mm precipitation in
central Veluwe (Fig. 355), but there have been years of 400mm and 1200mm precipitation.
|

|

|
|
|
|
|
Fig. 355 Distribution of precipitation in the Netherlands (Huisman, Cramer et al., 1998; page 18)
|
Fig. 356
Precipitation minus evaporation in the Netherlands
(Wolters-Noordhof, 2001; page 53)
|
|
|
|
If precipitation exceeds evaporation lakes and subterranean aquifers fill up. As soon as
these cannot be filled up in time, water runs off subterranean or along brooks and rivers (Fig. 357 and Fig. 358).
That part of the precipitation that reaches a stream is called
runoff. The water during rainfall will gather into rills and streams down
the slope. During and after the rain part of the water will soak into the
ground. If the soil is saturated with water the remaining water will stream
together in small streams and form a river. The groundwater flows also downhill and where the
water bearing layer crops the slope a source will come out. The surface water
and the subterranean water feed together a river. When the catchment area is large enough a permanent
river will be the result. An estimation is made that ⅛ of the annual runoff will reach directly overland the sea while
the remainder part will go underground.
the Netherlands
receive runoff from catchment areas of the Rhine (entering the Netherlands in Lobith), Meuse and Scheldt
rivers.
|

|

|
|
|
|
|
Fig. 357 Major soil types and average annual
runoff in the Netherlands (Huisman,
Cramer et al., 1998; page 21)
|
Fig. 358 Received runoff in the Netherlands (Huisman,
Cramer et al., 1998; page 13)
|
|
|
|
|

|
|
|
|
Fig. 359 The
river basin of the Rhine
(Paul Maas, opdrachtgever: Thieme Meulenhoff)
|
|
|
The river Rhine has a catchment area of 160 000km2
with an annual average of 1 775mm precipitation minus 1 392mm evaporation in the part of that area as far as Lobith. So,
approximately 383mm over an area of 160 000km2 produces 61km3/year.
So, on average 1942m3/sec of water should run off and enter at Lobith.
Levelling by seasons
Snow and ice in mountains level out seasonal fluctuations of rivers by storing precipitation in
winter, releasing it in summer[83] (see Fig. 359 and Fig. 361).
In Fig. 362 a rough approximation of discharge related to catchment area is
shown. A big spot indicates the mentioned values of the river Rhine and a line
is drawn for any catchment area producing a discharge in the Rhine
circumstances. However, if precipitation is more than the average mentioned the
line shifts upward, if evaporation or other reductions are more than mentioned,
it shifts downward.
As a rule of thumb the m3/sec
of discharge is 1/100 of the km2 catchment area[84], but any river has its own
graph, less regular than suggested here.
The relation of discharge to the water level near Lobith in Fig. 363 is important for the height of dikes and the draught of ships, but
it changes in time because of sedimentation and excavation.
Because precipitation and evaporation differ much per day, the
discharge of the Rhine differs daily (see Fig. 364), as unpredictably as the weather forecast.
|

|

|
|
|
|
Fig. 364 Daily
average discharge of the Rhine at Lobith (Lecture Marc F.P.
Bierkens UU Faculty
of Geosciences)
|
Fig. 365
Duration line of Rhine discharge at Lobith (Lecture Marc F.P.
Bierkens UU Faculty
of Geosciences)
|
|
|
|
Ranking Fig. 364 you can derive a ‘duration line’ as in Fig. 365, indicating how often you can expect a given discharge to be
exceeded.[85] From that figure you can
conclude that 50% of the time the discharge of the Rhine
did not exeed 2000m3/sec. The mirrored graph gives the percentages
of underspending.
The discharge of a river fed by a catchment area
increases some time after the first rainfall (see Fig. 366) and after the last rainfall it continues some time, depending on
the size of the area.
Suppose an unusual system of heavy showers follows the basin around
the course of the Rhine and those of its feeding rivers like the Main and Mosel
from Switzerland
to Lobith and everywhere in the basin drainage is optimal. A wall of water then
nears Lobith. How often will that happen, how long will it last? These are the
questions to be answered to calculate risks of flooding.
Static forces and the potential energy along a slope
The weight W of a bullet on a slope of a degrees can be
resolved in factors perpendicular and parallel to the slope (see Fig. 370). The force parallel to the
slope equals W·sin(a).
For example, if a = 30o
that force is ˝W, because sin(30o) = ˝.
|

|

|
|
|
|
|
Fig. 369
Stevin: Clootcrans
|
Fig. 370
Balance on different slopes
|
|
|
|
However, the distance d any bullet has to cover parallel to the
slope into the base equals the vertical height divided by sin(a). So, force
times distance (potential energy) remains the same at both sides of the summit.
For example, if a = 30o,
the force is ˝·W, but the distance d to cover is 2·h.
The ‘Clootcrans’ Stevin used as his logo (see Fig. 369) shows the equal potential
energy of bullets according to their slope by intuition (count those at the
corners in Fig. 370 half).
Potential acceleration
Force is defined as mass times acceleration (F = m·a).
At the vertical wall the potential acceleration equals the
gravitational acceleration g = 9.807 m/sec2.
If the masses of the bullets are the same, but the force F parallel
to the slope is reduced by sin(a) then the
acceleration ‘a’ parallel to the slope should be reduced by the same factor.
In case a = 30o,
a = ˝·g = 4,904 m/sec2.
Suppose we disconnect all bullets and supply every second a bullet
on the summit at both sides.
Acceleration ‘a’ is defined as velocity v divided by time t (a = v /
t).
As long as there is no resistance the velocity v of any bullet will
increase constantly with the time t according to v = a· t. But, the covered
distance will increase disproportionally, because every next second the bullet
has covered a larger distance according to its increased velocity.
So, we can conclude a source distributing an equal amount of bullets
per second produces a stream thinning downstream gaining mutual distance by
increasing velocity (see Fig. 371).
|

|
|
Source: http://team.bk.tudelft.nl/ > publications 2006
Hydrology.xls
|
|
Fig.
371
Bullets falling and rolling along a slope every second with a growing
distance and velocity
|
|
|
Calculating increasing velocity v and covered distance s along a
slope
The growing velocity v and
covered distance s shown in Fig. 371 are calculated as follows.
Between any two moments tp
and tq (tp<tq) velocity grows from vp
into vq with a constant acceleration a: vq –vp = a·(tq –tp).
Let the time interval (tq –tp) near zero. Then vq –vp = a·t,
or vq = vp + a·t.
At time t half way any tp
and tq the mean velocity vm equals (vp+vq)/2.
Here you can substitute vq .
So, vm=(vp+vp+a·t)/2
or vm=vp+ ˝·a·t.
The distance s covered at
any moment equals vmt if you take for vp the
velocity v0 at the beginning.
So, s = (v0 + ˝·a·t)t
or s = v0·t + ˝·a·t2, shortly
calculated as a time summing integral of s/t = v = a·t:

Supposed the bullets start
in rest (v0=0) and then begin to fall or roll without resistance,
then s equals ˝·a·t2 without initial C.
The velocity at the end of the slope is reached at slope length
d = ˝·a·t2 = ˝ ·g·sin(a)·t2.
And d = h/sin(a) (see Fig. 370). So t2 = (h/sin(a))/(˝·g·sin(a)) or 2h/g·sin(a)2.
So, tend = sin(a)-1·Ö(2·h/g).
At that
time vend = a·tend = g·sin(a)·sin(a)-1·Ö(2·h/g)
= Ö(2·g·h).
So, the
velocity at the end of the slope is independent from a: it is
the same velocity of a falling bullet at the end of the wall. The average
velocity along the slope is half of vend: vm:= ˝ Ö(2·g·h).
If a bullet of mass m [kg]
hits you with a velocity of v [m/sec], and you resist its force stepping back
slower bringing its velocity back to zero, the bullet has lost m·v·(v ‑ 0 m/sec)/2 = ˝ m·v2
energy.
That kinetic energy Ek
could have been built up falling or rolling h [m] with an acceleration a [m/sec2],
according to Ep = F·h = m·a·h. Falling or
rolling, the bullet lost Ep, gaining Ek, while Ep :=
Ek at last.
So, the process is described
as m·a·h := ˝ m·v2 [joule].
Running water in a pipe
Suppose running water is a stream of more or less cohesive
incompressible drops, flowing downstream in a volume per second of Q [m3/sec]
everywhere.
Suppose the bullets of Fig. 371 are cubic metres water
forced in a pipe of minimal cross section.
The average velocity will be the velocity at the end of the natural
slope Ö(2·g·h) divided by two: vm = ˝·Ö(2·g·h).
So, the cross section of a pipe with capacity Q should be at least
A = Q/vm = 2·Q/Ö(2·g·h)
[m2].
Its
water content is A·h/sin(a) [m3].
If the mass m [kg] of water relates to its volume [m3]
as r (normally 1000 kg/m3)
its mass equals r· A·h/sin(a) [kg].
A sudden obstacle at the end of the pipe (like a tap closed at once)
shows the large amount of energy built up in flowing water. Such an obstacle
has to resist a force F1 equal to the weight of the water column
divided by A [newton/m2] and a force F2 resulting from
kinetic energy Ek = ˝·m·v2 divided by some
distance s (braking distance) to get the force
(energy is force times distance). If that braking distance is
very small F2 increases into infinity, breaking the water pipe.
A water column of height h on a surface A produces a force F1 =
r·h·A·g
[newton].
A mass m = r·h·A/sin(a) [kg]
water with a velocity v = ˝·Ö(2·g·h)
[m/sec] reduced to zero over a distance of s metre (braking distance) produces
a force F2 = ˝·m·v2/s:
 or
or 
The kinetic force F2 is many times larger than F1
= r·h·A·g
caused by the weight of the water column (the difference is Ľ·h/s·sin(a)). In the
example of Fig. 372 a kinetic force of flowing
water is calculated as 500 times the weight of the water column.
|

|
slope angle
|
a
|
30.0
|
deg
|
(Input)
|
|
slope
|
one to
|
1.73
|
|
|
|
|
|
|
acceleration
|
a
|
4.9
|
m/sec2
|
|
|
|
|
|
height summit
|
h
|
1.0
|
m
|
(Input)
|
|
slope length
|
d
|
2.0
|
m
|
|
|
|
|
|
time to reach end of slope
|
t
|
0.90
|
sec
|
|
|
|
|
|
end velocity free flow
|
v
|
4.43
|
m/sec
|
16
|
km/hr
|
|
|
|
average velocity
|
vm
|
2.21
|
m/sec
|
8
|
km/hr
|
|
|
|
discharge
|
Q
|
1
|
m3/sec
|
(Input)
|
|
min. sectional plane of pipe
|
A
|
0.4516
|
m2
|
|
|
|
|
|

|
radius of pipe
|
r
|
37.9
|
cm
|
diameter
|
75.8
|
cm
|
|
|
content of pipe
|
C
|
0.90
|
m3
|
|
|
|
|
|
density of water
|
r
|
1000
|
kg/m3
|
|
|
|
|
|
braking distance
|
s
|
0.001
|
m
|
(Input)
|
|
force by weight
|
F1
|
4429
|
newton
|
452
|
kgf
|
|
|
|
kinetic force
|
F2
|
2213997
|
newton
|
225757
|
kgf
|
226
|
ton
|
|
proportion
|
F2/F1
|
500
|
|
|
|
|
|
|
pressure at tap
|
p
|
4912447
|
newton/m2
|
500912
|
kgf/m2
|
501
|
ton/m2
|
|
m height of rise
|
|
501
|
m
|
|
|
|
|
|
Source: http://team.bk.tudelft.nl/ > publications 2006
Hydrology.xls
|
|
Fig.
372
Water ram
|
|
|
That force is utilised in a
pumping device called ‘water ram’. The pressure p built up in the water ram by
suddenly closing the tap braking the flow to yield its kinetic force is
utilised to push up the water through a valve. Theoretically the water column
can be built up until 500 m. However, the pressure falls away shortly after the
valve opens, so the procedure has to be repeated often to near that theoretical
value.
Free flow
The cross section of a free flow A = Q/v will be smaller
downstream according to its increasing local velocity v = ˝ ·a·t (if
there are no other sources feeding the stream).
You can see that decreasing width already on the tap (see Fig. 373).
Since s = ˝·a·t2 or t = Ö(2·s/a) and consequently v = s/Ö(2·s/a) =Ö(s·a/2), the cross section on any distance from
the source will be A = Q/Ö(s·a/2).
|

|

|

|
|
|
Source: http://team.bk.tudelft.nl/ > publications 2006
Hydrology.xls
|
|
|
Fig. 373
Water flowing from the tap
|
Fig. 374
Simulation of 0.00004 m3/sec falling water
|
Fig. 375
A river stemming from different separate streams
|
|
|
|
|
However, what you see is the diameter, 2·r. And A = p·r2.
So, 2·r = 2·√(A/p.)
In Fig. 373, the water from the tap has
an intial velocity, perhaps comparable with the 0.02m level of the falling
water in Fig. 374. As soon as a critical
velocity is passed a continuous flow is falling apart in drops like rain. It
shows the limits of water cohesion.
A river
A river, stemming from different separate streams with smaller cross
sections (see Fig. 375) will end up flowing faster
in the end. Moreover, its resistance reduces because of less contact with its
bed, becoming more and more smooth (less rocky) downstream. However, its slope
reduces also coming closer to the sea. How do these circumstances balance
locally?
Until now, we supposed
flows, running without resistance.
But, any liquid flowing
along a surface encounters a shearing force in the opposite direction dependent
on its roughness. That force causes deceleraton or even partially flowing back
(turbulence).
Force is mass times
acceleration. If mass remains the same, the accelerations ‘a’ of previous
paragraph 3.1.5 should be reduced. How much
is that reduction in a stream flowing through a landscape?
Many parameters play a role,
but the result mainly will be that shearing stress reduces the force of water
and consequently its acceleration and velocity substantially only if the water
level is less than 2m to bottom. However, it always plays an important role in
transporting sediments.
So, a river can not adapt
its discharge, but rather its form to bring the water most efficiently to the
sea. However, that search for the most efficient course may take a very long
time, sometimes waiting for a year of extreme rainfall to improve the course,
clearing up bottle necks, looking for steeper slopes lessening its tress.
Shearing stress
Manning created the formula of Fig. 376 to calculate the force t every square
metre wetted surface exerts [newton/m2] in opposite direction of the
flow (‘shearing stress’).
|
 
|

|
|
|
|
|
Fig. 376
Robert Manning and one of his formulas
|
Fig. 377
Shearing stress
t due to different discharge suppositions and local
roughnesses and bed forms along 17.5 km of the river Meuse
(Grensmaas)
|
|
|
|
Fig. 377 shows t for different
circumstances a part of the river Meuse
(Grensmaas) ranging from 1 to 50 newton/m2. Fig. 380 shows the studied part in Fig. 377, folded along the boundary
of The Netherlands and Belgium
within its winter dikes.
The river Meuse for example
Fig. 378 shows a cross section of a
river like the river Meuse approximately half
way of its 925 kilometres course. Suppose the surface of its cross section
A = 300m2 and its discharge Q = 600m3/sec
(often in winter). In that case its water level is 5.7m and it transports a
mass m = 600 000kg of water per second over 2 metre (so,
velocity v = 2m/sec or 7.2km/hr). That represents Ek = 1.2
million joule kinetic energy over 2 m, and a force F2 = 600 000
newton equivalent to a weight of approximately 60 tons.
|

|

|
|
|
|
|
Fig. 378
Typical cross section and wetted surface of a river like the Meuse half way (Grensmaas)
|
Fig. 379The
influence of shearing force by different water levels in Fig. 378
|
|
|
|
According to Mannings formula in this circumstances the shearing
stress t would be 10
newton/m2.
If it shears over the river bed taking 100 m in the cross section
(‘wetted contour’), then perpendicular to that cross section in 1sec over a
length of 2m the river has to overcome 2 000 newton resistance. That is
only 0.3% of the local force of the river. And in this two metres we did not
even count the pushing power of many kilometres moving water coming down
upstream.
Low shearing stress
So, the influence of the shearing stress t on velocity and
acceleration on a water level of 5.7m is negligible, but in many centuries it
has given the actual form to the river by loosening material from the bed.
Water with a velocity of 2m/sec could even move stones of 0.5kg, but at the
bottom a shearing stress of 10newton/m2 will only move some smaller
sediment.
High shearing stress
However, at water levels in the same circumstances lower than 2m, t becomes more
than 1%, increasing into 80% on very low water levels (see Fig. 379). You can calculate it
yourself for different circumstances downloading http://team.bk.tudelft.nl/ > publications
2006 Hydrodynamics.xls.
So, in small brooks t will play an
important role on the resultant force, acceleration, velocity and kinetic
energy.
Kinetic energy per m3 water ˝ r·v2
In
Mannings formula r is the
mass of 1m3 water (mainly 1000 kg/m3). The kinetic energy
reduced by roughness like earlier shown by the water ram (see page 175) is ˝ m·v2
(see page 175).
So, r·v2
in the formula represents twice the kinetic energy per m3 water.
You can
measure the velocity v [m/sec] on different spots in the cross section to
calculate the average velocity (see Fig. 421).
Kinetic energy [newton·m] per m3
is the same as force per m2 like t [newton/m2].
So, the rest of the formula is a
dimensionless factor, but how to calculate it?
Roughness n
The roughness of river beds
is expressed in a roughness factor n [sec/m1/3] shown Fig. 430, ranging from 0.01 for very
smooth concrete until 0.1 sec/m1/3 for flooded tight forest.
Hydrolic radius R
R [m] in
Mannings formula is the ‘hydrolic radius’, the wet surface ‘A’ of the cross
section divided by the length of its
wetted contour ‘P’ (R = A/P). The larger ‘A’ is (for example
increasing by a larger discharge (see Fig. 378) the less influence the wetted contour has.
The surface/contour proportion is an
important factor in many physical phenomena like roads around an urban island
(public investment), volume/surface of buildings or growing animals
(insolation). If a volume increases by a third power of distance, a minimal
surface containing that volume increases quadratically (slower), while the
minimum contour (a circle) containing a surface increases in the same time
linear (again slower).
A ‘wetted contour’ of a river is not a
circle, but it increases slower than the contained cross sectional surface also
because the horizontal upper surface is ignored.
Fall and acceleration a
Most difficult to estimate
is local ‘a’ in Mannings formula. The total acceleration of a river can be
calculated according to page 174 and reduced by varying
shearing stress, but that average is locally changed by varying slopes and
forced by water masses upstream into increased acceleration in narrow cross
sections, partly compensated by higher water levels storing potential energy
for accelerations later.
Reduction of acceleration
The part of the river Meuse
studied, falls 10m (from 40 to 30 above sea level) over 17.5km length with
varying resistance (see Fig. 381). However, the total fall
of the river Meuse from source to sea is 409m
over 925km. That is the tangent of a = 0.0253 degree. So, you could
expect an average acceleration of a = g·sin(a) = 9.807·sin(0.0253) = 0.004
m/sec2, partly reduced by a substantial t in the many feeding brooks at
the boundary of the basin (see Fig. 383).
|

|

|
|
|
|
Fig.
380 17.5km of Meuse (Grensmaas)
|
Fig. 381
A fall of 10m along 17.5 km of the river Meuse
(Grensmaas)
|
|
|
|
Because v = a·t and consequently t = v/a, the
distance covered s = a·t2/2 = a·(v/a)2/2.
So, at distance s = 500km from source the velocity should be
v = √(2·a·s) = 66m/sec.
However, we counted v = 2m/sec, to reach Q = 600m3/sec
through a cross section (wetted surface) of 300m2. So the reduction
by t in all upstream shallow brooks
and small rivers of the basin together should be 97%!
Discharge
|

|

|
|
|
|
Fig. 382 Successive SOBEK cross-section trajects
along the Grensmaas
|
Fig. 383 Meuse river basin of 36 000 km2 through France,
Belgium, Germany and The Netherlands
|
|
|
|
If you measure the cross
section ‘A’ [m2] of a stream and the velocity v [m/sec], the
discharge Q = A·v.
However, you also can
measure the rainfall of the Meuse river basin in Belgium
and France
(23 500km2). If in that area at average in a year 1000mm rain has fallen of
which 200mm is evaporated or temporarily sunken down into the earth, then
Q = 800mm·23500km2/yr. That is 600 m3/sec of water
coming into the Netherlands
at the boundary of Belgium
averaged over a year (see Fig. 383).
However, in a a concurrence of circumstances like in january 1995, there
can be more rainfall (up to 350mm per day), less evaporation, no storage
in a saturated earth, faster discharge because that earth is frozen, but
starting to melt, delivering previously fallen water in the same time.
In such a case you can expect floodings.
A river has its largest
velocity on its surface, decreasing into the bottom.
The average velocity v is
often measured at 0.4·h (see Fig. 384). However, the velocity
distribuition over the cross section varies substantially (see Fig. 385).
|

|

|
|
|
|
|
Fig. 384
Velocity in a longitudinal cross section
|
Fig. 385
River cross sections with simulation of velocity profiles
|
|
|
|
Many rivers have a relation v = k·Qm, but ‘k’ and
‘m’ differ from river to river (in Fig. 386 Bovenrijn and Waal obey approcimately
to v = Q0.3).
|
 
|
|
|
|
Fig.
386 Flood and velocity in
Bovenrijn and Waal
|
|
|
Different sensibility of velocity for discharge
Fig. 387 shows that relation for two extremely different American rivers. In a
logarithmic representation the measurements fit very well a straight line. An
increasing factor ‘k’ shifts the whole line up, an increasing exponent ‘m’
makes it steeper (v more sensitive for Q). If the Iine is horizontal
(m = 0), there is no relation between v and Q whatsoever. Even if the
discharge increases, the velocity will not. These are stoic rivers having other
possibilities to give space to their discharge, for example in the lowlands.
The steep liners are nerveous ones, apparently limited in their cross sections
in the highlands.
|

|

|
|
|
|
|
Fig.
387 Different relations
between velocity and discharge
|
Fig. 388 SOBEK simulation of level related to discharge processed with correction for
spatial variations between successive crosssections of Fig. 382
|
|
|
|
Depth related to discharge
Many rivers have a relation depth D = c·Qf, but ‘c’
and ‘f’ differ from river to river (in Fig. 389 Bovenrijn and Waal obey approcimately
to D = 5·Q0.4).
|

|

|
|
|
|
Fig. 389
Depth related to discharge in Bovenrijn and Waal
|
|
|
|
Width related to discharge
Many rivers can be simulated
by an ellipsoid cross section (see ).
|

|
|
|
|
Fig. 390 Simulation of an ellipsoid cross section
|
|
|
For a river in weak soil
(not forced by artificial measures) it is easier to find space in width than in
depth, because sedimentation reduces depth.
Material from the river bed
(silk, sand and gravel) is transported dependent from the velocity of water.
|

|
|
|
|
Fig.
391
Erosion and sedimentation dependent from the velocity of water
|
|
|
From >0.2 cm particle
size we call it gravel (see Fig. 391).
Until <0.2 cm it is named
sand or silk (see Fig. 392, an enlargement of Fig. 391).
|

|
|
|
|
Fig.
392
Erosion and sedimentation at the boundary of silk < 0.0.005 cm and sand
>0.005cm dependent from velocity of water, detail from Fig. 391
|
|
|
In Fig. 392 until 0.05m/sec you
can conclude that the river bed is stable. Or the reverse: if you see a stable
bed, the velocity should be less than 0.05m/sec.
Silt
From a velocity 0.15m/sec
all loose silt is moving. So, if you see silt on the bottom, the velocity of
the water should be usually less than 0.15/sec. If you do not see silt, it
should usually be more. However, heavy clay densified into a cohesive plaster
layer needs a higher velocity to erode than you would expect from their
particle size.
Sand
From 0.45m/sec (ample
1.5km/hr, slowly walking) onwards all sand is moved. So, if you do not see
sand, the velocity will be probably more than 0.45m/sec.
Gravel and stones
At higer velocities you have
to look at gravel and stones in to estimate the water velocity (see Fig. 391). From 1m/sec
(3.6km/hr) you see stones of 1cm diameter rolling, from 1.45m/sec
(5km/hr) stones of 2cm, from 1.7m/sec (6km/hr) stones of 3cm, from 1.95m/sec
(7km/hr) stones of 4cm.
On that level the diameter of stones moved grows approximately
parabolically with the square of velocity. So, stone diameter » v2 like 1 » 12, 2 » 1.452, 3 » 1.72 and 4 » 22. That seems logical, because according to page 175 the kinetic energy of
running water (˝ m·v2) is proportional to the square of
velocity.
Higher velocities widen passages, lower velocities narrow them.
At the long term wider passages
of a river with lower velocities will be filled up with sedimentation and
narrow passages with high velocities will be widened by erosion or floodings.
So, by an equal discharge Q in older natural rivers the velocity v is equalised
as well. However we have artificially narrowed our rivers to save land and to
make them deeper for ships.
Width (w), depth (d) and stream velocity (v)
The study of the changes of
channel width (w) and depth (d), stream velocity (v) and suspended load with a
discharge Q = w·d·v is the next step for a better understanding of the
behaviour in a landscape.
Channel width, depth and
current velocity increase during rising water. This is no
surprise to anyone familiar with the regime of rivers, but the regular change
of each separately is amazing.
With the help of a wide
range of streaming conditions it was found experimentally (Leopold and Maddock,
1953) that width, depth, velocity and load increase as simple power functions
of discharge. This can be translated in the following
equations:
w = aQb d = cQf v = kQm
(see page 181)
The numerical values of the
arithmetic constants a, c and k are not significant for the hydraulic geometry
of streams. On the other hand the numerical values p,q and r are very
important. All these values are found by measurements. Leopold and Maddock found that the average for some 20 more or
less comparable stations in the United
States gave the following values:
b = 0.26 f = 0.40 m = 0.34
In these cases during a
flood the width of a channel at a specific cross-section will increase slowest (w =aQ0.26),
the depth (level) fastest (d = cQ0.4 ) and the velocity
in between (v = kQ0.34).
|

|

|
|
|
|
Fig. 393 Calculating v, w and d
|
Fig. 394 The geometry of the stream
|
|
|
|
Comparing measurements of
channel shape and stream velocity in a downstream direction gives surprising
results. Normally the discharge of a river downstream increases. The same
equations are found to apply at the different downstream cross-sections.
Research and measurements proved that:
Width, depth and velocity increase downstream.
According to Fig. 371 this empirical results also
reject the idea that streams in the mountains flow wildly and more rapidly than
downstream.[86] These higher streams are characterized by a flow in circulair
eddies with almost as much backward as forward motion.
The numerical value of the
exponents b and m from the equations above are not the same for changes
downstream as for changes with discharge passing an upstream cross-section.
In the downstream direction
the average values for the exponents become:
b = 0.5 f = 0.4 m = 0.1
Downstream, the width
of the channel will increase most rapidly, the depth a little bit less
rapidly, but the mean velocity will increase only slightly.
|

|

|
|
|
|
Fig. 395 Calculating v, w and d
|
Fig. 396 The geometry of the stream
|
|
|
|
It is believed that the
increasing depth downwards permits a more efficient flow in a river and so
overcompensates the decreasing slope. As a result a slight net increase in
velocity at mean annual discharge will take place.
Further mathematical
calculations of the hydraulic geometry equations suggests useful applications
of the principles.
The discharge is defined as Q
= wdv
and if w = aQb d = cQf v = kQm
then by substitution: Q
= (aQb)(cQf)(kQm)
or: Q
= ackQb+f+m
it follows that: a x c x
k = 1.0 and b + f + m = 1.0
As is stated above the
arithmic constants a, c and k are not important. But it is interesting that for
all the made measurements and calculations for the different cross-section b +
f + m =1.0 agree.
The morphology of a river
system depends mainly on climate, gravity, height,
slope, bedrock, soil type and vegetation. Human impact on the system cannot be
neglected and especially not downstreams with all artfiicial interventions
varying from storage reservoirs both for the generation of electricity and for
storage purposes of water and for alterations in the system itself and dumping
of materials in the system.
|

|


|
|
|
|
Fig. 397 Development of river beds
|
|
|
|
Wind, water and traffic flow
along the earth´s surface. Some of these flows collect into streams.
|

|

|
|
|
|
Fig. 398 Schematic of SHETRAN model setup.
|
Fig. 399 Salmon Abundance across the Eden
catchment
|
|
|
|
Fig. 400 shows a landscape with 24 x
24 squares (sloped mountain areas or a polder with outlets) with 4 possible
drainage directions, producing a converging
feather or tree like drainage system. Computer programme Jong (2003) ‘river(drainage.exe)’ (see http://team.bk.tudelft.nl/ publications 2003), made
from the ‘random walk’ example of Leopold and Wolman cited by Zonneveld (1981), arouses
such random landscapes producing drainage systems. The image is built up in
columns from upper left to down below. The programme prevents convergent arrows
and smallest circuits by changing lowest arrow 90o into right or
downward if they occur. So, the runoff tends towards ‘South East’ as if the landscape
has a main slope or a mein drainage outlet. Watersheds become visible
separating catchment areas. Why do they concentrate into separate basins and
converge into main streams?
|

|

|
|
|
|
|
Fig.
400 Directions of drainage in a landscape
|
Fig.
401 Surface streams caused by Fig. 400
|
|
|
|
Getting a feeling for runoff calculations
Run the program or take Fig. 401, draw the catchment basin
of an outlet and calculate the discharge Q for one hour taking arbitrary
European precipitation and evaporation values into account. Neglect
subterranian flows, width and depth of streams, obstacles or retardatons.
Suppose surfaces and altitudes, draw the altitude lines and estimate
velocities. An exercise like that makes you understand the problems elaborated
in next sections.
Truncation orders in river systems
You can divide a river
system in different truncation orders from source to the mouth of the system. Fig. 402 shows four methods. All the
ordering systems are more or less based on a method starting with the source
and going downstream. The first order is called a source river without any
tributaries and so on. The differences are more determined by the nomination of
the different tributaries than by the diffences in system. Strahler (above right) considers small source brooks
without tributaries above as first order. Streams collecting water from first
order rivers are second order rivers and so on. Try to divide Fig. 401 in such an order system.
|

|

|
|
|
|
|
Fig. 402
Four methods to distinguish ‘orders’ in a feather like drainage pattern
|
Fig. 403
Average number and length of orders in ‘random walk rivers’
|
|
|
|
Leopold and Wolman calculated that random rivers have 4.4 upstream branchings of lower Strahler orders according to Strahlers method at
average. In practice it varies between 2 and 5. The longer a river is the more
orders can be distinguished.
This ‘bifurcation ratio’ plays a rôle in traffic as
well, though street patterns and artificial drainage systems in flat lands are not like a tree but like a grid (compare Alexander (1966))[87]. If there are 20km streets per km2, you can raise some
7km of them into the order of neighbourhood roads with a higher capacity and
transform 2km into district ways with an even higher capacity. So, the optimal
proportion between the density of ways and sideways in a grid seems to be approximately a factor
three. Do not take it for granted, it is an easy rule of thumb, based on
calculations of Nes and Zijpp (2000) indicating factors 2 and 4 are suboptimal in
three different types of calculation.
Density of roads and orders of roads
Suppose a metropolis of 30km radius has 60 x 60 = 3600km2
surface with 2km/km2 district roads (see Fig. 496). There should be 7200km
district roads in a grid of average 1x1km. To calculate density from the grid
mesh bordered by 4km district roads, you have to
count them half because they serve adjacent meshes as well. Many of them would
be overloaded by through traffic when you would not raise 1/3 of them into city
highways (2400km in a grid of 3x3km, 0.67km/km2)
with a capacity of 3000 mv/h and less exits. However, on their turn they would
be overloaded. So, this argument produces a semi logaritmic range of orders (Fig. 404).
|
|
km nominal mesh
|
km/metropolis
|
km/km2 inclusive density
|
exclusive
|
mv/h
|
|
district roads
|
1
|
72000
|
2,00
|
1,33
|
1000
|
|
city highways
|
3
|
24000
|
0,67
|
0,47
|
3000
|
|
local highways
|
10
|
7200
|
0,20
|
0,13
|
10000
|
|
regional highways
|
30
|
2400
|
0,07
|
0,05
|
30000
|
|
national highways
|
100
|
720
|
0,02
|
0,02
|
100000
|
|
and so on
|
|
|
nearly 3.00
|
2.00
|
total
|
|
|
|
|
|
|
|
|
Fig.
404 Theoretical orders of urban traffic infrastructure
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The total density of ways is 2km/km2. One third of them we
have transformed into highways of several orders. So, the density of ways
includes the highways. Exclusing highways, there are 1.33km/km2
small district ways left. If we would like to reduce the amount of exits of
local highways to save velocity, we have to disconnect district ways into dead
ends. If we like to connect them mutually with extra parallel service roads
along side the city highway we need the inclusive density at least.
If we try to draw a system
of highways in a square of 60x60km we firstly draw a grid of 10x10km. There are 14 local highways of
60km, but 6 of them we transform into a higher order. So, their exclusive
density is 8x60/3600=0.13 indeed. However, we can not
fill 10km space between local highways with 3.3 city highways. So we choose 3
highways lowering the inclusive density from 0.67 into 0.60km/km2. This causes
a raise of exclusive district way density from 1.33 into 1.40, but on this
scale we can not draw them anyhow.
Comparing truncing in rivers and roads
For wet connections the same
applies when we call city highways supply channels, local highways brooks and regional highways rivers. In Dutch such orders of
water ways can be named more precise than in English.
|
Riviersystems
|
Road systems
|
|
Dutch
|
English
|
Dutch
|
English
|
|
hoofdrivier
|
mainriver
|
hoofdweg
|
highway
|
|
hoofdader
|
trunk stream
|
wijkverzamelweg
|
trunkroad
|
|
zijrivier
|
tributary
|
zijweg
|
sideroad
|
|
aftakking
|
distributary
|
zijweg
|
secundary road
|
|
beek
|
brook
|
buurtweg
|
tertiairy road
|
|
geul
|
channel
|
woonstraat
|
residential road
|
|
geultje
|
rill
|
woonerf
|
residential area
home zone
|
|
|
|
Fig. 405 Naming orders of river and road systems
according to Moens
|
|
|
Bifurcation ratio, orders and network density
In Fig. 406 left, the bifurcation ratio
of brooks before meeting a river is 20.
However, the same network
density could be reached with a bifurcation ratio 2 and 5 orders (Fig. 406 right).
|

|
|
|
Feather
like
|
Tree
like
|
|
density
|
29
sections
|
29
sections
|
|
bifurcation ratio
|
18
|
2
|
|
number of ‘orders’
|
2
|
5
|
|
|
|
|
|
Fig.
406 Feather and tree -like connection patterns
|
|
|
Multiplying and extending
these patterns into square surfaces (Fig. 407) tree like connection patterns seem to require a little higher
density to open up all parts and consequenly higher costs when restricted to
bifurcation ratio 2. I do not understand why. Is halving the number of outlets
responsible for a higher density? If somebody can design a lower density within
this boundary conditions or prove its possibility mathematically I will publish
it next time.
On the other hand, tree like
opening up every point of the area makes many variants and greater diversity of
locations possible when you have more space to lay out (Fig. 407).
|

|
|
|
Feather
like
|
Tree
like
|
|
density
|
96
sections
|
98
sections
|
|
bifurcation ratio
|
20
|
2
|
|
number of ‘orders’
|
2
|
6 or 9
|
|
|
|
|
|
Fig.
407 Feather and tree like connection patterns opening up a square
|
|
|
Perhaps opening up a square
in a tree-like way with bifurcation ratio 3 could reach the same or even lower densities
and consequently lower costs. Try it. Does it result in less nodes and longer sections, a better readability of
the area? The number and characteristics of nodes and the length of sections
are important for spatial quality. Which rôle does the length of individual sections
L play instead of total length per order in Fig. 403?
The average length L of a
random walk river section is a power its catchment area A (L=A0.64). If length L is given the
inverse the catchment area is a power of the length (A=L1.563, Fig. 408 and Fig. 409). All the figures are
experimental, obtained by observing many catchment areas and rivers.
|

|

|
|
|
|
|
Fig.
408 Catchment area related to the length of a river section
|
Fig.
409 Logaritmic representation of Fig. 408
|
|
|
|
Check Fig. 401 by counting the
corresponding squares in Fig. 400 of a specified order and
its length. Compare your measurements with Fig. 409 and Fig. 403.
A river can be described by
its morphology. It is the credit of William Morris Davis (1912, die erklärende
Beschreibung der Landformen (Leipzig und Berlin) that for the first time a
system is formulated based on development according to evolution. He describes
the evolution of the valleys of the first order rivers as a V-shape without a
valleybottom that develops in a wide valley with a valleybottom. This river
will develop at the end in a real lowland river as we all know in The
Netherlands from the river Rhine. Later
scientists built further on his theory and adapted it where it was necessary. Fig. 412 - Fig.
418 show such a development with adaptations.
A classification according
deposits is also developed. The faster the water
streams the coarser material can be transported as load. This means that at
decreasing velocity of streaming a river will deposit first the coarse
material. The slower the stream becomes
the finer the sediment will be that will be deposited. Near glaciers coarse material is sedimented and a lowland
river will deposit fine material as sediment.
Moreover a river in a flat will tend to meander. By doing so the meander
curves will move downstream due to the undermining of the outside curve by the
streaming water.
|

|

|
|
|
|
|
Fig. 410 River curves causing different vegetation
|
Fig. 411 Water flows causing different river bottoms
|
|
|
|
Every unevenness can cause
an alteration the course of the river; many different channels of a river can
be recognized in lowland river. So the water takes diverse and changing
courses. Lower sections still bear rough material wearing out the outside parts
of a bend into meanders, because rough material
laid down there in the same time becomes a water barrier until heavy showers
force a break through Fig.
413 and Fig.
415.
|

|

|
|
|
|
|
Fig.
412 Forms of deposit
|
Fig.
413 Move of Rhine near Neuss
from Roman times (a) via Middle Ages (b) until recently
|
|
|
|
In low lands finer deposits raise the bed in calm periods forcing water to
find easier courses. A high discharge of a river causes even an river system with many branches
in a lowland area. Such a system is called a braided river.
|

|
|
|
|
|
|
Fig. 414 Change of river behaviour in time
|
|
|
The morphology of the
braided river is not very stable; it changes often depending
the amount of water.
|

|

|
|
|
|
|
Fig. 415
Meandering river with historical deposits
|
Fig. 416
Twining river
|
|
|
|
|

|

|
|
|
|
|
Fig. 417 Delta development with river (R), top-sets (d) and
fore-sets (D)
|
Fig. 418
Mississippi
delta
|
|
|
|
The Rhine area downstream of Lobith is formed by both the process of meandering during quiet periods and braiding during periods with large differences of water
discharges (Fig.
419).
From Lobith Rhine
distributes water via Waal, Lower Rhine and IJssel in historically changing proportions.
|

|
|
|
|
Fig.
419 Historical distribution of Rhine
water from Lobith
|
|
|
The velocity v of water in a
river can be measured on different depth vertical lines h with mutual distance
stretches b of the cross-section B (Fig.
420). You can determine any partial discharge by
multiplying v x b x h.The summon of the outcomes in cross section A for the
different stretches b to get Q = S(v·b·h) is an approach for the discharge
In the equation v is the
mean stream velocity of the river and the velocity can easily be measured on
site.
For example: asked the river
drainage Q (Fig. 422), given hi, bi
and vi from profile subdivisions (Fig. 421).
|

|

|


|

|
|
height h
|
width b
coordinate B
|
velocity v
|
|
|
|
Fig. 421 Data from profile
|
|




|



|

|

|

|
|
profile subdivisions
|
drainage per subdivision
|
velocity
|
surface
|
drainage
|
|
|
|
Fig. 422 Drainage (profile subdivisions and velocities)
|
|
|
The depth H of the river in
a cross-section varies, but it can be measured on site. Then, the drainage Q(H)
can be calculated by a practical formula apparently characteristic for the
profile concerned. However, periods of high drainage Q or regular floodings in
winter change profile and … the formula. Comparing measurements like in Fig. 421 on different water heights
you often find a curve like a parabola, approached by Q = a·Hb or
H=(Q/a)1/b (Fig. 423). Parameters ‘a’ and ‘b’
should be found non-theoretically by experiment, seem to characterise the
profile.
|

|

|
|
|
|
|
Fig.
423 ‘Measurements’ Mi and
Q(a,B,H) = a·HB
or the inverse
H(a,B,Q)= (Q/a)1/B to get H on the y-axis
|
Fig.
424 Change of boundary condition downstream; a ‘drowning’
waterfall
|
|
|
|
Measurements deviate from
the formula because velocity varies. When measurements can not be simulated by
a smooth curve, it is probable that conditions downstream are changed by high
water levels. Two graphs should then be drawn; one until the point of change,
one for the higher values. When for example a waterfall downstream suddenly
‘drowns’ at increasing water levels (Fig.
424) the slope of the curve will change by the increase
of velocity.
Constants a and b can be
found by the least squares method provided by Excel using graphs (see Fig.
425). Enter the data of the measurements of height and
drainage calculated according to Fig. 423 in two columns. Make a
point graph and select it.
|

|

|
|
choose power,
|
click both lowest,
|
|

|

|
|
click axis,
|
choose logarithmic,
|
|
|
|
|
Fig. 425 Adding regression lines in Excel
point graphs
|
|
|
|
Choose ‘add trend’ in
‘graph’ from the main Excel window above, and graphs like Fig. 426 and Fig. 427 with power regression line
and formula are calculated by the program.
With R2 near to 1
you have a reliable formula. In Fig. 426 we used ‘measurements’ of Fig. 423 putting the independently
variable measurements on the x-axis this time to find a=0.0003 and b=8.7398.
|

|

|
|
|
|
|
Fig.
426 ‘Measurements’ Mi and Q(a,b,H) = a·Hb
|
Fig.
427 Logarithmic representation of Fig. 426
|
|
|
|
The logarithmic
representation log Q = log a + b log (H-H0) produces a straight line
easy to extrapolate to other heights and drainages. But be careful, there could
be jumps in velocity by downstream events. If you have made graphs before and
after the jump because measuremens could not be simulated by a smooth curve,
each interval in Fig. 427 has different slopes
representing different behaviour.
Just like wind, water slows
down by roughness of the bed. The cross length of
roughness in a wet profile P (Natte Omtrek) is calculated by summing
hypothenuses of triangles according to Pythagoras characterised by the square
root of (bi)2+(hi‑hi‑1)2
(see Fig. 420 and Fig. 429).
Considering the profile as a
function H=f(x) we can read the waterlevel H from accompanying left border x1=l
and right border x2=r as values from f(x) (Fig. 428). The length of roughness P
within the cross section (Natte Omtrek = wetted contour) and the surface of the
wet cross section A are both calculated as a function of H (Fig. 429).
|


|
Cross length by Pythagoras:

Surface wet cross section:
 
|
|
|
|
|
Fig. 428 Profile as a function
|
Fig. 429 Calculating wet cross section A and cross length of roughness
P (NatteOmtrek)
|
|
|
|
When we divide the surface
of the wet cross section A of a stream by this cross length of
roughness P we get a measure indicating what part of the flowing water is
hindered by roughness called ‘hydrolic radius’ R = A/P in metres.
Method Chézy
The average velocity of
water v = Q/A in m/sec is dependent on this radius R, the roughness C it meets,
and the slope of the river as drop of waterline s, in short v(C,R,s).
According to Chézy v(C,R,s)=CÖRs m/sec, and Q = Av = ACÖRs m3/sec. Calculating C is the problem.
Method Strickler-Manning
Instead of v=CÖRs, Strickler-Manning used

with roughness n taken from Fig.
430.
|
Characteristics of bottom
and slopes
|
n
|
|
|
from
|
until
|
|
Concrete
|
0.010
|
0.013
|
|
Gravel bed
|
0.020
|
0.030
|
|
Natural streams:
|
|
|
|
Well maintained, straight
|
0.025
|
0.030
|
|
Well maintained, winding
|
0.035
|
0.040
|
|
Winding with vegetation
|
0.040
|
0.050
|
|
Stones and vegetation
|
0.050
|
0.060
|
|
River forelands:
|
|
|
|
Meadow
|
0.035
|
|
Agriculture
|
0.040
|
|
Shrubs
|
0.050
|
|
Tight shrubs
|
0.070
|
|
Tight forest
|
0.100
|
|
|
|
Fig. 430 Indication of roughness values n according to
Strickler-Manning
|
|
|
Method Stevens
Instead of v=CÖRs Stevens used v=cÖR considering Chézy’s CÖs as a constant c to be calculated from local measurements. So,
Q = Av = cAÖR m3/sec and c is calcuated by c=(AÖR)/Q. When we measure H and Q several times (H1, H2
…Hk and Q1, Q2 … Qk), we can show
different values of A(H)ÖR(H) resulting from Fig.
429 as a straight line in a graph (Fig. 431). We can add the corresponding values of Q we found
earlier in the same graph reated to A(H)ÖR(H). When we read today on our inspection walk a new water level H1
on the sounding rod of the profile concerned we can interpolate H1 between
earlier measurements of H and read horizontally an estimated Q1 between the
earlier corresponding values of Q to read Q from graph.
|

|
|
|
|
Fig. 431 Graph used according to Stevens with ‘measurements’ of Fig. 426
|
|
|
However, from these
‘measurements’ c appears to be not very constant, but the graph remains a
practical way to estimate Q from H.
|

|
|
|
|
Fig. 432 Level
regulator with level as target
|
|
|
|

|
|
|
|
Fig. 433 Discharge
regulator with discharge as target
|
|
|
|

|
|
|
|
Fig. 434 ‘Manners’
of regulation
|
|
|
The fixed regulators are
called weirs (stuwen), manual or automatic
regulators are called gates (schuiven).
The colors of Fig. 435 indicate the area in the Netherlands
that would become submerged if there were no flood protection dikes. The
flooding area as indicated is supposed to occur during modest river floods (up to 4000 m3/sec at the
German/Dutch border) and a normal high tide at sea.
However, it was not always
like that. In 2000 years that area has increased into the current surface by
rising external water levels and falling ground levels (see Fig. 462).
|

|
duration
|
period
|
|
issues
|
|
1000
|
100
|
-
|
1100
|
|
settlement ancestors
|
|
500
|
1100
|
-
|
1600
|
x
|
Erection dikes, confined contours
|
|
250
|
1600
|
-
|
1850
|
x
|
Waterlogging control, developing drainage
|
|
125
|
1850
|
-
|
1975
|
x
|
Riverworks (regulation, normalisation
canalisation)
|
|
62
|
1920
|
-
|
1982
|
x
|
Zuiderzee works
|
|
32
|
1955
|
-
|
1987
|
x
|
Delta works
|
|
16
|
1975
|
-
|
1991
|
x
|
Major purification plants
|
|
8
|
1985
|
-
|
1993
|
x
|
Policy documents tuned (RO, WHH, Trprt, Milieu)
|
|
4
|
1993
|
-
|
1997
|
|
Pilot schemes, integrated approaches
|
|
2
|
1997
|
-
|
1999
|
|
Evaluation RWS-200 year
|
|
1
|
1999
|
-
|
2000
|
|
New water Policy 21st century
|
|
new approaches
|
x
|
determined by disasters
|
|
|
|
|
Fig. 435 Potential threads
|
Fig. 436 Reverse half time of
the Dutch water management
|
|
|
|
To cope with regular floods
Dutch water management started by erecting terps in the first milennium A.D. and dikes in the
next 500 years. At that time the dynamic water surface was confined and the
next 250 years the emphasis of water management became waterlogging control and
drainage of reclaimed land. Then, in a period of 125
years the Dutch regulated, normalised and canalised their rivers. In a continuing half time
of water management policy new priorities developed like Zuiderzee, Delta and purification works (see Fig. 436). In the last few decades
all these continuing efforts were integrated by national policy documents, pilot schemes and
evaluation for future safety.
Apart from its threats,
water as a medium for trade and transport and as a military barrier for
external attacks was also a crucial ally in the development of Dutch
independence and perhaps a factor in keeping the nation out of World War I.
In the past, the Dutch have
created again and again water corridors and water defence systems for the military defence of (parts of) the
country. In addition, all major cities developed their own defence system,
quite often this is still visible on today’s maps of the old cities. In the
east and south, huge wild peat areas offered some kind of natural protection
against invaders from the east and south east. Where the sub soil contained
solid sandy deposits, in other words where
realistic chances existed that enemies could penetrate, military fortresses were developed (Nieuwe Schans, Boertange, Coevorden, Grol, Doesburg, Mook, Roermond, etc., see Fig. 437) Also along the southern
flank of the river area cities developed as military fortresses against
invaders from the south (Grave, Den Bosch, Hedel, Willemstad).
In parts of the country,
through the ages there always have been various options to create water
corridors during (threatening) wartime, in particular in
north – south direction. These wet corridors were situated in between major military
fortresses. To get these systems activated, a well designed (and maintained!)
system of sluices, dikes and locks was developed, in combination with natural
water systems that could provide sufficient inundation water during critical
periods. Today, the remnants of
these provisions are cultural elements in the landscape. Quite often money is spent
on renovation and restoration, no longer for military reasons but to safeguard
a cultural heritage.
Paved (or railed) roads in
the water saturated soft soil areas in the Netherlands gradually started
developing from the middle of the 19th century. Around 1800, the best, safest and quickest way to
move from the government buildings in The Hague to the navy harbours in Den Helder and Hellevoetsluis was still taking a horse via the beach! That
is a major reason why through the ages all the major waterways in the Netherlands
were also used for shipping. Until late in the 20th century, most
domestic transport of cargo and passengers was done by ship
(‘trekvaart’, beurtvaart). In fact for all important
routes and waterways specific (sailing) vessels were developed. The remains of
this fleet are now the backbone of the leisure industry. Today, about 35% of
all the cargo transport in the Netherlands is still going via
waterways; compared to this figure in other countries this is extremely high.
The daily water management
of major waterways as shipping routes is still crucial. Shipping
developments on the international Rhine also determine the major nautical developments
on Dutch domestic waterways. The historic and today’s development of cargo
transport on the international Rhine (in other
words the economic importance of that river), has not been and is not determined
by (fluctuations in) the Dutch economy, but first of all by the German economy. The Rhine is the major
hinterland connection of the ARA ports (Amsterdam, Rotterdam, Antwerp), and shipping developments
have been coordinated and controlled by the International Central Commission
for Navigation on the Rhine (CCNR) since the defeat of
Napoleon (1813 Waterloo, Vienna Congress 1815). It is the oldest still
functioning international body in the world.
International trade always
has been important for the development of the Netherlands. More in particular sea
trade on a global scale. It has also determined the
intensive navy orientation of society. It is remarkable that for the protection
of the capital (Amsterdam, the old trade centre) the
so called ‘Stelling van Amsterdam’ has developed, while for the military
protection of the national government centre (The Hague) only a poorly functioning
water corridor was available.
The purpose of the Rhine
canalisation (3 weirs in the Lower Rhine/Lek branch, plus some bend cuts in the upper reach
of the IJssel river) was to gain more control,
during low river discharges (of the Rhine at the German Dutch border), of the
fresh water distribution via the two bifurcations (Pannerdensche Kop-PK-, IJsselkop -IJK-) to the rest of the
country (see Fig. 439). Extra fresh water to the
north is needed during the dry season, because the IJsselmeer
(IJssellake) evaporates about one cm a day during a warm summer day, causing
too many shallows in the navigation channels in the IJsselmeer
after some weeks of a dry period. In addition, such a dry period often occurs
in the growing season of crops in the adjacent polders around the IJsselmeer , so at that time an extra need exists for
fresh water. More fresh water coming down via the IJssel (being the main feeder of the IJsselmeer) can be achieved by closing the weir at Driel.
|

|

 
|
|
|
|
|
Fig. 439 Weirs directing water northwards and southwards
|
Fig. 440 IJK, PK, Weir
of Driel regulating Dutch water distribution
|
|
|
|
The Driel weir is the most important fresh water tap of the
country. By lowering (= partly or entirey closing the Lower Rhine) the so
called visor gates, a backwater effect is noticeable till upstream Lobith, so
also at both bifurcations IJK (more) and PK (less). Because the width of the major channel
in the Waal branch is 260 m, and the width of the IJssel
major channel only 80 m, the amount of discharge taken from the Lower Rhine will distribute over IJssel and Waal in the order of magnitude 40–60 % /
60-40 %, so as an average 50/50%. However, the lowering of the Driel weir is
only possible if first the two other weirs at Hagestein (Lek) and Amerongen (Lower Rhine) are lowered, with the purpose to
create sufficient navigable depth in the entire length of the river between IJK and the tidal zone near Rotterdam.[89]
Because the weirs are only
closed during dry periods (low discharge of the Rhine at the German-Dutch
border), the fresh water discharge coming down the Lek to Rotterdam will be minimised; as a consequence the salt
water intrusion from the sea may harm the drinking water inlet east of Rotterdam
along that river. This is not acceptable, so there must be compensation to
minimise that salt water effect. It can be done by first closing the Haringvliet sluices, in a way that a backwater effect is
created up till at least the Moerdijk zone. Then, all the fresh water
coming down both the Meuse and Waal rivers will be sent north to Rotterdam
and Hook of Holland. This surplus fresh water
is sufficient to stop the salt water intrusion as mentioned.[90]
So one can conclude that a
strategic water management of the IJsselmeer is determined by the flush regime
of the Haringvliet sluices, via the canalisation of
the Lower Rhine.
The major rivers and the sea
always have threatened the Dutch society during severe floods. The tidal characteristics
and the regime of the river discharges have determined the development of the flood
protection systems in the country. Due to large scale drainage and reclamation over a period of many centuries, major parts
of the land where peat deposits at the surface and in the subsoil exist(ed),
have subsided. This process is still going on as long as the polders are kept dry with artificial means (pumps, see
Fig. 468). Due to climate change,
expectations are that the sea level will rise and the regime of the major rivers will change
(higher peak flows, longer dry periods[91]). As a result, the dense
populated areas in the western and centre part of the country will further
subside and the river levels and sea level will rise (see Fig. 444).
In the past, dike breaches along the rivers have occurred frequently
during floods, more in particular during severe winters when ice jams blocked
the major streams. There are also well known examples of severe floods by storm
surges from the sea, the last major attack was
in 1953. During the last 50 years, strong political policy decisions on safety
against flooding have determined how flood control measures (coastal defence systems, dike strengthening along estuaries, lakes and rivers) have been
designed and implemented. Due to expected climate change, new standards and approaches
for adapted policies are considered or already carried out (Room for the Rivers
programme). Safety along the major
rivers can only be achieved in concert with measures taken by riparian
countries in all river basins situated upstream of the Netherlands.
The present map of the Netherlands is
fully determined by human intervention with the purpose of flood control and
safety. One has to distinguish the
rivers and the coastline.
Along the rivers, the
regulation, normalisation and sometimes canalisation (Meuse, Lower Rhine), in combination with
(confined) flood plain management and dike structures (often but not always with a public road on
top) have determined safety; as have the controlled discharge distribution over
the various Rhine branches Waal, Lower Rhine and IJssel) during all stages at two
bifurcations (Pannerdensche Kop, PK; Ijsselkop, IJK) and the artificial drains
at the downstream end of the rivers (Nieuwe Merwede, Bergse Maas, Keteldiep/Kattendiep. Note: the normalised major
channels of the river branches are state owned; however the land in
the flood plains is mostly owned by private people, including
foreign landownership).
Along the coastline, one has to distinguish at
least four major systems of coast development (see Fig. 438):[92]
1.
estuaries and (clay) island fixation in the south west;
2.
a closed sandy coastline in the west (dunes);
3.
a fully controlled lagoon in the centre with a primary (Afsluitdijk) and secondary (bunds
around reclaimed polders) defence system, and
4.
land reclamation in between sandy islands and a clay protection
dike in the north (Waddenzee).
There is a litoral drift of
the tide along the coast in northerly direction, tidal
differences fluctuate between the southwest , the centre
and the north east between 5m - 1,5m - 4m (see Fig. 441).
The line on Fig. 439 between Sluis (Zeeuws Vlaanderen) and Eemshaven (Groningen) is exactly 45 degrees to
the north arrow. It is a symbol, representing the 0-line (NAP, normal Amsterdam level, the one and only uniform
chart datum in the whole country).
Fig. 441 shows the effort of
increasing the elevation of dikes above the sea level along this line after the
rare desastrous floods of 1953. They are mainly elevated
to 4 metres above regular high tide (different along the coast). It shows also
the ground level in Holland, as far as Amsterdam being even lower than the bottom of the IJsselmeer. The blue and red bars left
in the drawing show the level of rivers and roads, canals and lakes in the
polders. This representation indicates the logic of crossings by tunnels rather
than by bridges even if the soil is weak, if dikes have to be crossed and if
the densely populated area offers many spatial barriers.
|

|
|
SURFACE WATER
|
|
SALT
|
BRACKISH
|
FRESH
|
|
cur.
|
stag.
|
cur.
|
stag.
|
cur.
|
stag.
|
|
deep
|
Oosterschelde, Waddenzee
|
Grevelingen, Veerse
Meer
|
Haringvliet
|
Biesbosch
|
Uiterwaarden Maas
Uiterwaarden Rijn
|
IJsselmeer, Oostvaarders
plassen
|
|
shallow
|
|
bank
|
|
swamp
|
|
bottom
|
|
|
GROUNDWATER
|
|
|
|
|
Fig. 441 Levels on the line of Fig.
439
|
Fig. 442 Kinds of water in the Netherlands
|
|
|
|
The many resulting kinds of
surface water (deep, shallow, bank, swamp, bottom, salt, brackish, fresh,
current, stagnant) in the Netherlands are an important basis
for its ecological diversity (see Fig. 442).
Heavy rainfall and seepage determine also the design criteria of water
management measures in the country. In populated and
industrialised areas, a severe rainfall with critical intensity must be pumped
out completely within a period of 24 to 48 hours.[93] This urges the need for adequate pumping and drainage systems in the flat and low situated areas where due
to wind effects, proper drainage by gravity
is impossible; in addition proper maintenance of these systems is necessary.
This can only be achieved by proper supervision and effective enforcement, so
also the institutional aspect of water management (legislation, rules and regulations, set up of
management authorities, finances, skill and staff, etc.) is a matter of crucial
importance.
At Lobith in February
normally a water level of approximately 10m NAP and 3000m3/sec is
measured. But in 1995 it was
approximately 17m NAP and 12 000m3/sec, the second highest
discharge of the century (1925: 13 000m3/sec). Evacuation of
200 000 inhabitants was ordered by the Royal Commissioner of Gelderland
Terlouw when floods threatened Betuwe area downstream of Lobith. One million cattle
had to be moved. It caused extreme traffic jams on roads the like of which had
never been envisaged. The dikes barely held out, becoming wetter and wetter.[94]
Afterwards, the real threat
of inland floods raised public awareness and the need to make plans to increase
safety. If the present state of inland dikes and other hydraulic
circumstances is not changed, we apparently have to expect threats of a
disaster like 1995 twice a century (a recurrence time of 50 years).
|

|

|
|
Source:
|
|
|
Fig. 443 Subsidence expected
by 2050
|
Fig. 444 Sealevel rise and
subsidence expected by 2050
|
|
|
|
But the hydrological
circumstances change. Perhaps we should expect more rain in winter (less in
summer) as a result of climate change. Germany
and Switzerland have drained
their meadows so much, that any rainfall upstream reaches the river Rhine faster than ever. Moreover, the west of the Netherlands
faces a general subsidence of at least -3cm until 2050 (locally –70cm,
see Fig. 443).[95] Increasing the height of dikes along the rivers is necessary, but
it does not solve the question how to drain the discharge into the sea while
its level rises through climate change (15 cm by 2050?, see Fig. 444).
Normal distribution of maximal discharges
Looking at the average
yearly maximal discharges of past years (see the 98 years in Fig. 445) you can calculate their
average maximum discharge (6.6454m3/sec) and their standard deviation (2.1408m3/sec) to draw a ‘normal distribution’ based solely on these two numbers (see Fig. 446).
From that normal probability
distribution you can extrapolate the probability per class of 1000m3/sec
wide (see Fig. 447).
|

|

|
|
|
|
Fig. 445 Extreme discharges of the river Rhine per year
|
Fig. 446 Probability
|
|
|
|
|
m3/sec year
maximum measured in 98 years
|
m3/sec class
|
probability/year
|
Year/probability
(recurrence time)
|
|
average
|
6 645
|
|
Ę
|
|
|
|
|
standard deviation
|
2 141
|
|
Ę
|
|
|
|
|
|
|
>1 000<2 000
|
0.58%
|
once in
|
174
|
year
|
|
smallest observed
|
2 280
|
>2 000<3 000
|
1.77%
|
once in
|
57
|
year
|
|
|
|
>3 000<4 000
|
4.37%
|
once in
|
23
|
year
|
|
|
|
>4 000<5 000
|
8.68%
|
once in
|
12
|
year
|
|
|
|
>5 000<6 000
|
13.87%
|
once in
|
7
|
year
|
|
average
|
6 645
|
>6 000<7 000
|
17.81%
|
once in
|
6
|
year
|
|
|
|
>7 000<8 000
|
18.38%
|
once in
|
5
|
year
|
|
|
|
>8 000<9 000
|
15.25%
|
once in
|
7
|
year
|
|
|
|
>9 000<10 000
|
10.18%
|
once in
|
10
|
year
|
|
|
|
>10 000<11 000
|
5.46%
|
once in
|
18
|
year
|
|
|
|
>11 000<12 000
|
2.35%
|
once in
|
42
|
year
|
|
largest observed
|
12 849
|
>12 000<13 000
|
0.82%
|
once in
|
122
|
year
|
|
|
|
>13 000<14 000
|
0.23%
|
once in
|
439
|
year
|
|
|
|
>14 000<15 000
|
0.05%
|
once in
|
1,961
|
year
|
|
|
|
>15 000<16 000
|
0.01%
|
once in
|
10,881
|
year
|
|
|
|
>16 000<17 000
|
0.00%
|
once in
|
75,115
|
year
|
|
|
|
>17 000<18 000
|
0.00%
|
once in
|
644,950
|
year
|
|
|
|
>18 000<19 000
|
0.00%
|
once in
|
6,887,859
|
year
|
|
|
|
>19 000<20 000
|
0.00%
|
once in
|
91,495,720
|
year
|
|
|
|
|
|
|
|
|
|
Fig. 447 Normal probabilities per discharge class of the river Rhine
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
However, that is only a very
first approach, because the formula for an asymmetrical distribution (see Fig. 365) or a distribution
otherwise different from the normal distribution may fit the data better.
The percentages are
represented less precisely and eloquently than their reciprocal value: the
number of years you can expect between two occurrences of that class
(recurrence time). That measure has
political value.
The Parliament of the Netherlands
once decided to accept 1 casualty per million inhabitants per year caused by
environmental disasters (accepted risk). So, the number of
casualties per class of discharge causing floods has to be calculated to plan
the measures to meet the accepted risk of that rare discharge. Which area is
flooded by which discharge, and how many people live there? Many studies have
been executed to get answers on that question. They make clear that 1 casualty
per million inhabitants per year would lead to unacceptable measures producing
other kinds of risks. So, the Parliament decided in 1960 to accept the higher
risk of a disastrous flooding of rivers once in 1250 years.[96] In other areas surrounded by dikes (dijkringen) that risk
acceptance is lower or higher according to their economic value (see Fig.
448).
|

|

|
|
Source:
|
Source:
|
|
Fig. 448 Current safety standards for floods (MNP, 2004)
|
Fig. 449 Proposed changes of safety standards (MNP, 2004)
|
|
|
|
However the ‘human and
economic value’ has increased substantially compared to the costs of water
safety management. So, these safety standards are in discussion (see Fig. 449).
If you number the discharges
Q from high to low (rank number r), in 98+1 years of experience the first largest
maximal discharge has a recurrence time of 99/1 year, the second (including the
first!) 99/2 and so on (see Fig. 450).
|
year
|
m3/sec
|
rank
|
recurrence time
|

|
|
|
Q
|
r
|
99/r
|
|
1901
|
5 058
|
77
|
1.3
|
|
1902
|
5 715
|
68
|
1.5
|
|
1903
|
6 081
|
60
|
1.7
|
|
1904
|
3 731
|
89
|
1.1
|
|
1905
|
6 697
|
44
|
2.3
|
|
1906
|
6 121
|
57
|
1.7
|
|
1907
|
5 058
|
77
|
1.3
|
|
1908
|
6 101
|
58
|
1.7
|
|
…
|
…
|
…
|
…
|
|
1925
|
12 849
|
1
|
99.0
|
|
…
|
…
|
…
|
…
|
|
1992
|
5 758
|
65
|
1.5
|
|
1993
|
11 100
|
4
|
24.8
|
|
1994
|
12 060
|
2
|
49.5
|
|
1995
|
4 112
|
84
|
1.2
|
|
1996
|
7 004
|
38
|
2.6
|
|
1997
|
3 912
|
87
|
1.1
|
|
1998
|
9 487
|
11
|
9.0
|
|
|
|
|
|
|
|
Fig. 450 Ranking maximum
discharge per year, calculating recurrence time
|
Fig. 451 A Gumbel graph of Fig.
450
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
If you plot them in a graph
with a logarithmic x-axis (Gumbel graph[97], see Fig. 451) you can extrapolate the
higher discharges to be expected roughly by a straight line. Fig. 451 shows a discharge of
approximately 16 500 m3/sec recurring every 1250 years with a
big spot. So, for any river you can indicate every observation y on that graph
if you know the last time that level was reached (x years ago). Nearly any kind of theoretical probability distribution (like the normal one on page 211) will also produce a nearly
straight line for the higher levels in the Gumble graph. That method is used for
many kinds of natural disasters like earth quakes and eruptions of vulcanoes.
However, the slope ‘s’ and
elevation ‘e’ of the straight line chosen have great effect. In Fig. 451 a line with formula Q(r)
= s·ln(r)+b m3/sec was chosen, where s = 1.43 and
e = 6.36.
One of the proposed measures
is, to inundate indicated polders preventively in case of emergency. But a 1m deep polder of
1km2 (1 000 000m3) would store 12 000m3/sec
water only for 83 seconds at least if it is not sloping. In case of sloping you
should half that capacity. If you would like to store 16 000m3/sec
during a week to be safe for many centuries because you cannot discharge that
amount into the sea because of sea level rising after these centuries, you need
10 000km2 (a quarter of the Netherlands). However, you can
reduce the needed storage because you still can discharge into the sea, be it
at low tide or by huge pumps. But this simple and much
too rough calculation shows at least the dimensions of the problem.
|

|
|
|
|
Fig. 452 Maximum water depth during a
flooding in Betuwe along the Rhine
after a dike breach and a peak discharge of 18.000 m3/s
|
|
|
So, construction of
retention basins or more general widening of the riverbed in the Netherlands solely cannot be a
substantial solution to avoid rare flooding in a river system. Dikes along the rivers have to be heightened, but
which height is enough? Deepening the river (filled up quickly with sediment)
or making the dikes higher increases the capacity to discharge, but moves the
problem to the west where more people live. So, retention in the Rhine
basin upstream has to increase to avoid extreme situations downstream. This is
discussed by the international Rijncommissie Koblenz.
|

|

|
|
|
|
Fig.
453
Schematic representation of a low land river
|
Fig. 454
Measures improving Rhine discharge
|
|
|
|
To be prepared for floods a landscape will have to be designed
mainly as a natural area (see Fig. 455).
|

|
|
|
|
Fig. 455 Anticipated vegetation structure and land use along the Dutch Rhine
as a ‘green river’
|
|
|
On 19 December 2006 the
Dutch Parliament accepted a Spatial Planning Key Decision (SPKD, in Dutch: Planologische
Kernbeslissing PKB) concerning a series of
measures along the rivers known as ‘Room for the river’ (see Fig. 456). However, the final set
of measures should be determined by commitment of local stakeholders and
administrators. To get that commitment Delft Hydraulics has developed a game to determine the effects
of any single measure in solving the problem.
|

|
|
|
|
Fig. 456 A series of measures known as ‘Room for the river’
|
|
|
As shown in the sketch map
of the Netherlands
(see Fig. 438), there are various major
coast forms, differing fundamentally.
For the design, strengthening and maintenance of the coastal defence, all these major forms
need continuously specific tailor made attention. A universal fact is that
disasters are needed to make progress. Also in coastal water
management, tragic disasters have determined human intervention in developing
the Dutch coast line. One can refer to the big flood in the southern part of
the former Zuiderzee in 1916, when severe flooding
occurred causing nearly 20 deaths and huge damage; this disaster accelerated
the political approval of starting the Zuiderzeewerken (Zuiderzee works) designed by Lely. And of course the storm
surge on February 1st, 1953, which initiated the
Deltawerken (Deltaworks).
In the past, coastal and
river works were done by trial and error and on a relatively small scale. If
the works that needed to be done were simply too big and complicated, land was
given up (again). In those days, coastal engineering was more or less a matter
of ‘’If we cannot do what we want, we will do what we can.’’. Apart from not
having proper large tools, current knowledge and practical experience were not
enough to justify efforts in coastal development on any sort of large scale.
Fundamental coastal research and model investigations were only developed in the Netherlands
from the early 1930s. At that time, three major civil engineering works were
developed, i.e. the Afsluitdijk (Enclosure dike, whereby the ‘Zuiderzee’ was renamed the ‘IJsselmeer’), the big lock for seafaring
vessels at IJmuiden at the end of the Noordzeekanaal (North Sea Canal) and the completion of the
Maaswerken (Meuse works; Julianakanaal locks, with the biggest head in the country).
Till then, water related research for Dutch clients was often done abroad, for
example in Karlsruhe (Rehbock laboratory).
The preparations and design
for the Zuiderzeewerken in the 1920s urged the need for developing a good
mathematical basis for proper tidal computations, to be able to predict
with sufficient accuracy changes in water levels along the coast of the Wadden Sea after the closure of the Afsluitdijk. In this
respect in particular one name must be mentioned: Lorentz. He developed modern
tidal calculations, needed to estimate the impact of the Zuiderzee works
(Afsluitdijk) on the tidal regime along the northern Dutch coastline. In fact, one can conclude
even after 75 years that the sandy bottom of the Wadden Sea
has still not reached a new equilibrium since the closure in 1932, due to the
severe changes in the tidal movements as introduced by human intervention at
that time.
For all major
infrastructure, political approval is
necessary by means of a special law being adopted by Parliament. Such a law not
only describes the need for the work itself, but also the financing and how
institutions are required for design and implementation. The Delta Act was adopted in 1956, three years after the
February ’53 surge. At the time, repair to the damage and building of new structures
was already going full speed ahead. So in fact the financing of those efforts
had not yet been approved by Parliament till 1956. The country was in a sense
at war, so military means were accepted. For nearly 25 years (in the period
1953 – 1977), the execution of the solid dams in the south west was never a
real political question: the need for implementation was simply a political
fact because ‘safety first’ was the guiding motive after the disaster in ’53
when about 1850 people were killed. Only in the mid-seventies, when the last
episode of the Deltaworks scheme started with the closure of the Oosterschelde (Eastern Scheldt), socio economic and
environmental changes on a national scale prompted the need for a complete
revision of the engineering approach to this major work (Fig. 457) showing many innovative
coastal constructions.
|

|
|

|
|
|
|
Fig. 457 Delta project
|
|
|
It is remarkable to notice
the huge level of human intervention since 1953, needed to close the estuaries
in the south west. As the crow flies over a distance of about 100 km between
Hook of Holland and Cadzand/Belgian border, 9 different ways have been used for
closing off tidal creeks and estuaries, involving (systems of) primary dams (years as
mentioned indicate year of commissioning). From north to south they are: the
Nieuwe Waterweg (floating movable barrier, 1998), Brielse Maas (sand supply, 1952), Haringvliet (sluices, dam and by passing lock, 1970), Brouwersdam (caissons and cable, 1968), Oosterschelde (open barrier, 1986), Veerse Gat (caissons, 1961), Westerschelde (open estuary, dike strengthening, 1985),
Braakman (sand supply, 1951), and Zwin (gradually closed by natural phenomena).
In addition there are 6
other solutions for the closure of so called secondary dams (some of them
located on a former tidal slack) in the Deltaworks scheme, for example the
Hollandse IJssel barrier (a main steel gate and a second one just for
safety reasons in case the first one has a failure, 1956), the Volkerakdam (caissons plus major locks, and sluices (1969),
Grevelingen (cable, minimising the tidal volume in the
Brouwershavense Gat before closure (1961), Krammerdam (major locks with a sophisticated salt/fresh
water control system, 1982), Markiezaatdam (compartment dam of clay and sand with a lock,
to minimise the tidal volume at the Oosterschelde barrier and to control water quality in the
Scheldt-Rhine canal, around 1980),
Zandkreekdam (sand supply, minimising the tidal volume in
the Veerse Gat before closure, 1960). To complete the variety
of closure works in this part of the Netherlands,
one must also mention the Sloedam and the Kreekrakdam, both needed for the
railway connection to Vlissingen (clay and sand dams, 1870).
Considering all this, in
the 20th century the Dutch have reached apparently a point that can
now be characterised as ‘we can do what we want”. Such a huge and costly scheme
could only be implemented because the Dutch society was prepared to allocate
the necessary funds from its own resources, so political support remained
consistently positive. On the other hand: if a country in the Third
World were to ask a donor organisation (for example the World Bank) to finance a closure
scheme in a complicated tidal area with at least ten solutions, this would
never been accepted. Such an investment for the safety of only 200,000
inhabitants behind the structures is according to present standards of
international donor organisations simply NOT considered as feasible (!).
Note that in 1990,
Rijkswaterstaat was awarded the Maaskant Prize for the
Deltaworks, in particular for the way
the whole project is flexible in its spatial planning and technical set up, and
for the way it has proven to be useful also for new sectors developed after the
period of design and execution, for example leisure and environment. For more
general information on these works, see the jury report.
The centre coast line of the Netherlands
between Hook of Holland and Den Helder
can be characterised by a system of sandy dunes. Because of the lateral
drift in northerly direction along the coast, there is some continuous ongoing
erosion of the sandy coastline(see Fig. 458). The effect over time is
visible at the Hondsbosse Zeewering, where the original tow of
the revetments at the seaside was constructed (stone construction, 1875) in
line with the low water line on the beach in those days. Today, the low water
coastline has moved over about 70 m in easterly direction.
In 1991, Parliament adopted
a coastal defence law, giving the green light
for regular sand supply (beach nourishment) to maintain the position
of the low water line as it was in 1991. Since then, year after year, at some
places along the entire coast, nourishment works are carried out outside the
tourist season. Like the closure of the IJsselmeer by the 30km Afsluitdijk in 1932 this major project of the fifties
caused changes of yearly natural sand transport in the North Sea and Wadden
Sea The sand moved mainly from the inland waters
as growing islands in front of these works. To stabilise
protruding beaches and islands, large amounts of sand from the sea had to be
added artificially to these beaches(see Fig. 459).
|

|

|
|
|
|
Fig. 458 Natural yearly sand transport
|
Fig. 459 Artificial incidental
sand supply
|
|
|
|
Over their entire length,
the sandy dunes are important for building up and maintaining a ‘fresh water
bubble’ in the sub soil, floating
on the salt groundwater underneath. This fresh water system is an extra
(groundwater) protection against salt intrusion in critical areas behind the dunes, for example
the Westland. In many cases, the fresh
water volume in the dunes is artificially kept above certain levels for
drinking water supplies in the west. The inlet water originates from
the major rivers in the country, Rhine and Meuse, and is pumped through
pipelines.
A special development is de
Kerf, west of Schoorl (Noord-Holland). There, in the late nineties,
the primary dune ridge was artificially cut to allow the penetration of salt
water during rather high tides (about twice a year). The environmental
development and habitat have been carefully studied and followed by many
institutions since then.
The Afsluitdijk is presently being renovated, to meet the
recent standards for flood protection and safety/reliability. Also the capacity
of the sluices may be increased shortly. Sluices, bridges
across the locks bypassing the sluices, and dike (alignment) had special design
criteria for military reasons. They really have worked: in 1940, Kornwerderzand was the only place in Holland where the invaders could not get
through. In the original design of the dam, space was reserved for the
construction of a rail track as well. A deep cut for the planned track is still
visible on the former island of Wieringen, alongside the motorway to
Den Helder. The excavated clay from
that deep cut has been used for the creation of the last refuge hill (terp) built in the Netherlands to
date; at Wieringerwerf in the Wieringermeer. Indeed it was used by
some locals after the German army blew up the surrounding polder dike at the
end of WWII. Today, on top of that
‘terp’ there is a public swimming pool (again the world upside down).
The sea defence system in
the north is rather complicated, because of the sandy islands, the Wadden Sea with all its environmental and morphological
extremes, the so called old ‘Landaanwinningswerken’ and the strengthened long clay sea defence
dike between the Afsluitdijk and the Dollard. For the purpose of this
chapter, the most interesting aspects are the auxiliaries in the sea coastal
defence system, for example the ferry terminals, harbour law outs and terminal structures, the various breakwaters (Harlingen, Delfzijl), navigational aid systems,
and the leisure facilities. They all can be used as informative and
illustrative examples when designing a specific issue in relation to coastal
engineering aspects. Whatever further intervention
will be needed in the near future, the fact is that for the 21st
century the situation of designing and constructing large scale works can now
be described as ‘are we still allowed to create what we can?’.
Finally,
a last aspect when it comes to coastal engineering, the logistics of the execution and implementation
of impressive works. It deals with the supply of material in isolated and so
far undeveloped areas. This can be illustrated with two examples from the past.
For more modern and contemporary equivalents, everyone can use their common
sense.
First, when visiting the Wadden islands in the north, many brick houses can be seen that have been
built through the ages. This is remarkable, because there have never been
brickyards on the islands. Even some lighthouses, like the famous Brandaris (Terschelling), were constructed exclusively with bricks. One may wonder where originally all those bricks came from.
This has everything to do with the flourishing Hanseatic
League in the past. Wooden sailing
vessels came from the Rhine basin, heading for the Hansa cities in the north and beyond (Baltic Sea). Bricks were transported by ship from brick yards in the river
area (flood plain), and handled manually. In those days, where no machinery existed,
this was done stone by stone by so called head loading. More astonishingly,
each stone of the Brandaris light house must have been handled this way at
least six times (or most probably even more), when being moved between the
brick yard somewhere in the flood plain to its final place in the structure. En
route they were brought on rather small vessels over dangerous and difficult
waters.
Second, a similar development can be seen on a larger scale, for
distant overseas destinations. The VOC vessels in the 17th-18th
century took bricks as ballast on their journey from Holland
to the Far East, for example to present-day Jakarta. When visiting the city today, one can still see the typical bricks
and tiles of Dutch origin, used in the construction of buildings there.
Design with nature
To stimulate local inland
movement of sand and clay from the sea (stopped after these
‘hard’ defence works) the policy of coastal defence has changed gradually into
a ‘design with nature’ approach.
|

|
|
|
|
Fig. 460 Slufter on the isle of Texel
|
|
|
This involves opening up
some ‘hard’ defences where it is safe (slufters) allowing the sea to come
in, bringing sand and clay into these calm inland waters causing the
development of beautiful dynamic natural areas calling the original state of the Netherlands
to mind.
Wetland areas may need drainage to be used for living and
agriculture. The draining was started to obtain more space for these
activities. The first method of draining was with the help of open ditches and trenches. The water was drained by sluices on lower lying waterways like
rivers or at low tide at the sea (see Fig. 461). Later when the difference in height of water between the drainage
area and the river or sea became too small or even negative, the land was
drained by pumps (see Fig. 462 and Fig. 468).
A polder is a piece of land that forms
a hydrographical entity. In low lying areas a polder is surrounded by
embankments or dikes. Even a lake can be transformed into land (see Fig. 461).
This reclamation is also called a polder
because the groundwater level is managed in an artificial manner. Such land
reclamations are always situated below the surrounding water level.
|

|

|
|
|
|
|
Fig. 461 A short history of polders
|
Fig. 462 Rising outside water levels and dropping ground levels
|
|
|
|
Draining an area starts a process of changes
in the soil. The ground level will settle and drop depending on the type of
soil. Peat soil will actually totally
disappear by chemical processes and the ground level will be lowered by the
equivalent of the thickness of the peat layer. Also the introduction of better methods and pumps will lower the groundlevel
(see Fig. 462).
It is obvious that since the groundwater level is managed
artificially , there are several desirable groundwater levels. The depth of the groundwater level depends on the activity that
will take place in that area and the type of soil. For grassland a high groundwater level is
no problem for growing, but having cattle on that land will be more
problematical as the cattle will destroy the grass by walking on it and no food
will be left. For crops the depth of the groundwater
level is dependent on the type of crop. Grasslands may be wetter, dryland crops should be dryer than 1m
below terrain (Fig. 463
|

|
|
|
|
Fig. 463 Crop yields for different open water
levels
|
|
|
For urban areas the groundwater level is kept
at approximately 1m below ground level for different reasons such as
foundations and wet crawl spaces. Also the construction of cables and pipes in the streets is easier under dry
circumstances.(see Fig. 464).
|

|

|
|
|
|
|
Fig. 464 Flooding of a canal in Delft
|
Fig. 465 Deep canal in Utrecht
|
|
|
|
Urban areas need dry crawl spaces to keep
unhealthy moist out of the buildings but they need wet foundations as long as they are made of wood.
Groundwaterlevel is often recognisable from open water in the
area. In higher parts of the Netherlands
like in Utrecht canals show a level of several metres below ground
level (see Fig. 465).
The distribution of polders worldwide
Lowlands with drainage and flood control problems cover nearly 1million km2
all over the world (Fig. 466) and nearly half the world population lives there because of water
shortages elsewhere (RWS (1998).
|
x1000 km2
|
1 crop
|
2 crops
|
3 crops
|
Total
|
|
North
America
|
170
|
210
|
30
|
400
|
|
Centra America
|
|
20
|
190
|
210
|
|
South
America
|
60
|
290
|
1210
|
1560
|
|
Europe
|
830
|
50
|
|
880
|
|
Africa
|
|
300
|
1620
|
1920
|
|
South
Asia
|
10
|
460
|
580
|
1050
|
|
North and Central Asia
|
1650
|
520
|
20
|
2190
|
|
South-East
Africa
|
|
|
530
|
530
|
|
Australia
|
|
310
|
120
|
430
|
|
|
|
|
|
9170
|
|
|
|
Fig. 466 Area of lowlands with
drainage and flood control problems
|
|
|
Inhabited or agricultural areas below high tide river or sea level
(polders) have to be drained by one way sluices using sea tides or pumping
stations (see Fig. 468, Fig. 471).
Fig. 467 is the oldest known example of draining by one way sluices at low
tide dating from the 11th century.
|

|

|

|
|
|
|
Fig. 467 The oldest one way
sluice found in the Netherlands
and its modern principle
|
|
|
|

|
|
|
|
Fig. 468 Pumping stations in the Netherlands
|
|
|
One way sluices lose their purpose when
average sea and river levels rise and ground level drops mainly because of the
subsidence of peat polders (Fig. 462). Drying peat oxidates and disappears and
so the ground level of the polder will drop below river or sea level.
The area is divided in smaller entities or compartments that are
surrounded by belt canals (boezemkanalen), protected by dikes and internally drained by races (tochten), main ditches (weteringen), ditches (sloten), trenches (greppels), and pipe drains. As the system of outlet canals(boezemkanalen) transports the water from the land to the river or
the sea and they are all connected with each other it is also possible to use
these waterways for shipping. The area is made accessible for shipping traffic
by locks.
Fig. 469 shows the belt system of Delfland and the compartments. Each
compartment has its own sluice or pump and outlet canal or ‘boezem’.
|

|
|
|
|
Fig. 469 The belt (‘boezem’) system of Delfland
|
|
|
The reclamation and drainage of the polders is done by pumps. The pumps
are driven by wind, steam or electricity depending the technical knowledge of
the time. The methods used depend on the depth of the polder. Draining
marshland is often done by one step of
pumping or even by a one way sluice when the land is adjacent to a tidal river
or the sea. But after settling of the soil in the course of time it can be
necessary to use more steps for pumping. Especially when the only force to
drive the pumps was by wind, rows of windmills were used for draining the
polder. The most famous row of windmills in the Netherlands are those of Kinderdijk in Zuid Holland.
The methods used for draining polders with different altitudes are pumping at once from the
deepest part using gravity by collecting first the water from the deepest level
or draining step by step compartments separated by dikes and weirs saving
potential energy (Fig. 471).
|



|


|
|
|
|
|
|
|
|
Fig. 470 Lowland system
|
Fig. 471 Drainage by one to three pumping
stations, in earlier times by a ‘row of windmills’ (‘molengang’)
|
|
|
|
Polders are optimally drained by a
regular pattern of ditches (see Fig. 472, Fig. 473).
|

|

|
|
|
|
Fig. 472 Wieringermeer polder
|
Fig. 473 Hachiro Gata Polder in Japan
|
|
|
|
|

|

|
|
|
|
Fig. 474 Variables determining distance L between
trenches
|
Fig. 475 Variables determining distance L between
drain pipes
|
|
|
|
The necessary distance L between smallest ditches (see Fig. 474) or drain pipes (see Fig. 475) is determined by precipitation q [m/24h], the maximum acceptable
height h [m] of ground water above drainage basis between drains and by soil
characteristics. Soil is characterised by its
permeability k [m/24h] (see Fig. 476).
L=2Ö(2kh/q) is a simple formula to
calculate L. If we accept h=0.4m and several times per year precipitation is
0.008m/24h, supposing k=25m/24h the distance L between ditches is 100m.
|
Type of soil
|
Permeability k in m/24h
|
|
gravel
|
>1000
|
|
coarse sand with
gravel
|
100
|
1000
|
|
coarse sand,
fractured clay in new polders
|
10
|
100
|
|
middle fine sand
|
1
|
10
|
|
very fine sand
|
0.2
|
1
|
|
sandy clay
|
0.1
|
|
peat, heavy clay
|
0.01
|
|
un-ripened clay
|
0.00001
|
|
|
|
|
Fig. 476 Typical permeability k of soil types
|
|
|
|
However, the permeability k [m/24h] differs per soil layer.
To calculate such differences more precisly we need the Hooghoudt
formula described by Ankum (2003) page 35.
Parcel ditches are used as property boundaries. In this way
agricultural and urban activities are easily to separate from each other. Any
use has its own requirements for parcel division. Systems of parcel
division have to take dry infrastructure into account. Different network
systems have to be combined in the polder for a good completion of drainage as
well traffic.
|

|
|
|
|
Fig. 477 Alternative systems of plot division in
polders
|
|
|
We will elaborate that in 3.4.16.
There are many types of water level regulators elaborated by Arends (1994) (Fig. 478, Fig. 479, Fig. 480).
Weirs
|

|

|

|

|
|
Schotbalkstuw
|
Schotbalkstuw met wegklapbare aanslagstijl
|
Naaldstuw
|
Automatische klepstuw
|
|

|

|

|

|
|
Dakstuw
|
Dubbele Stoneyschuif
|
Wielschuif rechtstreeks ondersteund door
jukken
|
Wielschuif via losse stijlen ondersteund door
jukken
|
|
|
|
Fig. 478 Types of weirs
|
|
|
Sluices
|

|

|

|

|
|
Uitwateringssluis open
|
Uitwateringssluis closed
|
Inlaatsluis open
|
Inlaatsluis closed
|
|

|

|

|

|
|
Irrigatiesluis
|
Ontlastsluis closed
|
Ontlastsluis flooded
|
Ontlastsluis open
|
|

|

|

|

|
|
Keersluis
|
Spuisluis
|
Inundatiesluis (military)
|
Damsluis (military)
|
|
|
|
Fig. 479 Types of sluices
|
|
|
Locks
To allow accessibility of shipping traffic you need locks at every
transition of water level.
|

|

|

|
|
Schutsluis
|
|

|

|

|
|
Dubbelkerende schutsluis
|
|

|

|

|
|
Gekoppelde sluis
|
Sluis met verbrede kolk
|
Bajonetsluis
|
|

|

|

|
|
Tweelingsluis
|
Schachtsluis
|
Driewegsluis
|
|
|
|
Fig. 480 Types of locks
|
|
|
Entrance and exit
Any regulator, culvert, sluice, lock or bridge requires a structure with
entrance and exit of water needing space themselves (Fig.
481).
|

|
|
|
|
|
|
Fig. 481 Samples of the ‘entrance’ and ‘exit’ of a structure
|
|
|
Civil engineering offices are involved with many water
management tasks (see Fig. 482).
|

|

|

|

|
|
01 Water
structuring
|
02 Saving water
|
03 Water supply
and purificatien
|
04 Waste water
management
|
|

|

|

|

|
|
05 Urban
hydrology
|
06 Sewerage
|
07 Re-use of
water
|
08 High tide
management
|
|

|

|

|

|
|
09 Water
management
|
10 Biological
management
|
11 Wetlands
|
12 Water quality
management
|
|

|

|

|

|
|
13 Bottom
clearance
|
14 Law and
organisation
|
15 Groundwater
management
|
16 Natural
purification
|
|
|
|
|
|
Fig. 482 Water managemant tasks in lowlands
|
|
|
|
|
|
For a long time now, maps have existed of The Netherlands showing
the areas governing their own water management (Waterschappen), and their drainage areas
(Fig. 483 above). Overlays show hydrological measure points (Fig. 483 below left) and the supply of surface water (Fig. 483 below right).
|

|
|
RWS (1985)
|
|

|

|
|
|
|
|
Fig. 483 Hydrological maps of Delft and environment
|
|
|
On the first map you can find the names of compartments,
pumping-stations, windmills, sluices, locks, dams, culverts, water pipes.
However, these maps are no longer available in hardcopy anymore by fast
development of GIS in the nineties.
The storage of water in the lower parts of The Netherlands will put
heavy demands on the surface. The 4th National Plan of water
management policy V&W (1998, stressing environment), and its successor ‘Anders omgaan met water’ V&W (2000) (stressing
security) marked a change from the accent on a clean to a secure environment,
as did the 4th National Plan of environmental policy VROM (2001) compared with its predecessors. Several floods in The
Netherlands and elsewhere in Europe have
focused the attention on global warming and water management. The future problems and proposed solutions are summarised in the
figures below. Storage is a central item in reducing the risks for lowlands.
|

|

|
|
|
|
|
Fig. 484 Dutch Policy documents
|
Fig. 485 Strategies: 1 care, 2 store, 3 drain
|
|
|
|
Public sector institutions dealing with infrastructure must spend a lot of money
over a time span, always longer than a budget year. Planned expenses must be properly argued
(transparency) in annual work plans and need the approval of Parliament
(democratic decision making). The approval must be based on a long term policy
(political consistency).
Water related infrastructure facilities are always multi functional; there are always more users and uses, so priorities must be set
after political debates (public disclosure) and approval, and the management must integrate the interests that
exists in society (integrated water management). The public must be informed on developments and criteria (regular
communication with media and NGOs), data must be accessible (preferably for free) reliable and
retrievable(web site). All this has to do with good
governance.
Integrated water management means that attention must be
given to many sectors. Often, first an acceptable vision is needed to start a
firm discussion. But usually a vision alone has no legislative status, it is
just a recommendation (reference is made to ‘Omgaan met Water’ –V&W, 1984- and ‘Plan Ooievaar’ -1986-). More is needed for generating fundamental commitments for the
infrastructure sector. In practice, means are always limited so choices must be
made based on priorities and criteria. Avoiding random and un-controlled diffuse discussions, a strong
target must be set and made visible to all involved parties in both the public
and private sector. Such a well documented target needs political approval in
Parliament, its implementation must be feasible in economic terms of course,
and also both in technical and socio-economic terms.
Yhis meant that Parliament must not only give its approval to a
policy target as such, but also to the finances and the institutional set up
needed for implementation over a longer period of years. Such a period is always
longer than the ruling period of an elected politician in power. So, there is a
need for political consistency to avoid a (sudden) change of
major political targets during the implementation period of infrastructure schemes.
One may guess how many cabinets with different political colour have ruled the
Dutch nation in the period 1953 – 1986, the implementation period of the
Deltaworks. During such a long period there always must one ministry as
implementing agent and an institution as executing agent that is accountable
for the project.
The above pleads for a gradual development of one or more Policy
document(s) with sufficient legislative
status. This cannot be done over night. The way this has been developed in the Netherlands
is elaborated hereafter, see also Fig. 484.
After World War II, in the late forties and fifties the rebuilding of the Dutch nation
took shape. In the late fifties it led to a public awareness that at least some
coordination was needed on spatial planning; it finally led to a first policy document on spatial planning around
1960. By law it was approved that a revision should take place every 10
to 12 years, and that the planning horizon of a policy document was 25
years. For the implementation, annual workplans of the
involved ministries and related public sector organisations needed approval of
Parliament (and –of course- still do). Also the way consistent spatial planning
had to develop at various levels (national, regional, local) was described. And
with additional proper legislation, matters such as disclosure, supervision,
enforcement and management (in the public sector) became organised as well.
New public awareness of problems in the sixties
The country developed further, but due to industrialisation and urbanisation, pollution of surface waters became
manifest. There was a growing public awareness that a new policy paper was
needed on the water management of surface waters. A first
version was adopted in Parliament in 1970, a period in which the second version
of a revised policy paper on spatial planning was also developed. But
because spatial planning and water management were two main responsibilities of
different ministries under politicians of different political parties and the
public sector organisations responsible for execution were still working in a
top-down approach, there was hardly any coordination between the working floors
of the two involved ministries during the preparations of these two policy
papers.
In the late seventies, traffic and transport in the Netherlands
became a real problem. In a period where the working culture in the public
sector changed from a top-down approach to a bottom-up attitude, and the
working floors of separate ministries were allowed to exchange information and
views directly with colleagues from other ministries, a first policy document
on transport developed. First there were some separate draft versions for different
sub-sectors and modes (rail-road-water-pipeline-transmission-telecom).
But Parliament forced the three main ministries involved (Economic Affairs,
Public Works, Housing) to prepare a second version in the late eighties on
inter modal and integrated transport issues, to be relevant also to water
management and spatial planning. In the meantime, a third and fourth version of
the policy paper on spatial planning developed, as well as a second and third
version of the policy paper on water management (revision compulsory by law,
every 10 to 12 years). Also in the late eighties, a first policy paper on
nature development and environment got Parliamentary approval, finally leading
to a situation at the beginning of the 21st century where four major
policy papers on infrastructure sub-sectors were aligned and
adopted by parliament: on Spatial Planning, on Water Management, on Transport
and on Environment and Nature (respectively the 5th, 4th,
3rd, and 2nd version, see again Fig. 484).
An important lesson learned from the development as described is the
fact that altogether the time for a more effective alignment of the policy
papers could have been shorter from the very beginning if the ministries had accepted
an internal working culture, to be characterised as ‘bottom-up and horizontal
external contacts on the working floor’.
Furthermore it is obvious that when every square inch of land
surface has at least a triple function, and every cubic meter of water multi
purpose function, adequate planning is only possible when integrated policy
plans are adopted by Parliament, and when consistent political support is more
or less guaranteed over many years (at least decades).
And it has been experienced during the numerous public disclosure
meetings throughout the years, in particular during discussions with well informed
NGOs, that the transparency of infrastructure plans and projects is really
crucial. Much time (and money!) would have been saved if, as part of the process
of public disclosure, relevant files and data had been made public and
accessible (web site in recent years) in advance, and if important NGOs had
been consulted at much earlier stages of planning preparations. We all have
noticed the negative image of more recent large scale projects, such as HSL
(High-Speed Line), Betuwelijn (railway), 2nd Maasvlakte (extension of Port of Rotterdam), dike strengthening, 5th runway at Schiphol, etc. One may guess why …….
Today, one may ask how the situation will be after a new revision
(following the law) of all these policy documents shortly. It is expected that
in the near future only one integrated policy document will be issued, dealing
with the complete national infrastructure (wet and dry), nature and
environment, and transport, including budget allocations (see last horizontal
bar and vertical column in Fig. 484). For an efficient implementation and execution, it includes that
further fundamental reform of public sector institutions is unavoidable.
No doubt more independent Agencies will be separated from the public sector (as
has been done recently with Rijkswaterstaat), and that as a whole the present number of civil servants in the
public sector will further decrease due to privatisation schemes and the streamlining
of public sector organisations. Legislation, rules and regulations will further
become adapted and aligned to international standards and developments (EU,
global warming, international waters, CO2 emissions, etc.). Technical and operational tasks will further shift from the
public to the private sector. EU-directives will further develop and determine
the daily management of infrastructure (water directives, bird habitat directives,
etc.).
Water boards are among the
oldest government authorities in the Netherlands. They literally form
the foundation of the whole Dutch system of local government; from time
immemorial they have shouldered the responsibility for water management for the
residents of their area. In polders this mainly involves regulating the water
level. It has always been in the common interest to keep water out and polder
residents have always had to work together. That is what led to the creation of
water boards. Due to mergers, there are 27 water boards in The Netherlands
(2006). Their borders don't coincide with municipal borders.
What is a 'waterboard'?
A water board is a public
body with a special function; it is in charge of the water management of a
certain area. In Holland
there are in total some 27 water boards, in the last hundred years many smaller
water boards have joined, so the number has decreased substantially.
Goals and tasks of waterboards
The general goal of water
boards is water management in the broadest sense of the word. In Holland where half of the
country is located below sea level, this requires special measures. The western
part of the country is for the larger part located below sea level; polders
determine the landscape and water management.
1.
Maintenance, construction and
keeping up the water defense in the form of dikes, dunes, quays and dams.
2.
Management of water level,
water quantity, water quality
3.
Taking care of waterways, roads
as traffic systems
Territories of water boards
are defined on the basis of watersheds, either naturally defined like in the
east or man-made like in the case of polders. Borders quite often cross
provincial and municipal borders
The structure of the water
boards varies, but they all have a general administrative body, an executive
board and a chairperson. The general administrative body consists of people
representing the various categories of stakeholders: landholders, leaseholders,
owners of buildings, companies and, since recently, all the residents as well.
Importance and financial contribution decide how many representatives each
category may delegate. Certain stakeholders (e.g. environmental organisations)
may be given the power to appoint members. The general administrative body
elects the executive board from among its members. The government appoints the
chairperson (Dijkgraaf) for a period of six years. The general administrative
body is elected for a period of four years (as individuals, not party
representatives). Unlike municipal council elections, voters do not usually
have to go to a polling station but can vote by mail or even by telephone.
The city of Delft and also the campus
of Delft University of Technology is located in a landscape that is composed of
polders. The watersystem of these polders is managed and maintained by a water
board that is called 'Delfland Water Board'.
|

|
|
|
|
Fig. 486 Delfland Waterboard
|
|
|
The campus area is located
in two polders (see ).
|

|

|
|
|
|
Fig. 487 The 'Wippolder'
|
|
|
|
|

|

|
|
|
|
Fig. 488 The 'Zuidpolder'
|
|
|
|
Delfland is one of our
country's twenty-seven water authorities. The area in which Delfland operates
is bordered by the North Sea, the Nieuwe
Waterweg and the Berkel en Rodenrijs line, Zoetermeer and Wassenaar. On an area
of 41,000 hectares, about 1.4 million people live and work, and approximately
40,000 businesses are established. This makes the Delfland region one of the
most densily populated and most highly industrialized areas of the Netherlands.
The region is furthermore renowned for its intensive glasshouse horticulture
both in the Westland
area and around Pijnacker.
The three key tasks of
Delfland - maintenance of dikes and dams, water level control, and water
quality control. These are intricately related. The manner in which you
construct and maintain quays, for example, has consequences for the quality of
the water. Delfland always performs its tasks from "a broad view"; taking into account
all possible relevant factors, a form of integrated water management. To
achieve tha, Delfland strives for cooperation with other authorities and
institutions both public and private. A good execution of the key tasks,
cooperation and consideration for natural qualities; these are the three
directives of Delfland's policy. The Water Board thereby does not limit itself
to the struggle against water, but also for water. Because no water means no
life. Water is life!
Maintenance of dikes and dams
The Delfland region is located
far below sea level. And if a dune or dike should collapse, the land behind it
would flood immediately. The consequences of a collapse in the Delfland region
would be felt as far as the Utrechtse Heuvelrug. To limit the danger, Delfland
maintains the sea and river flood defence structures and quays. Safety is, of
course, crucial in the management and maintenance of the dikes and dams. In
addition to safety, the past few years have also seen increasing attention
being devoted to the landscape, nature and recreation.
The main or so-called
primary maintenance of dikes and dams consists of two components: the seawall
and the river flood defence structure. This primary maintenance of dikes and
dams of Delfland must be able to withstand a wind-force and water level which,
on average and statistically speaking, do not occur more than once every 10,000
years.
Water management
Water management involves
the regulation of the water level in streams, lakes, ditches, moats and canals.
This is vital for developments, agricultural businesses, the shipping industry,
nature and recreation. The height at which the water level of an area is set
depends on the use and function of that area. The level in nature reserves and
protected areas, for instance, often fluctuates, while farmers prefer a
relatively low water level to prevent their land from becoming too wet. The
management of water levels is also of great importance for the shipping
industry. If the water level is too low, large ships will run aground; if it is
too high, the vertical clearance under bridges will become insufficient.
Water quality
Delfland ensures an optimum
quality of the surface water in its management region. This key task entails
the purification of wastewater and the limiting of discharges into surface
water wherever possible. After all, clean and pure water is important to
humans, but also to animals and plants. Delfland therefore creates conditions
that lead to a better-optimized habitat for plants, aquatic plants and animals.
This can be done by constructing nature-friendly banks for example, or through
ecological maintenance of waters and quays
The text below is derived from official papers concerning the way spatial
plans have to be checked on their
impact on water management in The Netherlands. From 1 November 2003 onwards the
‘watertoets’ is legally obligatory in
making regional plans, master plans and zoning plans in The Netherlands.
The ‘watertoets’ concerns all waters and
all water management aspects like:
1.
guaranteeing the level of safety;
2.
reducing floods, increasing resilience of water
systems: care, store, drain (see Fig.
485);
3.
sewage: care, store, drain; reducing hydraulic load of sewage
purification installations;
4.
water supply: right quality and quantity at the
right moment; counteract adverse effects of changes in land use on the need for
water;
5.
public health: minimising risks of water related
diseases and plagues, reducing risks of drowning;
6.
counteracting increasing subsidence and reduction
of land use possibilities;
7.
counteracting ground water inconvenience;
8.
surface water quality: achieving and maintaining
good water quality for people and nature
9.
preservation / realisation of proper ground water
quality for man and nature;
10.
counteracting drying out (verdroging): protecting
characteristic ground water depending on ecological values, cultural history
and archaeology;
11.
development and protection of a rich, varied and
natural wet nature.
In any of the plans concerned, a
description of the way the consequences of the plan have been taken into
account (water paragraph) has to be included.
Beyond safety and water inconvenience the
consequences for water quality and drying out have to be mentioned and how the
obligatory water advice of the water manager has been taken into account.
Generally:
1.
elaboration
of roles of different participants;
2.
products:
appointments, water advice and waterparagraph;
3.
spatially
relevant criteria;
4.
the
relationship with the obligartory environmental impact assessment;
5.
the
environmental impact assessment;
6.
compensation:
legislative aspects and examples.
Embedding in procedures:
1.
municipal
procedures: master plans, zoning plans, elaborations, changes and exceptions;
2.
regional
plans, their elaborations and non-legal provincial plans;
3.
environmental
impact assessment procedures for traced out roads;
4.
plans
for broadening roads and provincial roads;
5.
reconstruction,
land use - and ground clearing plans.
In 2007 the Province
of South-Holland
published indications of surface claims for water surface in zoning plans: 8,5% times the paved surface and + 1,5% x the unpaved surface.
The Waterboard Rijnland (around Leiden)
suggested in 2007 keeping 6% of the overall urban area to be water surface. The Waterboard Delfland claims volumes of water per specific surface
according to Fig. 489 . However, these global norms nowadays should be determined according to
the local context.[98]
|
|
m3/ha
|
|
paved surface (housing,
employment, greenhouse areas)
|
325
|
|
unpaved surface
(grassland, nature, leisure)
|
170
|
|
arable land
|
275
|
|
|
|
|
Fig. 489 Standards for water reservoirs inside and
outside the urban area
|
|
|
|
Water is the source of all
life on earth. The distribution of water, however, is quite varied; many
locations have plenty of it while others have very little. Oceans, rivers,
clouds, and rain, all of which contain water, are in a frequent state of change
(surface water evaporates, cloud water precipitates, rainfall infiltrates the
ground, etc.). The circulation and conservation of earth's water is called the
'hydrologic cycle' (see Fig. 351 and Verhallen, 1999).
There are five processes in the hydrologic cycle: condensation, precipitation,
infiltration, runoff, and evapotranspiration. These processes occur simultaneously
and, except for precipitation, continuously. The hydrologic cycle takes place
in the hydrosphere, this is the region containing all the water in the
atmosphere and on the surface of the earth.
What is the problem with water?
Shortage of fresh water
world-wide is already apparent right now but will be even larger in the future.
The world population is still growing, at this moment not all people have
access to good quality fresh water and finally the consumption of fresh water
per person is still increasing.
Water is the most valuable
of our natural resources. It is, however, predicted that an alarming percentage
of major cities are going to be running short of it in the next decade. How
will this rising demand for water be met? In the 2nd International Architecture
Biennale in Rotterdam
(Flood, 2005), the world wide problem of water shortage was the key issue of
the Biennale and its exhibitions.
The systems approach; water and water system
The hydrologic cycle is
based on a systems approach; the cycle is seen as a system. It is important to
realise that this approach is also needed in all planning and design. This
means that for every site the hydrologic cycle has to be defined and quantified
in headlines. For instance in Holland
we have a surplus of rainwater in winter, while we have a shortage in summer
due to higher evaporation and less rainfall. Hydrologists can calculate the
quantities related to the hydrologic cycle at a given site. Of course soil
conditions, topography and ground water table are also important to consider
the impact of the water cycle as a whole.
A dynamic aspect of water management
The hydrologic cycle is a
conceptual model that describes the storage and movement of water between the
different spheres; biosphere, atmosphere, lithosphere, and hydrosphere at a
given site or area. Water on earth can be stored in any one of the following
reservoirs: atmosphere, oceans, lakes, rivers, soils, glaciers, snow fields,
and groundwater. Water moves from one reservoir to another by processes like
evaporation, condensation, precipitation, deposition, runoff, infiltration,
sublimation, transpiration, melting, and groundwater flow.
The planetary water supply
is dominated by the oceans. Approximately 97 % of all the water on earth is in
the oceans. The other 3 % is held as freshwater in glaciers and ice caps,
groundwater, lakes, soil, the atmosphere, and within life. Water is continually
cycled between its various reservoirs. The typical residence times of water in
the major reservoirs is different. On average water is renewed in rivers once
every 16 days. Water in the atmosphere is completely replaced once every 8
days. Slower rates of replacement occur in large lakes, glaciers, ocean bodies
and groundwater. Replacement in these reservoirs can take from hundreds to
thousands of years. Some of these resources (especially groundwater) are being
used by humans at rates that far exceed their renewal times.
The need for water management
It is clear that we need a
certain strategy for water management that is based on the hydrologic cycle in
a certain area. Here we want to work out an example of water management policy
in Holland:
Water Assessment.
The Netherlands is
a highly urbanised delta of which a large part is situated below sea level. The
problem of water management is already an old one, like in other delta
landscapes. In the past decade the country has been faced with extremely high
river discharges which forced thousands of people to evacuate, with flooded
areas caused by extreme rainfall, with groundwater problems in urban areas and
drying out of certain nature reserves. It is widely acknowledged that, to
prevent a further increase of these problems, changes are necessary in water
management as well as in spatial planning. In contrast with what the name may
suggest, Water Assessment (WA) is a process of interaction during spatial
design, rather than a test on water aspects of a completed spatial plan
afterwards.
The objectives of Water Assessment (WA)
The objectives of WA are to
guarantee that water interests are taken into account in spatial and land use
planning, so that negative effects on the water system are prevented or
compensated for elsewhere. This integration of water in spatial planning works
in two ways: a plan is assessed on its implications for the water system and
the restraints that the water system puts on land use are made explicit.
WA is not meant to be a new
procedure, but a process of interaction that is fully integrated into existing
spatial planning procedures. When Environmental Impact Assessment or Strategic
Environmental Assessment (as prescribed by the EU) has to take place as well,
both assessments partly take place parallel and provide each other with
information.
Water Assessment as part of spatial and landuse planning
To ensure the integration
of water aspects into the spatial planning process, ‘Water Assessment’ has been
introduced in 2001. Water Assessment is a process in which water managers are
involved actively in the development of any spatial plan from the earliest
stages on. This instrument has only recently been introduced, but the results
up till now are promising.
The different steps in WA
1.
The initial phase; agreements
on water criteria and co-operation during the planning process. In the initial
phase, which starts as soon as the ideas about the plan start developing, the
spatial planning authority takes the initiative to inform the water authority.
The result of this initial phase is an agreement on the assessment criteria and
the further process to be followed.
2.
The developing phase; water
recommendation In this phase the water authority and the spatial planning
authority work interactively and creatively together on the design of the plan.
In the Water Recommendation - which is a formal advice - the water authority
informs the spatial planning authority on its findings and makes, if necessary,
recommendations for adjustments of the plan.
3.
The decision-making phase;
water paragraph Based on the Water Recommendation the spatial planning
authority makes the necessary final adjustments to the plan.
4.
The reviewing phase; a ‘go!’
for realisation
A qualitative aspect of water
The hydrologic cycle is not
only needed to get insight into the quantitative aspects of water and the water
system, it also forms the basis for the management of water quality. The
earth's water supply remains constant, but man is capable of altering the cycle
of that fixed supply. Population increases, rising living standards, and
industrial and economic growth have place greater demands on our natural
environment. Our activities can create an imbalance in the hydrologic equation
and can affect the quantity and quality of natural water resources available to
current and future generations. Water use by households, industries, and farms
have increased. People demand clean water at reasonable costs, yet the amount
of fresh water is limited and the easily accessible sources have been
developed. As the population increases, so will our need to withdraw more water
from rivers, lakes and aquifers, threatening local resources and future water
supplies. A larger population will not only use more water but will discharge
more wastewater. Domestic, agricultural, and industrial wastes, including the
use of pesticides, herbicides and fertilisers, often overload water supplies
with hazardous chemicals and bacteria. Also, poor irrigation practices raise
soil salinity and evaporation rates. These factors contribute to a reduction in
the availability of potable water, putting even greater pressure on existing
water resources.
Urbanisation
Large cities and urban
sprawl particularly affect local climate and hydrology. Urbanisation is
accompanied by accelerated drainage of water through road drains and city sewer
systems, which even increases the magnitude of urban flood events. This alters
the rates of infiltration, evaporation, and transpiration that would otherwise
occur in a natural setting. The eplenishing of ground water aquifers does not occur
or occurs at a slower rate. Together, these various effects determine the
amount of water in the system and can result in negative consequences for river
watersheds, lake levels, aquifers, and the environment as a whole. How to deal
with our water resources is one of the major problems in the future since the
world population is still growing, the consumption per person is still
increasing and the demand for industrial use of water also increases.
Water resources
On the basis of the
hydrologic cycle you can determine how much water from natural resources you
have available on the basis of natural renewal of the water quality. Renewable
water resources include waters replenished yearly in the process of the water
turnover of the earth. These are mainly runoff from rivers, estimated as the
volume per unit of time (m3/s, km3/year, etc.) and formed
either within a specific region or from external sources, including groundwater
inflow to a river network. This kind of water resource also includes the yearly
renewable upper aquifer groundwater not drained by the river systems. However
it should be noted that, on the global scale, these volumes are not large
compared with the volume of river runoff and are of importance only for
individual specific regions. Another important aspect is to take into account
how much time these processes take.
What we see now on a large
scale is that we renew water resources on the basis of technological means; by
waste water purification and even the production of fresh water from sea water
at an industrial scale. Even though this might technologically be possible, the
cost is extremely high. In ecological sense it takes also lots of energy and
material. So in the long run it is much more efficient to make use of water
resources in a conscious way; to not overuse, to store the rainwater in stead
of pumping it into the sea and to keep the different water qualities apart.
The planning and design on the basis of watersheds
The aspect of
sustainability in landscape planning is addressed in planning and design on the
basis of watersheds. A watershed is the geographic area where all water running
off the land drains to a given stream, river, lake, wetland, coastal water or
other waterbody. Watershed planning and management comprise an approach to
protecting water quality and quantity that focuses on a watershed as a whole.
This is different from the traditional
approach of managing individual wastewater discharges, and is necessary due to
the nature of polluted runoff, which in most watersheds is the biggest
contributor to water pollution. Polluted runoff is caused by a variety of land
use activities, including development, transportation, agriculture and
forestry, and may originate anywhere in the watershed. Watershed planning is
sometimes a difficult subject to define because of all the different ways in
which it has been practised throughout the world is depending on each
watershed's unique characteristics, people, and other factors (Verhallen,
1999).
Landscape planning
In landscape planning not
only the landuse types and their possible pollution is taken into account, also
the storage or infiltration of water for dry periods is part of the problem.
The location of both depending on stream direction of the waterways is crucial;
no polluting landuse upstream! The amount and location of waterstorage depends
on the quantities that are described in the hydrologic cycle.
1.
Inclusiveness and co-ordination
between people involved
2.
Watershed framework and the
hydrologic cycle for the region in question as a basis for the landscape plan
3.
Plan to preserve and/or improve
the quality of life and the environment
4.
Long term planning and
management
5.
Development of a watershed plan
A watershed plan
1.
Characterisation of the
watershed as a physical network (total area, land ownerships, natural
resources, environmental concerns, etc.)
2.
Prioritisation of environmental
concerns (water quality, urban growth, recreation, etc.)
3.
Implementation plan (strategy
for the long run, best management practices, funding opportunities, etc.)
In landscape planning the
approach should always be based the principles of watershed planning. Landscape
planning does take into account more aspects than watershed planning; the
topographical and historical aspects of the site and most important it develops
a strategy for the landscape development in the long run (Simonds, 1961, 1997).
It is not only a static description of aspects of the watershed alone, it looks
ahead on the basis of the principles defined in the watershed plan. In
landscape architecture the work of McHarg (1971) is a good example of a more
comprehensive and integrated approach to landscape planning than watershed
planning alone. Also Clay (1979) gives a series of examples from landscape
architecture in which water plays an important role and the principles of
watershed planning are applied. Note how old these plans are! For Holland, Boekhorst et al.
(1996) give examples of the work of Nico de Jonge in which water plays an
important role at the scale of the Dutch region. We can conclude with the
statement that no sustainability in landscape planning is possible without
taking into account the watershed and the hydrologic cycle.
An integrated approach of water management and spatial planning
The problem of water
management needs a comprehensive scope and approach (Verhallen, 1999). Planning
and design can contribute to that approach in a general approach for design and
water management; the water systems approach as an integrated approach for
landscape design at different levels.
I. Water forms the basis for the understanding and insight into the
landscape as a natural system.
- The start of any project should be the distinction of different
levels of the water system and their spatial form. In all cases you first
define the watershed and drainage pattern. In mountainous areas this is fairly
simple if you have a topographic map with the contour lines. In delta
landscapes like in Holland
you mostly use the polders as the spatial and hydrological units in the
landscape.
- A next step is the global
description of the hydrological cycle in the study area. Rainfall spread over
the year, evaporation and topography help you define the understanding of the
water system in headlines.
II. If you have done the
landscape analysis, you can start to apply the spatial representation of the
program to the existing site. In this phase of spatial organisation of the landuse
there are the following guiding principles as a basis:
- Water runs from high to low; use this in the location of the
different types of landuse
- Organise forms of landuse according to their rate of pollution;
the least polluting in the higher areas, the most polluting downstream.
- In Delta landscapes organise water flows from fresh to salt water
environments
- In the organisation of time, start with a long term strategy and
then work out the short term interventions.
- Another principle is to work from ‘natural’ to ‘artificial’
III. General principles for
the approach of the water management for the 21st century
- Conserve water at the place as much as you can locally
- Store what you can not conserve, locally
- Organise letting in and transport elsewhere of water. Make a
distinction and also a spatial separation of clean and polluted water; do not
mix them!
There are other networks than wet connections, for example the roads (dry connections) we add in this chapter. And they interfere. More kinds of networks
like those of pedestrians, cyclists, public transport, rail and their
characteristics we will elaborate later.
Everybody knows many names of wet and dry connections, regardless of
their function (Fig. 490). They seem to fit nearly logarithmically on a constant difference
of scale multiplying the mesh width each time approximately by 3. That rather
precise scale articulation has practical backgrounds.
|
NETWORK
|
BLUE LEGEND
|
BLACK LEGEND
|
|
density
|
mesh/
exit interval
|
|
NAME
|
nominal width
|
NAME
|
|
km/km2
|
km nominally
|
width 1%
|
|
m
|
|
|
0.002
|
1000
|
ł10000
|
sea
|
|
|
|
0.007
|
300
|
3000
|
lake
|
120
|
continental highway
|
|
0.02
|
100
|
1000
|
stream/pond
|
100
|
national highway
|
|
0.07
|
30
|
300
|
river/waterway
|
80
|
regional highway
|
|
0,2
|
10
|
100
|
brook/canal
|
70
|
local highway
|
|
0.7
|
3
|
30
|
race
|
60
|
urban highway
|
|
2
|
1
|
10
|
watercourse
|
40
|
district road
|
|
7
|
0.3
|
3
|
ditch
|
30
|
main street
|
|
20
|
0.1
|
1
|
small
ditch
|
20
|
street
|
|
70
|
0.03
|
0.3
|
trench
|
10
|
path
|
|
|
|
Fig. 490 Names of networks on the higher levels of scale[99]
|
|
|
However, in reality it is sometimes more, seldom less than 3 and
often the highest and lowest orders are missing. For example clay grounds do not need trenches and sandy grounds start their drainage by brooks. In the same way rural areas do not need streets every 300m. In The
Netherlands they start with roads every 1km as you can check on topographic
maps.
|

|
|
|
|
Fig. 491 The styling of wet connections
|
|
|
|

|
|
|
|
Fig. 492 The styling of dry connections[100]
|
|
|
These neutral names get their time-bound character by changing
function. Dry and wet networks get their contemporary meaning by ‘functional
charge’ in Fig. 493. Their density implicates the level of investment.[101]
|
Nominal mesh
width
|
30m
|
100m
|
300m
|
1km
|
3km
|
10km
|
30km
|
100km
|
|
Density (km/km2)
|
70
|
20
|
7
|
2
|
0.7
|
0.2
|
0.07
|
0.02
|
|
wet connections
|
|
|
|
|
|
|
|
|
|
name
|
trench
|
small flooded
ditch
|
a flooded ditch
|
watercourse
|
race
|
brook
|
river
|
lake
|
|
indicative width
1%
|
|
1m
|
3m
|
10m
|
30m
|
100m
|
300m
|
1000m
|
|
other names
|
|
|
stream
|
stream
|
stream
|
stream
|
|
|
|
|
|
urban canal
|
urban canal
|
urban canal
|
urban canal
|
industrial
canal/waterway
|
canal
|
canal
|
|
functions
|
draining
|
drainage pool (from
polders)
|
|
|
|
Nominal mesh
width
|
30m
|
100m
|
300m
|
1km
|
3km
|
10km
|
30km
|
100km
|
|
dry connections
|
|
|
|
|
|
|
|
|
|
name
|
path
|
street
|
main street
|
road
|
urban highway
|
local highway
|
regional highway
|
national highway
|
|
an exit every
...km
|
10m
|
30m
|
100m
|
300m
|
1km
|
3km
|
10km
|
30km
|
|
indicative width
|
10m
|
20m
|
30m
|
40m
|
60m
|
70m
|
80m
|
100m
|
|
functions
|
pavement
|
opening to a
hamlet
|
neighbourhood
street
|
district road, village road, country road
|
urban highway,
main road
|
urban highway
|
provincial
highway
|
national highway
|
|
|
footpath
|
residential walk
|
walking route
|
cycle route
|
cycle ride
|
|
|
|
|
Duurzaam Veilig (long-term safety)
|
Woonpad, free of
cars
|
Woonstraat,
restricted entry for cars
|
Erftoegangsweg,
sojourn function
|
GebiedsOnsluitingsWeg,
opening to an area
|
Stroomweg,
throughway
|
|
|
|
|
public
|
|
|
|
|
bus
|
express
|
fast bus
|
Interliner
|
|
Nominal mesh
width
|
30m
|
100m
|
300m
|
1km
|
3km
|
10km
|
30km
|
100km
|
|
railway line
|
|
|
|
|
tram
|
lightrail
|
regional
|
national
|
|
a supportive
base
|
|
|
|
|
300m
|
1km
|
3km
|
10km
|
|
functions
|
|
|
|
|
|
the underground/metro
|
local train
|
intercity train, Argus
|
|
|
|
|
|
|
hybrid systems
|
hybrid systems
|
hybrid systems
|
|
|
|
|
Fig.
493 The time-related functional charge of networks
|
|
|
The most efficient enclosure is made by surrounding the enclosed area with
a minimum length of road. As well known, the result is a circle. But in a
continuous network, it is approximated by a hexagonal system.[102] This minimal ratio between periphery and area is demonstrated 3D by
many natural phenomena (cells in a tissue) where preference is given to a minimal ratio
between outer area and inner content.
Soap bubbles
A good example is a cluster
of soap bubbles. A cluster of soap bubbles
forced into a thin layer produces a two-dimensional variant. The bubbles
arrange themselves in polygons with an average of six angles.
However, if one pulls a
thread through them, the nearest bubbles will re-arrange themselves again into
an orthogonal pattern (Fig. 494). Urban developments from
radial to tangential can also be interpreted against this background. The
interlocal connections pull the radial system straight, as it were. The
additional demand for straight connections over a distance longer than that
between two side roads (here called a ‘stretch’) introduces rectangularity.
Every deflection from the
orthogonal system then is less efficient.[103]
|

|

|
|
Hildebrandt and
Tromba (1989)[vvvvvvv]
|
|
|
Fig. 494 The formation of right angles
|
Fig. 495 Length (L) and width (W) of the mesh for a given net density of
(D=2)[104]
|
|
|
|
Marbles in a framework
This can be clarified by
engaging in a thought experiment: Imagine a rectangular framework
with hinged corners that is completely filled with marbles. If one re-shapes
this framework into an ever narrower parallelogram, then there will be space
for fewer and fewer marbles, so, in every case, the rectangular shape proves to
be optimal, in this respect. The only network that could compete with
this, which has lines running from a rectangular grid, is a triangular grid,
but it is immediately clear that it is inferior because of its unfavourable
perifery/area ratio. For instance, the
parallelogram in the thought experiment that became ever more skew, matches an
angle of 60° in an equilateral triangular grid. Apart from the disadvantage
caused by deviating from the right angle, an extra connecting line is needed to
cut the parallelogram into two equilateral triangles.
Mesh width and mesh length
Fig. 495 shows a sequence of relationships between mesh width and length in rectangular meshes with a net density of 2 km per km2 (the same density means the same
investment!).
Length and width of squares
are 2/density. The same density also occurs in a pattern of roads that go infinitely
in one direction every 0.5 km. Thus, when the length and width of the mesh 1/d
= 0.5 km, the ratio between length and width is at its limit.[105] In that case, where the net density is 2 km per km2 there can be no ‘crossroads’ any more.[106] This consideration only applies to an orthogonal system.
In connection with the red and blue legend one can imagine their
superposition as follows:
Urban area is radially crossed or tangentially surrounded by
infrastructure.
By superposition of the higher order over the lower order, the
density of the lower order decreases.[107]
By superposing the wet connections over or under the dry
connections, both networks interfere (interference, see page 3.4.5).
When one lays different (wet and dry) networks over each other, an interference occurs that defines the
number of crossings, and, because of this, the level of investment in civil engineering
constructions (Fig. 497).This can be done in different ways. Separating
instead of bundling them fragments space more. The diversity of interference
has important impacts on ecology and cultural identity.
|

|
|
|
|
Fig. 497 Interference between wet and dry networks.
|
|
|
The position of urban areas with respect to orders of magnitude of
water and roads dictates their character to a large extent. The elongation (stretching) of networks reduces the need for
engineering constructions when their meshes lie in the same direction.[108] If one bundles them
together, this also helps to prevent fragmentation. The aim of the ‘Two network strategy’, on the other hand, is to position water, as a ‘green network’, as far away as possible from the roads (in an alternating manner). However, this has
the effect of increasing fragmentation by roads and watercourses.
Mutually crossings of waterways seldom separate
their courses vertically (Fig. 498) as motorways do (Fig. 499).
|

|

|
|
|
|
|
Fig. 498 Crossing of separated
waterways
|
Fig. 499 Crossings of highways
|
|
|
|
More often their water levels are separated by locks or become inaccessible for
ships by weirs or siphons.
However, crossings between ways and waterways
have to be separated vertically in full function anyhow. And they often occur.
|

|

|
|
|
|
|
Fig. 500 Rivers, canals and
brooks
|
Fig. 501 Superposition races
|
|
|
|
|

|

|
|
|
|
|
Fig. 502
Interference with highways
|
Fig. 503
Interference with highways and railways
|
|
|
|
The same kind and level
|

|

|
|
|
|
|
Fig. 504 R=300m Sojourn area
road crossing for mixed traffic
|
Fig. 505 R=1km Opening up road
(GOW) single lane roundabout – with freely located cycle path and cyclists
having right of way
|
|
|
|
Camillo Sitte already showed T crossings have less conflict points (Fig. 506). Modern roundabouts translate a normal crossing
in 4 T-crossings.[109]
|

|

|
|
|
|
|
Fig.
506 Less conflict points in
T-crossings
|
Fig. 507 An actual roundabout
|
|
|
|
Before roundabouts came into use, attempts were made to design safer
T-crossings on town (R=3km) and district
(R-1km) level.
Town level
|

|

|
|
|
|
|
Fig. 508
Sketch Zoetermeer 1969
|
Fig. 509 Actual situation
|
|
|
|
District level
|

|

|
|
|
|
|
Fig. 510 Sketch for district Driemanspolder-West (Meerzicht)
|
Fig. 511 Actual situation
|
|
|
|
However, gaining safety this way produced faster driving. So
T-crossings did not produce more safety
after all. Moreover, non-perpendicular T-crossings make orientation more
difficult. Roundabouts are safer.
|

|

|
|
|
|
|
Fig. 512 Central guiding – at a crossing R=1km Opening up road (GOW) –
R=300m Sojourn area road
|
Fig. 513 Haarlemmermeer
solution – at a crossing R=3km Throughway – R=1km Opening up road (GOW)
|
|
|
|
Different kind and level
Especially when the canal is a belt canal with a higher level than the other waterways
many complications arise. Extra space is needed for weirs, dikes and sluices,
perhaps even locks and many slopes not useful for building. The slope the city
highway gets from crossing the high belt canal could force to make a tunnel instead of a
bridge. Anyhow, several expensive bridges will be necessary and some of them
will be dropped from the budget, causing traffic dilemmas elsewhere.
|

|
|
|
|
Fig. 514 Neighbourhood
street crossing canal and railroad in Utrecht
|
|
|
The slope behind the bridge in Fig. 514 is not steep enough to get
a tunnel under the railway high enough for busses (2.60m here is too low).
Count your crossings
(costs)
Fig. 515 shows how different dry
and wet networks in different orders cause crossings of different kinds.
|

|
|
|
|
|
Fig. 515 Interference of
dry and wet networks in different orders causing crossings of different kinds
|
|
|
|
Trenches and ditches become drains or (underneath roads) culverts in the urban area, but main ditches (3m wide) and water courses (10m) or even larger waterways have to be
crossed by bridges.
From 6 different kinds of
interfering crossing in Fig. 515, Fig. 516 counts 35 crossings in 5
types.
|
|
residential streets (20m wide)
|
neighbourhood streets (30m wide)
|
district roads
(40m wide)
|
|
main ditches (3m wide)
|
16
|
8
|
4
|
|
water courses (10m wide)
|
|
5
|
2
|
|
|
|
|
|
|
Fig. 516 Five types of
interfering crossings supposed in Fig.
515
|
|
|
|
|
|
And there are superposed
crossings as well.
|
based on pressure
|
or
|
tension
|
|

|

|

|
|
arch bridge (boogbrug)
approach ramp(aanbrug)
thrust (horizontale
druk)
deck (rijvloer)
trussed arch with upper and
lower chord (vakwerkboog boog met boven-
en onderrrand)
abutment (landhoofd)
|
beam bridge (balk- of liggerbrug)
abutment
(landhoofd)
overpass, underpass (bovenkruising, onderdoorgang)
deck (brugdek)
continuous beam (doorgaande
ligger)
pier (pijler)
parapet (leuning)
|
suspension bridge (hangbrug)
anchorage block (ankerblok)
suspension cable (hangkabel)
suspender (hanger)
deck (rijvloer)
center span (middenoverspanning)
tower (toren)
side span (zijoverspanning)
abutment (landhoofd)
|
|

|

|

|
|
trough arch
bridge (boogbrug met
laaggelegen rijvloer)
|
multiple span
beam bridge (balk- of
liggerbrug met meer overspanningen)
|
fan cable stayed bridge (waaiertuibrug)
cable stay anchorage (tuiverankering)
|
|

|

|

|
|
half-through arch bridge (boogbrug met tussengelegen rijvloer)
|
viaduct
|
harp cable
stayed bridge (harptuibrug)
|
|

|

|

|
|
deck arch bridge (boogbrug met
hooggelegen rijvloer)
|
cantilever bridge (kraagliggerbrug, cantileverbrug)
suspended span (zwevend brugdeel)
cantilever span (uitkragende zijoverspanning)
|
transporter bridge (zweefbrug)
trolley (wagen)
platform (platform)
|
|

|

|

|
|
fixed two-hinged three-hinged arch (ingeklemde, tweescharnier~,
driescharnierboog)
|
single-leaf bascule bridge (enkele basculebrug)
counterweight (contragewicht)
|
lift bridge (hefbrug)
guiding tower (heftoren)
lift span (val)
|
|

|

|

|
|
portal bridge (schoorbrug)
portal frame (portaal)
pier (pijler)
|
double-leaf bascule bridge (dubbele
basculebrug)
|
floating bridge (pontonbrug)
manrope (mantouw)
pontoon (ponton)
|
|
|

|

|
|
|
Bailey bridge (baileybrug)
|
swing bridge (draaibrug)
|
|
|
|
Fig. 517
Names of Bridges and their components
|
|
|
These types of bridges could be made of steel, concrete or wood.
Depending on the material they have a different maximum span (Fig. 350).[110] [111] [112] [113]
|
english name
|
dutch name
|
span in m.
|
notes
|
|
|
multiple span beam bridge
|
balk- liggerbrug met meer overspanningen
|
unlimited
|
|
|
|
viaduct
|
viaduct
|
unlimited
|
old-fashioned
|
|
|
ferry bridge
|
pontbrug
|
unlimited
|
|
|
|
suspension bridge
|
hangbrug
|
2000
|
wind-sensitive
|
|
|
fan cable stayed bridge
|
waaiertuibrug
|
1000
|
wind-sensitive
|
|
|
harp cable stayed bridge
|
harptuibrug
|
1000
|
wind-sensitive
|
|
|
cantilever bridge
|
kraagliggerbrug, Gerberligger
|
550
|
|
|
|
arch bridge
|
boogbrug
|
500
|
steel
|
|
|
trough arch bridge
|
boogbrug met laaggelegen rijvloer
|
500
|
? with draw connection
|
|
|
fixed two-hinged three-hinged arch
|
ingeklemde, tweeschanier-, driescharnierboog
|
500
|
? with draw connection
|
|
|
half-through arch bridge
|
boogbrug met tussengelegen rijvloer
|
500
|
?
|
|
|
deck arch bridge
|
boogbrug met hooggelegen rijvloer
|
500
|
?
|
|
|
beam bridge
|
balk- of liggerbrug
|
250
|
steel truss, framework
|
|
|
arch bridge
|
boogbrug
|
200
|
stiffened bars
|
|
|
floating bridge
|
pontonbrug
|
200
|
military
|
movable
|
|
lift bridge
|
hefbrug
|
150
|
old-fashioned
|
movable
|
|
portal bridge
|
schoorbrug
|
150
|
between supports with tube beam
|
|
|
beam bridge
|
balk- of liggerbrug
|
100
|
steel concrete
|
|
|
beam bridge
|
balk- of liggerbrug
|
100
|
concrete tube beam
|
|
|
transporter bridge
|
zweefbrug, transbordeur.
|
100
|
? old fashioned 1895-1920; 2 in europe
left
|
movable
|
|
double-leaf bascule bridge
|
dubbele basculebrug
|
100
|
|
movable
|
|
swing bridge
|
draaibrug
|
60
|
even as aquaduct
|
movable
|
|
arch bridge
|
boogbrug
|
50
|
hout
|
|
|
single-leaf bascule bridge
|
enkele basculebrug
|
50
|
|
movable
|
|
portal bridge
|
schoorbrug
|
40
|
? concrete
|
|
|
beam bridge
|
plaatliggerbrug
|
30
|
or wider with large construction height
|
|
|
beam bridge
|
balk- of liggerbrug
|
30
|
|
|
|
strauszbridge
|
ophaalbrug
|
25
|
|
movable
|
|
beam bridge
|
balk- of liggerbrug
|
20
|
2m wood truss, framework
|
|
|
beam bridge
|
spoorverkeer staal
|
15
|
small construction height
|
|
|
ship bridge
|
schipbrug
|
10
|
? te doesburg
|
movable
|
|
beam bridge
|
balk- of liggerbrug
|
10
|
wood
|
|
|
raft bridge
|
vlotbrug
|
10
|
? floating from under approach ramp
|
movable
|
|
crane bridge
|
kraanbrug
|
10
|
old-fashioned
|
movable
|
|
roll bridge
|
rolbrug
|
8
|
one example 67m
|
movable
|
|
clap bridge
|
klapbrug
|
8
|
without counterweight
|
movable
|
|
|
valbrug
|
5
|
old-fashioned (castles)
|
movable
|
|
|
oorgatbrug
|
1
|
for mast only, old-fashioned (hindeloopen)
|
movable
|
|
Bailey bridge
|
Baileybrug
|
|
military
|
|
|
|
|
fig. 518 Maximum span of
different bridges
|
|
|
|
|
|
|
The construction height
below deck is often limiting factor.
Costs of bridged P.M.
Tunnels
3D crossings need slopes. Fig. 519 shows a highway on 0.1m height without slopes. You have to dig out
the tunnel until –2.9m. By doing so, you
need cycle slopes of more than 80m at both sides.[114] The tunnel construction
extends to 197.13m width. Imagine the problems to keep it dry, imagine the
costs, imagine the problems you raise designing the adjacent neighbourhoods.
|
First calculation
|
|
talud
|
zijberm
|
rijbaan
|
middenberm
|
daglichtschacht
|
middenberm
|
rijbaan
|
zijberm
|
talud
|
|
m hoogte wegdek
|
0,10
|
|
|
|
|
|
|
|
|
|
|
m breedte met taluds
|
24,00
|
0,50
|
2,00
|
7,00
|
1,00
|
3,00
|
1,00
|
7,00
|
2,00
|
0,50
|
|
m
tunnelhoogte
|
2,40
|
|
|
|
|
|
|
|
|
|
|
brugdek
|
0,60
|
|
|
|
|
|
|
|
|
|
|
m totale breedte met 2 normale
fietshellingen
|
197,13
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
Fig. 519 First calculation of slopes in a tunnel for cyclists below a
highway
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 520 shows a highway on 2m with slopes on both sides, totally 43m wide.
The tunnel can be made on –1m, so the slopes meet nearly on 0m making the total
width 44.4m.
|
Second calculation
|
|
talud
|
zijberm
|
rijbaan
|
middenberm
|
daglichtschacht
|
middenberm
|
rijbaan
|
zijberm
|
talud
|
|
m hoogte wegdek
|
2,00
|
|
|
|
|
|
|
|
|
|
|
m breedte met taluds
|
43,00
|
10,00
|
2,00
|
7,00
|
1,00
|
3,00
|
1,00
|
7,00
|
2,00
|
10,00
|
|
m tunnelhoogte
|
2,40
|
|
|
|
|
|
|
|
|
|
|
brugdek
|
0,50
|
|
|
|
|
|
|
|
|
|
|
m totale breedte met
2 normale fietshellingen
|
44,40
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
Fig. 520 Second calculation of
slopes in a tunnel for cyclists below a highway
|
|
|
3.4.7
A
traffic network
A street is more than traffic space. However, this chapter restricts itself to traffic space, like
traffic specialist would do if (s)he had no attention for context. A street is not a
summing up of measures needed for traffic, but is is good to know which
measures are used by specialists. Many measures mentioned here, are no more
than rules of thumb to start with.
Any kind of traffic has characteristic measures.
Design measures are deduced from the
distribution of actual measures (see Fig.
521).
Normally the 5% largest measures are left aside for design.
|
|
|
|

|

|
|
|
|
|
Fig. 521 Dispersion of real car
widths in 2004;
95% < 1.80m [115]
|
Fig. 522 Width of parking places in 1980 [116]
|
|
|
|
However, these measures can change in time and occasionally not
apply. So, you need margins. For example, in Fig. 522 the parking space for a car is much wider than the width of an
average car, because at parking places people have to step in and out at both
sides. Moreover, taking the largest turning circle of cars you need space to
turn in, not only in width, but also in length. So, a street with cross parking should be wider than the 95
percentile of car lengths (5m).
That is why car parking requires a quarter of
pavement in the urban surface.
|

|

|
|
|
|
|
Fig. 523 1.20m for a pedestrian
|
Fig. 524 2.40m for a parked car
|
|
|
|
In The Netherlands normal paving-stones used on side walks are an
unit of measure easy for reference if you are walking on the street or taking
photographs (0.30x0.30m). From Fig. 523 you can learn a kerb is half a tile wide and for
walking you need at least two tiles
if you don’t have luggage. From Fig. 524 you can learn that the parking spaces of our Faculty are 2.40m
wide.
In a residential street occasionally you need space
for larger vehicles like moving vans, ambulances, vans of police, fire brigade or service vehicles, often necessary in residential areas.
Pedestrians carrying luggage or pushing
baby buggies need 1.5x more space than without such loads as shown in Fig. 525.
|
|
|

|

|

|

|
|
|
|
|
|
|
Pedestrian
50 + 2 x 5 @
60 cm[117]
|
Cyclist
75 + 2 x 15 @
100 cm[118]
|
Car 30 km/h
200 + 2
x 15 @
230 cm[119]
|
Bus 50 km/h
255 +2 x 25@
300 cm[120]
|
|
|
|
|
|
|
Fig.
525 Primary profile spaces
needed
|
|
|
|
|
|
A usual residential street gives way to two loaded pedestrians
walking both ways (for instance one with luggage and one with a baby buggy
passing each other, say 2m paved surface with 6 tiles of 0.30m + a 0.15m kerb +
0.05m margin) as sidewalks. On the roadway two vans should be able to
drive both ways with a margin because they swing a little when they move (say
6m). If you draw sidewalks at both sides the pavement will count 2+6+2=10m. That is
easy to remember for residential streets without parking places (as in
Fig. 522). With parking places and gardens it could be =20m (Fig. 526), but we do not yet take them into account. We will do that at page
265 and further.[121]
|

|
|
|
|
Fig. 526 A residential street
(2.5 + 2 + 2.5 + 6 + 2.5 + 2 + 2.5 = 20m)
|
|
|
However, you do not need that width of pavement all along the road.
Cars can wait when they see someone approaching from the other side. Pavement
can locally be narrower (for example 1+3+1=5m), slowing down the cars or just wider (for example
3+6+3=12m) to make more speed or to give children and pedestrians more space on
the sidewalks. A roadway of 6m width, has two ‘lanes’ for both directions. You can remove one locally. You can halve the
sidewalks locally as well, but do not remove at one side one of them
unnecessarily, otherwise pedestrians have to cross the road. If you do not have
to give way to large cars or speeds higher than 30km/h the lane can get the
minimum width of 2.30m. For even lower velocities without large vehicles the
pavement is suitable for mixed use with pedestrians, say 1.90+0.60@2.50m.
For higher design velocities you should take more margin for swinging. For normal cars at 30km/h you need 2.25m per lane, and 0.30m extra
is no luxury. But at 50km/h you need 2.75m per lane, and at 70km/h 3.25m. Along walls or obstacles,
drivers keep even more distance (obstacle fright) to prevent damage.
Drivers also keep distance to cars ahead. The higher the velocity, the more distance they will keep. Above 30km/h that growing
distance even decreases the capacity of the road (Fig. 527)![122]
That means, to keep the same capacity you need more lanes.
|

|
|
|
|
Fig. 527 A higher speed decreases
the capacity of the road
|
|
|
As you can see, roads designed for more than 2 000 cars per
hour in one direction (that is approximately 20 000 per day[123]) need at least more than
one lane per direction.[124]
Moreover, at 50km/h you have to give separate way to cyclists along the road and at 70km/h
at crossings as well if you accept the
Dutch appointments ‘Duurzaam Veilig” (see Fig. 573).
If you leave your home to go for a ride, you start on a ‘residential
street’ (some 20m wide) via a larger
‘neighbourhood road’ (say 30m) reaching an even
larger ‘district road’ (say 40m) and so on.
On the average every third road of each level you can make a turn to
a road of a higher level (see Fig. 528, do not take it too serious, it is a rule of thumb). The question arises at
which mutual absolute distance you have to draw them in urban design. To keep
it simple, we take 30m for the smallest residential paths, 100m for residential
streets, 300m for neighbourhood roads, and 1000m for district roads (Fig. 528).
|

|
|
|
|
Fig. 528 Four orders in a network
hierarchy
|
|
|
Public pavement for traffic and parking is
expensive. It has to be paid by lots a municipality can sell, surrounded by
that public space (municipal land development). The housing allotments below, include a substantial
area of expensive parking spaces as well. They are made by the computer
programme Standaardverkaveling.exe. Starting points are:
- centre lines of
surrounding roads on a multiple of 30m (preliminary main grid);
- roadways everywhere 6m wide, not needed everywhere,
but including a reservation for wider roads of higher level in the network
elsewhere;
- parking standard everywhere more than 1 parking place per
dwelling along the road, starting at least 5m from road corners, only
drawn along roads North and South (indicated as ‘N’ and ‘S’) in the drawing of
the urban island (an urban ensemble completely surrounded
by roads);
- sidewalks seldom smaller than 2m wide;
- no front gardens yet;
- dwellings 5x10m, 2 floors high with roof timbers of
3m on lots of 100m2 housing 2.25 inhabitants in rows not exceeding 40m to
avoid extra dilatation;
- path around the back 1m wide;
- green areas are drawn
East and South filling up the main 30m grid. They show the space saved by
design operations, but can be used to enlarge the lots for sale as well,
diminishing public space (pavement + green).
These starting points can be changed easily in Standaardverkaveling.exe.
However, for the time being they are kept constant below to study the change in
allotment performance by design transformations.
|

|

|
|
Fig. 529 30x30m
|
Fig. 530 30x60m W-E mirroring
|
|
|
|
|
The picture shows an urban island with three houses with gardens
surrounded by sidewalks and streets. North and South of the island there are
parking lots for 2 cars each. The allotment is mirrored at the other side of
the street.
The smallest urban island taken in consideration here has a grid
measure of 30x30m. The consequence of small urban
islands is an excessive surface of public pavement (here 76%!), leaving relatively little for
sale (here maximally 22%) paying for that public space.[125]
|
The effect of a first design transformation, W-E mirroring,
elongates the urban island reducing public pavement (here into 67%). The gained surface produces
a green margin of 9m drawn East and 2.50m drawn South. Now,
at that length, one side with parking places is enough to reach more than 1 parking place
per dwelling.
The shadow of the N side is best suitable for parking. Now, W and
E roads are used for entrance to houses at both sides and back gardens get more privacy. The lots for sale
differentiate in morning~ and evening sun lovers.
|
|
|
|
In Fig. 530 greenery is drawn East to get an idea
of road profiles and crossings without greenery in the
corner left below in the drawing, where circles are drawn with a radius of 10
and 30m. For children in the afternoon and in the summer evening green area can
better be designed in the West as well to have sunny playgrounds. That does not
change the counted figures left and below of the drawing.
|

|

|
|
Fig. 531 60x30m N-S Turning and
multiplying
|
Fig. 532 60x30m N-S mirroring
|
|
N-S turning and repeating gives both blocks South gardens. Now,
the short sides of the urban island are used for parking, forcing cross-parking to reach >1 parking places per dwelling.
The path round the back is enlarged at the expense of sidewalks to give proper front access to the Southern
block.
|
N-S mirroring introduces North gardens, drawn longer here to
get a partly sunny view on the N garden still. It differentiates the lots for
sale in size and suggests a different dwelling type for sun lovers with south
gardens and artistic life style with Northern light rooms like studios.
|
|
|
|
|

|

|
|
Fig. 533 60x30m elongating
|
Fig. 534 60x60m mirroring
|
|
To reach the same capacity of Fig.
532 by one sided elongating avoids the path round the back utilizing the
side walk, giving back a proper size to the sidewalks N and S. East gardens are suitable for people who like morning sun
in the garden and in the sleeping room. Pavement is still 66%.
|
Mirroring gives evening people a chance as well and both gardens
more privacy. It differentiates use and plantation. The enlargement of the
urban island again reduces the amount of pavement, now into 52% in favour of
the margins possibly used as green area: 9m East and 5m South.
|
|
|
|
|

|

|
|
Fig. 535 60x30m L-shape
|
Fig. 536
60x60m U-shape
|
|
Introducing perpendicular blocks provides streetcorners with front entrances in 2 directions. That
gives the beginning of an urban look and safety by private control of public space on both roads involved. To
improve that effect design solutions for corners, not implemented here,
would be nice. Such solutions will struggle with smaller or no gardens in the
corner.
|
Mirroring the L-shape produces U-shaped allotments with one open
side, here avoiding North gardens. It has the same
advantages as previous mirroring transformations, in this case reducing
pavement from 66% in Fig. 535 into 52% and introducing
green margins of 9m East and 5m South. S gardens go 0.5m around the back now, giving space
for ivy-covered side façades avoiding grafitti.
|
|

|

|
|
Fig. 537 90x60m Closing
|
Fig. 538 Elongating and adapting 100x60m
|
|
Closing the urban island with front entrances on every surrounding
street produces a usual allotment type of 90m length, leaving a 9m green
margin East to fill the urban grid of multiples by 30m. Limiting parking
places to N and S urges cross parking at both sides to have more than 1 parking
place per dwelling leaving little space for sidewalks.[126]
|
N-S elongating to 100m is easy by adding 2 houses West and
East. However, the shortage of parking places then forces parking at all
sides. By giving up cross parking N and S, there is space for 6 extra houses
in total. The reduction of pavement is 2% only, but the number of parking
places is 1.4 per dwelling. This time the green margin is distributed W and E
to make trees possible.
|
In Fig.
538 we leave the starting points of page 265 behind and start to look at a higher level. On that level new
spaces for mobility are needed. By the way, the elongated blocks of Fig. 538 exceed 40m and need an extra dilatation, which is expensive.
If we multiply the module (M) of Fig. 538 (100x60m) 5 times E-W and 3 times N-S (Fig. 539) we reach the mesh width (300mx300m) for neighbourhood
roads (30m width of pavement[127]) mentioned at page 265. We now have 15 modules together surrounded by larger neighbourhood
roads needing extra space.
Traffic production
These ‘neighbourhood islands’ we call ‘neighbourhood quarters’, because 4 of them make a neighbourhood.
|

|

|
|
|
|
|
Fig. 539 A neighbourhood, multiplying Fig. 538
|
Fig. 540 Profiles normalised
to 20, 30 and 40m
|
|
|
|
Suppose every urban island contains some 75 people going
out 4 times a day of which 3 by car. Suppose 1/3 of the car trips the driver is accompanied by
a passenger, 1 trip is done by walking or cycling. So, a block produces
75x2x2@300 car movements per day, because they are not only going out, they
are coming back as well. That normally means 30 car movements per hour per island. Let them use two
of four streets around the block. So, a residential street has some 15 car
movements per hour and much more in peak hours. And there are visitors as well.[128]
Space for facilities
The neighbourhood of Fig. 539 does not only need extra space for pavement of neighbourhood roads,
but also for neighbourhood facilities like green, water, a school,
shops and offices. Moreover, it has to accommodate facilities of higher level
like district roads (40m wide). They produce car movements as well, but in the
same time they make part of the modules involved unsuitable as residential
area. Moreover, not all modules will reach 56 dwellings per ha or a floor space
ratio (FSI) of 68% reached in Fig. 538, because many lots are larger than 100m2. Suppose there
are 1000 inhabitants per neighbourhood, it produces 1000x2x2@4000 car movements per day using half of the neighbourhood roads
available. So, a neighbourhood road has some 2000 car movements
per day or 200 per hour and much more in peak hours.[129] And there are visitors as
well.
Going on like that we can make a table with approximate measures (in
reality they will vary around that measure) for any type of road in a hierarchy
(Fig. 541, do not take it too serious: it is a rule of thumb).
|
Class
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
residential path
|
residential street
|
neighbourhood road
|
district road
|
urban highway
|
highway
|
regional highway
|
metropolitan highway
|
|
|
directly served area
|
estate
|
ensemble
|
neigh-bourhood
|
district
|
town
|
conur-bation
|
region
|
metropoli-tan
region
|
|
m radius | mesh | crossing distance
|
30
|
100
|
300
|
1000
|
3000
|
10000
|
30000
|
30000
|
|
directly served inhabitants
|
10
|
100
|
1000
|
10000
|
100000
|
1000000
|
3000000
|
10000000
|
|
number of dwelling
layers
|
1
|
2
|
3
|
4
|
6
|
7
|
8
|
10
|
|
Profile
|
|
|
|
|
|
|
|
|
|
Left half until median strip
|
|
|
|
|
|
|
|
|
|
profile key
|
m facade height
|
2,75
|
5,50
|
8,25
|
11,00
|
16,50
|
19,25
|
22,00
|
27,50
|
|
m private use
|
1,00
|
2,50
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m sidewalk
|
0,50
|
2,00
|
4,00
|
3,00
|
3,00
|
3,00
|
3,00
|
3,00
|
|
|
|
|
|
|
|
|
|
|
|
|
m cycle track1
|
|
|
2,00
|
2,00
|
3,00
|
3,00
|
3,00
|
3,00
|
|
|
|
|
|
3,50
|
1,00
|
1,50
|
|
1,75
|
|
|
|
m park1
|
2,50
|
2,50
|
2,50
|
2,50
|
2,50
|
2,50
|
2,50
|
2,50
|
|
m parallel road
|
|
|
|
3,00
|
3,00
|
3,00
|
3,00
|
3,00
|
|
|
m park2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,00
|
3,00
|
3,00
|
3,00
|
4,50
|
|
m cycle track 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,00
|
3,00
|
3,00
|
3,00
|
4,00
|
|
m hard shoulder
|
|
|
|
|
2,50
|
2,50
|
2,50
|
2,00
|
|
|
m lanes
|
1,00
|
3,00
|
3,00
|
3,50
|
6,50
|
13,00
|
16,25
|
26,00
|
|
m park 3
|
|
|
|
|
|
|
|
|
|
m median strip
|
|
|
|
2,00
|
4,00
|
4,00
|
4,00
|
4,00
|
|
Right half from median strip mirrored
|
5,00
|
10,00
|
15,00
|
19,00
|
28,00
|
33,00
|
38,00
|
48,00
|
|
|
|
m
total
|
10,00
|
20,00
|
30,00
|
40,00
|
60,00
|
70,00
|
80,00
|
100,00
|
|
|
|
m
pavement
|
8,0
|
15,0
|
23,0
|
28,0
|
41,0
|
54,0
|
60,5
|
79,0
|
|
Physical infrastructure
|
|
|
|
|
|
|
|
|
|
m width between facades
|
10
|
20
|
30
|
40
|
60
|
70
|
80
|
100
|
|
km/hour design velocity
|
10
|
30
|
50
|
70
|
90
|
110
|
130
|
150
|
|
m minimum lane width
|
1,75
|
2,25
|
2,75
|
3,25
|
3,25
|
3,25
|
3,25
|
3,25
|
|
|
|
number of lanes
|
1
|
2
|
2
|
2
|
4
|
8
|
10
|
16
|
|
Capacity (possible use)
|
|
|
|
|
|
|
|
|
|
vehicles/h capacity per
lane
|
500
|
1000
|
1500
|
2000
|
2000
|
2000
|
2000
|
2000
|
|
vehicles/hour capacity
|
500
|
2000
|
3000
|
4000
|
8000
|
16000
|
20000
|
32000
|
|
vehicles/24 hour
capacity
|
5000
|
20000
|
30000
|
40000
|
80000
|
160000
|
200000
|
320000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Use | Intensity
|
|
|
|
|
|
|
|
|
|
residential
|
|
|
|
|
|
|
|
|
|
directly served
inhabitants
|
10
|
100
|
1000
|
10000
|
100000
|
1000000
|
3000000
|
10000000
|
|
car
rides/inhabitant/day
|
2,00
|
2,00
|
2,00
|
1,00
|
0,20
|
0,10
|
0,05
|
0,02
|
|
%surrounding
infrastructure used
|
50%
|
50%
|
50%
|
50%
|
50%
|
50%
|
50%
|
50%
|
|
light vehicles/24 hour
intensity
|
20
|
200
|
2000
|
10000
|
20000
|
100000
|
150000
|
200000
|
|
|
|
cargo
|
|
|
|
|
|
|
|
|
|
kg cargo/inhabitant per
day
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
|
|
|
kg cargo/vehicle
|
10
|
100
|
1000
|
1000
|
1000
|
1000
|
1000
|
1000
|
|
cargo vehicles/24 hour
intensity
|
2
|
2
|
2
|
20
|
200
|
2000
|
6000
|
20000
|
|
|
|
service
|
|
|
|
|
|
|
|
|
|
service
visit/inhabitant/day
|
0,01
|
0,01
|
0,01
|
0,02
|
0,01
|
0,00
|
0,00
|
0,00
|
|
|
|
service vehicles/24
hour intensity
|
0,20
|
2,00
|
20
|
400
|
2000
|
2000
|
6000
|
20000
|
|
|
|
total
|
|
|
|
|
|
|
|
|
|
vehicles/24 hour
intensity
|
22
|
204
|
2022
|
10420
|
22200
|
104000
|
162000
|
240000
|
|
vehicles/hour intensity
|
2
|
20
|
202
|
1042
|
2220
|
10400
|
16200
|
24000
|
|
vehicles/hour peak
intensity
|
|
|
|
|
|
|
|
|
|
% use by car =
intensity/capacity
|
0,4%
|
1,0%
|
7%
|
26%
|
28%
|
65%
|
81%
|
75%
|
|
|
|
|
|
|
|
|
|
|
|
dB(A)
noise on façade
|
66
|
59
|
62
|
74
|
80
|
84
|
90
|
96
|
|
% devaluation
houseprice by noisewwwwwwww
|
10%
|
5%
|
7%
|
22%
|
34%
|
40%
|
48%
|
54%
|
|
|
|
Fig. 541 Approximate
characteristics of a road hierarchy as a model
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
All assumptions of Fig. 541 are arbitrary and can be changed in the similar spreadsheet
‘hierarchy.xls’. This spreadsheet draws the
adapted profiles as well. The text below explains the concepts.
Spatial measures
In Fig. 541 ‘m radius’ is a nominal measure (read 300m and think ‘something between 100m
and 1000m’ or ‘neighbourhood’, with a diameter of approximately 600m) for the
area involved. It applies the mesh width of the theoretical network as well,
the distance between crossings of roads of the same level (turn distance). ‘Directly served
inhabitants’ is as elastic as the nominal radius (read 1000
inhabitants and think ‘something between 100 and 10 000 inhabitants’).
The ‘Profile key’ gives a possible division of half the profile
including the median strip, summarised without the median
strip, supposing the other half is mirrored. So, the total distance between
façades is two times half the profile.
Traffic measures
The ‘km/hour design velocity’ shows which speed of cars is supposed
determining the ‘minimum lane width’ of the lanes out of which the roadway is
composed. The ‘number of lanes’ is determined by the expected number of
cars per hour calculated in line ‘vehicles/hour intensity’.
The actual intensity is something else than the capacity, the maximum
possible intensity without congestion, for example in peak hours. They are
compared in the % use by car = intensity/capacity. Above a certain
percentage (60%?) you can expect congestion in peak hours.
Non-residential traffic
The light vehicles/24 hour intensity is calculated here by multiplying
the number of directly served inhabitants, the number of car rides/inhabitant
per day and the %surrounding infrastructure used as we did already on page 269 for residential and
neighbourhood roads. There we mentioned already ‘there
are visitors as well’. In the neighbourhood it does not count so much, but on
roads of higher level cargo transport and service traffic is more important.
How to count that? Here we
found a very simple, but perhaps not very reliable way. We estimate the kg cargo/inhabitant/day and divide it by an estimated kg
cargo/vehicle to get the number of cargo
vehicles/24 hour. In a comparable way the number of service visits/inhabitant per day produces the service
vehicles/24 hour intensity. Summing these lines produces the number of vehicles/24 hour
intensity, which divided by 10 produces, vehicles/hour intensity.
Noise
The dB(A) noise on façade depends on many things like intensity
and distance to the façade. It is a rough estimate, but it determines %
devaluation of house prices by noise.
This chapter started by real measures of cars (Fig. 521), derived models about a hierarchy of roads with different capacity
and intensity (induction from particular into general). We neglected many
aspects of urban context. Now, we have to check how reliable these models are,
knowing that reality always differs (deduction form general into particular).
Deduction into a special
case
A complete survey should take more cases to check the theory. Here
we take one case only and we do not check all assumptions (hypotheses). In Fig. 542 The urban area
around Dordrecht, we find 6 levels of roads. The resolution does not permit to see
residential paths (1). But we see residential
streets (2, white) , neighbourhood
roads (3, yellow), district roads (4, same colour, but somewhat
thicker), urban highways (5, purple), highways (6, red), regional highways (7, red and orange). We have
drawn circles of nominally 3, 1 and 0.3km around parts we nowadays call city, district and neighbourhood.
Deviation of predicted
measures
Let us start with Papendrecht. It has some clear squares of approximately 500x500m neighbourhood
roads while our model states 300x300m. Should we adapt our model?
|

|
|
|
|
Fig. 542 The urban area around Dordrecht
|
|
|
Elsewhere (for example in the central part), there are smaller mesh
widths (sometimes 100m). The model
fits better the average. Moreover, we appointed: “read 300m and say ‘something between 100m and 1000m’ “. So, reality
deviates within the appointed tolerance of the model. If our model fits the
average, we can say: “Papendrecht has a relatively large mesh width for its
neighbourhood roads”.
Do we count the right
hierarchy class?
But perhaps there is more going
on. Do some of the drawn residential streets have neighbourhood road
characteristics? To decide that, we need to enlarge the detail (Fig. 543). No, the map is correct, all
streets with the square of neighbourhood and district roads are approximately
20m wide from façade to façade, perfectly according to what we stated in Fig. 541. The neighbourhood roads fit the prediction to be some 30m wide as
well. However, the district road is not 40m, but 50m wide. There are two
possible reasons.
Spatial context driven
deviations
There is something more to learn
from Fig. 542 after all. We supposed there
would be a district road every 1km, but in Papendrecht we see only one within a radius of 1km
(diameter 2km). However, there is interference with the network of rivers
clarifying why the second one is not realized. A second one here would not have
enough use to legitimate the cost. The river limits its bearing surface. The model supposes
a homogeneous topography while reality is heterogeneous. Nevertheless the
density of district roads is low comparing to the model, so the remaining one
needs more capacity.
Superposition
From Papendrecht we learn also
that a district road appearing in a grid of neighbourhood roads can take over a
neighbourhood function (superposition, we will discuss that in paragraph 3.4.4). That is another reason to
increase its capacity and thereby its width.
|

|

|

|
|
|
|
|
|
Fig. 543 A Papendrecht detail
|
Fig. 544 A central Dordrecht detail
|
Fig. 545 Dordrecht
some 350 years ago
|
|
|
|
|
So, we keep the model for the time being, because it keeps us
attentive on regularities in the existing urban tissue to be applied in urban
design.
The time-dependency of a
model
By the way, Fig. 543 and Fig. 544 illustrate how much surface can be occupied by non residential
functions, as we stated in paragraph 3.4.13. Fig. 545 shows what we call a city changes in time.
Holland’s oldest
city in the 17th century (Dordrecht) and Amsterdam were very large that time but
now we call their surface (R=1km) a district. All other cities in the Atlas of Blaeuyyyyyyyy from 1652 are even smaller. They had a radius
R=300m (walking distance). That is what we now call a
neighbourhood. On Bleaus maps you see closed urban islands everywhere with
closed corners as well. The urban density was much higher than we are used to
nowadays. One of the factors of decreased density is the mobility space we need
for cars and their parking lots. The way the urban islands became open
allotments in the 20th century is described by Castex and Panerai.
What would be the cause?
Fig. 546 and Fig. 547 show two allotments of 100 dwellings ( 225 inhabitants) in rows of
10 on 1.8 ha. So, there are 56
dwellings/ha and FSI= 56% while the floor space
per two storey dwelling is 100m2. From total area 62% surface is for
sale and 38% is public space including 1 parking place per dwelling and roadway
pavement of 3.2m wide.
|

|

|

|
|
|
|
|
|
Fig. 546 100 dwellings along
residential streets with parking in front of the house: 15% pavement, 23%
green area
|
Fig. 547 Reduced pavement by
residential paths, parking at 1 minute walk: 10% pavement, 28% green area
|
Fig. 548 Reduction of street
pavement, increase of green area comparing Fig. 546 and Fig. 547
|
|
|
|
|
However, in Fig. 547 parking is concentrated at the boundaries. People have
to walk 1 minute more than in Fig. 546 to reach their cars,
partly living at residential paths, saving 1/3 of pavement![130] That reduces municipal costs (or ground prices and taxes for private persons) substantially.
By doing so, there is 1/5 more green area (5% green of total area), resulting in a much
greener look without cars. That area could become public green, but it can be
sold as well reducing municipal costs again.
The disadvantage is, you
can not easily come close to your home with luggage, moving vans and other
vehicles. And you can not see your car from your home.
Multiplying a module like Fig. 547 by 8 around a centre,
produces a neighbourhood of 1800 inhabitants, enough for some facilities like a school (1ha black square in Fig. 549 to Fig. 551), playgrounds, some shops
and enterprises or public facilities. By locating parking spaces at the
boundaries of the ensembles, at daytime some residential parking space can be
used by users of the facilities, avoiding extra facility parking space.
|

|

|

|
|
|
|
|
|
Fig. 549 300m central road
|
Fig. 550 1800m peripheral one way road substituting 600m residential
street
|
Fig. 551 900m peripheral road
substituting 300m residential street, central parking
|
|
|
|
|
A central neighbourhood
road costs least pavement, but it divides the neighbourhood and the school in
two parts (Fig. 549). A peripheral road costs much more road length, unless it is part
of a grid used for adjacent neighbourhoods as well. A one way solution (Fig. 550) may half pavement and
barrier effect but causes detours. A one sided peripheral
road leaves the other side open to the field and causes long walking distances.
Concentrated parking on neighbourhood level could mean a 10 minute walk to your
car (Fig. 551).[131]
However, these choices are
often subordinate to the environment, mostly a district grid (Fig. 552).
Multiplying the module from Fig. 549 by 4 (7200 inhabitants)
the surface fits in a 1x1km grid of district roads (40 wide), leaving open a
30m surrounding margin and a centre (Fig. 552) in each district quarter.
That centre can be used for additional district green, facilities or housing
(4ha black square), utilizing concentrated residential parking in day time. The grid permits to leave out
1200 m neighbourhood streets according to the model of Fig. 541, but asks 8x90=720m extra
residential roads to give access to all ensembles.[132]
|

|

|
|
|
|
|
Fig. 552 A small district or
district quarter
|
Fig. 553 Same built-up area optically full or empty
|
|
|
|
Fig. 553 shows the optical
principle of leaving the centre open, applied in Fig. 552 on the level of the
quarter and on the level of its centre: the same surface left (4x6=24) gives a
more spacious effect located in the periphery (6x8-4x6=24 as well:
the ‘Tummers-De Bruin effect’). A positive side-effect is better accessibility
of the built-up area. On an even smaller scale Fig. 552 shows another principle of
central squares: do not make an X-crossing, give access roads along the square
a view on larger buildings (here schools). Berlage designing the Mercator square in Amsterdam called it the ‘turbine principle’.[133] The resulting T-crossings refer to Camillo Sitte as cited before (Fig. 506).
Network types on differrent levels of scale
|

|
|
|
|

|

|

|

|
|
R=1km
|
R=3km
|
R=10km
|
R=0.1-10km
|
|
Fig. 554 Shortest path
|
Fig. 555 Radial
|
Fig. 556 Stops
|
Fig. 557 Grid
|
|
for pedestrians
|
for the market
|
for public transport
|
for car(riages)
|
Neighbourhoods in a distict
The hexagonal grid proposed by the American traffic expert
Buchanan (1963) [134], Fig. 558 produces neighbourhoods of
R=300m suitable in a grid of R=1000m.
|

|
|
|
|
Fig. 558 The Buchanan grid put in a square 2x2km
|
|
|
Ensembles in a conurbarion
Fig. 552 showed how a regular grid
of district roads and neighbour streets solves some problems arising if you
look at an isolated neighbourhood only.[135] The most famous urban grid is built in Barcelona, designed by Cerdŕ (1867). He designed urban islands in squares of normally 133x133m (Fig. 559).[136]
A neighbourhood contained
25 islands (R=300m!) with bevelled 16m high building blocks making small
squares on all crossings (Fig. 560).[137] The islands are enclosed by residential streets of 20m wide (Fig. 561), neighbourhoods by
neighbourhood roads of 30m wide (Fig. 562), district (4
neighbourhoods) by district roads of 50m wide with a large median strip (Fig. 563).[138] A district had a market.
|
 
|
|
Fig.
559 Plan Cerdŕ (1867) in Barcelona
|
Fig.
560 A Cerdŕ neighbourhood
|
|

|

|

|
|
|
|
|
|
Fig. 561 Streets 20m
|
Fig. 562 Roads 30m
|
Fig. 563 District roads 50m wide
|
|
|
|
|
|
|
|
|
District quarters
Bach (2006) sums up the advantages of a rectangular
grid concerning its flexibility giving next
examples here all drawn at the same scale in a square of 1x1km.[139]
|

|

|

|
|
Fig. 564 Making a short cut as
long as the detour
|
Fig. 565 Easily providing a
centre
|
Fig. 566 Easily diminishing
access crossings
|
|

|

|

|
|
Fig. 567 Easily introducing one
way traffic
|
Fig. 568 Easily giving way to
other networks like cycle paths
|
Fig. 569 Easily accepting ongoing
green lines
|
|

|

|

|
|
Fig. 570 Exceptions draw special
attention
|
Fig. 571 Easy hinging to other
grids
|
Fig.
572 Crooked grids keep easy orientation
|
|

|
|
|
|
Fig.
573 A grid makes appointments like Dutch Duurzaam Veilig easy to explain
|
|
|
|
|
As discussed on page 250 by thought experiment, the
content of a crooked grid (Fig. 572) is less than a
rectangular one, while its outline is the same as the square. So, it will cost
more pavement per inhabitant..
According to Fig. 494 by increasing through
traffic towns changed from a spider into a fly in the regional web.[140]
|

|

|
|
|
|
|
Fig. 574 Utrecht from radials in 1866 …
|
Fig. 575 via tangents
into a large-scale grid
|
|
|
|
Regional networks within a national
network
|

|

|
|
R=30km
|
R=100km
|
|
Fig. 576 Regional networks
|
Fig. 577 National networks
|
|
|
|
National networks within an
international context
|

|

|
|
R=300km
|
R=1000km
|
|
Fig. 578 Fluvial networks
|
Fig. 579 Continental networks
|
|
|
|
The pedestrian is the basal connector of urban life and all
other kinds of its traffic. Not taking care for the pedestrian fragments the
residential area, the neighbourhood, the district and the town. It increases
casualties promoting the car and these processes
strengthen each other. So, care for the pedestrian is the core of urban design.
That (p)art of urban design is discussed thoroughly by Bach (2006).[141] So, in this chapter we only summarize some highlights from his
work. The cycle increases the velocity reached by human power in flat
countries, extending what we call slow traffic, elongating its tracks.
|

|

|
|
R=300m
|
R=300m
|
|
Fig. 580 Reichow: car first
|
Fig. 581 Runcorn: pedestrian first
|
|
|
|
|

|

|
|
|
|
|
Fig. 582 Cars dividing a
neighbourhood
|
Fig. 583 Traffic calming
|
|
|
|
Cyclists and pedestrians take the shortest way.
So, they introduce radial
lines and new crossings in car oriented grids that
force detours.[142]
|

|
|
|
|
Fig. 584 Radial with a minimum of
crossings
|
|
|
Busses
At the beginning of the
twentieth century the lay-out strategy of public transport lines by busses
changed from collecting travellers (Fig. 585) into connecting travellers (Fig. 586).[143]
|

|
|
|
|
|
Fig. 585 Collecting travellers
|
Fig. 586 Connecting travellers
|
|
|
|
Bus stations
There are two principally
different types of bus stations: island type (Fig. 587) and herringbone type (Fig. 588).
|

|

|
|
|
|
|
Fig.
587 An island type of central bus station
|
Fig.
588 A herringbone type of central bus station
|
|
|
|
Bus stops
|

|
|
|
|
Fig. 589 Bachs (2006) bus stop concerning passengers’
demands
|
|
|
|

|

|
|
|
|
|
Fig. 590 An artists’ bus stop
|
Fig. 591 A Curitiba bus stop
|
|
|
|
|
|
bus
|
tram
|
fast tram
|
(semi)metro
|
NS-sprinter
|
|
min.
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
|
km radius served area
|
0.3
|
0.3
|
0.5
|
0.6
|
0.8
|
|
max.
|
0.4
|
0.4
|
0.6
|
0.8
|
1.0
|
|
min.
|
0.3
|
0.3
|
0.4
|
0.7
|
1.5
|
|
km stop distance
|
0.4
|
0.4
|
0.6
|
1.1
|
1.8
|
|
max.
|
0.5
|
0.5
|
0.7
|
1.4
|
2.0
|
|
min.
|
12
|
12
|
18
|
30
|
40
|
|
km/h velocity
|
16
|
16
|
22
|
35
|
45
|
|
max.
|
20
|
20
|
25
|
40
|
50
|
|
min.
|
2
|
2
|
4
|
5
|
7
|
|
km average ride
|
4
|
4
|
7
|
10
|
14
|
|
max.
|
6
|
6
|
10
|
14
|
20
|
|
minutes ride
|
15
|
15
|
20
|
16
|
18
|
|
stops per ride
|
10
|
10
|
13
|
9
|
8
|
|
min.
|
1000
|
1667
|
3333
|
8000
|
13333
|
|
passengers per hour
|
2000
|
3333
|
6667
|
16000
|
26667
|
|
max.
|
3000
|
5000
|
10000
|
24000
|
40000
|
|
passengers per stop
|
200
|
333
|
524
|
1768
|
3457
|
|
|
|
|
|
|
|
|
Fig. 592 Some characteristics of urban public transport[144]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Light rail combines all
velocities.[145]
From Fig. 592 you can draw pictures like
Fig. 593.
|

|
|
|
|
Fig.
593 A metro from Fig. 592with 0.6km radius of
served area around a stop and 1.1km stop distance
|
|
|
Supposed you know the line length of Fig. 593 (for example 10km), you
can calculate the number of stops (9+1) and the km2 served area (10pR2 minus overlaps) of all stops together. Supposed you know the number of served
inhabitants per hectare (100) and the %inhabitants expected to use metro (14%,
see Fig. 592) you can calculate the
number of passengers per day (15144, Fig. 594). That will determine
whether the line is exploitable or not.[146]
|
km line length
|
10
|
|
inh. / dwelling
|
dwellings/ha
|
m2 Floor Space /dwelling
|
%FS (100%·
FSI)
|
|
distance between stops
|
1.1
|
|
|
number of stops (9+1)
|
10
|
|
|
km˛ served area
|
11
|
|
|
inh./ha
|
100
|
for example:
|
2,3
|
43
|
100
|
43%
|
|
number of served inhabitants
|
110195
|
|
|
|
|
|
|
14% passengers per day
|
15144
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 594 Calculating the profit of the metro line from Fig. 593
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|

|
|
|
|
|
Fig. 595 A railway station accessible for cyclists, pedestrians and
busses
|
Fig. 596 A railway station for
cars based on inner and outer turning circles of busses and cars
|
|
|
|
|

|

|
|
|
|
|
Fig. 597 Approaching the railway
station according to Bach (2006)
|
Fig. 598 Approaching the railway
station according to Calthorpe
|
|
|
|
Airports
Seaports
Inland ports
Increasing use of urban
subsoil
Urban development plans are increasingly determined by the urban
subsoil.
Problems and requirements associated with groundwater and load
bearing capacity can be solved technically (see chapter Fout! Verwijzingsbron niet gevonden. Fout!
Verwijzingsbron niet gevonden., page Error!
Bookmark not defined.).
In addition, the installation of cables, ducts and drains requires
more and more space under the built-up area. As a result, ever stricter
requirements have to be met with respect to the relative position of drains,
cables and ducts. And don’t forget underground storage space, for example for
the disposal of glass, paper and other recyclable materials from containers
placed in groups in the city. This often makes it difficult to find or make
underground space, no matter how much we would like to get rid of these ugly
containers by placing them underground.
Additional aboveground
facilities
This chapter does not only take a closer look at on the use of
underground space in urban areas, but also at space for beam transmitters and
other forms of overhead and underground infrastructure.
The branch points and transitions from regional networks to urban networks also play
an important part in urban development. Take for example the transition from
overhead high-voltage transmission lines via transformers to an underground electricity
distribution network. On the other hand a region may have ducts that do not occur in the
urban landscape, yet are important for the city.
Regional ducts
On a regional level, ducts generally have a different effect on the
use of topsoil than in towns, such as large underground water and gas
distribution pipes and underground conveyor pipelines from dock areas to users,
for example oil pipelines to the Ruhr region and Antwerp. On a regional
scale, however, electricity cables that are underground in cities are
aboveground in rural areas, such as the many high-voltage transmission lines
across the Netherlands.
Although the spatial use of ducts on a regional scale means fewer
restrictions on land use in urban areas, careful consideration must be given to
the installation of pipes in the countryside. The ducts and cables in the
transition zones from rural to urban areas restrict urban land use and urban
developments. Consideration must also be given go maintenance of infrastructure
in the country side.
Tunnels
In addition to pipes and ducts, more and more tunnels are being
constructed, such as road tunnels and rail tunnels under
waterways and rail tunnels to preserve the landscape. Examples that illlustrate
the state of art in 2001 are the Rotterdam rail tunnel under the Nieuwe
Waterweg, the Betuwe railway line for goods transport
(under construction), and the high-speed rail link through the “Green
Heart” (also under construction) of the Randstad.
Archaeological artefacts
This chapter elaborates on the different pipelines and their
restrictions and limitations.
The installation of underground drains and ducts obviously involves
much earth moving. As of 2002, statutory investigations must be carried out
into the presence of archaeological artefacts and traces prior to commencement
of building activities. Construction companies have a duty to report and to
conserve archeological finds. The decision to start digging depends on the importance of the
archeological find, as specified under the Malta Convention (1999). This convention has
been implemented in the Nederlandse
monumentenwet (Monuments and Historic
Buildings Act)
An archaeological survey was carried out as a pilot project prior to
the construction of the Betuwe railway line. During the archaeological survey,
important finds were made, from both prehistory and later eras. The finds
included the oldest skeleton ever found of a woman (Treintje) in the Netherlands,
and finds related to fishing such as a prehistoric boat, fishing nets and
fishing gear, as well as Medieval houses and farms.
This chapter does not aim at giving a complete list of all ducts and
cables that occur on a regional scale. The emphasis is on large distribution
networks for gas, electricity and water, as well as telephone networks, data networks, optical fibre networks and pipes to transport raw
materials from harbours to processing
plants including those in Germany
and Belgium.
There are also underground discharge pipes such as sewerage pipes and sewage pressure pipelines. Not all ducts in outlying areas are run underground. High-voltage
transmission lines are a good example of overhead use of cables.
In order to supplement drinking water supplies in the densely populated
western part of the Netherlands,
water from the rivers Rhine and Meuse are
pumped to dune areas through pipes. In the dunes the water is filtered and
purified into drinking water, and distributed to consumers.
All these ducts and cables have their own requirements for
installation which must be met by the surrounding area and the subsoil. This
not only concerns subsoil conditions and groundwater, but also topsoil
conditions related to land use.
Fig. 600 shows the position of cables and ducts in a street profile outside
the built-uparea in accordance with the Nederlands Normalisatie Instituut (Netherlands Standardisation
Institute).
It seems harmless and easy to place obstacles such as ducts and
cables underground whenever possible, and from an aesthetic point of view even
desirable . Furthermore, underground cables and ducts do not have a dividing
and / or barricading effect on the surrounding area as topsoil distribution networks.
Underground installation of cables and ducts, however,
has implications for the land above which is kept open (not developed) for
maintenance and management purposes. In addition, shrubs and trees are not allowed, as deep roots will
affect the ducts and cables. Tree roots, for example, could penetrate sewage
drains, causing blockages or subsidence of the soil. Moreover, ducts, cables
and drains are not easily reachted and dug up in areas covered with trees,
hedges and plants. Depending on the type of cable or duct, a strip of land is
reserved on either side which can vary from 1m to 50m.
Risks and costs
The risk of transported material exploding and a standstill of
underground transport also plays a role in the decision to keep topsoil free
from obstacles.
Sometimes the price tag put on underground pipework is a determining
factor in the decision-making process. Think for example of the laying of
pipework in subsoil with less load-bearing capacity. Many main sewage drains
are supported by piles.
With respect to electricity networks, risk consideration and possible loss of power through conduction
are reasons to choose for overhead transport in the countryside across greater
distances.
In summary, we can state that extensions, maintenance and
management, repairs to cracks and the clearing of blockages in overhead cables
and overground pipes are less costly, and that risks of transport are reduced .
In view of these considerations, pipes and cables are laid in open
areas as much as possible. The
Netherlands Standardization Institute has drawn up standards, the NEN standard for alignment, occupied
space, depth and distance between ducts and cables.
|

|
|
|
|
Fig. 599 NEN 1738
|
|
|
|

|
|

|
|

|
|
W.A. Segeren
and H. Hengeveld (1991) p. 273
|
|
Fig. 600 Position of pipes and cables outside built-up areas
|
|
|
Bundling of pipes not only prevents fragmentation of space and
needless use of space, but also reduces the barricading effect within the area.
It is recommended to check new development sites on existing
underground ducts and cable and their alignment. Information is available from
the provincial authorities.
We assume that there will be no changes to the power supply via
electricity networks in the foreseeable future.
A distinction is made between high-voltage grids with high kilowatt voltages
and low-voltage urban distribution networks (220 V).
High-voltage transmission lines have stress levels of 380 kV, 220
kV, 150 kV and 110 kV.
The mains voltage is driven up as high as possible, as high current
intensity causes heat loss.
After all: power (watt) = current intensity (ampere) X voltage (volt)
High-voltage transmission lines form an overhead distribution
network in the countryside. High voltage is transformed to medium voltage,
usually 10kV, in substations that work as distribution centres for urban and
industrial areas. In residential areas, the medium voltage in the transformer
station is coverted to low voltage (220 V).
High-voltage cables
aboveground
In principle, high-voltage grids are aboveground. Areas under
high-voltage cables must be kept free of obstacles in connection with swing
length of possible break in a cable. This means that building is not allowed
under high-voltage lines in areas exceeding 100m. In other words, a land strip
of 50m on either side of the high voltage lines must be kept free of permanent
obstacles. For further information on the width of a strip of land, see the
relevant NEN standards. High-growing
vegetation is not allowed either; temporary use of land is allowed for
recreational and agricultural purposes and for nature reserves. Apart from the
recreational use of land, such as parks or nature reserves, waterways and roads
may cross the strip of land below the high-voltage transmission line.
Safety measures prohibit construction under high-voltage
transmission lines[T.M.de8] .
People’s health must also be taken into consideration. Health aspects primarily
concern the problems caused the magnetic fields surrounding high-voltage cables.
Another health risk is a higher concentration of copper in areas with
high-voltage cable lines. Further research into health risks is recommended.
High-voltage cables
underground
High-voltage transmission lines are only laid underground if
no other solution can be found. The main reason for overhead construction is
the loss of power underground because the conductor, the oil insulating layer
used as a dielectric, and the earthed cable covering form a condenser, which
has a disruptive effect on the phase and causes energy loss in frequently wet
soil; air is a better insulator.
Interconnected regional
networks
The national electricity network is divided into
interconnected regions, allowing instant deployment of another network in the
event of cuts and peak loads.
The Netherlands
additionally uses electricity from the international European network. For
example, during times of massive use of electricity mainly in winter, it comes
from the Alpine regions (hydroelectric power stations). Conversely, at low-peak
times, the Netherlands
supply electricity to the Alpine regions by pumping up the water to help bring
to level the storage reservoirs in those regions. Coal or gas-powered plants
must always run at a minimum capacity to keep them on stand-by and for
technical reasons. Excess capacity can be used to supply other regions in Europe.
In the Netherlands,
high-voltage transmission lines usually terminate at urban boundaries. Via
substations, distribution substations and transformers, electricity reaches the
meter cupboard in our homes.
|
|
|

|
|
|
|
Fig. 601 The electricity network
|
|
|
Design problems can be considered from two angles:
·
alignment of new high-voltage transmission lines, and of
sites for linking stations and power plants;
·
changes to land use for areas around and under
existing high-voltage lines
Alignments of new pipes must satisfy the abovementioned NEN
standards, and take into account future land use and/or land reservation.
Adjustments over time are made only in exceptional circumstances. Cost is a key
factor in this respect, as are stagnation of transport and possible risks.
Changes to land use obviously involve major adjustments when an
extension of an urban area is concerned. The narrow elongated strips of land
beneath high-voltage lines make it difficult to fit in a new residential area.
In connection with safety and health aspects high-voltage lines
often determine the boundary lines of an urban extension.
·
One possibility is to leave the land under
high-voltage lines unbuilt. Temporary land use may be allocated for
recreational facilities, unorganised sports events etc.
·
A last solution would be to lay the high-voltage
cables underground.
Compared with overhead installation, the costs of placing them underground is
significantly higher. In addition, there will be considerable loss of power and
increased maintenance costs. Although there can be no development on the strip,
it can be allocated for recreational use. Road construction is allowed,
provided that ducts and cables are not “covered” by obstacles. This usually
means that pipework and cables are laid in a public green zone, for the
alignment area needs to be kept open for safety reasons and maintenance work.
·
A final option is the construction of a distribution
substation with transformers, from where underground
pipes form the distribution networks. Bear in mind that when you select a
location for a distribution substation, the switche and compressed air in
transformers make them quite noisy.
The Netherlands
has a national gas network ever since the discovery of
natural gas in exploitable quantities. The network is connected to the natural
gas extraction in Groningen
and the North Sea. One network runs from Groningen
and one from Noord Holland, from the pipeline landfall for extraction in the North Sea. Naturally the two networks are interconnected.
Urban gas used to be produced from coal. This production was connected
to local gas plants and had an urban distribution network. The networks were
interconnected to avert calamities in supply and to provide additional gas at
peak times. Most rural areas were not connected to a natural gas network. People
used bottled gas (butane gas) to cook, while homes were heated with domestic
fuel oil or coal.
Like the electricity network, the natural gas network has a
distribution system. Gas pressure in rural areas is higher than
in towns and cities. In distribution substations at a lower level the gas
pressure of 40 bar in the national network is brought down to 25 bar for house
service pipes.
The rural natural gas distribution network runs entirely
underground. The same restrictions are placed on them as on the national
electricity network with regard to obstacles to facilitate maintenance,
management and safety, think of the risk of explosions underground.
|

|
|
|
|
Fig. 602 The gas network
|
|
|
In other words, strips of land with
underground pipework must be free of obstacles - buildings and high-growing
vegetation. Tree roots can also cause maintenance and connection problems. The
width of the strips is significantly narrower than that of the electricity
network, it is approximately 10-20 metres (see applicable NEN standards).
Due to the water shortage in a number of water extraction areas water is brought from
elsewhere to relieve the shortage in these areas. To supply the western part of
the Netherlands with
drinking-water, large pipes have been laid from the Rhine
to the dunes where the water is infiltrated and purified. There are also water
pipes leading from the Biesbos storage reservoirs to water treatment plants in
urban conurbations, such as Rotterdam
and surroundings. In addition, water extraction areas should also be free of
pollution and polluting activities.
The network of water treatment plants to residential areas has a
comparable branch system with one or more water mains to supply towns and
villages, which branches off at the district and residential levels. To ensure
a more reliable supply of water in districts, the pipes are installed in a ring
structure.
From a design point of view, the maximum space occupied by rural
distribution pipes is at most ten metres, while urban distribution pipes take
up less space. Space usage depends on provincial and local acts.
|
|
|

|
|
|
|
Fig. 603 Drinking-water network
|
|
|
In general, pipes in rural areas are connected to the road network.
Vegetation is not desired in view of maintenance purposes. Furthermore, the
mains can be affected by roots. The
distribution network must be covered by a layer of soil of at least 90 cm,
which has to do with the frost limit. In the Netherlands, the fire brigade uses of drinking water to
extinguish fires.
Wastewater purification plants are usually located in
the country. Contaminated water and wastewater is transported through pressure
pipelines from the urban areas to water treatment plants. These plants usually have a collection and purification function
for a particular region. From the wastewater treatment plants pressure
pipelines run to the sea and the big rivers to discharge the purified
wastewater. In other cases, purified water is immediately discharged into the
storage basin.
Pressure pipelines for sewage water are subject to the same
standards that apply to the use of the space above the pipelines. Pipe
dimensions depend on the amount of sewage water that passes through them. The
option of installing two adjacent narrower drains, in case of reduced
discharging capacity is required due to a change in supply, is underused.
Here too, standards apply to pipe maintenance and the prevention of
pipeline breakage. NEN standards have been drawn up, sometimes
supplemented by local acts.
The space above pressure pipelines is subject to the same design
requirements and restrictions concerning use and vegetation as water pipelines.
A problem is also caused by the weight of the pipes. Appropriate measures must
be taken with respect to soils with less bearing capacity to prevent subsidence
of the pipe system. This explains why many sewage systems supported by piles.
Almost the whole telephone network runs
underground. Special NEN standards apply to
the installation of this network. Per region, the structure of the telephone
network consists of an underground cable running from a house to the central
exchange, and from there to an underground connection with the nodal point.
From the nodal point, a connection is established via beam transmitters to
nodal points in other areas.
In addition to this underground network, there
is also an aboveground network of beam transmitters. These beam transmitters are placed on tall
buildings while the transmission paths must be kept free from high-rise.
Current developments in mobile telephone and other
connection technologies will certainly influence the spatial use of beam
transmitters. A network of lower-scale beam transmitters, masts and receivers
has also been developed for the mobile telephone market. Research has shown
that this development might be pose health problems.
Developments in telephone satellite connections are bound
to play a prominent role in the future.
|
|
|

|
|
|
|
Fig. 604 Telephone network
|
|
|
In the Netherlands, physical space is also
used for transmitting radio and television signals via
transmission masts which transmit signals to receivers or aerials. Obstacles
can cause interference or distortion.
|

|
|
|
|
Fig. 605 Central antenna installation
|
|
|
In urban areas, cable networks transmit
these signals. The increased use of satellite connections will also result in
changes to spatial use.
Underground and overhead pipes are increasingly used to transport
raw materials from ports, sea ports or
otherwise, to industrial areas. Depending on the materials to be transported, a
number of restrictions must be observed. These cover safety measures for the
surrounding area, such as buildings and roads, and for transport, for example
pressure in gaseous substances, solution / dilution in liquids, suspension etc.
Certain substances also carry a risk of explosion: berthing can give static
electricity, causing devastating fires,
such as oil fires in sea ports.
In general, these pipes connect the port, the unloading quay, to processing plants. Although such pipes
primarily run overhead, we can also identify many, and longer, underground
pipes, connecting the port of Rotterdam to the Ruhr region and the port of Antwerp for instance. Materials,
transported through these underground pipes range from oil products to
semi-finished products for industry; this includes secret military pipelines.
The Netherlands
has also installed pipes from oil platforms in the North
Sea to transport oil products such as gas and oil to processing
plants and distribution companies.
In the Netherlands,
approximately 20% of raw materials are transported underground through
pipelines.
In terms of design, the use of space and corresponding restrictions
governing pipelines is comparable to those of the gas network. However, depending on the material to be transported,
additional measures are required.
With regard to the load bearing capacity of the soil, arrangements
must be made to prevent sagging and fractures .
Tunnels constitute a special group of
pipes.
The best-known tunnels in the Netherlands run under waterways,
and are designed for motorised traffic. The oldest tunnel, the Maastunnel in Rotterdam, dates from before the Second World War. Amsterdam
has several urban tunnels below the IJ, which connect new districts such as IJburg and Amsterdam Noord with the town centre.
A recent development is the construction of tunnels for rail
transport. The first one to run beneath a waterway was constructed in Rotterdam, and is a
relatively short tunnel. The Schiphol tunnel, which was constructed beneath runways and the airport hall, is
another example of a short tunnel. Both train tunnels have underground stations
which require a number of additional safety measures. More recent plans include
the construction of a tunnel with a railway link for goods transport between Rotterdam and the Ruhr
region, and a tunnel for the high-speed railway link (HSL) below the Groene Hart region. These underground
tunnels cover long distances. In principle, the goods transport railway tunnel
requires no ventilation, provided transport is run automatically. On the other
hand the HSL tunnel will need to be equipped with ventilation and escape
routes.
These tunnels are constructed for a variety of reasons, such as
nature conservation, reduction of noise pollution, fragmentation of the
landscape, visual considerations etc.
Research has to be carried out into the construction of these
tunnels with respect to location and method of construction, and safety of the
load carried, both passengers and raw materials. Think of the fires in the Mont
Blanc tunnel between France and Italy
in 1999 and in 2005, the Tauern tunnel in Austria
(2000) and the Gotthard tunnel in Switzerland (2001).
Underground metro networks are currently being
constructed in Amsterdam and Rotterdam. In general, these underground
systems are subject to the same standards as tunnels. Construction under
existing buildings and tunnels in particular will necessitate specific demands
as to construction and use. Metro systems must also have adequate escape routes.
|

|
There are a number of risk factors for tunnels, such as:
· risks
arising from soil conditions
· risks
arising from method and construction
itself and construction material, for example the choice
between one or two separate tunnel tubes with one-way traffic, or one tube
for freight transport and another for carrying passengers, or as in the
Channel Tunnel which uses ‘car trains’ and ‘lorry trains’
· risks
arising from how the tunnel is used (calamities!); the reliability of train, lorries and
cars and the type of products to be carried. Human errors in the construction
and the breaking of traffic rules cannot be ruled out. Management and
maintenance of these tunnelsmust be
carefully monitored.
Needless to say, use of space depends on tunnel size and length.
In principle, few restrictions apply to the use of space above tunnels.
|
|
|
|
Fig. 606 Tunnels
|
|
|
In rural areas, electric cables run overhead. In urban areas in the Netherlands
they disappear under the ground, after high-voltage is transformed to a medium
voltage of 50KV or 10KV. At district
level, voltage is decreased once more via a transformer kiosk to 380V
(industrial voltage) and 220V (domestic voltage). Transformer noise is caused by switching and compressed air.
In urban areas, gas pipe pressure is adjusted to domestic pressure.
This takes place in distribution stations, from where the gas is distributed
across a town via underground pipes.
Drinking water is distributed across urban areas via underground
pipes.
The sewerage system is treated on page 304, the drainage system on page 304.
The installation of the pipe network of water, gas and sewers has
some restrictions. It is obvious that the curves that the tubes make are
determined by the flexibility of tubes. The sewage network also needs a fall in
order to bring waste from the collecting point to the treatment plant by
pumping or under pressure.
Underground conveyor
pipelines
Underground conveyor pipelines for materials transported
from harbour areas also play a role in urban areas. These pipelines are often
bundled in pipe alleys, for which space has been allocated or reserved through
decisions at national level. On an urban scale, the layout of this space must
meet requirements with regard to safety, accessibility and repair work. In
general, this implies that the pipes are installed in public green strips, or
incorporated in larger park areas.
Underground transport
tunnels
Underground transport tunnels such as metro lines, tram tunnels and car tunnels play an important role in the
use of urban areas. Decisions on transport and construction have a major impact
on the urban area. Similarly, underground parking garages have a major impact
on urban development. Such spaces will need to be designated or combined with
the construction of intensively used buildings, such as shopping centres, large
apartment buildings and offices.
New developments with respect to the construction of underground bus
stations also require space, and will need to be a point of discussion in the planning process. The same applies to
underground distribution centres.
Underground storage
On an urban scale, decisions are also taken with regard to
small-scale underground material storage, such as the storage of glass, paper and other small-scale domestic
waste that is not collected from
door-to-door. This underground storage takes up considerable space, and is
often difficult to fit in into existing street profiles because of the high
density of underground cables, pipes, wires and drains. The containers must be safely reached by
users and therefor not be installed just anywhere in a neighbourhood.
The installation of cables
and pipes as part of preparing a site for habitation
With regard to planning and constrcution of a new district, the
installation of cables and pipes forms part of the process of preparing a site
for habitation. The advantage is that it minimises the risk of damage caused by
other construction activities. Building activities, however, require their own
power and water supply. In effect, this means that these pipes and cables are
installed in combination with provisional supply roads prior to the
commencement of building activities.
The overall installation of cables and pipes in a new district
usually begins with the construction of sewage systems and district heating
pipes.
Immediately after completion of the buildings, house service pipes
for sewerage and district heating are installed, and the other cables and pipes
including connections put in place. Approximately 6 to 13 weeks prior to
completion, local municipalities give permission for the installation of
underground infrastructures. Negotiations have meanwhile taken place concerning
the municipal green areas, as pipes and cables are often located in green
zones.
A public works time schedule
of the city of Rotterdam
An example of a public works time schedule of the city of Rotterdam is given below:
·
No later than 4˝ months before completion, plans
for making the site “liveable” have to be available. These include
specifications and shop drawings of the utilities, which are made once the
schemes with the road layout and the green areas are completed.
·
Public tendering. This procedure can take up to 6
to 8 weeks.
·
Branch pipes are installed 8 weeks before
completion.
·
Seven weeks before completion, drinking water
pipework is installed for legal tests, which may take some time.
·
Six to five weeks before completion, the utilities
companies can connect up gas pipes and electric cables. Installation of house
service connections can commence. Provisional supply pipes are converted to fit
the distribution network, or removed.
·
Four weeks before completion, house service
connections are completed, and telephone and central antenna systems installed.
·
The remaining 2 to 3 weeks are used to install
discharges and fnish paving.
Distribution networks are planned for urban and rural areas. They
include water, gas and electricity, as well as cable networks for telephone and
audio-visual appliances including computer networks. Computer cables are
primarily fibre optic cables rather than the well-known copper wires.
The choice of district heating with corresponding pipes system is
also made on this scale and fitted into the street profile. And don’t forget the wastewater discharge system and the sewage system either as a stand-alone or as
a combined system.
|

|
|
|
|
Fig. 607 District heating network
|
|
|
Use of space and relative
position
The use of space, the relative position and safety measures of the
different networks are laid down in municipal regulations. Although these may differ in terms of depth and pipe combination,
the regulations share similar principles. These regulations are available from
the local municipality, as are maps containing information on the position of
cables and pipes in the street profiles at district and urban level. Most
municipalities can provide these maps in digital format. Please note however,
that these maps do not specify all pipes, and that not all pipes are
registered. This is particularly the case for computer network cables. These have often been installed without specific permits, and are
therefore not included on plan drawings. This means most cables cannot be
marked out. These networks are usually found at a shallow depth (± 30cm below
ground level). Fig. 608 shows the location of cables and pipes in a street profile of a
built-up area as laid down by NEN standards.
Empty shells and
combinations
A number of municipalities have begun constructing networks using
empty cables (‘empty shells’), which will be use at a future date. The advantage of this method
is that streets need not be broken up to install new networks. Another recent
development concerns the combination of networks. In Amsterdam, for example, experiments are
carried out by installing fibre optic cables in sewage drains.
In addition, areas with high groundwater levels need a drainage
system. This system consists of canals and ponds, and a closed underground
drainage system to collect surplus groundwater, storing it for shorter or
longer periods before discharging it.
|

|
|
|
|
Fig. 609 Location of cables and pipes in built-up areas
|
|
|
In the first place, drainage systems are meant to make development
sites suitable for the construction of houses, and the maintenance of the area
in question, i.e. site management. Drainage systems are designed to keep the
ground-water table in built-up areas at an appropriate level to prevent water
problems with foundations, cellars and pipes, on the other hand these systems
are designed to discharge surplus ground water. The groundwater table is
artificially kept at a predetermined level by the municipality using pumping
stations.
Depth
The minimal depth ranges from several decimetres to approximately 80
cm below ground level. Depth is depends on existing foundations and pipes.
Areas with wooden piles foundations, for example, have a different groudwater
level: wooden piles must remain submerged to
avoid rotting. In later urban areas, however, concrete and other types of
foundation are used which are not affected by groundwater. The climate also
determines the depth of the groundwater level in urban areas. In times of
severe frost, ground saturated with water can freeze to approx. 80 cm below
ground level. The frozen ground can cause pipes to burst and
holes in the asphalt road surface. In the Netherlands, pipes are therefore
always installed deeper than 80 cm below ground level.
Rainwater
In addition to discharging surplus groundwater, the drainage system
also serves to discharge rain water and melt water which
permeates the subsoil. In built-up areas, excess water from hardened surfaces,
such as streets, squares and roofs, is usually discharged via a sewerage
system.
Underground, the drainage network consists of drainage pipes. Above
ground, it made up of ditches, canals and ponds: the ‘open water system’. Water
from drainage pipes is either discharged into open waters in urban areas, or
transported to drainage pools, also open water, in rural areas. Surplus water
in canals, waterways and ponds is discharged from the urban area to open
water outside the urban area. From
there, the water is carried to the rivers and/or the sea via a system of
waterways and pumping stations.
|
|
|

|
|
|
|
Fig. 610 Urban drainage
|
|
|
SewageUp until the early 20th century, domestic and industrial
wastewater was usually discharged
directly into surface water. In the 19th century, some towns already
used various pipe systems to carry this wastewater to areas outside the
built-up areas. During the course of the 20th century, sewage
systems were gradually installed throughout the Netherlands. Isolated farms and
houses are not always connected to the sewage system. Nevertheless, these homes must satisfy wastewater purification
requirements. This can be achieved by using individual water treatment methods.
Sewage systems are designed to discharge domestic water, industrial
water and excess rain water safely in such a way that it does not cause health
hazards. Contaminated water is purified until residual water can be safely
discharged into open water.
Autarkic systems
This chapter does not discuss buildings that use their own sewage
systems to re-use grey water, i.e. rainwater
to water the garden, clean buildings, wash cars, take a shower and the
re-use of shower water to flush the toilet, or their own purification systems
such as helophyte filters. These systems are highlighted in the context of “eco-friendly building”.
The common sewage system
A sewage system consists of a collecting
system, a transport system and a purification system. Particularly the
collecting system is relevant to this book. This system consists of pipes,
which collect wastewater and rain water and carry it to the sewage purification
or discharge points.
|
|
|


|
|
|
|
Fig. 611 Building block sewage
|
|
|
We can distinguish the following sewage systems:
·
combined systems including various improvements
·
separate sewerage systems, stand-alone systems including various improved
versions.
The combined system
In this system, all domestic and industrial water and precipitation,
rain water and melt water of snow and hail are discharged via one combined
system of pipes. Domestic connections and road connections are sloped towards
the collecting sewer system. The collecting sewage pipe is drained by a
pumping-station. Sewage water is transported to the sewage purification through
a pressure pipeline.
The big variable of this system is the amount of rainwater present. Large quantities of
rainwater will dilute the dirty sewage water, resulting in less efficient
purification. The management of the sewage purification plant is extremely
complex due to strong fluctuations in sewage water concentrations and discharge
peaks. The dimensions of the system is a problem. It is not economic to adjust
the diameter of the pipes to the biggest quantity of sewage water that needs to
be discharged. To minimize rainwater dilution and peaks in discharge additional
storage capacity is made that is directly connected to the system. If this
additional storage proves insufficient, overflows have been constructed to open
water. Contaminated water, rainwater and sewage sludge are then discharged onto
the surface water. It is obvious that this is the weakest link in the entire
process. The overflow system is constructed in such a way,
that the predetermined number of annual overflows is not exceeded. In the Netherlands,
this has been calculated to be 3 to 10 overflows per year. Approximately 10%
of rainwater is carried to surface water via overflows. This system is not the
most hygienic or efficient. This is why research has been conducted into
possible improvements, which resulted in a new system: a separate sewage system.
|
|
|

|
|
|
|
Fig. 612 Sewage systems
|
|
|
In this system, rainwater
is separated from domestic and industrial wastewater and discharged via its own
pipe system. Rainwater is always discharged directly onto surface water via
street inlets. Surface water is also affected by street contamination in the
form of spillages of petrol, oil, tyre abrasion and litter. In addition to
preventing this kind of pollution, discharge points are equipped with filters
to collect contaminants. The system combines drainage systems installed in the
past for site development with rainwater discharge systems.
Domestic and industrial wastewater sewerage is pumped by a sewage
pumping-station and discharge to a sewage purification plant. The size of the
pipes depends on the average of the highest wastewater production in 24 hours.
Drainage of rainwater is a different story. The amount of annual
precipitation, in the form of rain, hail and snow, shows considerable
fluctuation. Furthermore, part of the precipitation enters the drainage system,
part flows into the soil, part disappears through evapotranspiration and part
is absorbed by plants. Water that enters the system is collected and usually
discharged directly onto open water in built-up areas. Water from the streets
is collected via street inlets and enters the open water via a mud trap and
sometimes via helophyte filters.
The choice of a system
It will be clear that the choice of a system depends on the scale of
the district or village. The unity of a system is a prerequisite; a system is
only as efficient as its weakest link.
The sewage system is determined by discharge
quantities. These can be divided into dry weather discharge or wastewater and
rain water discharge or precipitation discharge. The required capacity per hour
for dry weather discharge is approx. a tenth of the daily discharg. The average
water use per person is between 100 l
and 150 l. Rain water discharge, on the other hand, fluctutates as the
amount of precipitation is spread unevenly over the
year. Reduction in precipation water is caused by evapotranspiration, the use
of water by plants and water absorption. This reduction of the original amount
of precipitation water is known as the runoff coefficient (see Fig. 613).
|
Building type
|
|
Content/ha .
|
Runoff coefficient
|
|
Old city centre
|
high-density building
|
350
|
0.8
|
|
Newer districts
|
closed buildings
|
250
|
0.6
|
|
|
open buildings
|
150
|
0.4
|
|
with parks and gardens
|
100
|
0.25
|
|
Undeveloped, unhardened terrains
|
|
|
0.15
|
|
Parks
|
|
|
0.5
|
|
|
|
|
|
|
Nature of the surface
|
|
|
0.9
|
|
Closed road surface
|
|
|
0.9
|
|
Clinker paving
|
|
|
0.8
|
|
Metalled roads
|
|
|
0.45
|
|
Gravel and cinder roads
|
|
|
0.25
|
|
|
|
|
Fig. 613 Runoff coefficient
|
|
|
Design considerations for
installing cables and pipes in built-up areas.
Built-up areas are intersected with rural cables and pipes. On this
level in particular, various NEN standards and municipal regulations
apply, causing complications, as the limitations from rural networks stand in
the way of urban developments in rural areas. This involves many hours of
negotiation to find a solution.
Every municipality in the Netherlands has its own
regulations, which can be inspected by municipal services. By and large, they
are all identical; regulations prescribe relative position and depth in
relation to the surface level. Differences are primarily manifest in
load-bearing capacity of soils, and ground-water tables and groundwater levels
tolerated by each individual municipality.
|

|
|
|
|
Fig. 614 Standard layout of cables and pipes in Rotterdam, Zevenkamp
|
|
|
|

|
|
|
|
Fig. 615 Standard layout of cables and pipes Den Haag
|
Negotiations on the position
of cables, pipes and drains
Negotiations on the position of cables, pipes and drains in a new
district, and corresponding municipal services, take place during the design
phase of an urban development plan. During these negotiations, alternatives and
potential design solutions are drawn up, taking into account technical aspects
of installation such as house service connections, pipe radius, junctions of
pipes, cables and drains, relative influence of the different pipes, and their
position in the street profile.
The position in the street profile determines the management and
maintenance of pipes and drains, as well as street furnishings such as trees,
lighting and street furniture.
Aboveground facilities
The design of public grounds largely depends on the underground
infrastructure. “Eco parks” and underground dustbins such as glass and paper containers are
often installed near squares or, in any case, near open urban spaces. These
should not be obstructed by cables and pipes.
The implementation plan regarding cables, pipes and drains for new
districts is laid down at an early stage in the land registry, and is available
from the local municipality.
Land registry plans
In principle, the position of all cables and pipes in existing
developed areas is laid down in land registry plans, which can be consulted in
the event of changes in town planning. The municipality of Rotterdam is a good example: this
municipality has stored all relevant data on underground networks digitally.
Other municipalities are in an advanced stage in digital processing of data, or
are nearing its completion. Nevertheless, there may still be a few surprises in
store, as not all installed and obsolete cables or pipes have been laid down,
digitally or otherwise. In some cases information may have gone missing. Even
computer network cables are not always registered
because they are temporary or because contractors do not think it necessary to
inform the city council.
Beam transmitters
With the development of a new district urban planners should take
account of beam transmitters that require physical space
in towns, i.e. height and position of the buildings. A building can form an
obstacle for these beam transmitters. Overall beam transmitter systems must be
guaranteed in towns for adequate and profitable transmission. This can cause
problems in existing built-up areas and thus requires the installation of a
more compact network to guarantee adequate transmission range.
Combinations
New developments in the field of distribution networks, i.e. pipes,
cables and wires, will take place to satisfy future demands for fast
communications and connections. For example: a combined system of cable and
wire ducts, or a combined system of sewer pipes and fibre optics cables, currently in an experimental stage in Amsterdam. Ducts are a particularly
interesting option due to the high degree of accessibility of these pipes.
However, the position of these ducts may pose problems: ducts located beneath a
building may give rise to private-law cases regarding access to a building.
Load-bearing capacity of the soil will need to be taken into consideration, if
these ducts are not incorporated into a building. Examples to solve such
problems are the communal trenches for cables and pipes used in England, and cable and pipe tunnels in the Netherlands.
The municipality
of The Hague is currently installing
“empty” pipes through which cables can run
to provide extra capacity for new, innovative applications.
The most recent development for communication uses satelites for
transmission instead of cables.
|

|

|
|
|
|
Fig. 616 Communal trenches for cables and pipes
|
|
|
|

|
|
|
|
Fig. 617 Cable and pipe tunnel
|
|
|
Contents
4.1 Introduction................................................................................................................... 313
4.2 Earth sciences.............................................................................................................. 315
4.2.1.... Geology......................................................................................................................... 315
4.2.2.... Geomorphology.............................................................................................................. 320
4.2.3.... Soil science................................................................................................................... 325
4.2.4.... Chemical compounds...................................................................................................... 334
4.3 Engineering.................................................................................................................... 338
4.3.1.... Earth sciences and the urban landscape (P.M.)................................................................. 338
4.3.2.... Sustainability (P.M.)........................................................................................................ 338
4.3.3.... Preparing a site for development....................................................................................... 338
4.3.4.... Methods for preparing a site............................................................................................. 339
4.3.5.... Urban functions............................................................................................................... 345
4.4 Applications for designers........................................................................................ 348
4.4.1.... Ground and design P.M................................................................................................... 348
4.4.2.... Site analysis P.M........................................................................................................... 348
4.4.3.... Working with slopes P.M................................................................................................. 348
4.4.4.... Historical examples of design........................................................................................... 349
The goals of this chapter on earth, ground and soil are:
·
To make you aware of the
relevance of this knowledge that can give your design approach a 'sense of time
and place'
·
To give you some background in
the scope, viewpoints and approaches in the earth sciences
·
To give you some background and
insight into the possibilities for applying this knowledge in the design
process
|

|

|

|
|
|
|
|
|
Fig. 618 Urban
developement and geology; the Mont Saint - Michel in France. A
small settlement around a monastry built on a rock in front of the coast. The
settlement and the rock form a magnificent ensemble; the church and steeple
enhance architecturally the verticality of the rock amidst the sea water.
Walking to the top, no cars are allowed in the city, you experience the
elevation. Above you have a splendid view or the surroundings.
|
|
|
|
|
In one chapter we cannot give you an introduction to geology, geomorphology
or soil science; just see it as a brief glimpse at the magnificent world behind
the earth sciences that determines and conditions all urban development to a
certain degree. Knowledge and insight into earth sciences can give your design an extra
quality and makes you more stable in the preaching, screaming and expression of
power of the environmental movements all over the world. It provides you with
.firm ground under your feet.
Earth, ground and soil are in most projects the basis on which all
construction and planting takes place. First comes the plotting of the contours
of the plan by surveyors, then the preparing of the site for construction and .finally
the construction and planting itself. Although in earth sciences the material
is the most visible, the dominant aspect of earth sciences is time and process.
In geology, time and process are the basis for understanding the material. In
the context of design and planning, geology plays a role on a large scale and
long term; the landscape development in the long run is for a
large part determined by the geological conditions of the site. Geomorphology is most important on the structural
level, whereas soil science more on the level of element and object.
Holland is very young in geological sense; especially in the west where the
dynamic coast landscape still changes. Note that in Holland there is no
natural rock; all rock, stone you see is imported. For foreign students; do learn about
the geology of your country, it will give you many insights and knowledge you
can use in planning and design. Geology is not so visible in the daily
environment but is of tremendous importance because of the long term effect and
processes.
Terminology and knowledge
domains
Earth, ground and soil are related terms but are different in many
ways.
·
Earth[147] is both abstract (the
earth) and concrete: what you can put your hands in… Earth is also referring to
the planet we are living on.
·
Ground[148] is concrete in the sense
that it is always substance matter; material
·
Rock[149] is a natural aggregate of
minerals; it is always hard material. You cannot transform it by hand like
ground and earth.
·
Soil[150] is the upper layer of the
earth, where plants grow. Is abstract; a man-made classi.cation on the basis of
explicit criteria. Soil is determining land use for a large part, especially on
the regional scale, for agriculture, horticulture and forestry.
The central problem of the earth sciences is to understand how our
planet works and how it came to be the way it is. The earth sciences comprise
three different but related knowledge domains: geology, meteorology and
hydrology. In the context of this chapter we take a look at geology and its
subdivisions. The other domains have been described in former chapters. Three
partial knowledge domains are specifically important in the context of urban
design and landscape architecture: geology, geomorphology and soil science. As
an example the figures below give an impression of the geology, geomorphology
and soil map of Holland.
|

|

|

|
|
|
|
|
|
Fig. 619 The
geological map of the Netherlands The main geological developments that have
formed the country are visible; the river system with the delta, the coastal
area with the dunes, the peat in the west and north east and the marine
sediments in the north and south west
|
Fig. 620 The
geomorphological map of the Netherlands
Here the glacial influences are clearly visible in the centre of the country.
Glacial ridges formed by the ice.
|
Fig. 621 The
soil map of the Netherlands
In the west you can see the peat and marine clays. In the east the sandy
soils and in also here the river landscape can be clearly distinguished.
|
|
|
|
|
|
  
|
What is geology?
Study of the earth, its forces, materials and
processes[151].
An important part of geology is the study of how earth’s materials,
structures, processes and organisms have changed over time.
Geologists address major societal issues that involve geologic
hazards and disasters, climate variability and change, energy and mineral
resources, ecosystem and human health, and ground-water availability.
|
|
|
|
Fig. 622 R: 10 000km>1000km >1m
|
|
|
Concepts and guiding
principles of geology
Geologists use three main principles, or concepts, to study earth
and its history.
The first concept, called plate tectonics[152], is the theory that the
earth’s surface is made up of separate, rigid plates moving and .oating over
another, less rigid layer of rock. These plates are made up of the continents
and the ocean floor as well as the rigid rock beneath them. Plate tectonics is
useful in the field of geology because it can be used to explain a variety of
geologic processes, including volcanic activity, earthquakes, and mountain
building. The mechanism that drives the earth’s crustal plates is still not
known, but geologists can use plate tectonics to explain most geologic
activity.
The second guiding concept is that many processes that occur on the
earth may be described in terms of recycling: the reuse of the same materials
in cycles, or repeating series of events. The geological cycle and the hydrological cycle are examples.
The third principle is called uniformitarianism[153]. Uniformitarianism states
that the physical and chemical processes that have acted throughout geologic
time are the same processes that are observable today. Because of this,
geologists can use their knowledge of what is happening on the earth right now
to help explain what happened in the past.
Geological time scales;
process and time in geology
Geologists have created a geologic time scale to provide a common vocabulary
for talking about past events. The practice of determining when past geologic
events occurred is called geochronology[154]. The geologic time scale
is generally agreed upon and used by scientists around the world, dividing time
into eons, eras, periods, and epochs.
|

|
|
|
|
Fig. 623
Geological time intervals
|
|
|
These time intervals are not equal in length like the hours in a
day. Instead the time intervals are variable in length. This is because
geologic time is divided using significant events in the history of the earth.
For example, the boundary between the Triassic and Permian is marked by a global
extinction in which a large percentage of earth's plant and animal species were
eliminated.[155]
Another example is the boundary between the Precambrian and the
Paleozoic which is marked by the first appearance of animals with hard parts.
Eons are the largest intervals of geologic
time and are hundreds of millions of years in duration[156]. In the time scale above
you can see the Phanerozoic Eon is the most recent eon and
began more than 500 million years ago[157]. Eons are divided into
smaller time intervals known as eras. In the time scale above you can see that
the Phanerozoic is divided into three eras: Cenozoic, Mesozoic and Paleozoic.[158] Very significant events in
earth's history are used to determine the boundaries of the eras.
Eras are subdivided into periods.
The events that bound the periods are wide-spread in their extent but are not
as significant as those which bound the eras. Finer subdivisions of time are
possible and the periods of the Cenozoic are frequently subdivided into epochs.
Subdivision of periods into epochs can be done only for the most recent portion
of the geologic time scale. This is because older rocks have been buried
deeply, intensely deformed and severely modified by long-term earth processes.
As a result, the history contained within these rocks can not be as clearly
interpreted.
Relative Time
Geologists create a relative time scale using rock sequences and the fossils contained
within these sequences. The scale they create is based on The 'law of
superposition', which states that in a regular series of sedimentary rock strata, or layers, the oldest strata will be at the bottom, and the younger strata
will be on top[159].
The three important cycles
of the earth as a geological system
The essential fact emerging from earth sciences is that the earth
can be viewed as a set of three separate but interconnected cycles:
·
the geological cycle of plate tectonics and
materials,
·
the atmospheric cycle (weather & climate) and
·
the hydrological cycle that describes the water
movement at large.
The geological cycle
The geological cycle governs the formation and
disappearance of solid land. The science of geology contains two central
insights.[160]
The first of these, arrived at in the eighteenth century, is that
the earth is very old and that its history can be read in the rocks on its
surface.
The second insight, gained in the late 1960s, is that the earth has
evolved and continues to do so.
The continents have not always been where they are now, nor have
they always had their present shape and it will also not stay the same in the
future. Instead, the surface of the earth has changed constantly, and the
continents have moved about, sometimes breaking up into pieces, sometimes
coming together again. This view of the earth, called plate tectonics, replaced
the old idea of a static and unchanging planet. The study of the rocks and
their history is the subject of geology, whereas the study of the forces that
drive the activity on the surface is part of the newer field of geophysics.
At the same time that the continents are moving, a smallerscale
geological cycle, involving the formation of rocks and their erosion into
sediments and soil, goes on.
It describes the dynamic transitions through geologic time among the
three main types of rock: igneous, sedimentary and metamorphic rock.
In river deltas and the eruption of volcanoes, new land surface is added to the earth.
At the same time, the inexorable forces of weather and time break down the
mountains.
|

|

|
|
|
|
|
Fig. 624 Plate
tectonics
|
Fig. 625
Formation of rocks
|
|
|
|
The atmospheric cycle
On the stage set by motion of the continents, the atmospheric cycle operates.
|

|
|
|
|
Fig. 626 The
atmospheric cycle
|
|
|
Powered by heat from the sun and the earth’s rotation, winds move
across the surface, carrying weather systems. Rainfall, temperatures, and other
day-to-day aspects of our environment change in response to the prevailing
winds and the jet streams. These weather patterns and their causes are the
subject of the science of meteorology.[161]
Over longer time periods, changes in the earth’s orbit or movement
of the continents alter the patterns followed by the winds and the temperatures
on the earth. Such changes in climate, of which the recurring ice ages are a
good example, have had a profound effect on the development of all life on
earth including people. Understanding long-term climate development is one of
the major research fields in the earth sciences.
|
  
|
The hydrological cycle
Intermediate between the slow, majestic
changes in the continents and the daily changes in the weather operates the
third great cycle — the hydrologic cycle, the cycle of the earth’s water, or
hydrosphere.
Water evaporates from the surface and returns as rain or snow.
Some water is locked up in the polar ice caps, but most resides in the oceans. Perhaps the
most poorly understood part of our planet, the oceans act as a great
reservoir for many natural and artificial R= 100 km surface= 300 km2
substances.
|
|
|
|
Fig. 627
R: 10 000km>100km >1m
|
|
|
Their currents help equalise temperatures on the globe, while at the
same time they spawn the major storm systems that have such an important
effect on human activities.
|

|

|
|
|
|
|
Fig. 628
Currents of the oceans
|
|
|
|
Geological scale; material
and space in geology
In geology we distinguish three main types of rock:
Igneous rocks are formed when molten rock cools, it is found in
three major forms:[162]
·
Granite is the lightest kind, formed
when magma from the earth's mantle rises to the surface. Then cools and
cristallises slowly in the earth's crust. By weathering it produces sand and
clay stemming from its different cristals.
·
Basalt is lava from a volcano that
has been spewed out and cooled on the surface.
·
Olivine is the heaviest kind, and
consequently seldom seen at the surface. Its mining has been proposed as a
solution for global warming, because it is slowly binding CO2.
Sedimentary rocks are formed if weathered or
eroded material is deposited on the bottom of rivers, lakes, seas and oceans.
Over long periods of time this sediment is buried and compressed. Often plant
and animal material is buried along with it and is found as fossils. Coal,
limestone and sandstone are sedimentary rocks.[163]
Metamorphic rocks are formed when rock is
structurally altered through intense heat and pressure. Marble is produced when
limestone is subjected to these stresses.[164]
Space
In order to understand geologic processes and to reconstruct the
geologic past, geologists work at different scales — scales that range from
microscopic to planetary. In order to work at these spatial scales, they use a
number of tools:[165]
·
At the microscopic level,
traditional tools include the petrographic microscope, used to identify minerals and examine rock textures.
·
Some geologic features are very
large, and geologists must create detailed maps to observe them completely.
Geologists use maps to record basic information, to examine trends, and to
understand processes and geologic history. For example, a map may record the
locations of historical earthquakes, helping to identify faults.
·
On a planetary scale,
geologists can map the earth’s surface using data from orbiting satellites.
Geologists also make maps reconstructing a view of the earth at some time in
the past; such maps are called paleo-geographic
maps.
|
  
|
What is geomorphology?
Study of the form of the earth and the forces
that are behind that forms; landforms and processes that shaped them.
Geomorphology seeks to understand landform history and dynamics, and predict
future changes through a combination of field observation, physical
experiment, and numerical modeling. Erosion, sedimentation, formation of
landforms are issues that are studied in geomorphology.[166]
|
|
|
|
Fig. 629
R: 10 000km>100km >1m
|
|
|
Geomorphology is practiced within geology, geodesy, geography, archeology and civil and environmental
engineering.
Concepts, guiding
principles in geomorphology
Geomorphology is based on the systems view of geology and is very
much process oriented at smaller time scales. It distinguishes three key
concepts:[167]
·
Landform; an element of the landscape
that can be observed in its entirety and has consistence of form
·
Landscape; earth surfaces
composed of an assemblage of subjectively defined, lesser surfaces including
its vegetation and artifacts.
·
Geomorphic system; a set of
related landforms and processes, usually defined in terms of a dominant agent
of geomorphic activity (water, gravity, ice, wind, waves, or organisms)
Process and time in
geomorphology
The main geomorphologic processes are:[168]
·
epigenous or exogenous
processes; these processes occur on the earth's surface, such as weathering,
erosion, transport and deposition.
·
hypogenous or endogenous
processes; these processes are influenced by forces in the earth's crust, such
as mountain building, heaving and subsidence, tectonics, volcanism.
·
extraterrestrial processes;
processes, where landforms are created by “alien” influences, such as an
asteroid collision.
Weathering is the disintegration and
decay of earth, rock, soils and their elements through exposure to the atmosphere.
Water plays a key role in weathering. Weathering takes place at the site; there
is no movement involved, in that case we speak of erosion.[169]
|

|

|
|
|
|
|
Fig. 630
Physical weathering
|
Fig. 631
Chemical waethering
|
|
|
|
We distinguish three types of weathering:[170]
·
Physical or mechanical
weathering involves the breakdown of
rocks and soils through direct contact with atmospheric conditions such as
heat, water, ice and pressure. Mechanical weathering is the cause of the
disintegration of rocks. The primary process in mechanical weathering is
abrasion (the process by which clasts
and other particles are reduced in size)[171].
·
Chemical weathering, involves the direct effect of atmospheric chemicals; for example
the disintegration by rain water that contains carbonic acid from the
atmosphere. Oxidation followed by disintegration is caused by rain water containing
oxygen from the air, particularly on ferriferous minerals. Chemical and physical weathering often go hand in hand. For
example, cracks exploited by mechanical weathering will increase the surface
area exposed to chemical action. Furthermore, the chemical action at minerals
in cracks can aid the disintegration process.[172]
·
Biological weathering always involves plants and
living organisms. Lichens and mosses grow on essentially bare rock
surfaces and create a more humid chemical microenvironment. The attachment of
these organisms to the rock surface enhances physical as well as chemical
breakdown of the surface microlayer of the rock. On a larger scale seedlings sprouting
in a crevice and plant roots exert physical pressure as well as providing a
pathway for water and chemical infiltration. Burrowing animals and insects
disturb the soil layer adjacent to the bedrock surface thus further increasing
water and acid infiltration and exposure to oxidation processes.[173]
Most weathering is a combination of three types and takes time.
Nearly all weathering involves water, mostly directly like frost, shattering,
wetting and drying. That is, weathering is climatically driven and thus the
term 'weathering'. Because weather and climate occur at the earth's surface,
the intensity of weathering decreases with depth and most of it occur within
less than a metre of the surface of soil and rock.
Geomorphology in design
For all design projects the topography and form of the land is a
starting point in the beginning of the design process. In Holland it is in most cases relatively easy
to oversee the form of the land because of its flatness. In most other
countries, it is not so easy to come to grips with the form of the land. You
need to analyse and research the contourlines from the topographic map by
making sections, analysing slope characteristics and analyse the water system.
|

|

|
|
|
|
|
Fig. 632 Ridge and Vally signature
|
Fig. 633 Land form in section
|
|
|
|
First some basic principles regarding contour lines. Motloch describes some basis
important principles in analysing contour lines and the relief or elevation.
First of all reading the contourlines on the topographic maps should first of
all give you an idea about valleys and ridges (Fig. 632). Secondly you should make a number of sections to see and
understand the form of the land as a whole. Making sections from the
topographic map is fairly easy and straightforward; see the diagram (Fig. 633) Thirdly, the water system should give you some complementary
information. If you know how the water runs, you get an idea of what the form
of the land is. Even if the water system is changed by man over time, it still
gives you information on the form of the land. You always start with the
natural system on a large scale to see how the overal structure of the land
form is. Then you add the man-made changes and additions like dams in rivers,
new waterways, locks and sluices, reservoirs etc.[174]
Formation of land by rivers
The formation of the land by rivers is an important research
subject in geomorphology. The development of a river as a whole over time is
determined by topography, geological material and climate.[175]
|

|

|
|
|
|
|
Fig.
634 River forms
|
|
|
|
Fig. 634, shows some basis patterns of rivers; they can be easily derived
from a topographic map and give immediately an impression not only about the
structure of the watersystem as such but also about the geology. Secondly you
need these patterns to define the watershed. Thirdly it gives you an idea where
in the riversystem as a whole the area is located; close to the source or close
to the sea.[176]
|

|
|
|
|
|
Fig. 635 Valley forms
|
|
|
|
Also if you take a closer look at the form of the valley by making a
cross section, you can learn about material, landform and formation. Fig. 635 shows some examples of valley forms, there are many more. It is important that you learn to see basic
topographic forms on a regional scale, in this case river valleys.
The IJssel
near Doesburg
Taking a closer look at river formation we can distinguish the
process of erosion and sedimentation, forming meanders (see Fig. 636).
|

|

|
|
|
|
|
Fig. 636 Direction of stream
erosion
|
Fig. 637 The river IJssel near Doesburg
|
|
|
|
Fig. 637 shows a large meander in the river IJssel north of Doesburg. First of all you see on the land the various stages in the
development of the meander; the pattern of blue lines shows the subsequent
steps in development, from west to east. On the lower left you see a man-made
shortcut for river traffic by boat.
The Seine in Paris
Another example of the formation of rivers and river landscapes
reflected in the urban landscape of Paris; the former course of the river Seine
(see Fig. 638) and how that can be read in the present urban pattern (see Fig. 639).
|

|

|
|
|
|
|
Fig. 638 The former course of the
river Seine
|
Fig. 639 Paris now
|
|
|
|
In the subsequent stages of urban development of Paris,
the former course of the Seine is still visible; see the
second extension of the walled city. Also in the name of the quarter 'Le Marais' (The Marsh), that is located in part of this former course of the
river Seine, the lower position of the area
comes back.
Polders
Polders are a special phenomena in the context of geomorphology. It
goes without saying that all polders are man - made. There are three types of
polders:[177]
·
Drained lakes, 'sea bed polders' or in Dutch 'droogmakerijen'
·
Marine sediments along the
coast that are diked (e.g. the Dollard)
·
Diked land in open water like the new IJsselmeer
polders in Holland
In the last decades, in Holland
no new polders are made anymore. Land is created by making of land above
waterlevel. In most cases sand is pumped inside the a ring dike like for
instance the 'Maasvlakte' (a recent part of the Port of
Rotterdam and the new islands being created for IJburg, a new urban extension in the water east of Amsterdam.
In many delta's all over the world, you can find polders, not only
in Holland.
|
  
|
What is soil science?
Soil science is the
study of soil as a natural resource on the surface of the earth including
soil formation, classification and mapping; physical, chemical, biological,
and fertility properties of soils; and these properties in relation to the use
and management of soils. Soil science explores the nature,
properties and use of soil to capture its value and to understand better its
critical role as a foundation of life.[178]
|
|
|
|
Fig. 640
R: 10 000km>10km >1m
|
|
|
People who study soil seek to comprehend fundamental global surface
processes on multiple scales that impact ecosystems functioning and
environmental health. Soil science is the key factor in food production and is a basis for
environmental and natural resource issues such as land use, soil contamination, ground water quality and waste disposal. [179]
Concepts, guiding
principles of soil sciences
Soil science studies the upper layer of the earth (±1.5 m) that
determines the suitability for plant growth and different types of landuse.[180]
Process and time in soil
science
Soils are porous natural bodies composed of inorganic and organic
matter. They form by interaction of the earth's crust with atmospheric and
biological influences. They are dynamic bodies having properties that reflect
the integrated effects of climate (atmosphere) and biotic activity
(microorganisms, insects, worms, burrowing animals, plants, etc.) on the
unconsolidated remnants of rock at the earth's surface (parent material)[181]. These effects are
modified by the topography of the landscape and of course continue to take
place with the passage of time. Soils formed in parent materials over decades,
centuries, or millennia may be lost due to accelerated erosion over a period of
years or a few decades.
Formation of soils is determined by five soil forming factors:[182]
1.
Parent material: The primary material from which the soil is formed. Soil parent
material could be bedrock, organic material, an old soil surface, or a deposit
from water, wind, glaciers, volcanoes, or material moving down a slope.
2.
Climate: Weathering forces such as heat, rain, ice,
snow, wind, sunshine, and other environmental forces, break down parent
material and affect how fast or slow soil formation processes go.
3.
Organisms: All plants and
animals living in or on the soil (including micro-organisms and humans!). The
amount of water and nutrients plants need, affects the way soil forms. The way
humans use soils affects soil formation. Also, animals living in the soil
affect decomposition of waste materials and how soil materials will be moved
around in the soil profile. On the soil surface remains of dead plants and
animals are worked by micro-organisms and eventually become organic matter that is incorporated into the
soil and enriches the soil.[183]
4.
Topography: The location of a
soil on a landscape can affect how the climatic processes impact it. Soils at
the bottom of a hill will get more water than soils on the slopes, and soils on
the slopes that directly face the sun will be drier than soils on slopes that
do not. Also, mineral accumulations, plant nutrients, type of vegetation,
vegetation growth, erosion, and water drainage are dependent on topographic
relief.[184]
5.
Time: All of the above factors
assert themselves over time, often hundreds or thousands of years. Soil
profiles continually change from weakly developed to well developed over time.
Soil formation
|


=

|

|
|
|
|
|
Fig. 641 R: 10 000km>1m
|
Fig.
642 Soil formation
|
|
|
|
Soil formation (see Fig. 642) is the process by which rocks are broken down into progressively
smaller particles and mixed with decaying organic material.[185]
·
(I).Bedrock begins to
disintegrate as it is subjected to freezing-thawing cycles, rain, and other
environmental forces
·
(II)The rock breaks down into
parent material, which in turn breaks into smaller mineral particles.
·
(III).The organisms in an area
contribute to soil formation by facilitating the disintegration process as they
live and adding organic matter to the system when they die. As soil continues
to develop, layers called horizons form. The A horizon, nearest the surface, is usually richer in organic matter, while
the lowest layer, the C horizon, contains more minerals and still looks much like the parent
material.
·
(IV)The soil will eventually
reach a point where it can support a thick cover of vegetation and cycle its
resources effectively. At this stage, the soil may feature a B horizon, where leached minerals collect. Natural processes that occur on
the surface of earth as well as alterations made to earth material over long
periods of time form thousands of different soil types.
Structure of the soil layer as a whole is based on the layers that
are resulting from the process of soil formation:
[186]
0-horizon: leaf litter, organic material;
A-horizon: plough zone, rich in organic matter;
B-horizon: zone of accumulation;
C-horizon: weathering soil, little organic material or life;
R-horizon: unweathered parent material.
|
  
|
Material and space in
soil science
In the scope of this chapter, we can only give you an idea of the
subject. Thus we have taken as example here, three soil types; sand, clay and
peat. We will take a closer look at physical properties, size, form and
chemical composition.
|
|
|
|
Fig. 643 R: 10 000km>1m>0.001mm=1m (clay)
|
|
|
Physical structure
Soil structure and soil mechanics are characterised by
differences in particle size, structure and texture. Physical qualities are determining the way
you can work with different types of ground in construction carrying man-made
structures like roads, buildings but also the characteristics for cultivating
and labouring the land in agriculture. The chemical characteristics are
important for plant growth.
Sand has a 'grainy' structure and
Silicium as the basic element
Clay has a 'sticky, gluey'
structure containing more minerals.
Peat has a soft structure. It can
take up water like a sponge, in that case it expands and gets heavy. Carbon is
the basic element.[187]
Particle size
Soil types are classified according to
particle size:
|
(large rock block
|
|
The smaller soil
fractions can be determined by assessing their settling velocity in water.
The smaller the soil fraction, the slower they settle in water, as their
specific surface is bigger. Sand fractions take approx. 1 minute to settle in
a normal glass of water, while silt fractions takes approx. 12 hours, and
clay fractions even longer.
The surface of the
particles per kg of dry matter is 10 m2 for sand, 100 m2
for silt and 1000 m2 for clay. The size of the surface is relevant
for the absorbing capacity of soil particles of nutrients on the one hand,
and pollution on the other hand.
|
|
small rock block
|
|
|
large stone
|
|
|
small stone)
|
|
|
coarse gravel
|
|
|
fine gravel
|
|
|
coarse sand
|
2000 - 210 m
|
|
fine sand
|
210 - 50
|
|
loam / silt
|
50 - 2
|
|
clay
|
< 2
|
|
|
|
Fig. 644 Fig.
32 Particle sizes
|
|
|
Sand fractions retain hardly any water or
nutrients. Silt fractions retain water reasonably
well (but not nutrients) and clay fractions retain both water and
nutrients, and these are responsible for soil contamination.
Identifying soil fractions
Soil fraction identification is carried
out on the basis of vegetation. For example coltsfoot indicates a high content of soil consisting of
particles smaller than 0.016 mm (16m). By rubbing a quantity of fine grained soil in our palms, we are
left with remnants of that soil in the lines of our hands. Loess in a dry state has a similar consistency to
flour, while sand is easily identifiable. And so on.[188]
|
 
|
|
|
|
Fig. 645 Soil fraction diagram
|
|
|
Ground water saturation
The ground is made up of solid constituents (mineral or organic),
soil particles with interjacent pores. These pores can be saturated with air, air and water, and water.
The term groundwater zone refers to the state of the
water in the ground (pores saturated with water), while capillary fringe refers to pores saturated
with air and water, and capillary water zone to zones filled primarily
with air. This is the pedologic (pedology is soil science)
classification of ground water.[189]
Soil water and ground water
In geology, subterranean water is divided into two groups; water in
unsaturated upper zone – soil water - and water in the underlying
saturated zone – groundwater.[190]
Soil water only partially fills the
voids between the (ground) particles with water, while the other voids are
saturated with air. Soil water corresponds with the capillary fringe and
capillary water zone. The interface between groundwater and the capillary zone
is known as the phreatic level or ground-water table.
Ground water
In general, the term groundwater refers to fresh water, responsible for all biotic processes. The majority of subterranean
water, however, is sea water. In the Netherlands
in particular, this subterranean sea water plays an important role in coastal
areas. It occurs virtually everywhere in the provinces of Holland and Zeeland, and is covered by a layer of fresh ground water. Freshwater has a lower specific gravity than salt water, and as such
“floats “ on the salt water. Seepage is a vertical groundwater flow; upward
movement from the ground water table to the surface under influence of water
pressure. The deep polders of Holland
and Zeeland (4 to 6m below ground level)
contain salt seepage water due to the absence of, or excessively thin layer of,
fresh groundwater due to (surface) water removal.[191]
Soil water
The water contained in the upper soil layer –soil water - can be categorised
according to moisture content. Even without the supply of (rain) water, soil
particles are surrounded by hygroscopically-bound water molecules; an
atmospheric humidity of 0 never occurs in nature. An increase in atmospheric
humidity leads to an increase in the number of molecules, bound hygroscopically
to the soil particles.
Capillary fringe
Under the influence of adhesive forces, soil particles are
surrounded by a layer of water due to the inflow of rain water. As the layers
surrounding the soil particles thicken, the particles begin to bond, while
open, air filled, pores remain. This zone is known as the capillary fringe.
Initially, these pores form a network. However, the increased supply
of water eventually causes all pores to fill up with water, allowing water to
flow freely between the soil particles. This last zone is known as the
groundwater zone. This zone is easily identifiable in the soil. When digging or
drilling a hole, water is accessed at a certain depth, a depth that will
eventually be at a constant distance in relation to the ground level. This
plane is known as the ground-water table or the phreatic level. The distance to the ground level is known as the groundwater level
and is expressed in cm’s below ground level. The groundwater beneath the
ground-water table moves freely.[192]
Capillary zone
The term ‘capillary zone’ is also used in pedology. This zone is found in the upper layers of the profile. This zone
is also saturated with water by capillary or adhesive forces, but it does not
have ground water as its source, nor does it form a connection with ground
water. It remained as gravitational water of the downward seeping water
following a heavy downpour.
Capillary action of the ground.
Water is primarily retained in the ground by capillary forces (see Fig. 646). The capillary action is caused by the affinity between the water
molecules (cohesive force) and the affinity of
soil particles on the adjoining water molecules (adhesive forces). Water placed in a
thin tube in a reservoir with water will rise due to capillary forces. The
level of water rise is determined by the thickness of the tube. When the water
is rising, the adhesive force between the tube and water is greater than the
cohesive force among the water molecules. This phenomenon also occurs in the
ground.
The smaller the particles, the more water is retained. The same
applies to the pores; the smaller the pores, the greater the water level can
rise. In other words, clay ground consisting of minute particles with
intermediate narrow pores will be characterised by a high ‘piezometric level’, compared with sand, which has large particles and pores. This also
implies that clay ground will be less easy to drain than sand ground, as clay
retains water better than sand.[193]
Capillary levels
Based on laboratory tests and field observations using dipsticks,
the following values for capillary piezometric levels above the ground-water
table have been determined.
|
Coarse sand
|
12 - 15 cm
|
|
Intermediate coarse sand
|
40 - 50 cm
|
|
Fine sand
|
90 - 110 cm
|
|
Sandy loam
|
175 - 200 cm
|
|
Loam
|
225 – 250 cm
|
|
|
Due to the capillary action of the ground, the groundwater is pulled
into a spherical shape between two ditches; the water level of the ditch acts
as the lowest point. That is important for the distance between ditches in
agricultural land, since different crops require different groundwater levels
(see …).
|
|
|

|
|
|
|
Fig. 646 Capillary action of the soil
|
|
|
Water-table classes.
Groundwater tables are divided into water-table
classes, where the highest average groundwater level (HMGL) and lowest mean groundwater level (LMGL) is processed. The groundwater level is determined in relation to
the ground level; the depth of the groundwater is representative.[194] The annual natural
fluctuation of the groundwater in the Netherlands is measured in tens of
centimetres. This movement is characterised by rust stains in the otherwise grey to
grey-blue groundmass. This staining is caused by the presence of iron in the
soil.
|
Gt
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
|
LMGL
|
-
|
-
|
Ł40
|
ł40
|
Ł40
|
40-80
|
ł80
|
|
HMGL
|
Ł50
|
50-80
|
80-120
|
80-120
|
ł120
|
ł120
|
ł120
|
|
|
|
Fig. 647 Main subdivision of water-table
classes (groundwater level in cms below ground
level)
|
|
|
Horizontal groundwater flow
Downward g roundwater flows are the result of differences
in groundwater levels in an area. Although the general direction of the
groundwater flow is known, it will need to be determined for local situations.
Flow is dependent on pore space and the size of the pores and, indirectly,
particle size. In addition, soil is not an homogenous entity due to stratification
in sedimentation, causing big fluctuations in permeability across relatively
short distances.
In addition to natural groundwater tables, the Netherlands
also has artificial groundwater tables, which are kept at a predetermined level
through pumping. Pumping also creates groundwater flows towards the pumping
plant.
Vertical groundwater flow
In addition to horizontal groundwater flow, we can also identify a
vertical movement of water in the soil. This is known as effluent seepage (Dutch: kwel), where the water ‘surfaces' from the ground-water, and
infiltration, characterised by ‘downward movement’ of water. The latter process
is a natural phenomenon that occurs under the influence of gravity. This
movement takes place in the profile zone above the ground-water table.
Technically, this is also the profile zone, where water is temporarily stored.
Seepage
Effluent seepage is caused by water pressure
from an elevated area to a low-lying area.
Effluent seepage can occur along hill ridges, when the groundwater level on the hill ridge is higher than the
adjoining areas. This causes a subterranean flow in the direction of the
lower-lying area. Springs are created in areas where the water issues to the
earth’s surface.[195]
Seepage along dykes
A similar phenomenon occurs in areas bordering big rivers, whenever the level of the river water is higher than the
neighbouring polders. Water rises to the earth’s surface along the dykes, when the water level of the rivers is higher than that of the land
behind the dykes. The pressure of the elevated water produces water movement
underneath the (porous) dykes. The seepage water rises to the surface along the
dyke. This explains why ditches are constructed alongside dykes to collect and
discharge water.
Seepage along the sea
This situation can also occur in the west of the Netherlands, as
polders are drained at a greater depth than storage basins and, for that
matter, big rivers and the sea. The effluent seepage in this area can be
saltwater, freshwater or brackish water, depending on the source of the water
from the storage basin or the water pressure from the salt groundwater. Seepage
water from the storage basin rises to the earth’s surface near the dyke.
Brackish and salt seepage water originating from the
brackish/saltwater bell in the subgrade of the west of the Netherlands
rises to the earth’s surface in the lowest sections of the polder, where the
freshwater layer has thinned as a result of drainage activities, causing salt
water to rise to the earth’s surface by pressure in the saltwater bell. This
phenomenon gives rise to the opinion that in the long term agriculture in Holland and Zeeland can
not survive unless it changes its products.
|

|
|
|
|
Fig. 648 Potential seepage areas
|
|
|
|

|

|
|
|
|
|
Fig. 649 Deep polders in the Randstad <5m-NAP
|
Fig. 650 Seepage areas in The Randstad
|
|
|
|
|

|
|
|
|
Fig. 651 Schematic hydrogeological
cross-section of the Netherlands
|
|
|
Supplemeted with a schematic not
quantitave image of the pattern of groundwater Fout! Verwijzingsbron niet gevonden.
shows flowlines for the deeper groundwater flow. The deeper groundwater
infiltrates in Overijssel, the Veluwe, the Utrechtse Heuvelrug and the coastal dunes. This causes seepage in the IJsselvallei, the Gelderse Vallei and the polder area of West
Netherland.
The exagerated heights (x 350) in
the cross-section causes a strongly deformed pattern of flowlines. In reality
the horizontal component of the pattern is more pronounced than the vertical
component.
Spread of soil
contamination
Soil contamination can be spread through the
soil by the flow of ground water. If this is to be cleaned up, it is essential
to have an insight into the speed and direction of the spread. For further
information on this topic, see chapter …, page …
Land use of sand, clay and
peat
These characteristics of soil determine their use:[196]
Sand
Pure sand is not a good basis for plant growth; dunes, deserts are
examples. The physical structure is such that sand does drain the water very
easily; it infiltrates into the upper layers at a rapid rate. Sandy soils in agriculture have the advantage
that they are easy to work and lack of nutrients for plants is not really a
problem because of fertilizers nowadays.
Clay
The structure of clay is firm and sometimes 'sticky', especially
when it gets wet. Clay soils are in most cases very fertile; they belong to the
richest agricultural soils. Young clay soils can be found in delta's and along
rivers. In most cases these soils have been in agricultural use for a long
time.
Peat
Peat is a very unstable soil; you cannot build on peat, it always
needs foundation. For agriculture it is very well suited for growing grass
(dairy farming) and horticulture. Peat soils can be found around Delft and the west of Holland in general. When exposed to oxigen,
peat reduces (a chemical way of 'burning') thus resulting in shrinking of the
soil. To make the peat fit for agricultural use, it has to be drained.
The part exposed to oxigen will shrink; a process you can see the results of in
all peat areas in Holland.
The Earth
Approximately 99% of the Earth’s mass is composed by the elements of
iron, oxygen, silicon, magnesia, nickel, sulphur, calcium and aluminium (see Fout! Verwijzingsbron niet
gevonden.). The solid core of the Earth is formed by the heaviest
elements iron and nickel with a liquid boundary. That makes a difference in
rotation possible such as happens if you rotate an egg to determine if it is
boiled, but operating like a dynamo causing the magnetic field of the Earth.[197]
A larger proportion of lighter elements and compounds compose its
mantle and crust (see Fout!
Verwijzingsbron niet gevonden.).[198]
|

|

|
|
|
|
Fig. 652
Contribution of elements composing the Earth by mass (the darker the bigger
the atomic mass)
|
Fig. 653
Contribution of oxides composing the
Earth’s crust by mass (the darker the bigger the density on the Earth’s
surface)
|
|
|
|
Cooling magma
In upward movements from
mantle to crust the composition of the residual liquid is changed as a result
of crystallisation of the cooling magma.[199] The first minerals to critallise contain a relatively high number
of AlO4-tetrahedrons. Continuous cooling
creates minerals with proportionally more SiO4- tetrahedrons. As a
result, the crystallised minerals will prevent each other
from adopting their own form. This explains the complete absence of beautiful,
big crystals in plutonic rock (igneous rock below the surface). That is why rock composition should be analysed with the aid of
a microscope.
The Earth’s crust
In the crust of the Earth most of elements are combined
into oxides with the lightest of the mentioned elements, oxygen (see Fout! Verwijzingsbron niet
gevonden.). The lightest oxide is water. Though its atomic mass is
bigger, at the Earth’s surface its extended density (mass per volume) is
smaller than those of the pure elements (see Fout!
Verwijzingsbron niet gevonden.). These oxides are the main
components of rock and raw material for ceramic industry. Because of their colours
they are also often used as pigments.[200]
|

|

|
|
|
|
|
Fig. 654
Molecular mass and density (extension) at the Earth’s surface of the most
abundant elements and oxides in the Earth’s crust
|
Fig. 655 Lower
density at the Earth’s surface of most abundant oxides compared to the main
elements
|
|
|
|
Olivine
The heaviest rock is olivine, recently recognised as a possible solution to global warming if
exposed to the atmosphere in a granulated form, because it has a natural be it
slow reaction with CO2.
|

|

|
|
|
|
Fig. 656 The
crystal grid of olivine
|
Fig. 657…and its green appearance as a crystal
|
|
|
|
Composition
Pure oxides are seldom found on their own. They are the basis of
many combinations with other elements (see Fout!
Verwijzingsbron niet gevonden.) forming more ore less pure grids
(minerals, crystals), on their turn combined into kinds of rocks, mixtures with
their own name (see Fout!
Verwijzingsbron niet gevonden.). A book on minerals is something else than a
book on rocks.[201]
|
 feldspars feldspars
 quarts
SiO2 quarts
SiO2
 plagioklases plagioklases
  pyroxenes
-SiO3 pyroxenes
-SiO3
 olivine
-SiO4 olivine
-SiO4
|

|
|
|
|
|
Fig. 658 Ideal
typical parts of grids.
|
Fig. 659 Groups
of minerals forming types of rocks
|
|
|
|
As a rule of thumb heavier (mafic) rock such as basalt looks darker than lighter
(felsic) rock like granite (see Fout! Verwijzingsbron niet gevonden.).
Heavier, mafic rock is found more abundantly on the bottom of the oceans, where
the crust is thinner, while lighter, felsic rock more abundantly on land.[202]
Main minerals of Igneous rock
Out of the huge number
of known minerals, only a minority are formed as igneous rock. Igneous rock primarily contains the following minerals:[203]
·
feldspar 59.5%
·
amphibole /
pyroxene 16.8%
·
quartz 12.0%
·
mica 3.8%
·
other minerals 7.9%
·
Feldspars include orthoclase, plagioclase, oligoclase;
they consist of the elements SiO2, Al2O3, Ca, Na, K, CaO, Na2O, K2O.
·
Amphiboles include hornblende, olivine, peridotite; they
consist of the elements Mg, Fe, Ca, AlO4, SiO4, OH
·
Pyroxenes include augite, hyperstone, diopsite; they
consist of the same elements as amphiboles, with the exception of OH.
·
Micas include biotite and muscovite; they form sheets,
which consist primarily of SiO4-, AlO4- and FeO4 tetrahedrons.
To a significant extent,
this composition also determines the chemical composition of the soil.
Design, planning,
construction and maintenance
Engineering of earth and
ground
Ground balance; cut and
fill
Environmental aspects
The legal aspects of
environmental quality of soils
Besluit
Bodemkwaliteit in Holland
Landslides
and geohazards
Earthquakes
Soils and ground-water
tables suitable for residential and industrial areas
Any adjustment or
improvement to the soil and ground-water table deemed necessary to enable the construction
and design of a residential and industrial area, must be carefully considered
during the planning stage, taking into account the technical possibilities and
limitations of the ground itself, as well as the groundwater. Not only are
these considerations vital to the ecological preconditions associated with
sustainable planning, they also underpin the existence conditions of an area,
and economically sound planning.
Accomodating the
environment
Traditionally,
differences in soil properties necessitated a differentiated approach to ground
use. Nowadays, economic factors and strategic planning prevail when deciding on
future use. No consideration is taken of the management and the preservation of
the (newly created) environment. Management can prove so costly and complex,
that even minimal cutbacks or setbacks will create serious maintenance and
environmental problems.
Sustainable impacts
Any intervention must
provide a certain degree of certainty that the newly created situation can be
sustained.
Furthermore, any
manipulation to the condition of the soil as a result of fill or lowering of
the groundwater level, or a combination thereof, will not only affect the
actual site, but also the surrounding area. This manipulation can cause
significant changes in the patterns of plant growth. In addition, abrupt
transitions between different areas will affect the visual and social harmony
of an area.
Assessment of existing and
future value
The values of the site
earmarked for development, land use, cultural-history, vegetation and ecology
of the area covered by the plan and the surrounding area must be analysed to
enable sound planning and assessments of future use.
There are two opposing
approaches to preparing a site for development:[204]
·
technically, any ground can be prepared for
development; in other words, the "foundation" does not determine the
site to be developed, but rather the demand. This approach does not focus on
sustainability of the newly created situation. Effectively, the issue of
management is left out of the equation altogether.
·
identifying the site to be developed is dependent
on the "foundation"; in other words, a site's potential for various
functions must be assessed, taking into account installation and management
costs. This ‘potential site’ selection is more ecologically sound.
Several preparation
methods can be identified. The ultimate choice of method has far-reaching
implications in terms of management of the existing situation, as well as the
design potentials of the new urban landscape.[205]
Lowering the polder level
To obtain the required
drainage, the level of the entire polder polder(site
preparation) is lowered via a pumping station. This can prove
problematic if only a section of the polder needs to be developed, and will
either involve creating a new (smaller) polder inside the existing polder,
which is then developed, or adjusting the rest of the polder to the new
groundwater table in line with use requirements.
The advantages of this
method include ease of execution and savings on embankment sand.
The disadvantages,
however, generally outweigh the advantages.
Given its many
disadvantages, this method is not applied to peat ground in urban areas.
Sagging
As the water level
drops, air will permeate the overburden, causing settlement of the ground (settlement or “sagging" of the ground is
caused by the replacement of water by air). Clay and sand grounds are
characterised by minimal setting. Peat grounds, on the other hand, are
extremely prone to setting due to their high concentration of water (over 90%).
In addition, peat oxidation sets in due to the presence of air, resulting in
additional loss of volume. As a result of this and the loss of water,
'settlement' occurs, a downward movement of soil that negates the effect of
lowering the polder level.
Wooden piled foundations and seepage
The pile heads of old buildings with wooden piled foundations
will begin to rot above water. Older trees are also affected by sudden lowering
of the groundwater level. Furthermore, deeper polders may be prone to increased
effluent seepage from the surrounding, elevated, areas.
These problems are
characteristic of many peatland agricultural areas, where levels have been
lowered for land development works to increase crop yield. Although at first
sight it appears that the existing landscape is being spared, and incorporated
in the design of the new neighbourhood, this is not the case.
Raising with sand pumped to the building site
The required dredge
spoil is usually derived from a dredge area, from where sand is
pumped through pipes to the building site. This method destroys all existing
structures of an area. The designer can create his design in a virgin area, and
only needs to take account of connections on adjacent neighbourhoods and roads.
This is effectively a "tabula rasa" method.
The advantages of this
method include the relatively low cost of sand by ‘high-volume dredging’, and
the immediate creation of a level building site, making the plan
"free" and "flexible". Private and public terrains are
gradually lowered and feeder roads are not overtaxed by heavy sand transports,
as in the following method.
|

|
|
|
|
Fig. 660 Raising with sand and lowering polder level
|
|
|
Costs
Cost disadvantages
include high pre-investment costs due to the need for extra embankment sand
caused by increased subsidence in the early stages. Before actual building can
commence, developers will need to wait several years for the subsidence to
halt, generating a further cost item.
To minimise these
disadvantages, a system of vertical drainage using 'sand piles' is applied –
very exceptionally in house construction. Pressurised water is rapidly
discharged upwards through the sand piles, causing accelerated subsidence.
Following completion of
building activities, the site is subject to all the usual subsidence problems.
Another disadvantage is that the existing landscape will disappear completely
under a layer of sand, requiring extensive ground consolidation for urban green
areas and gardens.
Examples of raising with
sand
This method is heavily
deployed in the west of the country in large-scale urban expansions.
The post-war urban
expansions in Amsterdam West are a well-known example.
|

|
|
|
|
Fig. 661 Raising with sand
|
|
|
Sand delivery per 'axe''
This method is similar
to the previous one, the main difference being that embankment sand is
delivered by lorry.
The advantage of this
method is that it enables a more selective approach, allowing for smaller
deliveries and thus phased land reclamation. More consideration can therefore
be given to the existing landscape features, which in turn might play a part in
the design. This method also allows for the sole raising of those areas that
are essential for the construction of roads and pipelines, thus not impacting
on other areas.
If the soil is not all
too marshy, urban greenery and gardens can be constructed on the original
overburden.
The elevated sections
are subject to all the previously mentioned disadvantages of subsidence.
Nowadays, vertical drainage is applied to these sections. Additional problems
include the provisions and costs involved in transporting sand overland.
This method is primarily
applied in new residential areas in the North and East of Rotterdam. In
general, this involves integrated land reclamation.
Impact of raising with sand on vegetation
Using sand to raise an
area has a negative impact on vegetation:
·
Embankment sand generally has a low nutrient
content. Although this may be ideal for certain types of vegetation, the growth
of most trees, as well as lawns and general gardening work depend on the
availability of soil with a higher nutrient content.
·
Due to its dense packing, embankment sand is not
easily permeable for roots. This is particularly true of reclaimed sand. The
area is not conducive to tree growth; furthermore, filling a small planting
hole with a more suitable soil type will not suffice, as the roots will be
contained within the planting hole due to the poor permeability of the
surrounding soil.
·
The weight of the sand compresses the old top
layer, creating a layer with poor water and root permeability. These highly
unsuitable plant growth conditions are exacerbated during construction
activities, when the ground is further compressed by heavy machinery.
Under-reamed platforms and light-weight fill-material
In this method,
mains-connected residences and streets are under-reamed with (concrete) piles.
Alternatively, under-reamed living platforms are created. Access roads and parking places
are raised with a layer of polystyrene, covered with
scoriaceous sand, while urban greenery and gardens are not raised.
The main advantage of ‘living
platforms’ is that house building can commence as soon as
the platform is complete (in the ‘raising with sand’ method, developers need to
wait 5 to 6 years after raising before building can commence). This allows for
phased building, thus incorporating existing landscape features. Furthermore,
there are no problems with subsidence. The raising of an area using lightweight
fill-materials has similar advantages.
The method of
light-weight raising has been applied in Capelle a/d IJssel; concrete living
platform designs have also been drawn up, such as Piet Blom’s expansion plans for Monnikendam.
Preventing the light-weight construction from floating
To prevent the light-weight
construction from floating, excessive groundwater rises must be prevented in
the event of heavy rainfall. The preconditions for this method include good
drainage and open water storage of at least 6 to 7% of the surface.
Costs
Both methods have one
main disadvantage: extortionate costs, roughly twice as high as raising with
sand. However, the long-term benefits include far lower maintenance costs.
Urban development (sub) plans must be entirely laid down in writing beforehand.
Light-weight raising methods are however characterised by slight subsidence in
the course of time. Raising increases the weight, thus causing further
subsidence.
Living layer
A more recently
developed method involves the use of a so-called living layer. This is a layer of
'pure' soil, poured onto the ground (separated by a plastic film). This ground
is usually partially polluted, and cannot be purified for a variety of reasons.
This method allows developers to build on contaminated ground.
Other forms
As well as the
abovementioned methods, an additional option involves floating constructions,
as demonstrated for example by Hans Huber’s graduation project of his 'Eco Building'
in the TU district. For his experimental project in Haarlem, Herman Herzberger designed floating homes that follow the sun’s movement. Other
development ideas include houseboat parks with their own mains infrastructure.
‘Situation-conscious’ site selection.
Situation-conscious
urban designers tend to prefer an accurate analysis of the soil conditions and
water economy, coupled to the issue of preparing a site for development, as an
integral part of planning.
Bijhouwer’s Kethel
The abovementioned
concepts are far from new. As early as 1948, the garden and landscape architect
Jan TP Bijhouwer carried out a study into the development
potential of the village of Kethel near Schiedam. Soil maps revealed the
location of the old village on top of a creek ridge, a sturdy clay ridge,
deposited by the flood current of the sea. Bijhouwer projected his development
plan on the position of the creek ridges in this area, while he chose the peaty
basin between the ridges to design a park. This park was eventually situated
here, by selecting suitable vegetation and installing generously sized bodies
of water. The development itself partially adhered to his original ideas.
|

|

|

|
|
|
|
|
|
Fig. 662 Bijhouwer, soil map of Kethel and surroundings
|
Fig. 663 Bijhouwer, development
plan of Kethel and surroundings
|
Fig. 664 Maas and Tummers Haagse Beemden
|
|
|
|
|
Applications in peaty basins intersected by wide sturdy ridges
In those parts of the Netherlands
where smaller peaty basins are intersected by wide sturdy ridges, Bijhouwer’s approach is ideal. This is by no means a ‘minority concept’: in
many areas of the Netherlands, peat is intersected by interstream ridges, creek
ridges and cover sand ridges, such as The Haagse Beemden, a big expansion
district in Breda, designed by the urban developer Leo Tummers and the landscapes architect Frans Maas.
The graduation project
of Peter Dauvellier, which touches on the
issue of preparing a site for development, compares the approach taken in
Kethel to that of the Holy district in Vlaardingen by virtue of their 'universal' approach
(integrated reclaiming).
Tanthof in Delft
A separate mention must
be made of Tanthof, a district in Delft.
The design of this area
has been met with substantial criticism because of its complex, 'drab' layout.
This criticism is however primarily targeted at the pattern of building blocks
and roads.
The main layout is
extremely sensitive to the underlying landscape. One key feature concerns the
narrow creek ridge that diagonally intersects the plan, deployed as a green
zone with a traffic-calming route, known as the Kethelrugpad. This ridge was
far too narrow to allow for concentrated development (as with the Kethel plan).
Rather, designers decided to take account of the local soil, loam and clay, to
plant ash and elm, slow-growing tree species that will take several years to
envelop the district, and will not do as well in the rest of the neighbourhood.
|

|
|
|
|
Fig. 665 Tanthof, Delft
|
|
|
In the heart of the
district, a park was designed around several old farms, also built on the spurs
of creek ridges. A narrow space was left for this park during raising; it forms
the transition with the open pasturage of Midden-Delfland.
In this respect, the
chief layout is in sharp contrast to the districts of Voorhof and Buitenhof,
where the landscape plays no part, and where more 'universal' traits prevail.
Unfortunately, the diagonal green zone has been kept extremely narrow, and made
‘spatially subordinate’ at road junctions. The orientation problems of this
district are therefore not the result of the design being excessively tailored
to the landscape, but rather stem from the fact that the landscape has been
given too subordinate a role to play.
Flooding and drainage
Seepage of water underneath houses and boggy gardens
are common occurrences in many parts of the Netherlands. This phenomenon is
known as flooding, and can be minimised
by installing sewers in built-up areas, which discharge water from streets and
concreted areas. Unhardened ground will nevertheless continue storing water
during groundwater table rises.
What measures can be
taken to prevent, eradicate or reduce the risk of flooding?
Sand grounds can be left
out of the equation, as dewatering of easily permeable ground is fairly
straightforward. Clay and peat grounds pose the biggest dewatering problems, as
they do not allow for easy water discharge due to adhesion, retaining the water
in narrow pores and corridors.
Existing drainage systems
Prior to being prepared
for development, the grounds acted as farmland or as pasturage. To prevent
excessive rise of the ground-water table during wet periods, clay and peat
areas are equipped with a drainage system in the form of cut trenches and/or
drains. In order to maintain the predetermined polder level (water level),
excess water is discharged via ditches through a pumping station or drainage
sluices.
Paved and ‘unhardened’ urban areas
When preparing a site
for development, drainage series are disrupted and ditches filled up, as they
do not "suit" the urban development plan, thus given the urban
developer sufficient freedom for his design. In a modern townscape, most of the
precipitation will eventually be discharged via the sewer system, as urban areas
primarily consist of hardened surfaces, so that water can only
be discharged artificially. Conversely, the ‘unhardened’ urban areas, the gardens and parks,
must have and maintain their storage capability to prevent the risk of
flooding.
The rise of the
ground-water level can be partially absorbed by underground storage of water
(in the crawl spaces of houses) and in sand bodies. This is however not an
ideal situation, as water in underground crawl spaces can give rise to
unpleasant smells, rising damp, and affect beams, floor heating pipes and
cables. Water in sand bodies underneath roads can cause subsidence, affect the
load bearing capacity and encourage frost heave.
In most cases, flooding can only be tackled with the aid of a new
drainage system, as the "old"
system is in many cases unusable for preparing a site for development.
|

|
|
|
|
Fig. 666 Water control in urban areas
|
|
|
Urban development and/or
destination aspects apply completely different criteria to the ground.
Buildings and infrastructure requirements are virtually identical, while
planting criteria are far less stringent and highly dependent on use. The
designer’s standpoint also plays an important role in this respect: vegetation
and use adapted to the soil, or vegetation tailored to use.
Criteria applied by all destinations.
Per destination and
implementation technique, various ‘ground criteria’ apply, including:
·
load bearing capacity:
ability of the ground to support buildings, roads and sewers (static load);
·
passableness: load
bearing capacity of the ground for carrying people (and machines) and dynamic
load;
·
relief:
altitude variations of the ground;
·
dewatering level: the
difference between the ditch level and the surface level to be dewatered;
·
dewatering: water
discharge from the ground to the ditches;
·
water retainability:
ability of the ground to retain water without groundwater support (i.e. without
capillary connection to the groundwater);
·
infiltration ability: the
amount of water that can penetrate the ground per unit of time;
·
closed water storage: additional
amount of water that the ground is capable of absorbing in addition to the
amount already present (depending on pore space, humidity level and
ground-water table);
·
open water storage: the
amount of water that ditches are capable of absorbing at a certain water level
(depending on open water surface area and the water level of the ditch); and
·
drainage:
discharge of excess water from the ditches to the discharge point.
With regard to drainage:
·
for
building: foundation frost-proof (frost line 0.6 m below surface level), installing
foundation 'in the dry', house service connection of pipes 'in the dry', no
water in crawl spaces (if required) – ground water at least 0.2 m below the
crawl space floor and groundwater below the foundation installation level due
to the risk of cracking to buildings caused by reduced load bearing capacity with increased water levels;
based on these criteria: ground-water table at
least 0.8 m below surface level;
·
for roads, parking areas and paths: top of the
capillary water below the frost line due to frost heave and thaw during
hardening; the substrate must always maintain as constant a bearing capacity as possible;
based on these criteria: ground-water table
0.7-1.0 m below asphalt;
·
for paths: good drainage, resistant to wind and
water erosion;
·
for pipes (water, gas, sewers): install house service
connections 'in the dry'; water pipes and sewers must be frost-resistant;
separate sewerage system: hydraulic slope to open water (R.W.D. = rainwater discharge); mixed
sewerage system:
discharge to emergency spillways; groundwater main sewers may be below the frost line;
based on these criteria: ground-water table 1.0 m
below surface level;
·
for electric wires: minimum cover layer 50 cm,
situated above groundwater;
·
for parks: minimal fluctuating ground-water table,
good water retainability of the ground, no hard, impermeable layer prohibiting root growth,
favourable global ground-water table, 1 m for trees; this may be less for plants:
pH groundwater: broadleaf 5
coniferous
4.5
N.B. other drainage requirements apply to
botanical gardens: keep the situation as natural as possible);
·
for sports fields: ground-water table in winter a
maximum of 50 cm below surface level due to passableness following rainfall;
·
for playing fields and camp sites: quick-drying
after rainfall; excessively low water levels affect grass growth in summer
With regard to open water, size and position is determined by:
·
civil criteria in relation to dewatering, storage,
emergency spillways and overflows
·
urban design criteria; ditch levels lower than
permissible maximum ground-water table.
With regard to bearing capacity:
·
for buildings: Pleistocene sand layer must be
sufficiently strong for building foundations (impermeable layers may be
perforated when hitting in poles; this may result in effluent seepage);
high-rise buildings will almost always have to be founded with piles on
Pleistocene substrate; for low-rise buildings, pending sufficient bearing
capacity of sand and clay ridges in peat and overflow embankments in clay
areas, shallow foundation of these layers is also allowed;
·
for roads: dig out sand or earth body above
surface level or cunet and fill up with sand; sand body on solid foundation or
to spread the load, use sand and clay ridges in the landscape if possible;
·
for parks and landscaping: bearing capacity less
relevant than drainage criteria.
Buildings
As a general rule,
buildings apply the following suitability criteria to the ground:
·
With regard to drainage:
o
for building: foundation frost-proof (frost line
0.6 m below surface level), installing foundation 'in the dry', house service
connection of pipes 'in the dry', no water in crawl spaces (if required) –
ground water at least 0.2 m below the crawl space floor and groundwater below
the foundation installation level due to the risk of cracking to buildings
caused by reduced load bearing capacity with increased water levels;
based on these criteria: ground-water table at
least 0.8 m below surface level;
·
With regard to open water, size and position is
determined by:
o
civil criteria in relation to dewatering, storage,
emergency spillways and overflows
o
urban design criteria; ditch levels lower than
permissible maximum ground-water table.
·
With regard to bearing capacity;
o
for buildings: Pleistocene sand layer must be
sufficiently strong for building foundations (impermeable layers may be
perforated when hitting in poles; this may result in effluent seepage);
high-rise buildings will almost always have to be founded with piles on Pleistocene substrate;
for low-rise buildings, pending sufficient bearing
capacity of sand and clay ridges in peat and overflow embankments in clay
areas, shallow foundation of these layers is also allowed.
Infrastructure
As a general rule,
infrastructures and pipes apply the following suitability criteria to the
ground:
With regard to drainage
·
for roads, parking areas and paths: top of the
capillary water below the frost line due to frost heave and thaw during
hardening; the subgrade must always maintain as constant a bearing capacity as
possible;
·
based on these criteria: ground-water table
0.7-1.0 m below asphalt;
·
for paths: good drainage, resistant to wind and
water erosion;
·
for pipes (water, gas, sewers): install house
service connections 'in the dry'; water pipes and sewers must be
frost-resistant; separate sewerage system: hydraulic slope to open water
(R.W.D. = rainwater discharge); mixed sewerage system: discharge to emergency
spillways; groundwater main sewers may be below the frost line;
·
based on these criteria: ground-water table 1.0 m
below surface level;
·
for electric wires: minimum cover layer 50 cm,
situated above groundwater;
With regard to open
water, size and position is determined by:
·
civil criteria in relation to dewatering, storage,
emergency spillways and overflows
·
urban design criteria; ditch levels lower than
permissible maximum ground-water table.
With regard to bearing capacity:
·
for roads: dig out sand or earth body above
surface level or cunet and fill up with sand; sand body on solid foundation or
to spread the load, use sand and clay ridges in the landscape if possible;
Vegetation
As a general rule,
vegetation applies the following suitability criteria to the ground:
With regard to drainage
·
for parks: minimal fluctuating ground-water table,
good water retainability of the ground, no hard, impermeable layer prohibiting
root growth, favourable global ground-water table, 1 m for trees; this may be less for plants;
pH groundwater: broadleaf 5
coniferous
4.5
N.B. other drainage requirements apply to
botanical gardens: keep the situation as natural as possible);
·
for sports fields: ground-water table in winter a
maximum of 50 cm below surface level due to passableness following rainfall;
·
for playing fields and camp sites: quick-drying after
rainfall; excessively low water levels affect grass growth in summer
With regard to open
water, size and position is determined by:
·
civil criteria in relation to dewatering, storage,
emergency spillways and overflows
·
design criteria for different vegetation functions
such as parks, sports fields etc; ditch levels lower than the maximum
permissible ground-water table.
With regard to bearing capacity
·
for parks and landscaping: bearing capacity less
relevant than drainage criteria.
·
passableness or access criteria apply to sports
fields.
Industry
Industry criteria
governing the ground will generally correspond with criteria applied to
buildings in general, and infrastructure. Additional criteria must always be
specified.
architects
Different levels of intervention
Ground at the level of
element:
materialisation of form
Ground at the level of
structure;
organising land use
Ground at the level of
process; a strategy
for
landscape development
The form and dynamics of
the land
We have chosen some prototypical plans from history where the
working with landform and ground is integrated into the plan and design of the
ensemble. We have selected four plans; the Villa d'Este at Tivoli, close to Rome; the Parc de Sceaux
at Paris; the Hawkstone Hall and gardens close to
Weston-under-Redcastle in the UK;
the Parc des Buttes Chaumont in Paris. All four have a different relation
with the
geological conditions of the site and are from different time
periods. All are examples where designers have made use of the geological
conditions and have integrated this into their plans. All are public space and
can be visited.
Villa d'Este in Tivoli, near Rome
The Villa d'Este was built on a steep slope in
Tivoli, a small town south of Rome. It was designed in the 16th century and is an example of a
renaissance garden.
|

|

|
|
|
|
|
Fig. 667 Villa
d'Este in Tivoli
|
|
|
|
The garden consists of two parts; the very steep slope with the
terraces just next to the house and the more .at part further away from the
house. House, garden, water, sculpture and site are beautifully integrated into
the plan forming a splendid unity that expresses the capacity of using site
characteristics
.
Parc de Sceaux in Paris
Sceaux is a relatively small ensemble compared to the other plans of
Le Nôtre.
|

|

|

|
|
|
|
|
|
Fig. 668 Parc de Sceaux in Paris
|
|
|
|
|
The composition is based on different axial systems. First the main axis that includes the castle. Secondly there are
two axes based on water; the grand canal and the cascade both perpendicular to
the main axis. Both are perfectly .fitted into the site; they are located in
naturally lower areas in the terrain. Le Nôtre made clever use of the site
conditions and integrated them into an intriguing composition. The structure
gives the composition an effect of surprise; you don't expect the water because
you don't see it from the building.
Hawkstone, Shropshire, UK
The plan is a series of interconnected itineraries; it does not have
a dedicated groundplan.
|

|

|
|
|
|
|
Fig. 669
Hawkstone, Shropshire, UK
|
|
|
|
It makes a clever use of the exceptional geological conditions of
the site; its location on the edge of the plains of Shropshire
and the steep side close to the house. The garden is not enclosed but open to
the views of the plains and is composed of different walks that make use of the
contrast between the steep rock and the open plains.
Parc des Buttes Chaumont in Paris
A park in the northeastern part of Paris, not far from Parc de la Villette. It was designed in the 19th century by Haussmann at a former quarry.
|

|

|
|
|
|
|
Fig. 670
|
Fig. 671
|
|
|
|
'Chaumont' refers to chalk. It still contains rocks, the highest being used as viewpoint. It
is an early example of 'reuse' of industrial sites, in this case a quarry for
chalk. The park gives a special experience because of its urban context; urban
nature referring to geological features of the site with a grotto and a
waterfall.
5
Life, ecology and nature
Contents.................................................................................................................................... 352
5.1 Natural History............................................................................................................. 353
5.1.1.... Long-term biotic changes................................................................................................. 355
5.1.2.... 400 000 000 years ago.................................................................................................... 356
5.1.3.... 230 000 000 years ago.................................................................................................... 357
5.1.4.... 65 000 000 years ago...................................................................................................... 358
5.1.5.... Pleistocene.................................................................................................................... 359
5.1.6.... Identifying plants
species................................................................................................. 362
5.2 Diversity,
scale and dispersion................................................................................. 366
5.2.1.... The
importance of diversity for life..................................................................................... 367
5.2.2.... The importance of diversity for human living....................................................................... 367
5.2.3.... Scale-sensitive concepts................................................................................................. 369
5.2.4.... Spatial state of dispersion as a condition of diversity.......................................................... 370
5.2.5.... 300km continental
vegetation areas.................................................................................. 373
5.2.6.... 30km national counties.................................................................................................... 375
5.2.7.... 3km Landscape formations.............................................................................................. 378
5.2.8.... 300m local life
communities............................................................................................. 383
5.2.9.... 30m ecological groups..................................................................................................... 386
5.2.10.. 3m symbiosis and
competition......................................................................................... 389
5.2.11.. 30cm individual
strategies for survival................................................................................ 390
5.3 Ecologies........................................................................................................................ 392
5.3.1.... Generalisation................................................................................................................ 392
5.3.2.... Six kinds of ecology........................................................................................................ 392
5.3.3.... Scale classification......................................................................................................... 393
5.3.4.... Cybernetics.................................................................................................................... 394
5.3.5.... ·Regulation
theory........................................................................................................... 399
5.3.6.... Separation and discontinuity............................................................................................ 400
5.3.7.... Selectors and regulators in the landscape......................................................................... 402
5.3.8.... Ecological networks........................................................................................................ 404
5.3.9.... Urban ecology................................................................................................................ 406
5.3.10.. Distribution and abundance of people................................................................................ 408
5.3.11.. Comparing and applying standards for green surfaces in urban areas................................... 411
5.3.12.. Urban perspectives.......................................................................................................... 419
5.3.13.. Human health in the urban environment............................................................................. 425
5.4 Valuing
Nature............................................................................................................... 429
5.4.1.... Assessing biotic values................................................................................................... 429
5.4.2.... Measuring rarity.............................................................................................................. 430
5.4.3.... The IJsselmeer case....................................................................................................... 433
5.4.4.... Replaceability................................................................................................................. 440
5.4.5.... Comparability Problems, which categories?....................................................................... 441
5.4.6.... Valuation bases.............................................................................................................. 441
5.4.7.... Valuing urban nature....................................................................................................... 443
5.5 Managing
Nature........................................................................................................... 446
5.5.1.... Main Ecological Structure (EHS) and nature-target types.................................................... 447
5.5.2.... Nature-target types for the higher sandy soils.................................................................... 450
5.5.3.... Nature-target types in fluvial areas.................................................................................... 451
5.5.4.... Nature-target types for the Marine-clay areas..................................................................... 452
5.5.5.... Urban nature................................................................................................................... 453
5.5.6.... Differences in diversity between and within regions............................................................. 455
Biodiversity
There are about 1.7 million
known species and new species are being discovered every day.[206] It is estimated that one successful new form is created each year, while, under the
present conditions, approx. 500 species per year become extinct. Some biologists estimate
the real number of existing species as being 10 million, others as many as 80
million, Zoest (1998) reports.
Distinguishing species from subspecies (taxonomy) is a constant on-going
task. For example, the authoritative Dutch work: Heukels’ Flora edited
by Meijden (1996) has recently
been drastically amended to accommodate the new international insights into the
organisation, differentiation and nomenclature of the plant kingdom. Viewed from this angle, we
live on an unknown planet with a rapidly diminishing biodiversity.
Nevertheless, the existing species represent an enormous genetic richness, of which we are hardly
aware.
A risk cover for life
Within any one species there
are as many variations as there are specimens, and just to make the problems of
ecological generalisation even greater, all these specimens live in different
contexts and micro environments. To question the meaning of this enormous diversity at the species,
genetical and habitat level is typically human, but it is not an ecological
question in the scientific sense. All we can do as Pianka (1994) does, is to observe that this biodiversity has
arisen due to evolution and that, in the past, when sudden environmental
changes took place, it was this that ensured the continuation of life up to the
present time. Life has survived all manner of catastrophes because there was always a species, or a
specimen of a species, that could survive in the new environment. The
extinction of the dinosaurs about 65 million years ago in the darkness, of
a kind of nuclear winter, following a meteoric collision with Earth, gave an advantage to night animals, and among them, mammals like ourselves. Biodiversity acts, therefore,
as the the risk coverage of life itself suggests Londo (1998).[207]
Plants first
|
Plant life, which
transforms carbon dioxide into food and oxygen for the animal kingdom, is the foundation of
this diversity.This forms the basis of the local food chain, down to the
smallest scale on the surface of the Earth. Thus, in urban ecology, if one
does want to begin with the basement and not the ridge tiles, when
reconstructing our oikos although for many this is the most interesting (caressible) part
of the housekeeping, attention should first be given to botanical diversity.
Dutch plants
Approximately 1,500 of the
250,000 known plant species, worldwide, 3,500 of the 100,000 toadstools and 500 of the 23,000 mosses are found in the Netherlands, in the wild. The
science of dividing plants into classes, orders, families and species is
known as taxonomy.[208] Taxonomy is based on kinships that can be deduced from evolution.
Against that background, plants can be given a name.
Heukels’ Flora provides the scientific access to
approximately 1,500 Dutch plant
species.
|

|
|
|
|
Fig. 672 Heukels’
flora
|
|
|
Insects are the largest group
To find one’s way in this
flora, some insight is needed into the genesis of life (see para. 5.1.6). Insects often cooperate closely in the reproduction of
higher plants, and of the 1,100,000 known species of insect, approximately
20,000 can be found in the Netherlands.
Compared to those, the other groups of creatures are almost negligible: approx.
500 of the 50,000 known vertebrates (30 reptiles, 300 species of birds, 100 mammals).[209]
Counting species or genetic complexity?
The question that comes to
the fore here is whether one can compare one-celled life forms with multiple-celled forms that undergo cell differentiation. Although they live
independently, their diversity among themselves can be likened to the internal
cell diversity of multiple-celled forms. Should we use the
number of species as the criterion for biodiversity? The disappointing
discovery that human beings do not have very many more genes than species that,
so far, have been considered to be much simpler, leads to a similar question,
even though it indicates exactly the opposite. As far as the criterion for
choosing the number of species is concerned, for the time being, we adhere here
to the present mid-way scientific position.
This history is excellently
documented on the bottom floor of the Naturalis Museum. This museum was designed by Fons Verheijen. The design process is
described in ‘Ways to study and research’, Jong and Voordt (2002) and
is thus worth a visit.
|

|
|

|
|
|
|
Fig. 673 Eras at
Naturalis
|
|
|
The oldest forms of life
The oldest forms of life are
single-celled marine organisms that later formed themselves into
threads of algae. They have produced oxygen from carbon dioxide for more than a billion years.[210] This form of life stagnated when carbon dioxide gases became
depleted after the excessive growth that took place during the Carboniferous and Permian eras and carbon ceased to oxidate
spontaneously. Fauna took over part of this oxidation process. Carbon dioxide fertilization is still a constant feature of
horticulture to cause profuse growth.The increasing amount
of CO2 in the atmosphere, not only leads to a
greenhouse-effect, but also to more profuse
growth and increased agricultural production. Ecologically, from the
point of view of biodiversity, this is not an advantage.
Revolutions during the last billion years
During the last billion
years there have been four important revolutions:[211]
|
600 million years ago:
|
Fauna began to adopt
chalky skeletons, so that suddenly their
historical development can be read in the sediments.
|
|
400 million years ago:
|
Life established a foothold beyond the sea.
Mosses and liverworts (Bryophyta) brought a green colour
to the wet parts of the land (5.1.2).
|
|
230 million years ago:
|
Many animal and plant
species suddenly became extinct, marking the end of the
Palaeozoic. This made way for the
Mesozoic, the Saurian Age. Seed-bearing plants started to develop, which had a completely
diploid life cycle. These plants fertilised
each other and dispersed diploid seeds (5.1.3).
|
|
65 million years ago:
|
The Cenozoic began with the extinction of the saurians and the advance of mammals (5.1.4).
|
Life gained a foothold
beyond the sea. Where the land was wet, it became green with mosses and liverworts (Bryophyta).These plants can not
establish themselves on drier areas because their structures are not
sufficiently developed to take in water and store it to use during drought;
they have no roots. In addition, they are dependent for reproduction on male
gametes that swim.
Early in their development,
mosses did not halve their genetic material by means of sex cells, but
sometimes duplicated themselves on a part of the female plant. Only then was the duplicated (diploid) genetic material divided
and dispersed as single spores that germinated as haploid organisms with a single set of genetic
material. Mosses are predominantly haploid. They are not included in Heukels’
Flora.
The earliest vascular plants
The next step was the
appearance of the first staghorn and club-mosses, the horsetails and the ferns (Pteridophyta, the first 15 families in Heukels’
Flora). These were the earliest
vascular plants, capable of transporting
water internally. They can thus grow higher than the mosses. However, although
fully grown ferns can withstand dry conditions because of their vascular
system, they still need water to reproduce sexually.[212] This is why the existing Pteridophyta are usually to be
found in moist, shadowy places and/or why they often reproduce themselves
vegetatively.
|

|

|

|
|
Flat-stemmed Club-moss
|
Giant Horsetail
|
Male-fern
|
|
Meijden (1999)
|
|
Fig. 674 Pteridophyta
|
|
|
Although small haploid forms
do exist, the predominant forms on which all higher plants are modelled are
diploid.
A family tree
Many plant and animal
species suddenly became extinct, marking the end of the
Palaeozoic. They gave way to the
Saurian Age, the Mesozoic. Seed plants began to
develop, with a completely diploid life cycle. They fertilised each other and
dispersed diploid seeds.
The following appeared,
successively:
gymnosperms (families 16-18 in Heukels’ Flora 1996: the conifers),
angiosperms (families 19-119 in Heukels’ Flora 1996: most of the flowering plants)
monocotyledons (families 120 to 140, to which lilies and grasses belong)
|

|
|
|
|
Fig. 675 Division of the
Plant Kingdom
|
|
|
This scheme gives a
didactically simpler division into subclasses than the currently accepted
scientific one shown in Heukels’ Flora 1996. In the mean time
DNA-research changed the supposed tree of life again, so the arrangement and
name giving of the Heukels’ Flora 2005 has changed again substantially.
CD-ROMs
This species specificy is
thus focused on the recognisability of these reproductive organs. Species are primarily
identified on the basis of these organs. This process is currently simplified
by using interactive CD-ROMs (Fig.
676 and Fig.
677).
Knowledge of species gives
insight into the constitution of the soils, climatic conditions and growth
possibilities. It is probably an important basis to give urban architects a
feeling of the genius loci.
|

|

|
|
|
|
|
Fig. 676 An interactive CD-ROM of Heukels’ Flora
|
Fig. 677 CD-ROM Marijnissen
|
|
|
|
These CD-ROMs give a good
picture of different ecological approaches in the Netherlands. The Nijmegen approach (Marijnissen) is less
orthodox taxonomically and more accessible for lay people. Another electronic
source is CBSs Biobase (see Fig. 805 ), elaborated on http://team.bk.tudelft.nl > Publications 2007
> Life.xls (see 5.1.6).
Taxonomy of plants
According to recent
evolutionary insights, plant taxonomy is built up as follows:
|
Class -da
|
Subclass -dae
|
Super order -florae
|
Order -ales
|
Family -ceae
|
Genus -ida, ids
|
|
|
|
Fig.
678 The taxonomy of Dutch plant families
|
|
|
According to accepted
interpretations of evolution, the lowest subclass, the liliidae (monocotyledons, such as lilies, grasses and orchids), were the most recent to
come into existence. However, taxonomy is not a static science; there is still no
agreement on the sequence of evolution and subdivision. The families in Heukels’
Flora of 1990 were still
not classified according to the present international standard. In 1996 and
2005 drastic changes were made to the classification system and thereby to the
nomenclature, much to the sadness of many.
The great extinction
The Cenozoic began with the extinction of the saurians and the advance of the mammals. A meteoric impact in the region of the Caribbean caused so much dust to enter the atmosphere
that, in the prolonged darkness that followed, plant growth stagnated and the
large plant-eaters died out. It was mainly night animals, mammals, for example,
that survived.
The last 2 million years
(the Quaternary or Pleistocene) has been occupied by ice
ages (glacials) and warmer interglacials
(see page 50).[213] The two most recent glacial periods, the Saalian (Fig. 679 ) and the Weichselian (Fig. 680 ), were interrupted by the
Eemian interglacial period.[214]
Ice ages in The Netherlands
The higher parts of the Netherlands
were formed in particular during the Saalian.[215] The Weichselian did not reach the Dutch area.
|
200,000 BC
|
150,000 BC
|
70,000 BC
|
15,000 BC
|
|

|

|

|

|
|
Saalian
|
Eemian interglacial
|
Weichselian
|
|
|
|
Fig. 681 The two most
recent ice ages
|
|
|
The forming of the Veluwe massif and the Gelderse Poort are clearly visible.
Holocene
The lower areas of the Netherlands were shaped from 10,000
BC onwards (Fig. 682 ).
|

|
|
See Fig. 71
|
|

|

|
|
|
|
Fig.
682 Temperature changes and deposits
|
|
|
For instance, deposits under
Delft to a depth of 18 metres beneath New Amsterdam
Level (NAP) is Holocene[216]; the Pleistocene extends to a depth of 400 metres[217]
Vegetation changes by temperature
Fig. 683 shows how climatic changes greatly influence the vegetation.
|

|
|
|
|
Fig.
683 The influence of climatic changes on vegetation
|
|
|
The picture that emerges
from pollen dating is one of changing landscapes and habitation (Fig. 684 ).
|

|
|
|
|
Fig.
684 Landscape changes since the last ice age
|
|
|
Paragraph 1.3.1 from page 50 on gives a closer picture
of this.
Naming
Identifying plants informing you about a
biological genius loci (history, soil, water level) of the location and its
rarity is a difficult job for laymen. However, on http://team.bk.tudelft.nl > Publications 2007
> Life.xls you will find an extract
from Duuren (1997) CBS Biobase containing all wild plants of The Netherlands with
many characteristics. You can sort this Excel sheet on any characteristic. Fig. 685 shows the first four columns. The sheet is currently sorted on
occurrence of urban wild species in the urban area of Zoetermeer. Wild parsnip occurs in nearly any km2
of the town.
|
Species number
|
Scientific name
|
English name
|
Dutch name
|
|
000922
|
Pastinaca sativa
|
Wild Parsnip
|
Gewone pastinaak
|
|
000101
|
Artemisia vulgaris
|
Mugwort
|
Bijvoet
|
|
000135
|
Bellis perennis
|
Daisy
|
Madeliefje
|
|
000188
|
Calystegia sepium
|
Hedge Bindweed
|
Haagwinde
|
|
|
|
|
|
|
Fig.
685 First columns of Biobase extract on Excel sheet
|
Primary identification criteria
By next 17 (yellow or grey headed) columns (Fig. 686) you can make your own rough selection to identify plant species
quickly. Suppose you find a herb (Growth form = kr) without prickles growing up
to your middle flowering in august. Wild parsnip (000922) will appear somewhere
in your selection.
|
Species number
|
Growth form
|
Prickles
|
Until knee (<50cm, low)
|
Up to middle (<100 cm)
|
Above middle (>1m, high)
|
January
|
February
|
March
|
April
|
May
|
June
|
July
|
August
|
September
|
October
|
November
|
December
|
|
000922
|
kr
|
|
|
1
|
|
|
|
|
|
|
|
1
|
1
|
1
|
|
|
|
|
000101
|
kr
|
|
|
1
|
1
|
|
|
|
|
|
|
1
|
1
|
1
|
|
|
|
|
000135
|
kr
|
|
1
|
|
|
|
|
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
|
|
000188
|
lk
|
|
|
|
1
|
|
|
|
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig.
686 First identifying characteristics of Biobase extract on
Excel sheet with rows of Fig. 685
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
If you like to identify a tree you should choose ‘bo’ as growth
form. You also can choose grass like (gr); bush or shrub (st); dwarf shrub
(dw); woody liana (lh); herby liana (lk) and epiphyte, which is a plant growing
on other plants (ep).
Secondary identification criteria
If your selection is still too large you can select further on
leaf form and flower colour (Fig. 687).
|
Leaf season
|
Leaf form
|
Calyx / kelkbladen
|
Petals / kroonbladen
|
Flower colour
|
Second flower colour
|
Pistils / stampers / stijlen
|
stamens / meeldraden
|
Sex / geslacht bloem
|
pollination / bestuiving
|
Seed form
|
Fruit type / vruchttype
|
Fruit colour / vruchtkleur
|
Light minimal
|
Light maximal
|
Moist minimal
|
Moist maximal
|
|
Z
|
5
|
|
5
|
F
|
|
2
|
5
|
C
|
IC
|
9
|
41
|
o
|
LS
|
VL
|
3
|
3
|
|
Z
|
6
|
|
|
F
|
B
|
1
|
5
|
D
|
IH
|
1
|
32
|
o
|
LS
|
VL
|
3
|
4
|
|
W
|
3
|
|
|
A
|
F
|
1
|
5
|
D
|
I1
|
1
|
32
|
o
|
LS
|
VL
|
3
|
3
|
|
Z
|
4
|
|
|
A
|
R
|
|
|
C
|
IH
|
1
|
43
|
o
|
HS
|
L
|
2
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig.
687 Second identifying characteristics of Biobase extract on Excel
sheet with rows of Fig. 685
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Some plants keep their leaves in winter (W), most have leaves in
summer only (Z). You can not rely fully on leaf form or flower colour because
one plant may have different leaf forms or colours simultaneously. If you doubt
you can select two characteristics simultaneously chosing ‘or’. Fig. 688 shows used codes for leaf form with proportion of length (L) and
width (W), colour, required light and moist.
|
leaf form
|
colour
|
sex
|
light
|
moist
|
|
1 line L>10W
2 lancet 3W<L<10W
3 elongated 2W<L<3W
4 (nearly) round B<L<2B
5 hand (compound or not)
6 feather
7 compound feather
|
A = white
B = brown
C = blue
F = yellow
G = grey
H = colourless
M = multicoloured
N = back
O = without flower
P = purple, violet, lila
R = red, rose
U = orange
V = green
|
A = monoecious
B = dioecious
C = hermaphrodite
D = polygamous
E = spore plant
|
VL = full sun
L = light
LS = light shadow
HS = half shadow
S = shadow
VS = full shadow
|
1 = aquatic
2 = wet
3 = moist
4 = dry
|
|
|
|
|
|
|
|
Fig.
688 Codes used in second identifying characteristics from Fig. 687
|
|
|
|
|
|
|
The orange or dark grey heads of columns in Fig. 687 are not very useful for identification, they give characteristics
to check your selection.
Environmental information
derived from plant species
After identifying plant species next 16 columns give interesting
information about the environment (Fig. 689). The last row of Fig. 689 shows community type according to Westhoff and Den Held from Fig. 722. The ecotope columns show the code from Fig. 724 Ecological groups. Inbetween these columns their classes of tolerance discussed in
paragraph 5.2.9 are shown.
The last columns show additional characteristics summed up in Fig. 691.
|
Food minimal
|
Food maximal
|
Acidity
|
Salt minimal
|
Salt maximal
|
Zinc
|
Groundwater
|
Root depth
|
Root depth 2
|
Flow maximum
|
Flow minimum
|
Ecotope 1
|
Ecotope 2
|
Ecotope 3
|
Ecotope tolerance
|
Community Westhoff
|
|
2
|
3
|
x
|
|
|
|
7
|
3
|
4
|
9
|
9
|
G47
|
G48
|
|
1
|
25Ba01
|
|
3
|
3
|
x
|
|
|
|
7
|
|
|
9
|
9
|
P48
|
P68
|
R48
|
2
|
17Aa01
|
|
2
|
3
|
x
|
|
|
|
9
|
1
|
1
|
9
|
9
|
G47
|
G48
|
|
1
|
25Ba
|
|
2
|
3
|
x
|
|
|
|
5
|
4
|
4
|
9
|
9
|
R27
|
R28
|
R47
|
2
|
17B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig.
689 Environmental information derived from plant species
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nutrients
|
acidity
|
salinity
|
dependency ground water
|
root depth
|
water flow
|
|
1 = poor
2 = moderate
3 = nutricous
x = indifferent
|
1 = acid
2 = moderate
3 = alkaline
x = indifferent
|
0 = fresh
1 = between
2 = brackish
3 = between
4 = salt
|
1 = hydrofyt
2 = wet freatofyt (obligatory)
3 = moisty freatofyt (obl.)
4 = moisty freatofyt (fac.)
5 = local freatofyt
6 = lime afreatofyt
7 = afreatofyt
8 = salt plant
9 = dune freatofyt
|
1 = < 10 cm
2 = < 20 cm
3 = < 50 cm
4 = < 100 cm
5 = > 100 cm
|
0 = unknown
1 = stagnant
2 = slow
3 = streaming
4 = fast
5 = very fast
9 = no sense
|
|
|
|
|
|
|
|
|
Fig. 690 Codes used for
environmental information in columns of
Fig.
689
|
|
|
|
|
|
|
|
Additional characteristics per plant species
|
Column head
|
description
|
|
Height belt / hoogtegordel
|
typical height belt of species
|
|
Areal position / areaalligging
|
position in European dispersion
|
|
Use 1 / gebruik 1
|
agricultural or herbal use
|
|
Germinating time / kiemtijd
|
month when growth starts
|
|
Life span / levensduur
|
1, 2, 3 or more years
|
|
Family Heukels’ flora
|
page number in authoritative Dutch flora of Fig. 672 and Fig. 678
|
|
Genus Heukels’ flora
|
subdivision of preceding family
|
|
Species / soort Heukels’ flora
|
subdivision of preceding genus
|
|
UFK_1940
|
occurrence in The Netherlands in 1940 per 5x5km2
|
|
UFK_1990
|
occurrence in The Netherlands in 1990 per 5x5km2
|
|
Protection rode
lijst
|
member of Dutch list of
rare and declining plant species
|
|
Protection
Natuurbeschermingswet
|
protected by Dutch law
|
|
Protection EHS doelsoort
|
target species in Dutch
ecological policy (see paragraph 5.5.1)
|
|
Protection Bern Convention Protection
|
protected by European law
|
|
European blue list
|
member of European list of
rare and declining plant species
|
|
Change in the Netherlands
since 1950
|
Difference between UFK_1940 and UFK_1990
|
|
Abundance per 25km2 1980
|
Number of 5x5km2 squares species was found in The Netherlands 1980
|
|
Abundance
per km2 Zoetermeer
|
Number of 1x1km2 squares species was found in the urban area of Zoetermeer 2000
|
|
Buytenwegh 2002 305723/24
|
found in the urban area of
a 2x1km2 district of Zoetermeer 2000
|
|
|
|
|
Fig.
691 Additional characteristics per plant species
|
|
|
|
For example Fig. 768 used columns Abundance per 25km2 1980 and
Abundance per km2 Zoetermeer to compare national and
local rarity in a graph.
Biodiversity
There are many estimates on
biodiversity described much better than I can do by Zoest
(1998). We know some
1.7 million well-described species but much more are unknown while some 100 000
species are lost since Linnaeus. The extinction rate is estimated 1000 per year now; the growth in
evolution as 1 successful species per year. Though we now know the genome of some, we still do not know how they work
let alone we know their mutual relations. Even how our own species works is
nearly completely unknown to us, though we already studied 3000 years on this
topic. Having some success by medicine, we seldom
understand exactly why. Compared with the combinatory explosion of unanswered
questions we understand almost nothing, otherwise we could invent species.
Possible principals punish researchers admitting that honestly and modestly.
Mythmakers win the competition. However, myths may be useful for survival.
Responsability
Every state bears its own
responsibility in this multitude of species like a modern Noah. Though The
Netherlands occupies less than 0.01% of the earth’s surface it entails
approximately 35 000 (2%) of the earth’s number of known species. Our
responsibility is proportional to their global, continental
(blue list), national (red
list) or local
rarity.
The concept of rarity and thus
responsibility is scale-sensitive.
Health
Depending on the definition of
health I estimate that roughly 80% of the human population is not healthy.
There are positive and negative relations between human health and biodiversity. The impact of
biodiversity on human health is unknown. Perhaps a small organism in some
square kilometres of the remaining rainforests on the long term appears to be a
necessary condition for our life by producing tiny quantities of chemical
compounds conditioning processes in our body and mind as catalysts. But we do
not know. How to calculate the risk of loosing them?
The reverse impact of human health
and growth on biodiversity is better known but not certain.
|

|
|
|
|
Fig. 692 Estimated
growth of world population
|
|
|
Health is a scale dependent concept in time. Though
world population is not healthy on an individual level, in the long term we are
a healthy species growing in numbers exponentially ousting other species,
living twice as long as some centuries ago.
And we are not only expanding in
number. Per person we need more and more living space in our homes and
neighbourhoods. In a wider context we reduced the space we need for agriculture
reducing biodiversity in rural areas at the same time.
Intensity of use
However, some 20 years ago Jong
(1985) found the intensity of urban use in The Netherlands was highest in shops (135
hours/m2year). After shops came offices, social-cultural facilities,
schools, home and garden (48 hours/m2year).[218] The other hours of the year (counting 8760 hours) in the urban
surface may be available for other species depending on the conditions we leave
them by design and use (distinguished by time scale). Some species accept or
even welcome our presence like that in step vegetation (for example greater
plantain, rats, mosquito’s, sparrows). Could we
welcome more rare species in our towns by creating ecotope cities or as
Tjallingii (1996) stresses ecological conditions? How does it interfere
with our health?
5.2.1
The importance of diversity for life
Risk-cover for life
Londo
(1997) considered diversity as a risk-cover
for life. In the diversity of
life there was always a species to survive or within a species a specimen that
survived. Survival of the fittest presupposes diversity from which can be
‘chosen’ in changed circumstances. Diminishing biodiversity means undermining
the resistance against catastrophes. From the 1.7
million species we know, we probably lost some 100 000. So, we not only
introduce ecological disasters, but we also undermine the resistance of life
against these disasters.
Ecological tolerance
|

|
The curve of ecological tolerance[219] relates the chance of survival of a species or ecosystem to any
environmental variable, for instance the presence of water. In that special
case survival runs between drying out and drowning (Fig. 693 ).
Imagine the bottom picture as a
slope from high and dry to low and wet. Species A will survive best in its
optimum. Therefore we see flourishing specimens on the optimum line of
moisture (A). Higher or lower there are marginally growing specimens (a). The marginal specimens however are
important for survival of the species as a whole.
|
|
|
|
Fig. 693 Ecological tolerance in theory and reality.
|
|
|
Suppose for instance long-lasting showers: the lower, too wet
standing marginal specimens die, the flourishing specimens become marginal, but
the high and dry standing specimens start to flourish! Long-lasting dry weather
results in the same in a reversed sense. Levelling the surface and water-supply
for agricultural purposes in favour of one useful species means loss of other
species and increased risk for the remaining.
But there is a less friendly ecological lesson hidden within this
scheme. Marginal specimens are important for survival of the species as a
whole. A reservoir of unhealthy specimens favours species. Death regulates
life. Health is also spatially scale-sensitive.
A realm of exceptions
Biodiversity in mankind is a crucial value in our quality of life.
As we are here we are all different and the very last comfort you can give a
depressed person is 'But you are unique'. Reading Philp
(2001) you should conclude that medicine hardly
discovered that uniqueness in the evaluation of medicines. It hinders
generalizing science using concepts as average and standard deviation.
Dieckmann, Law et al. (2000), Riemsdijk and
NOBO (1999) and Jong and Voordt (2002) are aware of that difficulty in ecology,
organization theory and design study. Evolutionary ecology (see Pianka, 1994) is only
comprehensible considering exceptions outside the limits of a normal test
population (3·standard deviation) as Philp (2001) described.
Diversity is also a precondition for trade and communication. If production
and consumption would be the same everywhere, there would be no economic life.
If we would have all the same perceptions and ideas, there would be no
communication. It is an important misconception to believe that communication
only helps bridging differences. Communication also produces
diversity by compensating each other and coordinating
behaviour by specialization. Diversity is a
precondition of freedom of choice, a fundamental right of any human.
Possibilities of choice
The World committee environment and development (1990) of chairwoman Brundtland[220] summarized the environmental challenge by
stating sustainability as leaving next generations at least as much
possibilities as we found ourselves.[221] But what are possibilities? 'Possibilities' is not the
same as economic supply. If our parents would have left us the same supplies as
they found in their childhood, we would be far from satisfied. 'Possibilities'
has to do with freedom of choice and thus variety. Our converging
Schumpeter-economy as Krupp (1995) described and converging culture of Fukuyama (1992) leaves no choice. In our search for the
alternative we find everywhere in the world the same hotels, the same dinners,
the same language. This century, the last 'primitive' cultures are lost and
with them an experience of life that no western language can express. After
looking at their dancers in the afternoon on our rain forest holyday we find
them back in the disco in the evening.
A world without difference
The most extreme consequence of this levelling out would be a world
without economy and even communication. If there were no longer any differences
in production factors, exchanging goods and services would no longer be
necessary. If total worldwide distribution of knowledge and consensus would be
the result of our communication age, there would no longer be anything
worthwhile to communicate. These thought experiments show clearly that
'difference' is also a hidden presupposition in communication and economy. The question remains on what
level of scale self-sufficiency is desired: global, continental, national,
local like Steekelenburg (2001) illustrates beautifully in his scenarios.
Quality
Quality can be measured in terms of possibilities of
use, experience and expectation for future generations. The way design can sustain a sustainable development in the
sense of Brundtland is to produce more ‘choices’ for man,
animal and plant. If there were one best solution for all problems of
architecture and urban planning, it would be the worst in the sense of choices
for future generations! This paradox pleads more for diversity than for uniform
solutions. Moreover, if there were a uniform solution, the designer would have
no task. Quality is always a function of variation.
|

|
Quality of possible experience
moves between diversity and uniformity, surprise and recognition. One step too
far into both sides brings us in the area of boredom or confusion.
This is a simple conception,
already recognized by Birkhoff (1933) and Bense (1954), but why did
it not succeed, why is quality always posed as an unsolvable question?
Because the concept of diversity
is scale sensitive and so is our experience.
|
|
|
|
Fig. 694 Quality = f(Variation)
|
|
|
When on one level of scale
we experience chaos, in the same time on an other level of scale we could
experience boredom.
Confusion of scale
As mentioned in the introduction, rarity, responsibility
for rare species and even health are scale sensitive concepts. So is quality.
But any discussion on variety and thus variables can fall prey to confusion of
scale. That means that even logic and science as forms of communication could
be prey to a scale paradox. The paradox of Achilles
and the turtle is a beautiful example of a scale-paradox in
time. The turtle says: 'Achilles cannot outrun me when I get a head start,
because when he is where I was at the moment he started I'm already further,
when he reaches that point I am again further and so on!’ This conclusion is
only incorrect by changing the time-scale during the reasoning. Russell (1919)
finds something similar on set theory. Russell bans sets containing themselves
and reflexive judgements[222] such as 'I lie’. This sentence is not only an
object statement, but in the same time a meta-linguistic statement about itself
producing a paradox. When I lie I
speak the truth and the reverse.
Scale paradox
|

|
The scale paradox[223] means an important scientific ban on
applying conclusions drawn on one level of scale to another without any
concern. The picture shows the possibility of changing conclusions on a
change of scale by a factor 3. There are 7 decimals between a grain of sand
and the earth. That gives approximately 15 possibilities of turning
conclusions. In the scale distance between a molecule and a grain of sand
applies the same. This ban is violated so many times, that this should be an
important criterion on the validity of scientific judgements.
If the scale-paradox influences
the concept of diversity, it influences any class stating a difference with
the rest.
|
|
|
|
Fig. 695 The scale paradox
|
|
|
An example of turning conceptions into their opposite by scale is
the duality of aim and means. For the government subsidizing a municipality the
subsidy is a means, for the
municipality it is an aim. So the
conception of means changes in a conception of aim by crossing levels of scale.
The turning of 'Zweckbegriff' into 'Systemrationalität' discussed by Luhmann (1973) may be a turning conception of the same
scale-sensitive character. In growing organizations integration on the level of the organization as a whole
means often disintegration of the subsystems and perhaps a new form of
integration in the sub-sub-systems. This scale articulated process is called 'differentiation'!
Avoiding confusion of scale
In Fig. 695 confusion of
scale is already possible by a linear factor 3
difference in level of scale. That is why in spatial planning we articulate
orders of size by a factor of approximately 3.
|

|
An element from the nearly
logarithmical series {1, 3, 10, 30, 100 …}
is the name (nominal value)[224] of an ‘elastic’ urban category ranging until those of the nearest
categories (scale range).
The name giving ‘nominal’ radius
r=10 then is the median of a chance density distribution of the logarithm of
radiuses between (rounded off) r=3 and r=30, with a standard deviation of
0.15. We chose a series of radiuses (and not diameters) because an area with
a radius of {0.3, 1, 3, 10km} fits
well with {neighbourhood, district, quarter, conurbation} or loose {hamlet, village, town, conurbation}
in every day parlance.
Then also the system of dry and
wet connections could be named in this semi logarithmical
sequence according to average mesh widths.
|
|
|
|
Fig. 696 Names and boundaries of urban
categories
|
|
|
State of dispersion
Form as a primary object of design supposes
state of dispersion.
|

|

|
|
|
|
|
Fig. 697 States of
dispersion r=100m
|
Fig.
698 Accumulation, Sprawl, Bundled
Deconcentration r=30km
|
|
|
|
Scale articulation of dispersed states
Scale articulation is especially important distinguishing states
of dispersion. State of dispersion is not the same as
density. Considering the same density different states of dispersion are possible (Fig. 699 ) and that is the case on
every level of scale again (Fig. 700 ).
|

|

|
|
|
|
|
Fig.
699 States of dispersion in
the same density on one level of scale
|
Fig. 700 One million people in two states of distribution on two levels of
scale (accords CC, CD, DC and DD).
|
|
|
|
Fig.
699 shows the use of the words concentration (C) and deconcentration (D) for processes into states of more or less
accumulation respectively. Applied on design strategies in different levels of
scale we speak about ‘accords’ (Fig. 700 ).
In Fig.
700 the regional density is equal in all cases: approx. 300inh./km2.
However, in case CC the built-up area is concentrated on both levels (C30kmC10km)
in a high conurbation density: (approx. 6000inh./km2).[225]
In the case CD people are deconcentrated only
within a radius of 10km (C30kmD10km) into an average
conurbation density of approx. 3000 inh./km2.
In the case D30kmC10km the
inhabitants are concentrated in towns (concentrations of 3km radius within a
radius of 10km), but deconcentrated over the region. This was called ‘Bundeled
deconcentration’ in NRO2. The urban
density remains approx. 3000 inh./km2.
In the case D30kmD10km
they are dispersed on both levels.
Urban sprawl
Urban sprawl in a radius of 10km hardly influences the
surrounding landscape when the inhabitants are concentrated in a radius of 30
(the two variants above in Fig. 700 ).
However, the urban sprawl in a radius of 30km
breaks up the surrounding landscape in landscape parks. By that condition the
sprawl within a radius of 10km is important again: the landscape parks are
broken up further into town landscapes. In The Netherlands until 1983 DC was
the national strategy (‘Bundled deconcentration’, ‘Gebundelde Deconcentratie’ from NRO2, RPD (1966)), after NRO3, RPD (1983) the policy changed into CC (Compact town’, ‘Compacte Stad’), but turned out in
practice as CD and even DD. The result of both strategies was disappointing.
|

|
|
|
|
Fig.
701 Urban sprawl in Randstad, The Netherlands
|
|
|
Distribution and abundance of organisms
In prominent ecology textbooks there are several
definitions of ecology emphasising dispersion or with an increasing awareness
of scale (in that case we will speak about spatial distribution):[226]
Andrewartha (1961), cited by Krebs (1994): Ecology is the scientific study of the distribution
and abundance of organisms.
•Krebs (1994): Ecology is the scientific study of the interactions that
determine the distribution and abundance of organisms.
•Pianka (1994): Ecology is the study of the relationships between organisms and
the totality of the physical and biological factors affecting them or
influenced by them.
•Begon, Harper et al. (1996): Ecology is the scientific study of the interactions that determine the
distribution and abundance of organisms, populations and communities.
Kolasa and Pickett (1991) seem to be the only ecologists fully aware of
scale articulation consequences avoiding confusion of scale.
Time-space scaling
|

|
Pianka (1994) stresses
relationships in a broader sense than spatial relationships. He adds a scheme
stressing scale in space and time, but does not detect any paradox.
‘Community and ecosystem phenomena occur over longer time spans and more vast
areas than suborganismal and organismal-level process and entities. (after Anderson
(1986) after Osmund et al.)’
Begon, Harper and Townsend (1996) distinguish organisms, populations
and communities.
|
|
|
|
Fig. 702 Diagrammatic
representation of the time-space scaling of various biological phenomena
|
|
|
That distinction looks like a distinction of
scale, but is primarily a distinction between different kinds of ecology:[227]
- autecology concerning populations of one species at a time within their
‘habitat’
and
- synecology concerning the community of different species in the same ‘biotope’.
On the level of organisms one could speak about
‘ecological behaviour’ as for instance Grime, Hodgson et al. (1988) elaborated as plant species bound ‘strategies
for survival’ like ‘competitors’, ‘ruderals’ and ‘stress tolerators’ as rôles in a play
concerned less predictable than communities reaching a well described ‘climax’.[228]
Global and continental
Ecological
typology is scale-sensitive. The subdivision of global life conditions in Fig. 703 distinguishes ‘biomen’[229] primarily by temperature and precipitation[230]. This variation is recognisable on a smaller level of scale
vertically in mountains. The average temperature and precitipation in the Netherlands
are near 10oC and 1000 mm. The natural vegetation in such conditions
is moderate deciduous forest, but grassland is not far from these conditions.[231] However, in the low countries of the Netherlands the availability
of water is much higher than to be expected from its average precitipation.
|

|

|
|
|
|
|
Fig. 703 Global and continental ecological typology
|
|
|
|
On a
continental level (r=3 000km) areas of vegetation like estuaries, salt vegetations, reed marsh, river accompanying, Atlantic heather, birch forest, oak-beach forest, pine-spruce forest, dunes, warm oak forest and high moor land are distinguished. On a map
types in a typology appear like legend-units in a legend (see Fig. 703 ). In The Netherlands, Northern Germany and Southern Denmark, the distinction of Fig. 703 (right) corresponds
with geological categories like Pleistocene (until 1 000 000 years old) and
Holocene (until 10 000 years old).
European level
On a European level of
scale different distinctions were made. Fig. 703 gave the most recent
one based mainly on forest types and Fig. 704 an earlier one based on
species[232].
|

|

|

|

|
|
|
|
|
|
|
Western (W), ‘Northern’ (N), Middle (M), ‘Eastern’ (O) andSouth-Eastern (ZO)
European vegetation areas.
|
Vliegenorchis H43
|
Herfsttijloos
|
Kleine Kaardebol
|
|
|
|
Fig.
704 Plants, characteristic for Middle-European vegetation areas (M)
in the Netherlands
|
|
|
In
The Netherlands the distinction of Fig. 703 (right) corresponded with geological categories like Pleistocene (until 1 000 000
years old) and Holocene (until 10 000 years
old).
Fig. 704 distinguishes grounds mainly older than 1 000 000 years
in Limburg as ‘Middle European vegetation area’ (M). Pleistocene and older grounds in South Limburg are nearly fully covered by
löss alternating with rock on surface, primarily consisting of chalk, marl and
limestone sometimes turning up elsewhere in The Netherlands as well. The rest
of The Netherlands as part of ‘West European vegetation area’ (W) is younger.[233]
Holocene and Pleistocene
On a
national level in The Netherlands Holocene and Pleistocene are the most
enclosing categories approximately separated by the 5m altitude[234], roughly a distinction of
clay (with peat and dunes) versus sand (intersected
by river clay or locally filled by high
moor land). The most urbanised
Holocene estuary area, botanically indicated
as ‘lagoon county’ is highly influenced by man and in the same time an
internationally rare cultural-natural monument of polders. It is ecologically divided further in many ways representing its
dynamic and unpredictable wet ecological diversity.
|

|

|
|
|
|
|
Fig. 705
Planning Ecological Infrastructure
|
Fig. 706
International rarity of landscapes
|
|
|
|
Based on
the synecological typology of Westhoff and Held (1969) and Held (1991), Bal, Beije et al. (1995);
Bal, Beije et al. (1995) defined 132[235] (in Bal, Beije
et al. (2001) reduced into 92) nature target types of
the national ecological infrastructure (EHS). However, Clausman and Held (1984) earlier had proved them to be inadequate
for the Holocene Zuid-Holland area. Too many transitional stages between sand,
clay and peat, influenced by a historical local diversity of cutting peat and
water management produced a variety of nature types nearly equalling the number
of grounds itself.
Different plants on Pleistocene and Holocene grounds
Apart from the sandy dunes, the
lower Holocene with clay from sea and rivers and low (wet) and high (acid) peat
has a very different vegetation compared with the higher and dryer pleistocene
covered with coarser sand and gravel.[236] The ecological difference between low Holocene and high
Pleistocene is clearly illustrated by dispersion of two species: meadow barley (veldgerst, Fig.
707) and wavy hair-grass (bochtige smele, Fig. 708).
|

|

|

|

|
|
|
|
Fig. 707 Dispersion of meadow barley (veldgerst)
|
Fig. 708 Dispersion of wavy hair-grass (bochtige smele)
|
|
|
|
Different plants in dunes and rivers
Holocene is subdivided in dune and river county, illustrated by the
dispersion of two other species, marram (helm, Fig.
709) and greater burdock (grote klis, Fig. 710). The remainder is
called Haf county with sea clay and peat.[237]
|

|

|

|

|
|
Meijden (1999) and Meijden, Plate et al. (1989) page 44 en 28
|
|
|
|
|
Fig. 709 Dispersion of marram (helm)
|
Fig. 710 Dispersion of greater burdock (grote klis)
|
|
|
|
General trees in The Netherlands
General trees in The Netherlands are alder (els), ash (es), sycamore (esdoorn), hawthorn (meidoorn), birch (berk), rowan or whitebeam (lijsterbes).[238]
|

|

|

|
|
Alder
(zwarte els)
|
Ash (es)
|
Sycamore (gewone esdoorn)
|
|

|

|

|
|
Midland
hawthorn (tweestijlige meidoorn)
|
Birch (berk)
|
rowan or
whitebeam (wilde lijsterbes)
|
|
|
|
|
|
Fig. 711
General trees in The Netherlands
|
|
|
|
|
Trees specific for Holocene and river grounds
Holocene and rivers are characterised by black poplar (zwarte populier), willow (wilg), dogwood (rode kornoelje) (Fig. 712).[239]
|

|

|

|
|
Black poplar
(zwarte populier)
|
Crack willow
(kraakwilg)
|
Dogwood
(rode kornoelje)
|
|
|
|
|
|
Fig. 712 Trees of Holocene and rivers in The Netherlands
|
|
|
|
|
Trees specific for
Pleistocene and dunes
Peistocene and dunes are characterised by scots pine (grove den), red oak (amerikaanse eik), beech (beuk), aspen (ratelpopulier), hazel (hazelaar), holly (hulst), locust tree (robinia pseudo-acacia) and rum cherry or black cherry (amerikaanse vogelkers).[240]
|

|

|

|

|
|
scots pine
(grove den)
|
red oak
(amerikaanse eik)
|
beech (beuk)
|
aspen (ratelpopulier)
|
|

|

|

|
|
hazel
(hazelaar)
|
holly
(hulst)
|
|
|
|
|
|
Fig. 713 Trees of Pleistocene and dunes in The Netherlands
|
Fig.
714 Flora districts according to Van Soest
|
|
|
|
|
|
Further elaboration of ecological
counties (districten) (Fig. 714) is given by Van Soest
(1929/32)[241]
5.2.7
3km Landscape
formations
Undisturbed ‘definitive’
vegetations
Obviously
any region in The Netherlands that has got the time for succession of vegetation types gets a
more or less ‘definitive’ vegetation. Coincidences of first establishments are
filtered out.
This
vegetation is not only dependent on soil, but also on climate, position in
respect to sea and ground water level. For example, peat will only remain at high
ground water level. In dry conditions it will settle, oxidate to CO2
en H2O and disappear leaving a lower mineral surface level.
In
this paragraph we will discuss landcape formations and typical forest
landscapes that would appear without impact of man at last. Agriculture and the
use of fertilizers caused a homogeneous landscape. But the agricultural surface
being reduced by economic conditions, an ecologically well-considered choice of
vegetation and management could restore regionally characteristic forest, kept open partially by wild grazing cattle. You can consider
this paragraph as a guide to planting, because trees occurring naturally in the
region will grow better. You can obtain regional knowledge about soils from
soil maps 1:50.000 with explanatory
discriptions of landscapes.
Natural forest types
Following
descriptions are derived from Leeuwen and Kraft (1959). With regard to these elaborations Van
Leeuwen’s nomenclature is obsolete but simple, useful and clarifying for
urbanists and not yet exceeded in that respect.
|
Forest
|
Natural
|
Reclaimed
|
|
Holocene
|
|
salicion[242]
|
Willow and poplar forests, often found on nutricious flooded areas like river
forelands. As coppice wood and wickers, willows are planted on
‘grienden’. Temporarily you will find these woods on other nutricious grounds
as pioneer vegetation.
|
Grass land on river forelands and ‘grienden’.
|
|
alnion incanae[243]
|
Alder and ash forests with densely shrubs on clay
or sandy nutricious grounds with high and often somewhat changing ground
water level or in the neighbourhood of streaming water. These forests
often contain some oaks and poplars as well[T.M. de9] .
|
Moisty grass land (meadows) sometimes with hedges (Rubion, alder), pollard
willows or poplars.
|
|
ulmion[244]
|
Oak, ash (somtimes elm or maple) forests on moisty, nutricious
sandy and not too heavy clay grounds with ground water level in reach of roots[T.M. de10] .
|
Settlements, horticulture, orchards, fields, grass land, elm lanes, country estates and dune woods.
|
|
sambuco-berberidion[245]
|
Hedges and thickets on most limy grounds
of Ulmion[T.M. de11] .
|
|
Pleistocene
|
|
rubion[246]
|
Hedges and thickets (hawthorn, sloe, roses,
blackberries) on nutricious, but not expicitly limy grounds[T.M. de12] .
|
Settlements, orchards and fields on rather dry grounds; grass
land on more moisty or very limy grounds.
|
|
carpinion[247]
|
Oak, ash (sometimes maple or beech) forests on nutricious, not too
wet loam grounds. [T.M. de13] In coppice wood
thickets you wil find hazel and hornbeam.
|
|
carpino-berberidion[248]
|
Hedges and thickets on most limy grounds of Carpinion[T.M. de14] .
|
|
violeto-quercion[249]
|
Oak (seldom birch or beech) forests or coppice wood on acid
but not extremely poor, ofthen loam containing or somewhat moisty sandy grounds[T.M. de15] .
|
Fields
|
|
vaccinio-quercion[250]
|
Oak (sometimes birch or beech) forests or coppice wood on on acid
extremely poor, sandy (sometimes loamy) grounds[T.M. de16] .
|
Prehistoric (neolithic) settlements, heath often later planted
with coniferous wood (drifting sand) or crops (if dry) or meadows (if wet).
|
|
Peat
|
|
betulon pubescentis[251]
|
Rarefied birch forests on somwhat dehydrated
peat grounds (very rare[T.M. de17] ).
|
Digged out or drained and manured meadows sometimes planted as
Alnion incanae.
|
|
sphagno-alnion.[252]
|
Birch (sometimes alder) forests with shrubs of alder
buckthorn, willows, bog myrthle on acid
peat grounds (rare).
|
Bluegrass lands, later usually drained and manured, sometimes
planted as Alnion incanae.
|
|
irido-alnion.[253]
|
Alder or willow (mostly coppice wood) in peat areas with very
hing, stagnating not too poor ground water, usually with rarified shrubs[T.M. de18] .
|
Moisty grass land, digged out or drained and manured meadows
mostly planted as Alnion incanae.
|
|
|
|
Fig.
715 Relation between original natural forest type and reclamated
landscape
|
|
|
Ideal typical profiles
The
situation of most important soils and corresponding vegetation is represented
in ideal typical profiles Fig. 716 to Fig. 719 never appearing in reality.
Corresponding forest types have been mostly disappeared since long and replaced
by grass and crops. They illustrate mutual arrangements of Dutch original or
natural landscapes. Soil maps give more detailed and realistic images.
The Northern coast formation of The Netherlands
|

|
|
|
|
Fig.
716 Ideal typical coast formation in Northern part of The Netherlands
|
Mid-West cost formation of The Netherlands
|

|
|
|
|
Fig.
717 Ideal typical coast formation in mid-West of The Netherlands
|
Peat, river and pleistocene sandy formations
|

|
|
|
|
Fig. 718 Ideal typical
peat, river and pleistocene sandy formations
|
|
|
Growing Peat
|

|
|
|
|
Fig.
719 Ideal typical ‘verlanding’ in
nutricious environments
|
|
|
Clay
|

|
|
|
|
Fig. 720 Ideal typical
boulder clay formation
|
South Limburg
|

|
|
|
|
Fig. 721 Ideal typical
formation of South Limburg
|
‘Original landscape’ is not the same as the
‘natural landscape’ appearing when human
impact would stop, especially when agricultural measures were very radical.
Succession
Organisms
influence eachother. In the beginning competition in fast growing homogeneous
pioneer vegetation is dominant. In the next
phase of succession different species alternate
their use of sun, water and minerals over the year and differentiate them over
the area in increasing specialisation. Primarily establishing plants cause a
micro climate and soil structure creating conditions for
other species. Under these conditions some newcomers get the opportunity to
built up reserves and become more competitive than their fast growing
predecessors. For exampe, they grow higher catching sunlight from their
neighbours or grow deeper surviving dry periods better by their longer roots.
In their shadow slow growing specialists settle.
Differentiation and
regulation
The
differentiating life community prevents large fluctuations of temperature and
moist, retains water and nutrients attracting new animals. Specific insects pollinate specific plants
and clear up plants weakened by competition in homogeneous vegetation. Birds control insect overloads,
disperse seeds. Large grazing animals keep spaces open, predators keep their number limited.
Reproductive cycles of every participating organism with its own consumptive,
productive and reproductive periods are geared to one another and find for
every phase the environmental circumstances they need, or die out. The rise of
mutual relations into a climax stage (Fig. 730) requires coordination in space and sychronisation in time. In general it
takes time.
Differerent communities
in the same biotope
In
the same type of biotope different life communities can develop, according to
the history of their development. Different (weather) histories after all,
change the biotope itself in different ways and select species differently. For
example, if papillionaceous flowers with their specialised
algae established in an early stage to combine nitrogen in the soil, an other
series of succession would follow then when they established later or never. If
not, vegetation is dependent on nitrogen manure from outside. And the
reverse, if there is an external nitrogen source in the beginning,
papillionaceous flowers would not survive competition.
Equal communities in
different biotopes
On
the other hand the same type of vegetation can disperse over different biotopes
as well. So, there is not always a one-to-one relation between biotopes and
life communities.
Especially
man plants on his fields and gardens species he wants to, regardless the
existing biotope accomodating it to his needs. He mostly reduces a mature
system into its pioneer stage to get homogeneous highly competing productive
crops. Then ecosystems do not reach their climax stage because human dynamic (grazing, mowing, burning
and digging) prevents succession into more differentated stages.
A first taxonomy of communities
Mutual
relations between species produce recognizable plant communities listed in 38
synecological classes from Westhoff and Held (1975)
summarised by Held (1991), subdivided in orders, unions and associations (partly elaborated in Fig. 722)[254]. Classes 32 to 38 elaborate
forests more in detail than Fig. 715 did obsoletely but simply. Some scientific names like Salicion (32Aa and
33Aa), Alnion (35Aa) remain the same, other forest types named in paragraph 5.2.7 changed.
|
code
|
class 01-38 ~ea
|
order A-C ~alia
|
union a-d ~ion
|
associatiion 1-99 ~tum
|
Dutch name class
|
01 Lemnetea Eendekroos-klasse
02 Zosteretea Zeegras-klasse
03 Ruppietea Ruppia-klasse
04 Charetea Kranswieren-klasse
05 Potametea Fonteinkruiden-klasse
………………………………….
29 Oxycocco-Sphagnetea Klasse
der hoogveenbultgemeenschappen en vochtige heiden
30 Nardo-Callunetea Klasse
der heiden en borstelgrasanden
31 Trifolio-Geranietea sanguinei Marjolein-klasse
32 Franguletea Klasse
der sporken-wilgenbroekstruwelen
32A Salicetalia
auritae
32Aa Salicion cinereae
32Aa1 Myricetum
gale
32Aa2 Frangulo-Salicetum
auritae
32Aa3 Alno-Salicetum
cinereae
32Aa4 Salicetum
pentandro-cinereae
32Aa5 Salicetum
pentandro-arenariae
33 Salicetea purpureae Klasse der wilgen-vloedstruwelen en bossen
33A Salicetalia purpureae
33Aa Salicion albae
33Aa1 Salicetum triandro-viminalis
33Aa2 Salicetum arenario-purpureae
33Aa3 Salicetum albo-fragilis
34 Rhamno-Prunetea Klasse
der eurosiberische doornstruwelen
35 Alnetea glutinosae Klasse
der elzenbroekbossen
35A Alnetalia
glutinosae
35Aa Alnion glutinosae
35Aa1 Carici
elongatae-Alnetum
35Aa2 Carici
laevigatae-Alnetum
36 Vaccinio-Piceetea Klasse
der naaldbossen
36A Vaccinio-Piceetalia
36Aa Dicrano-Pinion
36Aa1 Leucobryo-Pinetum
36Aa2 Dicrano-Juniperetum
36Ab Betulion pubescentis
36Ab1 Betuletum pubescentis
37 Quercetea robori-petraeae Eiken-klasse
37A Quercetalia
robori-petreae
37Aa Quercion robori-petreae
37Aa1 Querco roboris-Betuletum
37Aa2 Fago-Quercetum
37Aa3 Convallario-Quercetum dunense
38 Querco-Fagetea Eiken-beuken-klasse
38A Fagetalia
sylvaticae
38Aa Alno-Padion
38Aa1 arici remotae-Fraxinetum
38Aa2 onsortium van Carex remota & Populus nigra
38Aa3 runo-Fraxinetum
38Aa4 acrophorbio-Alnetum
38Aa5 iolo odoratae-Ulmetum
38Aa6 raxino-Ulmetum
38Aa7 nthrisco-Fraxinetum
38Aa8 rataego-Betuletum
38Aa98 lmion carpinifoliae
38Aa99 ircaeo-Alnion
38Ab Carpinion betuli
38Ab1 Stellario-Carpinetum
|
code
|
klasse 01-38 ~ea
|
orde A-C ~alia
|
verbond a-d ~ion
|
associatie 1-99 ~tum
|
Nederandse naam klasse
|
|
|
|
Fig.
722 Taxonomy of life communities according to Westhoff and Den
Held.
|
|
|
The next taxonomy
However,
that taxonomy was adapted again by Schaminee, Stortelder et al. (1995);
Schaminee, Weeda et al. (1995); Schaminee, Stortelder et al. (1996); Schaminee,
Weeda et al. (1998) . Fig. 723 gives an impression of the first classes only.
|
|
class 01-11 ~ea
|
order A-C, DG, RG ~alia
|
union a-d ~ion
|
association 1-99 ~tum
|
subassociatiion a-b
|
01 Lemnetea minoris
02 Ruppietea
03 Zosteretea
04 Charetea fragilis
05 Potametea
06 Littorelletea
07 Montio-Cardaminetea
08 Phragmitetea
09 Parvocaricetea
10 Scheuchzerietea
11 Oxycocco-Sphagnetea
……………..
|
|
klasse 01-11 ~ea
|
orde A-C, DG, RG ~alia
|
verbond a-d ~ion
|
associatie 1-99 ~tum
|
subassociatie a-b
|
|
|
|
Fig.
723 Taxonomy of life communities according to Schaminee.
|
|
|
This taxonomy at last was used in
nature conservation, simplified in nature target types we will discuss in 5.5.1 more in detail.
Based on ideas of Van der Maarel (1971), Runhaar, Groen
et al. (1987) divided Dutch
plant species in ecological groups (Fig. 724 ), suitable for estimating impacts of technical measures and
ecological potencies.
Fig. 724 below shows which ecological groups made progress in the last
century and which declined. It is clear that oligotrophe groups declined
substantially[255].
Ecological groups
classified by directly working conditions
This
subdivision restricts itself to conditions directly working on plants
like sunlight, moist and acidity. It avoids taking into account underlying
causes like soil type and water management complicating this classification.
These are important factors estimating the impacts of technical interventions
indeed, but they are originating in very different ways from higher levels of
scale.[256] For example, salty or brackish groups could not only be caused by
surface water but also by seepage. Seepage on its turn can cause very different
vegetations dependent on its chemical composition. Keeping classification
as close as possible to the plant, the number of subdivisions and their
presupposed explanation is limited. Moreover, the difference between ecotope
and vegetation fades away and classification concerns both.
A hierarchy in
classification
The
used characteristics show a certain hierarchy by which a higher characteristic
may not have to be subdivided further. For example within salty and brackish
environments salt proportion (salinity) is so dominant that no further subdivisions into nutriciousness
are necessary. On the other hand lower characteristics like soil spray (st) do not always have to
be added to higher characteristics.
Moreover,
hierarchy could cause different definitions of lower characteristics depending
on current higher characteristics. For example the degree of acidity in water depends strongly
on its proportion of bicarbonate (HCO3-
ions as buffer against acidification). On land other buffers are active. So, by
distinguishing land and water vegetations first you can combine both buffer
systems in the concept of acidity without losing their distinction but without
explanation of causes[257].
Main classification in
water, wetland and land vegetations
This
classification distinguishes primarily water (W), wetland (V) and land vegetations in
freshwater (if heavily loaded by organic pollution marked by ‘sa’, brackish (b)
and salty (z) environments). Land vegetations are subdivided further according
to succession stages of pioneers (P), grass land (G), brushwood (R), and forest (H), all of them subdivided
in wet (2), moisty (4) and dry (6).
Then
a distiction is made according to different degrees of nutriciousness from poor (oligotrophe) to rich (eutrophe). Within rich groups acidity does not make much sense, but within
poor groups it is essential because it regulates the availability of present
nutrients. In acid conditions existing organic material
can not be digested by any organism (pickled gherkins, dead bodies in peat).
More sp/ecific indexed
vegetations
Other subdivisions are
indicated by indexes. Wall vegetations (Fig. 725) like procumbent pearlwort (sagina procumbens, liggende
vetmuur), yellow corydalis (pseudofumaria lutea, gele
helmbloem) or ivy-leaved toadflax (cymbalaria muralis,
muurleeuwebek) get the index ‘mu’. Within moderately
nutricious environments pioneer and grass land vegetations can get the index
‘kr’ to indicate lime. Pioneer vegetations can get indexes like ‘st’, ‘ro’ and
‘tr’ to indicate soil spray, digged and treaded soil, often present in towns.
Some examples of coding ecological groups
For example treaded soil
is densified and relatively unaccessibe by water and air. Some plants are
specialised to such conditions. So, on pathways you will find well known P48tr
plants (Fig. 725) like plantain (plantago maior, grote weegbree), shepherd's-purse (capsella bursa-pastoris, gewoon herderstasje), knotgrass (polygonum aviculare, gewoon varkensgras), annual meadow-grass (poa annua, straatgras) or pineapple weed (matricaria discoidea, schijfkamille)[258].
|

|

|

|

|
|
procumbent pearlwort
P40mu
|
yellow corydalis
P40mu
|
ivy-leaved toadflax
P40mu
|
plantain
P48tr
|
|

|

|

|

|
|
shepherd's-purse
P48tr
|
knotgrass
P48tr
|
annual meadow-grass
P48tr
|
pineapple weed
P48tr
|
|
|
|
|
|
|
Fig.
725 Some wall and tread plants well known in urban areas
|
|
|
|
|
|
Plants indicating an
ecological group
Most
plant species appear in different ecological groups simultaneously. Plants
appearing in many ecotopes can live in many conditions, they have a wide
‘ecological tolerance’ and are less appropriate as indicators of specific conditions. Runhaar, Groen et al. (1987) distinguish two classes of
tolerance. Class 1 occurs in one or two very related ecotopes only; class 2
occurs in more types. Best indicators live in one ecotope only (class 1), but
they are often rare and difficult to recognise by laymen. So, to recognise an
ecotope you can best identify several species living together indicating the
same ecotope. The wider the tolerance the more species you have to identify to
be sure about the ecotope[259]. In the ecotope system
a species is classified in as many ecological groups as necessary to explain
2/3 of its presence. If species would be classified to all accidental ecotopes
they ever were found the classification would be little specific.
Less specific indicators
To
filter out less specific ecological groups taking up a major part of
The Netherlands the classification calculates all ecotope types back to the
same surface. For example sweet vernal-grass (anthoxanthum odoratum, gewoon
reukgras) appears optimally in poor grass lands (G22, G42), but in a lower
abundance and coverage also in more nutricious grass
lands (G27, G47). However, nutricious grass lands are very
common in The Netherlands and poor grass lands are
rare. The consequence is sweet vernal-grass occurs most in
nutricious grass lands in spite of its preference for poor grass lands. By
departing from relative occurrence per ecotope type commonness of nutricious grass lands plays no
rôle in classification.
Dependencies
Most animal species are
location bound by their dependency on specific plant species. That is why we
primarily concentrate on plants. For example the large copper butterfy (lycaena dispar, grote vuurvlinder) feeds only from june until half august on its host plant loosestrife (lythrum purple, kattestaart) and lays its eggs only on its breeding plant a water dock (rumex hydrolapathum, waterzuring) in weak condition (a healthy
specimen defends itself against damage by insects). This typical combination is
found in The Netherlands in peat counties between Friesland and Overijssel only. So, large copper butterfy is rare in The Netherlands.
|

|

|

|
|
|
|
|
|
water dock (waterzuring) V18,V19
|
large copper
butterfy (grote vuurvlinder)
|
loosestrife (kattestaart) R27,R28, H27,H28,V17
|
|
Fig. 726
Symbiosis of copper butterfy with breeding and host plant
Interactieve ETI CD-ROMs Heukels flora en vlinders
|
An other example of specific
dependency is a common night butterfly tyria jacobaeae (jakobsvlinder, Fig. 727) laying its eggs on common ragwort (senecio jacobaeae, jakobskruiskruid).
|

|

|
|
|
|
|
Fig. 727 Tyria jacobaeae and its breeding plant common ragwort on the roof of the faculty
|
|
|
Common ragwort is very poisonous except for Tyria jacobaeae’s caterpillar. It stores the poison. So,
the caterpillar and the butterfly are poisonous for their enemies.
Rare plants on poor grounds
If presence or digestibility of
minerals are a limiting factor, only rare specialists can survive. By manuring exactly these rare species loose competition
of common and fast growing species. A nutricion poor environment not only
selects rare species but also diminishes defence of plants. Weak plants are
better digestible by herbivores and insects. One often recognises
rare vegetation by a multitude of insects and their predators like birds.To
avoid leakage of catched ions on poor grounds plants build cholesterol in their membranes instead of sitosterol. However, sitosterol
makes cell walls stronger and plants less digestible by
herbivores (from cow to caterpillar). Where less herbivores survive the
ecosystem supports less species.[260] Cows on a richly manured meadow bend as far as they can over the
fence to eat grass from a neighbouring unmanured meadow, leaving the manured
grass uneaten. A farmer gladly puts an ill cow on an unmanured meadow.
Salt and acid diminish
digestibility of minerals leaving space for specialist
plants and peculiar ecosystems. Soured forests are rich in parasites. The abundance of great
titmouses increased in soured forests though they
suffered lack of calcium. Their eggshells became
thin.
Plants and insects
The relation of every Dutch plant
species with animals - particularly insects – is described in Weeda, Westra et al. (1985); Weeda, Westra et al. (1987); Weeda, Westra et al.
(1988); Weeda, Westra et al. (1991); Weeda, Westra et al. (1994) . The autoritive Meijden (1996) (see Fig. 672) refers to this
publication naming volume and page.
The question how animals recognise
‘their’ plants depends on perception of smell, colour and form. The
recognisability of plants for their matchmakers, the insects, culminates in their
reproduction organs, their flowers. The question how pistils recognise ‘their’ pollen is a vast area of mircoscopical research.
Fertilisation requires coordination in space and synchronisation in time between plant and animal.
Small populations at risk
After the problem of fertilisation the problem of seed dispersion follows. These problems occur on different
levels of scale. Topographic, demographic and genetic isolation of populations decreases genetic biodiversity and increases risk of dieing out. On a minimum
population area after 50 generations 10% of genetic
material may be left, decreasing adaptability and probability of survival. Genetic
deterioration becomes a big problem. A minimum population
area is not sufficient for conservation of genetic variation and impels making
gene banks of threatened species.
Connections between populations
This is an important subject for
nature conservation and spatial planning. The Dutch Nature conservation plan LNV (1990) and its succesors stimulate a main ecological
infrastructure (EHS, see paragraph 5.5.1) to connect important
natural areas by corridors for genetic exchange. This is more important
for mammals and reptiles than for birds, insects and plants. However, for mammals
and plants narrow corridors are very species-specific. Depending on their
lay-out they work for one species and not for other ones. For plants - the
basis of any food chain - isolation could even be preferable to avoid invasion
of fast growing common species. Rare species often grow and disperse slowly. So,
ecological infrastructure will haven little favourable botanical impact and
sometimes even negative[261]. For vegetation local diversity is a better investment than
connections.
According to Grime, Hodgson et al.
(1988) plants have three differerent
strategies for survival:[262]
1 growing fast,
reproduce and evacuate ("ruderals" like chickweed, stellaria media, vogelmuur);
2 develop competition power, then reproduce
("competitors" like rosebay willowherb, chamerion angustifolium, wilgenroosje);
3 endure difficult
circumstances other species avoid and reproduce when possible
("stress-tolerators" like cowslip, primula veris, gulden sleutelbloem)
Growing fast or slow
Cickweed can produce seed a fortnight after gemination.
It is record-holder of Dutch plants in that respect. The rosebay willowherb goes up fast to compete with other plants, but
can weaken by shortage of minerals and fall down. The cowslip is a specialist surviving in circumstances
other plants do not.
|
ruderal
|
competitor
|
stress-tolerator
|
|

|

|

|
|
Chickweed
(vogelmuur)
P48,P68
|
Rosebay willowherb (wilgenroosje)
R47,R67, H47,H62
|
Cowslip (gulden sleutelbloem) G43,G47kr,H43,H47
|
|
|
|
Fig. 728 Three strategies for survival according to Grime (1988)
|
|
|
Ruderals are found in newly
occupied areas (pioneer stage, see Fig. 730 ), stress tolerators in developed ecosystems (climax
stage) with less minerals.[263] Agricultural activity aims at fast growing crops like ruderals
and competitors. So, human impact is often not in favour of stress-tolerators.
Stress-tolerators are often protected plants.[264]
Generalisation is dangereous, especially if small differences
can produce great effects. That is the case in ecology. Biodiversity between
species and between specimens within any species is multiplied by the number of
contexts they live in. And the physical and social context of any location is
different from any other location because every location is unique if only
because of its location between the other locations of the Earth’s surface.
That diversity is a risk cover for life. But there are different differences.
Some of them we call ‘equality’. Equality is the basis of expectations. The
ecological expectations of our common future are gloomy. However, our
imagination covers more than expectations, it opens up possible futures as well
as probable ones. The modality of possibility requires an other way of
reasoning than probability.
In the advanced technology of pattern
recognition the emphasis on similarity shifts into a focus on dissimilarity
(Pekalska, 2005). Following that track
broadens the view into unexpected, improbable possibilities, opened up by
difference. Differences are observable at boundaries. So, it's worth the effort
to study boundaries rather than homogeneous areas. They determine the areas,
not the reverse. Perhaps it produces cross-border insight.
Besides autecology and synecology we know environmental science emphasising human society and
health, cybernetic ecology emphasising space-time
relationships, system dynamics ecology stressing abiotic points of
departure and chaos ecology stressing unpredictability
from minor earlier events.
Their
approach and terminology differ substantially:
|
|
naming abiotics
|
naming biotics
|
|
environmental science
|
environment
|
human society
|
|
autecology
|
habitat
|
population
|
|
synecology
|
biotope
|
life community
|
|
cybernetic ecology
|
abiotic variation
|
biotic variation
|
|
system dynamics ecology
|
ecotope
|
ecological group
|
|
chaos ecology
|
opportunities
|
individual strategies for survival
|
|
|
|
|
|
Fig. 729
Ecologies
|
|
|
The
sequence in this summary may reflect a decreasing human centred approach as we ask from urbanists on
their way from environmental scientists into designers of biotope cities or
even further. In that perspective of urban ecology, it is important to
understand the differences to avoid debates that paralysed thinking about
nature policy in the Netherlands for years.
Jong (2002) describes in her thesis the strikingly separated Dutch
development of the last four categories in Fig. 729 during the 20th
century. The clearest controversy - between the ‘holistic-vitalistic’ synecology and the ‘dynamical’ systems ecology - represents a beautiful example of spatial
dispersion in one species causing scientific diversity. Synecology primarily
developed in the Catholic University of Nijmegen (Westhoff) extending to Wageningen University of Agriculture in
the higher East of The Netherlands while ‘dynamic’ ecology originated from the
National University of Leiden (Baas Becking, Odum) in the wet lower West area.
System dynamics
System
ecology since Odum, E. P. (1971) distinguishes ‘ecosystems’
containing mass, energy and information within clear cut boundaries. In
particular at the boundary of an ecosystem inputs en outputs are observed and
measured trough time. The inside is concerned as a ‘black box’. Dependend on
external conditions these observations and measurements show a ‘behaviour’ useful to be expected in
other situations.[265]
|
|
PIONEER
|
CLIMAX
|
|
Energy
Net production
Food chains
|
high
linear
|
low
web
|
|
Community structure
Total amount of
organic material
Inorganic nutrients
Species diversity
Spatial diversity
|
small
extrabiotic
low
low
|
large
interbiotic
high
high
|
|
Life characteristics
Niche specialisation
Sizes of organisms
Life cycles
|
wide
small
short, simple
|
narrow
large
long, complex
|
|
Nutrient cycles
Mineral
cycles
Nutrient
exchanges
Reuse
|
open
fast
unimportant
|
closed
slow
substantial
|
|
Selection pressure
Growth strategy
Production
|
fast
quantity
|
controlled
quality
|
|
Homeostasis
Symbiosis
Nutrient
conservation
Coicidence
Information
|
undeveloped
small
high
little
|
developed
substantial
low
much
|
|
|
|
Fig. 730 System dynamic stages
|
|
|
A number
of scale classifications summarised by Haccou, Tjallingii et al. (1994), Klijn (1995), Kolasa and Pickett (1991) preceded Fig. 731. Such a classification is required to weigh rarity, replacebility, potential of territory and planned human artifacts.
The biological nomenclature is less articulated (factor
10?) than the urbanistic as yet (factor 3), but it proceeds to smaller measures
(from 10000km until m). That is why we fill the gaps by abiotic nomenclature as
coincidentally larger frames of smaller biotic components to get comparable
urban units (3km radius towns, 1km
districts, 300m neighbourhoods and so on). So, we consider the earth to be subdivided in biomen, a
continent in areas of vegetation, a
geomorphological unit in flora counties, a
formation in landscapes, a hydrological unit in communities described by Westhoff and Held (1969) and Meijden (1996), a soil complex ecological groups described by Runhaar, Groen et al. (1987) and Meijden (1996), a soil unit or its structural parts by cooperating or
competing organisms. In passing ecologies of different focus get their own
level of scale supposed to be optimal for their application. However, this
supposition is still arbitrary.
Territorial and taxonomic
classification
The synecological classification of communities and the system ecological
classification of ecological groups have their own levels of scale but their
intention is more taxonomic than territorial. So, biotic components have a
larger scale span than the scale classes employed here to be comparable with
urbanistic classes of smaller span. Synecological ‘classes’ can
take up kilometres, their subdivisions in ‘orders’, ‘unions’ and ‘associations’ can take up metres. An
ecological group (see Fig. 724) like P48 (pioneer vegetation on
moisty, very nutricious soil) can have a radius of 1km, but a vegetation P40mm
(on moisty walls) could be restricted to 100mm. An example of large scale span
on species level is known from fungi. Some of them are the largest organisms on
Earth, their mycelium extends to hunderds of metres.
Ecologies per scale
However,
to be able to compare different locations we keep up these names with the
supposed modal size (30m for ecological groups) as nominal measure.
|
nominally
|
abiotic frame
|
nominally
|
biotic components
|
ecologies
|
|
kilometres radius
|
|
10000
|
earth
|
3000
|
biomen
|
Geography
|
|
1000
|
continent
|
300
|
areas of vegetation
|
|
100
|
geomorphological unit
|
30
|
flora-counties
|
|
10
|
landscape
|
3
|
formations
|
landscape ecology
|
|
metres
|
|
1000
|
hydrological unit, biotope
|
300
|
communities
|
synecology
|
|
100
|
soil complex, ecotope
|
30
|
ecological groups
|
systems ecology
|
|
10
|
soil unit, boundaries
|
3
|
symbiosis and competition
|
cybernetic ecology
|
|
millimetres
|
|
1000
|
soil structure and ~profile
|
300
|
individual survival strategies
|
autecology
|
|
100
|
coarse gravel
|
30
|
specialization
|
biology
|
|
10
|
gravel
|
3
|
integration
|
|
1
|
coarse sand 0,21-2
|
0.3
|
differentiation
|
|
micrometres (m)
|
|
100
|
fine sand 50-210
|
30
|
multi-celled organisms
|
microbiology
|
|
10
|
silt 2-50
|
3
|
single-celled organisms
|
|
1
|
clay parts < 2
|
0.3
|
bacteria
|
biochemistry
|
|
0,1
|
molecule
|
0.30
|
virus
|
|
|
|
|
|
|
Fig. 731 Ecological units
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 731 is a preliminary and rough attempt to name abiotic and biotic
components by scale. Any level of scale has its own nameable diversity and
dynamics. It has to be discussed, elaborated and renamed by ecologists more
precise. Perhaps different approaches in ecology appear to have their own level
of scale, accessible to designers giving measure to the urban context on that
scale.
On
different levels of urban scale we could need different approaches; for
example:
• R=300m Communities in biotopes
• R=30m Ecological groups in ecotopes
• R=3m Symbiosis and competition
• R=30cm Individual
survival strategies
This paragraph discusses the one-sidedness of an emphasis on ecological
connections in nature conservation and spatial planning.
It traces back the track of Dutch nature conservation thinking, into the
typical Dutch ecologist Van Leeuwen stressing separations to restore the balance.
As a
student at the Faculty of Architecture in Delft my favourite lectures were
those of architect Aldo van Eijck and ecologist Chris van
Leeuwen.
|

|

|
|
|
|
|
Fig. 732
Aldo van Eyck
|
Fig. 733
Chris van Leeuwen
|
|
|
|
Both
emphasised the boundaries between spaces instead of the character of
the spaces intself.
‘The
boundary makes the difference; that’s where it happens’ they argued.
After
all, the task of urban and architectural designers is to draw boundaries.
Designers cannot do much more than drawing boundaries to make spaces visible
and usable.
|

|

|

|
|
|
|
|
|
Fig. 734 Van Eyck (1955-1960) Burgerweeshuis (Amsterdam)
|
Fig. 735 Van Eyck (1965) Sonsbeek paviljoen (Arnhem)
|
Fig. 736 The cell and its membranes
|
|
|
|
|
In the
seventies Aldo van Eijck could give a lecture without a break for six hours on
only a few images from Mali reporting his experiences of Dogon architecture (A.E.v. Eyck, et al., 1968). The Dogon live at a spectacular landscape boundary. Nobody wanted
to miss his rare and fascinating lectures and nobody in the overcrowded
classroom was bored for one moment by his humorous and furious criticism of
Western culture.
|

|
|
|
|
Fig. 737 An entrance as a seat: a ‘twin phenomenon’ or ‘in between realm’
|
|
|
I remember an image showing
the entrance of a hut with thick walls. The entrance had the form of a tree or
fungus (see Fig. 737).·
So,
you could sit in this boundary environment without being forced to choose
between inside or outside. You got coolness from the shade or warmth from the
sun simply by changing position. Van Eijck called such locations not forcing us
to choose ‘in between-realms’ or ‘twin phenomena’. He reproached our culture for forcing choices between false
alternatives: “Would you like to breathe in or out?”.
Van Leeuwen
The
emerging environmental awareness of the seventies made the lectures of Van
Leeuwen popular as well. Many remember them. Shortly before his death he
attended a conference dedicated to his work (D.J. Joustra, et al., 2004), organised by former students in urbanism and architecture. However, the speeches of
that conference showed very different applications, (especially in the field of
urban renewal) based on vague interpretations contrasting with Van Leeuwens own usual precision.
|

|

|
|
|
|
|
Fig. 738 Conference 2004
|
Fig.
739 Van Leeuwens references
|
|
|
|
He knew
the outdoor nature like no one else, but at the same time he was an armchair
scholar, writer of many dispersed articles and lecture notes (C.G. van Leeuwen,
1971) surprising colleagues and fascinating designers.
His
‘open-closed theory’ (Leeuwen, 1964) was the subject of dispute with his friend and close colleague
Westhoff from the University of Nijmegen at the former national
institute of nature conservation (RIN). Westhoff,
et al. (1975) developed according to Braun-Blanquet (1964) a Dutch synecological system of life communities now elaborated
by his successor (Schaminee, et al., 1995) and translated to nature target types (Bal et al., 2001) applied in the actual policy of the Dutch ecological network (NEN). However, that operational approach now loses foundation in the
perspective of climate change.
|

|

|

|
|
Source:
|
Source:
|
Source:
|
|
Fig. 740 Braun Blanquet
|
Fig.
741 Westhoff’s synecology…
|
Fig.
742 …translated into Dutch nature target types
|
|
|
|
|
Van
Leeuwen made field inventories himself for many years. Based on that experience
he emphasised transitions between such supposed life communities rather than
determining the communities themselves (Leeuwen, 1965). Precisely there he saw most rare species, especially if such a
transition was spun out along a broad strip (gradient) into an infinite range
of unnamed particular environments on a smaller scale. There the ecologically
most interesting specialists settled.
|

|
|
|
|
|
|
Fig. 743 Limes convergens
|
Fig.
744 Boundary rich
|
Fig. 745 Limes divergens (gradient)
|
|
|
|
|
Van
Leeuwen surprised colleagues by predicting the square metre where a specific
rare plant species could be found. For example I witnessed him when he was
already at an advanced age looking around and indicating the place where the
Carex pulicaris (‘flea sedge’, ‘vlozegge’) should grow.
However, the manager of the area never found that species on his territory. The
bystanders went on their knees and found the predicted flea sedge. Van Leeuwen
did it intuitively, based on ‘phenomenal’ field knowledge.
Gradient map in national
planning
This
line of thought was the guideline of the Dutch Second National Policy Document
on Spatial Planning (RPD, 1966), by which Van Leeuwen’s ‘Gradient map’ was published (see Fig. 746).
|

|
|
|
|
Fig. 746 ‘Gradient map’ in the Dutch Second National Policy Document on Spatial Planning
|
|
|
Citing RPD (1966) :‘Gradients are narrow zones with gradual
intermediate stages between landscapes with mutual strongly different life
circumstances. Examples are contact zones between salt and fresh water
environments, between relatively dry and wet areas, between poorly and richly
nutricious landscapes and slopes in high areas. Within or directly near these
gradual zones one finds a great gradation of environmental types in small
compass and as a result a large richness of plant and animal species. To this
richness belong nearly all rare plant species in our country. Moreover, here
are the regions where in the Netherlands natural edge of wood thickets can
develop.
Furthermore, the ‘conservative’
character of these transitional environments is typical. This assures
continued existence of species concerned at these locations, subject to not
disturbing the transitional environment fully by changes caused by modern
agricultural methods.’
5.3.5
·Regulation theory
However,
Van Leeuwen could not record that experience in writings otherwise than by
sketching a very theoretical framework known as ‘relation theory’. That theory is dispersed in many articles and elaborated in
different separate directions, always surprising by unexpected relations
between ‘down to earth’ examples. It led to his being made an honorary doctor
of the University of Groningen (1974), but the same University published a
doctoral thesis judging that theory to be invalid on mathematical grounds
(Sloep, 1983). However, the same critique applied also to other ecological
theories not studied by Sloep. Opposite that most readers and certainly
listeners got the feeling of a crystal-clear and simple framework, relevant to
many questions concerning design, spatial planning, urban renewal and nature conservation.
At last Van Leeuwen agreed to name his theoretical framework more precisely
‘regulation theory’, according to his cybernetic references of steering and disturbing.
One of
the first schemes I remember from Van Leeuwen’s lectures shows some basic
notions of that theory (see Fig. 747). Firstly it shows the possibility of a negative relation between
pattern and process in ecosystems in terms of spatial and temporal variation.
So, in general difference correlates to stability (often found near vague
boundaries), equality to change (often found near sharp boundaries). However,
I realised many years later this rule cannot be applied on any level of scale
if you take the scale paradox (see Fig. 823) into account.
|

|

|
|
|
|
|
Fig. 747 Spatial and temporal variation in the theories of Van
Leeuwen
|
|
|
|
According
to Ross Ashby (1957, 1956) ‘equality’ is not regarded as the
opposite of ‘difference’ but as its near-zero-value. After all, any imagined
difference can always be made more different by adding attributes of difference
(for instance difference of place, distance), but it cannot always be made less
different. A difference less than the least difference we can observe or imagine
is called ‘equality’. So, ‘difference’ and ‘change’, ‘equality’ and ‘stability’
in the scheme are all taken as values of ‘variation’ (the variable to be
distinguished spatially and temporally).
To
concern equality as a special kind of difference is contrary to the main
presuppositions of usual mathematics, the science of equality (you cannot count different categories)
and equations. However, chaos equations like yx+1=a·yx-(a·yx)2
where a>3.6 produce chaotic behaviour even different on different
computers using different roundings off (see Fig. 748).
The same
applies to very small differences of initial values in complex models producing very different
results.
|

|
 

|
|
|
|
|
Fig. 748 Chaotic behaviour of
yx+1=a·yx-(a·yx)2
where y0=0.001 and a = 4
|
Fig. 749 Reduction to the average
|
|
|
|
·The main problem
is, mathematical treatment of quantities presupposes qualitative categorisation
reducing differences to an ‘average’ (see Fig. 749), tacitly supposed in set theory.
Proceeding
that way, Van Leeuwen supposed processes of a second order on both pattern
(‘process on pattern’) and process (‘process on process’) called ‘differentiating’ and ‘steering’ with ‘equalising’ and ‘disturbing’ as zero-values (see the grey
arrows in left Fig. 747). Because these processes are changes as well, they are disturbing
and equalising by definition. Stopping a process of disturbing is disturbance
as well. Suddenly cleaning a ditch or decreasing the number of grazers could
deteriorate the condition of the ecosystem unexpectedly. The consequence of
this view appeared to be a recommendation not to change the condition too
sudden: clean the ditch or decrease the number of grazers slowly according to
the adaptation speed of the system.
So
according to Van Leeuwen it is easier to break down differences (equalising)
then create them (differentiating) and at the same time it is easier to
introduce changes (disturbing) than to guarantee duration (steering). This is a
simple verbal expression of the second law of thermodynamics in the perspective of
cybernetics. Within that interpretation ‘life’ is represented as a phenomenon
climbing up into local diversity and duration at the cost of global disturbance
located elsewhere.
Second order patterns and
processes
Regulation
theory became more complicated as soon as Van Leeuwen started to look for a
second order of patterns as well: ‘pattern on pattern’ (‘structure’, ranging from ‘separation’ causing difference, into its
zero value ‘connection’ causing equality) and
‘pattern on process’ (‘dynamics’, gradual (‘continuity’) or sudden (‘discontinuity’) changes and
stops, causing stability or change). Later I realised distinguishing levels of
spatial and temporal scales might simplify the argument
and put it into perspective. Perhaps the primary supposition about a negative
relation between pattern and process is limited to certain levels of scale
explaining exceptions. Perhaps concepts like ‘pattern on pattern’ are simply a
question of scale. ‘Difference’ is a scale sensitive concept
after all (see Fig. 823). Moreover, difference, equality, separation and connection are
direction-sensitive.
Ligitimate questions
Anyway,
many legitimate questions remain. I will summarise some, but not answer them
here. The very first question is: “Is this science?”. How could you make
categories as general as difference and change or separation and connection
operational for tests by empirical research? Should you not distinguish
different kinds of difference (for example abiotic, biotic differences,
differences observed on different levels of scale) to find mutual relations?
What causes what? Are the second order variations dominant? Does separation
cause difference or the reverse? How could you imagine separation without
difference?
Elaborating
these questions you come across fundamental epistemologic questions similar to
those I know from the debate about academic design (Jong and Voordt, 2002). They go beyond critics like those of Sloep because equality itself is
disputed. Consequently the use of categorisation presupposed in any variable is attacked. The very core of
that debate in practice is the question how to generalise solutions of
context-sensitive problems bound to specific unique
locations and contexts. That question applies to ecology as well, confronted
with a confusing diversity of species multiplied by a diversity of specimens
and contexts. Management theory also struggles with the
inapplicability of reduction into the ‘average’ (see Fig. 749) from empirical science (Riemsdijk, 1999).
From a
designer’s point of view many design decisions in specific contexts cannot be
supported by empirical research aiming at generalisation. “That conclusion does not apply to this specific location!”
designers complain. Van Leeuwen’s approach offered a terminology directly
fitting to design acts par excellence: separating and connecting. It functioned
as a great heuristic tool, but many applications fell prey to confusion of
scale by lack of scale articulation. Let us now go back to ecological practice.
Shortly
before his death Van Leeuwen offered me a clarifying example.
Between
meadowland and forest in natural circumstances a
fringe emerges through herbivore grazing (see Fig. 750 and Fig. 751).
These
animals mow with their long necks over the boundary of their reach without treading
or manuring (floating head). By doing so, they create prototypes of meadowland. In meadowland (a fringe laid out) without manuring, mowed without treading of note (‘hooiland’, an alternative etymology of ‘Holland’) you find species like Serratula Tinctoria (‘saw-wort’, ‘zaagtand’) not to be found elsewhere. Species rich steppe
grasslands like in the Ukraine and Russia
are comparable with meadowlands. Why are there species rich (hundreds per m2)
and species poor (one per ha) grasslands? Instability of a specific temporal
scale between dry and wet, cold and warm, fresh and salt seems to be the most
important factor.
Such an
instability reinforces itself: a dense, solid soil emerges with Plantago Major (the tread plant ‘common
plantain’, ‘weegbree’). Water remains there, but also flows away easily.
|

|

|
|
|
|
|
Fig. 750 Metaphors of wilderness
|
Fig. 751 Pruners, alternating grubbers, grazers
|
|
|
|
That is
why even more powerful alternations between wet and dry, cold and warm arise,
which cannot to be endured by many plant species. In Moscow dryness is locally
suppressed by the fire brigade, again reinforcing disturbance and condensation
of the soil. However, a slope stabilises. In the Netherlands plantago major
never grows on a slope, because the contrast between wet and dry is too small.
There, other plant species can survive stabilising the environment even
further. The Russian species rich steppe has, unlike a desert a stable water
balance horizontally and vertically. A desert becomes brackish by
evaporation and consequently rising water (ascending moist flow). Salinisation by irrigation is a well known
phenomenon. So, a linking between wet-dry, cold-warm, salt-fresh alternation
arises there, which does not happen in species rich steppes. Against temporal
changes there are stable spatial transitions based on selective separation.
What I
would like to bring to the fore is the importance of inaccesibility, isolation,
in this case for large mammals. As the concept of ecological networks
(ecologische infrastructuur) started its triumphal progress in the Netherlands
(D.de Bruin et al., 1987, ‘Plan Ooievaar’; primarily based on separation), connections are primarily
emphasised.
|

|

|
|
|
|
Fig. 752 The
‘Plan Ooievaar’
|
Fig.
753 Separation of nature and agriculture:
zoning, selection, regulation, ‘ecological
networks’
|
|
|
|
I would
like to set against that emphasise for a while one-sidedly, the importance of
separations to arrive at the middle (mi-lieu). The concept of ‘structure’ (litterally ‘brickwork’)
comprises both separation and connection. Exactly their combination produces
particular environments where specialists are at ease. Researching that kind of
environment could be named ‘structure ecology’. In terms of regulation theory both isolation and connection
are a value of separation. Connection is solely a zero value of separation.
Connection supposes separation, not the reverse. There are no windows without
walls. But there is ‘difference in separation’, always a combination of
separation and connection while separation directs connection.
The
first notable combination follows on the ‘basic paradox of spatial arrangement’ as Van Leeuwen named it: the
phenomenon of separation perpendicular to connection.
|

|

|
|
|
|
Fig. 754 Basic paradox of spatial arrangement
|
Fig. 755
Selectors
|
|
|
|
A road
is laid out to connect, but perpendicular to that connection it separates. That
is painfully felt at crossings. The solution to connecting perpendicularly to
the other connection is separating vertically (viaduct) or in time (traffic lights, see Fig. 754). However, there are more combinations of separating and
connecting. Deck, dam, gutter, pipe and bowl are examples of ‘selectors’ in one, two, three, four and
five directions, selectively connecting into the other directions. That
direction-sensitive connection quality cannot be imagined without separation
into the other directions. Selectors take care not everything is going anywhere.
Taps, lids, valves, wedges and wheels are regulators taking care not everything is always going somewhere.
Living organisms are complex combinations of selectors and regulators known in
technology as mechanisms on different levels of scale
(see Fig. 756, Fig. 757 and Fig. 758).
|

|
|
|
|
Fig. 756 Mechanical forms of selection and regulation by separating and
connecting
|
|
|
|

|

|
|
|
|
Fig. 757 Sluice closed
|
Fig. 758 Sluice
open
|
|
|
|
In the
doctoral thesis of Van Bohemen (H.D.v. Bohemen, 2004) strikes that the hundreds of millions (!) spent on ecological
connections are hardly judged on their ecological effect.
|

|

|
|
|
|
Fig.
759 Technical ecology
|
Fig.
760 Ecological connections
|
|
|
|
The
argument is: you have to build a wildlife viaduct before you can measure the
effect. That phase is now upon us, but it is recognised that just as in
epidemiological research cause and effect are
difficult to separate. And then we still focus solely on the effect on
populations of some species. Which effect the constructed connections show on
other species is even more difficult to determine. The deteriorating effect of
positive discrimination is well known from hanging on
nesting-boxes: other bird species were ousted, insects died out and the plant
species having them as postillions d’ amour disappeared.
The
impact of connections is sometimes demonstrably
negative. Examples include the import of alders from Eartern Europe in the
seventies or the connection of the Main-Danube canal. The connection of all parts of the world to each other
(globalisation) may be the greatest danger. Connecting genetically different
races could cause loss of biodiversity. That leads to the subject fascinating
me most: levels of scale. At what level of scale connecting is the best strategy,
and at what level of scale separating? The best argument for separating areas
is the emergence of subspecies, though it takes a lot of time. A crucial
question is: are we in the Netherlands in need of other large mammals than
grazers if they have better and more sustainable conditions elsewhere? Could
not we create in our wet country much more interesting ‘ecological conditions’
by separation (Tjallingii, 1996), conditions lacking everywhere else? Holland hooiland!
|

|

|
|
|
|
Fig.
761 Ecological conditions
|
Fig.
762 Separating flows
|
|
|
|
A more
moderate conclusion is that ecology cannot produce general statements, though
politicians would like to seduce you that way. That is what I learned from the
doctoral thesis of Mechtild de Jong (2002, see Fig. 763 and Fig. 764).
That
methodological problem of scientific generalisation in the context-sensitive
relations between one and a half million of species from which we know so
little, is something shared by ecology with context-sensitive design (Jong and
Voordt, 2002) and management sciences.
The
problem of the classical empirical ideal to produce generalising statements
(out of bits and pieces, to deduce subsequently from these statements
conclusions for specific cases) increases if you realise any species comprises
differently reacting individuals. That problem increases even more so, if you
realise that any individual arrives in a different context. The urbanist or
architect knows the problem only too well.
An
ecologist is not invited to copy solutions, but to bring a local field of
problems into a common solution by a unique concept. That is not solely an
ecological network, but a more complete ecological infrastructure.
|

|

|
|
|
|
Fig. 763 Separations in Dutch ecological thinking
|
Fig. 764 A genealogy of theories
|
|
|
|
Biodiversity in towns
Since 19th
century’s Dutch hygienic developments in the urban
area founded by Cohen (1872) and historically
described by Houwaart (1991) - the very
source of public housing policy and urban design - biodiversity in spaced towns outruns rural
biodiversity.
|

|
|
|
|
Fig. 765 Number of wild plant species per km2 in the lower and higher part
of The Netherlands
|
|
|
Fig. 765 shows that some square
kilometres in the urban area of Zoetermeer indicated in the left picture
have more that 250 wild plant species per km2. Local observers (like
KNNV Zoetermeer, reported by Jong and Vos (1995); Jong and Vos (1998); Jong and Vos (2000); Jong
and Vos (2003) ) counted even more than national ones (counted by FLORON,
reported by Groen, Gorree et al. (1995).
|

|

|
|
|
|
|
Fig. 766 Number of plant species per km2 in Zoetermeer and Enschede
|
|
|
|
The
urban area of Zoetermeer is more in contrast with the rural environment
characterised by cattle breeding than Enschede (indicated in the right
picture) surrounded by more natural equally rich areas. Fig. 766 shows both in more detail. Here we can see that infrastructure and industrial areas
contribute more than we would expect by intuition. Their verges, slopes and rough
grounds are less visited and disturbed by man and pet.
Counting species per km2
The
number of species per km2 is added up over several years. So, many species
could have been disappeared, they then only show the urban potential. Moreover,
some square kilometres could have been observed better than other ones, for
example the outskirts.
|

|

|

|
|
180
|
200
|
330 wild plant species
|
|
low-rise outskirts
|
high-rise
|
centre
|
|
Fig. 767
Number of wild plant species in 3 km2
of Zoetermeer
|
|
|
|
|
Even
when in the centre the plant observations were better than in the outskirts, Fig. 767 warns us for the intuitive
view that biodiversity always decreases from the outskirts into the centre. The
large number of observed species in the central km2 could also be
explained by urban age, abiotic variation like seepage, drainage, water level or intersection by infrastructure with verges and slopes, less influence of adjacent agriculture and manure of cattle
breeding dispersed by water or wind.
So, some
of these possible causes could be varied as means of design aiming urban biodiversity.
Rarity in the urban environment
Fig. 768 arranges some 500 urban plant
species from the 1500 known in The Netherlands in a sequence of national
rarity, naming 50 of them only. Their national presence in % of the 5x5km
observation squares is recognisable in the rising line. The spots show the
urban presence in % of 1x1km observation
squares in Zoetermeer. So, the spots above the line are more common in
Zoetermeer than in The Netherlands, the spots below less so.
|

|
|
Fig. 768 Local rarity (100% is very common) of approximately 500 plant
species (only partly named) in a sequence of national rarity
|
|
|
A number
of nationally rare plant species in the left side of Fig. 768 evidently found their place in urban ecotopes. In the wake of urban
plants and ecotopes rare insects and fungi have been observed in Zoetermeer,
but seldom nationally rare vertebrates.
In 1994,
it was established for the first time that the biodiversity per km2 in
Amsterdam. By Denters, Ruesink et al. (1994) and Vos (1993; Vos (1996) and Zoetermeer (Vos 1993, 1998) is up to five
times higher than in the agrarian surroundings of these cities. In saying this,
of course, it should be noted that the richness of species in urban ecosystems
differs from that of the classical nature areas.
The
agrarian surroundings of Amsterdam and Zoetermeer are not nature areas, but are
a series of monocultures closely oriented to economic production. It is no
wonder that the large cities show a more diverse range of species.
Nevertheless, the potency of the ‘urban district’ should not be underestimated.
Open
space in the Netherlands is reduced
by 12.5% urban and rural built area for 16 000 000 inhabitants with
ample 300 m2 average built area per person. When these inhabitants were concentrated in 16 conurbations of 1 000 000
inhabitants each within 10km radius (see Fig. 700 ) - regularly dispersed over the country - 10 open large landscapes
with a free horizon of 30km radius would be
available as open space. They would be accessible within 10km from everybody’s
house. In empty spaces of that measure bears and eagles could find their
habitat and the weekends could be filled by survival journeys we now look for in other
countries once a year.
Landscapes (geomorphological units)
However,
agriculture and urban sprawl have filled these potentially
open landscapes. If we name an area of 30km radius still a landscape as long as there are less
than 1 000 000 inhabitants, The Netherlands still have 10 landscapes
(see Fig. 769 ). But not for long, because there are landscapes with nearly
1 000 000 inhabitants and great pressure of urban sprawl. The size of
spots in Fig. 769 meets the average urban density in The Netherlands. So, where
they overlap the density is higher than average.
|

|
|
|
|
Fig. 769 Built and open space in The Netherlands
|
|
|
Keeping landscapes open
From Fig. 769 we can conclude that concentration within conurbations (r=10km)
does not help much in keeping landscapes open. Regional concentration (r=30km)
does. Regional deconcentration breaks landscapes up into landscape parks or
urban landscapes like happened in the Green Heart of Randstad (recently named Green
Metropolis or Deltametropolis). However, deconcentration within conurbations (r=10km) could help
making biotope cities. What kind of biotopes are they?
Possibilities of size
Form,
size and structure of components are conditions for the function of open areas though urban functions on
their turn can be the historical cause of form and structure. The landscape
consultancy H+N+S in Utrecht visualised the
functional charge for nature as a function of
size and altitude in Fig. 770 .
|

|
|
|
|
Fig. 770 Possibilities for nature by size and altitude
|
|
|
In Fig. 771 they summarised possibilities
of human recreation as well.
|

|
|
|
|
Fig. 771 Possibilities for recreation by size and altitude
|
|
|
The
smaller the area the less animals could find a habitat, but that is not the case for botanical biodiversity as far as
their distribution is not dependent on animals.
Parks, size and distance from residential areas
A
crucial space-time dilemma of urban planning is priority for either small open spaces nearby
residential areas or remote larger ones with more travel time but a better
survival of animal populations and recreational possibilities.
If on
any level of scale in a town the green area has a size equal to the maximal
walking distance (standard green structure, see Fig. 772 ), then the green area counts 1/10 of the total area. In that case
every inhabitant of a town (approximately 30km2, about 100 000
inhabitants) would have 30m2 town park. The same applies on a
district and neigbourhood level of scale for district parks and neigbourhoodparks.
If that reasoning is extended into ensemble green every inhabitant would have
have disposal of approximately 70 m2 public green area. In the Dutch
context that is a maximum (see Fig. 773), but it is an easily manageable target standard. Now you can work
out how much a town deviates from that
standard and which level of scale is favoured.
Both green surfaces in urban areas and their
distance to inhabitants can be expressed as a radius. In that case a radius r
represents a walking distance or an area a = p r2,
equal to a circular surface of the same size. That representation of surface is
more directly imaginable than huge numbers of hectares fastly increasing by a
growing scale. A radius grows slower, and by doing so it indicates orders
of size more easily. Fig. 774 shows some standards for
green surfaces and their distance to the served inhabitants that way. In that
figure we can observe that 'English Nature max.' proposes larger green areas at
a distance below 1000m and smaller areas further away than what we will explain
here as a ‘Standard Green Structure’. Furthermore, we can conclude that all
other mentioned (Dutch) standards are below that standard.
|

|

|
|
|
|
|
Fig. 774 Some standards for green
surfaces in urban areas
|
Fig. 775 Optimally accessible
green surfaces
|
|
|
|
The figures are calculated in a way explained in
this section. Greenery standards expressed in m2 per inhabitant
require suppositions about densities for comparison. These densities are taken
from the ‘Standard Green Structure’ to be explained below.
Nominal orders of size
If in a range of radiuses, you take after ‘r’ the next radius ‘R’
ample three times larger (R≈3.16·r), then the next area A is ten
times larger (A≈10r). It could encompass 7 smaller circles
(70%) in closest packing, and a surface proportional to ample 3 circles (30%)
as ‘tare’ (see Fig. 775).
If you take an easily nameable range of 'nominal' radiuses = {1, 3,
10, 30, 100, 300, 1 000, 3 000, 10 000, 30 000m}, then the
surface increases at average with a factor 10.
In this paper ‘nominal’ means, that if I name a surface ‘10m’,
then I will mean something in between 3 and 30m. So, ‘nominal measures’ are not
exact, they are 'elastic' between their neighbours, indicating an order
of size.
Standard Green Structure
But, greenery standards expressed in m2 per inhabitant
are still incomparable to those expressed in surfaces and distances. Within R
they suppose densities, and densities determine the amount of users and the
costs of maintenance. I will use a
'Standard Green Structure' to provide densities on different levels of scale for
comparison. Green surfaces are optimally accessible if they are located in the
centre of the urban areas they serve. In that optimal case the distance from
the boundary of an urban area involved (radius R) to the boundary of a central
green surface (radius r) is the maximum walking distance R-r (see Fig. 775). The 'average' distance is
approximately half R-r (depending on different densities within the residential
area). If the average distance to the green area is the same as its
radius, then in this paper we call that distribution of green areas over these
levels 'Standard Green Structure' (see Fig. 776). Moreover, in Fig. 776 some common names are
added. In this paper they are used to interprate other standards.
|
|
|
|
|
|

|
|
nominal
|
name
|
nominal
|
nominal
|
nominal
|
|
green area
|
|
urban area
|
‘average’ distance
|
max. distance
|
|
r
|
|
R
|
r
|
R-r
|
|
m
|
|
m
|
m
|
m
|
|
10000
|
landscape park
|
30000
|
10000
|
20000
|
|
3000
|
urban landscape
|
10000
|
3000
|
7000
|
|
1000
|
town park
|
3000
|
1000
|
2000
|
|
300
|
district park
|
1000
|
300
|
700
|
|
100
|
neighbourhood park
|
300
|
100
|
200
|
|
30
|
small public green
|
100
|
30
|
70
|
|
10
|
common garden
|
30
|
10
|
20
|
|
3
|
private garden
|
10
|
3
|
7
|
|
|
|
|
Fig. 776 A Standard Green
Structure
|
Fig. 777 Shift from average into maximum distance
|
|
|
|
In Fig. 777 the Standard Green
Structure is given in grey. However, most standards are based on the maximum
distance. So, for comparison we have to shift the dots half R-r to the right
(red dots) as used in Fig. 774.
Inhabitants
In this concept of a Standard Green Structure
the spatial distribution of green surfaces is determined, but not yet the
number of people served. They determine the density or its reciprocal value,
the land use in m2 per inhabitant. However, if a village of
10 000 inhabitants grows into a town of 100 000 inhabitants, it will
probably need a town park and if it grows into a conurbation of
1 000 000 inhabitants it will probably need a town park for every
township and an urban landscape for the conurbation. That amount of desired
untilled land was earlier provided as countryside around the village. In a
first approximation that will increase the land use of green surface within the
urban area.
|
Urban R(m)
|
Green r(m)
|
|
|
Ambition
|
Inhabitants
|
|
|
Ambition
|
Inhabitants
|
|
30 000
|
10 000
|
|
|
countryside
|
0
|
|
|
countryside
|
0
|
|
10 000
|
3 000
|
|
|
countryside
|
0
|
|
1
|
conurbation
|
1 000 000
|
|
3 000
|
1 000
|
|
|
countryside
|
0
|
|
6
|
townships
|
166 667
|
|
1 000
|
300
|
|
1
|
village
|
10 000
|
|
36
|
districts
|
27 778
|
|
300
|
100
|
|
6
|
neighbourhoods
|
1 667
|
|
216
|
neighbourhoods
|
4 630
|
|
100
|
30
|
|
36
|
urban islands
|
278
|
|
1 296
|
urban islands
|
772
|
|
30
|
10
|
|
216
|
building complexes
|
46
|
|
7 776
|
building complexes
|
129
|
|
10
|
3
|
|
1 296
|
buildings
|
8
|
|
46 656
|
buildings
|
21
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 778 Different ambition levels
|
|
|
|
|
|
|
|
|
|
|
|
Densities
|
Higher level
|
gross
|
|
|
|
|
|
|
|
tare = green
|
|
net (residential)
|
|
Lower level
|
|
|
|
|
|
|
|
|
|
|
|
|
|
net
|
|
|
|
|
|
|
|
|
|
Fig. 779 Net of higher level equals gross of lower level
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ambition
|
density
|
|
land use
|
|
|
gross
|
net
|
|
gross
|
- green
|
- rest =
|
net
|
|
|
inh/ha
|
inh/ha
|
|
m2/inh.
|
m2/inh.
|
m2/inh.
|
|
|
village
|
32
|
59
|
|
314
|
28
|
116
|
170
|
|
neighbourhoods
|
59
|
88
|
|
170
|
19
|
38
|
113
|
|
urban
islands
|
88
|
164
|
|
113
|
10
|
42
|
61
|
|
building
complexes
|
164
|
246
|
|
61
|
7
|
14
|
41
|
|
buildings
|
246
|
455
|
|
41
|
4
|
15
|
22
|
|
|
|
|
|
|
68
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 780 Standard Green Structure densities and land use on the ambition
level of a village
|
|
|
|
|
|
|
|
|
|
|
ambition
|
density
|
|
land use
|
|
|
gross
|
net
|
|
gross
|
- green
|
- rest =
|
net
|
|
|
inh/ha
|
inh/ha
|
|
m2/inh.
|
m2/inh.
|
m2/inh.
|
|
|
conurbation
|
32
|
59
|
|
314
|
28
|
116
|
170
|
|
townships
|
59
|
88
|
|
170
|
19
|
38
|
113
|
|
districts
|
88
|
164
|
|
113
|
10
|
42
|
61
|
|
neighbourhoods
|
164
|
246
|
|
61
|
7
|
14
|
41
|
|
urban islands
|
246
|
455
|
|
41
|
4
|
15
|
22
|
|
building
complexes
|
455
|
682
|
|
22
|
2
|
5
|
15
|
|
buildings
|
682
|
1263
|
|
15
|
1
|
5
|
8
|
|
|
|
|
|
|
72
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 781 Standard Green Structure densities and land use on the ambition
level of a conurbation
|
|
|
|
|
|
|
|
|
|
Comparing greenery standards expressed in surface, distance or m2
per inhabitant
Fig. 782 shows the m2
green area per inhabitant of different standards distributed over different
levels according to levels and densities supposed in the Standard Green
Structure. Figures for common and private gardens are added for comparison.
|

|
|
|
|
Fig.
782 Standards of green area
expressed in m2 per inhabitant on different levels of scale
|
|
|
If figures are given for the 'urban landscape'
(yellow) the ambition is apparently a conurbation with higher densities than a
town. However, most standards do have the ambition of a town. So, the Standard
Green Structure shown here is calculated with the ambition of a town. To change
that, use the spreadsheet mentioned earlier. That sheet shows how densities are
calculated for different ambitions. Moreover, it enables you to make your own
programme for urban green space according to the identity of the location.
Making a specific programme for urban green space
Given the ambition chosen in an other part of
the spreadsheet, the worksheet shows the result of your choices asking radiuses
of the urban and green area on two levels of scale (for example town and
district, see Fig. 783), and the number (1 to 6)
of green spaces on the lower level.
|

|

|
|
|
|
|
Fig.
783 Two levels of scale
represented in a 1000m grid
|
|
|
|
These choices can be made by five sliders and
the spreadsheet informs you directly about the consequences (see Fig. 784). On a copy of Fig. 774 two new green spots show
how your programme is in the proportion of the other standards.
|

|
|
|
|
Fig.
784 Choosing a programme
|
|
|
Distributing green areas according to the programme
The next worksheet shows a square with the same
surface of the largest circle you chose divided in 90x90 modules, telling you
how much modules you need of each category to fulfill your own programme (see Fig. 785).
The last problem is to increase the net
densities of each module to fulfill your programme.
A first visualisation
This exercise is real time accompanied by a
rough visualisation (see Fig. 786).
|

|
|
|
|
Fig. 786 A first visualisation
|
|
|
This figure does not represent building heights
but densities. To get an impression of building heights the vertical
exaggeration is estimated depending on the supposed floor surface per
inhabitant, the supposed height of a story and the supposed percentage of
built-up area within each module.
Connecting or separating
Ecological infrastructure could be important for distribution of animals
with a larger feeding ground or reproduction area than the same areas not
connected. However its effectiveness is species specific and not convincingly
proven. Their surface could be at the expense of larger concentrated areas.
|

|

|
|
Open area concentrated but
isolated
|
The same area connected
but deconcentrated
|
|
Fig. 787 The surface dilemma
of concentrating or connecting
|
|
|
|
Tummers and J.M. (1997)
defend central open areas instead of peripheral dispersion.
Spatial claims
Claims as mentioned in the 5th National Plan of spatial policy NRO5, VROM (2000) are summarized below left. The expected shrinkage of
agriculture surface cannot compensate the growth of other claims to the needed
zero on the fixed surface of Deltametropolis. So, many claims will not be
satisfied or perhaps be solved in space-saving combinations. From the drawing on page 135 of the mentioned plan one can count
the claims in the Deltametropolis. Below right these claims are expressed in
km2 and in circles of 1 and 3km occupying the same surface[266].
|
|
Nederland
|
|
|
|
Deltametropolis
|
|
|
|
1996
|
claims
|
|
|
claims
|
km radius
|
|
|
km2
|
low
|
high
|
|
high
|
3
|
1
|
|
|
|
|
|
|
km2
|
number
|
|
living
|
2242
|
390
|
850
|
|
210
|
7
|
3
|
|
working
|
959
|
320
|
540
|
|
120
|
4
|
2
|
|
infrastructure
|
1340
|
350
|
600
|
|
90
|
3
|
1
|
|
nature, recr & sport
|
5439
|
4770
|
4770
|
|
970
|
34
|
2
|
|
water
|
7653
|
4900
|
4900
|
|
380
|
13
|
3
|
|
agriculture
|
23508
|
-1700
|
-4750
|
|
-1050
|
-38
|
7
|
|
|
41141
|
9030
|
6910
|
|
720
|
23
|
18
|
|
|
|
Fig. 788
Claims derived from the national plan
|
|
|
Visualising the supposed
claims
These
circles are drawn at size in the figure below right. So, 10 circles of 3km
radius are put together to 1 circle of 10km radius. In the same way one can ’decompose’
any circle in 10 smaller ones to picture more precisely the location,
eventually till the picture has reached a photographic halftone appearance with
countable spots in different colours (pointillistic representation). This representation for instance shows at a glance the living
environments of metropolitan, conurbation or urban centre (1kmť or 10,000 people surrounded by 30, 10 or 3km urban area), urban outskirts (1kmť outside
the centre in at least 3kmť urban
area not bordering on green areas of the same size), green urban areas (such an urban outskirt bordered
on at least 1kmť green
area), village (1kmť
surrouded by green areas of the same size) or rural (0.3kmť or 1.000
people surrouded by green areas of at least 1kmť) and the
number op people enjoying such living environments[267].
Alternatives by design
With the
stock of too much paint indicated in the right figure below we can picture many
different perspectives of a future Deltametropolis. We necessarily have to omit
claims. The perspectives will not only differ in the
specific claims they accept or disappoint, but also in the way each colour is
concentrated in larger units in favour of their own function or dispersed in
smaller ones in favour of synergy with other functions. projects should support this own
function or on the other hand synergy.
|

|
The National Plan of Nature Policy LNV (2000) publishes on page 25 of its programme the newest
version of the accompanying map.
Deltametropolis counts three robust connections[268]:
·
randstadgroenstuctuur,
·
Nieuwe
hollandse waterlinie en stelling van amsterdam, and
·
the robust ecological
connection between Biesbos and IJmeer.
The biological identity of dispersed natural areas
and projects in a large part of Deltametropolis from this programme and their
role as aimed nature type (natuurdoeltype) is elaborated by the Province of Zuid-Holland and clearly
represented on the Internet http://home.wanadoo.nl/w.heijligers/Start/ndtkrt1.htm by W. Heijligers. On the accompanying map one can zoom in to the level of the
nature projects[269].
|
|
|
|
Fig. 791 Map of the National Plan of Nature Policy
|
|
|
Provincial elaboration and
local effect
Perspectives
and projects are evaluated in the way urban areas in the Deltametropolis
reflect this diversity and biological identity.
The
basic ecological criterion for evaluation is global diversity lo leave possibilities open
for future life. Diversity on a high level of scale is operational as rarity (as strong identity) on a lower level[270].
Comparing incomparable
values
|

|
Perspectives and projects are evaluated on the preservation and
production of worldwide (10,000kmť),
European (1000kmť) and
national (100kmť)
rarity of objects. So, rarity can be expressed
in kmť. The
second criterion, important for planning and design is replacebility of removed objects, expressed
in years. It evaluates the possibility of compensation of rare objects. Once
rarity of natural and artificial objects is determined on different levels of
scale, they can be evaluated with regard to their replacebility.
In Fig.
794 living areas of 1kmť or 0.3kmť designed and named by TKA TKA (2001), Hosper Hosper (2001) and H+N+ H+N+S (2001) in Almere (see Fig. 915) are located in a diagram for
evaluation.
|
|
Fig. 794 Rarity and
replacebility of natural and artificial objects
|
The
product of both gives an ecological value for comparison and subsequent
evaluation as discussed in 5.4 (see page 429). Natural areas are represented generally more right in the
diagram, because they are less replaceble than the mentioned artificial
objects.
Claims by growth
The
urban growth since the industrial
revolution culminates, especially in the developing countries where the
European hygienic history of towns repeats itself. Restricting ourselves to the
present Dutch situation claims on Randstad are bigger than ever and the
idea of an open Green Heart fades away by urban sprawl.
|

|

|
|
|
|
|
Fig. 795
Claims on Detametropolis area
|
Fig. 796
The supposed Green Heart
|
|
|
|
The 30
years old idea of high density conurbations have not been successful in
spite of national strategies like bundled concentration or compact cities. And if so, they would have been not effective (see Fig. 700 ) in saving surrounding landscape.
Metropolitan ambitions
It is an
example of ideas like high tech transportation solutions that have big
metropolises as a reference. However, Randstad does not yet reach the capacity
of a real metropolis making fast underground systems possible.
|

|
|
|
|
Fig. 797
The capacity of metropoles
|
|
|
From an
ecological point of view the condition of measure (see paragraph 5.3.3 on page 393) is less important when we concentrate on vegetation rather than on
big animals. From a human point of view we should bring nature closer to home (see page 411). That pleads for openness within the conurbation and not for
accumulation on every level of scale.
The 4th National Plan of Watermanagement Policy V&W (1998; V&W (1998; V&W (1998; V&W (1998) (stressing environment), and
its last successor ‘Anders omgaan met water’ V&W (2000) (stressing security) mark a change from accent
on a clean to a secure environment, just as the 4th National Plan of
environmental policy NMP4, VROM (2001) compared with its predecessors[271]. Several floodings in The
Netherlands and elsewhere in Europe has focused the attention on global warming and watermanagement. The future problems and proposed solutions are summarized in the
figures below[272].
|

|
In Fig. 798 above most left, global
warming, in the figure right the ground descend of the western and northern
part of the Netherlands are shown.
Bottom most left, different scenarios of temperature increase, right of it, the expected increase of precipitation in winter and decilne in
summer are shown.

|
|
|
|
|
Fig.
798 Expected problems
|
Fig. 799 Strategies: 1
care, 2 store, 3 drain
|
|
|
|
The storage of water requires heavy surface claims. The lowest areas
collect water and pollution, so local altitude lines, waterlevels and drain systems fix the possibilities and
risks for nature and human living. They have to be listed. Relatively high
locations favour both as concurrent functions. Lower areas are more suited for
water.
In the
short term energy saving by concentration is important
to stop global warming, in the long term sunlight will provide enough electric
energy to sustain the current worldwide demand several times.
The best
indicator of a clean environment is the presence of rare nature. Its greatest
threat is no longer the city but intensive agriculture.
The complex world of selectively separating and
connecting occurs right down to the smallest scale of biology: the cell and its
membranes (see Fig. 736). On that interfaces
substances are selected and allowed to make connections with each other. The
conditions for specific connections are created primarily by separating substancies
that should not be connected (preselection). That already begins with
the external membrane separating the inner environment from the entropic
outside world. That makes less probable processes possible inside. This range
of conditions and the endoplasmatic apparatus necessary to create the right conditions for
the right connection is often forgotten in understanding the isolated process
of connection operationally (monocausally).
The endless range of conditional functions in the environment seem to require another,
perhaps typically ecological way of thinking than the single function with one
clear product. Such processes are imitated in systems of retorts and pipes
being the armamentarium of chemistry (in Dutch: ‘scheikunde’, ‘skill of
separation’, not the skill of connection). Madame Curie needed four years to isolate 1/10 gramme of
radium from tons of pitchblende. To dissolve sugar in our coffee is a daily
activity taking seconds, but separating it afterwards takes much more effort. A
heap of manure is easily dispersed, but it takes years to get it out of the
ecosystem.
In the same way it is easier to destroy the
subtle system of selectors and regulators of a living organism than to
rearrange and synthesise it. A violent murder means demolishing separations,
starting with those of the skin. Suppose now an ecologically rare location is
surrounded by a range of conditional functions we still do not understand
completely. Is it wise then to make connections for a few cuddly populations
with botanically doubtful functions? Their equalising function in small areas
could be that of an elephant in a china cabinet. Other (migrating) animals than
grazers do not fit in our small nature reserves, but in vast eutrophic areas
elsewhere in the world. There they are needed as mineral transporters comparable with pipelines connecting one sided
high productive communities. A much larger number of smaller more rare species
of animals needing a smaller area could be supported better by diversification
of the botanical foundation. You can wait which superstructure develops
thereupon instead of taking the summit of a food web as a target in advance. You should not start
building a house with the roof.
Living in high densities
Being no
expert on human health the most extensive overview I
know in the joint field of medicine and urbanism is edited by Vogler and Kuhn (1957) some
50 years ago. They discuss many kinds of ‘civilisation damage’ in the urban environment from different medical specialist’s
points of view. I never found a reference into this comprehensive work and I
can understand it considering its size and age. So, I recoil from reviewing it
as well, the more so while I am not read up on more recent medical literature.
Apart from the disadvantages of living in high densities Vogler and Kuhn
emphasise, its benefits Jacobs (1961) some years later referred to were partly confirmed in
a psychological sense.
Crowding
Freedman (1975); Freedman (1977) and Baum (1978) discussed research
on crowding and behaviour concluding no
other impact of increasing density than intensifying existing negative or
positive social-psychological processes. However, by human biodiversity or social diversity - stage in the lifecycle, income or life style - some people like to live in
high densities, others do not. People with children mostly like low densities of
quiet suburbs. So, forced to live in high densities the impact could be primarily
negative. However, learning to live in high densities with children might turn
out positive by discovering advantages, adapting, compensating shortages and accommodating new functions.
Adaptation and compensation
Adapting
to an environment and compensating shortages by new
accommodations are essential characteristics of life. Life would never have
developed without these capacities. The possibility of adaptation and
compensation are often forgotten by researchers only interested in forecasting.
‘Arsenic is poisonous’, they predict. The prediction is based on 3x standard
deviation from the average (99.7% of the cases) and if
arsenic poison would be ever a global problem their solution would be removing
the cause only. But in Austria a village population of so called ‘arsenic
eaters’ (source unknown) since centuries got used to it. That is the way
evolution solved problems by adaptation and compensation increasing diversity,
not by global rules reducing diversity. Oxygen was once a global poison, now it is a prerequisite for aerobic life. Adapting, compensating
and accommodating are also ways designers study. When low temperature is a
problem of living in higher latitudes we compensate (accommodate) by building
acclimatised houses. It is unnatural because it disturbs the natural
distribution and abundance of homo sapiens. But since we make houses more than
3000 years it appears natural to us. What we call ‘natural’ apparently is time scale sensitive as well.
Regional differences in
health
A recent
survey into medicine use shows that the most well-to-do sandy region ‘Gooi’ has the lowest use of medicines in The Netherlands (Fig. 800 ). Insurance companies could decrease
their rates for these groups in the same time increasing their wealth (and
health). But to which extend Gooi-people owe their health to wealth and life
style, to lower housing density, to green area in their direct neighbourhood,
dry sandy soil or climate we do not know.
Local differences in health
Death
rates in the big towns in the nineties were 11% higher than elsewhere in The
Netherlands and there are substantial health differences between and
within towns(Fig. 801 ). However, they correlate highly with income differences causing
different (un)healthy lifestyles. For example they indicate that in a
low-income district the chance to die before the age of 65 is 50% higher than
in a high-income district. And rich people move from low-income wet peat and
clay districts into high-income sandy districts leaving a less healthy
population behind.
Causes of collective disease
Epidemiological
research seldom succeeds in
convincingly separating causal physical context factors like the urban
environment from other coinciding influences affecting health.
The
surveyors did not try to explain either comparing regions of The Netherlands
because epidemiological research is one of the most tricky disciplines urging
expensive longitudinal research extending decades to be
convincing. That is a great pity, because as long as statistical evidence fails
an even more tricky branch of statistics wins: risk calculation. Risk calculation seems rational, but often it is also the
calculation of fears and myths motivated by little more than sharing them in
collective fear.
Contributions by design?
Urban
design is not always the most effective solution in environmental problems remaining after the great
positive health effect of housing itself. Barton and Tsourou (2000) advise 12 key health objectives for urban planners in the
context of WHO healthy city project in which Eindhoven participates: healthy
lifestyles, social cohesion, housing quality, access to work, accessibility,
local low-input food production, safety, equity, air quality and aesthetics,
water and sanitation quality, quality of land and mineral resources, climate
stability. Evaluating their effectiveness again would urge expensive
longitudinal research extending decades to be scientifically convincing.
Stress
The more
we know, the more possible threads we become aware of to be calculated. That
raises fear and fear raises stress. Stress is suspect in raising or stimulating
diseases like cancer. Fear for cancer is so well-known a medical symptom that it got its
own name in medical vocabularies: ‘carcinophobia’. Designers in the wake of this
uncertainty already try to make solutions for possible problems. That is their
task, but they seldom evaluate the effectiveness and possible side-effects of
their solutions.
Avoiding risks may be risky
There is
something wrong in the state of medicine. King Average rules the kingdom of
exceptions human species comprises, but
in the same time exceptional occurrences are magnified by television
and newspapers. Television and newspapers bomb us by statistical exceptions,
distorting our perception of chance and magnifying impact. Risk is popularly
defined by chance x impact. The public shame of few physicians involved
intimidates the profession as a whole. And we still know little about our body,
our own nature yet. Honest physicians remain silent but that is what frightens
more.
Avoiding
any risk physicians prescribe too many medicines, order too many physical
examinations increasing the costs of medical care, increasing slowly appearing
side effects. Avoiding any risk raises new risks on other
levels of scale. Always avoiding to catch a cold may result in high
susceptibility for flu any time we leave a building or a car. Our hygiene drove
life out and nature in exile. Our biological resistance fades, the number of immunity
deficiency diseases increases. We do not get injuries enough to become vaccinated
by nature itself. We like dangerous holydays to flee from our unnatural
and boring safety, but we do not know real danger anymore and fall ill by
foreign food.
Costs of care
A secret
medical survey I heard of by a medical student in the seventies revealed that
half of our diseases at that time were
iatrogeneous (caused by physicians). I do
not know whether that was true or not and what the present state of medicine is
in this respect. That is why I fear the worst case. Insurance companies sell fear. We pay more for
safety than for anything else:
insurance, police, army, preventing fire, burglary and catching a cold. We fear
we can not pay all and we double our work until we die from the impacts of
stress. The life time we spend on worry is lost well-being, lost health and
life time. Our fear for exceptional possibilities raises new diseases of the
mind and we fear them as well. In reality our life is safer than ever, but we
do not dare to live with life: the risk to die. Life became strange to us and death as well, we fear the
unfamiliar because it could be unhygienic.
Carefree nature
In the mean
time numerous other organisms are going their own way, not fearing for anything
that is not actual and mostly without any apparent fearing at all. They live
from very slow to very fast.
I prefer
the slow living plants surrounded by their very fast pairing messengers of life-experience, the
insects. Plants are the basis of life’s pyramid. Added animal life only
selects and regulates like man does as well by harvesting, preserving, mowing
and gardening. Sometimes we visit them and walk in something totally else we
belong to historically but do not have to understand, something we should not
try to plan.
Releasing care
I think
it stimulates human health when we bring life close to everybody’s home and
living, but nobody knows, it is a hypothesis. Berg, Berg et al. (2001) give
an excellent overview in their essay about the relation between nature and
health concerning history, possible impacts on stress, fear, physical
resistance and personal growth. Nature puts the stressing concept of our own
importance into a relative perspective of one species between 1 700 000 ones or
more. They differ more from us than any people we tend to reject in social
conflict. Nature tempers forced choice as architecture should do as
well according to Eyck, Parin et al. (1968) .
The challenge of diversity
The
intellectual challenge of this century is to handle diversity instead of generalising it by
statistical reduction. Generalising research has diminishing returns, on the other hand design is promising, generating
study. Evolution and ecological succession is its model. Studying nature heals
social disappointment by disappointing presuppositions, prejudices. It
stimulates an active form of modesty. The more we know about nature the more we
appear to know not, and the more we want to know, to see, to experience. In any
town of The Netherlands specialised study groups of nature associations
contribute to atlases of birds by Hagemeijer and Blair , Bekhuis, Bijlsma et al. (1988), Beintema, Moedt et al. (1995), butterflies by Tax (1989) and Bink (1992), bats by Limpens, Mostert et al. (1997), amphibians and reptiles by Bohemen, Buizer et al. (1986) , mammals by Broekhuizen, Hoekstra et al. (1992), fishes by Nie (1996), plants by Mennema, Quene-Boterenbrood et al. (1980),
Weeda,
Schaminée et al. (2000) and mushrooms by Nauta and Vellinga (1995) multiplying our shrinking world of holiday
destinations by growing local universes we tended to overlook. In any town
nature writes a history of war and peace far more thrilling than television and
newspapers could do.
Nature
looks for its journalists because it only exists by the grace of those seeing
it.
A.
Any human has a right on 300m2
residential area in a radius of 10km, work and services included.
B.
Any human has a right on all
necessary sources of living within a radius of 30km. These sources have to give
access to products of 2000m2 agricultural land per person. This land should be
accessible within a radius of 1000km concerning the risk of stagnating
logistics.
C.
Agriculture has to be located in
areas with highest supply of water, minerals and sunlight. Towns and untilled
natural areas have to be located in areas with less minerals.
D.
Any human has a right on
untilled natural ground uninhabited by man within a radius of x from her or his
place of residence measuring at least a radius of x/3; x being {0.3, 1, 3 … 100
000 metre}.
E.
Dutch cities belong to the most
healthy in the world. So, any attention given to health in Dutch cities is
distressing in a perspective of the hygienic condition of cities in the second
and third world.
‘Nature’ is treated as a concept in this chapter and
thus as part of a culture that values nature (see Fig. 1010). This chapter gives some
insight into the types of natural area that can be distinguished. It is the task of the (regional, urban architectural or
architectonic) designer to choose and, in the appropriate scale size, those
combinations of these forms as a key unit, that make a clear, understandable,
comprehensive and feasible plan possible.
Biodiversity
is the ‘risk coverage for life’. The loss of biotopes for human beings, animals
and plants is the framework within which the seriousness of the environmental
problem is assessed. We will not dispute this here, but describe a method
whereby these values can be measured. From these points of departure it is
simple to evaluate on various scale and time levels to what extent an element
of nature is special or unique and replacable.
Heterogeneity is homogeneity on an other scale
In
valuing the Dutch flora and fauna on
a European level, we should be petitioning for the whole of the Netherlands to
be declared a Wadden area, because, at the European level, that is unique feature of our
region. But that would create a very undifferentiated picture of the Netherlands.
At the Dutch level, perhaps we ought to collect all the ecotopes of our
latitude within our national boundary, but if every country was to do that,
then there would be homogeneity at the European level. In other words, the
question is: What sort of variation do we want, and at which
level?
Rarity in space
As our
concern is with the biodiversity of the whole world, our priority must be to
assess the uniqueness of our nature within R =
10,000 km (the radius of the Earth is approx. 6,000 km). Uniqueness at the
continental level can be read off on the scale against the frequency of
occurrence of similar areas within R = 1000 km. At the national level, R = 100
km and at the local level, 10 km. Rarity is also culturally useful because it
makes cultural values comparable with ecological ones (Fig. 802 ). Moreover, rarity has a relation with the economic concept of
scarcity determining economic value.
|

|

|
|
|
|
|
Fig. 802
Comparing ecological and urban objects
|
Fig. 803
Evaluating the incomparable
|
|
|
|
Conditional evaluation
Conditionality
represented by tanks filled with liquids of different specific gravity
clarifies an other possibility evaluating categories of nature and
culture (Fig. 803 ).They could be named as conditional evaluation. This figure shows
the relation between increasing carrying capacity of ecological and economic
capital while diminishing economic and cultural pressure to avoid losses and to
find maximal social capital and quality for future generations.
Replacebility in time
A second
consideration could be the extent to which destruction of natural areas can be
considered to be irreversible. In other words, ‘how long would it take for a
similar area to revert to its original state: 1,000,000; 10,000; 100; or 10
years?.
Value as a product of rarity and replacebility
If a
certain kind of natural area is frequently found within a given radius, and if
it can be quickly brought back to its climax state, less value will be placed on this land than when this hardly ever
occurs and when it takes a long time to reach the present quality again. In
making a valuation, one should thus take the reciprocal value of the product
and count up the scores on each scale level. However, very many variants and
specifications are possible. This sort of evaluation has been put forward by Joosten
et al. (1992) for the Peel and it would be well worthwhile to work it out in
depth.
Interestingly
enough, this approach has also been found to be useful in establishing the
visual quality of the urban architectural and architectonic aspects of an urban
renewal plan (De Jong and Ravesloot, 1995).
Expressing rarity in
kilometres
The
local rarity of ‘x’ communities, ecological groups,
populations, formations, ecosystems or artifacts can be expressed as the
distance ‘y’ to the nearest x examples in the neighbourhood.
If the
criterium for rarity x equals 1, then y is
the distance to the next example in the neighbourhood (within this radius
<y, it can then be considered to be a unique example). From a given x, a
radius can thus be deduced (as a frame) outside of which the object is no longer unique or rare. If these
turn out to be the only x examples in wider surroundings (a broader
frame), then the object with x examples with that radius as a grain (unit) is rare again in that wider frame.
Rare on one level, common on
an other level
Suppose
that, within a radius of 30 km, another 10 examples of the same formation3
km can be found, but, further away, within a radius of 300 km, none at
all, then the regional 30 km rarity of these formations3 km
is low, but the subcontinental300 km rarity of this district30
km is high. Conversely, regionally, within a radius of 30 km, a formation
can be rare, but, it need not be nationally within a radius of 100 km. This
does not negate the fact that the nation may have a responsibility
continentally for these sorts of formation.
Involving human artifacts in
the comparison
The same
applies to artefacts. In Delft there is one, for the Netherlands, rare example of
profane-Gothic architecture. There are many more
examples from this period in Belgium, but, worldwide, they are only found in Europe.
The profane-Gothic example in Delft is thus locally rare within a radius
of 100 km; subcontinentally it is not
rare, but it is again rare, world-wide.
Determination of the grain
of comparison
The
question is whether people value this profane-Gothic building in itself or the
total urban architectural combination of a profane-Gothic building on a
Mediaeval canal. In deciding what is rare, people continue to use a coarser
grain when comparing one formation
with other examples. To liken this to the production of photographic prints,
the distance between the framework and the grains (units) (i.e. the resolution) plays a role in determining rarity.
Rarity resolution
If there
were no examples of this type of urban architectural combination in Belgium,
then one could also talk of subcontinental rarity. The rarity of combinations30
m within a subcontinental300 km framework still has a very
high ‘rarity resolution’ of linear 30/300000 = 0.01%.
For
designers, such precision is greater than that needed for a plan, while 10% is
enough to reach a decision on a design sketch. An urban architectural design is not rejected because the wrong
bricks have been suggested. For biotic components, in order to reach a rarity
resolution that is acceptable for making a decision, a grain must be maintained that bears
some relation to the frame
The resolution of plant and
animal data
If the
number of locations where a species is found, on earth or within the Netherlands,
is known, a frame, a grain (unit) and therefore a resolution (the ratio between the two)
is implicit. In the Netherlands, the grain, the sampling unit, is usually an
‘hour field’ of 5x5 km (with a radius of 3
km), which is the average walking distance per hour. For very many species it
is known in which hour field and sometimes even in which square kilometer,
topographically, they can be found and also partly to what
extent.
The rarity resolution of the
hour-field frequency measure
The
national rarity of a species is then known as
the ‘hour-field frequency’’, the number of hour fields in which the species occurs in the Netherlands.
Therefore, it has to do with the quality of the formation For example, for
every plant species from different periods, this is fairly well known, so by looking
at the development in the hour-field frequency over a number of years it is possible to determine whether a species is threatened within the Netherlands.
The arbitrary boundaries of
data
The
borders of the Dutch state are arbitrary, because what is measured as rare,
nationally, need not be rare regionally or internationally. The rarity
resolution of hour-field frequencies in
the Netherlands is 3% linear (3 km radius/100 km radius; area-wise it is less
than 0.1%: 25 km2 to 40,000 km2). In this book we will
restrict ourselves to a rough resolution. This can be 10% linear (1% of the
area) for nature valuations based on sampling hour fields as large as areas
with a radius of 10 km (more than 10 hour fields) in a frame of 100 km (more
than 1000 hour fields).
A local policy of rarity
A
municipality could, as was considered in Zoetermeer, for example, determine, for its policy on nature, that the accent
should be laid mostly on regional and world-wide rarity. If types of ecosystem occur in a municipality that are rare
worldwide, then, of course, these deserve to be treated with the greatest
urgency. After that, priority is given to things that are regionally rare in
preference to national rarities, providing that these occur in abundance
elsewhere in the world. In that case, it does not matter whether those things
are rare or whether they occur generally in the Netherlands. The aim of
municipalities is to create a special identity within their region and not to
try to differentiate themselves from towns outside the region. In simple terms,
this can lead to a policy that not only has ecological but also economic
significance.
We know that some (sub)species, such as the Zuyder Sea Herring and the small brackish-water
jellyfish Eucheilota Flevensis
became extinct after the closing of the IJsselmeer (Noordhuis (2000).
It is
known that the core area of the Marsh Fleawort (Weeda, Westra et al. (1991)
and the Black-tailed Godwit, a meadow bird (Beintema, Moedt et al. (1995), is in the Netherlands,
and that elsewhere they have an uncertain future. Surprisingly, the core area
for the Marsh Fleawort is Flevoland, where, after draining the land, it
appeared everywhere, spreading rapidly both on land and into the neighbouring
waters, but also quickly disappearing again. So we carry a great responsibility
when it comes to species like this.
Responsibility of The Netherlands
in numbers
Reading
van Duuren (1997) there are only two of the
35,000 species resident within our national boundaries for which we have the
responsibility of a Noah. Of the 1,732,000 known species on earth (only a small
part of the probable actual number), 35,000 of them are found in the Netherlands.
Expressed in another way, 2% of the total number of species on earth are found
within an area that is less than 0.008% of the total land surface on earth.
Thus the Netherlands is jointly responsible for a much greater number of
species than its area would suggest.
Insects and birds
Of
these, the largest number of species are insects. In the Netherlands there are
about 17,000 species of insect of which approximately 2,200
are butterflies (most of them only flying at
nignt), 4,000 hymenoptera, 4,500 are diptera and
30 other orders of which most of us have never heard. They are one of
the most important sources of food for the 366 species of bird found in this country. There
is a nation-wide interest in butterflies, but most of them are linked to rare
plants that demand species-rich vegetation. Their distribution can be seen from
the various butterfly atlases (M.H. Tax 1989; F.A. Bink 1992; van Halder, Inge
and Irma Wynhoff et al. 2000). In addition to the 111, mostly threatened, day
butterflies in our country, there are also 1,400 moths and small butterflies,
as named in CBS’s BIOBASE van Duuren (1997) .
Biodiversity
The
insects are part of the phylum arthropodaso too are many crabs, lobsters, prawns and water insects that are
important for birds.The table below shows ordered lists of the most
species-rich phyla of the 50 phyla that biologists have identified, and they
are represented according to how species-rich they are in the Netherlands.
|
BIOBASE CBS
Duuren (1997)
Name
|
Species
world-wide
|
Species in the Netherlands
|
% in the Netherlands
|
plants or
animals
|
rough 10%
estimate
|
|
arthropoda
|
1130000
|
21000
|
2
|
d
|
|
|
moulds and fungi
|
100000
|
3500
|
4
|
p
|
|
|
‘yellow algae’
|
9200
|
2200
|
24
|
p
|
|
|
threadworms or
elvers
|
12500
|
1700
|
14
|
d
|
|
|
green seaweeds
|
7000
|
1600
|
23
|
p
|
|
|
the angiosperms
|
250000
|
1400
|
1
|
p
|
|
|
lichens
|
20000
|
633
|
3
|
p
|
|
|
mosses
|
23000
|
533
|
2
|
p
|
|
|
Chordata
|
52000
|
470
|
1
|
d
|
|
|
ringworms
|
8000
|
350
|
4
|
d
|
|
|
flatworms
|
14000
|
330
|
2
|
d
|
|
|
wheel animals
|
1800
|
300
|
17
|
d
|
|
|
molluscs
|
53000
|
300
|
1
|
d
|
|
|
eye seaweeds
|
500
|
250
|
50
|
p
|
|
|
bacteria
|
1500
|
150
|
10
|
p
|
*
|
|
blue algae
|
1500
|
150
|
10
|
p
|
*
|
|
Coelenterata
|
8000
|
140
|
2
|
d
|
|
|
virus
|
1200
|
120
|
10
|
p
|
*
|
|
red seaweeds
|
3500
|
78
|
2
|
p
|
|
|
|
|
Fig. 805
Biodiversity according to the CBS Biobase
|
|
|
All
these plant and animal phyla play both a qualitatively and quantitatively
important ecological role for example in the IJsselmeer region. They are not always
given the attention they deserve. An exception to this, for example, is the
research carried out by the Mycological Research Work Group for the IJsselmeer
Polders (Zanen, Ger van and Piet Bremer et al. 2000) on the approx. 1,600
species of fungi (toadstools) that occur in Flevoland. Also important are the ‘yellow algae’ to which the beautiful siliceous sea weeds (diatoma) belong, that, world-wide,
have created our oil reserves. In the IJsselmeer region they are an important
source of food in the spring and autumn if enough silicates have dissolved in
the water to enable these organisms to form their skeletons. Elvers and worms are eaten by fish (e.g tubifex). The green seaweeds are a summer source of food,
especially in the Markermeer, where, because of turbidity, a few of the oldest organisms, blue algae do less well there than in
the IJsselmeer. These processes greatly influence the differences in the fish
and bird population between the two lakes. An important member of the green
algae for the Mute Swans and Gadwall ducks is the Wreath Seaweed, historically the forerunner of the higher plants and vegetables.
Aquatic and land vegetation
Together
with the few gymnosperms (mostly conifers) found here, both aquatic and land vegetation in the Netherlands is
made up of angiosperms. Most of the Markermeer and IJmeer are devoid of water plants
because the transparency of the water is rather poor, also at depth. However,
they have become really well-established at the edges, on the foreshores of the
sheltered Gouwzee and inside the dykes,
although, on the outer side of the dykes, they are slowly being pushed out by
the just-as-valuable Wreath Seaweed. They are very important for aquatic life and for birds in that they
stabilise the lake bed. The vegetation on the new land is still rather homogenous, because
most of it is made up of heavy clay that, especially in the areas
of salt marsh that are not yet ready for
agricultural exploitation, does not mature very quickly.
Regionally rare soils
Where
the surface soils are sand and loam, as in Pampus-West, an interesting vegetation can develop attracting a rich insect
(e.g. butterfly) and bird life. As in all the visionary plans, further research
needs to be carried out before these soils are excavated or covered for urban
purposes
Dutch
vegetation is one of the best researched in the world. Botanically, within the Netherlands,
Flevoland is not yet very interesting, but it has great potential, especially
along the inner edge of the dykes. Already, in East Flevoland, 50 red-listed (threatened) species are
found and summarised by Bremer and Smit (1995) . However, a varied vegetation
is in constant competition with productivity which is so valued by the birds of
this region. Although clay marsh, as a type of natural area to aim for is doing well there (Bal, D.,
H.M. Beije et al. 1995), it is an ecological community of few species that only
after 20 to 1000 years will grow into a richer peat bog (Londo, G. 1997).
One-sided focus on popular
species
Little
attention is often given to mosses and lichens. They will play an important role in the new land if peat formation establishes itself. The Chordata, the vertebrates, to which we also belong, can look forward all the more to
the active interest of nature work-groups. Of course, this applies primarily to birds. We will return to this
topic when we deal with rarity in Europe and the Netherlands. There are very
many other vertebrates both now and in the future that can play an important
role in the value placed on the region’s nature.
Using biological atlases to
find relations and potentials
In the Atlas
of Dutch Amphibians and Reptiles (Bohemen,
H.D., D.A.G. Buizer et al. 1986) and in the Atlas of Dutch Mammals (Broekhuizen, S., B. Hoekstra
et al. 1992) one can see what the distribution is with an accuracy of 5 km.
From this, it is noticeable that colonisation of the new land from the
surrounding old land, for example by the grass snake, is still in its initial phase. Constructing foreshores and islands
can stimulate this process. The question is whether, having created such
habitats, one should either wait until a breeding pair of the creatures in
question make the journey to their new habitat, and by chance survive, so that
perhaps in 30 years’ time the colonisation can begin, or one should actively
introduce them there. Within the category ‘mammals’, a beautifully illustrated
atlas is devoted to bats (Limpens, Herman, Kees Mostert
et al. 1997).
The role of fish in the
nitrate cycle
Fish, as
a group are, of course, of utmost importance to the IJssselmeer region, see the
Atlas of Dutch Freshwater Fish (Nie, Henk W. de 1996), of
which some have the status ‘protected species’. There are other species that we
would rather be rid of (e.g. bream colonisation). The dubious role of the widely occurring bream could well be reversed if an
entrepreneur, for example in Almere, would start using this source of food for the production of
cattlefood. In the Netherlands, ten times as much manure is produced as
household waste. Currently, the protein in cattle food is produced by blue algae in the root tubers of vleugelbloemigen
(clover, lucerne and other bean wearing plants) on an area three times as large
as the Netherlands, in countries in which children die of protein shortages.
However, it is more lucrative to feed these soyabeans to our pigs than to use
them to cure children of beri-beri.
Fish ponds
The
nitrate-rich decomposition product from protein, manure, finds its way into the
Randmeren, partly from Gelderland, where the phyla listed above (but not expanded on further here)
make them suitable for the Bream. Elsewhere in the world, to recycle this
manure, farms have fish ponds for carp and bream. If we were to follow this example, there would be no better
location in the Netherlands than the IJsselmeer region. However, this revolutionary breakthrough for nature in the Netherlands
is being hindered by the necessity to adapt the fishing laws: sport-fishermen are unwilling to waiver their right to the bream
to professional fishermen, who could supply a substantial source of cattle
food.
Mollusks and birds
A variety-rich phyla of mollusks (weekdieren), mussels and the like, 1% of which (approx. 300 varieties!) are found in the Netherlands
is, among other things, of great importance for the diving ducks in the area. The basis of
this is the enormous success of one exotic variety, the Zebra Mussel that appeared in the Netherlands
in 1826 from the Caspian Sea and from 1975 onwards, as the waters became richer
in nutrients, spread rapidly. Because of its capacity to colonise so quickly,
Zebra Mussels are now common in the Netherlands and in Europe. Their appearance
in North America in 1989 and has caused problems there (Gittenberger, E. and
A.W. Janssen 1998). They can block cooling water and drinking water systems.
Nevertheless, this mussel is the favourite, at the moment, of bird-loving Netherlands.
A number of details are important in laying out the bed of the Markermeer. Zebra mussels have a life-span of five years. They attach
themselves to hard surfaces and the adults seldom move elsewhere. They begin
life as one of the millions of eggs released by the female. The larvae move
like plankton by means of vibrating hairs until they develop a shell that makes
them sink to the bottom. There they actively creep around until they find a
hard, protected anchorage where there is not very much light. They can live at
depths (to tens of metres deep) much greater than diving ducks can reach. The
larvae eat bacteria, blue algae and very small particles of the sediment in the
lakes (detritus). As a mussel, they grow the fastest in nutritious, moving
water. They filter the water so actively, that they clean the entire IJsselmeer
twice a month. The activities of the Water Flea, a species in the lobster family, have a similar cleansing effect.
Mussel beds attract many other forms of life.
|
Percentage of the international bird population
Tempel and Osieck (1994) 4)
Symbol is similar to presence graph Jan.-Dec.
V winter birds Wintervogels
M whole year, especially in the winter
P whole year
N whole year, especially in the spring of s
L summer, nesting bird
|
IJMEER
|
MARKERMEER
|
GOUWZEE
|
IJSSELMEER
|
OOSTV.PLASSEN
|
LEPELAARSPLASSEN
|
TOWN
|
|
Water
|
V
|
carnivore
|
Goosander
|
|
|
|
4
|
|
|
|
|
V
|
carnivore
|
Smew
|
|
2
|
1
|
2
|
|
3
|
|
|
V
|
Zebra mussel
|
Scaup
|
|
5
|
|
44
|
|
|
|
|
V
|
fish
|
White-tailed
Eagle or Sea Eagle
|
|
|
|
|
n
|
|
|
|
V
|
plants
|
Barnacle Goose
|
|
|
|
|
2
|
|
|
|
V
|
plants
|
White-fronted
Goose
|
|
|
|
|
1
|
|
|
|
V
|
plants
|
Whopper Swan
|
|
|
|
|
1
|
|
|
|
M
|
plants
|
Greylag Goose
|
|
|
|
|
41
|
|
+
|
|
M
|
plants
|
Gadwall (duck)
|
|
1
|
|
3
|
4
|
|
+
|
|
M
|
plants
|
Pintail (duck)
|
|
|
|
|
7
|
|
|
|
M
|
plants
|
Wigeon (duck)
|
|
3
|
|
1
|
1
|
|
+
|
|
M
|
plants
|
Pochard (duck)
|
6
|
2
|
|
1
|
|
|
+
|
|
M
|
plants
|
Teal (duck)
|
|
|
|
|
13
|
|
+
|
|
P
|
fish
|
Grebe
|
|
|
|
4
|
|
|
+
|
|
P
|
Zebra Mussel
|
Tufted (duck)
|
5
|
4
|
2
|
3
|
1
|
2
|
+
|
|
P
|
plants
|
Mute Swan
|
|
|
|
1
|
|
|
+
|
|
P
|
plants
|
Coot
|
|
|
|
1
|
|
|
+
|
|
N
|
plants
|
Shoveler (duck)
|
|
|
|
|
1
|
|
+
|
|
P
|
fish
|
Caspian Tern
|
n
|
|
|
|
n
|
n
|
|
|
P
|
fish
|
Black Tern
|
|
n
|
|
64
|
1
|
|
|
|
reed
|
V
|
carnivore
|
Hen-harrier
(breeding)
|
|
|
|
|
n
|
|
+
|
|
N
|
carnivore
|
Spoonbill (not
breeding)
|
|
|
|
|
7
|
1
|
+
|
|
L
|
carnivore
|
Spoonbill
(breeding)
|
|
|
|
|
16
|
2
|
|
|
N
|
fish
|
Bittern
(breeding)
|
|
|
|
|
n
|
|
|
|
L
|
insects
|
Spotted Crake
|
|
|
|
n
|
|
|
|
|
grass
|
N
|
carnivore
|
Black-tailed
Godwit
|
|
|
|
|
1
|
|
+
|
|
N
|
carnivore
|
Ruff
|
|
|
|
|
n
|
|
+
|
|
brushwood
|
N
|
carnivore
|
Avocet
|
|
|
|
|
6
|
|
+
|
|
L
|
insects
|
Bluethroat
|
|
|
|
|
n
|
|
|
|
L
|
insects
|
Black-winged
Stilt/b
|
|
|
|
|
n
|
|
|
|
L
|
fish
|
Common Tern
|
|
|
|
n
|
|
|
+
|
|
forest
|
L
|
fish
|
Cormorant
(breeding)
|
|
|
|
|
15
|
7
|
|
|
P
|
fish
|
Cormorant (not breeding)
|
|
|
|
8
|
3
|
1
|
+
|
|
|
|
Fig. 807 The European responsibility
for birds
|
|
|
Bird and Habitat Directive
For the
benefit of the Bird and Habitat Directive, the European importance of the IJsselmeer region for birds is
expressed quantitatively as the percentage of their presence in the European population.
The threshold value is 1% of that population. Locations below that percentage,
but which nationally are one of the five most important locations for that
species are indicated with an ‘n’ in Fig. 807. In the second column, one can see whether the graph of their
presence between January and December peaks in the summer (L), the
winter (V) summer or whether it is a variant between the two.
Seasonal maxima by bird
migration
The seasonal
maximum outside the dykes for the Black Tern and the Scaup were 64% and 44% of the
European population, respectively. These birds seek the open water. Forty-one
percent of the Greylag Goose population winters within the
dykes of the Oostvaardersplassen or stays there the whole year
round. Of the European Cormorants, 34% breed (/b) in the wooded parts of the Oostvaarders- and
Lepelaarsplassen or stays (/nb) either there
or on the IJsselmeer. Of the spoonbills, 26% either stay or breed inside the dykes. The Tufted Duck population is found on all
the lakes in numbers that together comprise 17% of the European population.
Oostvaardersplassen
The
Oostvaardersplassen are indicative of how
valuable it is to have still water, reed morass, grass fields, brushwood and woods inside the dykes. There are
more species of birds here than anywhere else.
Differences between IJsselmeer
and Markermeer
The
IJsselmeer is the most important stretch
of water in Europe, particularly for carnivores, Mute Swans and ducks.
Despite
its large surface area, the Markermeer is still not as important as
the IJsselmeer, and, on a European level, is mainly important for ducks of the
same assortment.
In the IJsselmeer,
ten times more fish can be found than in the Markermeer.
Silt is a problem in the
Markermeer. It is restrained by the Houtribdijk to prevent it encroaching on
the IJsselmeer. The wind draws the silt up from the bed of the Markermeer. This
reduces the entry of light, preventing algae from doing their basic work and the waterplants
from expanding, except in the protected waters of the Gouwzee. The Zebra
Mussels become covered with silt. The
numbers of Tufted ducks and Pochards in the Markermeer are
decreasing correspondingly.
Map of the Natural
Vegetation of Europe
The
conclusion is that also the area within the dykes plays a role of international
importance. The Map of the Natural Vegetation of Europe (Bohn, Udo 2001) compiled by 102 geobotanists
from 31 European countries, is a milestone in international ecology. On this
map it can be seen how the narrow coastline between Belgium and Denmark offers
botanical potentials that are internationally rare. They are indicated as U2 on
the map: ‘vegetation complexes of dyked morasses with water-loving oak/ash
forests and ash/elm forests’. These cover less than 1% of Europe.
Rarity of Dutch woords
Beech
woods are typical of the
neighbouring countries, as far as the Alps, and further to the north, the
coniferous forests appear: ‘From Amersfoort until the Urals the landscape is
less surprising.’ (Constandse, A.K. 1967). Indeed, not all the area is covered with tree species with which
we are familiar. It is the long-term potentials that are important. In the
succession of overlapping ecosystems, this would be merely the natural and
varied final stage (climax) with open areas for special vegetation and fauna,
kept open by large grazers (Vera, F. 1997).
The
forests of the Flevopolders are largely an early
reflection of this end stage, but there are also beech and coniferous forests,
not characteristic of the region, that foster the establishment of special
vegetation such as internationally rare toadstools (Zanen, Ger van, Piet Bremer
et al. 2000). This leads to the question of whether, for the benefit of regional
diversity, one should allow clay morass, that is rare internationally, to be
cut across here and there by forests that are common elsewhere. However, due to
manure infiltration and acidity, the undergrowth in our forests does not
develop much further than stinging nettles or Wavy Hair-grass (Dirkse, G.M. 1994).
Continental and national
rarity
From the
view point of European diversity and rarity, the low areas of the Netherlands should be one large wooded morass. Viewed nationally, this would, of course, be monotonous.
Throughout the Netherlands, the natural succession towards a final stage is
artificially interrupted everywhere. It is held in various, often productive,
intermediate stages for the benefit of nature conservation or agricultural
goals. The artificiality of nature in the Netherlands as a whole is the result
of the simple fact that, without human intervention, half of our country would
be sea floor. What is maintained, can be likened to a picture taken of the
river delta at the beginning of history
with annually changing waterways and pioneering communities. Since 1000 AD,
this landscape has been increasingly stabilised by dykes. Since the end of the
Würm Ice Age, around 10,000 years ago, when the North Sea was still dry, the
seawater rose and fell periodically through the millennia, but it will now rise
faster and higher than ever.
Rarity of urban artifacts
Approx.
10% of this landscape is occupied by warmer urban buildings. The Dutch city — on water, with canals and
quays — and built on low land is rare internationally. Currently, in modern
cities, due to their more open planning, improved hygiene and/or nature
friendly policy, one can find a larger number of wild plant species per km2
than in many natural areas. This vegetation and its insect fauna are
mostly inhabitants of more southern, stoney areas, but they form a gene bank
for warmer periods and a refuge within the surrounding agricultural wilderness
for living creatures such as bats and birds. Many of the birds named can be
seen in towns (Melchers, Martin and Remco Daalder 1996). The Grebe and the fox are discovering the town as a
new natural area, while the House Sparrow is disappearing.
Architectural rarity
The
daring designs and organisation of Dutch environmental planning and
architecture as presented in the prize-winning Dutch pavilion by MVRDV at the world exhibition in Hannover is attracting world-wide
interest. A growing fascination can be seen in this pavilion for innovative
ways of cooperating with nature. Almere has built up a name for itself in the
area of architectonic experiments and has become a showcard for architectural
designs, but what it misses is an amphibian aquadistrict and water
architecture.
Artificial environment
The now
freshwater of the IJsselmeer region is maintained by installations such as
dykes and sluices. The policy determining the level of this water (high levels in summer and
low levels in winter) contravenes what would happen in nature. Within their own
territories, the Dutch Ministeries of Transport and Communications (V&W) and Agriculture, Nature and Food Quality (LNV) have developed into nature and environment ministeries: in
construction work and in carrying out agrarian management, working together
with nature is high on the agenda. Ministry of Transport and Communications
constructions such as earthworks, dykes, roads and their verges have become
objects for nature engineering (Aanen,P., W. Alberts et al. 1990). Their contours, layout and management have a demonstrable
ecological effect within the cities too.
A paradox of environmental
and nature policy on different scales
In the
past detergents and nowadays phosphate- and nitrate-rich water from the animal husbandry on the Veluwe reaches the IJsselmeer via the IJssel and the Markermeer via the Randmeren. There, it is transformed by sometimes too rapid growths of, and
thereby toxic, algae, grazing, and hunting water-creatures into large quantities of
vegetable matter, mussels and fish, which attract large numbers of birds. These birds, that come from far and wide, make this an area not
only of international importance, but also a rare area, nationally.
Due to
the success of environmental policy (e.g. phosphate-free detergents), less and
less nitrate and phosphate is entering the lakes. The reduced availability of
these minerals sets an upward limit on food production and allows other,
nationally rare, but less productive species to establish themselves. Perhaps
the age of migrating birds will be followed by an age of reptiles, amphibians
and mammals that, due to the lack of sandy areas and brushwood (foreshores and
islands) outside the dykes, have not yet colonised the region. With a view to
the future role of the region, it is important to gain insight into the
increasing complexity of this system.
National rarity of birds
The table below shows the ecotope of red-listed birds found in the IJsselmeer
region (Duuren, L. van 1997). The Red List reflects the national rarity
of species. It is a selection made from many other targeted species included in
realising a Primary Ecological Structure. The internationally rare species are also represented in this:
|
|
NEST
|
FOOD
|
mainly insects
|
|
Black Tern
|
BA
|
open
water
|
open
water
|
+
|
|
Little Grebe
|
C
|
open
water
|
open
water
|
+
|
|
Garganey duck
|
C
|
open
water
|
open
water
|
|
|
Bittern
|
BD
|
reed vegetation
|
reed vegetation
|
|
|
Sedge Warbler
|
C
|
reed vegetation
|
reed vegetation
|
+
|
|
Savi’s Warbler
|
C
|
reed vegetation
|
reed vegetation
|
+
|
|
Spotted Crake
|
D
|
reed vegetation
|
reed vegetation
|
+
|
|
Bearded Tit
|
DA
|
reed vegetation
|
reed vegetation
|
+
|
|
Spoonbill
|
DA
|
reed vegetation
|
reed vegetation
|
+
|
|
Great Reed
Warbler
|
BD
|
reed vegetation
|
brushwood
|
+
|
|
Ruff
|
B
|
brushwood
|
grassland
|
+
|
|
Common Tern
|
C
|
sandy, open
brushwood, pioneer
|
open
water
|
|
|
Avocet
|
DA
|
sandy, open
brushwood, pioneer
|
open
water
|
+
|
|
Kentish
Plover
|
BD
|
sandy, open
brushwood, pioneer
|
sandy, open
brushwood, pioneer
|
|
|
Ringed Plover
|
D
|
sandy, open
brushwood, pioneer
|
sandy, open
brushwood, pioneer
|
+
|
|
Redshank
|
C
|
grasland
|
grasland
|
+
|
|
Black-tailed
Godwit
|
CA
|
grasland
|
grasland
|
+
|
|
B Very threatened
BA Very threatened, important
internationally
BD Very threatened, vulnerable
C Threatened
CA Threatened, important internationally
D Vulnerable
DA Vulnerable,
important internationally
|
|
|
|
Fig. 808
The national responsibility for birds
|
|
|
Habitat combinations
important for birds
Judged
by its feathered visitors, the national rarity of the region can be listed as
open water, reed vegetation, brushwood, grasslands and sanctuaries (also on the land of South
Flevoland). Sanctuaries are important for birds during the vulnerable
moulting period, when their flying capacity and food menu is restricted. For this
reason, a favourite moulting place is the lonely Houtribdijk, because it is out of reach of predators and it offers sufficient
food. If also used for recreational purposes, then good organisation is
required. Wide vistas of open water is also a visual rarity, even though the Zeeland waters are not more than 100
km away. Ecologically, however, large expanses of water are not particularly
important (what is known is that the Scaup duck is moving away from the coast
in indeterminable numbers and that only the Cormorant has a flight range of more
than 1 km).
Recreation symbiosis
These
waters are mostly important for recreation, for those sailing in the ‘brown
fleet’ of old ships from the historically important harbours in the region. For
the real sea sailors, the Waddenzee and the North Sea are nearby.Other sailors
like to keep in sight of the shores. When the mast route from the Zeeland waters to the Friesian lake
region — the ‘Blue Arrow’ in the national plan —
becomes operational, then the IJmeer will become a junction of shipping lanes.
It is questionable whether this
recreational pressure will be favourable for moulting and breeding birds. There
will be great resistance against high-rise buildings along the shores, and
certainly on islands off the coast. A minority of the sailors is against the
compartmentalisation caused by islands and
foreshores. On the other hand, these supply isolated reed vegetation, brushwood
and grasslands, the areas of which are too small for non-swimming predators
which would otherwise make bird life impossible. For example, the Spoonbill has been forced out of the
Naardermeer by the fox. There is little differentiation in the Markermeer, in this respect. Greater differentiation in land/water transitions would create a more complex
system with more species of birds and of other creatures too.
Expressing
replaceability in years
Just as
rarity can be expressed in kilometres, so can replaceability be expressed in years. A
combination of both was first suggested by J.H.J. Joosten and B.P.M. Noorden
(1992) as a basic way of valuing an
ecosystem. This method has been worked out here and applied for the first
time in Almere in order to include human artefacts
in the comparison. This basis for comparison is important for many urban
architectural and political considerations. It is a consideration of basic
qualities in space and time. For
example, it is an alternative to earlier attempts to express nature in terms of
money or functionality for people (Maarel, E., van de and P.L. Dauvellier 1978; Groot, R.S., de 1992). On the other hand, it might offer the possibility of expressing
money in more general ecological definitions of scarcity and production opportunities. The
replaceability of an ecosystem or artefacts can be expressed as the number of
years needed to recreate that object.
Comparing natural and
artificial monuments
This
figure shows that a main port such as Schiphol and a blanket bog formation such as the Peel (both with an radius of 3km)
in a radius of approx. 300 and 100 km, respectively, are rare, but that the
time needed to create them is very different. It takes about 10 years to
rebuild a main port, but the destruction of blanket bog landscape takes at
least thousands of years to reverse. The value of both can be expressed by
multiplying both amounts: 3,000 for a main port and 1,000,000 for a blanket bog
landscape in our country. The values become more legible by choosing the
logarithm (the ‘number of noughts’): 3.5 and 6.
Rarity and replaceability
By
viewing rarity in combination with replaceability, a host of methodological queries arise, but they have managerial,
cultural, economic, technical, ecological and time–spacial departure points
which are urban ecologically relevant. Also even if one doubts the possibility
of putting this idea into practice, the mental exercise of thinking through
from these points of departure can lead to clarification in various scientific,
technical and managerial urban ecologically relevant areas.
What is replaceable?
Both the
IJsselmeer and the Oosterschelde are ecosystems that were
formed from a salty sea environment by human intervention during the last
century. To what extent can they be compared? This is important for determining
their rarity. In determining their replaceability, the question of
comparability also plays an important role.
The
replaceability of both systems can be initially viewed as being less than or
equal to their age, say 30 years. However, one could ask what should be
understood by ‘recovery’ in this context.
Supposed expectations on
succession
Would their
ecosystems experience the same succession if they were now exposed to
the sea for a number of years and then shut off from it again? There are a host
of examples in which small differences in the initial situation or differences in
intermediary situations (e.g., different weather conditions at crucial phases,
climatic changes that have started in the meantime, changes in recreational
use) can change the direction of the development, to give another result. Are
the different outcomes from such possibly different successions comparable and
accountable as one group of ecosystems? If one would answer ‘no’, then one
would not be able to give meaning to the concept ‘recovery’. In that case, one
should, on the grounds of deep ecological insight into succession variants and
how to influence them, have access to a sophisticated division of the ecosystem
categories that emerge in order to judge exactly whether the outcome of the
present succession can be considered to be reconstructable. To have such
confidence in ecological predictability is unjustifiable. The far-reaching
planning that would be needed to achieve a nature concept exactly is both
unnatural and paradoxical, if we want to consider and appreciate ‘nature’ as being outside human planning.
Initial situation
For this
reason, one has to harmonise the definition margins of the ecosystem category
with the predictability of its, by natural chance directed, existence, and
answer ‘yes’ to the question. In the same initial abiotic situation of a
large-scale transition from salt to fresh water, one must include in an
ecosystem category all outcomes of possible, and within reasonable margins,
spontaneous successions.
What is
meant by ‘the same initial abiotic situation’? Can this initial situation ever be achieved again? What effects do
we have in mind?: total resalination; unexpected overall oil pollution and the
resulting death of all life; building to saturation?
For a
realistic definition of the replaceability, one has to add the time needed to
return to a similar initial situation with the time needed for the succession
that follows.
Internal and interdependent
comparability
Within
one ecosystem, one can talk of an ‘internal comparability’, as being essential for defining its replaceability. For defining
rarity, the ‘interdependent comparability’ of a number of ecosystems is
necessary. In this way, the rarity of the IJsselmeer region can be relativised
by the presence of the Oosterschelde. This consideration is clarified by means
of an example.
The death of one is the food
of another
Love for
an animal or plant species is not always the best stimulus for gaining insight
into ecological coherency and perspective. In an ecosystem the death of one is
the food of another. Every human intervention in this is a choice, just as
building an urban district is a choice. To report on the ecological effects of
such a project, a broader insight is required than can be supplied by a few
indicator species.
Bird,
butterfly, plant, toadstool, reptile, mammal and bat work groups are active in almost every
town and city. They collect a wealth of information about their
fascination for the more attractive (caressible) species of the plant or animal kingdom. Full of idealism,
thousands of volunteers and hundreds of professional biologists go out and
about daily to make inventories. Because of this, atlases are now available
showing the distribution not only of categories already named, but also of
aquatic plants, molluscs and fish for the Dutch and sometimes European areas or
for urban areas, e.g. Amsterdam (Melchers 1991, 1996; Denters 1994), that register their occurrence up to an accuracy of 5 km and
sometimes even to 1 km.
Preference for specific
species or combinations
From
time to time, these distribution maps are amended. There are now
already a number of decades that can be compared, so the national or regional
presence of animal or plant species can be clearly seen. However, one should
realise that there are more and better observers than there were, so that some
species might appear to be expanding in numbers, while that might not, in fact,
be the case. A recent milestone in Dutch synecology is the overview made of all
plant communities, which is also available electronically (Alterra, Synbiosys). Because of this, one can gain a view of succession series and thus the planning for
each community. These possibilities will be utilised in the years to come in
national and provincial policies on the goal species for the EHS. These atlases have been very useful in writing this book. The
example below illustrates how, by referring to different sources, the
importance of garland weeds (kranswieren) for the Gadwall duck can be suggested.
Uncertainties
These
facts are by far not in a form in which they can be gathered together into a
definitive system description. Attempts to do this at national and regional
levels by the Dutch Ministry of Agriculture, Nature and Food Quality (LNV) and the RIZA, among others, are underway. For the
time being, the Ministry of LNV is placing an accent on the relationships
between vegetation and birds (Schaminée, Joop, and André Jansen 1998, 2001). The presence of certain birds can indeed be an indication of
combinations of environmental factors of different scales, because they put
different demands on their dynamic fouraging area compared with their peaceful
breeding or moulting site. The RIZA has recently produced a more complete
description of the IJssel- and Markermeer (Noordhuis, R. 2000), paying attention to the physical and chemical environment, the by
many underestimated role of plankton, aquatic plants, fish, water birds, birds
that breed in the Netherlands, reptiles, amphibians, mammals, their
developments and regional potentials.
An unpredictable young and
dynamic ecosystem
From
this emerges a dynamic picture of the IJsselmeer region — a young, artificial and
unpredictable ecosystem, with the seasonal, annual and decennial coming and
going of species, largely in an unclear
relationship with each other. Every year, new species are found in the IJsselmeer
region, while, at the same time, others disappear. It is difficult to find a
reference in the past to make a guess as to where it will go to in the end.
The
relation between the large water system outside the dykes and the just as
dynamic and increasingly valuable ecosystem on the new land is hardly
indicated, because the land, the Oostvaarders- and Lepelaarsplassen, are not included in the area of study of the publication.
Nevertheless, it is precisely this relationship that is important when making
decisions about whether or not to build outside the dykes.
A continuing debate
There is
no concensus about the way in which urban nature should be valued. This emerged
from a debate of biologists in the WLO Work Group for Urban Ecology held on 20 June 2001 at the
request of Bram Mabelis, following the publication of his article ‘Kwaliteitsmeters voor
stadsnatuur’ (Quality gauges for urban nature) in Levende Natuur
(Issue 6, 2000).
Source: Bram Mabelis’
article
During
that debate, other publications and methodologies were discussed. From that
discussion it appears that potential, time and scale are important concepts in
valuing nature. The usefulness of a methodology depends on the balance between
politics, design and science. Each of these three has its own character and
values.
The
texts of different reactions are given below:
IJsbrand Zwart:
Said
that, as an employee responsible for ecological policy in Almere, he is trying
hard to find a basic ecological map with valuations. Because of the fact that
Almere is only 25 years old, the present quality is limited and many facts are
missing. The soils (clay and building sand) have nothing special to offer.
Describing ecotopes fits in with his intentions to map the nature values of
Almere. Due to lack of data, however, it is impossible for him to use species
as a gauge. In his opinion, the methodology relies too much on existing facts
and qualities, because, in particular, the potentials that are present play an
important role.
Henk Timmermans:
Thinking
about quality sizes and weights for urban nature demands standardisation on the
one hand, and that could be done well by the institutes, and on the other, it
must fit in with, and be useful in practice. The latter must be done, and is
already partly done, by the municiple services. But they are all trying to
‘re-invent the wheel’. Therefore, cooperation has to be sought between the
various municiple services, the exchange between institutes could be brought up
to a higher level and the relationship between research and practice needs to
be improved. That is possible in a large project, but non of the participating
actors is powerful enough in capital or influential enough to initiate such a
project. Would not this be a coordinating task, and thereby a raison d’ętre,
for the WLO?
Robbert Snep:
confirms
the importance of quality gauges for urban nature. In this, it
is important to keep potential and present nature values separate. The present
nature value can be determined by making an inventory of nature values and by
monitoring target species. The potential nature value is determined by (a)biotic limiting
conditions, the spacial positioning (local, regional and national) and the
dynamics (management and interference). In working out methods for
inventorising and monitoring, as well as determining the potential ecological
value, many aspects are not taken into consideration (such as scale level,
completeness, trustworthiness, area coverage). A more refined working out of
the methods used and (where successful) their standardisation would be
desirable.
Taeke de Jong:
Quality
gauges for urban nature (Mabelis 2000; Zoest 2001) have managerial,
cultural, economic, technical and ecological uses and a function in
(time)environmental planning. All the uses earlier listed can be found in this
last function. Within environmental planning and urban architecture, each with
their own quality criteria (utility, appreciation and durability, in many
senses of the word, such as the ‘robustness’ of the design and the
capacity to remain functional in many different situations for many different
interested parties), the emphasis does not lie on the actual value of a region,
but on its potential value in the future. Essentially, this designer’s
perspective is essentially of another modality than that of the empiricus.
Urban architecture and environmental planning merely create conditions. They cannot bring about or predict utility, appreciation or
durability. There is a similar problem in ecology, that of unpredictability due to the lack of many,
still unknown and sometimes intangible, causal connections.
The danger of fixing
specialists’ preferences in valuation maps
For more
than 30 years, the urban architectural design profession has been objecting to
valuation maps that fix combined values from
a particular sector (see, e.g., the debate in the ‘70s about mapping the
environment), because surplus values can only be compiled from
partial values. These maps are made using information from different sectors
(management, culture, economy, technique, ecology, available capital). A ‘sieve
analysis’ is sometimes applied to all
these maps, brought together as layers in a GIS system, to form a stain chart with vetos. Once the vetos have been
established, then the role of those sectors in the decision process comes to an
end. The urban architectural conceptions that are still allowed to enter this
type of ‘hinderance chart’ or ‘limiting condition chart’, are often no more than ‘left-over options’ that produce insufficient or poor living environments. In
practice, all these sector charts have their own untraceable assumptions and complicated deliberation
systems that are mistrusted in political debate because they cannot be
understood in ‘simple round words’.
Playing specialists off
against one another
In this
confusion, the designer takes the opportunity to undermine all these interests
with a new concept that offers unforeseen
possibilities. In doing this, previous advice is shouted down by reactions from
sectors that have kept quiet up to that point and now see a new chance. The
agenda is quietly changed in favour
of those who are shouting the loudest at the decisive moment. The trick is to
be able to play out alternative ecological plans against each other in simple
round words or pictures. The valuation chart is used occasionally in this
process, but by continually referring to it lessens its power to convince,
because the other sectors bring their own valuation chart into the game,
whether or not from a hidden agenda. The political game of dice only looks at
the side that lies uppermost at the crucial moment.
Improving instead of
protecting
Whatever
way one measures it, everyone can see that ecological values are going down. It is important to find a method whereby not only registered
values are protected and stabilised, but where the value of ‘worthless’ areas can be increased in the hands
of designers so that they are given new chances in changing situations. Ecology
can offer vegetative images that stimulate designers’ imagination. For me, the aim of urban ecology is to operationalise the
design-relevant presuppositions of different ecological valuations in a
language that offers a framework for deliberation for designers and
politicians, and also for other sectors. My first attempt (Jong 2001) took rarity and replaceability as a point of departure for
valuation. These ecologically important variables are compatible with the way
of thinking of the urban architectural designer, but they also have an economic
meaning. They offer a design-technical and political framework within which
other sectors can also be considered.
As urban
architectural work and the political trade are both differentiated on the basis
of scale (European, national, provincial, regional, municipal), it is a good
idea, also in ecology, to differentiate by scale. Each scale range between a given grain
(unit) and framework of decision-making
has its own style of deliberation.
A grain of valuation
In
Mabelis’ systematics, two differences can be identified that have many
interesting theoretical implications. Mabelis’ grain is species-level, and the
framework is a referential area such as a park, neighbourhood, district or
town. After long hesitation, the grain taken in a variable framework when
planning Almere Pampus was the neighbourhood level
(radius 300 metres). By including ‘species-similar’ references in the wider
surroundings within the concept of rarity, many problems in establishing an
historical place-bound reference can be avoided. Therefore, unlike Mabelis’
system, the reference is not internal, but external: Are there similar systems in the (wide) vicinity? These references
would change simultaneously and detectably if, for example, climatic change
made the historical reference irrelevant. In addition to
that, the urban environment is already incomparable with historical references,
due to raising (using sand to prepare land for building), draining and a higher
average temperature, unless one restricts oneself to those district parks which
have a similar water management system as before urbanisation.
Indicator species
I agree
with Mabelis’ choice to use a number of indicator species, irrespective of their rarity and relationship to each other. If
the rarity can be valued at system-level, then valuing it at species-level
would lead to double valuation. Mabelis only measures the diversity of
indicator species. In itself, it is a valuation choice that can become opaque
and evoke discussion when the choice of indicator is made complicated by professional
ecologists. My question in Almere was: ‘From what scale and categories does one
choose the limits to a system, in order to be able to identify surrounding
systems as being comparable?’ I have not found an answer yet. Perhaps it is
completely unnecessary to make a systematic choice of category. On the one
hand, I am impressed by the enormous number of inventorial data that, due to
Schamineé’s efforts, have now been released by Westhoff’s plant community
School and built into the nature-target types of the LNV (Schamineé and Jansen
1998, 2001). On the other hand, I am also sensitive to the criticism directed
against such preconceived category formation. I am more inclined towards abiotically orientated types of
ecotope, because they can be directly influenced by urban architecture, and
indicate potentials. However, data and prognoses based on them are less
accessible.
Categories and types to
compare
New
categories are constantly emerging, especially in urban districts, or new
spacial constellations are recognised that do not fit into an existing typology. A similar sort of problem already exists within the designers’
profession when you try to set up a building typology, not to mention an urban
architectural typology. Every final year student will try to prove that their
design does not fit in there, and that it is thus a ‘new type’. In the 1950’s,
CBS’s Standard Company Categorisation (SBI) divided companies into the wood industry, steel industry, textile
industry, and so forth, but it collapsed as more industries came into being
that began to use a combination of all these materials. The statistics from the
old company categorisation became incomparable with those of the new one, so
that it was no longer possible to make long-term prognoses from this material. The same
thing happened with the land-use statistics. Each categorisation is thus a child of its time and carries along
with it hidden assumptions. The only aspect that remains is the level of the
species. I have to agree with Mabelis there, although taxonomy also turns out to be a
dynamic process.
Valuating potentials
I do not
know how the ecological valuation charts that van Zoest showed of Amsterdam were made. I am curious to
find out, and hope that their valuation systematology is simple enough for
designers to have access to their presuppositions. In that case, an interest
will also emerge in the ecological potentials of less valuable areas and that
is more challenging and more productive than a veto chart of valuable areas. For the
time being, in Almere, there is only talk of less valuable areas. Therefore
what it comes to here is extending the abiotic potentials. That demands design,
ecological design, and the creation of living conditions. When considering
nature development, one should perhaps have no other aims in mind than
diversity. After all, we value nature mainly in that it does lack human
influence. In that light, nature-target types are paradoxical. We do not
design a house to instigate a certain type of household. We design an oikos merely to make different
households possible.
Many kinds of context
There are many managerial, cultural, economic,
technical, ecological and spatial situations
(spacial contexts and perspectives in time) that influence ecological success,
whatever the plan. They can be incompatible on different scale levels, without
interfering with a rich natural habitat. It is thus possible for the aims for
nature at the provincial level to be mainly directed towards clay morasses,
while at the municipal level, local differences in soil and land use are
utilised for much more promising nature development on such tiny local areas
that they do not hinder the larger targets. In this way, national societies
such as the Natuurmonumenten and the ANWB can place the emphasis on recreational values
and national infrastructure, while the municipality can prioritise its
responsibility for housing.
Contradictions and conflicts solved by scale
Such contradictions are often a question of differences in scale
and are therefore not true contradictions. Management may direct on a national
level, follow on a regional level and direct again on a local level.
Nationally, culture may be focused on tradition, regionally on experimentation
and locally on tradition again, or vice versa. The national economy can
flourish, be retarded regionally, but within them, there may be successful
locations again. In a more physical–technical way one can direct one’s
attention nationally to specialising on European nature or economy, while striving
locally for function combinations that produce a better overall fulfillment of
life. Ecological diversity on a European level can produce homogeneity on a
national level and within the NW European building concentration there is
enough space left over for national distribution, and, within that, for
concentration again, regionally.
Effect analysis supposes expectations about the future context
The number of plausible perspectives on all these levels is so large that, unless
founded on a broad scenario, there is no possibility of carrying out an effect
analysis that will have any predictive value. National, regional and local
nature goals and presuppositions about managerial power, cultural developments,
economy, techniques, ecology and space are thereby essential. To arrange these
presuppositions scalewise, the following scheme can be applied:
|
|
radius
|
managerial
|
cultural
|
economic
|
technical
|
ecological
|
spacial
|
|
global
|
10000 km
|
directing
|
experimental
|
growth
|
integration
|
diversity
|
distribution
|
|
continental
|
1000 km
|
following
|
tranditional
|
shrink
|
specialisation
|
homogneity
|
accumulation
|
|
national
|
100 km
|
directing
|
experimental
|
growth
|
integration
|
diversity
|
accumulation
|
|
regional
|
30 km
|
following
|
traditional
|
shrink
|
specialisation
|
homogoneity
|
distribution
|
|
local
|
10 km
|
directing
|
experimental
|
growth
|
integration
|
diversity
|
accumulation
|
|
urban
|
3km
|
directing
|
experimental
|
growth
|
integration
|
diversity
|
accumulation
|
|
in the district
|
TKA
|
directing
|
traditional
|
growth
|
specialisation
|
diversity
|
distribution
|
|
Hosper
|
directing
|
experimental
|
growth
|
integration
|
diversity
|
accumulation
|
|
H+N+S
|
following
|
experimental
|
growth
|
specialisation
|
diversity
|
accumulation
|
|
|
|
Fig. 811 Presumed
perspective
|
|
|
Hidden suppositions about the future in plans
Urban architectural plans for the same region can differ in perspective.
The perspectives of the urban architectural plans of TKA, Hosper and H+N+S differ as to whether the authorities will be
directing or following at the district level, whether one would like to live
more traditionally or experimentally, or whether there is talk of
(de)concentrated specialisation or concentrated integration of functions.
The interpretation given here is arbitrary and
on higher scale levels it is uniform for the designs, but the scheme makes one
aware of suppressed presuppositions that designers and valuators have with respect
to different levels. These presuppositions differ among the participants in the
decision-making process. We can, however, realise them in part, especially at
the local level. If these presuppositions are explicit, a guess can also be
made of the effects of different plans after further research at the
neighbourhood level.
EHS
A main ecological structure (EHS) is established in nature
policy that is worked out further for each province.
|

|

|
|

|
|
|
|
|
Fig. 812 The EHS for the
Netherlands
|
Fig. 813 The EHS worked
out on Internet for the province of South Holland and the Gelderse poort
|
|
|
|
Nature target types
Nature conservancy sets certain types of nature as a target for
itself, in order to shape the main ecological structure in the Netherlands.
In Fig. 31 these nature-target types of the IKC/Ministry of LAVIN by Bal, Beije et al. (1995);
Bal, Beije et al. (1995); Bal, Beije et al. (2001) are linked to an urban
architectural scale.
|
|
Main group 1
|
Main group 2
|
Main group 3
|
Main group 41)
|
|
Name
|
almost-naturally
|
supervised-naturally
|
half-naturally
|
multifunctional
|
|
Radius
|
3km
|
>1km
|
300m
|
100m
|
|
Future picture
|
global
|
global
|
fixed
|
fixed
|
1.
STRATEGY
|
|
spacial scale
|
Landscape > thousands of ha.
|
Landscape > 500 ha.
|
ecotope/mosaic to approx. 100 ha.
|
ecotope mostly a few ha.
|
|
location
|
mostly process-determined
|
process and pattern-determined
|
process-, pattern- and species-determined
|
pattern- and species-determined
|
|
processes
|
not directed
|
directed integrally
|
directed in detail
|
directed in detail
|
|
patterns
|
not established
|
not established
|
established, perhaps a cyclical succession
|
established
|
|
directing variables
|
non
|
process-focused on landscape level
|
process- and pattern-focused up
to ecotope level
|
process- and especially
pattern-focused up to ecotope level
|
2. LAY-OUT
|
|
nature–technical
|
only in the
beginning phase
|
only in the beginning phase
|
perhaps
repeated
|
perhaps
repeated
|
|
environmentally
specialistic
|
only in the beginning phase
|
only in the beginning phase
|
permanent,
if necessary
|
non
|
|
Conservancy
|
|
Internal nature conservancy
|
non
|
non
|
partly
necessary
|
necessary
|
|
compartmentalising
|
non
|
non
|
possibly in
mosaic
|
possible
|
|
shared use
|
(very)
extensive
|
(very)
extensive
|
(fairly)
extensive
|
characteristic
|
3.
DEVELOPMENT
|
|
succession-stage
|
mostly
diverse stages
|
diverse
stages
|
a
stage/mosaic
|
a stage
|
|
extent
of development
|
on average
long
|
on average
long
|
rather
short
|
short
|
|
predictability
|
on average,
limited in the long run
|
on average,
rather limited in the long term
|
quite large
|
large
|
|
1) The characteristics of the
types in subgroup 4B (derived multifunctional types), apart from the
characteristics associated with shared use, they are the same as those of the
types from which they are derived.
|
|
|
|
Fig. 814 Overview of nature-target types
|
|
|
Nature-target types specified by physical-geographical region
The nature-target types are specified according to
physical-geographical region (Fig.
815 ).
|
Physical-geographical
region
|
Main
group
|
total
|
|
Landscape
scale
|
ecotope
level
|
|
1
|
2
|
3
|
4
|
|
3km
|
>1km
|
300m
|
100m
|
|
hl
|
Hilly land
|
1
|
2
|
12
|
2
|
17
|
|
hz
|
Higher sandy soils
|
2
|
3
|
19
|
2
|
26
|
|
ri
|
Fluvial area
|
0
|
2
|
12
|
2
|
16
|
|
lv
|
Laagveen
area
|
1
|
3
|
10
|
2
|
16
|
|
zk
|
Marine clay area
|
0
|
3
|
13
|
2
|
18
|
|
du
|
Dunes
|
1
|
1
|
16
|
2
|
20
|
|
az
|
Estuaries
|
0
|
3
|
8
|
1
|
12
|
|
gg
|
Tidal zone
|
2
|
2
|
2
|
0
|
6
|
|
nz
|
North Sea
|
1
|
0
|
0
|
0
|
1
|
|
|
Total
|
8
|
19
|
92
|
13
|
132
|
|
|
|
Fig.
815 Nature-target types per physical–geographical region
|
|
|
The following nature types have been established
as targets for the physical-geographical region ‘higher sandy soils’ (e.g. the Veluwe) (Fig. 816 ).
|

|
|
|
|
Fig. 816 Nature-target types for the higher
sandy soils
|
|
|
|

|
|
|
|
Fig. 817 Nature-target
types for higher sandy soils in local profile
|
|
|
For The Fluvial Area, the following nature types
have been established as targets (Fig. 818 ).
|

|
|
|
|
Fig.
818 Nature-target types for The Fluvial Area
|
|
|
|

|
|
|
|
Fig. 819 Nature-target
types for The Fluvial Area — 300m
|
|
|
|

|
|
|
|
Fig. 820 Nature-target
types for The Fluvial Area in local profile
|
|
|
For the Marine-clay areas, the following nature types
have been established as targets (Fig. 821 ).
|
3km
|
>1km
|
300m
|
100m
|
|
|
zk-2.1: clay–primeval morass
(including freshwater tidal landscape)
zk-2.2: wooded landscape on clay
zk-2.3: low fen morass
|
zk-3.1: freshwater community
zk-3.2: brackish water community
zk-3.3: salt and brackish brushwood
and landscape
zk-3.4: reedland and brushwood
zk-3.5 wet infertile grassland
zk-3.6: grassland rich in flowering plants
zk-3.7: peat heath
zk-3.8 thicket, mantle and seam
growth
zk-3.9: felling wood and osiers
|
zk-4.1: food-crop field
zk-4.2: grassland
zk-4B: target types from the main groups 1-4
zk-4B.3 reed culture
zk-4B.4: indigenous woodland culture
zk-4B.5: woodland culture with foreign
species
|
|
zk-3.10: woodland communities on Marine clay zk-3.11: woodland communities on peat-on-clay
zk-3.12 middle woodland
zk-3.13: park-stinzen woodland
|
|
|
|
Fig. 821
Nature-target types in Marine-clay areas
|
|
|
|

|
|
|
|
Fig. 822 Profile of
nature-target types in Marine-clay areas
|
|
|
The relation between abiotic factors in urban
areas and diversity of plant species is examined on 8 levels of scale.
Hypotheses on the abiotic origin of this diversity, especially within cities,
are listed on each level of scale. They are supported by examples from the
cities of Zoetermeer and partially Enschede.
Regions
If one compares regions (of a 30 km. radius)
with each other, other differences come to light than when, for example, one
compares groups of buildings (‘ensembles’ with a radius of 30 m). Travelling
through an urbanised landscape, on average, one sees, for example, that within
30 m. the extent to which land is being trodden on and exposed to sunlight varies, but
variations in ground and water management are often only evident at distances
greater than 30 km. Which differences in abiotic situations can, for each scale
level anew, explain the differences in richness of species? This question is
largely unanswerable, but for urban architects and civil technicians it is
crucially important, because these disciplines, certainly in new situations,
literally set the conditions of these variables. In the case of high-lying wet
and dry areas, should one bring about change every 100 km. or every 10 m?
Should one open up or drain water every 100m or every 1000m? This produces —
depending on the existing context — an entirely different diversity in the
initial abiotic situations. In addition, when one realises that one can do that
differently in one direction or another, that results in an infinite number of
design alternatives. Which of these alternatives produces the most extensive
ecological richness?
Towns
Towns are stonier, 1 to 3°C warmer, and are nowadays
cleaner, than their agrarian surroundings. They are, thanks to the 19th century
hygienists (see Houwaart, E.S. 1991), cleaner and more spacious
than a century ago. Urban environments are dynamic (there are few places that
have not been turned upside down at least once during the last 25 years), but,
viewed abiotically, they are also varied. For botanical diversity, the important
abiotic differences (in combinations of minerals, moisture, exposure to
sunlight, mowing management, disruption, treading on (extent of), (surface)
hardening (by constructing roads, heat capacity) are greater per square km.
than in agrarian areas and are often also greater than in nature reserves. On
what scale level should these variations be explained and utilised?
Hypotheses for design on different levels of scaele
For the time being, we will choose the following
points of departure (hypotheses):
|
Variation effective for
the vegetation
|
R =
|

|
|
the height, ground
|
30km
|
|
ground (‘floor’ or
‘bottom’ if you’re talking about a lake, canal, valley, etc, i.e. a surface),
water management
|
10km
|
|
seepage, drainage, water level, opening up waterways in towns and cities
|
3km
|
|
urban architectural
planning
|
1km
|
|
dividing land into lots
(distributing green areas)
|
300m
|
|
(surface) hardening (by
constructing roads), treading on (the extent of), manuring by pets, minerals
|
100m
|
|
difference in height,
mowing management, disruption
|
30m
|
|
exposure to sunlight
|
10m
|
|
One must interpret the radius between adjoining
radii, flexibly.
|
|
|
|
|
|
Fig.
823 Hypothetical working variations per scale-level in
urban-nature subsoils
|
Fig. 824 Scale paradox
|
|
|
|
Scale paradox
The scale paradox in urban architecture (see Fig. 824 and Jong, T.M., de 1995) teaches us that conclusions must be drawn from
the same scale-level (the smallest grain considered and the largest frame) as
that on which the premises were based. For example, in the above figure, if
every time one takes into consideration one small circle and its surroundings,
then one notices differences, while, on the contrary, when repeatedly comparing
small groups of seven with their surroundings (see also Kolasa, J. and Pickett,
S.A. 1991) one should conclude that they are alike. The
paradoxical notion ‘homogenous mixture’ indicates this dilemma exactly: at a certain
scale level it is homogenous and at a lower abstraction level it is
heterogeneous. The notion ‘bundled deconcentration’ is another example. For
such notions, an immediate question can be raised: ‘On which scale is the one
and on which scale the other?’. In addition, this figure shows that confusing
concepts like these are already possible where there is a factor 3 linear
difference in scale level. There is a 7-decimal linear difference between a
grain of sand and the earth, and so there are more than 14 confusing concepts
lurking in the background.
Scale articulated view on image and ecology
With this in mind, in Amsterdam, we have made an image
quality plan that attempts to find an optimum in tolerance
between surprise and recognition at each scale level (in their extreme form,
between chaos and order) as the sensory working of variation (Jong, T.M. de,
and Ravesloot, C.M. 1995). Diversity in ecology is
also sensitive at scale-level as both cause and effect, or rather as abiotic
condition and biotic effect. The crucial rarity of species, biotopes, plant
communities, ecosystems, landscapes, plant–geographical districts is just as
dependent on scale (globally, continentally and nationally, etc. rare). For
example, in Zoetermeer, a policy line was established
at some point that one should concentrate on globally (within a radius of
10,000 km) and regionally (within a radius of 30 km) rare species (and thus not
on nationally rare species). Insight into this demands a (as yet not available)
differentiated and long-term overview of combinations of species and their
ability to recover within 1, 10, 100 years, etc. (rarity in time). It thereby
becomes possible to deliberate rationally between different urban functions (a
main port is rare within 300 km and can recover within 10 years; a peat
landscape is rare within 300 km and can recover within a 1000 years). As there
are too few facts available, we do not deal with rarity and recoverability any
further in this article. A scale-based
view of diversity is a condition, and a good first step in the direction
of, such a scale-based view of rarity.
Zoetermeer and Enschede (approx. the same size)
are situated in areas that differ greatly in richness of species. The urban
areas of Zoetermeer and Enschede differ
little in diversity (not counting combinations of species). This complies with
Denters’s (1999) references that indicate that urban flora
differ very much ... from those in the immediate neighbourhood, whereas
striking similarities can be found between the flora of various towns ...’.
When one views these towns as a whole, at regional level, the age of the town
does not have much influence on the diversity. The influence of soils (clay and
sand, respectively) should also not be exaggerated because in preparing
low-lying land for building, sand is used as a material to raise the level of
the ground. In fact, in Zoetermeer,
that has not happened very much. Except for relief that is related to
infrastructure, in principal, the clay bottom has here only been partially
raised to approx. 40 cm using soil from within the urban, excavated from new
water features and building pits, thus creating a closed soil balance.
Waterways can be encountered approx. every 400 m. The
entire urban area here will be drained more or less to the same extent, to 1m. below
ground level.
Differences in diversity at urban level
In both Enschede and Zoetermeer there are large differences within the town in
richness of species (see Fig. 766). In both towns, the number
of wild plant species per square kilometre are shown in dots representing 10
species, such as is more precisely inventorised by Floron and by local observers (municipality and KNNV). Fig. 766 shows three widely
differing one-kilometre grid squares in urban architecture, extending from the
district Meerzicht (left) to the old village (right) in
Zoetermeer. The numbers of species found also differ significantly. In the
1970’s, Meerzicht was the third newly built district, following the high-rise
districts Palenstein and Driemanspolder that dominate the view from the motorway. From
there onwards, high-rise buildings were renounced in the newer, more northerly
districts.
Centre and periphery
New perifery districts in Enschede score
relatively high; old central districts, just as, for example in The Hague, score relatively low. In
Zoetermeer almost everything is new. What is noticably different in Zoetermeer
compared with Enschede is that the richness in species decreases from the middle to the edge in many
cross-sections. The largest number of species is to be found in the middle of
the town, in the old village. During the last 30 years, the town has grown round
this centre, first westwards and then in a clockwise direction. The edges of
town are sometimes less accessible and admissible for observers. Eutrophication from the rural surroundings can play a role.
There have been fewer disturbances in the old village in recent years than
elsewhere in the town.
Infrastructure
Apart from this, the centre is a concentration
of old high water courses and new, relief-rich infrastructure such as the fast train and the urban
motorways, with scarcely trodden-on verges. Both contribute to the
richness of the local species. Unexpectedly, in both towns, a concentration of
infrastructure appears to foster more species. Industrial premises also score
well.
The high, dry, chalk-rich railway line, along which vegetation is
regularly removed, produces, in between the maintenence clearances, and for
some one-kilometre grid squares, an extraordinary pioneer environment that thereby contributes to the local richness
of species. The banks of this looped-shaped fast train line have the largest
range of variations of exposure to sunlight imaginable. The only documented
example of ecological infrastructure at work along the fast train line, following
its opening in 1977, is the advance, in 1984, of the Cinnabar moth via a long
yellow ribbon of Ragwort from the dunes near The Hague (van Wely,1993).
Waterways
Waterways in the northern part of Zoetermeer are
suffering more and more from seepage containing phosphate and iron, made turbid by
algae. They were originally
maintained by vegetation-unfriendly dredgers, but this activity has been
restricted in recent years to that of keeping the flow of water open at
essential bottlenecks in the water system. Old water courses, sometimes with
water levels raised as much as 4m, that have been left undisturbed by the urban
architect, have clearer water, without any seepage and their banks are rich in
species, sometimes with rare flora. At the water’s edge, the rough banks of
ponds encircled with reeds, although picturesque, are influenced by seepage,
and so contribute relatively little to the richness of species.
Mowing habits
Whether removing mown vegetation from the sides
of motorways has contributed to the increase in species from 200 to 222 over
the entire motorway network between 1982 and 1988 (Vos, 1990) is difficult to prove. It is possible that
increases in shade and leaf-fall from planted vegetation and manuring by pets
from raised paths has worked against the desired empoverishment of these areas.
Moist grasslands that are rich in food are mown twice a year, and drier or wetter grasslands
only once.
Smaller scale differences in initial abiotic situations
The urban architectural variation at district
level (within a radius of 1 km) appears to influence the richness of species,
but can be disrupted by local elements such as the fast train line. The
variation in richness of minerals, moisture, sunlight, hardening of soil
surfaces and disruption is effective at this scale level, but, for urban
architectural ends, can only be evaluated by means of inventories which have a
smaller resolution than the usual square kilometre. The ‘mean-field assumption’
(Dieckmann, C.S. 2000) used in current statistical ecological
research is insufficient for that. For example, due to detailed planning,
mowing management can vary within a radius of 30 m. Schools could be brought in
for such labour-intensive inventories. For the urban nature type ‘nature in the
living environment’, a start has been made to inventorise abiotic factors
within a radius of 100m (Breems, S.C. 2000).
Conclusions
For a truly ecological urban architectural
design, it is necessary to conduct scale-based ecological research in towns, in
which differences in species richness and rarity within a radius of 1 km and
300, 100, 30 and 10 m are explained separately. To help balance a solution
against other functions, it is desirable to establish a measure of
recoverability (e.g. within 1, 10, 100 ...years). In opposition to current
urban ecological opinions, arguments can be put forward about the observed,
sometimes negative, influences of seepage, the unexpected positive influence of
business zoning and traffic infrastructure, and the limited influence of the
subsoil, pond verges and the age of buildings on botanical diversity. Herewith,
is also, for example, the much defended strategy of the two networks
(traffic infrastructure and water) refuted in its scaleless form.
6
Living, human density and
environment
Contents.................................................................................................................................... 457
6.1 Adaptation and Accommodation................................................................................. 459
6.1.1.... Human population........................................................................................................... 459
6.1.2.... Habitat, density and economy.......................................................................................... 460
6.1.3.... Population growth........................................................................................................... 462
6.1.4.... The urban environment..................................................................................................... 467
6.1.5.... Mobility between urban populations.................................................................................. 471
6.1.6.... The urban field is not homogeneous.................................................................................. 474
6.1.7.... The force of specialization................................................................................................ 476
6.2 Habitat............................................................................................................................. 482
6.2.1.... Dutch heritage................................................................................................................ 482
6.2.2.... Human impact................................................................................................................ 485
6.2.3.... The last millennium......................................................................................................... 490
6.2.4.... Reading topographical maps (Visser)................................................................................ 497
6.3 Density............................................................................................................................. 500
6.3.1.... Global densities10 000km...................................................................................................... 500
6.3.2.... Gross and net density..................................................................................................... 500
6.3.3.... A binary legend: net and tare surface................................................................................ 501
6.3.4.... (Sub)continental densities3 000 and 1 000km................................................................................ 502
6.3.5.... National densities and distributions300km............................................................................. 502
6.3.6.... Regional distribution100 and 30km............................................................................................. 505
6.3.7.... Density or real measure dots distribution........................................................................... 508
6.3.8.... Metropolis density30km...................................................................................................... 511
6.3.9.... Conurbation density10km.................................................................................................... 513
6.3.10.. Town
density3km............................................................................................................... 513
6.3.11.. District
density1km............................................................................................................ 514
6.3.12.. Neighbourhood
density300m................................................................................................ 514
6.3.13.. Ensemble
density100m....................................................................................................... 517
6.3.14.. Urban
island density30m.................................................................................................... 521
6.3.15.. Urban
details10m influencing density................................................................................... 522
6.4 Economy.......................................................................................................................... 524
6.4.1.... Dutch statistics.............................................................................................................. 524
6.4.2.... Public space.................................................................................................................. 525
6.4.3.... Urbanity......................................................................................................................... 526
6.4.4.... Population...................................................................................................................... 530
6.4.5.... Time and movement........................................................................................................ 532
6.4.6.... Dwellings....................................................................................................................... 533
6.4.7.... Public utilities................................................................................................................. 534
6.4.8.... Facilities........................................................................................................................ 538
6.4.9.... Businesses.................................................................................................................... 542
6.5 Environment................................................................................................................... 547
6.5.1.... Conditions...................................................................................................................... 548
6.5.2.... Emissions...................................................................................................................... 551
6.5.3.... Transmission.................................................................................................................. 559
6.5.4.... Immission and exposition................................................................................................ 563
6.5.5.... Creating standards.......................................................................................................... 568
6.5.6.... Environmental policy....................................................................................................... 571
6.6 Soil pollution................................................................................................................. 577
6.6.1.... Soil pollution................................................................................................................... 577
6.6.2.... General soil knowledge.................................................................................................... 578
6.6.3.... Soil pollution and building activities................................................................................... 580
6.6.4.... Exploratory survey.......................................................................................................... 582
6.6.5.... Follow-up investigation..................................................................................................... 586
6.6.6.... Causes of soil pollution.................................................................................................... 587
6.6.7.... Remediation methods...................................................................................................... 590
6.6.8.... Soil purification techniques.............................................................................................. 590
6.6.9.... Appendix saneringsregeling wet bodembescherming P.M. (remediation
regulations under the Soil Protection Act) 594
Adaptation and accomodation
This chapter deals with the adaptation of the human species to its
habitat (adaptation), and the adjustment of the human habitat to
the species (accommodation, technique).
The unmatched growth of human population is due to its faculty of
toolmaking and
consequently, its accomodating capacity. That accomodating capacity happens to
be the object of architecture and urban design.
Architecture and urban
design as a part of ecology
So, the chapter approaches architecture and urban design as human
ecology, a part of aut-ecology[273], necessary to understand the distribution and
abundance of this particular species and its remarkable artefacts on Global,
European, national, regional and local levels. Syn-ecologically it is
interesting to see how this species recently developed into a plague, ousting
other species and changing the environment (environmental ecology). From a viewpoint of systems ecology its
potential to survive on any level of scale in space and time could be studied,
taking global resources into account. Cybernetic ecology could
prove helpful for design and chaos ecology for management.
History as a laboratory
However, this chapter starts with a historical approach, because
history is a kind of laboratory unveiling suppositions of our existence we are
inclined to forget.
Anthropogenesis
For
millions of years, human characteristics have been tuned to the natural
environment in which people had to survive (adaptation).
Therefore, it is useful to acquaint oneself with this ‘reference’ environment as such, and, now and then, to allow this
nature to be the tutor of architectural (and mechanical engineering) forms.
Even in the most advanced studies into the development of autonomous robots,
the mechanics of insects are attentively observed. Also in the other
development that is thought to be important for the future — biotechnology — nature
is often ‘the tutor of art’ (‘Natura Artis Magistra’).
Human habitat
In the history of human
origins (anthropogenesis) , human adaptation and environmental determination have played a
major role. Different human-like animals such as australopithicus
developed and later became extinct. Approximately 2 million years ago, due to
climatic and environmental changes in Africa, homo habilis with larger brains
than its predecessors exchanged a forest habitat for savanna starting to
eat meat.[274] This species’ apparent use of tools has often served as a criterium to demarcate
humanity: the
capacity to oversee a series of acts of which only the first (e.g. the making
of tools) can be carried out immediately.[275] The use of language or fire as tools both suppose such an ability.
Subsequently, homo erectus developed with
many variants. Thirty thousand years ago only two species remained, homo
neandertaliensis and homo sapiens. The neandertalers existed at least 500 000 years, but became
extinct, leaving homo sapiens with a common ancestor in Africa
approximately 150 000 years ago as the sole human survivor.
Arboral
pre-adaptations?
The origin of the human
race, preceding homo habilis, should have produced a number of
ergonomically interesting ‘aboreal pre-adaptations’
(adaptations to the former forest environment), such as the ability to grasp
with the hands,
stereoscopic vision,
upright posture, the
production of a limited number of offspring at each pregnancy, a lengthy
up-bringing of the offspring, etc.[276] The tropical rain forest is then by no means as frightening as is it is
made out to be. It is a fantastic experience to cut a path for oneself through
this twilit environment: it feels as though one is returning home after 6
million years. All the senses are stimulated in a changing, yet balanced, way.
One can seldom see further than 100 metres ahead and is constantly obliged to
focus the eyes on objects both nearby and further away. Moreover, it is an
environment similar to a Gothic cathedral: full
of vertical light-seeking pilasters, in which, occasionally, the sun festively
forces its way to the bottom. This demands continuous attentiveness, but, on
the other hand, the senses seldom become overloaded.[277]
Savanna adaptations?
The 20tth century
witnessed the clearance of the last primitive forest peoples and their culture
and habitat. Nevertheless, a cultural-ecological study of these communities that are so closely
linked with our reference environment could be of importance for future urban
design.
The transition from forest
dwelling to life on the flat savanna lands must have made the eyes lazy, but
the hands and the head more diligent. Particularly in between these
environments people seek cover and build their own protective shelters.
With the help of technical
resources, the human species nowadays can maintain and organise itself to suit
its own wishes in every biotope (accommodation). In
general, such accommodation results in pioneer, grassland and brushwood
vegetations. Sometimes, mankind changes the dominance relationships in the
landscape to such an extent that, in places, the old situation remains
protected (nature conservation) or new
successions are allowed to come into being (nature development).
Habitat and density
Different populations live
in different densities (Fig. 825)[278].
|
HABITAT
|
% total land area on earth
|
% total world population
|
inhabitants per km2
|
|
Dry lands and deserts
Tropical forest/ shrub
crops
Grassland areas
Semi-forested areas
Mediterranean shrub
overgrowth
Temperate to cold area
Arctic/tundra area
Living area in the
mountains
|
18
15
21
7
1
10
16
12
|
4
28
12
39
4
1
<1
12
|
10
60
20
190
130
3
1
30
|
|
|
|
Fig.
825 Population densities in different habitats 1970
|
|
|
Habitat
and economy
Each habitat has resulted in
different forms of economic household management (Fig. 826). In mediterranean scrub and tropical grasslands
(savannahs) all types of economy have been found.[279]
|
|
Food-gatherers
|
Hunters
|
Pastorales
|
Nomads
|
Simple cultivators
|
Advanced cultivators
|
|
Equatorial forests
|
Siamang
|
Pygmies,
Melanesians
|
|
|
Amazone,
Nw.-Guinea
|
Indonesia,
Java
|
|
Tropical forest and scrub
|
Grand Chaco indians
|
the Bantu
|
the Bemba
|
|
Indo-Dravidians, South Americans
|
Bantus
|
|
Tropical grasslands (savannahs)
|
Australoids
|
Hadza (East Africa)
|
Nilotes
|
North American Indians
|
Hamites
|
|
Drylands and deserts
|
Bushmen and Australians
|
|
|
Bedouins,
Tuaregs
|
Oasis dwellers
|
Oases (riverine)
|
|
Temperate forests
|
Australians, Mesolithic Europeans
|
Tasmanians, Predmost
|
Iron Age Europeans
|
|
Chinese
|
Peasant
Chinese
|
|
Mediterranean scrub
|
Strand lopers
|
Californian Indians
|
Balkans
|
Berbers
|
Neolithic Iron Age, Maori
|
Medieval Europe
|
|
Temperate Grasslands
|
Paleolithic Europeans
|
|
Mongols
|
boerjaten, mongols
|
Siouan Indians
|
Pawnee indians
|
|
Boreal
|
Fuegians
|
Samoyeds
|
|
Lapps
|
|
|
|
Tundra
|
|
Eskimos
|
|
Lapps
|
|
|
|
|
|
Fig. 826 Habitats, economies and cultures
|
|
|
From this it appears that
there is no simple relation between habitat and household management, as
believed by physical determinists at the end of the last century.(Claval, 1976).
·
|
Population
|
km2 per head
|
heads per km˛
|
for 100 people
|
|
|
|
|
|
km radius
|
nominally
|
|
Food gatherers
|
|
Upper Palaeolithic (Eng.)
Australian aborigines
Tierra del Fuego islanders
Andamen Islanders
|
500
60
20
1
|
0,002
0,017
0,05
1
|
126
44
25
6
|
100
30
30
10
|
|
Developed
hunters/fishermen
|
|
Eskimos and Indians
Eskimos (Alaska)
Mesolithic man (Eng.)
Pampas Indians
British Columbians
|
500
80
25
5
0,1
|
0,002
0,0125
0,04
0,2
10
|
126
50
28
13
2
|
100
30
30
10
3
|
|
Arable farmers and nomads
|
|
Neolithic man (Eng.)
Pastoralists and nomads
|
1
0,25
0,03
|
1
4
33
|
5,6
2,8
1,0
|
10
3
1
|
|
Iron Age man (Eng.)
Middle Ages (Eng.)
|
0,25
0,05
|
4
20
|
2,8
1,3
|
3
1
|
|
Middle Age man
|
0,02
|
50
|
0,8
|
1
|
|
Swidden farmers
|
0,001
|
1000
|
0,2
|
0,1
|
|
Harrison, Weiner et al. (1964); Harrison, Weiner et al. (1970)
|
|
Fig.
827 Economies and population density
|
|
|
Density and economy
However, there is some
relation between household management and population density (Fig. 827)[280].
In the last two columns, the
areas are translated into the radius of a circle with the same or almost the same
area for a group of 100 people[281]
The same approximated sizes
will play an important role in comparing different urbanising models.
From hunting into agriculture
The transition from hunting to agriculture has had enormous societal consequences.
In the village Beidha, in Jordan,
the floor plan of dwellings changed from round to square during the 500 years
from 7000 BC. This reflects a probable social development towards sedentary
living with more task division and functional differentiation of the built
environment (Fig. 828).[282]
|

|

|
|
1 Living room
2 Storage places in the
neighbourhood
|
3 shops
4 community building
5 inner courtyard
living in storeyed
buildings
|
|
|
|
Fig.
828 Historical floor plans of dwellings that reflect the transition
from hunting to agriculture
|
|
|
Agriculture
If an animal or plant
species gains dominance in a new habitat, then, initially, the population of
these species can increase unhindered, but sooner or later it comes up against
boundaries in the carrying capacity of the environment (in terms of Opschoor and Weterings (1994) and Koten-Hertogs, Beckers-de Bruyn et al. (1995)
environmental utilisation space (milieugebruiksruimte),
or (in the case of human beings) boundaries, which they themselves fix, within
the existing biocoenosis (ecological community).
If we couple the beginning
of mankind with the use of tools, then the species is approximately 1 million
years old. Agriculture (the Neolithic revolution)[283] was invented
10,000 years ago (1% of 1 million!). By means of agriculture, the species was
able to enlarge, single-handedly, the carrying capacity of the environment and
thereby to increase its population according to from
approximately 4 million to 200 million by the height of the Roman Empire in
Europe and the Han Dynasty in China.
Overcropping and
agricultural innovations
Round about the beginning of
the Christian era this growth appeared to have slackened off, but, in the last
1000 years, growth has occurred again, which, as yet, appears to be exponential
(see Fig. 829).
The slowing down of growth
around the beginning of the era can be explained by the fact that all available
land at that time suitable for agriculture was in use[284]. Erosion occurred due to overcropping, forcing some
human communities to leave their homelands, and tribal migrations began to take place. Because of the
limitations of agricultural land, people learned to be more careful with the
soil by implementing two- or three-year rotations, by applying fertilizers
(nitrate cycle), by
improving the plough and the storage (of the produce), etc[285]. After the Neolithic Revolution, the next big revolution came with
the mastery of inanimate energy (Industrial Revolution beautifully described by Cipolla, 1970). Each
technological revolution created the conditions for far-reaching economic,
demographic, cultural and political revolutions and these, in turn, had
enormous ecological consequences.
Technical, agrarian and
hygiene innovations can counteract the original environmental limitations and
allow unlimited population growth for a time. Jong and Priemus (2002) discuss these and other approaches.
Medieval fluctuations
Fig. 829 shows that in Europe, during
the Middle Ages, significant population fluctuations occurred partly because of erosion and starvation,
and partly because of (pest) epidemics.
The new exponential growth has mainly taken place after the Middle Ages,
after technological developments had made their influence felt in the fields of
agriculture, trade and hygiene.
War and illness, such as the
enormous pest epidemic around 1300 A.D. interferes with population
dynamics in a similar way to the activities of
predators in a population of their prey[286].
|

|

|
|
|
|
|
Fig.
829 The supposed developments in population numbers in Europe
|
Fig. 830 Predator and
prey according to Lotke-Volterra
|
|
|
|
·
|

|
|
|
|
Fig.
831 Demographic crisis in Meulan, near Paris
1693-1694
|
|
|
Hunger
Historically, hunger is recognisable by the number of deaths, and
is often related to the staple food. Increases in the price of grain are
generally followed by more cases of death. Then, once the crisis periods have
ended, the numbers of births increase again. This relationship is not only
evident in history, but is still actual today, and will become more evident as
the current world population develops[287].
Unlimited and limited growth
If there was no immigration or emigration, and
the death rate remained constant, then population growth
would be completely dependent on the number of children born. If the number of
children k born to each individual was 1, then the population would
remain constant, if k<1 then the population would decrease, if k>1,
then it would increase. The total population y of parents y0
and children ky0 is then y0+ky0
(Fig. 832).
|

|

|

|
|
|
|
|
|
Fig.
832 Unlimited growth
|
Fig. 833 Adapted by
parameter
|
Fig.
834 Limited growth because of carrying capacity
|
|
|
|
|
Where death rates vary per
generation, there is also a variation in birth rates. To contain these
variations within one model, it is no longer sufficient to use a time-segment
approach.
Instead, one has to examine the population per cohort (Fig. 835)[288]. The branch of science that concerns itself with these activities is
called demography.
|

|
|
|
|
Fig.
835 Population in a certain period and per generation (cohort)
|
|
|
Growth that is limited by
the usable area of environment, or the carrying capacity of the ecosystem, is
represented by a logistic curve (Fig. 834). Should we, for the time
being, interpret the future of our population as one of unlimited or of limited
growth?[289] Many people like Meadows, Meadows et
al. (1992) think or hope, in view
of limited raw materials, that growth will be limited. The logistic curve works beautifully for fruit flies, but when
applied to the population of the United States, based on the demographic
statistics from 1790 to 1910, reality proved this mathematical approach to be
incorrect after 1950: growth is still exponential.
Technology
From technical history, we
have learnt how a succession of technological innovations, in its
totality (the ‘envelope curve’) can
be reinterpreted as exponential growth (Fig. 836).[290]
|

|

|
|
|
|
Fig.
836 The envelope curve and an example for transport technology
|
|
|
Chaotic growth
Fig. 837, and the following figures,
illustrate a reflexive chaos function chaosi+1 := a·chaosi – a·chaosi2 for example with chaos0 := 0.0016
and i := 0 … 15 that looks similar to a logistic curve on a=2, but which shows
chaotic shifts on higher values of the parameter a [291].
|

|

|

|
|
|
|
|
|
Fig.
837 Chaos using parameter a = 2
|
Fig. 838 Chaos using
parameter a = 3
|
Fig. 839 Chaos using
parameter a = 4
|
|
|
|
|
Death
has been largely and lastingly restricted by improved food, hygiene and medical
science to older age groups, although not everywhere to the same extent. The
most important variable factor that determines world population growth is the
fertility or reproduction factor.
Worldwide, of course, immigration and emigration play no role at all. The big question is: When
will the current exponential-like growth in population level off again? The
Earth is still able to feed a multiple of the current world population, but the
distribution is so uneven that an unacceptably large proportion of this
population is starving and dying. In time, not only will distribution be a
problem, but the total amount of food will become insufficient.
At the same time, during the
last 25 years, erosion has made 10% of the agricultural land
unusable. Rising world temperatures will intensify this process by causing more
deserts to form.
Changing predictions
According to CBS
calculations (see Fig. 840), the Netherlands
can expect population numbers to flatten off after 2030.[292]. In 2002 a maximum of 18
million was expected, in 2006 a maximum of 17 million, declining after 2040.
|

|
|
|
|
Fig.
840 The CBS population prognosis for the Netherlands, 2006
|
|
|
This development is expected
in most Western countries, due to the decreasing number of births. Elsewhere in
the world, so long as children are seen as the only form of health and pension
insurance, this
flattening off of numbers is not expected. The ecological crisis can then
largely be seen to be linked with development problematics.
|
|
infanticide
|
abortion
|
restricting coitus
|
|
Food gatherers and hunters
|
|
Australian tribes (the
Aborigine)
|
+
|
+
|
-
|
|
Tasmania
|
+
|
+
|
-
|
|
the Bushmen
|
+
|
-
|
-
|
|
Indians
|
+
|
+
|
+
|
|
Eskimos
|
+
|
+
|
-
|
|
Arable farmers
|
|
Indians
|
+
|
+
|
+
|
|
Africa
|
+
|
+
|
+
|
|
Oceania
|
+
|
+
|
+
|
|
|
|
|
|
|
+ = number of confirmed cases - = no reported cases
|
|
|
|
Fig. 841 Methods of restricting the population used by ‘primitive’ peoples
|
|
|
One of the most harrowing
Western influences is that, so long as the mother breast-feeds her child and carries it with her, natural
contraception is broken off. If the mother stops feeding her
child for just one day, then she immediately becomes fertile again. A mother
can feed her child for more than three years, but the Western example of laying
a child in a cot and feeding it with a bottle has gained a higher status. The
result is that a woman can become pregnant every nine months.
Western influence has not
only brought about higher fertility in the Third World, but
also a harrowing neglect of children still in their first phase of life. Every
time a new child is born to its parents: the youngest child always receives the
most attention. Contraceptive devices are used by almost all ‘primitive’
peoples[293].
Medieval population reduction
In the Middle Ages, hard
measures were taken to reduce the population. If an area of land became
over-used, at the very least or mildest, people were forced to move to marginal
land. The history of marginal small-holders, tinkers, bandits, in short ‘the
destitute’ ("ellendigen",
"uitlandigen" exactly meaning: ‘those who
have been turned off the land’) has never been written. The army, the cloister
and the celibate can be seen as forms of contraception in the Middle Ages.
In this way, one can also
explain how social norms in a farming community can be tightened (traditional
costume!). People who were unable to live by such high norms were
‘excommunicated’. The
exaggerated norms were used as ‘a stick to beat the dog’. Up to as late as the
20th century, in Staphorst, the
black sheep was actually forced into a cart and driven out of the village.
Industrial revolution
The biggest mass migration ever was
(and is) the movement from the country-side to the towns that resulted from the
Industrial Revolution[294]. The spatial and social consequences of that
process are summarised under the term ‘urbanisation’.
A progressive division between
production, exchange and consumption (working, transport, living and
recreation) has taken place, both in space and time, so that monofunctional
spaces and
interfunctional activities (activities that are only useful within a
series of activities) have come into existence. This division of functions does not
only take place between households, but also on the level of the individual
households themselves. For everyone, there is a separate time for living,
working and enjoying leisure. The household is losing its traditional functions
such as providing training, religion, assurance and by that it is losing size
and coherence.[295].
The use of time
How people spend their time gives a good indication of their daily
lives and their use of space. Less and less time is needed to sustain life.
Apes and people who currently live at subsistence level, and many households in
the past, need(ed) to spend 40% of their time on that. Nowadays, by dividing
tasks, we only spend approximately 8% of our time earning our daily bread, if
one includes children, pensioners and others exempt from paid employment.
Misfit
The fact, that communities whose main activities are unrelated to
the environment to which they have become attuned in the course of their
history, can lead to long-term, unbalanced, over- (or under) stress in the
organism. Insufficient adaptation to this stress causes lop-sized development.
For example, one can wonder why hardly anyone has perfect teeth or cannot see
clearly, without artificial aids, by his fiftieth birthday.
Crowding and disease
Living in closer proximity to others increases the risks of spreading
infectious deseases, anonimity, loss of social control and new
forms of criminality, even though according to Freedman (1975) the psychic effects
appear not to be too adverse. A new biological tendency has come into existence
that causes isolation, strongly polarising life into public and private spaces as Bahrdt (1957) described[296].
Accommodating to abnormal climates also sets physical demands on
this isolation. The resulting ‘inner environments’ not only become a new habitat for humans, but
also for birds, rats, mice, fleas, mites, fungi, bacteria, pets and house
plants. Asthma, as the third largest cause of death after
cancer, heart and vascular disease, is a problem mainly in temperate climates.
Stress
In addition to physical illnesses, there are also psychiatric
disorders that can
be linked with the new living environment, such as more frequent instances of
schizophrenia in inner
cities, although the cause can also be said to lie in the attraction of inner
city areas for sufferers of schizophrenia. Although many tests have been carried
out on sensoric deprivation (the lack
of sensory stimuli), one should perhaps talk instead of
‘motoric deprivation’ in the modern urban environment, in other
words, the lack of accompanying motoric sensations from the muscles, and, more
generally, the awareness of one’s own body and thereby of non-fictitious
‘reality’. The time spent in the car, in front of a television screen, at a
sports competition arouses all sorts of sensoric emotions which have no logical
motoric counterpart. Stresses cannot be resolved motorically by physical
exertion. This is one of the causes of obesity, heart and vascular disease.
Where people live in close proximity to each other and where internal spaces
are fragile, the ‘motoric sequel’ becomes systematically suppressed, from
childhood onwards. This could provide an explanation for the popularity of
sport and violence. Specialisation and the division of tasks
splinter the unity of life, not only spatially (this happens here, and that
there), but also in time (first this, and then that). The number of
interfunctional activities is
growing and is laying a heavy claim on tolerance to frustration, both for individuals and groups of people.[297].
Division of space and
time
People, animals, plants and
apparatus need space and time to remain functional and to realise their aims or
possibilities. At a certain level of intensity of use, they start to restrict
each others’ space and time so that displacement and waiting times occur,
respectively. Systematic planning (spatial) and organisation (temporal) in the functioning of human beings and society
become necessary as soon as either people or apparatus start to carry out, for
example, more than 0.01 hr/m2 of activities per year at a particular
site (the present levels for agriculture in the Netherlands). If an activity
takes place somewhere (a series of undertakings to meet a certain aim), then no
other activity can take place on that same site and time. Therefore, if the
intensity of use is greater than 0.01 hr/m2, one has to separate any
two activities in space (planning) or in time (organisation). If a separation
is made on a certain scale level, it is also necessary to connect it to another
scale level when, from time to time, activities such as natural or economic
cycles need to be linked. This combination of separations in general, and
connections here and there, and now and then, is a form of selection. Each
wall with a door, town wall with a gate, every prohibition with exceptions is a
selector[298].
Separation
Separations in space and
time can come into being because of physical
regulations or by territorial and prodecural consensus (‘you here, me there;
now you, then me’). At higher scale levels, arrangements prevail; at lower
levels, physical measures prevail. Consensus can be in the form of an order
(‘forbidden access’), which, in a democracy, is founded on delegating authority
to give orders within certain areas of responsibility. Consensus can also be
promoted by conducting an information or advertising campaign (‘stop certain
activities in this nature reserve’ or ‘come to the meeting’).
As soon as activities can be
divided by barriers, walls, arrangements or more informal consensus (culture)
and then by (spatial or temporal) selective links brought into association with
each other again (logistics!), then much higher intensities of use than 0.01
hr/m2·year are possible.[299].
Intensity of use is an important factor. It is one of the
factors that determines to what extent an environment can be supplied with
facilities (density of investment), by
guaranteeing a certain level of utilisation. The intensity of use also
determines the speed of aging, and is related to the contribution made to the
national product, energy density, ecological pressure, and the risk factor in
dangerous situations, etc. [300] Nevertheless, this measure is not used very much in Environmental
Planning because it is difficult to estimate the use of time and to bring this
to the same denominator as the use of space.[301]
In 1983, the intensities of
use of various spatial functions were, approximately like Fig. 842[302].
|
|
hr/resident·year
|
m2/resident
|
hr/m2·year
|
|
ACTIVITY
|
|
|
|
|
In and around the house
|
6552
|
137
|
48
|
|
Learning away from home
|
374
|
6
|
62
|
|
Moving
|
387
|
91
|
4
|
|
Social/cultural
|
539
|
8
|
70
|
|
Recreation
|
162
|
47
|
3
|
|
Sport
|
36
|
17
|
2
|
|
Shopping
|
238
|
2
|
135
|
|
Agriculture
|
11
|
1667
|
0.01
|
|
Exploitation of minerals
|
1
|
5
|
0.3
|
|
Industry
|
185
|
30
|
6
|
|
Public utility companies
|
8
|
10
|
0.8
|
|
Building firms
|
71
|
20
|
4
|
|
Trade
|
51
|
3
|
17
|
|
Transport &
communication
|
33
|
2
|
22
|
|
Other services
|
77
|
4
|
19
|
|
Government, etc.
|
61
|
1
|
102
|
|
Use of time: both paid and
unpaid
|
|
|
|
|
|
|
Fig.
842 Use of time/use of space = intensity of use
|
|
|
Residents optimise their use of time to
achieve a balance between maximising their income and the availability of free
time and space. They have thereby long been prepared to accept travelling times of three
quarters of an hour twice a day between their homes and their work[303]. Because of this, a
tentative effect analysis can be made of the various urbanisation alternatives in this
optimalising process. By doing this, however, an impulse is given to
far-reaching analyses of the economic, cultural and managerial effects.
Choices on different time scales
The use of time can be judged on different time scales: the daily
rhythm, the weekly rhythm, the yearly rhythm and
lifetime. On the first three time scales, the above-mentioned optimalising
process leads to recognisable questions of priority in everyone’s life in the
daily, weekly or yearly rhythm (see Fig. 843).
|
Am I going home early or late today?
|
Do I give priority to (a) the family or (b) to work?
|
|
This weekend:
|
will I be (a) at home or (b) am I going out?
|
|
This year:
|
will I be (living and enjoying recreation) (a) with someone else
or (b) alone?
|
|
|
|
Fig. 843 Setting priorities in the use of time
|
|
|
·
|
|
<tradition-directed
|
|
|
|
|
opportunity-directed>
|
|
rhythm
|
A
|
|
S1
|
|
|
|
S2
|
B
|
|
daily
|
a
|
a
|
a
|
a
|
b
|
b
|
b
|
b
|
|
weekly
|
a
|
a
|
b
|
b
|
a
|
a
|
b
|
b
|
|
yearly
|
a
|
b
|
a
|
b
|
a
|
b
|
a
|
b
|
|
|
|
Fig. 844 Alternative uses of time
|
|
|
Tradition- or opportunity
directed preferences
The (a) variants of Fig. 843 give more free time and strengthen the argument
for national distribution and for Bundled Deconcentration; the (b) variants are conducive to more income
and individual free space, thereby strengthening the argument for concentration
in the Randstad and for a Compact City strategy.
Eight alternative uses of time can now be distinguished (Fig. 844).
These possibilities of using time lead to different opinions about
how space should be organised. Political schools of thought can also be
positioned in this scheme. Traditionally (<) oriented parties (such as the
CDA) will choose (a) variants in all time scales
(A); opportunity (>) oriented parties (such as the liberals) will choose (b) variants (B); and the
socialists will
differentiate the variants into ‘blood groups’ (S1 and S2) that are,
respectively, more <tradition- or opportunity> oriented.
Dispersion of time in space
These time-use alternatives also lead to another use of space
between living, working and facilities and to another mutual proximity, other
transport needs and to another economic accent.
Within the Randstad, however, there are boundaries to the
maximalisation of collective free space within the opportunity-oriented>
perspective of urbanisation.
The process of specialisation and division of tasks in urbanisation,
splinters the unity of daily
and weekly life, both spatially (this is happening here, that there)
and in time (first this, then that).
In contrast to this, large and new freedoms have come into existence.
We become about twice as old as we did at the beginning of the last century,
and, in addition, have about twice as much free time.
According to CBS (1994) since World War II,
the number of people per dwelling has
halved, from 5 to 2.5 people, so that, within a radius of 10 metres (R = 10m),
we have at least twice as much space.
Within a radius R = 100m, we have small areas of green, and within a radius of
R = 1000m, large areas of green. We are suburbanised en mass in order to
have a magnificent view close at hand.
And there the story comes to a halt, because on each higher scale
level, the emptiness disappears.
Political parties choose different ‘accords’ of dispersion
Historically, the preferences for traditional- or
opportunity-oriented uses of time can best be read against the aims of
political parties with respect to space, expressed in their programmes over a
period of 40 years as th University of Amsterdam once found out. They can be
styled in ‘accords’ of the
concentration (C) and deconcentration (D) of urban areas on national, regional
and local levels (see Fig. 845 and
Fig. 700)
|
In a radius of
|
100km
|
30km
|
10km
|
|
|
(sub)national
|
regional
|
subregional
|
|
Liberal
|
C
|
D
|
D
|
|
Socialistic
|
D
|
C
|
C
|
|
Christian-democratic
|
D
|
C
|
D
|
|
‘Purple’
|
C
|
D
|
C
|
|
|
|
|
|
|
Fig. 845 Political ‘accords’ of dispersion
|
|
|
|
|
|
Traditionally, the liberals have
wanted a national concentration of urban areas, because that would benefit the
competitive position of the Randstad. On regional and local levels, however,
they have always preferred deconcentration to allow free choice of place of
residence or establishment. In contrast, up to the 1980s, the socialists favoured
deconcentration on the national level to encourage a fair distribution of
residence and employment opportunities throughout the country, but
concentration on the regional and local level for the benefit of public
transport and the political cohesion of minority groups. To preserve the
historical identity of the provinces, the Christian Democrats have
favoured national deconcentration. On a regional level, they have favoured
concentration in order to have provincial capitals with recognisable regional
religious and civil administrations. On local levels, they again favoured
deconcentration (suburbanisation) because, in their view, only small
communities can offer a caring society in which the family, the corner-stone of
society, can flourish. In this way, freedom, equality and brotherhood become
recognisable and controllable in different design principles and on various
levels of scale.
Changing preferences in national plans
But policies change by
different coalitions as you can see in the successing National Plans in the Netherlands
(see Fig. 846)
|
In a radius of
|
300km
|
100km
|
30km
|
10km
|
3km
|
|
2nd National plan
1966
|
Bundled Deconcentration
|
|
|
theory
|
|
C
|
D
|
C
|
|
|
practice
|
|
D
|
C
|
D
|
|
3rd National plan
1983
|
Structuurschets
Verstedelijking 1978: ‘new towns’ (‘PTT naar Groningen’)
|
|
Socialist period
|
|
D
|
C
|
|
|
|
|
Structuurschets
Stedelijke Gebieden 1983: ‘growth towns’
|
|
Liberal period
|
|
C
|
D
|
C
|
|
|
4th National plan
1988
|
Compact city: nodal points
|
|
|
C
|
C
|
D
|
C
|
|
|
|
|
|
|
|
|
|
Fig. 846 Changing preferences in national plans
|
|
|
|
|
|
|
|
The result of these
changing policies is urban sprawl (see Fig. 701).
Freedom of choice supposes diversity
The largest number of possibilities for future generations will be
achieved by realising maximum diversity in environments. Determining which
scale levels require which forms of diversity (legends), is the most important task that urban
architectural research has to face. The composition of the population and the
life cycle of every individual provides changeable patterns of time-use, and, for this, specialised spaces are
needed. One ‘best’ overall solution is the
worst solution. The intermediary forms between On-going Deconcentration (D100km
... D10m) and
Complete Concentration (C100km
... C10m) probably
offer more possibilities than these extremes in themselves, but they also
eliminate future possibilities for the Randstad, such as the availability of
free space of the size of the Green Heart that can
only be achieved where there is complete concentration. However, that, in turn,
interferes with the identity of towns and
cities, would require abandoning buffer zone politics.
According to Newton (1687, beautifully described by Feynman, Leighton
et al.,1977,1963), the
attracting force F between masses M1 and M2
is inversely proportional to the square of their distance d:
 (Newton, 1687), while
(Newton, 1687), while
 (Cavendish, 1798)
(Cavendish, 1798)
The factor G was measured by
Cavendish with a precision of 1% and until now again and again with greater
precision. The formula inspired traffic engineers to formulate the travel
benefit between urban populations in a comparable way.
Traffic flows by attraction
Human behaviour is more difficult to model than lifeless matter,
but, because of their large numbers, in the long term, people’s improbable
individual choices cancel out one another statistically into a main
probability. So, traffic between urban units can be modelled reasonably well in
proportion to their population, taking into account their mutual distance.
If we represent moving
people between sites of departure and destination according to their masses,
then the Newton formula can be adapted to actual reality. For example it can be
adapted by taking a power in the denominator of Newton’s formula (see page 471) other
than the square ‘2’.
Calculation traffic according to Newton’s formula
Completely according to Newton,
the power of attraction between two urban units would be proportional
to their populations p1 and p2 and
inversely proportional to the square (b = 2) of their mutual distance d.
But if you make G=a=1, you take the mass of both poles as 100 and change the
power b into 3 or into 7, then the function starts to look like the use of
different slow (b=7, like bikes) or fast (b=3, like cars or trains) means of
transport (see Fig. 847).
|

a:=1
b:= {3,7}
p1:=p2:=100
another notation is:

because d can be
represented as a power of e = 2,718 : eln(d)
|

|
|
|
|
Fig.
847 Traffic according to a modified Newton formula
|
|
|
However, according to this
graph, direct neighbours must exert a strong, almost infinite, force of
attraction, like lifeless matter does. In the case of humans, this would mean
that every desire to travel further would disappear, because the benefit of
staying home is infinite. Consequently, for travel calculations the coefficient
a / eln(d)·b of the populations p1 and p2
has to be adapted.
Adapting the coefficient of the populations
To make that coefficient
maximally equal to scale factor ‘a’ taken as 100% (a = 1), we have to make the
denominator minimally 1 by adding 1: a / 1+eln(d)·b.
Then, if scale factor a = 1 and the distance eln(d)·b is zero, the
force of attraction is 1 or 100% (see Fig. 848).
The graph now starts
beautifully at 1 at a zero distance, but by a growing distance the attraction
by fast traffic decreases to zero already below d = 5 in Fig. 848. To
stretch the graph you can subtract a constant b from the power:
eln(d)·b-b (see Fig. 849, where b=10). In the mean time, this
application shows the advantage of using the power of e instead of a power of
d.
Attraction reduced by costs and distance < 30km
In addition, the model also
has to take into consideration that not only the distance, but also factors
such as congestion or useless delay, can reduce the effect of masses attracting
each other. All such ‘costs’,
including travelling time, partly
increasing due to distance d, are summarised in current traffic models by the term ‘travel resistance’ c
(costs, see Bovy, P.H.L.
and N.J. van der Zijpp 2000). Between two populations, this travel
resistance is operationalised in the travel benefit function f(c) as an effect of c
(including distance d). This function reduces the attraction of the masses: the higher the costs, the
smaller the travel benefit.
Travel
benefit related to costs, calculated by traffic engineers
If the parameters are chosen
well, Fig. 850 is
supposed to fit in with the current empirical reality.
In the graph, the travel
cost c can be largely identified with the distance travelled in
kilometres.
|
Bicycle

Car

Train

|

|
Determining
parameters
|
|
starting
point
0 < a < 1
at
0.8, the function starts at 80% of the height.
a1 := 0.8
a2 := 0.5
a3 := 0.1
|
stretching
3 < b < 7
at 7,
the function deflects for the first time.
b1 :=
7
b2 :=
5
b3 :=
3
|
deflection
12 < b
< 20
at 20,
the function reaches its zero value for the last time.
b1 := 12
b2 := 18
b3 := 20
|
|
|
|
Fig. 850 The type of
log-logistic travel benefit function that is used in the WOLOCAS model, with which new VINEX districts were calculated
|
|
|
Thus, one can read from this
that the travel benefit of a car is, on average, greater after about 5 km than
that of a bicycle. After about 50 km, the travel benefit of a train is greater
than that of a car.
Modal split
However, at zero distance
there is of course no traffic, and looking at empirical statistics of different
traffic modes (see Fig. 851), the
curves do not look like the log-logistic utility curves of Fig. 850.
|

|

|
|
|
|
|
Fig. 851 Modal split
|
Fig. 852 Simulation of Fig. 851
|
|
|
|
They look more like normal
distributions drawn crooked to the zero distance border. If you simulate them
like that, the walking pedestrians and bikes look like a halve of such a normal
distribution. The curve of the car can be simulated as a normal distribution,
partly diminished by subtracting the curves of walking pedestrians, bikes and
mopeds like Fig. 853 shows.
|
|
|
|
walking
|
bike
|
moped
|
car
|
bus&
|
train
|
|
|
vertical scale factor
|
100
|
1000
|
100
|
15800
|
10000
|
11500
|
|
|
average at
|
|
0
|
0
|
7
|
25
|
-30
|
100
|
km
|
|
standard deviation
|
1,5
|
6,4
|
5,5
|
76,0
|
100,0
|
100,0
|
|
|
subtract
|
walking
|
|
20%
|
0%
|
75%
|
40%
|
30%
|
|
|
|
cycling
|
|
|
10%
|
75%
|
41%
|
40%
|
|
|
|
moped
|
|
|
|
0%
|
15%
|
30%
|
|
|
|
car
|
|
|
|
|
32%
|
27%
|
|
|
|
bus, tramway, metro
|
|
|
|
|
40%
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 853 Figures, used for the simulation
of Fig. 852
|
|
|
|
|
|
|
|
|
|
In between two highway exits or (public transport)stops
·
|

Here, f1(c)
is the log-logistic travel utility, and f2 is a sine with a period of
10 km superimposed on it.
|
|
|
|
Fig.
854 Fluctuations of travel utility with a periodic infrastructure of 10 km
|
|
|
In practice, the travel
benefit formula does not always decrease with an increasing distance or ‘travel
resistance’ by costs c. The formula is true in a homogeneous field, but
not in a heterogenous field of a network with exits or (public transport)stops.
Everyone knows that taking a exit further on can sometimes result in more
travel benefit. Suppose that the mesh width and exit distance of local highways is 10 km
on average. Suppose from my departure point, it is a 5 km drive to the next
local highway. Then, after 10 km, I am on the motorway, between two exits. In
that case, the travel utility of 10 km is smaller than that of 15 km. The graph
could therefore fluctuate when a radial motorway has an exit every 10 km (see Fig. 854).
Useful destinations
increased by distance
For a train, these
fluctuations are caused by the station stops: I
cannot end my train journey between stations in the event of my seeing no
utility any more in continuing the journey. With regional tracks occurring
regularly, every 30 km, even more fluctuations with a 30 km period are
superimposed on them.
|

f3(c) is a sine with a period of 30km and increasing
amplitude
|
|
|
|
Fig. 855 Fluctuations of the
travel utility with a periodic infrastructure of 3 and 10 km and with
increasing travel utility
|
|
|
Passing rarified zones without direct utility
It is clear that, in this
case, travelling 50 km has more utility than 40 km. In addition, the higher
design speed on these speed-specialised lines, less
plagued by stops and exits, lowers travel resistance, so that the kilometres
used to calculate c shrink in travel time. I will leave these sorts of
mathematical complication to more experienced calculators.
The conclusion could be that
well-thought-out construction or improvement of fast infrastructure results in
rarified zones designated as green areas, which
are positioned radially around human masses in the direction of other masses,
and have a greater travel utility for intersections situated further away than
for the pure log-logistic decreasing travel utility functions without
fluctuations. This is a beginning of the traffic concept for an interregional
network city.
Broadening the travel horizon increases the number of attractive
destinations
Without a division of tasks,
broadening the travel horizon in a homogenous urban field increases the
accessible area, and thus the destination possibilities by the square of its
radius. The proportion of these possibilities that is actually utilised within
an available budget in the form of money, means of transport and time, is the
scale factor a. That factor becomes smaller the
further (and faster) I travel to obain these possibilities. One can take this
increasing travel utility into consideration as an effect on the costs of
primarily decreasing travel utility function f(c), with an
increasing amplitude of stops or exits situated further and further away. In Fig. 855, it is
thus assumed that, at the first and second exit or stop on these lines, the
utility, and thus the amplitude, will increase due to increased destination
possibilities. This effect is strengthened by interregional task division".
Attraction between regions charged with task division benefit
In the current model
philosophy, a positive travel utility is expressed more purely as a factor of
the power of attraction of the masses, than just by the mass-effect-reducing
travel utility function f(c). For each urban concentration, a
traffic model can apply separate empirically determined corrections to the mass
effect. However, in the case of interregional task division that is not logical. The power of attraction
between regions, due to
increasing interregional task division, appears to be more like electromagnetic
attraction caused by a difference in positive and negative charges, which
supplement one another. However, where there are more than two tasks, there are
more sorts of charges than + and -, and the range is greater. It is essential
that the attraction is not a characteristic of a mass, itself, but
of its specialisation compared with other masses that are charged differently.
Alternatively, equal charges cause repulsion. For this, a separate, not
necessarily reducing, but accrediting, specialisation function will perhaps
have to be devised.
Making lost time useful
Then, in working out the
travel resistance c itself, the travel time as a cost
post will be taken as being almost synonymous with distance and other
inconveniences. However, travel time can be used as contact, work or rest time en
route. In particular, it will be possible to facilitate work time in the
future by means of communication technology. The remaining travel time does not
always increase with distance, but is mostly due to slowness and delays when
changing from one form of transport to another, and this can be included in c.
This is why the design of multimodal intersections and means of transport, and their
multifunctional, urban integrated and communicative equipment, is the primary
project for a Delta metropole. At the
same time, the most important item on the agendas of managers, designers and
key actors is the mutual determination of the identity of regions,
agglomerates and towns with respect to growth in task division. The new public
transport between them must not eliminate chance, but organise it. One cannot
confine oneself, then, to adapting c in existing models on the basis of
empirical starting points, when some costs can be changed into benefits by
shrewd design.
Attractions >30km
About 90% of all traffic
movements are kept within a radius of 30 km (region) around the departure
address. It is natural that traffic modelling focuses on that section. Commuter
traffic generates the problems that traffic specialists are hired to solve, so
they gear their models to these.
As far as I am aware, there
is still no model for the individual and collective benefits interregional
traffic (> 30km radius), caused by regional specialisation. The
attraction of mutually specialised masses should be greater than that of
mutually unspecialised masses. Why
would people travel at all, if there is no difference between departure and
destination? And if a difference far away promises great profits, how important
is distance then? If functions are specialised on a larger scale traffic
benefit can increase with distance.
Exchange, traffic implies specialisation
Trade rests on that
principle, and so does the ecological division of tasks between land and water,
and between male and female flowers that exchange their life experiences with
the help of insects, the travellors. On every scale level, life itself shows
the evolutionary effects of specialisation: combination by exchange. The
attraction of Disneyland has another travel benefit function than
commuter traffic, certainly when Parisians are becoming bored with it.
External specialisation by internal integration
In the Dutch Golden Age, Zaandam produced ships, Amsterdam used them. Amsterdammers with initiative
felt more at home in Indonesia than in Zaandam near by. Regular destinations
far away create an unknown zone close by, also recognised for commuters by Groenman (1960) as
‘ijle zone’. But that zone has its functional integration by other specialised
populations. During the period concerned, Amsterdam, already a metropole with
100,000 inhabitants, became a world city with a national web of punctual towing
boats (Vries, Jan de
1981). About 1600 AD the organising of the VOC by Van Oldenbarneveldt (Romein,
J.M. 1938,1971) gave
each of the United States of The Netherlands its own commercial part of the world changing
mutual competing and conflict into cooperation. It was external specialisation
by internal integration. Disneyland in Paris is a similar improbable example of
organisation and offshore entrepreneurial spirit. Organisation is a matter of
specialisation and combination.
External effort outgrowing internal integration
However, our colonial past
gives reason for us to be ashamed of expansion, certainly if it costs too much
energy. Ever since Stadtholder Willem III,
setting sail from Hellevoetsluis, exported our commercial democracy to England by conquering it, in a final
effort, with an armada three times larger than that of the Spanish, (Israel,
Jonathan I. 1995), we
would rather stay closer to home. Ever since Thomas Jefferson visited our
country in order to study our republican constitution (Eskens, E. 2000), the
roles have been definitively exchanged with Anglo Saxon players. From
Scherpenzeel (birth place of Peter Stuyvesant), no
one will establish a New Amsterdam again, if there is still enough space in
neigbour village Munnekeburen. Now investments from New York are welcome.
Whether foreign investments will come or not, again depends on the percentage
of key actors who, sometimes by chance, discover that it
would be better to grow (for example) coffee outside one’s own region, than at
home. If people are alert, this will not lead to exploitation this time, but to
cooperation.
Travel benefit fluctuating by distance
Between the region and the
world, however, there are still a number of scale levels on which the travel
benefit can be increased for some destinations by including rarified zones, for
example green areas close to home. If we show a
collective will for fast lines of interregional public transport, communication
and decisionmaking, then the travel benefit function in the travel models can
be adjusted. However, the question is: On what level do we want to spread our
towns and green spaces? Bundled deconcentration within the region (NRO2, RPD
1966, see Fig. 700 and
explaining text) has
been disposed of since 1983 (NRO3, RPD
1983, see Fig. 846): it
broke up the green spaces in urban landscapes. Its variant, a regional network
town, breaks green spaces into even smaller pieces.
Declining specialization by local congestion
The compact city (RPD 1988, see Fig. 846)
increases travel resistance locally due to congestion, whereby the strength of
cooperation between the big cities decreases in full accordance with prevailing
traffic models. That is a self-fulfilling prophesy. Wings that do not divide
their tasks, but without sufficient coordination go their own way, are probably
unable to make an international flight. Moreover, in the unintentionally
expanding compact city, green areas are only accessible by car. In addition, on
public holidays, part of the free weekend is claimed by traffic jams. That can
only be compensated by holidays in further-away places that make a joke of the
travel utility function. The result is a vicious circle of local travel
resistance and less cooperation based on reliable specialisation.
External competition by internal cooperation
The Delta metropole is not a regional, but an interregional
network city. It is
a world city not because of its masses, but because of spatial specialisation.
Urban masses become more attractive, if better and faster decisions can be made
than elsewhere in the world. That saves the energy of interregional competition for attracting international acclaim.
International power is achieved through interregional cooperation, based on a
division of tasks. In doing that, one aspires to create an international site
and expansion base for business establishments with extensive green and blue
spaces within cycling distance from home.
The classical trias
urbanica of management, culture and market is
recognisable in the centre of every medieval town, where
townhall and church made space for the market. This
is where the surrounding consumption and production converge, managed in the
town hall, reflected in church. This territorial division of spaces by task
has, since then, been subject to scale enlargement. Until after World War II, Bonn, Cologne and the Ruhr area, The
Hague, Amsterdam and Rotterdam had divided these tasks interregionally to
give managerial, cultural and economic accents, respectively. Due to the
movement towards a service economy after the war, cultural identity came to have more of an economic meaning.
The right diversity on the right scale
A culturally equipped town
or city furthers the chance of a productive meeting. Thereby, Amsterdam, gained
better chances of being chosen as a place of settlement by the key actors responsible. Rotterdam and the Hague regained
a cultural identity by means of international film and jazz festivals,
unmatched architecture, and decision-making culture. Making faster and better
decisions requires the lubricant of cultural eye-opening. In the much smaller,
but more central, inland Utrecht, the
‘captains of service’ confer
at the crossroads of polders, rivers and forests, with dunes and harbours on
the horizon. Here too, the converging peat, clay and sand diversify ecosystems
while from here they determine more uniformly the ecology as far as the Urals
(Constandse, 1967). Also
in the opinion of the youngest generation, growth should not be concentrated
there.
Direct, distribute, disperse and concentrate on the right level
There, key actors from the
heart of Europe are shown a route via the Rhine axis in their Delta over the Mondriaan-like network
called Holland (see Fig. 856).
|

|

|

|
|
|
|
Fig.
856 Potential continental, fluvial and national network systems
|
|
|
In addition, in the Delta,
rail and road transport via the south and east can be brought together on an
even greater scale along the European coasts to choose our water and air space as main
ports (and the reverse). This will be achieved, if
the foreign actors are received in a well-considered, cooperative network of
towns, each suited for its own task, attractiveness as a place to settle and
with it own identity. There
are large projects with small consequences and small projects
with large consequences. The Delta metropole is not directed towards projects
in which the one section expects to dominate the other, but, in the end, steals
an advantage.
Limitation shows the master
Does one section choose
projects that deprive the other of success, or can people delegate among
eachother so that, together, international functions can be given the best position in the whole
network? The latter requires subnational decision-making skills, regional
loyalty and again local decisiveness. If one chooses non-traditional regional
solutions, using traditional national means, the Delta’s inherited urban
constellation can be turned into an international novelty. One can grow
interregionally by trimming regionally, integrating by mutual specialisation, by
accepting one-sidedness in order to excel, and by developing the rest
elsewhere.
Specialisation as a paradox of scale
Managerial initiative,
innovation, growth, integration and versatility are a question of scale. In
contrast, on another scale, they require loyalty, tradition, trimming,
specialisation and one-sidedness.
The implicit presuppositions
of the Stedenland perspective (VROM 1998) that
preceded NRO5,
illustrate this kind of scale paradox. They are made explicit in Fig.
858. That perspective supposes national initiative and
subnational laissez-faire, national tradition and regional innovation, national
division of tasks, subnational integration, national concentration, local
dispersion.
|

|
|

|

Fig. 857 The Stedenland perspective
|
|
CONTEXT
and impacts within a PERSPECTIVE
|
|
Variable
per level of scale and period of change.
For example tentative nationally:
managerial: initiative (!) < > (?) laissez-faire 7
years
cultural: traditional (<) < > (>) experimental 15
years
economics: growth (+) < > (-) shrinkage 30 years
technical: specialisation (/) < > (x)
integration 60 years
ecological: heterogeneous (v) < > (o)
homogeneous 120 years
mass-space-time:
concentration (C) < > (D)
deconcentration 240 years
|
|
|
|
Fig. 858 Context organ (example: the Stedenland perspective (VROM 1998) and effects (grey))
|
|
|
According to the
combinatorial system, it is possible to play 1065 other chords/accords
on this organ. The Delta metropole accord is much the same. The difference is
that subnational deconcentration and a great effort to achieve technical
integration that facilitates the division of national tasks has been requested
(VROM 2001, 2002).
Specialisation supposes exchange
The division of tasks
consists not only of where projects are established, but also the network. A
didactive rule of thumb that, for each higher unit of road system, an
approximately three times larger mesh width should be maintained, turned out to
be more realistic than was first thought. It has been calculated in three
different ways that, by doing this, an optimum of accessibility and
construction costs is achieved (Nes, R. van
and N.J. van der Zijpp 2000). However, this would mean that, in the
Netherlands, there would have to be nine orders, each with its own design speed and exit frequency (Jong, T.M.
de and M. Paasman 1998): continental, fluvial, national, regional, local
motorways, urban motorways, district, neighbourhood and residential streets
drawn with a mesh width of 1000, 300, 100, 30, 10, 3, 1, 0.3, 0.1 kms,
respectively, if one draws the same mesh length and breadth. The first three
are drawn in Fig. 856, and if one styles the
remainder, then one gets a typology of dry connections with square meshes, as
shown in Fig. 492. These can be stretched
using the same mesh density as shown in Fig. 495.
Calculating missing links or simply drawing them?
In the absence of exact
knowledge about departure sites and destinations, designers can sketch in the
missing links with transparent, squared elastic paper. The design will
alternatively consider first the network as the directing force and then the
settlement site (Angremond, Kees
d’, Pieter Huisman et al. 1998; Jong, T.M.
de 1998). However, very many exits would have to disappear to improve travel
times and safety (Reuzer, Bart
and Marijn Schenk 1999). Though, especially within towns, the
national strategy is to reduce the number of orders at the expense of travel
time, but in favour of an assumed safety (Duurzaam Veilig; Sustainable Safety
Project). Therefore, the current travel benefit function remains calculable and negative. Is that what
we want?
Networks between specialised cities
|

|
|
|
|
Fig. 859 Population, socio-economic weight and connections in a radius of
1000 km
|
|
|
Fig. 859 gives a global impression of the population of
central Europe in 1996, with the highest densities shown along the Rhine. This figure also shows those centres that
score highly in a large number of socio-economic factors. The highest scores
are for London, Paris and Milan. Centres of secondary importance are Brussels,
Frankfurt and Munich. Amsterdam and Rotterdam are aligned with a large number
of centres of tertiary importance. The beginnings of a 21st century network,
with a mesh width of approximately 100 km are also visible in this figure. Southern
Europe and the large population of eastern Europe are attempting to join this
economic network. Railways parallel to the northern and western coasts form a
forerunner and starting point for, what is still, a hypothetical 300 km grid
(see Fig. 856. The Netherlands is situated
in the corner of this grid, as a terminal with main ports for transfer to air
and water.
The physical identity in Europe
At the end of the 20th century agriculture, due to a reduction of
its market coupled with higher productivity, lost its primary position in
national self-sufficiency. Globalisation leads to a division of tasks internationally
as Steekelenburg (2001) elaborates. The main task
for the Netherlands is trade
and the conservation of rare natural areas.
The lowlands of
Zeeland, Holland and Friesland as a whole, with a boundary consisting of young
dunes and older
ones, up to 5000 years old, together with their potential vegetations, are
viewed as rare on a European scale, within a radius of at least 1000 km. Dyke construction has enlarged the area and
diversity of the land in the course of a 1000 years, with Old Marine Clay
polders and
reclaimed land, albeit to the detriment of rare saline plant communities. By doing this, the largest area of potential
estuarine vegetation in north-western Europe has come into being.
Further inland there is a just-as-rare and irreplaceable zone of
potential reed swamp / swamp forest. ‘From Amersfoort to the Urals, one does
not encounter another landscape that is so full of big surprises’ (Constandse,
A.K. 1967). Further up-stream lies the largest, though
less rare, area within this radius, of river-dependent vegetation.
Rare in The Netherlands,
common in Europe
The sandy soils, situated on higher ground, form the beginnings of a potential European oak-beech
forest. Although not a rare form of vegetation, these
forests are highly valued nationally as recreation areas. Ecologically, pine
forests in our
country are viewed as recent, artificial anomalies.
|

|
|
|
|
Fig. 861
Nine types of landscape
|
|
|
Rare in Europe, common in
The Netherlands
If one looks in more detail at these important international
possibilities (in a section of 60 x 60 km), then the landscapes of very great
significance that one recognises are the Old Marine Clay polders, the reclaimed land and the peat exploitations in our
country in the neighbourhood of Leiden. In addition, the mud flats (Wadden),
the dunes, the Young Marine Clay polders, fluvial basins
and ridges are also of great international importance. The landscape types
identified by LNV show the Old Rhine to be an
extension of the fluvial area, surrounded by areas of peat lying
below the present water table (laagveen), bordering on areas of Marine Clay.On both
sides of the Old Rhine there is an interesting series of potential transitions.
|

|

|
|
|
|
|
Fig. 862 Internationally important landscapes
|
|
|
The Netherlands undisturbed
If, apart from providing a stable system of water management, the Netherlands
would be left undisturbed by human beings from now onwards, then the following
forests would come into existence:
|

|
|
Legends
1 salt-marsh vegetation with,
among other plants, sea lavender and salt-marsh grass: transitions from a
salt to fresh-water environment.
2 dune heath,
-grassland and
-thicket, dune birch forest and
dune oak forest, birch– common oak forest
3, 4 marsh fern–alder swamp, and
similar
5, 6, 7 ash–elm forest, and similar
8 blanket bog, and similar
9 moist alder, birch, common oak forest
10 dry birch–common oak forest
11 moist durmast oak forest, and similar
12 dry durmast oak, and similar
13 oak–hornbeam, and similar
14 millet grass–beech, and similar
15 woodrush–beech forest with
oak
16 beech forest, alder- and ash natural forest, and similar
|
|
|
|
Fig. 863
Potential natural vegetation
|
|
|
Only where water floods the land regularly or for a lengthy time,
where wind moves sand, and where grazing animals keep
meadows in forests open would vegetations other
than forest be able to maintain themselves.
Human impact
Against the background of this ‘nil variant’, in the following
paragraphs the effect of human intervention is demonstrated in images that have
been developed by the University of Utrecht (see Fig. 72)[304].
The influence of humans expresses itself
in draining,
raising,
hardening,
digging up,
treading upon, burning,
systematic grazing, mowing,
ploughing,
harvesting,
fertilising and polluting.
Because of these activities, earlier stages of plant successions are kept in
existence artificially.[305]
|

|
|
|
|
Fig. 864 Human
interventions in relation to dynamics
|
|
|
Decreasing ‘culturalness’ around settlements
For centuries, this
‘anthropogenically added dynamic’ decreased with the distance from residential
buildings
|

|
|
|
|
Fig. 865
Intensity-of-use gradients around farm and town
|
|
|
The intensity-of-use
gradient around farms and towns was strengthened by a
mineral gradient. For
centuries, traditional agricultural systems have enriched local soils with minerals to the
detriment of poorer soils further away, that thereby leave behind specialised,
and thus rarer, types of vegetation, such as hay fields, heathlands, shrublands
and forests. Where people stored minerals for use in agriculture, only a few
rapidly maturing species grew there. However, where people removed them, an
increasing diversity of slow-growing, but uncommon, specialist species,
cooperating of necessity in ecosystems, grew undisturbed and in scarcity. Over
the centuries, this has led to an increase in the number of plant species. [306]
Living between dry and wet
Farms and settlements on the
high, infertile sandy soils were mostly situated along rivers and streams. On
slopes between the lowest wet soils (known as ‘green soils’ in animal husbandry) and
higher, drier soils (‘common lands’ used as arable land) the
nitrogen cycle used in mixed husbandry gave the best chances of survival. Fights took
place to secure these scarce sites, so that, once established there, the
tendency was to concentrate, organise and defend the common land. The result
was a village (esdorp, in
Dutch) built around a village green or brink. This
concentric village shape contrasts sharply with the ‘linear village’ (lijndorp, in
Dutch) from which, along both sides, and at 90ş angles to the village street,
strips of fertile but wetter peat soils were colonised and drained. In the dijkdorp, farmsteads, also positioned at 90ş angles to the street were built
on the higher, drier ground at the side of the street, which followed the
highest line of the dyke.
|

|
|
|
|
Fig. 866
Traditional and present-day ecological processes with respect to landscapes
|
|
|
Homogeneity by artificial manure
Modern agricultural methods,
especially the discovery of artificial manures round about 1900 have changed these
developments drastically from rare, infertile and thus species-rich biotopes
into biotopes that are equally fertile overall and thus to biotopes that are
predictable, but with few species. [307]
Settlements on sandy grounds
In Fig. 867 Steegh (1985) designed a concept for the development
of settlements on sandy ground
|

|

|

|

|
|
1000 na Chr.
|
1200
|
1700
|
1900
|
|
|
|
|
|
|
Fig.
867 An ideal-typical development of a settlement on sandy ground
|
|
|
|
|
|
Terp villages on Marine Clay areas
However, the oldest
settlements that are still recognisable date from Roman times. Since those
times, churches, farms, and sometimes settlements, in coastal areas, especially
in Groningen and Friesland, have been built on raised mounds of earth (a terp).(Fig. 868).
|

|

|

|

|
|
|
1200
|
1350
|
1830
|
|

|

|

|

|
|
500 v. Chr
|
500 n. Chr
|
1200
|
1900
|
|
|
|
|
|
|
Fig.
868 The ideal-typical development of terp villages on Marine Clay areas
|
|
|
|
|
|
|

|
|
|
|
Fig. 869
Historical conditions for situating settlements along the water’s edge
|
|
|
Roman settlements on the loess soils of South Limburg
The best preserved land
surveying outlines from the Roman times are of the loess region of South Limburg: an underlying NW-SE and
NE-SW grid of 707 x 707 metres or fractions of this. By creating lots of land
by cutting it into blocks (‘quadrangulation’) in
this rational way, Roman army veterans were rewarded with a villa as a
retirement present. Steegh (1985) shows how these developed further in his ideal
types ‘Willerich’,
‘Willerrode’ and ‘Wilderbaan’ (Fig. 870).
|

|

|

|

|
|
150 na Chr.
|
1000
|
1500
|
1900
|
|
|
|
|
|
|
Fig.
870 The ideal typical development of settlements on the loess soils of South Limburg
|
|
|
|
|
|
Development of these
settlements in feudal times around 1000 AD
Following the decay of the
Roman Empire, the feudal court system began to use material from the most
strategically situated villas (not too high, not too low, along a road
crossing a nearby stream or river) to build a curtis or sala with
an encircling wall in the form of a shield from which the farms (tenures or casae) around
were managed. The agrarian surplus was sent to the Lord of the Manor via the old Roman road. Since the time of
Charlemagne, one
tenth of the produce had to be given to the church, so the local manager built
a church to collect these tythes himself and so that he only needed to maintain
a priest. A smithy, brewery and safety-seeking small-holders formed a compact
village centre and the curtis became the castle.
Development of street
villages around 1500 AD
Wetter areas allowed a
larger number of village wells to be dug, so these villages had a more dispersed shape. A tenant farmer, whose land
bordered on water, who later gained independence, would divide his land among
his children into a larger number of units. In this way, a street village was
formed, comprising easily defendable ‘closed courtyards’. This
is still a well-known type of farm building, even today, in the landscape of South
Limburg. Millers’ dwellings were added to the water mills and the lord of the
castle built a new castle with gardens bordering the water, thereby displacing
a number of farms that had occupied that land.
Later developments
Sometimes, the Lord of the
Manor systematically developed waste ground into a street village such as ‘Willerrode’. The
church remained on the site of the old castle in the centre of the village,
where now the lord levied tolls, and an inn to accommodate the post stagecoach
was built. After centuries of stagnation, the construction of a tramline to the
coal mines in the vicinity brought about far-reaching
changes. The inn became a centre for the mineworkers. The higher personnel
built houses along the tramline and a mineworkers’ colony, ‘Wilderbaan’, grew
up with its own shops, a new church and a patrons’cloister, financed by the
mine owners, with boys and girls schools. Supply industries established
themselves there with workers’ districts and bungalows built on sites which had
the nicest views. On pages 161-162, Steegh (1985) names many villages where elements of ideal
typical ‘Willerich’ are recognisable.
The Netherlands about 1000
AD
Round about 1000 AD, the human population lived on terps (in Friesland), along the rivers, behind the dunes, and, in a
more dispersed form, on the sandy soils.
|

|

|

|
|
1000
|
1500
|
1900
|
|
|
|
|
|
Fig. 871 The ideal
typical development of settlements on sandy soils behind the dunes
|
|
|
|
|
After
1000 AD
From 1000 AD onwards it is people who have determined the appearance
of the Netherlands. No longer they adapted their life to the country, they
started to accommodate the country to their life (see Fig. 72, Fig. 872 and Fig. 873 are enlargements).
|

|

|
|
|
|
|
Fig. 872 Natural regions before 1000 AD
|
Fig. 873 Settlements in the Netherlands about 1000 AD
|
|
|
|
Rising sea level
After about 1000 AD, the sea advanced in the south of the country.
The Delta waterways came into existence, but the free play of water and land
was prevented by dams built by the rapidly growing population.
|
.
|

|

|
|
(see also Fig. 72)
|
|
Fig. 874 (Fig. 873) 1000 AD.
|
Fig. 875 1100 AD
|
Fig. 876 1300
|
|
|
|
|
Land, no longer on loan from
the Emperor: the end of feudalism
The ecological history of the low-lying lands is closely linked to
reproduction, family links, illnesses and occupations, in short, to the ecology
of the human species.
Count Dirk II married a
descendant of Charlemagne and, in 987, was granted full ownership of his
fiefdom in North Holland by Emperor Otto III. Dirk III extended
the fiefdom to include wet lands in the south. The only people who lived there
at that time, were those living along the Old Rhine and at
its mouth, at Leiden (Lede,
water course Vries (1962)). In 1063, Dirk V was the
first to adopt the title Count of Holland, but it was not until approximately 1100 that
the name Holland came to
be used for the whole county. What happened during that century?
Making your own land
There is evidence of an enormous expansion in agriculture and
settlement in the centuries immediately subsequent to 1000 AD. In particular,
people learnt how to reclaim and cultivate peat bog (fen).
|

|

|

|

|
|
1000
|
1100
|
1200
|
1300
|
|

|

|

|

|
|
1500
|
1500
|
1700
|
1920
|
|
|
|
|
|
|
Fig. 877
The ideal typical development of old and new peat settlements
|
|
|
|
|
|
Colonisation
In the course of a century, the Netherlands was far-reachingly
colonised. There were a number of small towns at this time. Around 1300, these
towns began to grow. There was also growth on the sandy grounds, and forests
started to disappear. The sea retreated in some places and advanced in others.
By about 1300, there was hardly any ‘nature’ left any
more.
|

|

|

|

|
|
1000
|
1500
|
|
1900
|
|
|
|
|
|
|
Fig. 878
The ideal typical development of new settlements on the clay soils
|
|
|
|
|
|
The reconstruction made by the University of Utrecht for NNAO (see Fig. 72) shows an unmatched colonisation of these
low-lying lands. The first dateable information about the participation of
Dutch farmers in the colonisation of peat areas in eastern Germany (Hollerbroek) appeared in 1113. These farmers were
especially welcome because of their skills in draining low-lying areas.
Democratic water boards
Dirk VII’s brother,
Count Willem I, had a grandson, Floris V, ‘The blokes’ God’, who was married with
Beatrix. By founding democratic water boards, he
prioritised agrarian development that was based on the growth of population
resulting from draining the land. He met with resistance from feudal
aristocracy, such as Gijsbrecht van Amstel, who were becoming empoverished, which, in
1296, cost him his life.
Growing wealth replacing
taxes by toll
Towns, and particularly Dordrecht, were centres for the toll system of Holland
and needed to extend the trading basis on which they were founded. Most of them
were granted their town charter in the 13th century. This was the century
during which the influence of Holland grew to such an extent that Count Willem
II became
the Holy Roman King of Germany with his polder model. The Pope was making
preparations to crown him as emperor when he was beaten to death on the
slippery Friesian ice. However, his grand nephew, Willem III, was able to marry the daughter of the French
king and arrange marriages for his own daughters to the English king, Edward
III and the
Bavarian emperor, Ludwig.
Feudal interference
However, that last-mentioned strategy led to renewed feudal
interference. The emperor went fishing for the fattened cod that Otto III had
allowed to slip off his hook (the Hook and Cod Disputes (de
Hoekse en Kabeljauwse Twisten)). Struggling to free themselves from the
aristocratic–feudal ‘Hooks’ were the ‘Cod’-supporting farmers and citizens,
such as those of Delft.
Ecological influences on
trade economy
The County of Holland remained relatively free from the pest
epidemics that had
brought about a demographic reversal in Flanders and the
towns of the Hanseatic League. Bruges partly
lost its cloth trade to Holland (Leiden). The movement of herring shoals
from the Baltic Sea to the North
Sea, and herring gutting skills that had been discovered in the mean time, gave
fishermen there an ecological advantage. They sailed to wool-rich England and
gradually took over the freight trade. After 1500, partly due to the St.
Elizabeth flood in 1421, Dordrecht was
forced to relinquish its position as main port to Delft, Rotterdam and Amsterdam.
After the Treaty of Utrecht in 1475,
the towns of Holland took over the Baltic trade from the
Hanse as Jansen (1995) describes. Counts became Stadtholders. For one more century Holland accepted a
foreign head-of-state before starting to fight for definitive freedom.
Crucial waterways
The making of dykes, widespread partition of land and draining in Holland
encouraged population growth. This caused the peat areas to settle and allowed
little by way of occupation other than animal husbandry, fishing and shipping.
For this reason, the Hollanders were dependent on grain from the regions around
the Baltic Sea. Fortunately, the Hanse preferred to transport their Baltic
goods via the, in the mean time deepened, waterways of Holland, to their
entrepot in Bruges, than over the dangerous North Sea. In exchange for the much
reduced damage to their ships by using this route, the Hanseatic League paid
tolls to the Counts of Holland.
Tax relief, Republic and
Public Works
This income for the Counts brought tax relief to the farmers. As
they had made their own land, they no longer saw themselves as being bound by
the requirements of the feudal system (Jansen (1965)).
Uneven economic growth reduced any natural areas that still existed
to a few areas of blanket bog. The low-lying peat bogs were used as fuel, and
winds exposed the underlying Marine Clay. The Mast Forest in Breda was
planted to provide shipping with masts. However, the impulse of Golden Age
slowed down when people began to live off their private means instead of
investing. This resulted in the wet land of Woud (1987) being left behind and caused the French to
establish a department of Public Works in 1798.
The first Republic since Rome:
The United States of The Netherlands
Then, in 1585, Antwerp capitulated to the Spaniards, led by the Duke
of Parma. Antwerp, with its multicultural way of life
and its urban hinterland, had become the trading centre of the 16th century
world. It was the northern entrepot for products from countries around the Indian
Ocean as Bouman
(1979) describes. This is where modern banking and economic individualism
bundled into companies began. During the following four years, almost half
(approx. 38,000 people) of its largely Protestant inhabitants fled to the north
as Israel (1995) describes, thereby laying the laissez
faire foundations of the partly immigrant-inhabited metropole of Holland
and its trade emperium.The French did not help the young Republic gain acceptance
and sovereignity, as the Orange’s continued to hope, but they did help by
diverting the attention of Philip II, and thus the Duke of Parma, southwards.
That gave Maurits opportunities and Van Oldenbarneveld succeeded
in bringing competing parties together to form the VOC. That Maurits continued to believe in
predestination, and thus in aristocracy, cost Van Oldenbarneveld his life.
The early urbanisation of
Holland
Around 1550: more than half of the population
of Holland lived in towns that had grown up for the purpose of conducting
trade.
|

|

|

|
|
|
|
|
|
Fig. 879 1550
|
Fig. 880 1675
|
Fig. 881 1800
|
|
|
|
|
|
|
|
The Golden Age and the economic decline that
followed.
Around 1675: the towns in the west had
grown fast. A network of tow-barge canals had come
into existence.15 Development on the sandy soils had come to a halt.
Around 1800: following the impoldering
of North Holland, large areas of blanket bog were reclaimed. More dykes were
built. From a hydraulic point of view, the land was in a deplorable state.16
Recovering land and nature
This is how the relatively recent nature of the Netherlands, has
come into existence. It is so different from anywhere else in Europe that a
separate legend unit is needed to register it on the European nature map of
Bohn (see Fig. 860). The task of impoldering the land was completed
with the use of the steam engine. To work on the remaining ‘waste grounds’, the
Heide- and Grondmij were
established at the end of the 19th century. These relatively new natural areas
were later reduced again to provide employment during the 1930s, when
unemployment levels were so high.
Artificial fertilisers
Artificial fertilisers were discovered
round about 1900. Since then, fertilising areas of soils with low-mineral
content has favoured rapidly maturing crops, to the detriment of slowly
maturing specialist species. Animal husbandry, drainage and atmospheric
deposition have all contributed to this process. Just as it is easier to
dissolve sugar in coffee than to take it out again, so will much time be needed
before these levels of fertilisation are cut down. For this reason, it is not
just rarity expressed in kilometres that counts, but also (ir)replaceability in
years. One can use the product of these two values to gauge the value of
natural areas against
the rarity and replaceability of human
artifacts.
Around
1850: the growth of industry in Twente and in North Brabant. Impoldering of lakes caused by peat
exploitation in the western fenlands. The digging out the peat of the blanket
bogs of the higher eastern areas.
Around
1900: western areas were still the most urbanised.
The population of Amsterdam exceeded 500,000. The railway network was completed.
Around
1930: industrialisation on the sandy soils reached
a peak. Conurbations began to form everywhere.
Around
1960: land reclamation and the Delta works, in
addition to large urban and industrial expansion.
|

|

|

|

|
|
|
|
|
|
|
Fig. 882 1850
|
Fig. 883 1900
|
Fig. 884 1930
|
Fig. 885 1960
|
|
|
|
|
|
In the second half of the
19th century, two cultivation associations, the Heidemij and the Grontmij were established to bring new nature areas
under cultivation again, that had originated since the Golden Age.
Land consolidation and nature management
These associations played an
important role in land consolidation (ruilverkaveling).
|

|
|
|
|
|
Fig. 886 Before land
consolidation
|
Fig. 887 After land
consolidation
|
|
|
|
An interest in nature
conservation and management arose at the beginning of the
1900s. Since 1970, there has been an increasing interest in managing nature and
in introducing policies to conserve nature by consolidating land. At present,
land consolidation is also an instrument to nature conservancy policy-makers
(in riverine and peat bog areas).
Road and air transport play
a large new role, but a threatened environment requires a place of its own,
too.
|

|
 
 
|
|
|
|
|
Fig. 888 The Netherlands
in 1989
|
Fig. 889 Ideas for 2050
|
Map images of higher grounds in The Netherlands
|

|

|

|

|
|
South Limburg
1. edge of valley
2. stream
3. wooded side of valley
4. settlement
5. arable land
6. grassland with wooded banks
|
North-Limburg
1. arable land on a fluvial terrace
2. old fluvial dunes
3. hedged landscape
4. old fluvial beds
5. river
6. settlement
|
North -Brabant
1.
dune ridge (duinrug)
2. small peat
bog/fen mere
3. stream
4. woodland along a
stream
5. settlement on
old arable land
6. fluvial- or
water meadows
7. cultivated land
outside the valley of a stream
8. planted forest
|
1. road
2. grassland
3. arable land
4. remains of a
woodland
|
|

|

|

|
|
|
1. parabolic-shaped sand dune
2. small arable field on flatter terrain
3. grassland between hill ridges
4. woods on a country estate
|
Achterhoek
1. hill with old arable land
2. little field on plain surface
3. grassland of lower grounds
4. little wood
|
heathland reclamation
1. heath
2. field
3. grassland
4. wood
|
|
|

|
|

|

|
|
1. contour of lateral moraines (stuwwal)
2. old farmland on flank of lateral moraine
3. grassland surrounded by wood
on moisty grounds
4. settlement
5. wet woods (broekbos)
|
6. grassland of younger relamations
7. farmland of younger relamations
8. planted coniferous wood
|
Lateral moraines of West Twente
1. contour of lateral moraine (stuwwal)
2. meltwater ridge
3. settlement
4. old farmland on Eastern flank of lateral moraine
5. grassland on moisty plans
6. heath
7. planted coniferous wood
|
Ash trees along the valley of a stream
1. field (es)
2. stream valley (beekdal)
3. tableland
|
|
|
|
Fig. 890 Landscape elements on maps of higher grounds in The Netherlands
|
|
|
|
|
|
Map images of lower grounds in The Netherlands
|

|

|

|
|
|
terp landscape
1. terp with buildings
2. field
3. grassland
|
Parcelled landscape of West Friesland elongated lots
1. regional village (streekdorp)
2. orchard
3. grassland
|
Parcelled landscape of the
northern Netherlands (slagenlandschap)
1. stream
2. road village (wegdorp)
3. lot border
4. grassland
5. farmland (bouwland)
|
|
|

|

|

|
|
|
Water collection on dune landscapes
1. dune ridge
2. lower part of dune area
3. digged perpendicular watercourse (dwarswetering)
4. small wood dyke (houtkade) bordering village area
5.
surface dune relic (donk)
|
Beach banks between Leidenand Haarlem (strandwal)
1. road village
2. country estate on ridge
3. wet wood on sea side valley
4. canal for shipping digged sand
5. bulb field on digged part of sea side ridge
6. grassland in moisty sea side valley
|
peat bog area with peat stream
1. stream with regional village
2. grassland
3. digged perpendicular watercourse
4. small wood dyke bordering village area
5.
surface dune relics
|
|
|

|

|

|

|
|
Nature areas beyond the dyke(s) in South
West Netherlands
1. salt marsh (schor)
2. mud flat (slik)
3. sea dyke
4. farmland
|
The dyke system of SW Netherlands
1. dyke planted with trees
2. dyke village
3. creek relic
4. farmland
5. grassland on creek bed
6. pool as relic of bursting of the dike (wiel)
|
Fluvial landscape
1. abandoned river bed
2. settlement
3. raised old arable land
4. country estate
5. orchard
6. field
7. grassland
|
Country estates of West Utrecht
1. river
2. field
3. grassland
4. orchard
5. country estate
|
|
|
|
Fig. 891
Landscape elements on maps of lower grounds in The Netherlands
|
|
|
|

|

|

|

|
|
A peat bog (fen) with excavated
waterways
1. regional village
2. grassland
3. digged perpendicular watercourse
4. small wood dyke
|
The peat bogs (fens) of NW Overijssel
1. water region village alongside watercourse
2. marsh wood (moerasbos)
3. grassland
4. pool from peat extraction
|
The peat bog (fen) at Kamerik
1. buildings on clay ridge
2. canal with rest of building alongside
3. grassland parceled out in strips
|
A peat bog (fen) with lakes and drainage systems
1. regional village
2. grassland
3. lake (plas)
4. ring-dyke
5. polder with grassland and field
|
|

|

|

|

|
|
A fenland community along a canal
1. canal
2. perpendicular canal (wijk)
3. farm
|
Fenland communities along canals
1. canal
2. back canal (achterdiep)
3. perpendicular canal (wijk)
4. peat extraction with farm
5. strip with dwellings
|
Fen community along a canal that gives dual access ’
1. road alongside canal
2. perpendicular canal (wijk)
3. strip with dwellings
4. farm
|
North-east polder (Noordoostpolder)
1.
road with
farms surrounded by wood belts
2.
canal
3.
fields
4.
wood with
unimproved roads
|
|
|
|
Fig. 892
More recent landscape elements on maps of lower grounds in The Netherlands
|
|
|
The Earth’s surface
counts 511 185 932 km2 and
6 501 085 722 humans (estimation march 3rd 2006).
So, the gross population-density is nearly 13 inhabitants per km2
(nearly 8 ha per person).
|

|
|
|
|
Fig. 893 Global density
from <1 until >100 inhabitants per km2
|
|
|
However, people usually do not live in the
sea. The net population-density on land is about 44 inhabitants per km2
(about 2 ha land per person), because about 29% of the Earth’s surface is
land. So, the measure of density is most dependent on the kind of surface you
take into account.
Having excluded the oceans as tare surface to measure globally net human density on the Earth’s surface, the question arises
if, on continental level, you should take all land into account, including the
arctic areas, mountains, deserts, forests (continentally gross), or only the habitable
land (continentally net). After all, for application
in urban design, the aim is to compare inhabited areas. If so, what is
habitable land? Looking at Fig. 893, many areas count less than 1 inhabitant per km2,
mostly useless for agriculture and sustainable settlement. We can call that
‘tare surface’ on a continental level (see Fig. 894). The remaining ‘net surface’ with a higher (‘net’)
density, usable for any form of settlement, we can call ‘habitable land’.
|
Higher level
|
gross
|
|
|
net
|
tare
|
|
Lower level
|
gross
|
|
|
|
net
|
tare
|
|
|
|
|
Fig. 894 Net, tare and gross on
different levels of scale
|
|
|
|
|
|
|
However, most of these habitable surfaces
are actually used for agriculture, some for urban concentrations. These urban
areas sometimes count more than 5000 inhabitants per km2
(50 inhabitants per ha). Urban areas are most interesting to us if we
would like to compare metropolises, conurbations, towns, districts,
neighbourhoods and so on. Going on systematically with the interval boundaries
1-10-50-100 into 500-1000-5000 in the legend of Fig. 893, the legend units of highest density would become
invisible on the scale of the map. Moreover, the intervals are not equal. That
means the shown pattern is accidental. The pattern is changing by the choice of
intervals. They are chosen to produce the most striking pattern, but if
population grows, the chosen intervals may become insufficient to see any
pattern. Moreover, on an urban scale we are most interested in subdivisions
between 1000 and 10000. So, changing scale to visualise details we have to skip
the lowest densities calling them ‘tare’.
On any level of scale from the gross surface
you can subtract relatively unused areas as ‘tare surface’, resulting in gross and
net density. On a lower level of scale the net surface becomes gross surface
from which you can subtract other kinds of tare. So, to compare densities
properly, you have to distinguish levels of scale, each with its own legend
(see Fig. 895) to determine gross and net density.
|
|
m nominal radius
|
binary legend
|
|
Name frame
|
frame
|
grain
|
net
|
tare
|
|
Global
|
10 000 000
|
1 000 000
|
continents
|
oceans
|
|
Continental
|
3 000 000
|
300 000
|
habitable lands
|
lakes
and waste lands
|
|
Subcontinental
|
1 000 000
|
100 000
|
urbanised areas
|
rural
areas
|
|
National
|
300 000
|
30 000
|
urban networks
|
landscapes
|
|
Subnationaal
|
100 000
|
10 000
|
urban regions
|
landscape
parks
|
|
Regional
|
30 000
|
3 000
|
conurbations
|
town
landscapes
|
|
Subregional
|
10 000
|
1 000
|
towns, quarters
|
town
parks
|
|
Urban, local
|
3 000
|
300
|
districts, villages
|
district
parks
|
|
District
|
1 000
|
100
|
neighbourhoods, hamlets
|
neigbourhood
parks
|
|
Neighbourhood
|
300
|
30
|
ensembles
|
dispersed
greenery
|
|
Ensemble
|
100
|
10
|
lots
|
opening
up (access) area
|
|
Lot
|
30
|
3
|
houses
|
gardens,
patios
|
|
Dwelling
|
10
|
1
|
living rooms, studies, bedrooms
|
inaccessible
space, wet rooms, circulation and storage spaces
|
|
Room
|
3
|
0,3
|
sitting areas, dinettes, beds
|
walking
area, cupboards, closets, windowsills
|
|
Place
|
1
|
0,1
|
action-surrounding space
|
commodities
|
|
|
|
Fig. 895 Fifteen levels of scale to
distinguish 15 different kinds of density
|
|
|
On a European level of scale, adding an
extra interval boundary of 200 inhabitants per km2, you can observe
a central urbanised axis of more than 200, surrounded by ‘rural’ areas of less
than 200 inhabitants per km2. However, at a regular distance within
these ‘rural’ areas, there are some conurbations (London, Paris, Lyon, Milan, Munich, Prague, Berlin, Hamburg; see Fig. 897). Some of these do have the highest European density
measured within a local radius of 30km.
|

|

|

|
|
|
|
Fig.
896 Continental densities
|
Fig. 897 Subcontinental densities
|
Fig. 898 Legend
|
|
|
|
|
So, there are not only
different densities, but also different distributions, producing
patterns interesting from a viewpoint of design.
The Netherlands as a whole counts more than 42000km2 (sea excluded) and 16300000 inhabitants, that is about 390 inhabitants per km2 (about 4 inhabitants per
ha) with extremes ranging from 0 to 20 000 inhabitants per km2
if you take smaller areas into account.
The reciproque of population density is land use. The advantage of a land-use unit is that
different destinations of use can be discerned. In the Netherlands, the land
use is about 2700 m2 per inhabitant, roughly divided as 1500 m2
of agrarian land per inhabitant, 500m2 of water, 300 m2
of nature areas and forest, 300 m2 of urban areas and
infrastructure, 100m2 industry and recreation. [308]
Of this 300m2 urban area, only about 160m2 are
‘residential areas’[309]. According to CBS’s definition of ground
statistics, these are homes with green areas, hardened
surfaces and primary facilities, such as local shops, schools for pre-school
and primary education, as well as other residential facilities such as caravan
camps, house-boat harbours, service flats, etc.[310]
|

|
Fig. 899 shows the distribution of this residential
part of the urban area, divided over 40 statistical (COROP) areas, expressed in the absolute sense and
per inhabitant according to CBS
(1994) .
The residential area per inhabitant varies
in space. In the west of the Netherlands, an average of about 100 square
metres of residential area is available per inhabitant; in East Groningen,
about 300 m2 ; and in a number of other places between those two
extremes, about approx. 200 m2 per inhabitant[311].
So, ‘norms’ for the number of m2 of residential area
per inhabitant differ regionally. That also applies for other facilities,
such as (daily) recreational areas or drinking water basins. Apart
from variation in space, land-use norms also show a variation in time: they
change.
So, the use of Planological Index Numbers for the
amount of space needed for facilities is relativised by these spatial and
temporal variations.[312]
|
|
in dots of 100 m2 per inhabitant.
|
|
|
|
Fig. 899 Residential area per COROP area
|
|
|
Population
density divided by the number of occupants per
household
If one divides the density of inhabitants by the local average
number of occupants per household, then one arrives at the local density of homes[313]. However, since WW2, the number of people per
household, especially in the towns, has dropped from about 5 to 2.5[314]; and this number continues
to fall. This, by the way, was the main reason for scarcity of housing in the
later post-war period, and for the urban explosion after 1960. There are not
only great variations in time in the number of people per household, but also large
regional differences. The number of people per household is the lowest in the
Randstad and here the numbers have decreased the most rapidly in the last 50
years. In Fig. 701, the urban areas in the Randstad in 1965 are
compared with those in 1995.
During this period, the Randstad hardly grew in numbers of
inhabitants (from 5.3 million to 6.1 million). The extension of urban area was
caused, among other things, by fewer people living in one household (family
dilution).
The objects to be counted should be equal. That is why the floor
surface, to be measured in m2 is much better
a measure to get a ratio of climatised volume per earth area than the number of
houses of different size (as often done). For example the Dutch housing policy
Secretary of State 1973-1977 Van Dam approximately doubled the number of houses
produced per year in the Netherlands by halving their floor surface.
Coincidentally the demand of one person households for smaller houses was
increasing. It was a great political succes, but few politicians realised that
Van Dam did not increase the newly built floor surface (and building effort)
substantially.
Drawing the real measure dot
distribution
The regional spatial effect becomes obvious when you redraw the map
in real measure units of 100,000 and 10,000 inhabitants, counting 300m2
per inhabitant (the approximate overall urban spatial use mentioned on page 502). In Fig. 701 these are shown as circles with a radius of 3
and 1 km, respectively. Read: ‘3 km radius’ or ‘3 km in the round’ and say:
‘town’. Read: ‘1 km radius’ and say ‘district’ if part of a town or ‘village’
if separate. If circles overlap, then one has to conclude that the urban
density is higher than the average national density. If there are about ten 3km
circles (1 million people) within a radius of 10 km, then you can talk of ‘conurbations’ and draw
them as one circle of 10km.
Growing conurbations by growing land use
According to this representation, the old situation of 1965 (Fig. 701) was characterised by three large and three small
conurbations and only a few small (separate) towns. In 1990, the first thing
that strikes one is the dilution of households: the conurbations had grown, sometimes even
losing inhabitants into suburban settlements. One can call this form of
expansion ‘deglomeration’. This influences not only the built-up
areas drastically, but also the open areas in between. As soon as urban areas
are no longer surrounded by rural areas of the same order of size as the urban
area, a reversal in the image of the urban area occurs: the town is no longer
situated in the countryside, but the countryside is now enters the town, a
reversal pointed out by Tummers
and Tummers (1997,see Fig. 787)
Fragmentation of urban and rural areas
The fragmentation of urban
and rural areas on different scale levels can be visualised in the legend in Fig. 769.[315] The figures shown in this
table are not absolute. They can be interpreted with a tolerance of up to the
previous or the next figure shown in that column. The legend units shown in red
are represented as circles with a size that reflects the present average urban
spatial use in the Netherlands of approx. 300 m2 per person: 160 m2
urban residential area, 60m2 working area and 80 m2 of
infrastructure (a part of it lies outside the built-up area and therefore does
not need to be regarded as an urban area).
Dry
and wet infrastructure
For linear-shaped legend elements, a similar sort of semi-logarithmic series is
possible. Fig. 492 shows nine levels of access.[316] Something similar is
possible for drainage (Fig. 491). ‘Without information to the contrary’, in the
(former) low peat areas, the legend units are considered to be completely
filled with the named networks. In clay aeas the lowest orders with higher
network densities disappear. In dunes, nature conservancy areas, and higher
sandy grounds, even more lower orders disappear. In urban areas, ditches and
drainage channels disappear. Their function is taken over by a relatively
fine-meshed underground drainage network.[317]
Distinguish existing and future population
Fig. 769 shows a legend for representing the dispersion
patterns in a stylised manner on a regional scale. On the basis of this,
regions can be compared. The estimated economic, cultural and/or managerial
efforts needed to
realise the areas drawn into the design can be indicated using different
thicknesses of lines. The thinnest lines represent existing areas. This more or less reflects the importance of
the element in the design. At the same time, this provides an elegant way of
distinguishing existing areas from the new ones proposed (the ‘planning layer’). Apart from this, the legends are literally
‘open’ in the sense that the circular legend units can still be coloured with
functional accents or identities. For the time being, the circles can be seen
as ‘little magnifying glasses’ which conceal unfilled-in details of towns,
villages, hamlets, landscaped parks, urban landscapes or urban parks. The
drawings function as ‘colouring pictures’ that have not yet been filled in.[318]
Drawing the existing situation
To draw the existing situation in different plan layers, one layer, the number of inhabitants per
municipality, can be shown according to actual CBS statistics in real measure
circles of 100,000,10,000 and 1000 inhabitants (see Fig. 900).
|

|
|
|
|
Fig. 900 Population statistics
per municipality, drawn as circles of 3, 1 and 0.3 km radius of 100 000,
10 000, and 1000 inhabitants (300m2/inhabitant). These
circles represent the built-up area such a population needs at average in The
Netherlands. Their location is roughly determined by the urban topography
read from the map.
|
|
|
In such a pointillistic representation, a higher density than the
current average in the Netherlands can be read off directly from overlapping
circles. Dispersion within a municipality is quite accurately determined by the
position of the built-up area on the map (see Fig. 900).
Adding existing local plans
To that has been added the capacity of existing municipal
residential building plans, which, according to the New Map of the Netherlands
2000, is roughly estimated as being 570 000
inhabitants (see Fig. 901). This capacity has been aggregated with that
of the existing built-up area to create a basic map for the year 2005, thereby making
it possible to compare the designs. In this way, ten 1km units of 10 000
inhabitants (for example Amstelveen and
Nieuwegein) could be aggregated into one 3km unit of
100 000 inhabitants. In a simple way, this represents locally increasing
urbanisation, as distinct from expansion in general.
Adding existing national
plan NRO5
In Fig. 902 the remaining capacity of 5th
National Plan of Spatial Policy NRO5 (intermediary scenario for 2030) has been
drawn onto this background as a reference. That figure shows the mapped images
of the existing situation, the plans that, according to the New Map of the Netherlands,
are being carried out, and the part that remains after being subtracted from
that for NRO5, according to the EC intermediary scenario (ABF).
Interpreting plans
Fig.
903 shows the interpretation of NRO5 used in Fig. 902. In the same way other plans can be added.
In OMA, 7, 12 and
13 squares of 25 ha are converted into circles of 10,000 inhabitants (Fig. 904). Ten circles in the centre of Rotterdam, within a
radius of about 3 km are aggregated to a circle with a radius of 3 km (100,000
inhabitants).
Adding complementary plans
OMA’s and TKA’s designs
(see Fig. 904 and Fig.
905 respectively) are calculated back to the numbers of inhabitants from the
design sketches, and, after subtracting the existing local plans, are
distributed according to the topography of the drawings.
|

|

|
|
|
|
|
Fig. 905 Interpretation TKA
|
Fig. 906
Interpretation Snozzi
|
|
|
|
Summarising and comparing
with an alternative
Snozzi’s design is
interpreted exclusively and globally from the drawing (Fig. 908). In H+N+S’s design,
ABF estimated the capacity of the Green Heart to be 51 000 homes. This means about
100 000 inhabitants, represented as one dotted circle of 100 000
inhabitants in the middel of the summarising drawing of Fig. 907, because
although a dispersion of 100 inhabitants (shown by small dots) might be
possible, it is no longer visible or discernible. OMA, TKA and H+N+S’s designs
could now be represented in one drawing (see Fig. 907).
Snozzi’s design includes the
entire Delta metropolis and is therefore drawn separately (see Fig. 908) The legends are restricted to units of 100,000 (3 km radius) and 10,000
inhabitants (1 km). In the background, units of 10,000 inhabitants have been
divided into units of 1000 inhabitants (300 m), where the topography requires
it. This has not been done in the design layer, which improves overall
comparability.
A comparison of quantities
and rough morphology
Fig. 909 compares
NRO5 with five alternatives: developing the South
flank only, the Green Heart only, the North flank only, developing these three
together, or following Snozzi’s design.
|
Context
|
Population x 1000
|
|
OMA, South flank
|
|
H+N+S Green Heart
|
|
TKA, North flank
|
|
Total
|
|
Snozzi
|
|
recognisable on the map as:

|
Now present
|
Existing plans
|
NRO5-EC trend
|
|
100 000
|
10 000
|
1000
|
Inhabitants + existing plans
|
|
100 000
|
10 000
|
1000
|
Inhabitants, including existing plans
|
|
100 000
|
10 000
|
1000
|
Inhabitants + existing plans
|
|
100 000
|
10 000
|
1000
|
Inhabitants + existing plans
|
|
100 000
|
10 000
|
1000
|
Inhabitants + existing plans
|
|
Name:
|
2000
|
2005
|
2030
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Urban centre
|
710
|
700
|
988
|
|
1
|
|
|
800
|
|
|
|
|
700
|
|
|
8
|
|
780
|
|
1
|
8
|
|
880
|
|
|
|
|
700
|
|
Urban areas outside the centre
|
2818
|
2810
|
2448
|
|
|
11
|
|
2920
|
|
|
|
|
2810
|
|
|
25
|
|
3060
|
|
|
36
|
|
3170
|
|
9
|
|
|
3710
|
|
Urban green areas
|
415
|
410
|
655
|
|
|
16
|
|
570
|
|
|
|
|
410
|
|
|
35
|
|
760
|
|
|
51
|
|
920
|
|
|
3
|
|
440
|
|
Village centre
|
1337
|
1890
|
2090
|
|
|
16
|
|
2050
|
|
|
|
|
1890
|
|
|
|
|
1890
|
|
|
16
|
|
2050
|
|
|
24
|
|
2130
|
|
Rural living
|
251
|
400
|
505
|
|
|
|
|
400
|
|
|
10
|
|
500
|
|
|
24
|
|
640
|
|
|
34
|
|
740
|
|
|
|
|
400
|
|
Working area
|
512
|
380
|
454
|
|
|
|
|
380
|
|
|
|
|
380
|
|
|
|
|
380
|
|
|
|
|
380
|
|
|
|
|
380
|
|
Total
|
6043
|
6590
|
7140
|
|
1
|
43
|
|
7120
|
|
|
10
|
|
6690
|
|
|
92
|
|
7510
|
|
9
|
27
|
|
8140
|
|
9
|
27
|
|
7760
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 909 Five alternatives for NRO5 and their population specified to
their urban or rural context
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
It can be concluded from Fig. 909, that OMA already realises the NRO5 programme in the South wing, while TKA exceeds it already in the North wing. The
three plans together exceed the NRO5 programme by 1 million inhabitants. Snozzi arrives at an extra capacity of over 600,000
inhabitants. These extra capacities are mainly achieved in urban areas outside
the centre. Centres score lower than in the NRO5 design. To answer economic
questions by this kind of representation further differentiation of the
comparison into contexts of living and costs can be elaborated by calculation.
Misleading density
comparisons if the compared surfaces differ
Density measures are
abstract ratios of objects per area. To compare different areas, in principle,
their surface has to be exacly the same, otherwise very different values could
appear (see Fig. 910).
|

|

|

|
|
|
|
|
Fig. 910 The same person at 1 or 2 m2 results in very different
density values of 10000 or 5000 inhabitants per ha
|
Fig. 911 Misleading image of densities applied on the different surfaces
of COROP areas
|
|
|
|
For example, the statistical COROP areas, based on temporary socio-economic and
administrative boundaries, differ too much in surface to allow any comparison
of variables like density with surface as a factor (see Fig. 911, where Rotterdam has a lower density than some
smaller suburban areas).
A misleading regular GIS-grids
Even a regular, exacly equal square km grid applied in
GIS-applications can
produce misleading images. An occasional boundary could divide a concentration
or not, leading into very different images and conclusions, loosing essential
information and design qualities (see Fig. 912).
Data to compare contexts of
living and their costs are lost in an average representation, while the easier
to draw dot representation gives a more realistic image. Moreover, they can be
counted per km2 and by doing so, immediately translated in more
abstract densities, while the reverse is impossible.
|

|

|
|
|
|
|
Fig. 912 Two average density interpretations of the same dispersion
|
Fig. 913 Combinatorial possibilities of
arrangement between emptyness and full coverage
|
|
|
|
From a viewpoint of design the grey values inbetween emptiness and
full coverage give mathematically proven the most possibilities of arrangement
(see Fig. 912, column in the middle) and probably the highest
chance for high quality solutions. On page 518 we try
to find other relations between density and quality, depending on the
definition of quality.
Mistakes using densities as
a standard
While more advantages can be found in a representation of real
measure dots distribution, density has the advantage to express an attribute of
a site in one single number. That is why density is still very popular by
administrators, developers and managers to formulate standards for design.
|

|
|
|
|
Fig. 914 The Amsterdam harbour islands, developed
as residential area
|
|
|
However, densities are boundary-sensitive. So, if somewhere high densities are reached
and used elsewhere, the comparison could be very disappointing. The residential
plans for Amsterdam harbour islands (see Fig. 912) reached very high densities, often used as
reference that such densities can be reached without loss of quality. However,
when taking the surrounding water into account by measuring the reached
densities, their value would become much lower considering the effect of Fig. 910.
Comparing designs by real
measure dots distribution
Such mistakes can not be made representing plans by real measure
dots distribution.
|
Normalisation into 4 visions of 50 000 new inhabitants
within a square of 10x10km.
|
|

|

|

|

|
|
Zero variant
|
TKA ‘residential’
|
Hosper ‘recreation’
|
H+N+S ‘nature’
|
|
Fig. 915 Comparing plans for Almere Pampus
|
|
|
|
|
|
Three plans for Almere Pampus, normalised into the same capacity were
represented that way. This representation gives a rough, but direct idea of the
visions. For many kinds of specialists like
travel engineers, housing specialists, civil engineers this representation
gives necessary starting points for evaluation. For every desired square
kilometre you also can find the population density or floor-space index (FSI), because every dot represents 1000
inhabitants, now drawn by a circle of 30 000 m2 floor space
(100m radius net dots). If you like to count more or less than 30m2
floor space per person, then the circles have to be drawn only a little larger
or smaller.
Extreme gross and net dots
In Fig. 900 the dots of 1000 inhabitants had a radius of
300m (about 30 ha or 300m2 per inhabitant). These dots represent the
average urban area an inhabitant needs for all urban facilities in The
Netherlands according to the figures mentioned on page 502. However, in Fig.
915 they had a radius of 100m (about 3 ha or 30m2
per inhabitant, the average floor space you appoximately need for living only).
|

|
|
|
|
Fig. 916 Extreme gross and net dots
|
|
|
Within a district the gross dots of Fig. 900 would often overlap (see Fig. 916). Net dots already
give some idea about the mutual arrangement of dwelling areas. In Fig. 915 the urban facilities other than homes have to
be imagined in between the ‘net dots’. In Fig. 916 the allotment of a district quarter is drawn
showing the surface other than dwellings like surrounding facilities like green
areas, pavement, schools and shops. However, the gross dots overlap, showing there is more than that, apparently
outside the local district. So, measuring the density of a district with
district facilities only (district tare) will be higher than the density of a town
including town facilties (town tare). The same applies for any level of scale you
take into account.
Comparable surfaces in urban
areas
By counting the digits of the
number of m2, we could name these categories with a useful
tolerance by their nominal radius (see Fig. 917). For example, you can name an area with a
surface between 10000 and 99999 m2 (5 digits): ‘R=100m’ (ensemble).
|
Digits
|
Min. area
|
Max. area
|
Min. radius
|
Max.
radius
|
Nominal
radius
|
Gross
|
Tare
|
|
|
Smin
|
Smax
|
Rmin
|
Rmax
|
Rnom
|
|
including for example
|
|
|
m2
|
m2
|
m
|
m
|
m
|
|
|
|
10
|
1000000000
|
9999999999
|
17841
|
56419
|
30000
|
metropolis
|
landscape parks, metropolitan infrastructure and facilities
|
|
9
|
100000000
|
999999999
|
5642
|
17841
|
10000
|
conurbation
|
town landscapes, conurbarion infrastructure and facilities
|
|
8
|
10000000
|
99999999
|
1784
|
5642
|
3000
|
town, town quarter
|
town parks, town water, town infrastructure and facilities
|
|
7
|
1000000
|
9999999
|
564
|
1784
|
1000
|
district,
district quarter, village
|
district parks, district water, district infrastructure and facilities
|
|
6
|
100000
|
999999
|
178
|
564
|
300
|
neigbourhood, hamlet
|
neighbourhood parks, small water, neighbourhood infrastructure and
facilities
|
|
5
|
10000
|
99999
|
56
|
178
|
100
|
ensemble
|
small public green area residential public space
|
|
4
|
1000
|
9999
|
18
|
56
|
30
|
urban island, property, building complex
|
pavement directly opening up building complexes, open space in private
parcels (lots, plots)
|
|
3
|
100
|
999
|
6
|
18
|
10
|
|
gardens, unbuilt places, patios
|
|
2
|
10
|
99
|
2
|
6
|
3
|
building segment,
|
rooms, unbuilt spots
|
|
1
|
1
|
9
|
1
|
2
|
1
|
building part
|
inaccessible spaces
|
|
|
|
|
|
|
|
|
|
|
Fig. 917 Ten different tare categories,
ten different density measures
|
|
|
Though the range of surface difference is still a factor of nearly
10, this restriction is strict enough to get roughly comparable densities.
However, even by that tolerance there are still ten different urban density
measures to be confused. So, a gross density D100m is something else
than a gross density D300m, but a net density D300m in
this scale range is the same as a gross density D100m.
Tokyo-Yokohama is the
largest metropole, counting nearly double the number of inhabitants of the next
five between 15 and 20 mln (see Fig. 918). New York covers
the largest area. However, the way the
areas are counted may differ making the comparability doubtful.
|
Nation
|
Urban
Area
|
Population
|
Km2
|
Density
|

|
|
Japan
|
Tokyo-Yokohama
|
33200000
|
6993
|
4750
|
|
United
States
|
New
York
|
17800000
|
8683
|
2050
|
|
Brazil
|
Sao
Paulo
|
17700000
|
1968
|
9000
|
|
South
Korea
|
Seoul-Incheon
|
17500000
|
1049
|
16700
|
|
Mexico
|
Mexico
City
|
17400000
|
2072
|
8400
|
|
Japan
|
Osaka-Kobe-Kyoto
|
16425000
|
2564
|
6400
|
|
Phillipines
|
Manila
|
14750000
|
1399
|
10550
|
|
India
|
Mumbai
|
14350000
|
484
|
29650
|
|
India
|
Delhi
|
14300000
|
1295
|
11050
|
|
Indonesia
|
Jakarta
|
14250000
|
1360
|
10500
|
|
Nigeria
|
Lagos
|
13400000
|
738
|
18150
|
|
India
|
Kolkota
|
12700000
|
531
|
23900
|
|
Egypt
|
Cairo
|
12200000
|
1295
|
9400
|
|
United
States
|
Los Angeles
|
11789000
|
4320
|
2750
|
|
Netherlands
|
Amsterdam
|
1100000
|
324
|
3400
|
|
Netherlands
|
Rotterdam
|
1325000
|
531
|
2500
|
|
|
|
Fig. 918 The largest of 1200 cities listed by
demographia.com
|
Fig. 919 1200 cities between the density
lines 30 000 and 700 inhabitants per km2
|
|
|
|
On the density lines of 30 000 and 700 inhabitants per km2
(see Fig. 919) you find Mumbai and Atlanta as the
largest cities, with incomes of €2 000 and €19 000 rper capita
espectively. The €/capita income (see Fig. 920) and $/capita gross domestic product (GDP,
see Fig. 921)
are very roughly related to metrolopitan density.
|

|

|
|
|
|
Fig. 920 Density related to €/capita income in 14 cases
|
Fig. 921 Density related to $/capita gross domestic product in 161 cases
|
|
|
|
However the sources differ and the figures change rapidly. Van
Susteren (2006) compared
101 metropoles on many aspects using different sources.
The municiality of Amsterdam has an
average density of 4400, the municipality of The Hague 6500 inhabitants per km2.
Are these figures comparable? No. The administrative municiality of Amsterdam
comprises more vast empty areas than The Hague. Such empty areas have to be
subtracted as tare surface. In Fig. 922 and Fig. 923 the built-up municipal area is dotted, but if
you count the adjacent municipalities with more than 50% commuters into the
central city, comprising at least 15% of their working population (see
conurbation definition page 528), then the densities of these ‘conurbations’
are lower (2700 and 3300 inhabitants per km2 respectively).
|

|

|
|
|
|
|
Fig. 922 Population and floor space of Amsterdam
|
Fig. 923 Population and floor space of The Hague
|
|
|
|
Using population statistics per district and drawing dots
representing 1000 inhabitants with a radius of 100m (30m2 floor
space per inhabitant), you can get an idea of the diversity of densities within
these average conurbation densities (see
Fig. 922 and Fig. 923).
Deriving density from a
distribution of dots
In Fig. 923 a km grid is drawn. You can count the dots per
grid cell to determine the local density per km2. However that
depends on the location of the grid (see Fig. 912). It is better to make a mask of 1km2
and shovel that mask over the drawing to find the highest density. Multiplying
that figure by 100 gives the density of inhabitants per ha. Dividing it by the
average household size gives an estimate of the number of houses per ha.
You can also estimate the floor-space ratio (FSI: floor-space index) multipying the inhabitants by the used average
(here 30m2 at home, but you have to add other floor space, say
30+20=50m2) per inhabitant. A hundred times FSI gives %floor surface on a
conurbation level. High densities may suggest high rise buildings (at a
smaller-scale map, the dots could be drawn piled-up to suggest high-rise).
However that conclusion is put into perspective on page 520. Inbetween home-dots you have to imagine the
tare space for urban facilties. The largest of these are industrial areas,
parks and natural areas like dunes.
Town densities are incomparable if you do not precisely define the
boundaries of the towns compared. To determine the main national subsidies for
municipalities the distance between buildings has to be less than 100m to
determine the ‘built-up area’ as a factor in subsidy calculation. That mainly means excluding ‘open area’ like agricultural areas, natural areas and
parks larger than 100m in any direction as tare surface of higher order. The
question if you have to include national or regional highways and waterways
crossing the town and other facilities to calculate density has to be solved.
Many adminstratively bounded districts include
such tare surfaces of higher order, not to be included to calculate district
density. So, statistical figures about their total area are not reliable.
|

|

|

|
|
|
|
|
|
Fig. 924 Inhabitants and surface of administrative districts in the municipality
of Amsterdam
|
Fig. 925 The figures of Fig. 924 excluding districts of more than 1000 ha
and 20 000 inhabitants
|
Fig. 926 The same figure as Fig. 925 concerning the municipality of The Hague
|
|
|
|
|
Fig. 924 shows the great difference in size of
administrative districts in Amsterdam making
these incomparable in principle. In Fig. 925 districts of more than 20 000 inhabitats
are excluded. They should be subivided to be comparable with the smaller ones.
In the rough approach of Fig. 917 you should exclude also districts with a
surface counted in m2 of more or less digits than 6, that is 2
counted in ha, but we can take an even rougher boundary. Excluding three
districts of more than 3 digits (>999 ha) in Fig. 925 already gives an interesting view, but the
question remains if you have to include urban highways and waterways crossing
the district, town parks and other facilities derived from page Error! Bookmark not defined. (see also Fig.
993) to calculate density.
Rough boundaries of district
density
In Fig. 925 and Fig. 926 the drawn line y=50·x (‘inhabitants= 50·ha’)
represents the density of 50 inhabitants per ha. So, the slope indicates the
density. In both municipalities there is a concentration of districts with a
higher density above this line. If you draw a line from 0(0) into
20 000(50), then you get the line of density representing
20 000/50=400 inhabitants per ha. Below that line none of the districts
appear. However, on lower levels of scale with closer fitting boundaries you
may find higher densities. You can also estimate the floor-space ratio (FSI: floor-space index) multipying the inhabitants by the used average
(for example 50m2) per inhabitant. A hundred times FSI gives %floor
surface on a
district level.
Boundaries
Subdividing a municipality in partial
municipalities, districts and neigbourhoods (see Fig. 927) raises questions of financial responsibility for
(re)arrangement and maintenance of public space. So, determining the boundaries of that units
becomes increasingly important on lower levels of scale. The smaller the area,
the more the boundary surfaces count in relation to the enclosed surface. That
is why such boundaries are often drawn on the middle of a shared road or
waterway. If they are drawn on one side, the other side has to pay for it.
Subtracting tare of a higher
order
In the beginning, private plots are sold,
also paying for the surrounding public space as designed. However, if their
neigbourhood comprises surfaces used by adjacent neigbourhoods as well, the
costs have to be shared (tare of a higher order). That applies on every level
of scale, from national scale until common roofs and walls in buildings and
common hedges in gardens. So, in the initial exploitation scheme of a
district or neigbourhood, these surfaces have to be distinguished as tare of a
higher order. A neigbourhood density calculation can use this financial
distinction by subtracting such tare surfaces from the piece of map you take
into account (the map cutting).
The result is a net neighourhood surface, which is, according to Fig. 917, the same as the gross surface of all ensembles
involved (see Fig. 929). Politicians are still interested in the
reached number of houses per ha, but they do not often distinguish these
surfaces. By using the ‘net house neigbourhood density’ (in fact
the average ‘ensemble house density’) you can name a higher figure than using the
‘gross house neigbourhood density’. However, as argued on page 503, floor space is more reliable than the number
of houses to determine densities.
|

|

|
a
|
m2 Map cutting
|
|
b
|
m2 Non district surface of higher order
|
|
c
|
m2 Common district surface
|
|
d
|
m2 Gross neighbourhood (a - b - c)
|
|
e
|
Number of houses
|
|
f
|
Gross house density per ha
(10 000 · e / d)
|
|
g
|
m2 Common neighbourhood infrastructure and facilities
|
|
h
|
m2 Net neigbourhood (d - g)
|
|
|
=m2 gross ensemble surface
|
|
i
|
m2 Total floor surface
|
|
|
|
|
|
|
Fig. 927 Partial municipality Osdorp of Amsterdam, divided in 5 districts
|
Fig. 928 The 500x500m neigbourhood indicated in the middle of Fig. 927
|
Fig. 929 Primary figures to know on neigbourhood level
|
|
|
|
|
|
Non residential surface
There could be many (political, social, financial, technical,
ecological, spatial) reasons to distinguish residential and non residential
surface. Non residential initiators may have to pay
more for their plots per m2, they may need more parking space or
other public facilities, they do not contribute to the number of inhabitants
supporting shops and so on. That distinction may be not primarily important to
determine the total %floor surface your design offers, but the distinction is
often asked, especially if the non residential area is a substantial part of
the total area. If you would like to take up that distinction in your density
calculation, you need to specify more (see Fig. 930).
|
h
|
m2 Net neigbourhood
(d - g)
|
p
|
Average dwelling occupation
(inh./dwelling.)
|
|
i
|
m2 Total floor surface
|
q
|
Inhabitants per hectare ((e x
p)/(h/10000))
|
|
j
|
m2 Non-residential surface
|
r
|
Net residential surface (h - j)
|
|
k
|
m2 Non-residential private
surface (ca. 60% j)
|
s
|
m2 Housing floor surface
(gf.+storeys.)
|
|
l
|
m2 Total
private surface (k + u)
|
t
|
Net house density (10000 e/r)
|
|
m
|
m2
Ensemble public surface (h-l)
|
u
|
m2 Private residential surface
|
|
n
|
m2 Total built-up surface
|
v
|
m2 Public paved residential
surface
|
|
o
|
%built-up, 100xGSR or GSI (100·n/h)
|
w
|
m2 Public green residential
surface (r - u - v)
|
|
|
|
|
|
|
Fig. 930 Secondary figures to know on neigbourhood level
|
|
|
|
|
|
|
|
|
|
|
|
Subtracting the non residential surface (j in Fig. 930), including the surrounding public space) from
the net neighbourhood surface (h in Fig. 930, mentioned earlier in Fig. 929)produces a third surface you can take as a
basis to name an even higher house density: the net residential neighbourhood
surface (r in Fig. 930).
Private and public space
Both total residential and non residential surfaces have to be
distinguished in private and public space. If you do not want to measure the proportion
of public space in a not yet designed non residential area (j in Fig. 930), you can take 60% as an approximation (k in Fig. 930), but you have to measure the private
residential surface (u in Fig. 930) and the paved residential surface (v in Fig. 930) to check the third category, the green
residential surface and water (w in Fig. 930).
Inhabitants per hectare
If you know the average dwelling occupation (p in Fig. 930) and the number of
houses (e in Fig. 930) you can calculate the number of inhabitants on
the gross neighbourhood surface (h in Fig. 930). If you know the housing floor surface (s in Fig. 930) and the average floor surface per inhabitant
(for example 30m2) you can divide them to get the number of
inhabitants supporting the facilities of the neigbourhood.
Built-up surface and
building height roughly determine the floor space
The %built-up surface (100xGSI, Ground Surface Index) is an important part of private surface to
determine the kind of environment your design produces (think about shadows).
It is much work to measure that surface in a neighourhood, but a free
downloadble brain scanning computer application called ImageJ may help,
if you have a topographical map in TIFF. format. If you know the number of
storeys you can roughly calculate the floor space by multiplying it by the
built-up surface. However, some buildings cover open space loosing floor space
to be subtracted.
Measuring and calculating
The Excel sheet below gives these measures of
neighbourhood density in their
mutual relationship to make calculation easy. But you still have to measure
many surfaces from the map or drawing.
|

|

|
|
|
|
|
Fig. 931 An Excel sheet calculating of different kinds of density
|
Fig. 932 Amsterdam Kinkerbuurt visualisation of surfaces per ha
|
|
|
|
The urban development office of Amsterdam study
group Kinkerbuurt from the
sixties of previous century found an elegant way to visualise key factors of
neighbourhood land use (Fig. 932).
Five kinds of density
|
|
for example
|
expressed as FSI
|
|
% floor space on gross
neighbourhood (i/d)
|
114%
|
1.14
|
|
% floor space on net
neighbourhood (i/h)
|
117%
|
1.17
|
|
% floor space on net
residential surface (s/r)
|
119%
|
1.19
|
|
% floor space on a particular
ensemble
|
133%
|
1.33
|
|
% floor space on a particular
town island
|
140%
|
1.40
|
|
|
|
|
|
Fig. 933 The output of calculation: five kinds of density
|
|
|
|
|
Fig. 933 shows the output of the Excel sheet: there are
five kinds of increasing density you can distinguish, dependend on what kind of
surface you take into account.
If you do not only take the floor space, but also the housing
density, then there are another five.
Private to be sold / public paved / green
The private surface P raises
the profits to be maximised, the public space A-P the costs to be minimised.
However, a high amount of green, parking space and easy acces by paved
circulation space may increase the ground price per m2
of private lots. So, the proportion privat / public paved /
green has to be optimised according to local context.
Politicians, project developers, housing corporations, professional
colleagues or buyers often want to know the proportion of private plots to be
sold, public paved and public green surface in the
net residential area, determining qualitative and financial characteristics.
If three factors total 100%, you can visualise the proportion in a
triangular graph earlier done in Fout!
Verwijzingsbron niet gevonden. for three soil components. The Excel-sheet creates such a graph in a
necessarily orthogonal way giving a cross in the appropriate cell (see Fig. 934) to be interpreted as a very rough rounded off
indication.
|
|
red
|
|
|
|
|
|
|

|
|
|
|
|
|
|
In the Osdorp neigbourhood example of Fig. 928 the 46% net residential private ground to be sold
and 27% pavement resulted in 26%
public green are calculated in the Excel sheet of Fig. 931.
However, the graph with three 100% corners rounds these figures
off into 40/30/30. The surface public green and pavement are rounded off at
the cost of residential private ground to be sold. The graph is pessimistic
about the profits.
So, this graph only can be used for a very rough comparison with
other neigbourhoods, or has te be redrawn in a more precise triangular way
like Fout! Verwijzingsbron niet gevonden. according to the real figures given as well.
|
|
Private to be sold>
|
100%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 60% 60%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50%
|
|
|
|
|
|
0%
|
|
|
|
|
|
|
|
|
40%
|

|
|
|
 x x
|
20%
|
|
|
|
|
|
|
|
|
|
30%
|
|
|
|
40%
|
|
|
|
|
|
|
|
|
|
|
20%
|
|
|
60%
|
|
|
|
|
|
|
|
|
|
|
|
10%
|
|
80%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0%
|
100%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
green
|
0%
|
10%
|
20%
|
30%
|
40%
|
50%
|
60%
|
70%
|
80%
|
90%
|
100%
|
grey
|
|
|
|
|
Pavement
>
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 934 40% Residential private ground to be sold, 30% pavement and 30%
public green
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Simplified dimensions
The division of a neigbourhood in ensembles
mostly results in homogeneous residential or non residential areas. So, on this
level that functional distinction will no longer play an important role.
We can concentrate on basic formal surfaces as total area A,
built-up surface B, floor surface F, private surface P, non-specified public
surface A - P and average building height or average number of storeys S. The
gross ensemble surface A is equal to the net neighbourhood surface (see h in Fig. 930). So, neigbourhood infrastructure and
~facilities are excluded, and there is only one basis for density: F/A (FSI). The coverage of the total surface A by
buildings B/A (GSI) is a primary variable.
B multiplied by the average number of storeys S (if façades are
vertical) produces the floor surface F.
Spacemate
If F = S · B, then F/A = S ·
B/A. To compare ensembles with different A, Permeta draws a
diagram called Spacemate, plotting F/A against B/A. In Fig. 936 both are given as percentage of B and F from
the total area A. Moreover, the diagram is extended from 0 into 100%. So, B on
the horizontal axis includes also unusual, mostly theoretical high densities.
In that diagram the %floor surface as a
function of %built-up area appears
as a straight line starting in the origin with a slope according to the average
number of storeys. Any ensemble appears as a spot according to %F and %B (Fig. 936).
|

|
|
|
|
Fig. 936 Spacemate: floor surface as a function of built-up surface
according to Permeta
|
|
|
In Fig. 936, 6 theoretical parcellations are drawn
on 1 hectare (approximately 1 quarter of a nominal ensemble R=100m). The 8
actual ensembles in Osdorp, Amsterdam West as
measured by Permeta are given as numbers. They have all less than 20% built
area, and the theoretical parcellations have more. For example, ensemble 6 has
the highest %built surface, but not the highest %floor surface.
Intensifying floor surface
Making plans to increase density in
existing areas, political targets are often expressed in increasing FSI (%floor
surface/100). The Spacemate is primarily made to visualise the qualitative
effect of such operations. Permeta calculated many examples, real or made by
students, on different spots in the diagram to show the effect. A computer
programme shows different photographs of ensembles categorising them in
clickable surfaces of the Spacemate.
To intensify the floor density you have to increase the building
height or the average number of storeys (arrow crossing lines of floor density
with the same number of storeys in Fig. 936) or without increasing the number of storeys
you have to increase the %built surface (arrow parallel to lines of floor
density with the same number of storeys in Fig. 936). By increasing the %built-up surface
(decreasing open surface A ‑ B) more, one can cross the lines
of floor density with average 3 storeys in horizontal direction even decreasing
the number of storeys to 2 (draw it yourself).
Most design alternatives will appear on 50% built-up area (see Fig. 913). Then the potential of urban-architectural
quality and the length of façades, where building and open space are connected
is highest (structural quality). However, lower levels increase the potential
of open space, afforded views and green space (form quality), higher levels increase the support for schools,
shops and other population-dependend facilties (functional quality). So, there are at least three components of
urban quality direcly related to the %built-up surface.
More than 50% built-up area
Parcellations with more than 50% built area have
seldom courts or streets larger than 10m width.
|

|

|
|
|
|
|
Fig. 937 Ensemble in Venice 1: 5000; 200x200m
|
Fig. 938 Auction Aalsmeer 1:25000, ha grid of 1kmx1km, one building nearly
covering a district
|
|
|
|
Such urban areas have no cars like Venice (Fig. 937) or they have internal traffic in buildings
like the flower auction in
Aalsmeer (Fig. 938).
The use of open space
The elegantly simple and useful diagram by Permeta is
complicated without necessity by introducing %unbuilt/%floor (OSR), or in
formula: (A-B)/F. It is supposed that factor determines the use of open space:
little unbuilt area compared to a large available floor space would give a
pressure of floor-space users on the unbuilt area and for example a shortage of
space for cars.
However, the intensity of use of public space (part of the open space) is not
very dependend on use by local inhabitants. The traffic intensity of
residential streets usually is 1% of its capacity (see Fig. 541) The expectation of urban liveliness (intensity) by design is overestimated in districts other
than for example the city of New York. In student plans, that overestimate is
frequently represented by drawing too much people in suburban public space. A
global calculation proves that you must be
economical with the crowd pullers to get some lively places in the city.
And to feed that, you need still a lot of quiet suburbs in the conurbation.
Empty streets
That calculation goes approximately this way. According to the
ground usage statistics of CBS, in The Netherlands we have
approximately 1 billion m2 circulation area, whereas our population
of about 16 millions (including home-bound children and elderly) is on the
street at the most half an hour per person per day. This means that, on 100m2
public area through the daytime, at average you will see someone driving or
walking approximately one minute within a quarter of an hour. Assume that you
call a public space as ‘urban’ in contrast with ‘suburban’ if you come across
someone on 100m2 for one minute long each minute (‘urban intensity’). How much public space can be then ‘urban’?
Stealing liveliness from the
suburbs
You must make almost 2000m2 street elsewhere quieter for
100m2 urban intensity, but not too quiet, otherwise people cannot
come to the urban space you want to make ‘urban’. That ends up then on 5% of
the paved area. If you divide 3% of it concerning the districts, you keep still
2% for the concentration of urban crowd pullers. You should not subdivide urban
crowd pullers too much;
because you lure more people out of their house with bigger free choice-serving
centres. You can at most try to make the public space so attractive, that
people exchange the street to their television for a little bit longer than a
half hour per day. Can a master plan contribute to that, or should you trust
the architectural development?
Multipying the Built-up surface by the number of
Storeys produces the Floor surface B x S = F (if all façades are vertical). So,
the number of storeys S = F/B. If we make F = 100% of the Area A (FSR=1), then
the Area is fully covered with one storey, half covered with two storeys,
but doubling the number of storeys again
reduces the profit of open space (see Fig. 939). So, piling up storeys is subject of
diminishing returns in terms of open space, while the visual impact of the high rise on open
space increases.
|

|

|
|
|
|
Fig. 939 Diminshing returns of open surface by increasing high rise
building
|
Fig. 940 Progressively increasing Built-up surface by decreasing number of
storeys on 100% F/A
|
|
|
|
The Built-up surface B is the complement of open surface. The
%Built-up (of A) is dependend on the number of Storeys S if we keep FSR or %Floor
surface (of A) constant. You can try different %Floor values yourself to change
Fig. 940. The profit of open space
does not increase much above 5 storeys (blue spot in Fig. 940).
Non-vertical façades
The Built-up area B is recognisable on the topographical map as the
vertical projection of the building on the ground-level. However, for example a
pyramid will have
less floor space than a cube. So, F < S x B. The same
applies for buildings with different heights, extended parts, internal voids and
non-vertical façades.
The urban island is the
best level to avoid coincidental differences that could disturb a reliable
density comparison. An urban island is bordered by the axis of
public infrastructure that opens up or encloses private properties in closest
surrounding not intersected by other infrastructure. So it encloses no other
public infrastructure than dead-end streets, opening up backyards and garages,
water and green area only functional to the smallest publicly opened-up urban
area.
|

|
|
|
|
Fig. 941 The urban island
|
|
|
An ensemble encloses
several urban islands + ensemble infrastructure, a neighbourhood encloses
several ensembles + neighbourhood infrastructure and so on. The %floor surface per area
of an urban island is equal or higher than any other useful density measure by
lack of urban tare, except the %floor surface of a
particular plot (FAR). Jong (2001) made an interactive
computerprogramme showing the behaviour of an orthogonal island changing any of
the determining design measures (Fig. 941).
Multiplying urban islands into a neighbourhood
Any higher level of scale adds its own tare decreasing the density. The programme shows in a next window the
considerable surface occupied by dry and wet infrastructure on every
higher level (Fig. 941).
|

|
|
|
|
Fig. 942 Adding dry and wet infrastructure
|
|
|
Green surfaces and
surfaces for amenities are not
yet shown in this window. It should be clear that such infrastructure of higher
order should not be counted in the density of the lower order when they lack in
other locations to compare. On this level of scale these surfaces are location
factors by which the external context of the urban island differs,
but not its density. They become comparable by density measures on a
higher level of scale.
Many questions about the influence of
urban details of a closed buiding block on density like built width and length, the building depth, the width and length of court,
the width of streets, the width and length of island, the built-up surface, the
%built-up, the average height of storeys, the number of storeys, the date and
hour of sunlight, solar angle limits, the outer wall ratio limit and the surface of
outer wall are answered quickly by experimenting with all these measures in a
downloadable spreadsheet (see Fig.
943). These parameters can be changed easily to find their influence on
density. By experimenting with this spreadsheet you are warned for dark
buildings, courts or streets changing them.
|

|
|
|
|
Fig. 943 The %built-up
spreadsheet
|
|
|
|

|

|
|
|
|
|
Fig. 944 FSR(Built with)
|
Fig. 945 FSR(Number of storeys)
|
|
|
|
Many graphs like Fig. 944 and Fig. 945 can be constucted according to their hidden
supositions about these parameters.
|
Every year, as far as I
can remember, the the national bureau of statistics CBS has produced the Statistisch Jaarboek
(earlier a more extensive Statistisch Zakboekje). Since 2006 it is also
available in English (Statistical Year Book).
This inexpensive publication gives an overview and a popular extract of CBS
statistics (referring to much more data, to be found on http://www.cbs.nl/).
An example for direct use in urban design
There, for example, you
can find characteristics of 240 urban facilities. Dividing their number by total population of The Netherlands you
can calculate how many people you need to support each facility at average.
How many schools, restaurants, petrol stations has a Dutch district of
10 000 inhabitants at average? The deviation from this average
determines the functional profile or identity of a region,
conurbation, town, district or neighbourhood.
Intellectual substance
Those who are familiar
with this pocket book are mostly of the opinion that one is not an
intellectual unless one has a subscription to it. I support this view. At
some point early in the year, as soon as my new copy falls through the
letter-box, I settle down in a comfortable chair to look through it. Then, I
am unavailable for a few hours, as, with the help of this impressive
statistical material, I see numerous popular myths collapse before my eyes.
|

|
|
|
|
Fig. 946 The Dutch statistical year book 2008
|
|
|
Manipulating figures in Excel
It appears in the bookshops
at the same time as the inexpensive CD-ROM. Like the website http://www.cbs.nl/ this is a great blessing, because now all the tables can be
transported to Excel and then the feast of selecting and working with this
material can begin.
|
1 Population
1.1 Population
1.2 Health and
well-being
1.3 Education
1.4 Culture,
recreation and other uses of time
1.5 Legal protection
and safety
1.6
Residence
2 Employment, incomes and
social security
2.1
Employment and wages
2.2
Incomes, property and expenditures
2.3 Social security
|
3 Businesses
3.1 Demography of
businesses
3.2
Business book-year accounts
3.3
Automation and research and development (R&D)
3.4 Agriculture and
fisheries
3.5 Energy and
minerals
3.6 Industry
3.7 Building
industry
3.8 National trade
and service industry
3.9
International trade
3.10 Traffic,
transport and communication
|
4 Government, politics and
management
4.1 Government finances
4.2 Politics and management
5 Macro-economy and the
money and capital market
5.1
National accounts
5.2 Money
and capital market
5.3 Producer and
consumer prices
6 Geography and
environment
6.1 Geography
6.2 Environment
|
|
|
|
Fig.
947 The content of the Statistisch
Jaarboek 2001
|
|
|
A number of establishments
are listed for every organization and branch. To give an impression of the kind
of data you can find and manipulate, I have taken my CD-ROM Statistisch Jaarboek
2001 with figures from 2000 and put the relevant urban architectural tables
from the chapters indicated in Fig. 947 in
Excel.
It is up to you to make the
same graphs with more recent figures and to compare them with those of 2000.
National territory
In 1996, the Netherlands
occupied a territory of 41,526 km2 , divided over various provinces
and land-use categories, as shown in Fig. 948. Of these categories, forest,
nature and water can be seen as public facilities, to a
greater or lesser extent. Built-up areas occupy a relatively small area.
|

|
|
Legend: water, built-up,
nature, forest, agriculture
|
|
Fig.
948 Land use in different provinces (from below: agriculture, forest,
nature, built-up, otherwise, water) in
the Netherlands
|
|
|
The
lengths of roads
In 1999, the Netherlands had
117,430 km of surfaced roads (if one was to include unsurfaced roads, this
would be approximately 95% of the total road network). The growth of this road
network is shown in Fig. 949. Although not all means of transport
are public facilities, they form, together with the surfaced roads, a transport
system (Fig. 950).
|

|

|
|
Legend: highways, roads
outside and inside the urban area
|
Legend: motorcycles,
business and private cars
|
|
Fig.
949 Extent of paved roads
|
Fig.
950 Means of transport
|
|
|
|
The density of roads
Outside the built-up areas,
the prevailing road network has an average mesh width of approx. 1 x 1 km
(density 2 km per km2). Within built-up areas, the mesh width is almost 100 x 100 m (20 km per km2).
Motorways have an average mesh width of approx. 30 x 30 km (0.07 km per km2).
|
|
length
|
surface area
|
density
|
average mesh width in
km
|
|
motorways
|
2256
|
29261
|
0.077
|
30
|
|
outside the built-up areas
|
54820
|
26060
|
2.104
|
1
|
|
inside the built-up areas
|
60354
|
3201
|
18.85
|
0.1
|
|
total extent of surfaced
roads
|
117430
|
29261
|
4.013
|
|
|
railways
|
2808
|
33873
|
0.083
|
30
|
|
|
|
|
|
|
|
Fig. 951 The density of
the road network
|
|
|
|
|
|
|
The density of the railway
network can be compared with that of the motorways.
Approximately 135 people are
needed as a support base for a kilometre of road.
For the classification of
urbanity the numerical values for the neighbourhood address densities of the
different municipalities are categorised into five groups or classes.
|

|

|
|
Legend: urban centre,
urban, suburban, village, countryside
|
|
Fig. 952 Inhabitants by
urban CBS environment category
|
Fig. 953 On the map
|
|
|
|
The boundaries of the
classes have been chosen in such a way that all the classes contain about the
same number of residents. In this way, the following categories can be
distinguished:
·
very strongly urban
municipalities with a neighbourhood address density of 2,500 addresses or more
per km2 ;
·
strongly urban
municipalities with a neighbourhood address density of 1,500 to 2,500 addresses
per km2 ;
·
moderately urban
municipalities with a neighbourhood address density of 1,000 to 1,500 addresses
per km2 ;
·
hardly urban
municipalities with a neighbourhood address density of 500 to 1,000 addresses
per km2;
·
non-urban municipalities
with a neighbourhood address density of less than 500 addresses per km2.
The number of residents who
live in these environments is therefore divided rather similarly, with small
variations in age.
In NRO5, the
RPD used a similarly grouped classification to that of a stipple chart, for
reading off a location.
Order of
municipality by size
On 1st January 2000, this
population was resident in 537 municipalities. When
one lists these municipalities according to size, one gets the ‘ordering’ of
municipalities (rank size). In Fig. 954, using the ordering in this list, 1 in 40 of the
municipalities is named. This does not produce a straight line, because the
size of municipalities from the largest, downwards, diminishes rapidly, at
first, before slowing down. When the y axis is made logarithmic, the
graph becomes clearer (Fig. 955).
|

|

|
|
|
|
|
Fig.
954 Ordering
municipalities using a power trendline in Excel
|
Fig.
955 Ordering municipalities, expressed logarithmically, using a
trendline in Excel
|
|
|
|
Then it also becomes clear
that, for the smallest municipalities, the trendline is no longer accurate:
reality decreases faster for populations from below 10,000 to the smallest
municipality (Schiermonnikoog),
probably due to the geographical restrictions of the island boundary.
Order of conurbations
The historical boundaries of
municipalities cut through the reality of amalgamated built-up areas (urban
conurbations), so
that these graphs give an incorrect picture of the Ordering of urban areas.
However, the Yearbook also gives a table of urban conurbations of over
100,000 inhabitants. The somewhat out-of-date definition of this type of conurbation is given in the Yearbook as follows:
A central town with
surrounding municipalities that (on 31st May 1960) fulfilled the following
conditions:
- more than 50% of the commuters resident there must be employed
in the central town;
- in addition, the above-mentioned commuters must comprise at
least 15% of the working population of the central town.
This table is shown next to
the upper section of the municipality table (Fig. 956) in Fig. 957.
In general, municipal
density is much higher than conurbation density.
|
|
|
|
|
|
|
inhabitants
|
km˛
land
|
no.
inhabitants
/ha.
|
|
|
|
|
|
|
Amsterdam
|
731288
|
165,13
|
44
|
|
Rotterdam
|
592673
|
208,61
|
28
|
|
DenHaag
|
441094
|
67,92
|
65
|
|
Utrecht
|
233667
|
61,42
|
38
|
|
Eindhoven
|
201728
|
87,31
|
23
|
|
Tilburg
|
193116
|
117,42
|
16
|
|
Groningen
|
173139
|
80,15
|
22
|
|
Breda
|
160615
|
127,00
|
13
|
|
Apeldoorn
|
153261
|
340,30
|
5
|
|
Nijmegen
|
152200
|
53,70
|
28
|
|
Enschede
|
149505
|
140,04
|
11
|
|
Haarlem
|
148484
|
29,45
|
50
|
|
Almere
|
142765
|
131,62
|
11
|
|
Arnhem
|
138154
|
98,57
|
14
|
|
Zaanstad
|
135762
|
74,50
|
18
|
|
DenBosch
|
129034
|
85,00
|
15
|
|
Amersfoort
|
126143
|
62,88
|
20
|
|
Maastricht
|
122070
|
57,01
|
21
|
|
Dordrecht
|
119821
|
80,58
|
15
|
|
Leiden
|
117191
|
22,16
|
53
|
|
Haarlemmermeer
|
111155
|
180,01
|
6
|
|
Zoetermeer
|
109941
|
35,59
|
31
|
|
Emmen
|
105972
|
340,56
|
3
|
|
Zwolle
|
105801
|
95,35
|
11
|
|
Ede
|
101700
|
318,29
|
3
|
|
|
|
|
|
|
|
|
inhabitants
|
km˛ land
|
no. inhabitants
/ha.
|
|
|
|
|
|
|
Amsterdam
|
1E+06
|
365,12
|
27
|
|
Rotterdam
|
989956
|
355,50
|
28
|
|
DenHaag
|
610245
|
187,50
|
33
|
|
Utrecht
|
366186
|
140,93
|
26
|
|
Eindhoven
|
302274
|
181,27
|
17
|
|
Leiden
|
250302
|
87,26
|
29
|
|
Dordrecht
|
241218
|
153,42
|
16
|
|
Heerlen
|
218078
|
109,22
|
20
|
|
Tilburg
|
215419
|
159,47
|
14
|
|
Groningen
|
191722
|
126,09
|
15
|
|
Haarlem
|
191079
|
76,67
|
25
|
|
Breda
|
160615
|
127,00
|
13
|
|
Amersfoort
|
154890
|
121,50
|
13
|
|
DenBosch
|
154368
|
118,55
|
13
|
|
Apeldoorn
|
153261
|
340,30
|
5
|
|
Nijmegen
|
152200
|
53,70
|
28
|
|
Enschede
|
149505
|
140,04
|
11
|
|
Arnhem
|
139576
|
126,50
|
11
|
|
GeleenSittard
|
127322
|
98,13
|
13
|
|
Maastricht
|
122070
|
57,01
|
21
|
|
Zwolle
|
105801
|
95,35
|
11
|
|
|
|
|
|
Fig. 956 Municipalities > 100,000 inhabitants
|
Fig. 957 Conurbations > 100,000 inhabitants
|
|
|
|
From these tables, it
appears that some conurbations (Heerlen and Geleen–Sittard) are
composed of municipalities smaller than 100,000 inhabitants, while a number of
municipalities (Almere,
Zaanstad,
Haarlemmermeer,
Zoetermeer, Emmen and Ede) with
more than 100,000 inhabitants are missing, partly because, due to commuting,
they have been included in the conurbation of a larger municipality nearby. Fig. 958 shows the Ordering of the
agglomerates in Fig. 957.
Going beyond The national order
In the Netherlands, two
large conurbations dominate the ordering. If Amsterdam had
2 million inhabitants, the
ordering would fit better into the formula. When we map the deviations from the
formula (Fig.
959), then Amsterdam or Rotterdam, and,
to a lesser extent, The Hague, are
incongruous. This can indicate an international position, which has its own
order. Following this line of thought, then, Utrecht falls within the national ordering.
|

|
|
|
|
Fig.
959 Deviations from the ordering
y = 1000000·x-0.767 in the higher regions
|
|
|
Compared to other continents
Compared
with Asia, Europe is not only small, but, in contrast to all other continents,
its population is much older (Fig.
960 en Fig.
961).
|

|

|
|
(1) Including Russia, excluding Turkey. (2)
Including Turkey.
|
|
|
Fig.
960 Number of residents per continent
|
Fig.
961 Age range per continent
|
|
|
|
Population development in the Netherlands
|

|

|
|
|
|
Fig. 962
How the Dutch population has developed (see also Fig. 840), using a polynomal trendline from Excel
|
|
|
When you make a chart in
Excel to show how the Dutch population has developed (omitting the years
between the 10s), you discover that, for a century, every 10 years, the
population has increased roughly by a million. Select a chart and click on the
toolbar ‘chart/add trendline’ and you will find the above menu (see also Fig. 425). If
you choose a third-degree polynomial and, from ‘options’, click on ‘show equation
in chart’, then you get the above result. A polynomial appears to fit in well
here, and allows interpolation between the available years, but it has no
rational linkage at all with reality. To find that kind of formulas is the task
of demography (see page 464). So,
it should not be used for extrapolation.
Population characteristics
After World War 2, the
number of people per household (which almost equates with ‘occupance per
dwelling’)
decreased from 5 to 2.3 and the expectation is that it will decrease even further.
From an urban point of view, this is an important figure because this halving
of occupancy meant that, for the same population, twice as many dwellings had
to be built (Fig.
963). Family dilution has mainly come about due to the increasing
number of single-family households (Fig.
964).
|

|

|
|
|
|
|
Fig.
963 Average number of people per
household
|
Fig.
964 Number of people per household
|
|
|
|
Ageing
The population continues to
age, but
the question is whether, under the new politics, the number of immigrants will continue to grow as was forecast in 2001.
|

|

|
|
|
|
|
Fig. 965
Changes in age range
|
Fig. 966
Proportion of first and second generation immigrants
|
|
|
|
Time utilisation
|

|

|
|
|
|
|
Fig. 967
Time utilisation in 1997
|
Fig. 968 Use
of free time in 1997
|
|
|
|
Daily population movements
The average total distances
travelled, mainly
by car, per person per day is fairly constant at 35 km (Fig. 969). Commuting accounts for almost 10 km of this distance (Fig. 970).
|

|

|
|
|
|
|
Fig.
969 Total distance travelled per means
of transport
|
Fig.
970 Distance travelled per motive and
means of transport
|
|
|
|
Removals
In 1999, 1,696,000 Dutch
people moved to another place of residence in the Netherlands.
More than a million of these changes of address were within the same
municipality (3 km radius), more than a quarter of a million within the same
province (30 km radius) and almost 0.4 million from one province to another
(300 km radius).
|
Removals in 1999 within
|
3km
|
30km
|
300km
|
total
|
|
|
1058000
|
267000
|
371000
|
1696000
|
|
|
See Fig. 971
|
See Fig. 972
|
See Fig. 973
|
|
|

|

|

|
|
Number of removals
|
|
Fig.
971 Municipal
|
Fig.
972 Provincial
|
Fig.
973 National
|
|
|
|
|
The
largest number of removals took place within and between the provinces South
and North Holland.
How many of each kind
On 1st
January 2000, in the Netherlands, there were approximately 6,588,000 homes, the
value of which totalled € 575,945,000,000, divided into categories, as shown in
Fig. 974
|
|
year
|
population x 1000
|
number of dwellings
|
|
support base in persons
|
Home
|
1999
|
15760
|
6390100
|
|
2.47
|
|
Own home
|
1999
|
15760
|
3303700
|
|
4.77
|
|
Rented home
|
1999
|
15760
|
3086400
|
|
5.11
|
|
Home with central heating
|
1999
|
15760
|
89700
|
|
176
|
|
Flat/appartment, etc.
|
1999
|
15760
|
1965000
|
|
8.02
|
|
End of terrace-/terraced house
|
1999
|
15760
|
2689900
|
|
5.86
|
|
Home with a garden or grounds
|
1999
|
15760
|
75600
|
|
208
|
|
Home with a garage and/or a carport
|
1999
|
15760
|
33600
|
|
469
|
|
A detached house
|
1999
|
15760
|
979400
|
|
16
|
|
A semi-detached house
|
1999
|
15760
|
755800
|
|
21
|
|
A 1 or 2-roomed home
|
1999
|
15760
|
580500
|
|
27
|
|
A 3-roomed home
|
1999
|
15760
|
1273800
|
|
12
|
|
A 4-roomed home
|
1999
|
15760
|
2164100
|
|
7.28
|
|
A 5-roomed home
|
1999
|
15760
|
1556300
|
|
10
|
|
A home with 6 or more rooms
|
1999
|
15760
|
815400
|
|
19
|
|
|
|
|
|
|
|
|
Fig.
974 Housing categories and their number in relation to the total
population of the Netherlands
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
So, on every 19 inhabitants
there was a dwelling with 6 or more rooms.
Price and age
From Fig. 975 and Fig. 976 you can determine the average
age and price of dwellings.
|

|

|
|
|
|
|
Fig.
975 Number of homes per year of construction
|
Fig.
976 Value of home per year of construction
|
|
|
|
Singles
rent, families buy mainly new houses
The majority of people in
the Netherlands live in accommodation that was built after World War II,
between 1960 and 1990 (Fig. 977). Single-person households are mainly accommodated in rented homes.
Couples usually buy their own living accommodation (Fig. 978).
|

|

|
|
|
|
|
Fig.
977 Occupancy per year of construction
|
Fig.
978 Occupancy in own or rented houses
|
|
|
|
Less energy companies and water boards
The number of water boards has decreased from 32 in 1990 to 20 in 1998.
However, the number of employees or cubic metres of water produced remained the
same (Fig.
981). As with agrarian firms, this indicates
concentration.
Decreasing energy and water production
|

|

|
|
Note 3: Including
power installations(>50 GWh per year), in the context of joint ventures,
exploited by energy distribution companies and industrial companies.
Note 4: Excluding
multi-utility companies.
|
|
|
|
|
Fig. 979 Production
value of utility companies
|
Fig.
981 Water production
|
|
|
|
Selective increase of facilities for health and welfare
|
Establishments for:
|
year
|
population
|
number
|
growth per year
|
support base
|
|
after-school care
centres
|
1998
|
15654
|
992
|
18%
|
15780
|
|
hostels caring for
vagrants and homeless people
|
1999
|
15760
|
228
|
5%
|
69124
|
|
host-family care
centres
|
1998
|
15654
|
189
|
1%
|
82826
|
|
half-day
crčches/nurseries
|
1998
|
15654
|
169
|
9%
|
92628
|
|
full-day crčches/nurseries
|
1998
|
15654
|
1749
|
16%
|
8950
|
|
family doctors’/
general practitioners’
(gps’) practises
|
2000
|
15864
|
4809
|
0%
|
3299
|
|
established general
practitioners (gp)
|
2000
|
15864
|
7217
|
1%
|
2198
|
|
childrens’
independently homes
|
1998
|
15654
|
789
|
4%
|
19841
|
|
homes for the mentally
handicapped
|
1999
|
15760
|
151
|
2%
|
104372
|
|
homes for the those
with sensory handicaps
|
1999
|
15760
|
12
|
-1%
|
1313352
|
|
community care centres
|
1999
|
15760
|
75
|
3%
|
210136
|
|
childrens’ hospitals
and hospices
|
1999
|
15760
|
13
|
1%
|
1212325
|
|
medical day centres for
infants
|
1999
|
15760
|
56
|
8%
|
281433
|
|
psychiatric hospitals
|
1999
|
15760
|
76
|
-1%
|
207371
|
|
dentists
|
1998
|
15654
|
7030
|
-1%
|
2227
|
|
nursing homes
|
1999
|
15760
|
334
|
0%
|
47186
|
|
care homes for the
elderly
|
1998
|
15654
|
1380
|
-1%
|
11344
|
|
crisis centres for
women
|
1999
|
15760
|
80
|
25%
|
197003
|
|
independent dispensing
chemists
|
1998
|
15654
|
1547
|
|
10119
|
|
hospitals
|
1999
|
15760
|
136
|
-2%
|
115884
|
|
|
|
|
|
|
|
|
Fig. 981 Number of health
facilities compared with the size of the Dutch population
|
|
|
|
|
|
|
|
Fig. 981 is a
table showing 20 different types of public health facilities. By
dividing the population by the number of facilities, a potential support base
emerges that indicates the number of inhabitants that would be needed to
support this type of facility. Due to an irregular, historically determined
distribution of the facilities and the factors determining their establishment
at a specific location, their distribution is, of course, unevenly concentrated,
which, in turn, means that the actual support base, locally, can also vary.
The growth figures for the
latest available year, compared with the year prior to that, give an indication
of the figures for the years to come, but, in the longer term, they must be
calculated more closely in the light of
rational expectations of their expected use.
More outdoor facilities for
young children and less (larger) for the elderly
Fig. 982 and Fig.
983 show the growth of facilities for children and
elderly not reflecting the number of users (dependent on growing Dutch
population), but rather the number of establishments.
|

|

|
|
|
|
|
Fig. 982 Development of facilities
for children
|
Fig. 983 Facilities for the elderly (care homes for the elderly)
|
|
|
|
Decreasing number of schools
|

|

|
|
Note 1: Number of departments.
Note 2: Including practical education.
Legend top down: primary, special, secondary,
technical and vocational training, technical and vocational guidance, higher
technical and vocational, scientific.
|
Note 3: University Preparatory
Education (vwo),
Senior General
Secondary Education (havo),
Junior General
Secondary Education (mavo),
Preparatory Vocational
Education (vbo) and
Learning Path
Supporting Education (lwoo)
|
|
Fig. 984 Development in
the number of schools
|
Fig. 985 The average
support base of Fig. 988
|
|
|
|
From Fout! Verwijzingsbron niet gevonden. you can learn
you need a conurbation of more than 1 000 000 inhabitants for a university,
a town of >100 000 inhabitants for technical and vocational schools, a
district of >10 000 inhabitants for secondary and special schools and a
neigbourhood of more than 1 000 inhabitants for a primary school.
Equal number of pupils
|

|

|
|
Note 1: Including
part-time education.
|
|
|
Fig. 986 Expected number
of pupils
|
Fig. 987 Establishments
and users of primary schools
|
|
|
|
An equal number of pupils
combined with the decreasing number of schools shown in Fout! Verwijzingsbron niet gevonden.,
means a development into larger schools.
Less (and larger) schools
(at a larger distance)
|
Establishments for:
|
year
|
population
|
number
|
growth per year
|
support base
|
|
primary education
|
1999
|
15760
|
7224
|
-1%
|
2182
|
|
day-release
learning path
|
1999
|
15760
|
70
|
-4%
|
225146
|
|
vocational
learning path
|
1999
|
15760
|
75
|
-7%
|
210136
|
|
higher
vocational education
|
1999
|
15760
|
65
|
-3%
|
242465
|
|
special
forms of education
|
1999
|
15760
|
1255
|
-2%
|
12558
|
|
secondary
education
|
1999
|
15760
|
635
|
-6%
|
24819
|
|
scientific
education
|
1999
|
15760
|
13
|
1%
|
1212325
|
|
|
|
|
|
|
|
|
Fig. 988 Number of educational facilities compared with the size of the
Dutch population
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
More cinemas and film theatres, more money for monuments and
historic buildings
|

|

|
|
Note
2: Including two drive-in cinemas
Note
3: Excluding non-specifically equipped performance rooms
|
|
Source: (Cinemas) Dutch Federation for Cinematography; (film theatres)
Dutch Film Theatre Association
|
Legend top-down: general buildings, dwellings, churches, charity
buildings, castles and estates, agricultural buildings, mills, civil
engineering works, urban facilities, remaining.
|
|
Fig. 989 Cinemas and film theatres
|
Fig. 990
Expenditures on historic building projects
|
|
|
|
Cinemas are just one
category of facilities for culture and recreation summarised in Fig. 991. There
you can conclude their number did not increase in 2000.
Facilities
for culture and recreation
|
Establishments for:
|
year
|
population
|
number
|
growth per year
|
support base
|
|
amusement hall l
|
1998
|
15654
|
420
|
|
37272
|
|
amenity park
|
1998
|
15654
|
35
|
|
447263
|
|
ballet theatre
|
1997
|
15567
|
2
|
-6%
|
7532471
|
|
cinema
|
1999
|
15760
|
461
|
0%
|
34187
|
|
cabaret theatre
|
1997
|
15567
|
20
|
2%
|
761849
|
|
casino or lottery
|
1998
|
15654
|
40
|
|
391355
|
|
creativity centre
|
1997
|
15567
|
63
|
|
247097
|
|
dance theatre
|
1997
|
15567
|
8
|
6%
|
2048304
|
|
dance theatre
|
1997
|
15567
|
13
|
-2%
|
1173400
|
|
zoo
|
1999
|
15760
|
27
|
|
583712
|
|
film theatre
|
1999
|
15760
|
57
|
-2%
|
276495
|
|
music and creative arts
centre
|
1997
|
15567
|
52
|
|
299367
|
|
hotel with 1000
over-night stays per year
|
1999
|
15760
|
29053
|
4%
|
542
|
|
academy of fine arts
|
1997
|
15567
|
244
|
|
63800
|
|
yacht harbour
|
1997
|
15567
|
400
|
3%
|
38918
|
|
camping grounds, holiday chalet complexes, youth and group accommodations
|
1999
|
15760
|
3595
|
-3%
|
4384
|
|
museum
|
1997
|
15567
|
942
|
1%
|
16526
|
|
mixed museum
|
1997
|
15567
|
19
|
|
819321
|
|
industrial and
technical museum
|
1997
|
15567
|
260
|
|
59873
|
|
fine arts museum
|
1997
|
15567
|
102
|
|
152619
|
|
historical museum
|
1997
|
15567
|
491
|
|
31705
|
|
natural history museum
|
1997
|
15567
|
50
|
|
311342
|
|
museum of ethnology and
folk history
|
1997
|
15567
|
20
|
|
778355
|
|
musicians’ performance
stage
|
1997
|
15567
|
50
|
1%
|
310514
|
|
music school
|
1997
|
15567
|
129
|
|
120675
|
|
muziektheater
|
1997
|
15567
|
44
|
4%
|
355413
|
|
theatre for operettas, musicals and revues
|
1997
|
15567
|
8
|
1%
|
1954030
|
|
horticultural gardens,
show gardens and arboretums
|
1999
|
15760
|
104
|
|
151541
|
|
different types of
performing platforms
|
1997
|
15567
|
4
|
-2%
|
3736106
|
|
place of performance
for ensembles
|
1997
|
15567
|
9
|
0%
|
1729679
|
|
place of performance
for improvised music
|
1997
|
15567
|
13
|
5%
|
1219356
|
|
place of performance
for large orchestras
|
1997
|
15567
|
6
|
1%
|
2731071
|
|
place of performance
catering for 300 concerts per year
|
1997
|
15567
|
189
|
1%
|
82409
|
|
puppet theatre
|
1997
|
15567
|
13
|
2%
|
1203642
|
|
open-air sports
facility
|
1997
|
15567
|
4090
|
|
3806
|
|
indoor sports facility
|
1997
|
15567
|
2115
|
|
7360
|
|
theatre
|
1997
|
15567
|
78
|
0%
|
200780
|
|
playhouse
|
1997
|
15567
|
48
|
-2%
|
321413
|
|
watersportclub
|
1997
|
15567
|
950
|
0%
|
16386
|
|
zeil- en surfschool
|
1997
|
15567
|
90
|
|
172968
|
|
swimming bath
|
1997
|
15567
|
710
|
0%
|
21926
|
|
swimming bath complex
|
1997
|
15567
|
140
|
3%
|
111194
|
|
open-air swimming bath
|
1997
|
15567
|
245
|
-2%
|
63539
|
|
indoor swimming bath
|
1997
|
15567
|
325
|
1%
|
47899
|
|
|
|
|
|
|
|
|
Fig.
991 Number of cultural facilities compared with the size of the Dutch
population
|
|
|
|
|
|
|
|
Facilities ordered by number, divided by population: support base
Throughout
the Yearbook 2001, numerous tables are included that mention the number of
established faclities for many organizations and branches. The numbers of 244
types of establishment are summarised in a downloadable Excel sheet allowing to adapt the figures into more recent years or to
determine their trend. Divided by the real or expected national population of
the relevant year the average support base needed for each type of facility is produced.
In Fig.
992 some of these facilities and their average population
support base are mentioned. So, on a next tab of the sheet you can make an
average programme for any urban area. However, some areas do have more swimming
pools than the average, others more theatres. The deviation from the average
offers a profile determining the identity of the place. Many facilities are
still missing, such as prisons, police stations, ministeries, embassies,
surrogate family homes, boarding schools, monasteries and convents, but these
can be added.
|

|
|
|
|
Fig.
992 244 types of establishment ordered by number and their support
base shown logarithmically
|
|
|
From this, one can see that,
for a population of 100,000 inhabitants, a ‘town’, most facilities can find a
sufficient support base. For those who would like to know more about these
urban facilities on the level of a town, Fig.
993 gives an enlarged picture.
Facilities sustainable on town level
|

|
|
|
|
Fig. 993 Ordering of facilities for 100,000 inhabitants
|
|
|
This graph has a certain
multi-staged characteristic. In the steep vertical parts, urban growth
apparently allows little growth in the level of facilities that it can offer.
For populations between 55,000 and 100,000 inhabitants, the number of types of
facility hardly increases at all. In the horizontal parts, a little growth can
deliver much more facilities. With 25,000 inhabitants (a village or large
district) one already has a support base large enough to support half the
number of known facilities. A 1000 inhabitants (neigbourhood) give support to
1/3 of the district facilities. To examine that lowest part from 10 000
inhabitants in more detail, Fig.
994 gives an enlarged picture.
District or village facilities
|

|
|
|
|
Fig. 994 Ordering of facilities for 10,000 inhabitants.
|
|
|
6.4.9
Businesses
|

|
|
|
|
Fig. 995 Business establishments in
1999
|
|
|
On 1st January 1999, there were 752,825 active businesses in the Netherlands, divided into the main categories as shown in Fig. 995. A number of these are more finely subdivided in the
paragraphs below.
Agriculture and Fisheries
In 1999 there were still more than 1 million active agrarian firms in the Netherlands
(see Fig.
996).
|
Establishments
for
|
year
|
population
|
number
|
growth per year
|
support base
|
|
agricultural, hunting and forestry firm
|
1999
|
15760
|
106815
|
|
148
|
|
fishery firm
|
1999
|
15760
|
745
|
|
21155
|
|
|
|
|
|
|
|
|
Fig. 996 Number of agrarian firms compared with the size of the Dutch
population
|
|
|
|
|
|
|
|
Larger farms
The increase in the scale of these firms can be seen in Fig. 997.
|

|
|
|
|
Fig. 997 The increase in the scale of agrarian firms
|
|
|
The scaling-up of individual farms while the surface remains equal
implies decrease of the number of farms (Fig.
998), but increase of the number of large farms (Fig. 999).
|

|

|
|
|
|
|
Fig. 998 The development in the order of size of agrarian firms
|
Fig. 999 The growth of agrarian firms larger than 100 ha. (with a radius
of 1 km)
|
|
|
|
The surface farms need
The surface areas in hectares in these charts have been recalculated
into radii used in urban architecture (Fig.
1000).
|
|
from
|
To
|
Radius
|
Number of firms
|
|
-
|
m2
|
m2
|
in m
|
1990
|
1995
|
1998
|
1999
|
2000
|
|
Without arable land
|
|
|
10
|
2714
|
2061
|
1691
|
1585
|
1769
|
|
0,01-< 1 ha
|
100
|
9999
|
30
|
10046
|
8453
|
7010
|
6515
|
6086
|
|
1-<
10 ha
|
10000
|
99999
|
100
|
49556
|
45253
|
41076
|
39613
|
37355
|
|
10-<100 ha
|
100000
|
999999
|
300
|
61906
|
56568
|
54038
|
52712
|
51042
|
|
100
ha of meer
|
1000000
|
9999999
|
1000
|
681
|
867
|
1058
|
1120
|
1231
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 1000 Areas in hectares recalculated into radii used in urban
architecture
|
|
|
|
|
|
|
|
|
|
|
Industry
|
Establishments for:
|
year
|
population
|
number
|
growth per year
|
support base
|
|
chemical
industry
|
1998
|
15654
|
327
|
1%
|
47872
|
|
clothing and fur industry
|
1998
|
15654
|
77
|
8%
|
203301
|
|
electrical apparatus industry
|
1998
|
15654
|
390
|
0%
|
40139
|
|
food-processing and drinks industry, tobacco processing industry
|
1998
|
15654
|
891
|
1%
|
17569
|
|
furniture and related industries
|
1998
|
15654
|
382
|
-3%
|
40980
|
|
glass, earthenware, cement and chalk industry
|
1998
|
15654
|
276
|
3%
|
56718
|
|
industry
|
1998
|
15654
|
6433
|
1%
|
2433
|
|
leather, leather goods and footwear industry
|
1998
|
15654
|
41
|
-7%
|
381810
|
|
machine and apparatus industry
|
1998
|
15654
|
915
|
3%
|
17108
|
|
metal products industry
|
1998
|
15654
|
1093
|
4%
|
14322
|
|
office-equipment and computer industry
|
1998
|
15654
|
24
|
-8%
|
652258
|
|
paper (goods) and carton (goods) industry
|
1998
|
15654
|
203
|
15%
|
77114
|
|
publishers, printers, reproduction
|
1998
|
15654
|
654
|
-1%
|
23936
|
|
rubber and synthetic-material processing industry
|
1998
|
15654
|
351
|
1%
|
44599
|
|
textile industry
|
1998
|
15654
|
178
|
-5%
|
87945
|
|
transport vehicles industry
|
1998
|
15654
|
332
|
-3%
|
47151
|
|
wooden, cork, and cane goods industry (excluding furniture)
|
1998
|
15654
|
194
|
5%
|
80692
|
|
|
|
|
|
|
|
|
Fig. 1001
Number of industrial branches compared with the size of the Dutch population
|
|
|
|
|
|
|
|
Building Industry
|
Establishments for:
|
year
|
population
|
number
|
growth per year
|
support base
|
|
building company
|
1998
|
15654
|
31459
|
1%
|
498
|
|
building company specialised in finishing off buildings
|
1998
|
15654
|
8514
|
4%
|
1839
|
|
building company specialised in b&u, gww, excluding
excavation
|
1998
|
15654
|
14268
|
0%
|
1097
|
|
building company specialised in preparing building sites
|
1998
|
15654
|
1095
|
3%
|
14296
|
|
building company specialised in hiring out building machinery and
personnel
|
1998
|
15654
|
479
|
-1%
|
32681
|
|
building company specialised in installation
|
1998
|
15654
|
7103
|
-1%
|
2204
|
|
|
|
|
|
|
|
|
Fig. 1002
Number of companies in the building industry compared with the size of the
Dutch population
|
|
|
|
|
|
|
|
Retail and inland Trading
|
Establishments for:
|
year
|
population
|
number
|
growth per year
|
support base
|
|
florists
|
1998
|
15654
|
3900
|
|
4014
|
|
bookshops
|
1998
|
15654
|
1100
|
|
14231
|
|
building material retailers
|
1998
|
15654
|
1300
|
|
12042
|
|
computer retailers
|
1998
|
15654
|
500
|
|
31308
|
|
pet shop
|
1998
|
15654
|
1500
|
|
10436
|
|
diy retailers
|
1998
|
15654
|
3900
|
|
4014
|
|
chemists
|
1998
|
15654
|
1700
|
|
9208
|
|
chemists selling medical goods, perfumes and cosmetics
|
1998
|
15654
|
2100
|
|
7454
|
|
durable consumer goods and other forms of consumption -
|
1998
|
15654
|
50500
|
|
310
|
|
cycle shops
|
1998
|
15654
|
2300
|
|
6806
|
|
audio and amplification equipment retailers
|
1998
|
15654
|
700
|
|
22363
|
|
glass, porcelain and earthenware retailers
|
1998
|
15654
|
700
|
|
22363
|
|
greengrocers
|
1998
|
15654
|
2200
|
|
7116
|
|
wholesalers
|
1998
|
15654
|
61496
|
|
255
|
|
wholesale suppliers of business requisites and packaging
|
1998
|
15654
|
2524
|
|
6202
|
|
wholesale suppliers of raw materials and semi-fabricated goods
|
1998
|
15654
|
10420
|
|
1502
|
|
wholesale suppliers of wood, building materials, iron and metal goods
|
1998
|
15654
|
5727
|
|
2733
|
|
wholesale suppliers of machinery, apparatus, accessories and parts
|
1998
|
15654
|
13899
|
|
1126
|
|
wholesale suppliers of non-food consumer goods
|
1998
|
15654
|
21193
|
|
739
|
|
wholesale suppliers of food, spices and energisers
|
1998
|
15654
|
7733
|
|
2024
|
|
(textile) handicrafts shop
|
1998
|
15654
|
600
|
|
26090
|
|
household goods retailers
|
1998
|
15654
|
900
|
|
17394
|
|
household linnen retailers
|
1998
|
15654
|
100
|
|
156542
|
|
ironmongery (hardware) and tool shop
|
1998
|
15654
|
700
|
|
22363
|
|
jewellers
|
1998
|
15654
|
1500
|
|
10436
|
|
jewellers selling costume jewellery
|
1998
|
15654
|
300
|
|
52181
|
|
cheese shop
|
1998
|
15654
|
600
|
|
26090
|
|
stationers
|
1998
|
15654
|
2000
|
|
7827
|
|
kitchen equipment retailers
|
1998
|
15654
|
500
|
|
31308
|
|
dress fabric retailers
|
1998
|
15654
|
400
|
|
39135
|
|
lamp and lighting retailers
|
1998
|
15654
|
400
|
|
39135
|
|
retailers of leatherware and travel goods
|
1998
|
15654
|
300
|
|
52181
|
|
lingerie retailers
|
1998
|
15654
|
700
|
|
22363
|
|
furniture shop
|
1998
|
15654
|
1700
|
|
9208
|
|
furniture shop with home textiles, lighting goods and floor coverings
|
1998
|
15654
|
5000
|
|
3131
|
|
musical instrument retailer
|
1998
|
15654
|
400
|
|
39135
|
|
sewing and knitting machine shop
|
1998
|
15654
|
200
|
|
78271
|
|
opticians
|
1998
|
15654
|
1100
|
|
14231
|
|
perfumery
|
1998
|
15654
|
300
|
|
52181
|
|
poulterers
|
1998
|
15654
|
300
|
|
52181
|
|
health-food shop
|
1998
|
15654
|
300
|
|
52181
|
|
shoe shop
|
1998
|
15654
|
1600
|
|
9784
|
|
shoe shop with leatherware and travel goods
|
1998
|
15654
|
1900
|
|
8239
|
|
butchers
|
1998
|
15654
|
3700
|
|
4231
|
|
off-licence
|
1998
|
15654
|
1100
|
|
14231
|
|
sweet shop
|
1998
|
15654
|
400
|
|
39135
|
|
toy shop
|
1998
|
15654
|
700
|
|
22363
|
|
sports and camping-gear retailers
|
1998
|
15654
|
1600
|
|
9784
|
|
supermarket, grocers
|
1998
|
15654
|
3500
|
|
4473
|
|
tobacconists
|
1998
|
15654
|
1700
|
|
9208
|
|
textile supermarket
|
1998
|
15654
|
400
|
|
39135
|
|
textile retailers
|
1998
|
15654
|
9900
|
|
1581
|
|
garden centre
|
1998
|
15654
|
600
|
|
26090
|
|
paint and wallpaper shop
|
1998
|
15654
|
700
|
|
22363
|
|
fishmongers
|
1998
|
15654
|
700
|
|
22363
|
|
carpet shop
|
1998
|
15654
|
500
|
|
31308
|
|
foods, spices and energisers
|
1998
|
15654
|
16300
|
|
960
|
|
shop
|
1998
|
15654
|
66800
|
|
234
|
|
shop selling glass, porcelain and earthenware; household articles or
toys
|
1998
|
15654
|
2300
|
|
6806
|
|
shop selling durable household goods
|
1998
|
15654
|
3800
|
|
4120
|
|
photographic shop
|
1998
|
15654
|
800
|
|
19568
|
|
retailers of medical and orthopedic goods
|
1998
|
15654
|
100
|
|
156542
|
|
retailers of kitchen apparatus, other electrical goods and audio
equipment
|
1998
|
15654
|
2400
|
|
6523
|
|
interior decorators, general assortment
|
1998
|
15654
|
1300
|
|
12042
|
|
home furnishing retailers
|
1998
|
15654
|
1100
|
|
14231
|
|
|
|
|
|
|
|
|
Fig. 1003 Number of
trading companies compared with the size of the Dutch population
|
|
|
|
|
|
|
|
Inland Services
|
Establishments for:
|
year
|
population
|
number
|
growth per year
|
support base
|
|
job centres/employment bureaus for assessing, attracting and selecting
personnel
|
1998
|
15654
|
1300
|
|
12042
|
|
architectural and technical design and drawing consultancy
|
1998
|
15654
|
13200
|
|
1186
|
|
suppliers of spare-parts and accessories for cars
|
1998
|
15654
|
400
|
|
39135
|
|
car servicing company
|
1998
|
15654
|
3500
|
|
4473
|
|
tyre servicing company
|
1998
|
15654
|
200
|
|
78271
|
|
job pools (job-opportunity projects)
|
1998
|
15654
|
100
|
|
156542
|
|
garage for
industrial vehicles, trailers
|
1998
|
15654
|
800
|
|
19568
|
|
petrol station
|
1998
|
15654
|
1600
|
|
9784
|
|
bookkeepers, accountants
|
1998
|
15654
|
13200
|
|
1186
|
|
cafe
|
1998
|
15654
|
12700
|
|
1233
|
|
cafeteria, snack bar
|
1998
|
15654
|
10400
|
|
1505
|
|
bodywork repair firms
|
1998
|
15654
|
1500
|
|
10436
|
|
catering (w.o.
party-catering)
|
1998
|
15654
|
1600
|
|
9784
|
|
car tyre wholesalers and trade intermediaries (middle men)
|
1998
|
15654
|
300
|
|
52181
|
|
wholesalers and trade intermediaries in spare-parts and accessories
for cars
|
1998
|
15654
|
1500
|
|
10436
|
|
hotel, b&b (bed & breakfast),
conference centre
|
1998
|
15654
|
2500
|
|
6262
|
|
camping ground
|
1998
|
15654
|
1700
|
|
9208
|
|
camping ground or holiday chalet park, bungalow park
|
1998
|
15654
|
2800
|
|
5591
|
|
cantine (incl. contract catering)
|
1998
|
15654
|
800
|
|
19568
|
|
cantine and catering
|
1998
|
15654
|
2400
|
|
6523
|
|
hairdressers
|
1998
|
15654
|
11300
|
|
1385
|
|
testing or checking office
|
1998
|
15654
|
500
|
|
31308
|
|
dry cleaners
|
1998
|
15654
|
1400
|
|
11182
|
|
motor cycle retailers
|
1998
|
15654
|
500
|
|
31308
|
|
private car garages
|
1998
|
15654
|
13000
|
|
1204
|
|
advertising agency
|
1998
|
15654
|
12200
|
|
1283
|
|
restaurant
|
1998
|
15654
|
9700
|
|
1614
|
|
restaurant, cafeteria, snack bar
|
1998
|
15654
|
20400
|
|
767
|
|
beauty salon, pedicure or manicure
|
1998
|
15654
|
13600
|
|
1151
|
|
cleaners for buildings and transport vehicals
|
1998
|
15654
|
6400
|
|
2446
|
|
temporary employment agency
|
1998
|
15654
|
900
|
|
17393.55
|
|
holiday chalets or bungalow park
|
1998
|
15654
|
1100
|
|
14231
|
|
|
|
|
|
|
|
|
Fig. 1004
Number of service-providing firms compared with the size of the Dutch population
|
|
|
|
|
|
|
|
Traffic, Transport and
Communication
|
Establishments for:
|
year
|
population
|
number
|
growth per year
|
support base
|
|
inland shipping company
|
1998
|
15654
|
4200
|
-1%
|
3727
|
|
forwarders, ship-brokers or chartering brokers
|
1998
|
15654
|
1620
|
-5%
|
9663
|
|
road freight haulage companies
|
1998
|
15654
|
9750
|
5%
|
1606
|
|
loading, unloading and trans-shipment companies
|
1998
|
15654
|
320
|
7%
|
48919
|
|
airports and other air transport services
|
1998
|
15654
|
30
|
0%
|
521806
|
|
air transport companies
|
1998
|
15654
|
10
|
0%
|
1565419
|
|
storage/warehousing companies
|
1998
|
15654
|
510
|
2%
|
30694
|
|
pipeline transporting companies
|
1998
|
15654
|
10
|
0%
|
1565419
|
|
post, courier services and telecommunications companies
|
1998
|
15654
|
2520
|
11%
|
6212
|
|
travel agencies
|
1998
|
15654
|
1030
|
-5%
|
15198
|
|
travel organisations (tour operators)
|
1998
|
15654
|
550
|
0%
|
28462
|
|
taxi firms
|
1998
|
15654
|
2520
|
-7%
|
6212
|
|
tourist information offices
|
1998
|
15654
|
440
|
19%
|
35578
|
|
tram and bus/coach companies
|
1998
|
15654
|
290
|
-6%
|
53980
|
|
land transport service companies
|
1998
|
15654
|
390
|
8%
|
40139
|
|
water transport service companies
|
1998
|
15654
|
240
|
9%
|
65226
|
|
weighing and measuring companies
|
1998
|
15654
|
110
|
-15%
|
142311
|
|
ocean-going shipping companies
|
1998
|
15654
|
510
|
-9%
|
30694
|
|
|
|
|
|
|
|
|
Fig. 1005
Number of transport companies compared with the size of the Dutch population
|
|
|
|
|
|
|
|
Definition
We define environment as ‘the set of conditions for life’
(Hendriks 1993). In this definition, both
‘conditions’ and
‘life’ can
be more closely specified. By means of substitution, more precise concepts of
the environment emerge, such as ‘the set of physical conditions required for
plant life’ or ‘the set of managerial conditions required for animal life’.
|
conditions
|
life
|
|
managerial
|
human
|
|
cultural
|
|
economic
|
animal
|
|
technical
|
|
ecological
|
plant
|
|
mass/time/spatial
|
|
|
|
Fig.
1006 Substitution possibilities in
defining environment
|
|
|
One can presume a sequence of conditionality in both columns (one cannot imagine management
without a culture to carry it; one cannot imagine animal life without plant
life, etc.). That becomes an issue as soon as one attempts to weigh the importance
of different environments against each other.
Different environments
However, also without the above presumption, these substitution
possibilities allow 18 more precise environmental definitions to be made. We
can summarise managerial, cultural and economic conditions as ‘societal
conditions’ and
the remaining ones as ‘physical conditions’. In this way, the number of environmental
definitions is reduced to 6. Plant and animal life-forms can be summarised as
‘non-human life-forms’ (12 environmental definitions), but they can also be
more precisely distinguished in the five ‘kingdoms’ currently recognised in biology,
with homo sapiens as the sixth category, bringing the number of
environmental definitions up to 42. This figure increases further, if we define
a species-specific environment for every species.
Physical conditions for human life
The current environmental definition of ‘physical surroundings of
society’ (more or less according to Udo de Haes in Boersema,
Peereboom et al. (1991) ) is just one of the
environmental definitions identified above.
|

|

|
|
|
|
|
Fig. 1007 Environment
according to Udo de Haes
|
Fig.
1008 Environment in technical sense
|
|
|
|
Udo de Haes’ formulation can be expressed as
a technical definition, by reducing it to ‘the set of physical conditions for
human life’. However, by doing this, the ‘mutual relationship’ between physical
surroundings and society becomes less ‘causal’ than those postulated as a condition
for human life. In other words, an asymmetry is assumed in the
‘relations’ between society and the physical environment.
After all, one cannot imagine people, let alone a society, without
physical surroundings, but one can imagine physical surroundings without
people. A physical environment is thus a technical condition for human
and societal life. Because of this, a specific physical environment is not the cause
of one or other form of human life[319], such as physical determinism at
the end of the last century would have led one to believe. Human beings adapt themselves
to existing conditions (adaptation) or change physical conditions
(accommodation) exploring its possibilities, but they can
not surpass its boundary conditions[320].
Conditions determine what is possible
Technical conditions are
related to what is possible, while causal relations have
a bearing on what is probable within that possibility. After all, what is
probable is,
by definition, also possible, but not everything that is possible is
also probable. So, there are improbable possibilities. One cannot predict these, so one has to design them.[321]
In the same way as the set of probable futures is a subset of possible
ones, the set of causes is a subset of conditions. Every cause is a condition
for something to happen, but not every condition is also its cause (a last
added condition for something to happen). So, there are more conditions than
causes, often operating as (ceteris paribus) suppositions hidden in causal
reasoning. Economy can be studied as long as the dykes do not burst, that is
such a hidden supposition (a technical condition not discussed) of economic
reasoning. In everyday life we are not aware of the many background conditions making
life possible.
Conditions making other conditions possible.
The foundation of a house can be a condition for that house, but in the
same time not its cause. The cause may be an economic one. On its turn a house
can be a condition for a household (it can create the possibility of a
household) but in the same time not causing it. According to the technical
definition of environment the house belongs to the environment of the household
making a household possible like the foundations belong to the environment of
the house on their turn making the house possible. So, there can be a sequence
of conditions making each other possible and a design is summing up these
technical conditions in a drawing.
Design makes possible, not probable
The above argumentation gives an exact indication of what the
responsibility of the designer is,
in contrast to that of the researcher. If (s)he designs a home, (s)he must not
do it in a way that presumes its occupancy by a specific type of household -
that would be an encroachment on the freedom of choice of the future occupants
– her or his design must keep possibilities open for its occupancy by different
sorts of households.
The same sort of dilemma exists in ecology. It is not always possible to
forecast where a certain ecosystem will come into existence. Many subtle
factors and initial conditions determine its emergence. We cannot cause
an ecosystem. We only can create the conditions under which a set of
ecosystems can exist, while others can not.
With this conditional
environmental definition, environmental problems are simply ‘missing conditions
for life.’ These problems now can be specified further in a technical sense
(see Fig. 1006), by
specifying ‘conditions’ (physical or social) and ‘life’ (human or other).
For the other forms of life,
human beings have become a plague, the cause of many environmental problems.
But it is also dangerous for the species itself. In a life time the human
population has doubled. The agricultural surface is in danger to be halved by
desertification, erosion and contamination. It will decrease even further if we
use its products as fuel for our cars. So, you can count on a quarter of the
grain area per person compared to the conditions a century ago. The
productivity per ha. increased more than twice, but that progress stagnated
(see Fig. 1009). Many
environmental problems seem marginal compared to that doom scenario.
|

|
|
|
|
Fig. 1009 Doom scenario: increasing human
population, decreasing agricultural surface
|
|
|
Using the technical definition
chosen here, environmental problems are easily definable as missing conditions
for life, and environmental regulations as actions designed to provide for
them. These do not have to be the same as the eventually lost conditions, they
also can be new conditions.
Creating new conditions
instead of restoring old ones
For a technical definition
environmental measures do not need to be directed only on restoring an earlier
situation (that is often an illusion by the actual human population), they can
also create new life-sustaining conditions (see 6.5.6, page 571). This
perception of environmental problems distinguishes designers from researchers.
The relations between organisms and their surroundings (including that of the
human society and its physical environment) can still be only very partially
understood. However, they do not need to be completely understood to restore
lost conditions, and to create new ones.
Taking away the causes is
not enough
In addition, many environmental
problems cannot be solved any more by removing the
cause.
We cannot return any more to the
situation of 10,000 years ago. At that time, there were an estimated 3 million
people on earth and at least 50,000 species more than there are now.
And, because we cannot go back,
we have to do more than just maintain the old environmental conditions. We have
to create new ones.
What is meant by ‘conditions’ and
‘life’, can turn out to be different when put into practice. For example, the
abiotic conditions for plant life are contained in an environmental concept
that is different from those for animal life. In particular, the construction
of ecological connections creates new abiotic conditions for certain forms of
animal life. Viewed from their predominantly botanical understanding of the
environment, the authoritative plant ecologists Westhoff and Van Leeuwen (see page 396), value
separation more than connection by ‘ecological infrastructure’.
One can define abiotic, biotic,
technical, economic, cultural and managerial conditions for different forms of
plant, animal and human life (see Fig. 1006). General
technical environmental definitions of these different substitutions form just
as many environmental concepts, in which apparently conflicting opinions about
environmental problems and regulations are brought to the fore.
It is thus impossible to talk
about ‘the environment’ in general, and to put a general stamp of
‘environmentally friendly’ on one or the other regulation. Every
interference with the surface of the earth increases the possibilities of the
one species, to the detriment of other ones.
In agriculture, for
instance, we create optimal conditions over enormous areas of land (by
fertilisation, hydraulics, etc) for a few plant species, with the result that,
with such strong competition, every other species is eliminated. In urban
architecture, we optimise in favour of the human species and, within that, for
each location, according to certain societal categories. Thus, for each
intervention, we must specify which environment we are talking about.
In that perspective, we can now
define urban design and architecture as supplying, research- and design-based
conditions for human life by constructing buildings and organising space
(whether or not on a larger scale than that of a single building). Urban and
architectural problems consist of the (future) absence
of those conditions. The aim of urban and architectural research is to draw attention to,
anticipate or formulate in a programme these (missing) conditions. Therefore,
it includes not only anticipatory, explanatory and problem-indicative research,
but also design research and effect analysis beforehand (ex ante) and
evaluating research after completing the construction (ex post). The aim
of urban and architectural design is to present these conditions in
a realisable spatial relationship.
Environment is the set of conditions for life in general. Ecology is the research into the probability
of these conditions, and technical ecology is the (design related) research
into their possibility. Environmental planning is the provision of conditions
for life in general by means of research, design and policy (of course, as far
as these can be appreciated by human beings), viewed from the higher scale
levels to the lower ones (an inward-directed approach). In a similar way, environmental technical design is viewed from the lower scale
levels to the higher ones (an outward-directed approach).
With respect to the environment,
two standpoints, one of them anthropocentric and the other ecocentric, can be discerned. The first standpoint should view every aspect from
the point of view of human beings (nature as part of culture, see Fig. 1010), and the
second one, from the point of view of ‘nature’ (culture being part of it). As
‘nature’ is a human concept, the debate between anthropocentrists and
ecocentrists, that flares up once in ten years or so, invariably veers in
favour of the anthropocentrists. Thus, an ‘ecocentric standpoint’
includes only that part of the anthropocentric standpoint that attempts to
distance itself from human biases (έποχη,
epochč) in depicting and organising the environment (the conditions for life).
Due to this, the concept ‘anthropocentric’ has, in fact, become useless,
because as long as animals and plants are unable to speak an understandable and
convincing language, every standpoint is, by definition, anthropocentric.
|

|

|
|
|
|
|
Fig. 1010 Culture (C) and nature (N)
|
Fig. 1011 Conditional or operational approach
|
|
|
|
There are direct requirements
for human life which, if missing, cause loss of comfort or
even the death of people, and indirect requirements (such as the
existence of plants and animals) that, should they be missing, would adversely
affect these direct requirements. The existence of direct requirements for life
is thus linked to indirect requirements and, in turn, these are linked to
requirements that lie even further away (conditional links). For example, for many organisms, the necessary existence of oxygen in
the air is, itself, indirectly dependent on the existence of photosythesis by
plants. It is these indirect requirements that are often either easier to
influence by conditional design or (if they have been irretrievably
lost) by providing a new form, than to ‘tackle’ the missing direct requirement operationally
as being the ‘cause’ of the problem (see Fig. 1011).
A quiet study room can be a
requirement for studying. Noise from neighbours leads to the problem that this
direct requirement for studying is destroyed. Indirect conditions that can
restore this direct requirement can, in this case, be: adopting a complementary
living rhythm (so that the noise occurs at times when no one is studying),
thick walls or quiet neighbours. Noise from neighbours can thus be solved in
more ways than just by ‘removing the cause’.
By providing missing direct
requirements (to solve environmental problems) one can, in addition, adversely
affect other (mostly indirect) conditions. In building a house, one provides,
in a direct way, requirements (an ‘environment’) for human life, but, by so
doing, one adversely affects the environment for other life forms and thereby
perhaps the indirect conditions for human life. Thus, not only living
requirements, but also environmental measures (the provision of certain
conditions), are conditionally linked with each other.
For example, to save energy,
there is no sense in letting sun enter the house if that house does not stand
in the sun, but, in reverse, there is. If the last-mentioned condition is not
met, then it would be senseless to provide the first-mentioned requirement.
Environmental measures can become each others’ conditions or restrictions,
without, however, also being each others’ direct cause.
Environmental problems (missing conditions) have a conditional link with
each other in this way. After all, one environmental problem can facilitate
another one, without directly causing it. Eliminating the direct causes
(operationally) without analysing the condiotions, followed by creating
(conditionally) all related requirements for success has often be shown to be
ecologically counterproductive.
For example, one cannot bring a
manure-polluted drainage ditch back to its original state by stopping the
manure pollution as Nienhuis (1993) and Hekstra, Strien et al. (1993) show. In the short term, manure pollution is irreversible. The same
sort of problem occurs in medical science: a complaint appears to have a direct
cause, but the true cause may lie in shortages elsewhere in the body, so that,
unexpectedly, one of the conditions of the body that would otherwise ensure
that this sort of complaint does not manifest itself, is not met.
Environmental strategies are combinations of environmental
regulations, such that they enable and even strengthen each other, both in the
time taken and in the sequence of requirements, without creating new problems. Environmental
tactics is one of the locally or
temporarily (politically, culturally, economic, technically) adapted effects of
the strategy to the various situations.
6.5.2
Emissions
In this section, a number of technical aspects of environmental hygiene are
brought to the fore that are important for making short reports on
environmental effects and
environmental policy plans. There is much
literature about this subject primarily summarised in Boersema, Copius
Peereboom et al. (1991) to be completed with recent figures from RIVM
(2001).
Environmental hygiene, spatial planning and nature conservancy are
policy sectors concerned with the unwanted side-effects of human activities. In
spatial planning and nature conservancy, in the first place, this has to do
with the mechanical effects such as management, disruption, and small and large
interventions in nature and space. Environmental hygiene is mainly concerned
with material and energetic effects, among others, on materials, people, other
organisms, systems and entire geographical areas, including nature reserves.
In order to be able to estimate the unwanted side-effects of all sorts
of activities in a
given location, beforehand, it is best to divide these activities into living,
traffic, nature and agriculture, businesses and incidental activities. These
categories can be subdivided into a multiplicity of activities for which, for
each activity, emission factors are
known. By multiplying these factors by the number of inhabitants, jobs, or km2
, one can gain an impression of the emissions. This emission is
dispersed by air, water, the ground or other dispersion agents, and eventually
has a negative effect on materials, people or other organisms. These can be
summarised in the following diagram:[322]
|
economic activity---->
|
direct effect of emission ---->
|
indirect effect of transmission
---->
|
end-effect,
exposure
|
|
SOURCES
(page 553)
1. Homes
2. Traffic
3. Agriculture
4. Businesses
5. Incidents
|
EMISSIONS
(page 555)
1. Inorganic
2. Energetic
3. Mechanical
4. Information
5. Potential emissions
|
DISPERSED BY (page 559)
1. Air
2. Water
3. The ground
4. Food chains
5. Transport
|
OBJECTS
(page 563)
1. Materials
2. People
3. Other organisms
4. Systems
5. Locations
|
|
|
|
Fig.
1012 The chain of environmental
effects
|
|
|
In this table, no account is taken of unwanted socio-economic
side-effects. All that is given is a checklist to assess the environmental
effects. The nature of sources, emissions,
dispersing media and objects is dealt with in more detail, respectively, in
pages 553 - 563.
By estimating the expected emission, transmission, immission and
exposure, one can make a report of the environmental effect for an activity or
for an entire area. However, in such a report, no policy will still have been
formulated to restrict these effects.
A policy to restrict environmental effects
A policy of that kind must weigh-up the unwanted side-effects against
the useful effect of the intended activity, or of the situation that has come
into being, which can then be expressed in an environmental policy plan. A similar
consideration occurs due to standardisation. Standards to
reduce the damage that many objects suffer due to different human activities,
originate in these objects. Initially, it can be established where the limits
of damaging influences need to be set, in order to prevent that particular
object from suffering an adverse effect.
Standards
This can lead to quality standards being
set for the ground, water and air, that, in turn, lead to the setting of limits
for emissions from a wide range of activities. Finally, one can bring about
changes in the harmful activities themselves by linking the processing, the
product, or the particular establishment as a whole, to standards and
regulations. These are summarised in Fig. 1013[323].
|
STANDARDS, applied to:
|
|
the source
|
the emission
<----
|
the dispersing medium
<----
|
the object
<----
|
|
product standards processing standards
|
emission standards
- emission ceilings
|
quality standards
|
exposure and immission standards
|
|
EXAMPLES OF NON-NUMERICAL STANDARDS (‘Policy starting-points’)
|
|
‘Avoiding at the source’ (of the emission)
|
‘Combating at the source’ (of the emission)
‘Best technical means’
‘Most practical means’
|
‘standstill’ principle
|
‘no effect’
‘no adverse effect’
|
|
EXAMPLES OF NUMERICAL STANDARDS
|
|
Lead content of petrol
|
max. 99.2 metric ton CO2 per year in the Netherlands
|
average % of oxygen in the water
|
EPEL value
|
|
|
|
Fig. 1013 Standardising to reduce adverse effects
|
|
|
All standards contain a policy-based consideration of the useful effect
of various activities compared with their unwanted side-effects. This is an
economic consideration, which is examined further in Section 6.5.5, page 568.
This standardisation, intended as a feed-back system on human activities
in order to prevent negative side-effects, must, of course, be achieved by
sanction possibilities.
The Environmental Management Law offers the integral legal framework to
accommodate these standards. The international, national, provincial and
municipal environmental policy plan can
play an important role in this. Whether the standards in the environmental
policy plan must be adapted beforehand (by a licencing system), or afterwards (by environmental
accountancy) is not yet of importance for the technical
aspects of environmental hygiene. In both cases, these remain the same.
For the registration of emissions in an area, more facts about the
sources are necessary.They can be gained according to Fig. 1014 (a further elaboration of Fig.
1012)
|
Sources
|
Subdivision
|
|
1. housing, temporary-stay
recreation
|
1.1 households
1.2 encroachment onto public space
1.3 public green areas
|
|
2. traffic, infrastructure
|
2.1 cars and other petrol-powered vehicals
2.2 routes used for transporting dangerous substances
2.3 railways and other electrically powered routes
2.4 shipping
2.5 airways
2.6 cables and pipelines
2.7 beam transmissions (e.g. for radio and tv)
|
|
3. nature
agriculture, forestry,
nature recreation
|
3.1 natural areas
3.2 forestry
3.3 arable farming
3.4 glasshouse cultivation (incl. mushrooms)
3.5 open-air horticulture and fruit growing
3.6 animal husbandry, fisheries
|
|
4. business, day recreation
|
4.1 mineral exploitation
4.2 historical manual skills
4.3 industry
4.4 public utility companies
4.5 building industry
4.6 services
|
|
5. incidental activities
|
|
|
|
Fig.
1014 Overview of the sources
|
|
|
In1977, the total emissions for
all provinces in the Netherlands were estimated by means of collective
registration, supplemented by individual registration. For example, for Gelderland,
the emission registration for the four most important emissions gave the
picture of Fig. 1015[324].
|
gram per day
|
Carbon monoxide
CO
|
Sulphur dioxide
SO2
|
Nitrogen oxides
NOx
|
Hydrocarbons
CxHy
|
per:
|
|
Housing
|
12
|
4
|
6
|
13
|
inhabitant
|
|
Traffic
|
200
|
8
|
54
|
48
|
inhabitant
|
|
Nature
|
|
869
|
32
|
690
|
km2
|
|
Glastuinbouw
|
362
|
1346
|
317
|
43
|
job
|
|
Glasshouse cultivation
|
107
|
5
|
5
|
35
|
job
|
|
Firms
|
180
|
588
|
266
|
393
|
job
|
|
|
|
Fig.
1015 Four important emissions per
source category
|
|
|
The figures given above are clearly out-of-date, but the type of table
made for different years provides comparative material for assessing policy.
For the benefit of an initial global reference for emission factors for a
particular area, one should use a more recent version of such figures (http://arch.rivm.nl/environmentaldata/).
Combustion emissions and other types of emission
Emissions occur due to the processing of fuels or raw materials. This
causes combustion emissions and
process emissions, respectively. Energy saving could lead to
a significant reduction in combustion emissions. The following table gives some
insight into the relation between both types of emission during the 1970s.[325]
|
|
Combustion emissions
|
Process emissions
|
total
|
|
1Tg = 1000 000 000 kg = 1 mln ton
|
g/inhabitant/day
|
g/inhabitant/day
|
Tg/year*
|
|
carbon dioxide
|
CO2
|
8920
|
90
|
46.04
|
|
carbon monoxide
|
CO
|
286
|
49
|
1.71
|
|
nitrogen oxide
|
NOx
|
108
|
6
|
0.58
|
|
sulphur dioxide
|
SO2
|
70
|
8
|
0.40
|
|
hydrocarbons
|
CxHy
|
33
|
25
|
0.30
|
|
aerosols, dust, soot
|
|
20
|
0.13
|
|
|
hydrated calcium sulphate (gypsum)
|
CaSO4
|
|
427
|
|
|
salt
|
NaCL
|
|
67
|
0.34
|
|
sulphuric acid
|
H2SO4
|
|
22
|
0.11
|
|
|
|
Fig. 1016 Relation between combustion
emissions and process emissions
|
|
|
Types of emission and environmental stress
To estimate the nature of the end effect and the manner of dispersal,
the emissions need
to be distinguished from each other, either by source or by groups of source,
as in Fig. 1017 (an elaboration of Fig. 1012).
|
Types of emission
|
Subdivision
|
Examples
|
|
1. inorganic emissions
|
1.1 metallic
1.2 other inorganic
|
copper, lead, mercury
CO, SO2, NOx
|
|
2. organic emissions
|
2.1 pure
2.2 halogenic
2.3 oxygenic
2.4 nitrogenic
2.5 sulphuric
2.6 metallic
2.7 other inorganic
|
methane, toluene, benzene
vinyl chloride
alcohols, esters
amino acids
thiols
organic mercury
organic phosphorus
|
|
3. mixtures
|
3.1 complex mixtures
3.2 aerosols
3.3 solid waste
3.4 microbic
|
BZV (biological oxygen consumption), CZV (chemical oxygen consumption), kjeldahl (method for measuring nitrogen)
fly ash, industrial waste
tetanus, botulism
|
|
4. energetic emissions
|
4.1 heat
4.2 sound
4.3 radiation, magnetic
4.4 radiation, radioactive
4.5 magnetic field
|
cooling-water
traffic, industry
light, infra-red, ultra-violet, radar, ether waves
alpha-, beta-, gamma-
high-voltage transmission lines
|
|
5. mechanical emissions
|
5.1 disturbance
5.2 small interruptions
5.3 substantial interruptions
|
treading on the ground, mowing, vibrations, up-rooting, digging
ploughing, vandalism, clearing ground, building
explosions
|
|
6. information
emissions
|
6.1 visual
6.2 olfactory
6.3 others
|
horizon pollution
bad smells
misleading sounds
|
|
7. potential emissions
|
7.1 emission reduction
7.2 risk
7.3 variation in emissions
|
cloth filter, sedimentation plant, lpg (liquid propagaz) tank, (waste)
storage
day–night variations
|
|
|
|
Fig.
1017 Types of emission
|
|
|
Further information is given briefly below about a few of these types of
emission.
Material emissions
Metallic inorganic compounds can produce accumulating pollution that is
heavily poisoned. For water pollution, mercury and cadmium, in particular, and compounds of these
substances, are on the black list. The black list is a
European list of the most dangerous substances for the environment that may not
be released in any quantity at all.
The other inorganic compounds include: carbon monoxide, sulphur dioxide, nitrogen oxides, halogen compounds, phosphates and
arsenic. These include, therefore, the
quantitatively most important emissions and the majority of the combustion
emissions. Special attention is given to a few of
these below.
Carbon monoxide (CO) is formed when combustion is
incomplete. It is a poisonous, colourless and odourless gas. The total amount
of CO throughout the world remains surprisingly constant, despite increasing
(industrial) production. In addition, CO occurs naturally in the atmosphere,
due to the oxidation of hydrocarbons. However, CO is effectively oxidised to CO2,
so CO only remains in the atmosphere for 0.1 of a year.
Sulphur dioxide (SO2) is a colourless gas with a
suffocating smell. It irritates the mucous membranes and the lungs, but, apart
from this, it is not so damaging. It occurs naturally in the atmosphere, among
other things as a result of volcanic eruptions. A high concentration of SO2
is indicative of pollution by tiny particles (aerosols).
Sulphur dioxide is extracted from the atmosphere by oxidation to SO3
, which reacts with water to form sulphuric acid (H2SO4). Together with other
substances, this is the cause of acid rain.
This is the reason why more and more lakes in Canada, Scandinavia and
the Netherlands have become sterile, why forests have lost their vitality or
have been declared as dead, why heather has been taken over by grass, why wood
and agricultural yields have declined and why our cultural heritage has
been irreversibly harmed. A small part of the SO2 is immediately
washed out and absorbed by vegetation and water. The time that SO2
stays in the lowest part of the atmosphere is in the order of a number of days,
and, under certain conditions, a number of hours.
Hydrogen sulphide (H2S) is a smelly, poisonous,
inflamable gas, that irritates the eyes and the respiratory tissues. It is released
into the air by natural bacterial decomposition processes, but also by many industrial processes. It disappears from the atmosphere via
oxidation to SO2 or due to the activities of certain bacteria. It
remains in the lowest part of the atmosphere from a few hours to a number of
days.
The nitrogen oxides (NOx, i.e.
NO, NO2 and NO3) originate from nitrogen and oxygen in
the air at temperatures higher than 800°C. NO occurs in the first instance, but
as it cools, it is partly transformed in the atmosphere to NO2. NO
is a colourless gas that, in itself, is not harmful.
The reddish-brown NO2, on the other hand, is much more
harmful due to its irritating effect on the muscous membranes. NOx
is finally oxidised to nitrate and stays for about five days in the atmosphere.
NOx, in combination with hydrocarbons, can form all manner of new
compounds in the atmosphere that can contribute to ‘photo-chemical smog’. This
results, among other things in ‘PAN’(peroxide-acyl-nitrate) and formaldehyde (HCHO).
Of the inorganic halogen compounds, it is mainly the compounds with
fluorine (F) and chlorine (Cl) that are important.
Hydrofluoride (HF) is a very corrosive, poisonous
fluid, that, due to its low boiling point (19.4°C), is easily emitted as a gas
(of importance as a potential emission from storage sites). It is a cumulative
poison, i.e. it builds up inside organisms.
Chloride gases enter the atmosphere mainly as a result of
industrial accidents and
leakages, as an insecticide, or due to burning plastics.
The phosphates are
mainly important in water pollution. They can cause such an enormous richness
of food in the water that it becomes devoid of oxygen.
Organic ammonia (NH3) occurs especially in the
bio-industry. It stays for about seven days in the
atmosphere.
Of the hydrocarbons in the atmosphere, only about 15% originate
from human activities. However, this amount has another composition, and is
concentrated in a relatively small area. The natural hydrocarbons come from the
decomposition of organic material and emissions from plants, especially certain
trees. Above pine forests and
citrus cultivations a
haze can often be seen due to photo-chemical smog formation. The majority of hydrocarbons
disappear from the atmosphere due to photo-chemical smog formation. They remain
for quite a long time in the atmosphere; methane (CH4), for example, remains there for
about four years.
However, the length of time that these substances remain in the
atmosphere is dependent on reactivity. A total of 150 different hydrocarbons
have been identified in car exhaust gasses. They are released mainly due to incomplete
combustion and by evaporation. From the many different hydrocarbon compounds, a
number of examples are given below.
The group of halogenic hydrocarbons contains a large number of black-listed
substances, such as alpha-, beta-, gamma- hexachloro-cyclohexane, the PCBs (polychloro-biphenyles) and PCTs (polychloro-therphenyles), hexachloro-benzene, hexachloro-butadiene, pentachloro-phenol and
trichloro-phenol.
The chlorofluoro-hydrocarbons (CFKs, such as freon) belong to the halogenic hydrocarbons. They are used in cooling systems, as a propellant in spray cans, and are not poisonous in themselves.
However, they can harm the ozone layer of
our atmosphere, so that there would be no resistance any more to ultra-violet
rays. [326]
The other material emissions include
complex mixtures, aerosols, dust or particulate matter in the air, solid waste
and free-coming bacteria, viruses (sick buildings!) or genetic material.
Mixtures
The complex mixtures include a large number
of emissions from mostly organic material that can be largely biologically
decomposed, and therefore their exact chemical composition does not need to be
known. For these complex mixtures, standards are used such as BZV (biological oxygen consumption), CZV (chemical oxygen consumption) or the Kjehldahl method for measuring nitrogen.[327]
Areosols
The aerosols are
tiny solid and/or fluid air-borne particles that have such a slow rate of fall
that they can be considered to float or drift. They originate naturally, enter
the atmosphere through combustion processes, or are formed in the atmosphere by
chemical reactions (e.g. by photo-chemical smog). Rain or snow is formed by condensation
and sublimation, respectively, on the aerosols. Compared with the air over
oceans, the average pollution of the air over rural areas by aerosols is ten
times higher. Above small towns, air pollution by aerosols is 35 times higher,
and above large cities 50 times higher than over the oceans. In unfavourable
situations, this figure can increase to 4000 times or more.
Fine dust or particulate matter (PM)
Fine dust or particulate matter in the air (particles <10mm notated by PM10) of
different substances could be dangerous for human health. That is why the European
standard from 1st of January 2005 is maximally 40 mg/m3 average
per year, with maximally 35 times per year a 24-hour average exceeding 50 mg/m3.
Enduring exposition seems to be more dangerous than short exposition, but in
2005/2006 many Dutch building projects were rejected by jurisdiction based on
measurements and prognoses of exceeding the short 24-hour average exposition
standard. However, a distinction should be made in more dangerous
‘
7 µg/m3 along the West Coast until 3 µg/m3 in the
Eastern part of the countrydependent on the location from West to East a municipality may
subtract 7 to 3 µg/m3 from the
measurements to reach the maximally 35 days exceeding the 50 mg/m3
24-hour average
particulate matter, the European picture becomes less threatening
(see Fig. 1018).
|
|
|
|
|
|
Fig.
1018 Calculated PM10 concentrations with and without
|
|
|
Fig. 1019
|
|
|
|
|
Fig.
1019 2005 (left) and 2006
(right) prognoses of exceeding European standards for particulate matter in
2010
|
|
|
Kuypers (2006)
A more precise evaluation of
health effects of different PM components may change the imminent social and
economic effects of these standards up to now even more.
claims plantation can clean the
urban air. A tree could take the equivalent NO2 and PM10
of a car driving 10 000 km.
Energetic emissions
Energetic emissions include warmth, sound, electromagnetic and
radioactive radiation, and changes in the magnetic field. With
the exception of radioactive radiation, in so far as it originates from
radioactive substances that are dispersing, this is a form of emission, the
spread of which is very predictable. If these emissions occur, it is known that
almost all objects in the vicinity will be subjected to immediate exposure.
Because of that, in measuring emissions (as in the case of sound), certain
aspects of the exposure can already be included. The unwanted side-effects of
energy-in-motion emissions can, on the basis of a named characteristic, best be
controlled within the framework of spatial planning.[328]
Mechanical emissions
Mechanical emissions, such as disturbances, small and
substantial interruptions, are, within the framework of environmental hygiene,
not generally considered to be ‘emissions’. They are a part of the working
field of spatial planning, ‘urban management’ and nature conservancy. However,
logically and systematically, they fit in with an overview of types of emission
and environmental stress, such as that shown in Fig. 1017. These emissions can also be
largely controlled using spatial planning regulations.
Information emissions
Information emissions include all influences that disturb the
functioning of our ability to form images by sight, smell, taste, touch,
balance, and voluntary movements. They are subjective, difficult to measure,
and traditionally belong partly to the working field of spatial planning.
However, a lot of research still needs to be carried out in this area. For
example, if symptoms of psychiatric illness could be linked to urban living
conditions (e.g. in the form of sensoric or motoric overloading or
deprivation), then interesting new requirements could be placed on urban
surroundings.
Potential emissions
Potential emissions include emission-reducing regulations, risks and variations in emissions.
Emission-reducing regulations and risk management are
part of the continuing responsibility of all engineers. The variation in emissions makes
it somewhat more complicated to set standards than to fix an average. Local and
temporary periods of peak stress are,
after all, the most dangerous. Variations in stress can be cyclical, subject to
trends, and/or can increase abruptly, in leaps.
Transmission is especially important for material
emissions. It contains the propagation of energetic, mechanical, informational
(noise) and potential influences (risk) and of material by air, water, the
ground or via food-chains, mainly the territory of specialists and extensive
computer programs.
Transmission includes the
transport, dilution, dispersion, conversion and removal of material in and out
of the air, water, ground, food-chains and other relocating systems.[329]
Air pollution
We will go into the spreading of
air pollution the most thoroughly below. In addition, ground
and water pollution is partly a result of pollution in the air, so that, also
from this view point, priority must be given to gaining a better understanding
of air pollution. In this respect, it is important that a distinction is made
between vertical and horizontal air movements.
Where
there are no vertical air movements in a stable atmosphere, pollution stays at
low levels and can become highly concentrated locally. Horizontal air movements
are important in predicting where air pollution will occur. For water
pollution, especially important are the horizontal displacements, and only in
the case of deep lakes or seas do vertical displacements also play a role. The
displacement of ground pollution is largely dependent on ground water currents,
and possibly on human transport.
The sun acts as the motor for all
air movements. Sunlight is partly intercepted by the atmosphere and, especially
in the higher layers, warms it up. The lowest layers of air receive their heat
mainly from the surface of the earth, which is warmed up during the day,
releasing its heat again by radiation at night. Because of this, the lowest
layer of air (to about a height of 10 km), the troposphere, has, in
principle, an upwards-decreasing temperature. However, the stratosphere, that lies
above it, becomes warmer in its higher levels. If rising air comes into contact
with warmer layers of air, it stops rising. There is thus little exchange
between the troposphere and the stratosphere, also with respect to air
pollution. The troposphere is approximately 10 km high and contains about 80%
of the total mass of the atmosphere. This is where almost all weather phenomena occur; this is where the largest
warming up and cooling down takes place, and where the air pollution increases
and decreases due, respectively, to emissions being released and washed away.[330]
Polluted air remaining low
Warm air rises until the
surroundings become warmer, but, in retaining its own heat content, rising air
also cools off due to expansion. This cooling off process amounts to about 1°C
for every 100 m that the air rises.[331] An air bubble warmed up by the surface of the earth that is 2 degrees
warmer than its surroundings will thus rise 200m if the surroundings of the air
bubble stay the same, and it will rise more than 200m if the surroundings
become colder.
It is clear that if the lowest
part of the troposphere has become relatively warm because of a number of hot
days, there will be very little rising air, so that the air pollution will stay
below. One can talk then of a stable atmosphere. Especially after the night
time cooling off of the lowest layers of air due to radiation from the earth’s
surface, temperatures, that rise with height, can occur the next morning.[332]
Inversion
If a chimney doesn’t rise above
the point where the temperature starts to go down again, as is normal in the
troposphere, then the smoke stays held in the lowest layer of air, because the
surroundings are too warm to allow the air to rise. Such a situation is called inversion (an inverse temperature
gradient).
In the course of the day, a rise
in temperature in the lowest layer of air can cause the inversion to disappear.
However, that does not happen if there are clouds in the sky, or if the rise in
temperature is insufficient to make the lowest layer of air much warmer than
the layers above it. Because of this, an inversion can last for several days.[333]
Moisture
The amount of moisture in the air is just as important for the development of
vertical air movements. Moist warm air, rising from the surface of the earth,
cools down by expansion and, above a certain height, loses its moisture by
condensation. This condensation produces heat that causes the air to rise
further and then to cool down further, thereby producing more condensation. The
height at which condensation begins forms the flat underside of the cloud layer.[334] Thus, because of the heat development that then occurs, a loss of
moisture can cause the air to rise even more.
At ground level, the air is
warmed up the most in the tropics and the least at the poles. Because the air
in the tropics is continually rising, warm air moves northwards in the higher
layers, partly due to it cooling down over the subtropics, and then it sinks to
the lower layers of air in our latitude (see Fig. 218). The
continually sinking air at the poles produces a cold northerly wind, that meets
the warm humid air masses from the south in our latitude. This results in a lot
of condensation and precipitation in our latitude, in cold polar air wedging
its way under rising warm air until this too is heated up by the earth’s
surface. Because of this, the polar front in our latitude produces a much more turbulent
weather pattern than elsewhere.[335] On the one hand, this is good for the mixing and dispersion of air
pollution, but it also makes air pollution less predictable than in tropical or
polar climates.
Southwestern winds
The sun rises in the east because
the earth rotates eastwards. The atmosphere rotates with the earth. Therefore,
in contrast to polar air masses, tropical air masses have a strong eastward
impulse. As they move towards the north, this eastward tendency persists, so
that tropical air in our latitude comes mainly from the southwest. As
relatively stationary polar air masses move southwards, they become
increasingly confronted with the earth’s rotation and thus have a tendency to
move westwards in relation to the earth’s surface. Because of this, in our
latitude, cold polar air masses come mainly from the northeast.[336]
Polar front
The eastward tendency of the
tropical air and the westward tendency of the polar air, when they meet in our
latitude (the ‘polar front’), cause air movements that circulate in an
anticlockwise direction.[337] In low pressure areas (depressions), into which
the winds always blow, this is usual. That means, for example, that the winds
are southerly if a depression lies to the west of the Netherlands, and
northerly if the depression lies to the east. Based on this, a number of
frequently occurring circulation patterns can be identified for Europe, and
their frequency over the years can be established statistically.
From this, statistical indicators
have been formulated of expected weather types, and these
can be applied to dispersion models for air pollution.
Coastal circulations
A very frequently occurring type
of circulation, on a smaller scale, occurs systematically in coastal regions.
Because of the alternation between day and night, there is also an alternation
here between sea and land winds. A sea wind
occurs along the coast when the sun shines strongly and, due to this, the land
warms up faster than the water, causing a difference in air pressure. At night,
the land cools off faster than the sea, causing a wind to blow from the land,
seawards.[338]
Turbulence
Based on climatological factors,
regularity in wind direction, as mentioned above, applies to flat, open spaces,
but not to built-up urban areas. Very many smaller circulations occur there
that are summarised by the concept ‘turbulence’. Where there are eddies behind
buildings, the only way of predicting turbulent air movements in these urban
areas to any extent, is to place maquettes in wind tunnels, on a revolvable
platform. To carry out very exact tests on them, such maquettes must be built
by specialists, because it is very important to simulate the roughness of the
material and it is impossible to position gauge points on a normal maquette.[339]
Mathematical models of wind
circulation
For sources in relatively open
areas, mathematical models can be applied. One can distinguish pollution-point
sources, such as
chimneys, line sources, such as
main roads, and surface sources, such as an
industrial sites. The most frequently used dispersion model is the Gaussic Plume
model, of which
there are a number of variations. In addition, there are ‘grid models’ and ‘trajectory models’ as
described in KNMI KNMI De Bilt (1979). In the Gaussic Plume model, it is assumed that air pollution is
dispersed perpendicular to the direction of the air movement, according to a
statistical distribution.
Grid models divide the space into
box-shaped units, by means of a co-ordinate system whereby the input and output
is calculated per box.
Trajectory models are based on
forward-moving box-shaped units of air, each unit of which has input and output
values.[340]
The concentration of air
pollution substances can be shown in three different ways:[341]
-
volume/volume (unit ppm)
-
weight/weight (unit ppmm)
-
weight/volume (mg/m3)
RIVMs national gauging network for air pollution was drastically modernised
in 1985 and now comprises 68 gauge points. In
addition, TNO manages ten more points, and the provinces and municipalities 80
and 20, respectively.
Deposition
Apart from the dispersion of air
pollution, the fall-out (deposition) of particles and the washing out
of air polluting substances in rainwater, chemical changes in the air pollution
itself also play a role in the total transmission of air. However, not much is
yet known about these processes. Most of what is known concerns photo-chemical
smog, in which
mainly the chemical composition of combustion emissions changes under the
influence of light.
Smog
Photo-chemical
smog mostly occurs as a result of ‘ground inversions’ caused when the lowest
layers of air cool down faster than the layers of air above. Because of this,
condensation occurs in the lowest layers of air (fog), and, as there is an inversion, the
pollution also stays trapped in these layers. Aerosols serve
as nuclei for condensation and the drifting drops of water catch the remaining
pollution, whereby all manner of reactions occur. The formation of ozone (O3)
under the influence of sunlight can play an important role in these reactions.
However, compared to water pollution, chemical and biological reactions in air
pollution do not play such a large role.
Pollutants enter water by deposition from the air, by draining out of
polluted ground and by direct discharge. Thus, in the pattern of currents in a
river, one can find pollution-surface sources on the surface of the water, line sources along the banks and point sources at the location of the discharge. Apart from
these sources of pollution, the following means of ‘removal’ also play a role:
–
extractions, removal to groundwater, to tributaries;
–
reactions of a physical, chemical or biological nature.
Based on this input and output, a
balance can be drawn up for each stretch of river. As one can talk here of a
one-dimensional current movement, the concentrations can be
calculated using rather simple models. However, after 1965, models were
developed that could also handle two-dimensional situations (as in shallow lakes, bays and
harbours).
Mathematical models of water
pollution
Insight into bio-chemical
processes also became more advanced. Before 1965, already, the models took into
consideration the deterioration of dissolved oxygen and the decomposition of
organic material from waste water. Between 1965 and 1970, the oxidation of
reduced nitrogen compounds was also included in the models. Between 1970 and
1975, three-dimensional situations, such as deep lakes and seas, were
included in the models. The water masses were thereby divided up into layers
(stratification). In
addition, the growth and death of algae, and the
physiological reaction of organisms to temperature, sunlight and the
availability of food materials were described. After 1975, the behaviour of
toxic substances in biological processes (among others, their accumulation in
the food chain) was researched, as well as their transport on floating
particles and sediment.[342]
Because of the increasing
complexity of the models, it has to be recognised that their reliability is
decreasing. For this reason, one-dimensional models are still being used.[343]
In chapter 6.6 Soil pollution, page 577 and further
you can find a more comprehensive treatment. Here we restrict to some
fundamentals. Ground pollutants can be transported in the ground water. They
can held and removed by absorption into soil particles, precipitated by
chemical processes and dissolved again, and (partly) decomposed by
micro-biological processes, especially in the thin zone that is not completely
saturated with water.
The speed, direction and depth of
a groundwater current depends very much on the type of soil and the variation
in subsoils. In principle, three-dimensional current models are available for
this, but these need to be fed with an extremely large amount of detailed
information about the subsoils. This information is largely unavailable, so one
has to make do with simpler current models. For regional studies, in
particular, taking the relatively limited depth of the water transporting
systems into account in relation to the extent of the region, a calculation in
two dimensions is usually sufficient.[344]
Absorbtion
The speed and direction of
groundwater currents are, of course, initially dependent on the
type of ground. For removing pollution by absorbing it onto the surface of soil
particles, the specific surface area of a solid soil particle is important. For clay, for example, this is
larger than for sand. The more acid the environment, the more difficult it is
for pollutants to attach themselves to the soil particles. Acidity, therefore,
leads to some pollution of the groundwater. In addition, of course, as time goes
on, the whole surface area can become saturated, so that larger amounts of
pollution come to be transported in the groundwater currents. In that case,
certain substances can still be precipitated out of the water or dissolved into
it again. The solubility of chemical substances is also dependent on the
acidity (pH) and on the
‘redox potential’ (Eh).
Conversion
Micro-biological decomposition
and conversion processes are generally the most effective in the thin zone that
is not completely saturated with water. Especially in the transition zone,
where the presence of oxygen may or may not still play a role, can anaerobic
decomposition processes (without oxygen) be of great
significance. Among the well-known micro-biological conversion processes are
nitrification,
denitrification and sulphate reduction.
Data
For a quick orientation regarding
the possible risks of extending pollution that has appeared on or in the
(water) bed, reference can be made to archive information (van Duijvenbooden
1982). Among other sources of information, reference can be made to:
–
geological maps
–
ground maps
–
topographical maps
–
hydrographic charts
–
geo-hydrological mapping (surface contour charts, seepage/infiltration
charts, quality charts)
–
geo-electrical mapping
–
individual reports and data.
By studying the information
listed above, a preliminary insight can be gained of the local direction and
speed of the groundwater currents. If information on substances is available,
then it is also possible to estimate their transport.
Points of interest
Attention should be given, among
other aspects, to: [345]
–
the structure and composition of the soils (clay/peat with low k* and high CEC; sand with
large k and low CEC, pH, redox; and the mud
and organic-material content); [346]
–
the geological structure (presence of pockets of sand in contrast to
layers of clay, heterogeneities, holes, stratification);
–
the hydrological situation (seepage/infiltration, current direction and
speed, location of the watershed, drainage or infiltration channels);
–
topography (on the basis of height characteristics, gives a first
impression of the probable current direction).
–
If necessary, extra information can be collected in the field (van
Duijvenbooden 1982).
Exposed objects
Determining
the end effect (see Fig. 1012) is the
final and most difficult part of every environmental-impact statement. The
first thing that has to be established is which objects situated in the
neighbourhood of the environment-damaging activity are the ones on which the
effects have to be determined. In this section, the types of object
distinguished are materials, people, plants and animals, (eco)systems, or
entire areas. When there is no clear prior agreement regarding on which objects
the effect has to be reported, there will always be criticism afterwards on the
effect report that is delivered.
If one already has a list of
objects on which one has to report, then the question still remains of which
effects have to be reported.
Damage
If the object is people,
then one can still distinguish absolute effects (such as the mortality rate) from
gradual effects (such as the illness rate). To be
able to view the effects against each other and against the useful effect of an
environment-damaging activity, it is desirable, though usually impossible, to
quantify it to a common denominator. Of course, especially in the United States,
frequent attempts have already been made to express the damage caused by
environment-damaging activities in terms of money. The table below pictures
this for the Netherlands (1978).
|
Damage to
|
mln.guilders
|
no. guilders per
inhabitant
|
|
materials
health
commercial crops and
livestock
lost residential value
|
110
1000
85
1400
|
8
71
6
100
|
|
total estimative damage
|
2600
|
185
|
|
|
|
Fig. 1020 Damage due to
air pollution in the Netherlands estimated in 1978
|
|
|
Costs of damage
The most reliable datum in
this table is ‘damage to materials’. The way in which ‘damage to health’ is
calculated is already indicative of the dubious assumptions that have to be
made when expressing this damage in terms of money. The costs of early death
were estimated as the (discounted) income that the deceased would have earned
had there been no air pollution. The amounts used to arrive at the costs of
illness were ‘loss of production’ and ‘the costs of curative care’.
There are, though, three
methods of approach for damage due to death:
- The ‘human capital’ approach;
- The ‘costs of risks’ approach;
- The comparison with costs made to prevent unnecessary death.
The method used in Fig. 1020 is the ‘human capital’ approach.
For the second approach, wage differences – that can be interpreted as ‘risk
surcharge’ – are used as the point of departure. To determine the value of a
life, the extra wage paid for a 1% higher death risk is, for instance, multiplied
by 100. The third approach ought to be based on the amount that the Dutch
society is prepared to spend on ‘the most expensive patient in the Netherlands’.
For example, a vaccine
should not cost more than € 18 000,- per life year gained (NRC Handelsblad
2003-07-06).
Distinguishing the environmental part of damage
It must be clear that, even
if the nature of the effect can be described clearly and unambiguously, it is
usually difficult to quantify[347]. In addition, it is difficult to separate the effects of
environment-damaging activities from other influences. In this way, the ‘lost
residential value’ in Fig. 1020 is estimated on the basis of differences in house prices observed in
transactions in Rijnmond. However, the house-price differences are also
dependent on house characteristics (type of home, house size, year of
construction, with garden, etc.) and the characteristics of the district in
which the house is located (green facilities, nearby shops, noise levels,
accessibility, etc.)
To be able to determine the
effect of a home located in a foul-smell zone from these fixed variables,
complicated regression analyses and daring assumptions are necessary. Instead
of 1.4 billion guilders, a few changes in the assumptions would have given 1.7,
2.4 or 3.3 billion guilders as the lost residential value in the Netherlands.
[348]
Dose-response of living objects
The effect of environmental
pollution on living organisms can be shown in the form of a dose-response
diagram (Fig. 1021).
|

|
|
|
|
Fig. 1021 Dose-response relation
|
|
|
A similar diagram can be
drawn for poisoning a large number of individuals with different doses. The
dose that causes death in 50% of the cases, within a given time, is called ‘the
lethal dose at 50%’ (LD50).[349]
It is clear that dose-effect
relations are only known for a small number of substances on a small number of
organisms. It is, of course, difficult to establish the dose-effect relations
for human beings empirically, so there are still many knowledge gaps in this
area.
Research has established
that the worst damage to materials is brought about by the action of SO2
on painted steel, galvanized steel and on zinc foil. Research (Fig. 1022) was
set up by Jansen and Olsthoorn (1982) consisting of:
–
Measuring the concentration of
SO2;
–
Determining the exposed
quantity of materials;
–
Establishing the dose-effect
relations;
–
Making an economic evaluation
of the effects.
In this research, only
maintenance costs, the costs resulting from reduced economic lifespan and
substitution costs were taken into account. Indirect costs (for example, those
resulting from the failure of affected parts) were not taken into account.
The costs listed above were
estimated using a number of formulas by which, if the concentration of SO2
in the air is known, the reduction of the galvanized layer, the length of
protection of the paint layer, or the lifespan of the construction part were
derived. These sorts of formula, in fact, represent dose-effect relations.
Recalculated as costs and added up, it is possible to give a dose-effect
relation for the whole of the Netherlands.
|
Doses in
mln.kg SO2
|
Effect of damage in mln.
guilders.
|
Dose per inhabitant
kg SO2
|
Effect per inhabitant
Damage in guilders.
|

|
|
1300
1200
1000
900
800
700
600
500
400
300
|
225
177
151
123
92
74
56
40
25
18
|
93
79
71
64
57
50
43
36
29
21
|
16
13
11
9
7
5
4
3
2
1
|
|
|
|
Fig.
1022 Dose-effect
relation of SO2 on a range of metal constructions in the Netherlands
(1978)
|
|
|
|
This dose-effect relation is
thus composed of different dose-effect relations that are only related to a
certain material part of the damage not including health effects.[350]
|
For people, the lethal
doses of a lot of poisons are known, as well as many of their clinical
characteristics and side-effects (the absolute and gradual effects). The
branch of medical science that concerns itself with poisonings is
‘toxicology’ see: Sangster (1987).[351] The process by which humans take up, re-absorb, transform,
apportion, store and excrete poisons can be summarised in the following
diagram.[352]
Contrary to materials,
human beings, animals and plants can develop resistance to repeated exposure to
poisons. However, a slow build-up of toxins is equally likely to have
sudden, serious consequences. In addition, the effects of different types of
pollution can be increased by their interaction. One example of this is
evidenced by smokers’ increased susceptibility to the adverse effects of air
pollution. As a rule of thumb, one can say that if air pollution increases by
10%, the mortality will increase by approximately 1%.[353]
|

|
|
|
|
Fig. 1023 Toxicological
access routes into the human body
|
|
|
Historical disasters
As the literature on
toxicology is fairly easy to access, we will restrict ourselves here to human
exposure to a few historical cases of severe air pollution (Source: KNMI 1979)
In December 1930, the narrow
and heavily industrialised Meuse valley, in the neighbourhood of Leige,
experienced weather conditions, which – for almost a week – hindered the spread
of the pollution produced there. The result was that a large number of people
became ill due to respiratory problems, and, before the end of that week, 60
people had died. It is not clear whether very high concentrations of sulphur or
florides were the cause of the disaster, because no pollution measurements were taken at that
time.
A disaster that has been extensively researched is the
one that hit the small town of Donorain in the valley of the River Monongahela
in the State of Pennsylvania in the United States in 1948. Also here,
unfavourable meteorological conditions, together with the hills that encircle
this industrial town, hindered the dispersal of air pollution. The result was
that thousands of people became ill, mainly with respiratory complaints and
problems with the eyes, nose and throat. During this 7-day period, 20 people
died.
Even worse was what happened
in London from 5-9 December 1952. The majority of Great Britain was covered in
fog at that time. Elderly people in particular became ill, suffering from heart
problems or respiratory difficulties, and had to be taken to hospital. Even
after the worst period of pollution had subsided, more deaths occurred than was
usual for December. The total number of deaths rose to between 3,500 and 4,000
above the usual number of deaths in December. The extremely high concentrations
of soot and sulphur dioxide were probably the cause of this disaster
In the Netherlands, air
pollution has not led to a demonstrable number of deaths (that is
something else tnan calculated decrease of lifetime-expectenace or brain
performance), but there were obvious increases in the numbers of both illnesses
reported and hospital admissions, such as in the period 26-30 January 1959 and
4-6 December 1962. In Rotterdam, in 1959, the amount of smoke in the open air,
and, in 1962, the sulphur dioxide concentrations, reached extremely high
levels. In both these cases, too, it was long periods with no wind and bad
vertical exchange that caused increasing concentrations of toxins in the air.
Hardly anything is known
about the extent to which material pollution has caused the disappearance of
plant and animal species. For a number of species, such as lichens, a clear link can be made with air
pollution. The extinction of plants and animals is largely due to the loss of
their biotope. This is mostly caused by light and heavy mechanical
interferences, such as agriculture, urbanisation and road building. For
instance, lowering the water level of ditches can cause a significant reduction
in the diversity of vegetation.
However, a correlation does
not always have to be a causal relation. The distance to a farm and the related
reduction in agrarian activities can also offer a better explanation for local
diversity, even if there is already a correlation with the water levels in
drainage ditches. Water levels in themselves can correlate with the distance to
the farm, if that farm is situated on higher ground so that the water level in
the nearby drainage ditches is deeper than in those further away.[354]
The effect of various forms
of environmental stress on eco-systems and related geographical areas or
utility zones is largely unknown. The effect of the ‘mechanical emissions’
named in Fig. 1017, such
as treading on the ground, mowing, up-rooting, digging, ploughing, clearing the
ground, and building, is the easiest to determine.
The vulnerability of
different geographical units to light or heavy interferences is recorded on
environmental charts.
Vulnerability charts are compiled to show the vulnerability for
each environmental theme. More will be
said about this in the following section. The old objections to environmental
charts are, that these divert attention away from the interferences, their
alternatives and effects, so that only alternative locations are discussed.
These are less of an issue now that the instrument of environmental impact
assessment (MER) is available.
Although by far not everything is known about the environmental effects on
plants, animals and ecosystems, an interesting part of the MER series has been
published, entitled: Effect prognoses. Part
V: ‘Plants, animals and ecosystems’.VROM/LNV
(1987)
In the previous sections,
the unwanted side-effects of the activities summarised in Fig. 1014 are described. Effect reports
can be compiled along these lines. However, in this section, the focus is no
longer on ascertaining the effects, but on the policy-wise reduction of those
effects
|

|
|
Fig. 1024 Threshold,
limiting and target values
|
|
|
Accepted risks
The starting point is the
end effect on people, ecosystems and economic functions, as shown in the
previous diagram. In the totality of risks, to human beings an individual
chance of dying of 10-5 per annum is accepted by government; the maximal
acceptable level of risks. For
each single activity or substance, the maximal acceptable level is 10-6
per annum.[355] For illness (effects with a threshold value) comparable levels are
given, as well as for disturbance resulting from noise or foul smells. For
ecosystems, a similar sort of approach is developed. The maximal acceptable
level is achieved when the concentration of a substance is the same as the
calculated concentration, whereby protection is offered to 95% of the species
in an ecosystem. However, in many cases these norms appeared to be unattainable
(RIVM 2003).
Negligible effects
It is assumed that below 1%
of this maximal acceptable level the effects are negligible. This marks the
target value of all emissions and environmental effects: the value that
should be eventually achieved[356]. Between both levels there is a so-called ‘grey area’ within which targets for a certain period can
be formulated using verifiable threshold values[357].
As soon as these threshold
values have gained the legal status that they may not be exceeded, they are
referred to as ‘limiting values’[358]. If such values may only be exceeded when reasons are given, then
they are referred to as ‘guide values’[359]. Before these values are fixed, one can refer to them as environmental
quality targets[360], and
after that, as environmental quality requirements[361].
Target values
As a target value can only
be reached in the longer term, for the shorter term, one can fix lower limiting
values for what must be achieved during a certain year as an interim step
towards the year in which the target value has to be achieved. An example of
environmental quality targets is the table of target and limiting values of
priority substances from the first National Environmental Policy Plan (see Fig. 1025).
|
substance
|
target value
|
limiting value
|
average
|
concentration around the sources
|
% reduction for the benefit of the target value
|
% reduction for the benefit of the limiting value
|
reference
|
|
trichloro-ethene
surface water
tetrachloro-ethene
surface water
benzene
phenol
etc
|
50
0,1
25
0,1
1
1
|
50
2000
10
100
|
0.65
2,0
1,0
3,5
2
0,008
|
80
30
40
(185)
2
|
35-40
95
20
98
97,5
50
|
35-40
75
|
IMP
1987
IMP
1987
base
doc
MP
|
|
|
|
Fig.
1025 Target and limiting values of priority substances and the
percentages of necessary reductions in emissions that result from this.
Amounts in ?g/m3 for air (or ?g/l for water)
|
|
|
Time to reach target values
Regarding the priority
substances, after
thoroughly studying the effects of each substance, target values will be
prepared in a ‘basic document’ for the general environmental quality of water,
ground and air. In the grey area, for phasing the policy, limiting values must
be fixed that indicate how far the protection will extend during the period
agreed. This takes place on the basis of an economic consideration.
Weighting costs and environmental quality
|

|
The costs of this
protection increase progressively with the quality of the environment that we want to achieve in
this way. It is not always possible to achieve an immediate recovery of
environmental quality to the target value. One only has to think of the
amounts of money involved in soil decontamination to understand that complete
recovery of environmental quality not only financially, but also technically,
takes time to achieve.
Limiting values include a
consideration whereby the damage to exposed objects is weighed against the
economic interests associated with the activities involved.
In so far as this damage
can be expressed in terms of money, this consideration is rather simple.
After all, the costs of the damage can be added to the costs of protecting
the environmental quality for every protection level imaginable. From this,
for a certain threshold value, an economic optimum is obtained.[362]
|
|
|
|
Fig. 1026 Net societal costs after deducting environmental damage
|
|
|
Threshold values
However, in section 6.5.4, it
became clear how open to interpretation the concept ‘damage’ is, and how dependent this is on the value we
place on the protected objects. In addition, the graph does not run as
continuously as in Fig. 1026.
Locally, a small additional protection effort can suddenly save a species of
fish. These sorts of quality aspect are therefore expressed as verifiable
threshold values. For
example, a threshold value can be established for the oxygen content of water,
above which a species of fish will certainly survive.
A legally established limiting
value will go further than the economic optimum, as
other values are also taken into consideration than those that can be expressed
in terms of money.
The limiting value can be
established regionally; it can also be differentiated according to different
functions (special environmental quality).
Special environmental quality is the opposite of ‘general environmental
quality’. Based on separate general protection levels for drinking water,
inland fisheries and shellfish, norms were established in, for instance, the
Indicative Long-term Water Programme (IMP Water). Each
of these protection levels is based on different criteria.
Different supposed uses of damaged objects
The criterium for fishing
water can thus be a dose-effect relation for a
certain species of fish and a certain form of pollution. Also the consumability
of the fish that will be caught can be used as a criterium for the quality of
the water in which the fish will have to be caught. It is clear that the
criterium for drinking water will be different again from that needed for fish.
Levels of standards
Setting norms takes place on
different managerial levels, beginning with the European level. The higher the
managerial level and the larger the area over which the norm must apply, the
more flexible the norm has to be to encompass all eventualities and to maintain
a certain feasibility.[363]
The length and frequency of exposure
The length and frequency of
exposure are essential considerations when setting
norms. Certain norms may be exceeded for a short while, but not too often. In
addition, it can be established that excesses, if they take place at all, may
not follow each other within a certain interval of time. Human beings or
organisms need time to recover from a certain excess. From this it appears
that, in many cases, setting norms demands a statistical approach. This
approach, whereby norms can be given an average value, must not lead, though,
to ignoring periods of peak stress. Exact
values remain necessary, therefore, not only as a means of evaluation, but also
especially because of their role as an indicator and as a maximum value for
incidents (’98 percentile, and similar).
An example of these sorts of
peak sensitive exposure norms are the so-called EPEL and MAC values . The MAC values are hygienic values for companies, fixed by the
national MAC commission under the terms of the Working Conditions Law (ARBO). The
MAC values are the Dutch version of the American Threshold Limit Values (TLV).[364]
The association of Dutch municipalities (Vereniging van Nederlandse
Gemeenten VNG) made a list of approximately 700 businesses
and 80 installations categories. For each category that list recommends to keep
a distance in metres (zone) from quiet and mixed residential areas.
A downloadable Excel sheet offers that extended list in selectable
parts.
|
code
|
Distance to quiet residential areas
|
Distance to mixed areas (one category lower)
|
|
0,0
|
0
|
0
|
|
1,0
|
10
|
0
|
|
2,0
|
30
|
10
|
|
3,1
|
50
|
30
|
|
3,2
|
100
|
50
|
|
4,1
|
200
|
100
|
|
4,2
|
300
|
200
|
|
5,1
|
500
|
300
|
|
5,2
|
700
|
500
|
|
5,3
|
1000
|
700
|
|
6,0
|
1500
|
1000
|
|
|
|
|
|
Fig. 1027 Category codes of
businesses and recommended distance to keep from residential areas
|
|
|
|
|
For different kinds of nuisance (odor, dust, noise, danger, quiet areas, traffic, visual, soil,
air) different distances are given.
The largest distance determines the category of nuisance (see Fig. 1027). Distance to mixed areas are one
category lower than to quiet residential areas.
From effect- into
source-directed standards
The development of
environmental quality requirements originates from the exposed objects (risk
criteria, dose-effect relations). From this end effect, limits can be set on
the indirect and direct effects of activities and on the activities themselves
(see Fig.
1012 and Fig. 1013).
Non-accepted exposure
effects result in limiting values for the media air, water and the ground, from
which environmental quality norms can be derived.
Emission limiting values and emission ceilings follow from this, as well as requirements and
norms for products and processes towards which the activities lead.
The advantages and
disadvantages of norms on the source and emission side compared with norms on
the exposure and environmental quality side lie, on the one hand, in the area
of the practical applicability of issuing licences and, on the other hand, in
the possibility of objective under-pinning and the mutual consideration of
different environmental stresses.
Process and product standards
Applying quality and
imission norms can, after all, in principle, prevent the sum of all sorts of
different activities (e.g. industry, traffic and home heating, as sources of
air pollution), even though reasonably clean in themselves, from causing,
nevertheless, an unwanted or unacceptable situation. On the other hand, they do
not help to grasp the specific possibilities that can exist in an individual
pollution-reducing source. Process and product norms have the advantage that
they tackle pollution at source. However, they make an approach based on
regional conditions impossible. Emission norms and ceilings have a sort of
intermediary position between both.
International principles: sustainable development and biodiversity
The ‘Brundtland Committee’ (World
commission on environment and development, 1987) declared the principle of
‘sustainable development’ (to leave at least as many possibilities for
future generations as your generation encountered). Since Agenda 21 (UN 1992),
‘biodiversity’ became an issue of these ‘possibilities’.
Core aim of the first National Environmental Policy Plan (NMP1)
The core aim of the first
National Environmental Policy Plan (Ministry of Traffic, Spatial Planning and
Environment (NMP) VROM (1989)
was the preservation of environmental-usage space (milieugebruiksruimte) for
the benefit of ‘sustainable development’[365].
So, the production of
new environmental-usage space by building, the many possibilities of gain by
urban and architectural design are thereby overlooked.
Building, health and biodiversity
After all, the proper task
of building is to increase the utility of the space for human beings and their
future generations. Building is good for human health, because, without
buildings there would be distinctly fewer survivors. In addition, buildings can
increase the biodiversity of an area[366]. This means not only gains for human health, but
also demonstrable gains in terms of
biodiversity in the built-up environment. [367]
From the 500 wild plants
that are found in Zoetermeer, Fig. 768 shows, above the line, the
species that already occur more frequently in urban areas than on average in
the Netherlands. Thus one can conclude that building not only takes over
existing environmental utility space, but
also produces — and to a much greater extent — environmental utility space for
human beings, plants and, in some cases, even for animals. If one doesn’t
include that environmental effect in the calculation, then the bookkeeping of
the environmental utility space is incomplete.
Urban and architectural contributions to environmental problems
However, in environmental
policy the building industry is not appreciated for her environmental profits,
but merely its negative impacts are taken into account (see Fig. 1028). In a supplement
of the NMP (Ministry of VROM 1990) for
the building industry, it has been established what ‘contribution’ this ‘target
group’ (other target groups are: agriculture, traffic and transport, industry
and consumers) makes to each field of problems (theme) within the estimated
total for the Netherlands:[368]:
|
THEME
|
SPECIFICATION
|
CONTRIBUTION
|
|
Climatic change
|
air conditioning, isolation foam
|
23% of the total CFC use
|
|
|
energy from fossil fuels for commuter traffic, the production of
building materials, and heating
|
> 33% of the total
CO2 production
|
|
Acidification
|
commuter traffic, building materials, heating
|
>16% of the total NOx and SOx production
|
|
over-manuring
|
household waste water, emissions into the ground and into groundwater
|
24% of the total nitrogen and phosphorus production
|
|
Dispersing environmentally damaging substances
|
solvents, preservation, upkeep, asbestos, heavy metal emissions when
insufficiently re-cycled
|
9% of the volatile organic substances, 40,000 tons of heavy metals,
7,000 tons of pigments
|
|
Removal of waste materials
|
building and demolition waste
|
20% of the total waste
|
|
Disturbance
|
noise and foul smells due to traffic, building, production and
quarrying building materials
|
2.85 million homes suffering from (serious) disruption due to traffic, 25% of the population in small towns irritated by foul
smells
|
|
Wastage
|
careless use, not much re-cycling
|
120 milliom tons of raw materials per year, 90% of which are primary
raw materials
|
|
Internal environment
|
health effects due to building materials, moisture, quality of the
internal air, sound, vibrations
|
number of homes above the reference value: 90% NOx, 80%
radon, 80% airborne sound insulation, 60 % respirable substances, 15%
moisture problems, 6% carbon monoxide, 40% of the offices are ‘sick’
buildings
|
|
Damage to ecologically functioning area
|
building surface with isolated ground ecology, quarrying for building
materials
|
3,100 km2 of hardened surface, 1,000 ha/year open-cast
mining, of which 500 ha of definitive changes in destination
|
|
|
|
Fig. 1028 The contribution of the
building industry to environmental problems in the ‘90s
|
|
|
The building industry was
able to bring about reductions of spare parts of more than 20%, for example, by
not applying foam containing CFKs to insulation material or by not basing air
conditioning on these compounds, or by rendering them totally redundant. This
applies to more of the contributions named in this table.
In ‘Environmentally
considered building’ started by the Ministry of Traffic, Spatial Planning and
Environment (VROM), discussions took place with the industrial branch as to
which reductions in the different types of environmental pressures could be
achieved in the long term (target values) and various shorter term limiting
values that had to be met before a certain year.
Environmental problems and targets
The NMP1 distinguished
environmental problems according to the level of scale they can be solved (not
according to their effect, which is always local):
|
- Global problems: ozone layer and climate change[369];
- Continental problems: border crossing air pollution, ozone on
living level, acidification, smog, heavy metals[370];
- Fluvial problems: rivers, regional waters, salty waters,
water bottoms[371];
- Regional problems: accumulation of pollution, over-manuring,
pesticides, heavy metals, removing waste, soil pollution, drying up[372];
- Local problems: noise pollution,
smell pollution, urban air pollution, inside environment[373].
|

|
|
|
|
Fig. 1029 Conditional suppositions of
norms/standards
|
|
|
According to these levels,
targets were elaborated into standards according to limit values (see Fig. 1029) in
cooperation with international, national, provincial and local authorities.
From an effect-oriented into a source-directed policy
The NMP1 marked a change
into source-directed policy by making separate appointments with target groups
like:
- agriculture;
- industry;
- refineries;
- energy supply companies;
- building companies;
- trade, services and governmental institutions;
- traffic;
- consumers;
- waste processing companies;
- participants in the water chain;
However, effect oriented
measures remained actual for:
·
problems herited from the past;
·
source-directed measurements
not coming in time;
·
preventing calamities;
·
failing source-directed
measures.
The source-directed measures
were distinguished into:
·
emission directed;
·
volume directed;
·
structural measurements like
integral chain management, energy saving and quality improvement.
These measures were
discussed with the target groups (see Fig. 1030).
An agenda to discuss with target groups
The NMP used the following policy outlines as an agenda to the
discussions with target groups:
|
effect oriented (main emphasis of the ‘70s:
ground, water, air)
|
|
source oriented
(the ‘80s)
|
emission oriented (removal at source)
|
|
|
volume oriented (less consumption and
production)
|
|
|
structural
|
energy saving (energy)
|
|
|
|
integral chain management (material)
|
|
|
|
quality improvement (information)
|
|
|
|
Fig. 1030 Outlines of environmental
policy
|
|
|
In these ‘policy outlines’,
environmental care is recognisable within effect, emission and volume oriented
policy. It is only when it comes to ‘structural’ policy that innovational
environmental techniques are dealt with.[374]
Strategic
agenda
The government itself
handled a strategic agenda of:
·
reducing uncertainties;
·
making choices from scenarios;
·
formulating themes, instruments
and cooperation.
These themes, instruments
and cooperation are elaborated below.
Environmental themes supposing each other
Since the first National
Environmental Policy Plan environmental themes have been: wasting,
removing, disturbing, drying up, spreading, acidifying, over-manuring (the
‘VER-thema’s’ in
Dutch)[375].
|
However, a conditional
analysis of these (VER-) themes " (zie Fig. 1031)[376] shows they overlap. For example wastage has been tacitly
presupposed as an environmental problem in all of them. If wastage is the
main problem, then sunlight, rain, and
leaf-fall in the autumn should also be avoided. The theme words are
interpreted here according to their meaning in everyday language[377].
In a professional sense, a
clarification of that is presupposed, but is sometimes forgotten. What is
meant by ‘dispersion’ is the dispersion of environmentally toxic substances,
excluding CO2 (climate).
The
tacit presupposition is thus: ‘in so far as it is not connected with the
dispersion of acidifying or manuring substances, or CO2 .
|

|
|
|
|
Fig. 1031 Environmental themes
from the NMP, shown according to their conditionality
|
|
|
However, in everyday
language, one cannot imagine climate problems, acidification and over-manuring
without the dispersion of substances responsible for this. Ecologically, this
dispersion is irrelevant, in so far (again, according to everyday language) as
it causes no disturbances. However, ‘disturbance’, in
professional language refers mainly to disturbance of the living environment
due to noise, foul smells, insecurity, and is thus, in contrast to climatic
problems, very local. The tacit presupposition is then: disturbance in so far
as it is not connected with drying up, interior environmental problems and
dispersion.
Double counting
The government prefered to
convert environmental effects into these themes. That means that, in effect
analysis, there
is a danger of double counting, due to environmental values that presuppose
each other. In methods such as LilfeCycleAssessment, an
attempt is made to add up the effects by theme, but if a certain environmental
pressure has more than one effect, it is unjustifiable to include that pressure
several times in the calculation.
Calculations by RIVM
That is why for each theme,
the environmental planning bureau RIVM yearly checking governmental policy
results, repeatedly asked itself the same question:
‘and why is that bad?’. The conclusion remained unchanged, that it is hardly
possible in the Netherlands to determine the effects on health, but that, for
each theme, ‘a possible loss of biotopes’ should be regretted.
|

|

|
|
|
|
|
Fig. 1032
Calculating impacts of target group ‘agriculture’ on every theme, reduced to
impacts on biodiversity and health
|
Fig. 1033
Calculating themes from contribution of every target group, reduced to impacts
on biodiversity and health
|
|
|
|
Instruments and cooperation
NMP1 distinguished the following instruments:
·
regulations by law;
·
liability;
·
financial regulations;
·
environmental care in
companies;
·
product norms;
·
information and public
relations;
·
technology;
·
energy saving.
in cooperation with: international, national, provincial and
municipal institutions.
.
National policy documents after NMP1
|

|
There are four more recent
national policy documents with environmental criteria for
plans on different levels of scale from the Ministries VROM, LNV and V&W:
- The 5th National Plan of Spatial Policy NRO5, VROM (2000),
- The National Plan of Nature Policy LNV (2000),
- The 4th National Plan of Environmental Policy NMP5, VROM (2001),
- The 4th National Plan of Watermanagement PolicyV&W (1998) (stressing environment), and
- its successor ‘Anders omgaan met water’ V&W (2000) (stressing security).
Some of these policies are
elaborated in a regional policy. The
RIVM is supposed to test plans on the subjects of health, environment
and nature.
Some of the produced
criteria are summarised below.
|
|
|
|
Fig.
1034 Four national plans concerning the environment
|
|
|
European policy
P.M.
Choice of location
The choice of location for a building, complex or new neighbourhood
depends on position, orientation, land shortage and potential soil pollution,
and as such comes with a price tag attached. Readers are not expected to “know”
the contents of this chapter. Those factors that play a part in the choice of
location are marked with a question.
As well as determining
the choice of location, this topic is also of interest to urban planners and
architects. After all, most contracts depend on the commencement date of
building activities, allowing sufficient time to obtain the relevant permits
and to plan activities. A lack of knowledge concerning soil pollution –
including the relevant permits – will delay activities.
Soil protection act
This chapter offers
guidelines for carrying out research in the context of the decontamination
clauses of the Wet Bodembescherming (Soil Protection Act),
with the emphasis placed on "terrestrial soils". Detailed information
will be given on a range of pedologic properties and concepts. Examples of
potential areas affected by soil pollution are also included, as is a brief
summary of remediation techniques.
Surveys to obtain a clean soil statement
This monograph, coupled
with a concluding report, will enable building contractors to carry out
exploratory and preliminary surveys into soil pollution to initially obtain a
“clean soil statement”.
Clean soil statement depending on purpose
Until comparatively
recently, planning permission applications needed to include a so-called
"clean soil
statement". This has been replaced by a suitability certificate,
indicating intended purpose. As a result, the soil no longer needs to be
completely "clean", provided it is deemed suitable for its designated
use. Building work cannot commence until this declaration has been issued. This
certificate is not only concerned with the topic of soil pollution, but also
with “cleaning”, soil remediation, if pollution has been detected.
Protocols and methods
To encourage greater
understanding of the underlying problems, this thesis shall focus on the
protocols involved in the investigation procedure into
(likely) contamination (and resulting reports), and highlight a number of
pedologic concepts.
This chapter is
concerned with outlining the different types of contamination, coupled to
industry activities, their prevention and location in the townscape and
landscape. Current and developed remediation methods have been included for the
sake of completeness. The underlying idea is that decontaminating and preparing
a terrain for development follow naturally from one another, or could even be
carried out in unison, thereby influencing the overall design.
Suitability for future purposes
The term ‘soil
pollution’ denotes a negative impact on soil quality,
which affects the soil to such an extent, that it is rendered unsuitable or
less suitable for its intended purpose.
The soil must be
protected in such a way, that future generations can make use of it. This means
that the soil must not be damaged, or become irrevocably damaged, in accordance
with the concept of sustainability.
Different types of damage
When analysing our
exposure to substances in the soil, we can identify different types of
damage/exposure. In the case of soil pollution, this exposure includes inhaling
VOCs (volatile organic compounds),
consuming soil particles when drinking water, etc.
The situation is
exacerbated by the consumption of dangerous substances that put our health at
risk. The level of exposure is expressed in ADI (acceptable daily intake).
Please note that ADI differs from person to person. As such, an average figure
applies.
Functions of soil
With regard to soil
pollution, it is advisable to consider the different functions of the soil,
and the relevant quality assessments to be adopted.
·
supportive function for
buildings, roads and other constructions
·
productive function: growth
medium for natural vegetation and agricultural crops to feed people and
animals.
·
filter function for water
·
ecosystem function; life in
the soil makes a major contribution to the cycle of C, N and S.
To acquire a better
understanding of these functions, it is essential that we have a general understanding of the
concept of soil.
Soil and ground
What is the difference
between soil and ground?
·
The term ‘ground’
refers to all the loose natural materials found at the earth’s surface. In
terms of composition, it is an undefined material. The material consists of
mineral matter and organic components that can be retraced to plant remains and
conversion.
·
The term ‘soil’ refers to the arrangement of the individual
soil particles, their size and how they occur in nature. Chemical, physical and
biogenic processes play an important part in soil formation.
A closer definition
The Dutch language fails
to differentiate the terms ‘soil’ and ‘ground’. This problem can be solved by
including a definition.
Soil and ground are made
up of solid, liquid and gassy constituents. Solid constituents are divided into
mineral and organic constituents.
The naming of ground
types is based on particle-size distribution of the mineral particles. Please note that
most grounds do not have a homogenous particle size. In other words: the
designation ’sandy ground’ implies that the majority of particles fall under
the particle size fraction of sand.
Particle size
We can distinguish the
following particle size fractions:
·
to
2µ: clay fraction or clay
·
2µ
to 50µ: silt or loam
·
50µ
to 2000µ: sand (2000µ= 2 mm)
·
2 mm to
64 mm: gravel
Organic matter
The organic matter in
ground is made up of decomposed plant remains. If these remains form a thin
layer on the soil surface, we refer to them as humus, which is brown-black in
colour. Thicker layers of organic material (up to several metres thick) are
known as peat.
Due to excess water, the plant material has not been converted into humus.
Peat is primarily converted into humus following drainage of moist peatland, in
particular under influence of oxygen.
Water contained in the ground can take on different forms. A
distinction is made between
·
groundwater:
this water fills all pores between the particles, both big and small, and flows
freely.
·
The upper
limit of the groundwater is known as the ground-water table or phreatic level.
·
The depth
(or height) of the ground water is always measured in relation to the ground
level
·
capillary
water: this water saturates the fine pores and fissures of the
ground, and is unable to move freely.
·
swell water and adhesion water: water in and around the solid soil particles.
·
Capillary water, swell water and adhesion water are also known as
soil water.
The colour of drilled water
The groundwater level of
a terrain can easily be established through soil drilling. In the Netherlands,
the ground beneath the ground-water table – fully saturated by water – is grey in colour
due to iron having the bivalent oxide FeO.
Above the phreatic level, iron only occurs as Fe2O3, which is rusty in colour. This method is not 100% foolproof
however, as numerous grounds in the Netherlands contain little or no iron.
Groundwater tables
Groundwater tables are
divided into water-table classes, where the highest mean groundwater level (HMGL) and lowest mean groundwater level (LMGL) groundwater level is processed. The groundwater
level is determined in relation to the ground level; the depth of the
groundwater is representative.[378] The annual natural
fluctuation of the groundwater in the Netherlands amounts to several
centimetres (10 or more). This movement is characterised by rust stains in the
grey-blue groundmass.
|
Gt
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
|
GHG
|
-
|
-
|
<40
|
>40
|
<40
|
40-80
|
>80
|
|
GLG
|
<50
|
50-80
|
80-120
|
80-120
|
>120
|
>120
|
>120
|
|
N.B. groundwater level in cm's below ground level.
|
|
|
|
Fig. 1035 Main subdivision of the water-table classes
|
Groundwater flows
Downward g roundwater flows are the
result of differences in groundwater levels in an area. Although the general
direction of the groundwater flow is known, it will need to be determined for
local situations.
In addition to horizontal groundwater flow, we
can also identify a vertical movement of water in the ground. This is known as
effluent seepage (kwel), where the water ‘surfaces' from the ground-water, and
infiltration, characterised by ‘downward movement’ of water.
Soil pollution can
spread through the soil through groundwater flow. An insight into the degree,
velocity and direction of spread is therefore essential.
|

|
|
|
|
Fig. 1036 Horizontal groundwater
flow
|
|
|
Soil vapour
Soil vapour occurs in all areas where the pores of the
soil are not saturated by water. This air plays a part in all biogenic
activities in the ground, but can also be relevant for the different chemical
processes in the soil.
The composition of this
soil vapour can vary strongly. The air is usually more or less identical to the
atmosphere. However, because of the chemical pedological processes and soil
pollution, the composition can differ significantly from the atmosphere, and
even be toxic.
On the basis of the
solid constituents of the ground, it can be classified into sand, clay and
peat.
·
sandy ground; this ground primarily consists of mineral soil particles
with a particle size of 50 to 2000 mu, while the clay content (particles) is
less than 8% of the overall weight per unit of ground; ground permeability is
good
·
clay; this ground contains at least 25% clay fraction; ground with
a clay content of 8-25% is known as sandy clay; ground permeability is poor or
non-existent.
·
peat ground; this ground is primarily made up of decomposed plant remains
other than humus. The organic dust content must be at least 22.5% of the
weight. The other constituents are mineral and can contain particle sizes of
clay and sand.
Until comparatively
recently, planning permission applications needed to include a so-called
"clean soil
statement".
This has been replaced by a suitability certificate, indicating intended
purpose. A soil survey report needs to be submitted during the application
stage. The investigation must be carried out in accordance with the "Soil
Protection Guidelines".
If the exploratory survey (historic survey) reveals signs of soil pollution, a
follow-up investigation will be required.
Historic survey
When drawing up his
historic survey report, the investigator makes use of standardised survey
setups, as well as municipal information and assessments. In many cases, the
relevant council can provide information on behalf of the "historic survey".
Based on the outcome of the survey, an exploratory investigation is instigated
if serious contamination is suspected. The sole purpose of this investigation
is to indicate the incidence of serious soil pollution.
Setup
and criteria
The setup and criteria
which the investigation must satisfy are laid down in two protocols:
· "Protocol voor het oriënterend onderzoek" (naar de aard en concentratie van
verontreinigende stoffen en de plaats van voorkomen van bodemverontreiniging)
("Exploratory survey protocol" (into the nature and concentration
of contaminating substances, and the location of soil pollution) SDU, The Hague
1993).
· "Protocol voor het nader onderzoek" (naar de aard en de concentratie
van verontreinigende stoffen en de omvang van bodemverontreiniging) deel 1,
SDU,'s Gravenhage 1993.
·
("Follow-up investigation protocol” (into the nature and concentration of contaminating
substances, and the scope of soil pollution) part 1, SDU, The Hague 1993).
On the basis of both
protocols, an overview is included of the survey methods to be deployed,
including information relevant for building contractors. If you wish to carry
out this survey yourself, you will be required to comply with these protocols.
|

|
|
|
|
Fig. 1037 Research strategies in
protocols
|
|
|
|
|
|

|
|
F.P.J. Lame and R. Bosman (1993)
|
|
Fig. 1038 Exploratory survey
protocol
|
|
|
Terrestrial soils and waterbed soils
As demonstrated by the
above diagram, the exploratory survey is divided into terrestrial soils and
waterbed soils, while the survey itself is divided into an exploratory
investigation with a concluding report, and a more detailed investigation in
the event of soil pollution. This investigation is also concluded with a
report.
An exploratory survey must be carried out at all times to obtain a
suitability certificate to commence building work. This process involves
collecting information and data on past and present use of the site, as well as
the soil conditions, soil composition and the (geo)hydrologic setting. This
might also involve the pollution crossing terrain boundaries, from the location
"outwards", and "outwards" towards the location. Pollution
might also concern the ground beneath the buildings, in particular if we are
dealing with a permeable soil such as sandy ground.
The investigation
includes an on-site visit. During this visit, soil drillings can be carried out
to gain an impression of the soil composition and the likely contamination
detected through sensory perceptions (colour and odour).
Please take your own
safety into consideration; be careful when inhaling and touching substances. If
you need to smell and/or touch something, please do so in small quantities at a
time.
Terrestrial soils
The sampling strategy of
the follow-up investigation is based on information obtained from this
"field visit" – such as location and structural condition of the
buildings.
With regard to
construction work, we will confine our research to terrestrial soils. In cases
of contaminated subaqueous soils, readers are referred to the research methods
detailed in the above literature.
As previously mentioned,
this information needs to include details on:
·
past and present use of the site
·
the soil composition and geo-hydrologic settings
of the site.
As a minimum,
information on past and present use of the site must contain the following
details:
·
past
purpose(s) of the location and immediate surroundings;
·
location of
occurrence of possible sources; for example legal or illegal dumping and
discharging, leaking (underground) pipes and tanks. Council registrations of
pipes and storage tanks are a useful tool in detecting the source of
contamination.
·
information
on potentially contaminating activities, such as production processes, storage
and transfer locations. Remember also to draw up an inventory of the relevant
substances. An indication of the location of these activities, if possible,
will simplify inventory activities and the investigation.
·
methods and
materials used in the past for preparing a site for building, including opening
up the site.
·
details of
in-situ cables, pipes, debris, consolidations.
·
past and
present activities on adjoining terrains.
·
investigations
into soil pollution on neighbouring or adjacent terrains
·
inventory of
past users of the terrain, with their activities from approx. 1900.
As a minimum, this
information must encompass the following:
·
on-site soil
composition, both shallow and deep (over 10m); information obtained from soil
drilling tests and drilling;
·
depth of the
ground water
·
horizontal
and vertical movements of the ground water (effluent seepage, seepage and
groundwater flows)
·
position of
water channels and other surface water (also drained)
·
presence of
groundwater sources and groundwater drawoff
·
prevention
of brackish and/or salty ground water
·
results of
earlier soil surveys on-site or in the immediate surroundings; also include
past surveys into soil pollution.
Adding contaminating substances and microbiological activities
It is advisable to
incorporate into the survey research into the properties of contaminating
substances and microbiological activities. Although it is not compulsory to
include this information, it can provide a valuable insight into the problems,
and assist in selecting an investigation strategy and, if need be, determining
the remediation method.
Past and present use
The information on past
and present use of the site, as well as the information on soil composition and
geo-hydrologic settings of the site, needs to be incorporated into the
exploratory survey report, including relevant sources.
How can we obtain the
relevant information?
·
use recent
maps: topographical, from the land registry and maps of pipelines and mains, as
well as soil and geological maps including legends. The local council office
can usually provide historic data.
·
use of old
and recent aerial photographs, which can be obtained from the municipal
topographic service and numerous aerial photography firms. Additional tools
include infrared and other recordings falling under the heading of ‘remote
sensing images’.
·
exploratory
visit to the site, carrying out field observations and soil drillings to take
samples.
·
investigation into archives, permits and
dossiers (under the Nuisance Act) relating to past and present use of the
terrain
·
interviews
with (former) employees and the local community
·
use of
archives of different municipal, provincial and government institutes
·
branch-information
concerning past use of the terrain in relation to possible contamination
·
historical
information from council and water boards.
This information must be incorporated in the report, concluding
the exploratory survey.
If all (writing desk)
investigations indicate the likelihood of soil pollution, the survey must be
extended to include information on the nature and concentration of the
contamination collected on-site and laboratory analyses. This effectively is
the start of the exploratory survey; a certain degree of in-depth research is
required. A section of the preceding research must be expanded and deepened, as
the results of the exploratory survey indicate a suspected case of soil
pollution and a rough understanding of the contaminating substances. The
distribution of these substances has also been mapped out in outline. On the
basis of this information, a strategy is developed for the research methodology
in general, and samples taken. The selected method(s) are subjected to tests, essential
for eliminating potential mistakes and focussing the investigation, if need be.
This survey reveals
whether we are actually dealing with soil pollution, and is concluded with a
report, indicating the presence of soil pollution and recommendations for
"further research".
In the event of a
contaminated land soil, it is not necessary to examine the groundwater,
provided the mobility of the contaminating substances is negligible. It would
however be wise to do so, as most contaminating substances are either soluble
in water or present in liquid form in the ground.
Sensory perceptions of
contamination – by smell and/or perception or the identification of something
"different" in the ground - is not really objective, but rather
indicative. In addition, complicating factors must be taken into consideration,
such as potential health risks for the observer.
Visual perceptions can
also be clouded by the natural colour of the soil.
With regard to safety, VROM
(Environment Ministry) has produced a series of publications. When carrying out
a soil sample, a certain degree of care must be taken, not only by those taking
the sample, but also by onlookers. As a minimum, warning signs must be
displayed in the event of assumed contamination. Even better would be to
temporarily close off the site.
In principle, there are
different contamination types and therefore different sampling strategies.
Homogenously spread
contamination requires evenly distributed sampling. This is based on 1000 m2
spatial units (RE) in
the horizontal plane. Per RE, 3 drills must be carried out, whereby the
resultant ground samples are put into a mixed sample of the suspect layer and
analysed.
An alternative sampling
method is used for heterogeneously distributed contamination in known and
unknown place of occurrence. As the preceding investigation has determined the
type of contamination and its spread, a specific sampling method can be drawn
up.
Needless to say,
research results will need to be tested.
The exploratory survey
is concluded with a report. In the event of actual soil pollution, a follow-up
investigation will be carried out in accordance with the applicable norms.
In principle, anyone can
carry out the survey, provided the details on past and present use have been
incorporated in the final report. The same applies to information on soil
composition and the geohydrolic setting. Soil samples that require analysis can
be carried out in a specialist soil analysis laboratory on the instructions of
the researcher.
The exploratory survey
can also be entirely outsourced to a specialist research agency.
|
|
|

|
|
F.P.J. Lame and R. Bosman (1993)
|
|
Fig. 1039 Protocol for follow-up
investigation
|
|
|
The follow-up of an exploratory survey
Having completed the
assessment of the exploratory survey, plans are now drawn up for a follow-up
investigation (including additions to the exploratory
survey).
The aim of this
investigation is to establish the nature and concentration of the contaminating
substance(s) in both the horizontal and vertical plane.
An insight into the
local soil composition is essential, as is soil sampling. Regulations have been
drawn up for this purpose. Soil sample analyses and results interpretations
must be carried out in accordance with the protocol.
A follow-up report is
drawn up on the basis of the results.
The contents of a follow-up investigation
This report must
comprise the following information[379]:
·
nature of
the pollution
·
concentration
of the pollution
·
extent of
the pollution
·
need for
remediation
·
urgency of
remediation
N.B. this report does
not offer advice on whether remediation is required, nor on the remediation
method. These decisions are taken by the relevant institutions.
In principle, anyone can
carry out this follow-up investigation. However, due to the substantially more
complex nature of this investigation – in particular with regard to the
behaviour of substances and pedologic research, it would be advisable to enlist
expert help.
A systematic approach
has been drawn up to determine the level of urgency for carrying out soil
remediation work. This approach is partially based on the existence of
unacceptable risks in the event of serious soil pollution. The eventual
decision to carry out remediation work is taken by the competent authority.
This problem falls
outside the scope of this dissertation.
Further information is
contained in the Urgentie van bodemsanering (urgency of soil remediation),
published by the SDU.
In view of the fact that
most incidences of soil pollution are likely to occur in industrial sites, we
have confined our research to these areas. It must however be noted, that these
terrains are also found in built-up areas, and that a petrol station and garage
in a residential area may also be a potential contributor to soil pollution.
Causes
In general, the causes
of pollution on industrial sites include[380]:
·
leaking
(underground) storage tanks and company sewers.
These types of leaks are frequent occurrences, spanning longer periods.
In addition, the replenishment of tanks can cause numerous problems.
·
Old storage
tanks for central heating oil are often located in the vicinity of residential
buildings
·
discharges
directly into the ground of the industrial site
·
dumping
company waste on own site
·
land fills
containing own company waste and/or waste matter such as ash, waste products
and cinders from incinerators.
·
calamities
such as fire, explosions, floods, pipe fractures etc.
Ignorance, mistakes, leakages and accidents
Many contaminating
substances have entered the ground in the course of time due to ignorance,
mistakes, leakages and accidents such as spillages when transferring material
or fuel.
The absence of clear
operational regulations governing the handling of raw materials and the end
product with regard to storage, transfer and carriage, as well as the disposal
of waste matter, have almost certainly contributed to soil pollution.
The often lackadaisical
attitude of managers and operational staff is a further culprit.
In addition to
industrial sites, soil pollution regularly occurs in waste dumps (rubbish
tips), storage yards of (polluted?) ground, mines, quarries, gas and oil rigs
and salt extraction areas etc. Pollution may also be generated by the re-use
of, for example, previously contaminated building materials, as concrete
aggregate. In Rotterdam for example, contaminated debris of WW2 aerial
bombardments is still causing significant problems. Agriculture and horticulture are also
potential polluters due to their use of pesticides and fertilizers.
The standards governing
the most frequently occurring forms of soil pollution are drawn up in a
"test table" for ground and groundwater in the Leidraad Bodemsanering
(Soil Clean-up Guidelines). These standards are subject to alterations, and can
be amended in line with recent surveys. As such, it is essential that the most
recent tables be used. It seems best therefore to use the term "indicative
target values", which are divided into A, B and C values.
·
The A value is the reference value.
If this value is exceeded, we are dealing with contamination[381]. The A value differs per soil types, as
adsorption processes are particularly relevant in clay and peat grounds. In
other words: if this (contaminated) ground has an A value, it is suitable for all purposes.
·
The B value is an indicator of
contaminated soil; it does not reveal to what extent the soil is contaminated.
Further research is required in accordance with the “exploratory survey” protocol.
·
The C value is the actual test
value. In this case, soil remediation is required in accordance with the
“follow-up investigation” protocol.
The system of A, B and C
values was replaced in 1995 by a system of clean soil target values[382] (new A value) and soil remediation intervention values[383] (C value). The intervention values are based on risk assessments,
highlighting risks to the eco system as well as risks to man.
Industrial sites are
categorised as follows in soil pollution surveys:
·
former gas
factories
·
former and
existing industrial sites
·
former and
existing car and machine wreck depots
·
former and
existing tips in general
·
former and
existing goods transhipment sheds
·
former and
existing borrow areas (coals, oil, salt, gas, clay, rocks etc.)
Costs
In 1991, soil
remediation costs amounted to approximately 84 billion Dutch Guilders, and
primarily concerned remediation of former industrial sites.
Company operations
The relationship between
soil pollution and industrial sector is self-evident. The risk of soil
pollution is effectively dependent on company operations [384].
|
|
|
Business operation
|
Pollution
|
|
metal and galvanic industry
|
all kind of heavy metals,
cyanids aromates and chlorinated solvents (Tri and Per)
|
|
paint and dye industry
|
all kind of heavy metals,
PCB’s, aromates and chlorinated solvents (Tri and Per)
|
|
graphic industry
|
idem
|
|
textile industry
|
chlorinated solvents (Tri and
Per)
|
|
chemical lavendaries and textile cleaning service
|
all kind of heavy metals, pak’s
and chlorophenol
|
|
carpentry and wood preserizing
|
|
|
tanning and leather working industry
|
hydrocarbons and chromium
|
|
petrol stations
|
mineral oils, aromatics and
lead
|
|
garages
|
mineral oils, aromatics, lead
and battery acid
|
|
breaker’s yard
|
all kind of heavy metals
|
|
pesticide industry
|
halogenated, hydrocarbons,
aromatics, mercury, tin and arsenicum.
|
|
|
|
Fig. 1040 Overview of prominent
forms of soil pollution per operation
|
|
|
Soil pollution can take
on different forms, depending on chemical composition, phase (gas, liquid,
solid) and ground type. Clay ground particles for example can be contaminated
through adsorption,
immobilising the particles. The intervention values (previously B and C values) differ for clay
grounds and sand grounds. Sand ground is unable to form a compound with
contamination particles.
Types of form
Incidences of pollution:
·
solid form –
solid particles: metals, compounds of heavy metals and metalloids
·
adsorption -
cation: adsorption of soluble salts of heavy metals to clay particles and
organic components of the ground (humus or peat)
·
adsorption -
molecule: molecule adsorption of aliphatic and aromatic compounds to organic components
of the ground
·
liquid phase
(insoluble or poorly miscible in water): mineral oil, petrol and organic solvents. Liquid occurs in the soil in droplet form or as a film
surrounding the ground particles. In this type of pollution, the specific
weight of the liquid plays an important part. Liquids that are heavier than
water will form a layer above a poorly permeable layer, while liquids lighter
than water will form a layer on the ground-water table.
·
soluble in
water: occurrence in groundwater
·
gas phase:
aromatics (BTEX), volatile components of petrol, diesel oil and other mineral oils, volatile chlorinated hydrocarbons.
Types of content
The above pollution
types can be divided up into a number different categories, which in turn can
be categorised per industry sector.
Pollution types:
·
heavy metals and metalloids: chrome, cobalt, copper, cadmium, nickel, arsenic, zinc, tin, mercury, lead and antimony. Occur as metal and as oxide, sulphate, nitrate, halogenated, carbonated or silicate forms.
·
complex cyanides and free cyanides
·
aliphatic and aromatic hydrocarbon and mineral oils.
·
volatile halogenated hydrocarbon:
Trichloroethylene, Perchloroethylene
·
non-volatile halogenated hydrocarbon:
Polychlorobiphenyl (PCB), different types of pesticides
·
other compounds: ammoniac, acids, lye, phosphates, sulphates, nitrates
Remediation techniques have been under development in the Netherlands
since 1980. As soil remediation is a relatively new technology, large-scale
techniques are still being developed.
Remediation methods can
be categorised into two main groups, with a third group acting as a combination
of the main groups[385].
·
soil recovery
·
isolating the pollution
·
combination of isolation and recovery.
Soil
remediation by excavating, followed by soil purification or tipping.
The primary purification
techniques[386] involve:
·
thermal and
extractive methods for removal and
·
biological methods for alteration.
Tipping must be considered, if there are no adequate
soil purification techniques for this specific situation[387]. Temporary storage is considered if the purification plant has a
limited capacity[388].
Soil remediation through
in situ purification is currently under development. In addition to
not having to excavate the ground, other advantages of this method include its
relatively low costs and no interruptions to the company operations[389]. The techniques applied include flushing out the contaminated
soil ("washing"),
extraction of polluted air streams, chemical or biological conversion and
removing pollution via an electric field.
Most contaminated soils
are cleaned up by excavating, followed by soil purification. In situ soil
purification occurs on a limited scale, but will become increasingly
commonplace in future.
This
process effectively involves containing the spread of the pollution. This can
be achieved in a number of different ways[390]:
·
installing vertical and horizontal screens, such
as sheet piling, building plastics, mastic layers, bentonite-cement slurry
walls etc.
·
pumping up groundwater and/or infiltration water.
·
using fixation techniques; immobilising the
pollution.
Isolation is primarily
used in cases of extensive pollution, where "hot spots" – places with
the highest pollution levels - are isolated in order to prevent further spread
before complete remediation, or in order to be cleaned up first[391].
In cases, where it is
not (yet) possible to recover the soil for all types of pollution, the
unrecovered areas are isolated.
Soil purification
methods are aimed at removing the pollution or converting the pollution into
components that pose a minimal, or acceptable, risk to man and the eco system[392]. The latter method comprises biological degradation and
conversion of the pollution. The characteristics, on which the soil
purification process is based, are determined by the specific (chemical)
properties of the pollution.
The most prominent
properties are:
·
phase: gas, liquid, solid (volatility, boiling
point)
·
solubility in water or in another
solvent
·
adsorption/absorption (electric properties)
·
chemical stability
·
thermal stability
·
magnetic properties
·
biodegradability/convertibility
·
weight and form of the particles
·
size and shape of the particles.
Information needed for soil purification
In addition to the soil
purification technique, the "remediability" of the ground also plays
an important part, as soil purification comes with a price tag attached. Soil
remediation experts will need specific information, such as the nature and
concentration of the pollution, the presence of other contaminants and debris,
plastic, cinders, vegetation remnants etc. Knowledge of the soil in terms of
grain-size frequency distribution, organic dust content and moisture content
are also essential factors in the world of soil purification.
This chapter will focus
on the following purification techniques:
·
techniques for excavated grounds;
· in-situ soil purification techniques;
·
isolating contaminated sites.
Thermal soil
purification involves increasing the temperature of the
ground to such an extent, that the contaminating substances are evaporated
and/or decomposed and evaporated. The techniques used during this process fall
outside the scope of this dissertation.
Application: all types
of organic contaminations.
In principle, this
method can also be applied to heavy metals and their compounds, provided
temperatures reach approx. 800o C.
Thermal soil
purification can be applied to any type of ground. However, grounds with (a
high content of) organic material will be susceptible to burning. Clay and loam
grounds require more energy for this process than sand ground. Furthermore,
measures must be taken to guarantee a uniform ground supply.
In thermal soil
purification, the contaminated substances are evaporated, and the vapours
filtered. The resultant emissions are subject to severe criteria under the Wet
op de Luchtverontreiniging (Air Pollution Act).
The extraction process
is divided into a number of phases:
·
putting the contaminated ground into contact with
extracting agent (dissolved in water)
·
separating extraction particles from the clean
ground through rinsing out
·
purifying the (contaminated) extract
Application: suitable
for removing heavy metals, metal compounds and organic pollution.
This method is ideal for
purifying sand soils, due to the proportionately low adsorptive forces between
sand grain and contaminant. Due to the relatively high adsorptive forces of
clay and loam grounds, this method is unsuitable, or less suitable, for these
ground types.
Biological soil purification of excavated grounds
In
this process, organic contaminants are decomposed or converted by
micro-organisms into compounds that are not harmful, or virtually harmless, to
man and the eco system.
A distinction is made
between a mineralisation process with anorganic end products, and degradation with
incomplete mineralisation.
These biological
processes are however known to cause highly toxic inorganic compounds such as
chlorinated derivatives due to the decomposition of organohalogens. It
is of vital importance that employees working on site be adequately protected.
This biologic soil
purification method is based on landfarming and bioreactor techniques.
In landfarming, the
contaminated ground is spread in a thin layer across a suitable terrain and
cleaned by natural microbiologic processes. The degradation process is
stimulated by adding oxygen, cultivating the ground (ploughing), adding lime
and nutrients for the decomposing organisms, and by proper water management.
|

|
|
|
|
Fig. 1041 Landfarming diagram
|
|
|
We can identify two
bioreactor techniques: a
dry form, comparable with composting solid waste, and a wet form in so-called
soil slurry reactors.
This technique can only
be applied to organic compounds.
In principle, this
method is suitable for all ground types, but is usually applied to sand grounds
due to its high permeability and ease of cultivation.
The disadvantages of
this method include the long duration of the soil purification process, and
difficulties in reaching the target values.
Volatile compounds are
removed by extracting soil vapours, and subjecting them to surface clean-up.
This process is known as soil vapour extraction,
and is solely applied to volatile substances such as perchloroethene,
trichloroethylene,
petrol,
benzene,
toluene,
xylene,
ethylbenzene and methylene chloride.
This method can only be
applied to permeable grounds such as sand.
Disadvantages include
difficulties in reaching the target value, longevity of the process (can take
several years) and, in the case of mineral oil, the leftovers of heavy
components.
The process of bio
restoration consists of optimising the conditions for
micro-organisms responsible for ground purification.
This method is primarily
applied to sand grounds, as the contaminant must be easily degradable. As a
result, this method is mainly used in pollution types involving mineral oil and
low molecular weight polycyclic aromatic hydrocarbons.
This method also has its
disadvantages: it takes a long time to achieve the target value, if it is
achieved at all.
Contaminants are extracted
from the ground through the infiltration of a water-based extracting agent,
causing a chemical reaction. The extracting agent, containing the dissolved
contaminants, is then pumped up and cleaned above ground. Liquid extraction can continue until the desired target value
has been reached.
Application: primarily
in easily permeable grounds such as sand grounds. This method is suitable for
all pollution types that are soluble in extracting agents, including heavy
metals,
low molecular weight polycyclic aromatic hydrocarbons,
low molecular weight halogenated solvents, phenol and benzene.
The total duration of
this process ranges from several months to several years. It is not always
possible to achieve the target value.
The method of
electro-reclamation is based on three direct current transmission
lines: electro-osmosis, electrophoresis and electrolysis.
Ions or ion complexes
are transmitted through liquid between the soil pores under influence of an
electric field. This causes the polluting ions to be carried to the electrodes
and removed via a pumping system.
Application: this method
is ideal for purifying clay soils contaminated by heavy metals.
Its main disadvantage however is its energy inefficiency.
Conclusion in-situ soil purification techniques
The above in-situ soil
purification techniques are currently operational in the Netherlands. A certain
degree of experience has been gained with most of these techniques, in
particular underground contamination and polluted petrol stations. At
present, it is virtually impossible to achieve the A value using these
techniques. Furthermore, they are only suitable for homogenous areas. The
remediation methods take a relatively long time to implement. Having said that,
these in-situ soil purification methods also have a number of advantages,
including underground remediation, tackling deep contaminations without the
need for earth moving, and causing minimal disruption.
It is clear from the
above, that researchers in the Netherlands are currently on a steep learning
curve in terms of remediation techniques, learning from every new piece of
technology, unveiling new and at times unexpected information. In my opinion,
promoting in-situ soil purification is highly desirable, given its advantages.
One solution would be to increase the costs of tipping, and inspecting tipping
activities. It might also be useful to carry out a feasibility study into the
use of A-value as a follow-up remediation value. Greater flexibility in
remediation policy would promote the use of these relatively simple techniques.
A polluted soil is
screened off, thus containing the spread. This method can involve closing off
the site and preventing potential spread via soil vapours.
This civil-engineering
isolation technique is based on the erection of impermeable walls
of steel, bentonite-cement slurry walls and grout curtains. Preventing sideward
spread alone will not suffice, as the upper surface and lower surface must also
be isolated.
This technique can be
applied to all areas. Disadvantages include the behaviour of isolation walls in
the course of time. Only steel walls are moveable.
Geo-hydrologic isolation involves pumping up the groundwater of a
contaminated site, preventing the spread of pollution in the groundwater. This
pumping action can be combined with water infiltration from an adjacent area.
Application. This
technique is difficult to apply in built-up areas, as soil layers are generally
prone to settling during water drawoff. The degree of settlement depends on the
ground type.
This technique releases
(lightly) polluted water that needs to be discharged. This cannot simply be
done into a sewer or open water, so the water has to be cleaned prior to
discharging.
Site management and inspection
All the above isolating
techniques require adequate site management and inspection, even in the event
of (partial) failure of the technique.
Living layer in urban areas
A special isolation
method is being applied to a number of urban areas. Ground that is proving
difficult to clean due to the surrounding buildings, is isolated from all sides.
The overburden is partially excavated and isolated. A layer of clean ground,
known as the living layer, is
applied on top of the insulating layer. When using this terrain for building
work, care must be taken that this upper insulating layer is not
"infiltrated". This method is currently being applied in the city
centre of Amsterdam.
One of the biggest
problems associated with contaminated sites is that they contain a significant
amount of urban, industrial, building and demolition waste in addition to
polluted ground.
Pollution is rarely of a
singular nature; it is usually characterised by a combination of contaminating
substances, which frequently need to be extracted in different ways from the
ground.
Some substances are
impossible to extract from the ground, or require extraction methods that have
not yet been discovered. In this case, isolation is currently the only solution
available.
Combining soil purification and site preparation
Purification
of contaminated soil requires a lot of shifting of the ground. As such, might
it not be wise to draw up a plan of approach for preparing the site, as well as
a soil purification plan, and effectively combine these two plans? The
underground infrastructure can be installed during or immediately after
clean-up.
In instances, where a
site is located in the middle of a remediation area, where space is at a
premium, this combined approach can yield some surprising results.
Involvement of experts
The follow-up
investigation can be carried out by anyone, provided this is done in accordance
with the exploratory survey and follow-up investigation protocols, and the
requisite details and documents have been submitted in report form to the
relevant municipality. It is however recommended that the relevant surveys are
carried out by an expert. Soil samples may prove problematic; these can be
analysed by specialist laboratories in accordance with the methods indicated.
(A list of ground survey laboratories has been included.)
Technical laboratories
carrying out these surveys have acquired a certain reputation in this field and
are therefore often readily accepted as authoritative by local authorities.
These laboratories usually include an executive body, leading to a conflict of
interests.
Contents.................................................................................................................................... 595
7.1 Mapping............................................................................................................................ 596
7.1.1.... Introduction.................................................................................................................... 596
7.1.2.... Types of maps................................................................................................................ 597
7.1.3.... Perception and reading of (topographical) maps................................................................. 600
7.1.4.... Map analysis and interpretation........................................................................................ 607
7.1.5.... Making of maps and communication................................................................................. 609
7.1.6.... Legends for municipal zoning plans.................................................................................. 612
7.2 Child
perception............................................................................................................ 622
7.2.1.... Introduction.................................................................................................................... 622
7.2.2.... The growing scale of perception........................................................................................ 623
7.2.3.... Field of vision.................................................................................................................. 625
7.2.4.... The composition of a scene............................................................................................. 626
7.2.5.... Conclusions for urban design........................................................................................... 627
7.3 Composition
analysis................................................................................................... 629
7.3.1.... Variation........................................................................................................................ 629
7.3.2.... Scale levels.................................................................................................................... 630
7.3.3.... Focus............................................................................................................................ 632
7.3.4.... Morphological reconstruction............................................................................................ 633
7.3.5.... Structure in terms of openness and closedness................................................................. 633
7.3.6.... Functional differentiation.................................................................................................. 635
7.3.7.... Intention......................................................................................................................... 637
7.4 Legends........................................................................................................................... 638
7.4.1.... Resolution and tolerance................................................................................................. 638
7.4.2.... Scale-sensitivity.............................................................................................................. 639
7.4.3.... Unconventional true scale legend units.............................................................................. 640
7.5 Scales
of separation.................................................................................................. 643
7.5.1.... Potentials rather than functions........................................................................................ 643
7.5.2.... Conditional considerations............................................................................................... 645
7.5.3.... The context and perspective of consideration..................................................................... 646
7.5.4.... Relief between built-up and vacant areas........................................................................... 650
7.5.5.... Interaction with exterior spaces........................................................................................ 654
7.5.6.... An academic example of urban architectural rules.............................................................. 657
7.6 Boundaries
of imagination.......................................................................................... 659
7.6.1.... Creativity........................................................................................................................ 659
7.6.2.... Possible futures.............................................................................................................. 661
7.6.3.... Environment, the set of conditions for life........................................................................... 664
7.6.4.... Starting by difference....................................................................................................... 665
7.6.5.... The importance of diversity in ecology............................................................................... 667
7.6.6.... Conclusion..................................................................................................................... 669
Outline
The concept of mapping is basic
to the visual representation of the earth. Maps used to be dominated by a
strategic and military use, nowadays the use of maps has extended to use for
quite different types of applications like wayfinding, tourism, travel and also
spatial planning.
In urban design and landscape
architecture, we see maps as a form of visual representation of the landscape
be it urban, rural or infralandscapes. Maps can also be looked at from an
artistic point of view. Especially old maps are sometimes pieces of art.
Landscape architects and urban designers cannot work without maps; an striking
difference with architects. It is not only important to learn how to read and
interpret maps; the relation between map image and field image needs special
attention and takes time to learn. In the design process it means that
abstraction and reduction play an important role in urban design and landscape
architecture due to sheer size and scale. So maps and cartographic techniques
are basic for the representation of study areas and design interventions alike.
Finally you should be able to
make use of cartographic information in your drawing of plans at different
levels. Problems of reduction and enlargement, of representation of hierarchy
and of a 2D-representation of spatial situations should be basic knowledge for
a designer.
'Mapping' is not always referring
to making maps. It can also be used in a metaphorical way. In this context for
instance 'cognitive mapping' (Downs & Stea, 1973) is used but also in
expressions like 'mapping the city' that has nothing to do with maps as such
but with a way of visualising urbanity.
Cartography and maps
What is a Map? A map is a graphic
representation or scale model of spatial concepts, a means for conveying
geographic information. Maps are a universal medium for communication, easily
understood and appreciated by most people, regardless of language or culture.
Basic to the understanding of the
concept of maps is that it is a "snapshot" of an idea, a single
picture, a selection of concepts from a constantly changing database of
geographic information.
Modern Maps
Maps became increasingly accurate
and factual during the 17th, 18th and 19th centuries with the application of
scientific methods. Many countries undertook national mapping programs.
Nonetheless, much of the world was poorly known until the widespread use of
aerial photography following World War II. Modern cartography is based on a
combination of ground observations and remote sensing.
Cartography or mapmaking (in
Greek chartis = map and graphein = write) is the study and practice of making
maps or globes. The cartographic process rests on the premise that there is an
objective reality and that we can make reliable representations of that reality
by adding levels of abstraction. Maps are basically geographical or
topographical models of the land. Maps function as visualisation tools for
spatial data. Spatial data is acquired from measurement and can be stored in a
database, from which it can be extracted for a variety of purposes. Current
trends in this field are moving away from analogue methods of mapmaking and
toward the creation of increasingly dynamic, interactive maps that can be
manipulated digitally.
Standard features on modern maps
are: a scale that is used for precise interpretation of phenomena, conventional
signs with legends, a table that contains supplemental information about the
specific places on the map, and the practice of orienting maps so that North is
at the top and East to the right of the map.
Cartography and communication
Maps are a universal medium for
visual communication about the earth. Cartography is related to, but different
from other forms of visual communication. Cartographers must pay special
attention to coordinate systems, map projections, and issues of scale and
direction that are in most cases of relatively little concern to other graphic
designers or artists. But, because cartography is a type of graphical communication,
some basic insights to the demands of cartography can be learned from the
practice of graphical communication and statistical graphics.
Maps are traditionally subdivided
into topographic and thematic maps.
Topographic maps
Topographic maps are meant to
give the most accurate as possible description of the surface of the earth and
the objects that are on that surface like roads, rivers, buildings etc. and
their names. Topographic maps are general reference maps showing coastlines, cities,
and rivers and use contour lines to show elevation differences. All topographic
maps have a military origin; they were first of all made for military use.
Nowadays this has changed — military still use topographic maps — many other
people make use of topographic maps, realtors, hikers, geographers etc.
Nowadays most topographic maps are made on the basis of aerial photographs.
In Holland topographic maps are
called 'Topografische kaarten', in Britain 'Ordnance Survey Maps', in France
'Cartes IGN'. Note the difference with a 'topological map'!
A topological map is a very
general type of map that show relations but not exact locations, the kind you
might sketch on a napkin. The maps of the Metro in Paris, the Underground in London
and the railway maps of the Dutch Railways are examples of topological maps.
|

|

|
|
|
|
|
Fig. 1042 The topographic positions
of the Metro stations
|
Fig. 1043 The topological
representatin. To see the differences, focus on one line for instance line 1;
Porte de Vincennes to Étoile on both maps
|
|
|
|
Thematic maps
soil maps, geological maps,
census maps, historical maps show only a certain aspect like soil types,
geology, distribution of population, history of places or events are thematic maps.
Census maps focus on population
characteristics of a country. Census maps are thematic maps focusing on
population distribution as well as data on such items as age, ethnicity, and
income. Census maps help governments provide services to its citizens and plan
for the future.
Types of maps being used in urban
design and landscape architecture are — besides topographical maps — soil maps,
land use maps, historical maps, road maps, hydrological maps etc.
A more modern division can be
made between 'map sorts' and 'map types'
Maps sorts
Maps sorts refer to how maps are
used; the function of maps. The most important use of maps is orientation.
Whether to get across town or across the world, maps are crucial for
navigation. They can help us discover the distances between objects and their
relative orientation to one another.\
There are:
1.
Orientation maps
2.
Planning maps
3.
Maps for prognosis
4.
Management maps
5.
Educational maps, atlases
Map types
Map types refer to the different
methods of mapmaking. There are nine 'map types':
1.
Chorochromatic maps
2.
Choropleths
3.
Isoline maps
4.
Point distribution maps
5.
Diagram maps
6.
Dot maps
7.
Movement maps
8.
Spatial models
The types of spatial information on a map
Any map contains different types
of spatial information:
1.
Topographic; defines the
location (where?)
2.
Thematic; defines the attribute
or quality of the information (what?)
3.
Thematic cartography involves
maps of specific geographic themes oriented toward specific user groups.
4.
Temporal; defines the time
(when is topographic and/or thematic information defined?)
Use of maps
The predominant use of maps is
for orientation and way finding. Maps can also be used to analyse the land, the
topography or any geographical phenomena represented on maps. Designers and
planners use maps as basis for their work: to study the form of the land,
occupation and land-use, spatial developments and change. This is done by map
analysis, for instance by comparing maps from different time periods. A special
topic in urban design and landscape architecture is to study the relation
between field image and map image. That is part of the visual research of the
site. You should always use topographic maps as a basis for your work; no road
maps, no city maps (unless you are analysing the road system)!
Geographical information systems (GIS)
Nowadays GIS is an important part
of map production, mapping and geographical research. GIS is a digitally based
system that adds content to the visual representation on the map. Note that this is different from
labeling. For instance the green colour on the map can refer to grassland but
in a GIS-system any surface on a map can contain information about that
surface. This information can be updated, changed and extended easily. So it
offers a possibility for a wide range of applications. The software of ESRI —
like ArcInfo, ArcView — is still most used and more or less a standard
(www.esri.com).
Learning GIS takes quite some
effort and time. There is no way we can teach GIS in the context of this
course, this is only a short course on visualisation in urban design and
landscape architecture. GIS is a specialist tool that has a different scope and
content; it is one of the many research tools for urban designers and landscape
architecture. Unfortunately we don't have a structured introductory course in
GIS in the department yet, it will definitely come in the future. Steffen
Nijhuis (S.Nijhuis@tudelft.nl) is one of the specialists at GIS and its
applications in the department of Urbanism.
The Dutch government is
responsible for the production of maps of the country. In former days the
Topographic Survey, and
nowadays the land registry (kadaster), is
officially assigned the task of producing topographic maps on the scales
1:10,000 1:25,000 1:50,000 1:100,000 and 1:250,000. Other standard maps include
soil maps, geomorphological maps and geological maps. These maps do not cover
the whole country. Soil maps, geomorphological maps and geological maps have a
standard scale of 1:50000. These maps are based on 1:50,000 topographic maps,
which are printed in grey on these maps.
Other maps
There are several other maps,
such as historical maps, older topographic maps (the most important is perhaps
the topographic military map dating from around 1850 on a 1:50,000scale),
waterway maps, sea charts, water board maps, motorway maps, cycling maps, maps
showing administrative boundaries, maps illustrating demographic spread, etc.
All topographic maps are based on a grid of 1:50,000 (see Fig. 1),
from map 1 in north-western part of the country to map 62 in the south-eastern
part of the country. These 1:50,000 maps
are subdivided into Western (W) and Eastern (O) maps, for example : in Amsterdam
no 25 O, the O stands for east. The same system is used for larger scales and
is further subdivided (see Fig.
1044).
|

|
|
|
|
Fig. 1044 Subdivision of topographical maps 1:50,000
|
|
|
|
25
|
Original military map nr. 25
|
|
|
|
|
|
|
|
|
|
|
25 west
|
25 oost
|
Divided in West and East
|
|
1:50,000
|
|
|
|
|
|
|
|
25 A
|
25 B
|
25E
|
25 F
|
Divided in 8 maps A-H
|
|
25 C
|
25 D
|
25 G
|
25 H
|
|
1:25,000
|
|
|
|
|
|
|
|
25 AN
|
25 BN
|
25 EN
|
25 FN
|
Divided in N=North and Z=South
|
|
25 AZ
|
25 BZ
|
25 EZ
|
25 FZ
|
|
25 CN
|
25 DN
|
25 GN
|
25 HN
|
|
25 CZ
|
25 DZ
|
25 GZ
|
25 HZ
|
|
1:10,000
|
|
|
|
|
|
|
|
Fig. 1045 Coding of Dutch topographical maps on different scales
|
|
|
|
|
Map reading; from form to content.
Reading maps is for a great deal
a matter of pattern recognition and being able to see structure. A map is in
some or another way a model of reality that is reduced to the structure of that
reality that is represented. Map reading includes the capability to read:
longitude and latitude, relief or elevation, land use, hydrological system,
administrative boundaries etc. Map reading, therefore, means the interpretation
of various symbols, colours or grayscales, type of lines.
|

|
|
|
|
Fig. 1046 Different
legend units in a Dutch topographic map
|
|
|
Legends; the reading of maps
You cannot 'read' a map without
legend and scale. Sometimes the legend is also called the 'key'. You can
distinguish three types of legends on topographic maps:
1.
Labels; e.g. a colour green
means 'forest'
2.
Symbols or icons; e.g. a
pumping station is represented by a symbol that is identical anywhere on Dutch
topographic maps even though all pumping stations have a different form.
3.
Scale representations; e.g.
parcels do have the same form as they have in reality, but are scaled down.
Scale; determining size and distance
Scale is relative size. A map or
relief model, to be most useful, must accurately show locations, distances and
elevations on a given base of convenient size. This means that everything
featured on the map or model (land area, distances, rivers, lakes, roads, and
so on) must be shown proportionately to its actual size. The proportion chosen
for a particular map is its scale.
The scale of a map can be defined
simply as the relationship between distance on the map and the distance on the
ground, expressed as a proportion, or representative ratio.
Different
scales
1:25.000
scale
1:5.000 scale
Scale means relative size; for
instance on a 50.000 scale, 1 cm represents 50.000 cm or 500 m.
Different
scales of the same area
Fig. 1047 - Fig. 1050 show the Faculty of Architecture building and
surroundings. The parcelling and form of the buildings is according to the real
form; scale representations.
|

|

|
|
|
|
Fig. 1047
1:50.000 (2x2 cm= 1km2)
|
Fig. 1048
1:25.000 (4x4 cm= 1km2)
|
|
|
|
|

|

|
|
|
|
Fig. 1049 1:10.000 (10x10
cm= 1km2)
|
Fig. 1050 1:5000 (20x20 cm= 1 km2)
|
|
|
|
Importing images from an electronic source at the appropriate scale
Importing the image of an area
from an electronic source with a yardstick at the appropriate scale into a word
processor similar to Fig.
1047 – Fig. 1050 could be
done as follows. Make the image in the window of the electronic source exactly
15 cm wide (and for example 10 cm high). Copy the map to the clipboard
(Ctrl+C). Note the name of the place, district and street. Note the nominal
size of the yardstick in m (for example 70m like Fig. 1050) and the
size on the screen in cm (for example 2.50 cm.) measuring it with a real ruler
from screen. Put these measures and the desired scale in an Excelsheet with
formulas as given in Fig. 1051.
|

|
|
result:

|
|
|
|
Fig. 1051
Calculations to import an image at the appropriate scale in a word processor
|
|
|
Put the map in the wordprocessor
using Ctrl+V. Keep the image selected. Select ‘lay-out’, ‘image’, ‘width’ and
enter at ‘width’ according to ‘cm wide
in Word’ (8.40 in Fig.
1051). Press ENTER. The figure has the desired scale when
you print it. Don’t forget to quote the source under each map used because of
copy rights. Don’t make more than one hard copy and only for personal study
purposes.
Screensize and printsize
However, the screen you are
looking at right now is often not A4. To check that you can adjust the zoom
percentage of the screen until you have an A4 of 21,1cm width (for example 95%,
dependent on the type of screen). Click ‘Image’ and ‘Ruler’. Check the number
of centimetres above the text on screen with a real ruler. Measure from the
centre line of the surrounding streets the size of an urban island. Check with
the yardstick in the image whether you have done it properly! Note attributes such as in this example:
there is a public space at the rear and a park on the edge of the urban island.
Add photographs if you have.
Why do we need to adjust the planimetric scale?
The smaller the scale of a map
is, the fewer the features that can be accommodated. Obviously, therefore, the
larger the scale the more comprehensive the map.
Conversion table
1 km = 1000
m = 100.000 cm
1
km2 = 100 ha = 1.000.000 m2
Map projections
A map projection is any of many
methods used in cartography (mapmaking) to represent the three-dimensional
curved surface of the earth or other body on a plane, a two-dimensional space.
The term "projection" here refers to any function defined on the
earth's surface and with values on the plane, and not necessarily a geometric
projection.
|

|
|
Source:
|
|
Fig. 1052 A map projection
|
|
|
This process always results in
distortion to one or more map properties, such as area, scale, shape, or
direction. Because of this, hundreds of projections have been developed in
order to accurately represent a particular map element or to best suit a
particular type of map. Data sources for maps come in various projections
depending upon which characteristic the cartographer chooses to represent more
accurately (at the expense of other characteristics).
Different types of projections
In the case of the 'Mercator
projection', it preserves the right angles of the latitude and longitudinal lines
at the expense of area, which is distorted at the poles, showing the land
masses there to be larger than they actually are.
Flat maps could not exist without
map projections. Flat maps can be more useful than globes in many situations:
they are more compact and easier to store; they readily accommodate an enormous
range of scales; they are viewed easily on computer displays; they can
facilitate measuring properties of the terrain being mapped; they can show
larger portions of the earth's surface at once; and they are cheaper to produce
and transport. These useful traits of flat maps motivate the development of map
projections.
Coordinate system; the defining of location
A coordinate system is just a way
of systematically denoting and labeling points in space. Numbered aisles in
supermarkets, grids on road maps, and lines of latitude and longitude on the
Earth are all coordinate systems which we use every day. Coordinate systems are
usually based on two lines, or axes, which are most often perpendicular to one
another. In a city, for instance, one building may be "two blocks north
and four blocks east", from another, in which case the compass directions
of north and east are used as a basis for the grid of the city.
|

|

|
|
Source:
|
Source:
|
|
Fig. 1053 Projecting on a plane
|
Fig. 1054 Calculations
|
|
|
|
The dawn of the Great Age of
Discovery, some five hundred years ago, greatly increased the demand for
accurate maps and charts. The explorers needed maps which covered areas much
more vast than those we have yet constructed; they required maps of nothing
less than the entire world which they were exploring. Indeed, much of the work
of these early explorers involved making newer, more accurate maps of little-
or never-traveled regions.
|

|

|
|
Source:
|
Source:
|
|
Fig. 1055 Latitude, longitude
|
Fig. 1056 Elevation
|
|
|
|
Even still, it was not until
about a century ago that a standard coordinate system to describe locations on
the Earth's surface was adopted. An international convention devised the
now-familiar system of latitude and longitude and fixed its reference points. A
line of longitude (a meridian) passes through both the North and South Poles.
They are labelled according to their angular distance from the prime meridian
which passes through Greenwich, England by international agreement. Meridians
are labelled between 0° and 180° East or West of the prime meridian. Lines of
latitude (often called "parallels") are parallel to the Equator, and
are labelled according to angular distance from the Equator- between 0° and 90°
North or South. Any point on the surface of the Earth can be uniquely specified
by just these two coordinates, latitude and longitude.
The lines of latitude and longitude
are not straight, since they are on the surface of a sphere. Nevertheless, if
one looks at a small enough region, like a city or a town, that region of the
Earth is nearly flat, so the lines of longitude and latitude appear straight
and seem to form a square grid. Note that close to the Poles, where the
meridians converge, the slant of the meridians is quite noticeable, even on
small scales, so even if they appear straight, they won't form a square grid.
GPS (Global Positioning System)
What is GPS? The Global
Positioning System (GPS) is an American worldwide radio-navigation system
formed from a constellation of 24 satellites (space vehicles) and their ground
stations. It is built and operated by the US Dept. of Defense for military use.
Europe is working on its own
system called 'Galileo'; it will be available in a couple of years and will be
more accurate. GPS uses these "man-made stars" as reference points to
calculate positions accurate to a matter of meters. In fact, with advanced forms
of GPS you can make measurements to better than a centimeter!
GPS receivers have been
miniaturized to just a few integrated circuits and so are becoming very
economical. And that makes the technology accessible to virtually everyone.
These days GPS is finding its way into cars, boats, planes, construction
equipment, movie making gear, farm machinery, even laptop computers. Soon GPS
will become almost as basic as the telephone; part of 'ubiquitous computing'.
The GPS User Segment consists of
the GPS receivers and the user community. GPS receivers convert satellites'
signals into position, velocity, and time estimates. Four satellites are
required to compute the four dimensions of X, Y, Z (position) and Time. GPS
receivers are used for navigation, positioning, time dissemination, and other
research.
> Navigation in three
dimensions is the primary function of GPS. Navigation receivers are made for
aircraft, ships, ground vehicles, and for hand carrying by individuals. All
navigation systems in cars are based on GPS. In sports like sailing GPS is used
to determine positions and navigation.
> Precise positioning is
possible using GPS receivers at reference locations providing corrections and
relative positioning data for remote receivers. Surveying, geodetic control, and
plate tectonic studies are examples.
Elevation
In geography, the elevation of a
geographic location is its height above mean sea level (or some other fixed
point). Elevation is mainly used when referring to points on the earth itself,
while altitude is used for points in the air, such as an aircraft. Difference
in elevation is also called 'relief'. Relief is in general the showing of a three-dimensional surface on a
map; the showing of hills and valleys is
not substantially different from that of representing a statistical surface
such as the rainfall distribution. People are notoriously poor at reasoning in
three dimensions and so it is no surprise that many people find relief harder
to interpret than most other information on a map. There are more than a dozen
distinct methods for showing relief and so the map designer has a wide choice.
It is more or less a convention
in cartography to use darker tones/colours for higher elevations and lighter
for lower.
Making 3-D models of topographic maps
Still a comprehensive work,
making a 3-D map on the basis of a topographic map.
Haaften (2001) gives a short
outline how to do this. Gill (2006) is more extensive in that sense.
The ‘Meetkundige Dienst’ RWS measured the elevation of The Netherlands every 5 metre. It
resulted in a database called ‘Algemeen Hoogte Bestand’ (AHN) with X, Y and Z
coordinates for every measure point to be imported in a CAD or GIS application. The database is divided in smaller parts than Fig. 1044 because of its enormous size (>50Gb). To get grip
on this incomprehensible multitude of figures you can get some of the databases
and load them one by one in Excel using an application developed for that
purpose ( Fig. 1057).
However, it is still difficult to
recognise the topographic features, because incidental vegetation disturbes the
image. So, the database is aggregated into another database with 25x25m cells
(see Fig. 1058). But even
then it is difficult to recognise the Mekelweg in Delft.
Learning to read maps by combination of sources
The more you know about the
background of an area in terms of soils, geology the better you will be able to
understand the form of the landscape and what you see on the map. Nonetheless
all urban designers and landscape architects should be able to read and
interpret maps of areas, even though you have never been there or you are not
familiar with.
Learning to read maps is a matter
of doing; only by experience you gain more insight. The legends and scales as
such are not very difficult to understand but the interpretation is the tricky
thing. Reading and interpreting contour lines is even for experienced map
readers difficult. In Holland we have the disadvantage of not having any
mountainous region so there is less possibility to practice that aspect of map
reading.
Reduction and analysis
Analysis of maps always needs
reduction. Reduction of maps (Leupen et al., 1997) is a basic technique in map
analysis. Reduction is based on abstraction but is not the same. When you
reduce information on a map, it might be one aspect. For instance when you want
to analyse the water system, you could leave out the road system in order to
focus. Depending on the purpose you leave out information in order to emphasise
other information. In case of abstraction you generalise, that is you lower the
scale and depending on the size you leave out detailed information. For
instance on the map 1:400.000 of Holland, the city of Delft is represented by a
small point or circle whereas on the scale 1:25.000 you can distinguish the
street patteren, main plaza's etc.
Working with layers
The working with layers is very
well known technique in map analysis. Formerly with (transparent) paper, now
with digital layers like they can by used in Illustrator. Say you want to
research the relation between occupation pattern and elevation of a certain
area. You then first make one layer with only the dwellings of that area. Then
you do the same for the elevation. By comparing the two you might find a
relation; for instance at Walcheren, in the province of Zeeland, you will find
that the occupation pattern is related to the higher areas; the ridges of the
former creeks. Like in statistics; finding relations is one, secondly you will
have to research whether these relations have also causal relations or are
haphazard. These research by means of layers can be done in an analogue way
(mostly with transparant paper) or digitally like the layers in Illustrator.
The principle here is that you
research vertical relations in the landscape.
Still one step further is to make
use of GIS. Nowadays analysis of maps is more and more done with GIS. The
digital analysis of geographical information and cartographic information is
not only cheaper as soon as information is available in digital form, it gives
also opportunities for larger scale research with almost infinite amount of
data.
Comparing maps in time
Analysis of maps by comparing
maps of the same area from different time periods. Historical development can
be analysed by comparing maps from different time periods of the same site. For
the city of Delft, Geurtsen (1988) did such a study for the urban development
of the city.
|
   
|

|
|
|
Source:
|
|
Fig. 1059: The
development of the city of Delft according to Geurtsen
|
Fig. 1060 Compare
this historical analysis with the present situation!
|
|
|
|
It can also be shown in one map,
like Ven (2004) did for the polders around the Dollard, up in the north in the
eastern part of the Province of Groningen.
|

|

|
|
:
|
Source:
|
|
Fig. 1061 Showing
the process of landscape development; the making of polders in the Dollard
area in the northeastern part of Holland, the process of the subsequent
polders in time
|
Fig. 1062 The
topographic map of the area.
|
|
|
|
Analysing of places by means of maps
Analysis of maps by comparing
different aspects of the map. Maps represent spaces, places by horizontal and
vertical elements. Horizontal elements are: roads, roadsystems, watersystems,
parcelling. Vertical elements are: built structures, differences in elevation,
plantation. This we call a spatial and/or visual analysis.
By adding the flows of people,
material, energy and information you can get an idea how a place works and
functions.
In most countries the relief is
much more outspoken than in Holland. Formally Holland does not have 'hills' and
'mountains'; the highest point in the South (Vaals) is less than 400 m above
sea level. Even though the differences in elevation are not outspoken, in Holland
small differences in elevation can make great differences in occupation and
land-use.
The only way to analyse the basic
topography is to make an analysis on the basis of contour-lines.
Cartographic drawing
Maps can be seen as a form of
visual communication — a special-purpose language for describing spatial
relationships. Although it is perhaps unwise to draw a direct analogy between
cartography and language, concepts such as "grammar" and
"syntax" help to explain, at least metaphorically, the sorts of
decisions cartographers make as they compose maps. Cartographers seek to make
use of visual resources such as colour, shape and pattern to communicate
information about spatial relationships. The analogy with language also helps
explain why training in principles of effective cartography is so important —
it allows us to communicate more effectively.
Drawing maps — cartographic
drawing — is a specialist activity. Urban designers and landscape
architects should have a basic
understanding and insight in cartographic principles.
Keep in mind that cartography in
whatever form is a way of communication. What you want to communicate defines
the way you are going to work on maps.
Making maps; from content to form
1.
Classification and typology.
You start out with a classification and typology of the geographical
information you have. It is clear that this distinction forms a direct relation
with the legend.
2.
Generalisation and reduction of
maps. Sometimes information is too detailed and needs to be generalised into
more global classes or types. Any change in this sense refers at the same time
to scale and legend. Every scale has its own legend.
3.
Abstraction and diagrams. Any
cartographic representation as a map can be considered as a form of
abstraction. Sometimes it helps to add diagrams to give additional information
next to the map.
Upscaling and downscaling
Re-scaling; upscaling and
downscaling. In general downscaling is easier than upscaling. If you compare in
an atlas the same area at different scales, you can see the effect of downscaling
and upscaling. A different scale shows a completely different image, not just
diminishing in size. So every scale has its own image and its own legend.
Technically, downscaling is
always always possible as long as you adapt the legend and reduce information,
whereas upscaling is only possible if you add new information. In practice you
can always 'diminish the size' of maps but not 'enlarge' them. You cannot
enlarge or reduce maps without changing the legend! A number of factors
influence the options for re-scaling. First you have to identify and measure
the area you want to reproduce. For your ease, you will select a rectangular
shape including the core area (e.g. protected area, watershed, ancestral
domain, or other) and its environs of ecological, cultural and economic
significance. If the core of a protected area is a mountain, the rectangle will
include the downhill catchments and possibly the settlement areas where most
dependent communities reside.
Making cartographic models
The choice of the scale and hence
the size of the model should take into account the need for accuracy as well as
the need for enough space in which physically to construct and store the model.
Maps and mapping in Holland
Holland has a long cartographic
tradition. From the 16th century on Dutch cartographers made maps, not only of Holland
but also of other parts of the world. In many cased there were military uses
for maps; sea maps, maps of fortifications and topographic maps of an early
stage. At the end of the 18th century the first ‘Topographic office’ was
established based on French ideas and models. The main goal was a military
cartography of the whole country. In 1932 the ‘Topographic service’ was
formally established still under military rule. Between 1876 and 1953, a series
of 25.000 maps was produced of the whole country; the so-called ‘Bonne-sheets’.
Gradually this series was
replaced by a series on 25.000 based on the stereographic projection. In 2004,
a new organisation was set up; the ‘Topographic service Kadaster’. This
organisation is a formal part of the government service that has independent
tasks of producing basic maps, of registration of real estate. It is a public
service open to everybody. Nowadays most topographic information is
digitally-based information.
In Holland we now have basically
three scales in topographic maps; 50.000, 25.000 and 10.000.
The TOP10vector is the basis for
all Dutch topographic maps. From this TOP 10vector, the 25.000 and the 10.000
scales can be directly derived. The 50.000 scale needs to be generalised
otherwise it will be unreadable. This digital information forms the basis for
the production of paper maps, for GIS information, maps for special purposes.
All topographic maps can be
ordered at the website of the topographic service; www.tdn.nl
GoogleEarth and Web-mapping
Maps have traditionally been made
using pen and paper, but the advent and spread of computers has revolutionised
cartography. Most commercial quality maps are now made with map making software
that falls into one of three main types; CAD, GIS, and specialised map
illustration software.
'Web-GIS' is the culmination of
what is regarded as a 'Geospatial Data Infrastructure' or 'GDI.' A GDI is a set
of institutional, technical, and economical arrangements used to enhance the
availability of correct, up-to-date, to-the-point and integrated geospatial
data with regard to timeliness and price affordability, all of which combine to
support efficient decision making processes. A GDI is composed technically of
geographic information systems, networks, computers, and a plethora of software
applications (Plewe, 1997).
Web-GIS consists of a sequence of
geo-processing tasks that are distributed over server-side and client-side
computer systems. A client is a Web browser. A server consists of a Web server
and a Web-GIS software system. A client requests a map or makes a
geo-processing request over the Web to a remote server. The Web server
translates client requests into internal codes and invokes GIS functions by
passing formatted requests to Web-GIS software. The later software returns
results that are reformatted for interpretation by the client browser or with
additional functionality from a plug-in or Java applet.
Maps generated by a Web-GIS are
often called 'Web maps (Plewe, 1997).' They are an interface between a client
and the GDI. The design of Web maps is critical for the correct communication
of geospatial databases. Conventional and historical GIS analyses have
traditionally evolved around constructions using paper maps. With the advent of
the Internet, the practices of GIS had to be migrated into the Web environment.
GoogleEarth
GoogleEarth has really
revolutionised web-mapping in every sense of the word. For the first time in
history, maps of the entire world are available for all those who have
internet. For urban design and landscape architecture the possibilities are
hard to oversee; we still discover new types of use beyond the already existing
of getting maps freely at almost every conceivable scale. Especially in the
field of interpretation the possibilities are still to be further discovered.
The development of GoogleEarth goes so fast, both in getting more detailed
information and in the applications that you can use it for, that you have to
keep track frequently to keep up to date. Do regularly download the user
manual; it is also free and excellent.
At present, there are few formal
standards for the design of Web maps. The visual perception of Web maps is
decidedly different from paper maps. This perception is a fundamental
consideration during a design phase for Web-GIS. Digital map authoring (i.e.
cartography) tends to be more constrained in its available toolset than that
used for paper map design. Subsequently, Web-GIS strive to 'emulate' paper map
productions and presumably this weighs considerably in any Web-GIS selection.
Web-GIS does offer an acceptable differentiation from conventional GIS through
the use of animation, rotation functions, three-dimensional viewing, user
interaction, and other multimedia presentations (Beddoe, 1997).
Representing objects, their environment and development
Specific problems associated with
urban development within rural areas require knowledge of the city itself and
of the surrounding countryside. This task needs up-to-date and reliable
planning information, including development strategies, processes that take
place in and around the city and the spatial spread of characteristic elements.
Maps are a good method to lay down information and
processes. For the town planner, analyses and interpretations are essential
methods to identify and understand processes, and the possibilities and
limitations of a region. Regional analyses and interpretations constitute the
most important arguments and motives for a design.
Knowledge of the city and
surrounding countryside can be derived from maps. When maps are not available
or out-dated, aerial photographs and satellite images can be used.
Maps of the Netherlands are
numbered according to grids.
The European Commission and
the European Parliament have reached agreement about Guidelines for the set up
of a foundation of infrastructure for Spatial Information in the European
Community or Infrastructure for Spatial Information in Europe or INSPIRE. For the
moment INSPIRE is targeting on the development and execution of environmental
management. But the list of information belonging to INSPIRE is more extensive
and will give information all kind of subjects belonging to the Spatial
Sciences.
The more abstract language
of the guideline should be translated into a more practical one for
interpretation and definition of a number of specific standards and the
description of a limited list of spatial data.
INSPIRE has five basic
principles (INSPIRE 2007):
- Data are once gathered and maintained where it is most
efficient.
- The possibility should be given to combine data of different
sources and that these data can be consulted by many users for different
purposes.
- Spatial data should be gathered on one level of the government
and it should be possible to use these data on all levels of the
government.
- Spatial data that are necessary for a good public policy should
be available without any restriction.
- It should be easy to discover what spatial data are available,
the suitability of these to evaluate and what kind of conditions are
committed to it.
There are no specific
guidelines or techniques to translate the information to the practice.
Accessibility should be guaranteed by internet and by an EU-internet portal for
all publicly available information of the EU-member states and the guarantee of
the interchangeability of the information.
Spatial data belonging to
INSPIRE:
Since 2010
- Geographical names
- Administrative units
- Traffic networks
- Hydrographic data
- Protection zones
- Altitudes
- Identification of ownership
- Cadastral register of land plots
- Groundcover
- Ortho photographs
Since 2013
- Spatial definitions of statistic units
- Buildings
- Soil
- Geology
- Land use
- Human health and safety
- Public services
- Environmental security services
- Production and industrial facilities
- Facilities for agriculture and aquaculture
- Demography
- Registered regions for waste, groundwater, zones of nuisance,
mining etc.)
- Regions with natural risks
- Atmospheric circumstances
- Meteorological characteristics
- Oceanography
- Sea regions
- Habitats and biotopes
- Distribution of species.
More information is to be
found on website http://inspire.jrc.it/
The Law on spatial Planning 2008 prescribed
colours symbols and codes for municipal zoning plans summarised in the tables
below.
|
code
|
Dutch
|
English
|
R
|
G
|
B
|
C
|
M
|
Y
|
Pantone
|
|
|
Grens
|
boundary
|
255
|
255
|
255
|
100
|
100
|
100
|
|
|
A
|
Agrarisch
|
agricultural
|
235
|
240
|
210
|
10
|
5
|
20
|
7485U
|
|
AW
|
Agrarisch met waarden
|
agricultural with values
|
210
|
225
|
165
|
20
|
15
|
35
|
580U
|
|
B
|
Bedrijf
|
business
|
180
|
095
|
210
|
35
|
60
|
00
|
258U
|
|
BT
|
Bedrijventerrein
|
industrial estate
|
200
|
160
|
215
|
20
|
30
|
00
|
522U
|
|
BO
|
Bos
|
forest
|
100
|
170
|
045
|
55
|
10
|
100
|
369U
|
|
C
|
Centrum
|
center
|
255
|
200
|
190
|
00
|
20
|
15
|
706U
|
|
CO
|
Cultuur en ontspanning
|
culture and entertainment
|
255
|
060
|
130
|
00
|
90
|
35
|
Rubine Red U
|
|
DH
|
Detailhandel
|
retail
|
255
|
160
|
150
|
00
|
40
|
30
|
1625U
|
|
DV
|
Dienstverlening
|
provision of services
|
240
|
145
|
190
|
05
|
40
|
05
|
701U
|
|
G
|
Groen
|
greenery
|
040
|
200
|
070
|
50
|
00
|
80
|
360U
|
|
GD
|
Gemengd
|
mixed
|
255
|
190
|
135
|
00
|
25
|
45
|
156U
|
|
H
|
Horeca
|
hotel and catering industry
|
255
|
105
|
035
|
00
|
70
|
90
|
Orange 021U
|
|
K
|
Kantoor
|
office
|
235
|
195
|
215
|
05
|
20
|
05
|
250U
|
|
M
|
Maatschappelijk
|
social
|
220
|
155
|
120
|
05
|
35
|
50
|
157U
|
|
N
|
Natuur
|
nature
|
130
|
165
|
145
|
40
|
15
|
40
|
557U
|
|
R
|
Recreatie
|
recreation
|
185
|
215
|
070
|
20
|
05
|
85
|
380U
|
|
S
|
Sport
|
sports
|
130
|
200
|
070
|
45
|
05
|
90
|
3B2U
|
|
T
|
Tuin
|
garden
|
200
|
215
|
110
|
15
|
05
|
65
|
584U
|
|
V
|
Verkeer
|
traffic
|
205
|
205
|
205
|
20
|
20
|
20
|
427U
|
|
W
|
Wonen
|
living
|
256
|
255
|
000
|
06
|
00
|
97
|
102C
|
|
WA
|
Water
|
water
|
175
|
205
|
225
|
25
|
05
|
10
|
290U
|
|
WG
|
Woongebied
|
residential area
|
255
|
255
|
180
|
00
|
00
|
30
|
600U
|
|
|
Overig
|
remaining
|
235
|
225
|
235
|
05
|
10
|
10
|
663U
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 1063 Legally prescribed colours for main uses in Dutch zoning plans
|
|
|
|
|
|
|
|
|
|
|
|
|
code
|
|
Dutch
|
English
|
|
L
|

|
Leidingen
|
cables and pipes
|
|
L-B
|
|
Brandstof
|
fuel
|
|
L-G
|
|
Gas
|
gas
|
|
L-H
|
|
Hoogspanning
|
high
tension
|
|
L-HV
|
|
Hoogspanningsverbinding
|
high
tension connection
|
|
L-L
|
|
Leidingstrook
|
strip
for cables and pipes
|
|
L-O
|
|
Olie
|
oil
|
|
L-R
|
|
Riool
|
sewer
|
|
L-W
|
|
Water
|
water
|
|
|
|
|
|
|
WR
|

|
Waarden
|
values
|
|
WR-A
|
|
Archeologie
|
archaeology
|
|
WR-C
|
|
Cultuurhistorie
|
history
of civilisation
|
|
WR-E
|
|
Ecologie
|
ecology
|
|
WR-G
|
|
Geomorfologie
|
geomorphologie
|
|
WR-L
|
|
Landschap
|
landscape
|
|
|
|
|
|
|
WS
|

|
Waterstaat
|
water management
|
|
WS-WB
|
|
Waterbergingsgebied
|
water
store area
|
|
WS-WK
|
|
Waterkering
|
dam
|
|
WS-WL
|
|
Waterlopen
|
watercourse
|
|
WS-WS
|
|
Waterstaatkundige
functie
|
water
management function
|
|
|
|
|
|
|
Fig. 1064 Legally prescribed
patterns for main double uses in Dutch zoning plans
|
|
|
|
|
|
|
|
|
|
|
|
|
Dutch and analogue
representation
|
|
English and digital
representation
|
transp
|
|

|
geluidzone (R255 G155 B0)
|

|
noise zone (R255 G155 B0)
|
60%
|
|
industrie
|
|
|
|
|
spoor
|
|
|
|
|
weg
|
|
|
|
|
|
|
|
|
|
|

|
luchtvaartverkeerzone (R155 G50 B205)
|

|
air connection zone (R155 G50 B205)
|
60%
|
|
|
|
|
|
|
|

|
milieuzone (R0 G155 BO)
|

|
environmental zone (R0 G155 B0)
|
60%
|
|
bodembeschermingsgebied
|
|
|
|
|
geluidsgevoelige functie
|
|
|
|
|
geurzone
|
|
|
|
|
grondwaterbeschermingsgebied
|
|
|
|
|
stiltegebied
|
|
|
|
|
waterwingebied
|
|
|
|
|
zones Wet Milieubeheer
|
|
|
|
|
|
|
|
|
|
|

|
reconstructiewetzone (R56 G133 B94)
|

|
Reconstruction law zones (R56 G133 B94)
|
60%
|
|
extensiveringsgebied
|
|
|
|
|
landbouwontwikkelingsgebied
|
|
|
|
|
verwevingsgebied
|
|
|
|
|
|
|
|
|
|
|

|
veiligheidszone (R0 G0 B255)
|

|
safety zone (RO GO B255)
|
60%
|
|
bevl
|
|
|
|
|
leiding
|
|
|
|
|
lpg
|
|
|
|
|
munitie
|
|
|
|
|
vervoer gevaarlijke stoffen
|
|
|
|
|
vuurwerk
|
|
|
|
|
windturbine
|
|
|
|
|
|
|
|
|
|
|

|
vrijwaringszone (RO G255 B255)
|

|
protection zone (R55 G205 B0)
|
60%
|
|
buisleidingenstraat
|
|
|
|
|
dijk
|
|
|
|
|
duin
|
|
|
|
|
molenbiotoop
|
|
|
|
|
radar
|
|
|
|
|
spoor
|
|
|
|
|
straalpad
|
|
|
|
|
vaarweg
|
|
|
|
|
weg
|
|
|
|
|
|
|
|
|
|
|

|
Wro-zone (R255 GO BO)
|

|
Law of spatial planning zone (R255 G0 B0)
|
60%
|
|
moderniseringsgebied
|
|
|
|
|
ontheffingsgebied
|
|
|
|
|
verwerkelijking in naaste toekomst
|
|
|
|
|
wijzigingsgebied
|
|
|
|
|
|
|
|
|
|
|

|
overig (R100 G100 B100)
|

|
remaining (R100
G100 B100)
|
60%
|
|
|
|
|
|
|
|
Fig.
1065 Legal and environmental
zones
|
|
|
|
|
|
|
|
(bah)
|

|
bedrijf aan huls
|
|
|
(cw)
|
cultuurhistorische waarde
|
|
|
(iv)
|
intensieve veehouderij
|
|
|
(rw)
|
recreatiewoning
|
|
|
(-rw)
|
recreatiewoning uitgesloten
|
|
|
(sdh-..)
|

|
specifieke vorm van detailhandel
|
|
|
(-sdh-..)
|
specifieke vorm van detailhandel uitgesloten
|
|
|
|

|
digitale grens
|
|
|
|
|
|
|
|
Fig.
1066 Examples of functional
indications
|
|
|
|
|
|
|
code
|
Functieaanduidingen SVBP2008
|
Functional indications
|
|
(as)
|
aanlegsteiger
|
jetty
|
|
(a)
|
agrarisch
|
agricultural
|
|
(ab)
|
agrarisch bedrijf
|
agricultural business
|
|
(al)
|
agrarisch loonbedrijf
|
agricultural wage labour business
|
|
(agw)
|
agrarisch met waarden
|
agricultural with values
|
|
(ak)
|
akkerbouw
|
farming
|
|
(abp)
|
ambachtelijke be- en verwerking agrarische producten
|
|
|
(aqc)
|
aquacultuur
|
|
|
(aq)
|
aquaduct
|
|
|
(aw)
|
archeologische waarden
|
|
|
(az)
|
asielzoekerscentrum
|
|
|
(atl)
|
atelier
|
|
|
(at)
|
attractiepark
|
|
|
(ac)
|
autocircuit
|
|
|
(bsd)
|
baggerspeciedepot
|
|
|
(bb)
|
bed & breakfast
|
|
|
(b)
|
bedrijf
|
|
|
(bah)
|
bedrijf aan huis
|
|
|
(b≤ )
|
bedrijf tot en met categorie..
|
|
|
(b= )
|
bedrijf van categorie ..
|
|
|
(bw)
|
bedrijfswoning
|
|
|
(bt)
|
bedrijventerrein
|
|
|
(beb)
|
beeldbepalende boom
|
|
|
(bp)
|
begraafplaats
|
|
|
(be)
|
belwinkel
|
|
|
(bh)
|
beroep aan huis
|
|
|
(bi)
|
bibliotheek
|
|
|
(bs)
|
bioscoop
|
|
|
(bot)
|
bollenteelt
|
|
|
(bm)
|
bomenteelt
|
|
|
(bd)
|
bordeel
|
|
|
(bo)
|
bos
|
|
|
(bow)
|
bowlingbaan
|
|
|
(brk)
|
brandweerkazerne
|
|
|
(br)
|
brug
|
|
|
(cs)
|
caravanstalling
|
|
|
(ca)
|
casino
|
|
|
(c
|
centrum
|
|
|
(coc)
|
congrescentrum
|
|
|
(cc)
|
creativiteitscentum
|
|
|
(cr)
|
crematorium
|
|
|
(co)
|
cultuur en ontspanning
|
|
|
(cw)
|
cultuurhistorische waarden
|
|
|
(dr)
|
dagrecreatie
|
|
|
(da)
|
dansschool
|
|
|
(dh)
|
detailhandel
|
|
|
(dhg)
|
detailhandel grootschalig
|
|
|
(dhe)
|
detailhandel in brand en explosiegevaarlijke goederen
|
|
|
(dhp)
|
detailhandel perifeer
|
|
|
(dhv)
|
detailhandel volumineus
|
|
|
(dv)
|
dienstverlening
|
|
|
(ds)
|
dierenasiel
|
|
|
(dt)
|
dierentuin
|
|
|
(di)
|
discotheek
|
|
|
(db)
|
drafbaan
|
|
|
(do)
|
drugsopvang
|
|
|
(evz)
|
ecologische verbindingszone
|
|
|
(ew)
|
ecologische waarde
|
|
|
(ek)
|
eendenkooi
|
|
|
(e)
|
erf
|
|
|
(ev)
|
evenemententerrein
|
|
|
(fz)
|
feestzaal
|
|
|
(ft)
|
fruitteelt
|
|
|
(ga)
|
garage
|
|
|
(gs)
|
geluidscherm
|
|
|
(gw)
|
geluidwal
|
|
|
(gm)
|
gemaal
|
|
|
(gd)
|
gemengd
|
|
|
(gmw)
|
geomorfologische waarde
|
|
|
(gz)
|
gezondheidszorg
|
|
|
(gt)
|
glastuinbouw
|
|
|
(go)
|
golfbaan
|
|
|
(g)
|
groen
|
|
|
(gr)
|
gronddepot
|
|
|
(gv)
|
grondgebonden veehouderij
|
|
|
(gh)
|
groothandel
|
|
|
(ha)
|
haven
|
|
|
(h)
|
horeca
|
|
|
(h≤ )
|
horeca tot en met horecacategorie
|
|
|
(h= )
|
horeca van categorie..
|
|
|
(hs)
|
houtsingel
|
|
|
(hw)
|
houtwal
|
|
|
(hv)
|
hovenier
|
|
|
(ijs)
|
ijsbaan
|
|
|
(i)
|
infrastructuur
|
|
|
(ik)
|
intensieve kwekerij
|
|
|
(iv)
|
intensieve veehouderij
|
|
|
(ic)
|
internetcafé
|
|
|
(iw)
|
internetwinkel
|
|
|
(jh)
|
jachthaven
|
|
|
(jo)
|
jeugdopvang
|
|
|
(jop)
|
jongeren ontmoetingsplek
|
|
|
(ji)
|
justitiële inrichting
|
|
|
(kv)
|
kamerverhuur
|
|
|
(kp)
|
kampeerboerderij
|
|
|
(kt)
|
kampeerterrein
|
|
|
(k)
|
kantoor
|
|
|
(kab)
|
kartbaan
|
|
|
(ks)
|
kas
|
|
|
(kz)
|
kazerne
|
|
|
(kb)
|
kinderboerderij
|
|
|
(kijs)
|
kunstijsbaan
|
|
|
(ll)
|
laad- en losplaats
|
|
|
(lb)
|
landingsbaan
|
|
|
(lw)
|
landschapswaarden
|
|
|
(lbr)
|
leiding brandstof
|
|
|
(lg)
|
leiding gas
|
|
|
(lhs)
|
leiding hoogspanning
|
|
|
(lhv)
|
leiding hoogspanningsverbinding
|
|
|
(lo)
|
leiding olie
|
|
|
(lr)
|
leiding riool
|
|
|
(lwa)
|
leiding water
|
|
|
(ls)
|
leidingstrook
|
|
|
(lp)
|
ligplaats
|
|
|
(lh)
|
luchthaven
|
|
|
(lv)
|
luchtverkeer
|
|
|
(m)
|
maatschappelijk
|
|
|
(ma)
|
manege
|
|
|
(mrk)
|
markt
|
|
|
(me)
|
meer
|
|
|
(mo)
|
militair oefenterrein
|
|
|
(mz)
|
militaire zaken
|
|
|
(mb)
|
modelvliegtuigbaan
|
|
|
(mob)
|
monumentale boom
|
|
|
(mc)
|
motorcrossterrein
|
|
|
(md)
|
munitiedepot
|
|
|
(mu)
|
museum
|
|
|
(ms)
|
muziekschool
|
|
|
(mt)
|
muziektheater
|
|
|
(nso)
|
naschoolse opvang
|
|
|
(n)
|
natuur
|
|
|
(nlw)
|
natuur- en landschapswaarden
|
|
|
(nw)
|
natuurwaarden
|
|
|
(nb)
|
nutsbedrijf
|
|
|
(nv)
|
nutsvoorziening
|
|
|
(oe)
|
oever
|
|
|
(on)
|
onderwijs
|
|
|
(os)
|
ontsluiting
|
|
|
(ov)
|
openbaar vervoer
|
|
|
(ovs)
|
openbaar vervoerstation
|
|
|
(od)
|
openbare dienstverlening
|
|
|
(op)
|
opslag
|
|
|
(pf)
|
paardenfokkerij
|
|
|
(ph)
|
paardenhouderij
|
|
|
(pd)
|
pad
|
|
|
(pa)
|
park
|
|
|
(pg)
|
parkeergarage
|
|
|
(p)
|
parkeerterrein
|
|
|
(pb)
|
partyboerderij
|
|
|
(pah
|
passantenhaven
|
|
|
(pp)
|
pitch & putt
|
|
|
(ps)
|
plantsoen
|
|
|
(pl)
|
plein
|
|
|
(prr)
|
praktijkruimte
|
|
|
(pr)
|
prostitutie
|
|
|
(raamexploitatie)
|
raamprostitutie
|
|
|
(rv)
|
railverkeer
|
|
|
(r)
|
recreatie
|
|
|
(rw)
|
recreatiewoning
|
|
|
(re)
|
religie
|
|
|
(ri)
|
risicovolle inrichting
|
|
|
(rr)
|
rivier
|
|
|
(sau)
|
sauna
|
|
|
(shu)
|
schiphuis
|
|
|
(si)
|
seksinrichting
|
|
|
(sit)
|
sierteelt
|
|
|
(sil)
|
silo
|
|
|
(ske)
|
skeelerbaan
|
|
|
(skb)
|
skibaan
|
|
|
(sl)
|
sluis
|
|
|
(sa-..)
|
specifieke vorm van agrarisch
|
|
|
(saw-..)
|
specifieke vorm van agrarisch met waarden
|
|
|
(sb-..)
|
specifieke vorm van bedrijf
|
|
|
(sbt-..)
|
specifieke vorm van bedrijventerrein
|
|
|
(sbo-..)
|
specifieke vorm van bos
|
|
|
(sc-..)
|
specifieke vorm van centrum
|
|
|
(sco-..)
|
specifieke vorm van cultuur en ontspanning
|
|
|
(sdh-..)
|
specifieke vorm van detailhandel
|
|
|
(sdv-..)
|
specifieke vorm van dienstverlening
|
|
|
(sgd-..)
|
specifieke vorm van gemengd
|
|
|
(sg-..)
|
specifieke vorm van groen
|
|
|
(sh-..)
|
specifieke vorm van horeca
|
|
|
(sk-..)
|
specifieke vorm van kantoor
|
|
|
(sle-..)
|
specifieke vorm van leiding
|
|
|
(sm-..)
|
specifieke vorm van maatschappelijk
|
|
|
(sn-..)
|
specifieke vorm van natuur
|
|
|
(sr-..)
|
specifieke vorm van recreatie
|
|
|
(ss-..)
|
specifieke vorm van sport
|
|
|
(st-..)
|
specifieke vorm van tuin
|
|
|
(sv-..)
|
specifieke vorm van verkeer
|
|
|
(swr-..)
|
specifieke vorm van waarde
|
|
|
(swa-..)
|
specifieke vorm van water
|
|
|
(sws-..)
|
specifieke vorm van waterstaat
|
|
|
(sw-..)
|
specifieke vorm van wonen
|
|
|
(swg-..)
|
specifieke vorm van woongebied
|
|
|
(spt)
|
speeltuin
|
|
|
(sz)
|
speelvoorziening
|
|
|
(sp)
|
spoorweg
|
|
|
(s)
|
sport
|
|
|
(spc)
|
sportcentrum
|
|
|
(sph)
|
sporthal
|
|
|
(spv)
|
sportveld
|
|
|
(spz)
|
sportzaal
|
|
|
(sq)
|
squashcentrum
|
|
|
(sd)
|
stadion
|
|
|
(ste)
|
steiger
|
|
|
(str)
|
strand
|
|
|
(shs)
|
strandhuis
|
|
|
(sth)
|
studentenhuisvesting
|
|
|
(stw)
|
stuw
|
|
|
(su)
|
supermarkt
|
|
|
(tn)
|
tennisbaan
|
|
|
(tr)
|
terras
|
|
|
(th)
|
theater
|
|
|
(t)
|
tuin
|
|
|
(tb)
|
tuinbouw
|
|
|
(tc)
|
tuincentrum
|
|
|
(tu)
|
tunnel
|
|
|
(uv)
|
uitvaartcentrum
|
|
|
(vw)
|
vaarweg
|
|
|
(vh)
|
veerhaven
|
|
|
(ve)
|
ven
|
|
|
(vb)
|
verblijfsgebied
|
|
|
(vr)
|
verblijfsrecreatie
|
|
|
(vl)
|
verenigingsleven
|
|
|
(v)
|
verkeer
|
|
|
(vep)
|
verkoop eigen producten
|
|
|
(vml)
|
verkooppunt motorbrandstoffen met lpg
|
|
|
(vm)
|
verkooppunt motorbrandstoffen zonder lpg
|
|
|
(va)
|
vertrek- en aankomsthal
|
|
|
(vij)
|
vijver
|
|
|
(vk)
|
viskwekerij
|
|
|
(vt)
|
volkstuin
|
|
|
(vu)
|
vulpunt lpg
|
|
|
(wm)
|
waardevolle boom
|
|
|
(wa)
|
water
|
|
|
(wb)
|
waterberging
|
|
|
(wk)
|
waterkering
|
|
|
(ws)
|
waterstaat
|
|
|
(ww)
|
waterweg
|
|
|
(wz)
|
waterzuiveringsinstallatie
|
|
|
(we)
|
weg
|
|
|
(wel)
|
wellness
|
|
|
(wei)
|
welzijnsinstelling
|
|
|
(wn)
|
wielerbaan
|
|
|
(wt)
|
windturbine
|
|
|
(wtp)
|
windturbinepark
|
|
|
(w)
|
wonen
|
|
|
(wg)
|
woongebied
|
|
|
(wl)
|
woonschepenligplaats
|
|
|
(wp)
|
woonwagenstandplaats
|
|
|
(zee)
|
zee
|
|
|
(zo)
|
zend-/ontvangstinstallatie
|
|
|
(zbo)
|
zorgboerderij
|
|
|
(zoi)
|
zorginstelling
|
|
|
(zw)
|
zorgwoning
|
|
|
(zb)
|
zwembad
|
|
|
|
|
|
|
Fig. 1067 Functional
indications
|
|
|
|
|
|
code
|
Bouwaanduidingen SVBP2008
|
|
|
[aeg]
|
aaneengebouwd
|
|
|
[am]
|
antennemast
|
|
|
[bg]
|
bijgebouwen
|
|
|
[gs]
|
gestapeld
|
|
|
[kap]
|
kap
|
|
|
[ka]
|
karakteristiek
|
|
|
[nr]
|
nokrichting
|
|
|
[ond]
|
onderdoorgang
|
|
|
[pd]
|
plat dak
|
|
|
[tae]
|
twee-aaneen
|
|
|
[vrij]
|
vrijstaand
|
|
|
[sba-..]
|
specifieke bouwaanduiding
|
|
|
|
|
|
|
Fig. 1068 Building indications
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
Fig.
1069 Indicating measures in
Dutch zoning plans
|
|
|
|

|

|

|
|
|
|
|
waarde
|
minimum
|
maximum
|
|
|
|
|
s128
|
x
|
s129
|
x
|
s130
|
x
|
J
|
betekenis
x
|
|
|
s128a
|
a
|
|
|
|
|
aantal
|
aantal
|
|
|
s128b
|
b
|
s129a
|
a
|
s130a
|
a
|
aantal
|
bedrijven
|
|
|
s128c
|
c
|
s129b
|
b
|
s130b
|
b
|
aantal
|
bezoekers
|
|
|
s128d
|
d
|
s129c
|
c
|
|
|
aantal
|
bouwlagen
|
|
|
s128e
|
e
|
s129d
|
d
|
s130c
|
c
|
aantal
|
gebouwen
|
|
|
s128f
|
f
|
s129e
|
e
|
s130d
|
d
|
aantal
|
parkeerplaatsen
|
|
|
s128g
|
g
|
s129f
|
f
|
s130e
|
e
|
aantal
|
rijstroken
|
|
|
s128h
|
h
|
s129g
|
g
|
s130f
|
f
|
aantal
|
sporen
|
|
|
s128i
|
i
|
s129h
|
h
|
s130g
|
g
|
aantal
|
winkels
|
|
|
s128j
|
j
|
s129i
|
i
|
|
|
aantal
|
wooneenheden
|
|
|
s128k
|
k
|
|
|
|
|
|
maatvoering
|
|
|
s128l
|
l
|
s129j
|
j
|
s130h
|
h
|
m2
|
bebouwd oppervlak
|
|
|
s128m
|
m
|
s129k
|
k
|
|
|
%
|
bebouwingspercentage terrein
|
|
|
s128n
|
n
|
s129l
|
l
|
s130i
|
i
|
m
|
breedte
|
|
|
s128o
|
o
|
|
|
|
|
graden
|
dakhelling
|
|
|
s128p
|
p
|
s129m
|
m
|
|
|
m
|
diepte
|
|
|
s128q
|
q
|
s129n
|
n
|
s130j
|
j
|
m
|
hoogte
|
|
|
s128r
|
r
|
|
|
|
|
m
|
bouwhoogte
|
|
|
s128s
|
s
|
|
|
|
|
m
|
goothoogte
|
|
|
s128t
|
t
|
s129o
|
o
|
s130k
|
k
|
m
|
hoogteligging vlak
|
|
|
s128u
|
u
|
s129p
|
p
|
s130l
|
l
|
m
|
lengte
|
|
|
s128v
|
v
|
s129q
|
q
|
s130m
|
m
|
m2
|
oppervlakte
|
|
|
|
|
s129r
|
r
|
s130n
|
n
|
m2
|
vloeroppervlakte
|
|
|
s128w
|
w
|
s129s
|
s
|
s130o
|
o
|
m2
|
bruto vloeroppervlakte;
|
|
|
s128x
|
x
|
s129t
|
t
|
|
|
m2
|
bvo vloeroppervlakte;
|
|
|
s128y
|
y
|
s129u
|
u
|
s130p
|
p
|
m2
|
netto vloeroppervlakte;
|
|
|
s128z
|
z
|
s129v
|
v
|
s130q
|
q
|
m2
|
woning vloeroppervlakte;
|
|
|
s128aa
|
aa
|
s129w
|
w
|
s130r
|
r
|
m3
|
volume
|
|
|
s128ab
|
ab
|
s129x
|
x
|
s130s
|
s
|
|
vrije tekst
|
|
|
s128ac
|
ac
|
s129y
|
y
|
s130t
|
t
|
|
vrije tekst
|
|
|
s128ad
|
ad
|
s129z
|
z
|
s130u
|
u
|
|
vrije tekst
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 1070 Meaning of
standard symbol values
|
|
|
|
|
|
|
|
|
|
|
|

|

|

|
|
|
|
|
|
Fig.
1071 Examples of lines
|
|
|
|
|
Combining different sensory impressions
Experiments
with babies, reported by Piaget and
Inhelder (1947), keep me fascinated from the first time
I read about them until now, because of the practical and design implications
of the idea. Firstly, they gave the children an object to feel by touching
behind a screen making sure they could not see it. Then they showed the same
object, making sure they could not touch it. Piaget and Inhelder questioned at
what age the children would combine these two totally different sensory
impressions into one concept. On the average it appeared to be on the
age of one and a half years old. These conclusions were criticized later (it
happens earlier) but the idea has remained the same.
Concept formation
Combining
different sensory impressions synaesthetically into a concept of any object involved, means
more than a conditional Pavlov-reflex. Starting up your digestive system when a
bell rings does not yet mean that you can imagine them as a concept, and they
are not the same after all. It means that if you feel the object without seeing
it, you can make a visual imagination of the object without seeing it. It is
the very start of logical operations like
‘not’, ‘or’, ‘if … then’. It explains the fascination of young children for the
game of peek-a-boo or
hide-and-seek: mother hides herself and calls you. You
can hear her voice, but you do not see her. You now are looking for her,
because you have the visual imagination you like to check completing your
concept.
Moving experience
In
later investigations Piaget and Inhelder emphasized the importance of the motoric
ability for imagination capabilities and learning. You
can change your visual impression by moving physically. This possibility causes
continuous experiments by children. I remember my niece celebrating her first
birthday. Grandma held her on her lap saying ‘Quiet my darling, quiet!’. But
she stayed crying all the time kicking her legs. I had been reading Piaget
recently and said: ‘Give her to me’. Grandma handed me the child and I helped
her kicking legs to move her body up and down to see my face alternating with
the background. She started laughing! Grandma, somewhat embarrassed, thought
she loved me more then her, but I explained her the baby was experimenting
parallax: changing object and context by
moving up and down. She did not see me as a person, she tried to understand the
difference between my face and my background first. That is why moving on a seesaw is so
fascinating for children.
Object constancy
She
should have experienced object constancy earlier: mother is not there; she appears in
the door and walks into your direction. Her face enlarges until it fills your
total scope of vision: is that large object the same object appearing as a
small face peeping around the door? You throw toys out of your box, they bring
them back. Repeating experiences like that show constancy of changing objects:
different, gradually enlarging impressions link up to one imaginable object.
That is why swings and
merry-go-rounds are
important. Later on you run away from your mother and look back. She became
very small and to regain your safety you run back to enlarge her.
Your mother is
not yet a person, but ‘something large and warm’, like my three years old
daughters described their concept of ‘mother’ when I asked them ‘What is a
mother?’. The other way round dangerous things are ‘large and cold’. A car is
not dangerous when it is far away, because it is small.
Pain
There
we are. The dangerous things at home are well known when you are three years
old, because they are nearby and large, cold, solid and hard. They can hurt
when you run too fast. You learn by collision. But once you are in the street
you have to run faster to discern objects further away than at home and it
takes years to learn that there are objects running faster than you, becoming
large, cold, hard and painful very quickly. That is why playing tag is so
important. Young animals are short-sighted to learn discerning objects nearby
first by little movements causing parallax. The vision, radius of awareness and speed
grow with the years of childhood. I think the radius of awareness grows
exponentially, but it is a hypothesis.
Which
programme of requirements we can conclude per level of scale?
The radius of awareness
If the radius of awareness grows exponentially it could happen like Fig. 1072 shows. The
radius R should be interpreted elastically between its neighbors (R=10m means
‘between 3 and 30m’). If psychologists would study that relation and name the
values children observe in every stage of their growth, it would be a great
help for designers to determine their legend units and composition.
|
years old
|
m radius R
|
area of awareness
|

|
|
0
|
1
|
Action space
|
|
1
|
3
|
Room
|
|
3
|
10
|
House
|
|
5
|
30
|
Yard
|
|
7
|
100
|
Neighbours
|
|
9
|
300
|
Neighbourhood
|
|
11
|
1000
|
District
|
|
13
|
3000
|
Town
|
|
Fig.
1072 Hypothetical scales of awareness
by age
|
|
|
Observable variables
To
get an idea of the realities these measures indicate, see Fig. 1073. The question is: ‘Which observable
variables vary on every level of scale?’.
|

|

|

|

|
|
|
|
|
|
|
0 year: R = 1m
|
1 year: R = 3m
|
3 years: R = 10m
|
5 years: R = 30m
|
|
|
|
|
|
|

|

|

|

|
|
|
|
|
|
|
7 years: R = 100m
|
9 years: R = 300m
|
11 years: R = 1000m
|
13 years: R = 3000m
|
|
|
|
Fig. 1073 Growing awareness by
scale
|
|
|
|
|
|
|
|
|
|
|
|
Let
us first try to look as a child on different ages.
I
am sorry in this text it’s a boy like I was, rewrite it yourself for a girl if
you think it’s relevant.
A baby street like a room (3m)
You are one
year old. The front door opens and they put you in a buggy. Suddenly at one
side, all kind of unknown objects whiz by. Some objects on the far side stay
longer. You don’t have any influence, because they drive your car. You
cannot stay to experiment parallax properly. So, you look forward. There, all
kinds of objects enlarge, become
dangerous, but they pass aside and disappear. Suddenly your driver turns. You
shake in your buggy. The scene changes dramatically. They drive you in a dark
hole. Slowly in becomes lighter. You hear voices, but you see dresses,
trousers, legs, shoes and tiles as different colour surfaces. Looking
upward you see bodies towering above you, faces and hands. Suddenly they shake
you and drive you in a white hole with cars whizzing by. Another shake makes
your scene well-known until they take you out of the buggy. They hold you
before a wall that opens after some jingle with a turning hand. You smell
something you are used to. You are ‘home’.
A toddler street like a house (10m)
You are three
years old. You can walk! That means,
you can change the world around you by walking through a black hole. Sometimes the hole is
gone, but in the mean time you learned to open the wall, standing on your toes
and stepping back, pulling a handle down. There are several worlds, but there
is one you can open by pulling a handle aside. In that room there is noise,
wind, movement and very much space. You may run. They often
call you back. If you fall, it’s hard. Between the tiles there are blades and
ants. Sometimes there is a drain cover with holes aside somewhat lower. But if
you want to look inside they call you back: “dangerous!”. You find
pieces of soft brown clay, but they hold you back: “dirty!”. You may
not even step on it. They take you into another room by turning a corner.
Suddenly you are standing in the sun. Here plants are huge and not standing on
a windowsill, but in the ground. So, they can not fall down if you run through them.
But they call you back: “dirty!”. Some have prickles, so you stay walking on
the pavement. There are several pavements: stepping
down they are darker with smaller stones. But if you step down they call you
back: “dangerous! We said that earlier!”. Stupid: that was the drain cover.
A young child street like a yard (30m)
You are five
years old. Your father takes you to school in the morning, your mother from school in the
afternoon turning 5 corners. They moved
into a house with a garden and a gate to a path, going to a playground and to a street with cars and large trees. You may not
play in the sand around that trees, it is dirty. You’ve got
marbles, but there are not much groves to play marbles. You like to go to the
far side, but it is too dangerous. You’ve got a bike, but you may
not leave the pavement with the large tiles. If you stay
riding on that pavement, going around the corner three times, you come back
from the other side! Your friend has no bike, so together you play on the
playground. But it is too childish, your little sister plays there with your
mother on the wipperchicken and the slide. My friend
had a secret hut there, but they cut off plantation. So, it is
not very secret anymore. But he has a real Play station on his computer!
A child street like a school (100m)
You are seven
years old. You may cross the street in front of your house. Your new friend
lives there. His neighbour has a motorbike. He is repairing it in front
of his house. Round the corner lives an ugly man. You ring his bell, run away
and look around the corner how angry he is. Your mother takes you to her work.
You never knew she has a room there as well. Your portrait is on her desk, but
you cannot play there. You get a chocolate in a café with strange people. Your father
showed you how to go to Grandma by bus and you got a ticket to try yourself. The driver tells you where to
go out. You see large buildings where people work, but they don’t live there
and there are no children.
A child street like a village or neighbourhood (300m)
You are nine
years old. You may cross all the streets until the district way. You can go to
school, the sports field, the hairdresser and to Grandma by bike. You’ve got
roller skates on your birthday, but you only may skate on
the skate ground at five minutes cycling. There are shops where you can buy stickers, but your new
friend makes them on his computer. He takes
you to the computer shop, but you like the car models you can buy next door.
Your pocket money has doubled last year, but it is still not
sufficient. If you help Grandma cleaning her house three times you can buy a
Ferrari.
A child street to explore (1000m)
You are eleven years old. You
climb the old church-tower and see your house from above, your
school, your swimming pool and the fields outside the city where you cycled with your friends. You see
your own daily life like a bird. Apparently there are many more districts in town. The city ends somewhere. Next year
you will go to high school in another district. You will loose friends of
your neighbourhood and find new ones from elsewhere.
A teen-ager street to meet (3000m)
There are students from other
cities and countries in your class. In the geography class you
learn countries and cities by heart. You visit them on holiday. You are not a
child anymore. You have seen your city by night. There are right and wrong
disco’s. You have
got a newspaper round to be able to pay for your girlfriend next time. You look
at her lighted room from behind a tree in the street where she lives. Where
could you make an appointment next week? She often goes to a volleyball ground
hidden behind a large office building in her neighborhood. There you can sit,
beyond neon lights, unnoticed
by others, pretending to look at the games together.
Growth
From the second year on, children
grow linear with their age to the adult stature of their nationality (see Fig. 1075). After 10
years old they outgrow a car (Fig. 1074). So,
children have less overview than adults.
|

|

|
|
|
|
|
Fig.
1074 Growth of an average child in the USA
|
Fig. 1075 Adult length
variation by nationality
|
|
|
|
The growing eye
Moreover, their field of vision is smaller. So, their vision is closer to the
fixation center with less attention to context. Context
sensibility seems to be primarily the task of hearing. But, to
determine the direction of noise is more difficult for children than
for adults. Deaf people compensate their failing sense by developing a larger
field of vision earlier.
|

|
|
|
|
|
Fig. 1076 A
child’s average field of vision, and an adult’s average field of vision in
degrees from center
|
|
|
|
Fixation point
Visibility is highest in the central fixation point, declining
into the boundaries of the field of vision (see Fig. 1077).
|

|

|
|
|
|
|
Fig. 1077 Visibility
represented by Anderson (1984)
as a third dimension in the field of vision
|
|
|
|
Because of their limited field of
vision children have to move their head more often than adults to build up a
concept of context. Adults
complain wrongly about lack of concentration then. They have to change focus themselves to understand the composition of a
scene as well. Design helps to balance recognition and surprise. Too much
recognition causes boredom, too much
surprise chaos (see Fig. 1079).
Components and details
A scene comprises components and details. To design a
quickly understandable scene we have to make larger components externally different
from each other, but internally filled with characteristic details recognizably equal to distinguish the
particular component from the other components with other characteristic details.
That art is called composition.
|

|

|

|
|
|
|
|
|
Fig. 1078 Components
|
Fig. 1079 Quality as a working of variety
|
Fig. 1080 Design means of variety
|
|
|
|
|
Any level of scale mentioned in Fig. 1073 needs its
own composition. On any level of scale components and details have new
characteristics of categorization and orientation.
Observable differences
Your action space (R=1m) has hard and soft, movable and non-movable components in different
colors. Your room (R=3m) has a door, corners to play, eat and
store, different in light, material and visibility. These are
the legends for designing a child street like a room.
Your house (R=10m) has differences of accessibility, control, light, noise, temperature, wetness, differently
suitable for playing, personal care and rest. What could we use to distinguish
the components of a child street like a house? Your yard (R=30m) is differently covered, planted and lighted by the sun. There are
components of the house extending in the garden or the street (in-between realm). You behave
differently at the back or front side. There are
formal and informal places, hard and soft places, places of recognition and surprise. What is the
difference between lawn and pavement, terrace and walk? Are there
in-betweens to hesitate where to go?
Your school (R=100m) has spaces to sit and to run, compete, watch, play and learn. Your
village or neighborhood (R=300m) has spaces to buy, walk and ride a bike. Your
district (R=1km) has spaces of living, business, traffic and parks. Your city (R=3km) has spaces to meet and retire, atmospheres and cultures to explore.
Resolution
A field of vision comprises a
largest measure in reality (frame, expressed as R) and a
smallest visible detail (grain, expressed as r). Both
change the observed composition if you approach an object or a scene. The
distance from the observed composition is approximately equal to its frame.
If the frame of a picture
represents a reality of radius R = 10m and the grain a radius
r = 10cm, the resolution r / R is 1%. You will call
the result a ‘drawing’. If frame
and grain differ less (say 3%), it is a rougher sketch, stressing
the concept. If they differ more, it could be a more precise blue print (0.1%). Object and details of a blue print lay
too far apart to understand the composition or concept immediately, they get
their use primarily for realization.
Legends for design
On every level of scale the map
you draw may have a different legend. For example, in a drawing with a frame
R=10m, you can draw tiles in the pavement (10cm), the kind of plantation, the
furniture of the street and the entries of homes. These are adult categories.
Make a sketch to group them more roughly into less components, comprising child
categories. But what do you choose as components and their legend units in
other frames? You have to dissect or group them into components suitable for
child perception on different ages. Fig. 1081 gives an
overview of variety per level of scale named in this article. You could
interpret it as guiding principle for design: try to change softness every
meter, light every 3m and so on. However, for example light and shadow could be
changed very successfully on other levels of scale as well. The table is only a
starting point to be extended.
|
years old
|
0
|
1
|
3
|
5
|
7
|
9
|
11
|
13
|
|
|
m Radius of
frame
|
1
|
3
|
10
|
30
|
100
|
300
|
1000
|
3000
|
learning
|
|
differences to experience:
|
|
|
|
|
|
|
|
|
|
hard-soft
|
x
|
|
|
|
|
|
|
|
danger
|
|
movable|non-movable
|
x
|
|
|
|
|
|
|
|
operational abilities
|
|
color
|
x
|
|
|
|
|
|
|
|
recognition
|
|
windows|doors
|
|
x
|
|
|
|
|
|
|
orientation
|
|
light|dark
|
|
x
|
|
|
|
|
|
|
imagination
|
|
shelter|corners
|
|
x
|
|
|
|
|
|
|
to escape adult movements
|
|
function|time
|
|
x
|
|
|
|
|
|
|
every time having its own place
|
|
visibility
|
|
x
|
|
|
|
|
|
|
hide-and-seek
|
|
accessibility
|
|
|
x
|
|
|
|
|
|
rules
|
|
control
|
|
|
x
|
|
|
|
|
|
other people
|
|
noise
|
|
|
x
|
|
|
|
|
|
context
|
|
temperature
|
|
|
x
|
|
|
|
|
|
kinds of clothes
|
|
wetness
|
|
|
|
x
|
|
|
|
|
hygiene
|
|
ceiling|shelter
|
|
|
|
x
|
|
|
|
|
in-betweens to hesitate, to decide
|
|
plantation
|
|
|
|
x
|
|
|
|
|
nature
|
|
sun
|
|
|
|
x
|
|
|
|
|
nature
|
|
formal-informal
|
|
|
|
x
|
|
|
|
|
different behavior
|
|
recognition|suprise
|
|
|
|
x
|
|
|
|
|
initiative
|
|
run|compete
|
|
|
|
|
x
|
|
|
|
ambition
|
|
watch, learn
|
|
|
|
|
x
|
|
|
|
to learn
|
|
possibility to buy
|
|
|
|
|
|
x
|
|
|
expensiveness
|
|
possibility to walk
|
|
|
|
|
|
x
|
|
|
interest
|
|
possibility to ride a bike
|
|
|
|
|
|
x
|
|
|
ride
|
|
urban functions
|
|
|
|
|
|
|
x
|
|
exploration
|
|
meet|retire
|
|
|
|
|
|
|
|
x
|
projection|identification
|
|
atmosphers|cultures
|
|
|
|
|
|
|
|
x
|
identity
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig.
1081 Legends for design
|
|
|
|
|
|
|
|
|
|
|
|
A composition is not only
determined by components, but also by details directing your fixation. We only
mentioned characteristic details, determining components. But there are also
marking details, determining boundaries, connecting details determining
in-betweens and striking details labelling the whole scene.
Establishing a legend by composition
Composition analysis is not only a research method for analysing the balance between repetition and diversity in existing urban architectural units, but
also a design method to achieve this sort of balance and to explore its possibilities. In
composition analysis, there appears to be an infinite
number of possible types of balance. These extend artistic freedom by challenging the possibilities to their
limits. Within this are boundaries of survival value, future value, practical
value, and experiential value. Composition analysis is a systematic form
of establishing a legend in the research
and design process. Establishing a legend is an unexpressed supposition in
every structure- and function analysis.
The composition analysis
discussed here has been developed for the image-quality plan of the Amsterdam
district ‘De Baarsjes’. by Jong and Ravesloot (1995). The following pages are an literal quotation taken from this
document.
The starting point is that image
quality is an outcome of variation in surroundings.
Too little variation (monotony) results in
boredom, and too
much variation (chaos) in
overloading (see Fig. 1079). For every
individual, there are boundaries and optima of recognition by repetition and of surprise by change. This relationship says nothing
about the importance of built-up surroundings, but rather about its potential
to accommodate different sorts of meanings.
Scale
That this simple relationship has
not been utilised earlier, even though much psychological research has a
bearing on it, can be ascribed to scale problems at the time of implementation.
For this reason, we will consider images on different scale levels separately
(district image, neighbourhood image, block image, etc.).
Components and details
Within each image, we will make a
scale differentiation between components and details (see Fig. 1078). We consider
parts larger than one tenth of the image as components that define the
composition. We will call everything smaller than one tenth a ‘detail’, for the
time being.
Different components
The components of an image can be
more or less alike (see Fig. 1080). If they
are rather different, then the contrast is strong, otherwise it is weak. Between the
most and the least similar components within an image, one can distinguish a
smallest discernable and a largest discernable contrast. If all the components
are similar (non-contrasting), then we call the composition homogenous, and if they
differ, heterogeneous. One can
observe a relationship between compositions of similar components, a relationship
that can be either balanced or unbalanced. For the same contrast, the same
composition and the same relationship, it is still possible to discern
variation in composition. Similar components in a composition can be grouped in
a more or less compact form.
Diversity and repetition
on different levels of scale
Variation on one scale level
(e.g. between the components) does not obstruct the occurrence of monotony on the other scale level (e.g. between the
details within a component). In particular, it is the application of different
principles on different scale levels that adds ‘tension’ to the image. One can now arrange the design
strategies into scale levels in ‘accords’ between
diversity (V) and repetition (R), for example:
|
ACCORDS
|
A
|
B
|
|
between buildings
|
Repetition
|
Diversity
|
|
between components:
|
Diversity
|
Repetition
|
|
between details:
|
Repetition
|
Diversity
|
|
|
|
Fig. 1082 Variation accords
|
|
|
The traditional
architectonic accord A (Repetition at the building and detail
levels, but Diversity on the levels in between, ‘RDR’) differs from the modern
accord B (‘DRD’). After all, present architecture is mostly valued for the
unique contour (D) of the building as a whole and for the originality (D) of
the details, while between both these scale levels, repetition (R) is valued as
‘architectonic clarity’.
Three examples of style and scale
In Fig. 1083, three periods of architectural style, and, for the
sake of brevity, the three scale levels linked to them are shown. A tholos for Asklepios in Epidauros, with a radius
of 10 metres; Palladio’s Villa
Rotonda, with a
radius of 30 metres; and Berlage’s
Mercatorplein in the district De Baarsjes, with a
radius of 100 metres. In each period, and on each scale, components and details
can be seen which indicate to what extent one can talk about diversity or
repetition. 6
Perceiving different
compositions approaching a building
When we approach a façade, we first
look at the composition of the different components and then at the details. By
doing this, in each case, we have a different frame, depending on our distance
away from that object. So, at a distance of 10 metres from our façade , when we
turn our heads, the whole façade is within our vision (10-metre radius). Using
a wide-angle lens, we can see
our appartment (3-metre radius), and using a standard lens, a window or a door
(1-metre radius).
To assimilate the total image of the
street, we need to
view it from a distance of about 30 metres. In each case, we position what we
see within a larger frame. We see an image in a radius that is approximately
the same as our distance away from that image.
Fading details by increasing distance
The more we extend that distance
away from the image, the fewer details we see: the elements of façade are
rougher than those of our house when we stand near to it. We only have an image
of our block of houses thanks to the fact that we have walk around it at some
stage. It is a conceptual image, but it is
thereby no less important, because it helps us to find our way. This is also
the case with our neighbourhood, district and urban images.
|

|
|
|
|
Fig. 1083 Components and details of images in a radius of 10, 30 and 100
metres.
|
|
|
By chance, the tholos has a diameter of
20 metres and thus a radius of 10 metres. The components of a radius of about 3
metres appear in the image of the map as the central cellaand the
components of the peristyllum.
Distinguishing
components
When one looks at them, they
appear to be an entrance section and the flanking parts of the pillared
gallery, and the roof section and foreground laid out in a similar way. The
division of the components of the same order of size is, of course, free and is
not linked to an orthogonal or hexagonal grid. The capitals, triglyphs and other ornaments are contained as details
in a frame of 1m radius.
The components of the Villa
Rotonda differ more. The middle section is dominant.
The special (B) according to Tzonis, Lefaivre et al. (1989) is flanked by the common (A) , repeating components following the
classical scheme ABA.7 On the
map, a large central section C appears, flanked by similar ABA schemes, in
which, this time, the peripheral area can be included as the most common
component. In the image of Mercatorplein, the area is
the central component (30m in radius), flanked by an approximately equally
large groups of house façades in the corners and along the lengthy sides. The
details consist here of façade (10 m) window and entrance sections (3 m). The
image of a block (of buildings) can also be described within a radius of 100 m.
Details, components and
frame
For our analysis, we
differentiate the following images by their details, components and frame (with
radius expressed in metres):
|
|
detail
|
|
component
|
frame
|
ACCORD
|
|
|
<
|
|
>
|
|
BAARSJES
|
|
district image
|
|
100
|
|
1000
|
R
|
|
neighbourhood image
|
|
30
|
|
300
|
V
|
|
ensemble
|
|
10
|
|
100
|
R
|
|
street image
|
|
3
|
|
30
|
V
|
|
façade image
|
|
1
|
|
10
|
R
|
|
house image
|
|
0,3
|
|
3
|
V
|
|
finished image
|
|
0,1
|
|
1
|
R
|
|
|
|
Fig. 1084 Variation accord for De
Baarsjes
|
|
|
In De Baarsjes all
the neighbourhoods within the district image look alike (R), but within each neighbourhood,
the squares, and the block and street groups (‘ensembles’) vary
greatly (V). Within each separate ensemble, the blocks and streets are again very similar (R), but within each
block and street, the façades vary (V). Within the façades, appartments are repeated (R),29 but within each
house image, the finished image varies (V).
The primary difference in an image determines the dominant component
In the first
instance, the variation in the district image is read against the variation
among its components. As large
units as possible are chosen as components within the image, wherein a maximal repetition
of characteristic details can be found. It is as if one scans the image
with a searchlight the size of a component, until one has caught the most
repetitive part of the bundle. When, by doing this, one connects the definable
diversity (between the components) and the repitition (within the components)
so closely to the scale level of the district and its components, it becomes
very important where one chooses to place (focus) the boundaries of the
district components (and thus the boundaries of the formulated homogeneity).
Looking for internal
homogeneity of components
To establish the remaining
image-defining variations within each district component, a neighbourhood image can be formulated by looking for relatively
homogeneous neighbourhood components that differ maximally among themselves at
that level.
Symmetry of roads
If, for example, a road lies
between two district components, then this road accentuates the difference
between the district components, or, alternatively, the similarity within a
district component. In the one case, that can lead to the establishment of an
asymmetric street profile, and, in the
other case, to a symmetric one. For instance, in the case of De Baarsjes, the
focus determines the symmetry of the Hoofdweg. When one
reaches the Postjes neighbourhood, we can
distinguish, for various reasons, two different district components on both
sides of the Hoofdweg. For this reason, the walls of the streets on the
opposite side do not need to be the same (<>). Once past the Postjesweg,
a striking symmetry between the street walls becomes evident (><). This
gives the impression that one is entering a homogeneous neighbourhood.
Dividing and articulating
How, now, do we determine the
focus? Following Van der Hoeven and Louwe’s example, Hoeven and Louwe (1985) the urban area is ‘morphologically
reconstructed’ (see the Fig. 1085) First, the area covered by the district is divided
as equally as possible in the two main directions, using the most
characteristic repetitive detail: a building block of 72 by 360 metres. In this
way, the present district image has been reconstructed with an accuracy of
approx. 100 metres. This conceptual design intervention is called ‘dividing’. Globally
speaking, the second intervention,
‘segmenting’ or
‘articulating’, means connecting main roads and waterways to the surroundings
and taking the consequences for the primary zoning. Thus, a more differentiated
topological scheme arises that, in turn, is more closely aligned to present
actuality.
|
Dividing
|
Articulating
|
Tailoring
|
Detailing
|
|

|

|

|

|
|
|
|
Fig. 1085 Morphological reconstruction of the
urban area De Baarsjes
|
|
|
A third intervention cuts
the otherwise homogeneous parts apart and ‘adds’ them to the existing
topography. An analogy to the work of the tailor, the cutter, the couturier or
dressmaker, this intervention is known as ‘tailoring’. The
next intervention, ‘detailing’,
temporarily divides the area internally into components that are considered to
be homogeneous, identified by characteristic internally repeating details. The
connecting details can be found between the components, just where their
differences culminate. These can be points or lines, which either represent the
surrounding components or are in contrast to them.
Divisions and connections
Structure (coherence) is the
way in which grouped parts form a whole or the sum of divisions and
connections. The concept forms a separate category between form and function,
because the same structure can take on different forms and can have different
functions, and vice versa. Coherence always arises between different
parts; in the drawing, these are the legend units.
Cohesion and adhesion
One can refer to the
coherence between one kind of legend unit as cohesion. The
coherence between different kinds of legend units then has to be called
adhesion.8 Coherence can be stimulated by nearness in space and realised by separating or
connecting infrastructure.
Polarisation between open (a) and closed (b) sides
Spatial elements such as a
neighbourhood, a house, a chair, a cupbourd, a television set, a person are
often polarised, on the
one hand, towards an open ‘front’ where
the connections are concentrated and the communication with other elements
takes place, and, on the other hand, to
a closed ‘back’ in which the ‘functions characteristic of the system’ are
concentrated where they can operate sheltered from the outside world. One
cannot reverse this polarity with impunity without jeapodising the function.
For example, it is pointless placing a TV set, a cupboard or a chair with their
fronts against a wall. One only puts a person in a corner (with their front
against a wall) if one wants to ‘gag’ them (Fig.
1086).
Scales of polarisation
One can recognise polarity between openness and closedness on different
levels of scale and can give them meaning as ‘structure’ in design and
research. The polarities at different scale levels influence each other. The
polarity of a wall of a small room (3m radius) or of a forest edge (100m
radius), interfers with human polarity (1m radius) by causing hinderance or
back-coverage.[393]
Motoric and sensoric polarisation of rooms and houses
In the
left hand Fig.
1087, a study has an ‘open’ window-side and an ‘walled-in’
door-side. This sensoric polarity is realised within a radius of 3m. If one considers accessibility as ‘the distance to the front door” (radius
10m), then on a greater scale and in a motorical sense, the door-side is the most ‘open’ side
of the room and the window-side is the most ‘closed’. The polarities change
meaning according to the scale and are directed antipodally (‘contrapolar’).
The right-hand Fig. 1087 is a sketch of a house with a through lounge in which the front door, back door, corridor,
staircase, hall, cables, piping and wiring, in short the communication
functions, are concentrated in the small aisle on one side, and the ‘system
characteristic‘ living
functions on the other side , in the large aisle. This is the motoric polarity
(c) from the left-hand drawing that extends for a distance of 10m. The sensoric
3m polarity that divides the house on two sides into a window side and a walled-in zone is here perpendicular (‘orthopolar’).
Breaking boring polarisation by design
The three standard hobbies
of ‘creative’ architects: ‘the front door in the living room’, ‘the staircase
in the living room’, or ‘the kitchen in the living room’ all breach the 10m
motoric polarity, so that the objections to them (draught, smells, people
walking through) have to be solved mechanically.
Ensemble and urban island polarisation
The ensemble is polarised within a radius of 30m towards the open,
communicative, public front and a more closed, protected ‘private’ back.
|

|

|
|
|
|
|
Fig. 1088 Polarity 30m
|
Fig. 1089 Polarity 100m
|
|
|
|
Its most ‘open’ side is
where the street crosses with another street or enters a more
important street or square; its middle is the most ‘closed’ part.
Polarisation on higher levels of scale
This polarity can be spread
over more than 100m. Within the radius of 300m, one can be polarised towards
‘neighbourhood centre’ and ‘neighbourhood green’; within a
radius of 1000 metres towards ‘district centre’ and ‘district green’. In a similar
manner, within a radius of 3 km, the town has an open ‘town centre’ and a
more closed ‘periphery’. However, this is a motoric interpretation of ‘open’
and ‘closed’. A more sensoric interpretation talks about closed ‘inner city’
and open ‘outside areas’[394].
Function as values of use on
different terms
The built-up and unbuilt upon surroundings have
different values, such as short-term experiencial value, medium-term practical value, long-term future value and
extremely long-term survival value. By definition, this has to do with the value
for people, including the value for plants and animals, in sofar as we, as
people, recognise that value.[395]
For experiencial value ‘shape’
is enough; one doesn’t need much structure for this. For the other values,
increasing amounts of structure are needed. These have to be designed in that
way, because structure is the ‘condition’ for these values.
Practical values
Practical values can be
subdivided into economy, culture and administration. 9 These can be
recognised in the medieval town (see the
market square of Delft) as the following:
|
Social differentiation
|
Urban differentiation
|
|
administration (aristocracy)
|
castle, palace
|
|
culture (spirituality)
|
church, cloister
|
|
economic basis (citizens, serfs)
|
market, shops, dwellings, small traditional trade businesses
|
|
|
|
Fig. 1090
Trias urbanica in
the Middle Ages
|
|
|
Trias urbanica
Pierre George’s definition George (1961can be called ‘trias urbanica’.
By subdividing further, as a result of social differentiation, it is possible
using Jakubowski’s (1936) 10 and
Parsons(1966 and 1977) systematique to imagine a ‘trias politica’ from Montesquieu
and Derathé (1973), a ‘trias cultura’ and a ‘trias
economica’.
|
Social differentiation
|
Urban differentiation
|
Politics
|
|
|
legislative power
|
town hall
|
|
legal/administrative
|
law court/government services
|
|
executive power
|
police station, prison, barracks, military training ground
|
|
|
|
Culture
|
|
|
religion/ ideology
|
churches, monuments, signs
|
|
art/science
|
museums, institutes, libraries
|
|
up-bringing/education
|
socio-cultural facilities, schools
|
|
|
|
Economy
|
|
|
production
|
firms, banks, offices
|
|
exchange
|
distribution points, infrastructure
|
|
consumption
|
living, health service, recreation
|
|
|
|
Fig. 1091
Social and urban differentiation in modern times
|
|
|
Concentration and
centralisation
Functions can be concentrated or
deconcentrated spatially,
but apart from that, each function can also be centralised or
decentralised in a
hierarchical order.[396]
So, there are 4 possibilities of form related to function:
|
FUNCTION
|
|
FORM
|
|
|
concentration
|
deconcentration
|
|
centralisation
|
Concentration of
centralised functions
|
Deconcentration of
centralised functions
|
|
decentralisation
|
Concentration of
decentralised functions
|
Deconcentration of
decentralised functions
|
|
|
|
Fig. 1092
The difference between concentration and centralisation demonstrated
|
|
|
In the concept of
‘centre’ a morphological and a functional meaning have to be discerned.
Desirable possibilities
Intentions can range from tradition-oriented to
opportunity-oriented. They are proportioned as are probability and possibility
within what is desirable.[397]
More than a programme of
requirements
A design is traditionally
preceded by a programme of requirements, compiled
according to the wishes of the commissioning body. In order to meet these
requirements, the designer has to create the conditions in his proposals that
will lead to the fulfilment of these requirements. In doing this, he himself
sets additional requirements based on past
experience and on his expectations regarding future use and perception.
Robustness
The finished design will be used
and perceived in a different way than the commissioning body and designer had
envisaged. A design to be used in different ways and contexts we call ‘robust’ That
quality often leads to a plea for flexibility, ‘leave
possibilities open’. This means making fewer design efforts.
However, from that point of view,
one can also defend an environmental diversity that offers freedom of choice and with which one not only makes allowance
for the unsuspected, but also facilitates it. This means putting more effort
into design.
Art and kitch
A painting such as ‘the child
with a tear’ that prescribes emotions in us, emotions that we have to feel
every time we look at it, is no more art than sentimentality (kitch). A true
piece of art enables one to feel different emotions every time we look at it.[398]
Unexpected use
Nature has no wishes.
Nevertheless, we try, as people, to make a programme of requirements for nature development.23. That is
as paradoxical as the order ‘Be spontaneous’. We do that based on a primitive
and often inaccurate picture of how plants, animals and human beings will use
the environment that we design. We are repeatedly surprised by the way in which
the surroundings that we have designed are put to use by nature.
Unintended possibilities
We cannot make a programme of
requirements for nature: each species has its own programme of requirements,
about which we have little understanding and there are at least 1,500,000
species in addition to homo sapiens. All we can do is to create
environmental diversity and wait to see what use nature will make of it. While
ever one is unable to base the programme of requirements on prognoses,
diversity remains a form of risk coverage for perceptive-, practical-, future- and
survival values. This design intention seems to me to be important, not only
for nature, but also for human beings, as long as we believe in their freedom
of choice. Image quality can be related directly and in a design-
oriented way to variation in surroundings.[399]
The vocabulary of design
The legend is the vocabulary of design. A
legend unit is a type and any legend is a result of (sometimes
hidden) typology (for example living, working, recreating,
travelling in CIAM’s functional typology).
According to Jong and
Engel (2002) typology in design study is not the same as top-down categorizing
in empirical research. A type is not a category, a model or a concept but the
raw material for design. A type combines incomparable categories. For example
form and colour are incomparable: you can not speak about redder than round. A
type has to be designed to become a model, a design that can be realised. Types
are chosen because of their potential for design. They seldom lack aspects of
form. So, a design legend often can not be explained by words.
Resolution, the distance between frame and grain
That is why design sometimes begins with a
collage assembling reference images into a larger composition (collage,
montage). In
that case the reference images are the legend, sometimes even summarised and
explained apart from the composition. The reference images should not be taken
litterally then, but interpreted as general types. In a
later stage the composition becomes a realisable design and the legend
transforms in homogeneous lines or surfaces indicated by form or colour. Their
external form in the drawing is its smallest detail, its ‘grain’,
supposed to be homogeneous inside. Compared with the measure of the composition
as a whole (‘frame’) the
grain determines the resolution of the drawing. The measure in reality of
frame and grain could be expressed in their rough radius R={…1,3,10,30,100m….}
and r={…1,3,10,30,100mm….}. So, a resolution r/R=0.1 may concern a sketch,
r/R=0.01 a drawing, r/R=0.001 a very precise blue print.
Tolerance, the preciseness of the drawing
Apart from the concept of resolution you
have to consider the tolerance of a drawing. For example, if in an early
stage of design you sketch a line indicating a road your intention is an
approximate location, though it may be drawn in high resolution. Discussing the
drawing with parties concerned a tolerance of 10m from the core of the line may
be supposed. A drawing entails often different tolerances. The existing objects
you want to keep in the design could be drawn with a small tolerance. Their
exact location is determined. However, the designed lines start with a large
tolerance and in the course of the design process their location is more and
more precise; the tolerance decreases. If you draw the existing objects by
narrow lines and the designed objects by thick lines your most important
message comes to the fore best, while the objects everybody knows already shift
to the background.
Frame and grain
Your legend is scale sensitive. For example, using the
CIAM typology of living, working, recreating and travelling for a regional
sketch (R=30km and r=3km) tacitly supposes design decisions like dividing living, working and recreational
areas concentrated within a radius of 3km. However, using it for a district
sketch (R=1km, r=100m) hides other design suppositions[400]. So, frame and grain (scale) determine the meaning of your design
vocabulary (legend).
|

|

|
|
|
|
|
|
Fig. 1093 The region Veluwe-Arnhem-Nijmegen 60x60km
The radius of its grain
is R=300m in reality; on scale 1:25
000 it is r=1.2cm
|
Fig.
1094 The sub-region Arnhem-Nijmegen 20x20km
The radius of its grain
is R=100m in reality: on scale 1:10 000 it is r=1cm
|
|
|
From sketch into blue print
In Fig. 1093 the radius of the smallest legend unit (grain) covers 1% of the radius of the
whole map (300m) and a surface of approximately 30ha. So, it is not a rough
sketch or precise blue print, but a drawing. Fig. 1094 is a drawing as well, but with a smaller
frame and grain. In both representations the legend distinguishes built-up
area, forest, heathland, agriculture, water and highways. What kind of legends you
would choose planning the area? There are infinitly more possibilities than the
CIAM legend, topographical and density stereotypes. They all introduce hidden
design decisions.
A legend in grain spots of the same surface
makes the produced map countable as a surface programme. Such quantity and
surface sensible spots can be grouped together into larger surfaces or
subdivided into 10 smaller spots each, increasing resolution eventually into
that of a photograph at last. However increasing resolution makes the map less
accessible for analysis.
Design
principles as a legend
Steenbergen and Zeeuw (1995); Steenbergen and Reh
(1996); Steenbergen (1999) and Reh discerned principles of landscape design as
legend units (types) for the national planning agency of the rural area: urban
nodes, rural estates and castles, plantations, landscape theatres and
streamlands. In 2003 students tried to find them on a large 1:10 000 map
of Fig. 1093 (Fig. 1096) and glued them as spots of two sizes (300m and
1000m) from Fig. 1095.
|
Grain
|
Legend
|
|
Radius real
|
surface real
|
radius on scale
|
diameter on scale
|
Red
|
Orange
|
Yellow
|
Green
|
Blue
|
|
m
|
ha
|
cm
|
cm
|
meaning
|
|
300
|
30
|
1,2
|
2,4
|
urban node
|
rural estate
|
plantation
|
landscape theatre
|
streamland
|
|
1000
|
300
|
4,0
|
8,0
|
|
|
|
Fig.
1095 Legend-units
landscaping r={300m,1000m}
in a frame R=30km 1:25 000
|
|
|
Existing urban nodes, rural estates and castles,
plantations, landscape theatres and streamlands in the region of Fig. 1093 were
glued in grey shade first, planned ones in clear colour later.
There are many existing rural estates and castles in that region. Vista’s and other forms of accompanying landscapes
were generalised in the glued spot. Plantations are colonised surfaces by which the programme
is put on stage by intended or unintended grid like landscape architecture.
They could be found not only in the rural, but also in the urban area, going
beyond the stereotypic town-landscape dichotomy. Landscape theatres are recognisable natural, agricultural or
urban systems of views and routes by which the physical, biological or cultural
origin of the landscape could be experienced. Streamlands are locations where the dynamics of natural or
urban life can be experienced.
Physical
quantities as a legend
On
every level of scale (R={30km, 10km, 3km, 1km, 300m, 100m}) such maps were made
with shifting unconventional legends (Fig. 1097).
|

|

|

|

|

|
|
week
1 30km
|
week
2 10km
|
week
5 1km
|
week
6 300m
|
week 7 100m
|
|
Landscape
|
Town and traffic
|
Infrastructure
|
Physics and soil
|
Materialisation
|
|
|
|
|
|
|
|
Fig.
1097 Exercises BkM1U 06 2002
|
|
|
|
|
|
|
Quantified human activities as a legend
To indicate traffic in a
frame R=10km (Fig. 1094) spots
of Fig. 1098 were
used.
|
Grain
|
Legend for a regular Monday
|
|
Radius real
|
surface real
|
radius on scale
|
diameter on scale
|
Red:
people average per hour using a
station or motorway exit
|
Orange:
people living at home
|
Yellow:
people working
|
Green:
people recreating
|
Blue:
people caring or studying nature
|
|
m
|
ha
|
cm
|
cm
|
|
|
100
|
3
|
1,0
|
2,0
|
100
|
1000
|
500
|
<100
|
<10
|
|
300
|
30
|
3,0
|
6,0
|
1000
|
10 000
|
5000
|
<1000
|
<100
|
|
|
|
Fig.
1098 Legend-units town and traffic r={100m, 300m} in a frame R=10km, 1:10 000
|
|
|
Different legends on different scales
Infrastructure was studied in a frame of R=1km,
physics and soil in a frame of 300m.
|

|

|
|
|
|
|
|
Fig. 1099 The town of Arnhem
6x6km.
The radius of its grain
meets R=30m in reality; r=1.2cm on scale 1:2 500
|
Fig. 1100 The railway
station neighbourhood 600x600m of Arnhem
The grain is R=3m in
reality, 1,2cm on scale 1:250
|
|
|
|
Money as a legend
Existing and planned infrastructure was studied
in spots of investment according to Fig. 1101.
|
Grain
|
Legend
|
|
Radius real
|
surface real
|
radius on scale
|
diameter on scale
|
Red
investment
crossing
|
Orange
investment
trace
|
Yellow
investment
multiple land use
|
Green
investment
milieu
|
Blue
investment
waterworks
|
|
m
|
m2
|
cm
|
cm
|
meaning
|
|
10
|
300
|
1.0
|
2.0
|
€ 10 mln
|
€ 10 mln
|
€ 10 mln
|
€ 10 mln
|
€ 10 mln
|
|
30
|
3000
|
3.0
|
6.0
|
€ 100 mln
|
€ 100 mln
|
€ 100 mln
|
€ 100 mln
|
€ 100 mln
|
|
|
|
Fig.
1101 Legend-units infrastructure r={10m, 30m} in a frame R=1km, 1:1000
|
|
|
Problems and opportunities as a legend
Physics and soil was studied by problem and
opportunity spotting according to Fig. 1102.
|
Grain
|
Legend
|
|
Radius real
|
surface real
|
radius on scale
|
diameter on scale
|
Red
|
Orange
|
Yellow
|
Green
|
Blue
|
|
m
|
m2
|
cm
|
cm
|
meaning
|
|
3
|
30
|
1.2
|
2,4
|
|
|
|
|
|
|
first: problems
|
Safety
|
Noise
|
Light (sun/ artificial)
|
Ecotope
|
Wind
|
|
then: opportunities
|
|
10
|
300
|
4.0
|
8,0
|
|
|
|
|
|
|
Fig. 1102 Legend-units physics and soil R={3m, 10m} in a frame R=300m, 1:250
|
|
|
Creative design starts with doubting its most
self evident supposition: its vocabulary.
An
important starting point for designing, forming policy on, and researching into
legend units is the level at which one
wants to separate or mix them. I deal with the scale-segmented approach here.
However, the terms employed in this are only used here to indicate the extent
of an area and thus have no functional meaning other than ‘potentials’ for
functions.
Scale falsification
This
approach is based on the discovery that ‘scale falsification’ (see Fig. 695) can occur in most urban architectural argumentations when one
derives the argumentation from another scale level than that on which the
inference is implemented. For example, this has been the case with the division
between living and working. The radius within which the hinderance was
determined was much smaller than the radius within which living was separated
from working. In addition, the scale-segmented approach renders designers’
paradoxical concepts, such as ‘bundled deconcentration’, understandable and acceptable. The same applies to the separation
and mixing of red, green, blue and black.
The paradox of a homogeneous
mixture
The
concept of ‘mixing’, for example, of mixing built-up and vacant areas, is
scale-dependent. What in a large radius is called mixing, can be segregation in
a small radius. These conceptual confusions cannot arise any more in the legend
proposed. Different principles for arranging can be recognised immediately on
the map, according to scale.
Accords of distribution
The
distribution of the urban area within a radius of 10 km has hardly any
influence on the landscape around, if this is concentrated within a radius of
30 km. (see Fig. 700, the two upper variants CC and CD). However, the distribution
within a radius of 30 km breaks the landscape around into landscape parks. Under that condition, the distribution within a radius of 10 km
again becomes important: the landscape parks are further divided into urban
landscapes. Until 1983,13 the national strategy was DC (Bundled Deconcentration, see Fig. 846). After thatRPD (1983), the policy was changed to CC (Compact City/Town), but, in practice, the strategy was CD and even DD.
Shape, size and adjacent
legend units
Shape and
size do not in themelves give an indication of the probable function, but rather of possible functions; of functions such as nature and
recreation (see Fig. 770 and Fig. 771).
Due to
technical developments, some traditional urban functions (such as certain types of
distribution) have become less dependent on the size of the built-up area
around (the ‘area capacity’: the number of residents within a certain radius). Others (such as
commuter traffic, public transport, urban nature and recreation) are still, or
have become even more, dependent on that size. A table of potential functions
could also be set up for each radius of the built-up area, even though it would
have a more temporary character.
Value and adjacent legend
units
The
internet is used a lot by estate agents. This is one of their messages:
‘...
project developments of houses, appartments and detached villas will also be
situated at the water’s edge. In Almere, houses have been built at the edge of the lake, with a
mooring place for a boat, so that one gets the idea of being on holiday in
one’s own house, whatever the season. Rotterdam makes use of its water-rich
environment and Amsterdam is planning a new development at a location still
occupied by water. Nieuwegein has its river bungalows along the banks of the
Lek and there are many other locations where one can live at the water’s edge.
Who would not want to live at the side of the largest expanse of water in the Netherlands,
the North Sea, and watch the sun sink into the sea every cloudless evening?
But, of course, we cannot all live at the water’s edge, so some people go and
live on it. Houseboats and boat conversions decorate the sides of the water in
all shapes and forms, irrespective of municipal and ministerial policies to
discourage them. Hardly any new moorings become available, and permits are
hardly ever issued for them any more. A boat conversion without a mooring
permit is like a house without a building permit.
The remaining alternative is to live far away from the large areas of water and
to buy a pleasure (!) yacht in which one spends as much of one’s free time as
possible. The yacht harbours on the Veluwemeer and the IJmeer, the Veersemeer
and the Biesbosch, Nieuwkoop and Vinkeveen, Loosdrecht and the Sneekermeer
offer these floating cabins, tired of tramping through the waterways all
summer, places where they can hibernate through the winter en masse. Because
another fact is that: it is nice on the water as long as it doesn’t rain (too
wet) and as long as it is not frozen over (too dry). But now let’s return ...
to the shore.
Because so many people are charmed by the restful effects and wide expanses of
water, with the many additional recreational possibilities close at hand, these
locations are more expensive than other spots.
If living at the water’s edge is restricted to the narrow ditch at the bottom
of a back garden, then there are hardly any financial consequences. But if that
narrow ditch becomes a stream, then the price of the plot is already higher.
And should that stream broaden out into an often depicted slow-moving lowland
river, flanked by summer and winter dykes, then the situation becomes very
attractive for many people. Consequently, ... the more cubic metres of water
that move along the banks of the waterway, the higher the square-metre price of
the land becomes.
Maas van Vliet
Estate
agent/ surveyor, Nieuwegein
Here,
the economic function of the transition between buildings and water
is defined. However, there are other functions and other transitions that must
be valued and considered.
Boundaries between legend
units
Apart
from the colour combinations red and blue, one can distinguish on different
scale levels the following margins between red, green, blue and black:
|

|
|
|
|
Fig. 1103 Urban architectural
agendas with respect to legend and scale
|
|
|
Drawing creates boundaries. The decision as to where one draws a boundary, and why there, in
particular, depends on the agenda.[401]
Each cell in Fig. 1103 has values and dilemmas that must be weighed up, not only economic,
but also spatially, ecologically, technically, culturally and managerially.
These considerations become simpler when one places those values in a
conditional context (Fig. 1104).
|

|
|
|
|
Fig. 1104 Urban operations arranged conditionally
|
|
|
This
figure shows, for example, that one cannot imagine management without culturally based
collective concepts and shared presuppositions,
but reversely, one can.
As a
result, one cannot imagine culture without an economy that makes
a decent existence possible, but reversely, one can. One cannot imagine economy without technical
infrastructure: because, if the dykes break, the economy in the above-mentioned
sense, does not exist any more. One cannot imagine technique without raw materials and raw
materials cannot be imagined unless there is a time–space connection.
Weighting the uncomparable
Fig. 1105 gives an example of considerations using the above
values, and summarized conditionally.
Futures
Anybody has an implicit idea about the probable future. It directs
your decisions. When somebody else judges your design (evaluation), (s)he can
reject your design from another idea about the future.
So, it is important to make explicit your idea about the future for
an honest judgement of your study. Try http://team.bk.tudelft.nl, publications 2003, FutureImpact.exe (Fig. 1106) to make your ideas about the future explicit in a
design relevant way.
The aspects ‘management’, ‘culture’ and so
forth, are deliberately operationalised in an abstract way in extreme values
(initiative(!) versus executing(?), traditional(<) versus innovative(>)
and so forth), so that they mean something at each order of magnitude. Then
they gain another working on each scale level, whereby their meaning shifts
according to scale context.
Frame and grain of your object determine your context
Deciding among incomparable spatial, ecological, technical, economic,
cultural and managerial values (evaluation) is
dependent on the size of the project, the context within which the programme or
intention is determined and the probable future in which the impacts of the
intervention are anticipated within the term of a given planning horizon. In a
second sheet of the computer programme you can fill in the frame(O) and
grain(o) (size and resolution) of the object you have in mind. By doing so, the
rest is context (see Fig. 1107).
|

|
|
|
|
Fig.
1107 Determining object, local context and impacts
|
|
|
What targeted (P) and non targeted (I) impacts
you expect from the object you have in mind in that context? Once you have made
explicit where you expect the object to have its impacts (not even
specifying them), you can ask the computer programme to make the framework of a
priliminary study proposal by pushing the button below (see Fig. 1107).
Planning horizon and
changing perspective
The perspective determines the manner in
which one guesses effects, and this perspective changes in a rather
unpredictable way, for example, at national level, as follows,:
|

|
|
|
|
Fig. 1108
Changing perspective
|
|
|
The
predictability decreases with increasing periodicity (in an upward direction).
Geographical and historical variation in
context.
Fig.
1109 represent the same sorts of outside spaces in Venice, and are on the same scale as a ArchitectenCie’s design for the harbour island in IJburg Amsterdam. The extent to which the geographical and historical context can determine the outcome is
obvious from this. From these images, the potential of exposure of stone to
water also becomes evident, and the
significance of the margin between built-up and vacant areas.
|

|
Venice 1 x 2 km
|

|
Venice 200 x 200m
radius 100m
< canals every 100m
< ^ streets every 30m
< opened up internally
by inner streets
< occasionally with
front
to the water
|
|
|
|

|
Venice 200 x 200m
< interior
< line of sight over
the
water
< concave avenue
|
|

|
IJburg 1 x 2 km
|

|
IJburg early design
Harbour island 200 x
200m
the same scale
< interior
< line of sight
< more room to see
< greater margin
< convex avenue
|
|
|
|
Fig. 1109 Geographical variation of conceptions
|
|
|
A primary separation of
legends
The
examples of Fig. 1109 illustrate how important the margin is between built-up and vacant
areas, and how much potential this margin has for a coherent urban image. Vertical segmentation on the façade surface gives
motives for placing greenery, lighting, street furniture, pedestrian crossings and
possibilities for interaction with adjoining water. In this way, public space is segmented by the façade in a manner
that everyone understands. A number of examples are given below of this type of
margin and the possibility for differentiating the outside space in relation to this with
green and blue.
Inward and outward view
An urban
architectural plan can be given shape starting
from either the inside or the outside space.
At the
buildings level, the first principle starting with the outside is geared
towards large, detached constructions that are expressive on all sides. Within
this, as many external functions as possible (parking, traffic, light, air,
greenery) are internalised. This leads to a relatively large outside area and so to large
façades. Walled-in feelings are compensated by windows overlooking vacant
and empty spaces, courtyards or inner squares within 10
metres from each room.
Outward extensions
Reasoned
from inside outwards, a possible break in the building line is made in the form
of ‘cold extensions’ such as platforms, balconies, galleries and oriels (‘external margin’
extensions) that leave the façade surface with a sudden jump in temperature
(the skin) as undisturbed as possible. This is in turn, in itself, favourable
for restricting the outside surface, although every extension also causes cold
transition areas.
Inward extensions
In
contrast, the second principle in the same scale tends towards the
externalisation of functions, towards buildings that are less independent within themselves and
with internal breaks in the building line (building backwards into an ‘internal
margin’). By doing this, the outside space gains more protected and covered
external spaces such as inner corners, porches, arcades and walled-in balconies.
Recessing and extending
parts of a façade
A
systematic combination of both gives the façade a horizontal and/or vertical
relief:
|
Horizontal relief
|
small space
|
large space
|
vertical relief
|
traffic space
|
lodging space
|
|
top floor
|
recessing
|
extending
|
|
|
intermediate floors
|
extending
|
recessing
|
corner
|
recessing
|
extending
|
|
ground floor
|
recessing
|
extending
|
flank
|
extending
|
recessing
|
|
|
|
Fig. 1110
Horizontal and vertical relief
|
|
|
Systematically
building recesses, setting the building back in an internal margin in a horizontal
relief is appropriate mainly for the ground floor, at the level of public use,
and – because of exposure to the sun – on the top floor. Building outwards can easily take place where there is unused
space, so on the intermediate floors. Put the opposite way: platforms, ramps and extensions on the ground floor, recessed
floors and overhangs on the top floor or roof
(Wright effect), lends itself more to special locations and to large outside
spaces. These accentuate the contours of the building.
Horizontal relief
|

|
Oud
Boven, Freijser et al. (1997)
15% horizontal extension
on the 1st floor
|
|

Coenen
|

Mecanoo
|
|
|
|
Fig. 1111
Examples of horizontal relief
|
|
|
|
|
|
Vertical relief
To achieve a vertical relief in the façade, one can choose to recess the corners and extend on the sides of
the building (for example, at the entrances to the building), extending
both over the floors, or one can choose for the reverse: fortress-like
extensions at the corners and recesses
in the sides of the ground plan. The latter is less suitable because of traffic
considerations and lends itself to special situations such as car-free streets.
|
Lourijsen

|
Brandes

|
|
De Bazel

Greiner

|
Brandes

|
|
|
|
|
Fig. 1112 recessed corner
|
Fig. 1113 extended flank
|
|
|
|
|

|
<
Atelier PRO
extension on the corner and flank
|

|
< Wils
extension on the corner,
recess in the flank
|
|

|
< Wils
Boven, Freijser et al. (1997)
page 65
30% horizontal recess on
the first
floor 1e
40% horizontal extension
on the
ground floor.
|
|
|
|
Fig. 1114
Combinations
|
|
|
|
|
|
|
|
Sculptural effect
Where
there is increasing non-systematic variation in recessing and extending, the
sculptural effect increases at first, but then
it decreases again because of fragmentation.
|
Loerakker

|
Van Herk

|
|
|
|
|
Fig. 1115
Examples of combinations of horizontal and vertical relief
|
|
|
|
Structural effect
By,
introducing a pattern on the smallest scale (internal or external balconies),
from a distance, the façade gains a structural effect.
|
Mehrtens

|
Benthem en Crouwel

|
|
|
|
Fig. 1116
Repetition 3m>30m
|
|
|
The recognisability of the
ensemble
One can
leave these choices entirely to the architect or, from the beginning, link it
to the context in order to ‘add lustre’ to a special location. By doing this,
an urban architectural ensemble (street, square, building
complex in a radius of approx. 100 m) becomes more recognisable as an entity,
compared with other ensembles. After all, such choices have a greater effect if
they are repeated between the buildings themselves. For example, recessed
corners of blocks of buildings (see Cerda’s Barcelona) only create a broadening urban architectural image if the same
principles are used in the next and/or opposite block, also if the symmetry in
which this occurs is incomplete.
Differences on higher levels
of scale
When one
lets such choices depend more on the context at a higher scale level, that
requires an urban architectural typology of location variants in a
broader context. One can then look for the context on the district level (1kmĄ) up to the European level (3000kmĄ).
The
larger the context in which the location variants of open spaces and especially
open water occur, the more scarce and thus the more precious they are. That
applies to the corners of an island such as the south-west corner of the
Harbour Island (Haveneiland) in IJburg, but also for IJburg as the inner corner of the IJsselmeer, or for
Amsterdam as a corner of Europe, where lines from south and east converge on
sea- and airports. One can leave such location factors for what they are, but
one can also exploit them urban architecturally, and cash in on their scarcity.
Homogeneity by mixing places
In an
age in which residents bring ideas back home with them from holidays spent in
all parts of the world, reminders of Venice or St. Petersburg can also play a role, but by
careful interpretation, optimalisation, transformation and realisation, these
must be adapted in such a way that they become rare in their own right. To what
extent can the combinations that have come about in Venice, be used as a model
for those in Amsterdam, and to what extent are they divorced from our time or
place?
Interaction with sun, wind,
water, earth, life, living outside
The
effect of the outside space on the margin, and vice versa, is also
connected here with climate (for example, with the amounts of sun and wind) and
orientation (their direction), but, in particular, it is connected with the
size of the open space along which the margins lie and the extent to which they
are enclosed. Spaces that are totally, or for the most part, enclosed
horizontally, such as empty spaces and voids (up to a breadth of 20m),
courtyards and inner squares (20m or more in breadth)
offer, in each case, another context for designing the margin. In the last two,
it makes rather a lot of difference whether these are part of the
through-traffic structure (outside courtyards and squares) or not (inner
courtyards and squares).
|

|
incorporated up to 30 metres in a building
empty spaces
voids
|
|

|
length smaller than 5 times the breadth:
enclosed, otherwise through-going spaces:
passages, streets, avenues
|
|

|
up to 30m in breadth
interior courtyards, small inner squares
exterior courtyards and small outer squares
|
|

|
more than 30m
courtyards, inner squares
courtyards, outer squares
with less than 50% road surface: courtyard,
otherwise a square
|
|
|
|
Fig. 1117 Outside spaces
|
|
|
Squares
|
|
|

market square for animals
(Beestenmarkt) in Delft
approx. 40 x 50m
|

Main market square (Grote
Markt), Haarlem
|

Mercator Square
(Mercatorplein), Amsterdam approx. 80 x 140m
|
|
|
|
|
|
Fig. 1118 Squares
|
|
|
|
|
Margins
|

Gouda Abken BV, approx. 20m
|
P.M.
Schiedam by Van de Seyp and
Van Dijk,
approx. 10m
|
|
|
|
|
Fig. 1119 Margins in courtyards and streets
|
|
|
|
Widths
|

Ede Brauwere
|

Rotterdam
Crooswijk Malschaert
|
|
Fig. 1120 Small outside space with continual
horizontal relief
|
Fig. 1121 Large outside
space with vertical relief every 80m.
|
|
|
|
The depth of relief
Relief
that has a rather small depth can, nevertheless, greatly influence the
appearance of streets, as we know from experience in existing districts where
plastic window-frames that have been moved to the
façade surface interfere with the recognisability of the street.
The fequency of relief
The
frequency of the relief is related to the length and
height of the façade. The minimal frequency is 0. A small frequency is once per
façade (e.g.once vertically between two side streets or once horizontally
between the lowest and highest floors). Each frequency larger than that gives a
more unrestful image and, in special cases, may be accepted or even requested.
The rules given here only apply to building lines (alignments) and
façades. A distinction is made between ground-floor façades (BG), intermediary
floors (TV) and the floor directly under the roof (DV).
1.
The building lines are the
outside boundary of the façade surface, unless it is established in the
following rules that at a particular depth, over a certain area, and at a
certain frequency, it is permitted to extend and/or recess a building with
respect to the building line.
2.
The particular characteristic
of the planning area within a town is ‘powerful and urban’. This leads to the
general rule that deviations from the building line should strengthen the
vertical character of the buildings and, with a view to this, must extend above
each other over a number of floors.
3.
Acceptability and the
desirability of having differences between the façade surface and the building
line is established by four fixed characteristics of the urban architectural
plan. These are:
a.
the position of the building
with respect to water;
b.
the position of the building
within the urban district;
c.
the position of the façade with
respect to the public space that borders it;
d.
the position of the façade with
respect to the sun.
Each of these characteristics leads to a series of different public spaces.
Each series is divided into a series of types (rules 5-8). For each of the four
characteristics in each series a general rule is given (rules 8-12).
5.
Water in the planning area is
divided into four types on the basis of breadth, as follows:
W1 >100m : external water
W2 50-100m : internal water
W3 25-50m : waterways
W4 <25m : canals
6.
The planning area is divided on
the basis of centrality in three types of urban area, as follows:
IJ1 centre, up to 300m from the
southernmost point of the harbour
IJ2 central area, 300-1000m around the
centre
IJ3 periphery, urban areas around the
central area
7.
Public space in the planning
area is divided into ten types, grouped into streets (S), squares (P) and
courtyards (H), as follows:
S1 1>10 b, where b is 24–48m: main
street
S2 1>10b, where b is 12–24m: street
S3 1> 5b, where b is 4–12m : lane
S4 1> 5b, where b is <4m
: passage
P1 built-up on one side, remaining
sides W or S
P2 built-up on two sides, remaining
sides W or S
P3 built-up on three sides, remaining
sides W or S
P4 built-up on all four sides.
H3 built-up on three sides, remaining
side W
H4 built-up on all four sides.
8.
The façades are divided
according to their position in relation to the sun’s orbit (Z), by the hours of
the day, as follows:
Z1 0–6 hrs : night façade (N–E)
Z2 6–12 hrs : morning façade (S–E)
Z3 12–18 hrs : afternoon façade (S–W)
Z4 18–24 hrs : evening façade (N–W)
9.
Because of traffic, the corners
between S1 and S2 are recessed from the corner to 3m.
All the other corners are built along the building line to at least 5m from the
corner.
The rules below only apply then to the remaining surface of the façade.
10.
The general rule for recessed
building surfaces with respect to the building line in connection with their
location with respect to the sun’s orbit is that the less exposure to the sun,
the smaller the percentage of the façade surface that is allowed to deviate
from the alignment of the building. For Z1, the desired deviation from the
remaining façade surfaces according to rule 10 is 20%, for Z2 this is 40%, for
Z3 60%, and for Z4 80%.
11.
The general rule for the depth
of the recess with respect to the alignment of the building in connection with
location by water and public space is that from at least 1% of the bordering
public space in the south-west of the planning area (luw) to at least 5%
of it in the north-east of the planning area (ruw) are recessed inside
the building alignment.
12.
The general rule for the
frequency of recessing with respect to the building alignment is that the nearer one comes to the centre, the
‘liveliness’ of the façade increases. In the connection with the above
sentence, the frequency with which recessing occurs amounts to a maximum of 3
times for each 100m of building alignment on the north-west side to at least 9
times for each 100m of building alignment on the south-east side.
Creativity means leaving out at least one self evident
tacit supposition. We found a systematic way to
examine hidden presuppositions in
science and technology. We provisionally call it 'conditional analysis' and use it in ecology, design,
education and in making computer programs. It has more to do with possibilities
than with probabilities or necessities. It gives some insight in the
boundaries of imagination and thus design.
Conditional analysis
It is based on the simple
comparison of two concepts A and B, putting
the question 'could you imagine A without B?' and the reverse question.
Temporarily we take in consideration only the pairs of concepts that make
possible a different answer on both questions.
As soon as we can imagine A
without B but B not without A we call A a (semantic) condition for B. As soon as we find a concept C that we
cannot imagine without B but B without C we can, we have semantically a 'conditional range' of concepts ABC out of which
the hypothesis emerges that we cannot imagine C without A, but in the reverse
we can. Though introspective, these comparisons turned out to give consensus
based on a possibility of falsification.
Culture supposes life,
life supposes matter
Let us for instance conditionally
compare the ecological concepts Abiotic, Biotic and Cultural phenomena (A, B and C). I cannot imagine
cultural phenomena without biotic (because culture presupposes at any time
living people and functioning brains), but biotic phenomena without cultural I
can (for instance plants). I cannot imagine biotic
phenomena without abiotic phenomena, but abiotic phenomena without biotic I can
(for instance light, air, water, soil). So the hypotheses to be controlled are:
'I cannot imagine cultural phenomena without abiotic phenomena, but abiotic
phenomena without cultural I can.'. If we confirm that hypotheses we can draw a
conditional scheme like this:
|

|
It
seems to be a Venn diagram out of set-theory. But it is not, because
set-theory presupposes more than the concept of presupposition itself. It
presupposes for example the concept of 'element' and any equality of the
elements (according to the criterion of the set). Jong (1992) supposes less.
A
semantic Venn diagram does not yet need these and perhaps other
presuppositions. The drawn borders are no inward formulated borders of sets
and elements, but outward boundaries of eventually vague and continuous
conception.
The ABC model represents phenomena outside culture, but is
itself a concept and thus culture.
|
|
|
|
Fig. 1122
The ABC model
|
|
|
This raises the philosophical
question whether there is any difference between 'preconception' (presupposition, assumption) and 'precondition' (prerequisite) at all. The environmental
crisis taught us however that there appeared preconditions for life we did not preconceive beforehand. We consider
'environment' in an ecological sense as the set
of conditions for life, known or yet unknown.
Nature a human concept
or the reverse
In Fig. 1010 two very different ecological
presuppositions that have a direct influence on the way people design a
landscape or townscape are drawn: 'Man is part of nature' and 'Nature is only a
human concept' ecocentrism and anthropocentrism).
A paradox of argument
Both
suppositions contain a paradox. The anthropocentric way of thinking would imply
that physics and biology ('N') cannot find anything new from experiment or
observation that is not already included in the existing set of concepts (C) or
its combinations (idealistic position). Wittgenstein (1919, 1959;
Wittgenstein (1963; Wittgenstein and Hermans (1986) said: 'The boundaries of
our world are the boundaries of our language.', and: ‘About which you cannot speak you have to be silent.’ It was a
reason to suspect him of mysticism.
The ecocentric view however would
imply that we cannot communicate such observations. To take these observations
serious, we have to regard them as a not yet cultural part of the natural world
N (materialistic position).
Logic as culture
Let us now consider culture (C) as an intermediate between the picture
('N') and the portrayed in the natural world (N). Wittgenstein supposes that the picture and and the
portrayed have their 'logical form' in common. Formal logic however cannot cope with expressions like
exclamations, questions, proposals (like designs) and orders: they have no
logical form. That is what occupied the later Wittgenstein (1953). In my opinion these
linguistic expressions are the very solution to the paradox of ecocentric
thinking. Questions are the definition of an emptiness at the
boundaries of knowledge, proposals and designs are excursions in an unknown,
but nevertheless imaginable and perhaps possible future world.
Culture as a set of
suppositions
This brings me to a specification
of culture, creativity, science and art. Culture is the set of suppositions in communication.
Suppose we had to explicate all presuppositions of our communication before we
could start with it, in that case we would seldom have time to communicate. Fortunately we don't have to
explicate every time all these preconceptions, we simply take them for granted
and call them culture. That is easy, but it also keeps 'self-evident' concepts
out of discussion. Creativity just starts with disclaiming these apparently
self-evident preconceptions, science
starts with doubting them.
Art as a ripple at the outside boundary of culture
Art is a ripple at the outside boundary of culture
denying conventional and adding unconventional presuppositions by poičsis. We need art or technique to
make new concepts outside conventional language. Science on itself does not
provide that.
Different futures
Probable ecological, economic and cultural futures are gloomy
from a viewpoint of inevitable environmental developments. But are the probable
futures the only ones that we have to take in consideration? Empirical research is limited to the
probable futures. Design, or technical research is limited to the broader set
of possible ones.
I cannot imagine the probable without the possible. The reverse I can.
What is probable must be by
definition possible.
|

|
|
|
|
Fig. 1123 The
modality of the possible
|
|
|
Boundaries of causal
thinking
Predicting probable futures requires causal thinking on an empirical basis. We cannot predict possible futures as
far as they are not probable: we have to design them. They are invisible for
probability-calculations. They are fundamentally ab-normal, outside the 95%-area
of probability. Designs cannot be calculated or predicted. If so, they would no
longer be designs. Design produces possibilities, conditions, freedom of choice, difference.
Design does not cause
futures, it makes them possible
Every line a designer draws is a
precondition for further drawing, but not a cause for the rest of
the design process. In the same way the performance of the resulting building,
the behaviour of its inhabitants, is not caused or even necessarily aimed by
the designer, but only made possible in a universum of possibilities opened by
the design. Every line a computerprogrammer writes is a condition for the rest
of the program, but not the cause of its performance. On the other hand one
single missing line can 'ceteris paribus' be called the 'cause' of its break‑down.
Conditions of life
In the same way global life has
no single cause, but many conditions of which lacking one on a single place and
moment can indeed cause the death of an individual. Special conditions of
sunlight, moist and minerals do not cause special life‑forms (let alone
that they can be aimed by norms of sunlight, moist and minerals per location),
they only make different life‑forms possible. The relation conditional
<> causal has its analogies in the dualities possible
<> probable, designing <> predicting, means‑directed <> aim‑directed, and probably ecocentric
<> antropocentric.
What kind of thinking do we need
for design study?
|

|
I cannot imagine causes without conditions, the reverse I can. We
have to make a step back from causal
thinking about probabilities into the broader area of conditional thinking about
possibilities. Every cause is a condition for anything to happen, but not
every condition is also a cause. The foundation of a house may
be a precondition but not a cause of its existence. Causal thinking is
conditional thinking, but conditional thinking is not always causal.
Suppose we read in the paper: 'The crash of the cars was caused
because one of the drivers lost control of his wheel.' That sounds plausible
until an extraterrestrial descends, saying: 'Nonsense, the collision was
caused by two objects approaching eachother with great speed.'
|
|
|
|
Fig. 1124
Causes under conditions
|
|
|
If he is right, the paper is
wrong, because if the cars would not have been approaching eachother and one of
the drivers would have lost control there would have been no collision. So it
is only a cause under the tacit precondition of approaching cars. Every causal
conclusion is based on innumerable tacit conditions called 'ceteris paribus presuppositions'.
Any cause supposes
conditions
|

|
|
|
|
Fig. 1125 Conditional thinking
as a ceteris paribus environment of causal thinking
|
|
|
I cannot imagine social possibilities without any economic conditions. The reverse I can.
I cannot imagine economic possibilities without technical
conditions. The reverse I can.
This gives a semantic conditional
sequence of possibilities. In stable technical
conditions economic initiatives can cause technical or social change. But when
the dikes burst the technical 'ceteris paribus' for economic determinism are
lacking.
Changing conditions
The ceteris-paribus
presuppositions of causal explanations also change on different levels in time.
That means changing causal explanantion. They also can be changed by design forcing
shifting explanation about the effects. Innovative design implies removing some
preconditions and making new ones. Design makes ceteris non paribus.
Innovative
design implicates always removing suppressed conditions and making new ones.
Loose from that conditions change in different wave-lengths:
Now we can point out a week
component in causal thinking. The ceteris-paribus presuppositions of causal
explanations change on different levels and can be changed by design ... by us.
Comforting the causal
trapped
Professor
Helmar Krupp (1996), former director of
the Fraunhofer Institut in Karlsruhe studied physics, pilosophy and
sociology. He came to the conclusion that the individual no longer can
influence the evolution of society. Society behaves as a system with its own
dynamics. Individuals have to submit to this dynamics. In the conference 'The
mind of technology', Delft, 27 november 1996, De
Jong tried to comfort him by emphasising design. The limitations of research
could be broken by design.
Probable ecological, economic and
cultural futures are gloomy from a viewpoint of inevitable Schumpeter dynamics or Fukuyama-expectations. But are the probable futures
the only ones that we have to take in consideration? Empirical research is
limited to the probable futures, design, innovation or technical research to
the possible ones. And that creates hope.
Form supposes a legend
I cannot imagine a representation or drawing without indicated differences, an (eventually
tacitly presupposed) vocabulary or legend (key to symbols). The legend is the vocabulary of the drawing. Only by
drawing differences one can make forms
and only by making different forms one can make structures. Function presupposes a structure within which the
function operates.
The same form by
different structures
Nevertheless, within one set of
forms (for example a box of blocks) you can imagine different ways of
connecting them (structures) and within different structures you can imagine different
functions. In the reverse the same function often chooses different structures and the
same structure is often built in different forms or materials. So where the
design process lays the initiative is free. It can be either a causal, aim-directed (purposive) process starting with the function
(funcionalist position) or a conditional, means-directed process (formalist or structuralist
position).
The sequence of aims
and means
When the number of aims is smaller than the number of means you better can use aims as independent variable with the means as dependent variable. In architecture and certainly
urban planning the number of means is smaller than the number of aims. In that
case you better can variate the means to see what gives the greatest amount of
possibilities for future generations.
Environment in the technical and ecological sense of Hendriks (1993) is the set of
conditions for life (see Fig. 1008). In this definition
'conditions' can be interpreted as ecological, technical, economic, cultural or
administrative preconditions. These substitutions result in 5 different usual
concepts of 'environment': the administrative environment, the cultural
environment etc. The concept 'life' can be substituted in the same sense as
'social life, cultural life, life of men, animals, plants
etc, multiplicating the meanings of the concept of 'environment'.
Building conditioning
life
Building is a prerequisite for human and other life.
Building and urbanization has
ecologically more positive effects on the environment than
negative. In contrast with other productive branches it produces more
'environment' than it costs. It produces an environment for humans without which
they would not survive at the same rate. But it also could produce a better
environment for a variety of plants and animals than many places outside the
built‑up area (see Fig. 766).
Making th city a source
of life
Vos (1993) and Denters, Ruesink et al. (1994)
reported that for instance in the Dutch cities Zoetermeer and Amsterdam, you can find 1/3 and 1/2 of the
total amount of botanical species in the Netherlands. Within the city of Zoetermeer
one square kilometre counts even 350 wild self breeding species outside the
gardens. That is 7 times more species than an agricultural square kilometre in
the direct surroundings and as much as a square km in the natural environment
of natural reserves as the Dutch dunes. Of course we cannot say that the value
of an urban ecosystem equals that of the dunes, but we signal a potential that
we could improve. To improve the contribution of urban design to the solution
of the ecological crisis we have to emphasize more the production of positive
effects and its research than the reduction of the smaller negative effects.
The sun as source of
the city
Let me give another example of
environmentally decisive design. The development of photovoltaic cells can destroy many
gloomy prophecies. The photovoltaic cell deminished a factor 14 in price since 1975
(see Fig. 14); another factor 8 and it
outruns the economic efficiency of fossil fuels. The only problem is a cheaper
way of slicing sand. The last two centuries technical problems like that never
waited longer than 10 years for their solution.
Let's destroy all gloomy prophecies by design.
Design makes a
difference
The very
beginning of any range of semantic conditions seems to be 'difference'. Any concept presupposes
'difference'. Difference on itself cannot be defined because the concept of 'definition' already presupposes making difference with the
rest. But also the concepts of 'making', 'with', 'the', and 'rest' presuppose
'difference'. So in the sentence concerned, 'difference' was already at least
five times presupposed! Even the concept of equality (as necessarily presupposed in the concepts of
'gathering' and 'counting' and therefore in set‑theory and mathematics)
presupposes difference. As soon as you accept that there are 'different
differences', for instance more or less difference ('variation'), you have to accept that
equality is a special case of difference.
Difference makes
possible
According to Fig. 1130 there should be a more specific
relation between difference and possibility than the conditional one in Fig. 1129. However, I did not yet find a
more convincing consideration than a picture like Fig. 1130.
Yet this question is essential
for designers. If after all their profession as producers of possibilities has a specific relation with differentiation,
than it has a difficulty with the accepted scientific practice of
generalization.
Equality is a special
kind of difference
Ashby (1960) and Leeuwen (1971) noticed that given a
difference you always can imagine more difference, but not always less. The
least kind of difference we call equality. Nevertheless, there must be a
difference of place or moment left to establish that equality, otherwise the
comparison has no sense. So we can draw an important conclusion: equality is a
special kind of difference and not the opposite of it.
The search for equality
ends somewere
Many scientists feel
uncomfortable with that conclusion because their profession is based on
equations that conceive regularities in sets of n>1
'comparable' facts. Designers on the contrary do
not, because their profession is based on originality in every single n=1 case.
Without that originality their design would not be a design, but a prediction. The very
concept 'concept' presupposes any equality in the observations
conceived in the concept, but the concept 'conception' presupposes something different from earlier
observations. Conceptualization always needs a reduction of diversity.
The sense of difference
Vision, hearing, smelling,
touching all need differences or changes in the environment. As soon as there
is some repetition within these perceptions, we 'recognize' it, which is the
basis of cognition and conceptualization. (Re)cognition however is only based on similarity, it reduces the differences that still can
be perceived. So conceptualization changes sometimes chaos in surprize,
sometimes surprize in recognition, sometimes recognition in boredom.
Deminishng returns of reductive science
|

|
Causal thinking is a special way of reducing diversity. It
reduces similarities in repeating sequences of phenomena to the more general
concepts of cause-effect relationships. Causal explanation has the more value
the more reduction of different cases is possible by abstraction.
Alas, nowadays there are not so much phenomena left that can be
explained monocausally. They largely have been
explained earlier. What is left are context sensitive effects that can be caused by many different
'causes' or causes that can bring about many different effects, dependent on
small differences in the environment where the 'cause' is introduced.
Striking a match can cause little damage here, and big damage there. So
monocausal (or 'paucicausal') research shows deminishing
returns, especially on environmental (context sensitive) issues.
|
|
|
|
Fig. 1132
Deminishing returns of monocausal (or paucicausal) research
|
|
|
Means and aims can only be chosen
on the basis of a supposed causal relationship between both. Otherwise thinking
about means and aims is senseless. The same means applied here have other
effects as applied there. Apart from that they are also scale-dependent and
therefore subject of misconceptions.
Ecological tolerance
The
curve of ecological tolerance (see Fig. 693) relates the chance of survival
of a species or ecosystem to any environmental variable, for instance the
presence of water. In that special case survival runs between drying out and
drowning.
A risk-cover for life
Variety is a risk-cover for life. This is not only true for the variety in the
abiotic conditions, but also for the variety of ecosystems, species and of
genetic possibilities within each species. Life survived many disasters thanks
to biodiversity. In the diversity of life there was always a species to survive
or within a species a specimen that survived. Survival of the fittest
presupposes diversity from which can be chosen in changed circumstances.
Deminishing biodiversity means undermining the resistance against catastrophes.
From the 1.5 million species we know, this century we lost approximately 50000.
So, we not only introduce ecological disasters, but also undermine the
resistance of life against these disasters.
Biodiversity supposed
in any quality of life
Biodiversity in mankind is a crucial value in our quality
of life. As we are here we are all different and the very last comfort you can give
a depressed person is 'But you are unique'. Diversity is also a precondition
for trade and communication. If production and consumption
would be the same everywhere, there would be no economic life. If we would have
all the same perceptions and ideas, there would be no communication. It is an
important misconception to believe that communication only helps bridgeing
differences. Communication also produces diversity by compensating eachother and coordinating
behaviour by specialization.
Freedom of choice
supposes diversity
World commission on environment and development
(1987, Committee Brundtland, see ) summarizes the environmental
challenge by stating sustainability as leaving next generations at least as
much possibilities as we found ourselves. But what are possibilities?
'Possibilities' is not the same as economic supply. If our parents would have
left us the same supplies as they found in their childhood, we would be far
from satisfied. 'Possibilities' has to do with freedom of choice and thus variety. Our converging
Schumpeter-economy described by Krupp (1996) and Fukuyama (1992)-culture leaves no
choice. In our search for the alternative we find everywhere in the world the
same hotels, the same dinners, the same language. This century, the last
'primitive' cultures are lost and with them an experience of life that no
western language can express.
Trade and communication
suppose diversity
The extremest consequence of this
levelling out would be a world without economy and even communication. If there
are no longer any differences in production factors, exchanging goods and
services would no longer be necessary. If total world wide distribution of
knowledge and consensus would be the result of our communication age, there
would no longer be anything worthwile to communicate. These thought experiments
show clearly that 'difference' is also a hidden presupposition in communication
and economy.
Quality can be measured in terms of possibilities of
use, experience and expectation for future generations. The way design can
sustain a sustainable development in the sense of Brundtland is to produce more
choices for man, animal and plant. If there were one best solution for all
problems of architecture and urban planning, it would be the worst in the sense
of choices for future generations! This paradox pleads more for diversity than
for uniform solutions. Moreover, if there was an uniform solution, the designer
would have no task.
Quality is always a function of
variation (see Fig. 694). Quality of possible experience
moves between diversity and uniformity, surprise and recognition. One step too
far into both sides brings us in the area of boredom or confusion. This is a
simple conception, already recognized by Birkhoff (1933) and Bense (1954) see also Koutamanis (2002), but why dit it
not succeed, why is quality always posed as an unsolvable question?
Different diversities
at different scales
Any discussion on variety and
thus variables can fall prey to confuson of scale. That means that even logic and
science as forms of communication are prey to the scale paradox. The paradox of
Achilles and the turtle is a beautiful example of the scale-paradox in
time. The turtle says: 'Achilles cannot outrun me when I get a headstart,
because when he is where I was at the moment he started I'm already further,
when he reaches that point I am again further and so on!'. This conclusion is
only incorrect by changing the time-scale during the reasoning. Something
similar is found by Russell on set-theory. Russell (1919) bans sets containing themselves and reflexive
judgements as 'I am a liar'.
Premises of conclusions to be drawn at the same scale
|

|
The scale paradox means an important scientific ban on
applying conclusions drawn on one level of scale to another without any
concern. The picture shows the possibility of changing conclusions on a
change of schale by a factor 3. There are 7 decimals between a grain of sand
and the earth. That gives approximately 15 possibilities of turning conclusions.
Between a molecule and a grain of sand applies the same. This ban is violated
so many times, that this should be an important criterion on the validity of
scientific judgements.
The scale-paradox is not limited on concepts of diversity. An
important example of turning conceptions into their opposite by scale is the
duality of aim and means. For the government subsidizing a municipality the
subsidy is a means, for the municipality it is an aim. So the conception of
means changes in a conception of aim by crossing levels of scale. The turning
of 'Zweckbegriff' into 'Systemrationalität' by Luhmann (1973) may be a turning
conception of the same character.
In growing organizations integration on the level of the organization as a whole
means often desintegration of the subsystems and perhaps
|
|
|
|
Fig. 1133 The scale paradox
|
|
|
a new form of integration in
the sub-sub-systems. This process is often called 'differentiation'!
Obedience to nature
called freedom
The computer sustains the design
process and spatial design sustains or even enlarges our freedom of choice.
Enlarging the diversity of inside and outside space offers after all new
possibilities and thus new freedom of choice. Concerning the possibilities of
future generations of world population since Bruntland, we call the maintenance
of that freedom 'sustainable development'. Environmental planning takes into account the simultaneously
appearing loss of possibilities and freedom of choice for future generations.
Extending freedom of
choice by design
The building process however has
in this sense more positive than negative ecological effects. The best way
design can sustain a sustainable development in the sense of Brundtland, is to
produce more choices (possibilities) for man, animal and plant. If there were
one scientificly tested best solution for all causally formulated problems of
architecture and urban plaming, it would be the worst in the sense of choices
for future generations. This paradox rises when we consider science only as a
method of optimizing probable effects. I would like to state that technical
science has more to do with possibilities than with probabilities.
Sutaining design by
computing
Computerprogramming not only sustains design and freedom of
choice, it also forces us to make clear hidden presuppositions and that is the traditional task of art and
science.
In that perspective the task of
technical science is to make clear the preconditions (or presuppositions) of
technical performance, the task of technical ecology that of life performance.
The presuppositions about the
design process, as they are differently hidden in a designers' mind and in
design sustaining computer programs, have something in common with the
preconditions of technical and biological performance. If our theory can cope
with both, it will concern a more essential thing about design, building and
ecology.
Designing the
improbable
The possibility (the set of conditions) of an event is something different from a
cause (and subsequently the probability) of an event. Every cause is a condition for something to happen, but
not every condition is also a cause. The design of a house does not cause the
behaviour of a household. It only makes more ways of behaviour possible than
there would have been possible without a house. It allows freedom of choice,
offers conditions. In the same way the design of a computerprogamme is no good when it forces the user into a specific
way of thinking, it should give the opportunity for different ways of thinking.
Ecology is the science of conditions, prerequisites for different life‑forms.
Global Iife by its enormeous differentiation is not monocausal and thus not
predictable or 'aimable'. Death of individuals on the other hand, is
predictable by pointing out any essential condition for life lacking. Man as a
part of life is essentially not predictable as long as we believe in freedom of
choice.
Sustaining the possible
In ecology, technology, design
and computerprogramming conditional thinking is as important as the
operational, aim‑directed, causal thinking we are used to. The
methodology of causal and probability thinking is largely developed. But what
methodology do we need when we do not only ask questions about the cause or aim
of a phenomenon, but about the conditions under which a phenomenon could
possibly appear, its possibility?
Abler, R. & J.S. Adams; ; Gould,
P. (1971) Spatial organization - The Geographer’s view of the world. In: (Englewood Cliffs NJ) Prentice Hall Inc.
AER (1979) Kolen en Uraan. Een overzicht van relevante aspecten met betrekking tot
het gebruik van kolen / uraan voor elektriciteitsopwekking ('s-Gravenhage) Staatsuitgeverij
Akker, C. v. d. and M.
E. Boomgaard () (2001) Hydrologie. (Delft) DUT Faculteit Civiele
Techniek en Geowetenschappen.
Alexander, Christopher (1966) A
city is not a tree. (London) (s.n.)
Allen, S. (2000) Mapping the unmappabIe:
on notation In: Allen, S. [ed.]; 31-47
Ambroziak, B.M.; Ambroziak, J.R.
(1999) Infinite perspectives - Two thousand years of three-dimensional
mapmaking. (New York) Princeton Architectural Press
Anderson, D.R. (1984) Testing
the field of vision. (St. Louis) Mosby
Andrewartha, H.G. (1961) Introduction
to the Study of Animal Populations (Chicago) University of Chicago Press
Angenent, W.J. (1987) Kaartlezen
- Handleiding voor kaart- en kompasgebruik (Utrecht) HES
Angremond, Kees d';
Huisman, Pieter; Jong, Taeke de; Schiereck, Gerrit Jan; Thissen, Wil; Broos,
Philip; Herbergs, Ben [eds.] (1998) Watertovenaars. Delftse ideeën voor nog
200 jaar Rijkswaterstaat. (Rotterdam) Beta Imaginations Publishers
Ankum, P. van (2003) Polders
en Hoogwaterbeheer. Polders,
Drainage and Flood Control (Delft) Delft University of Technology, Fac. Civiele Techniek en
Geowetenschappen, Sectie Land- en Waterbeheer
Appleton, J. (1986) Some
thoughts on the geology of the picturesque (j) Journal of Garden History
6(1986): 270-291
Arcy Thomson, W. d’ (1961) On
growth and form. (Cambridge
UK) Cambridge University Press
Arends, G.J. (1994) Sluizen
en stuwen. De ontwikkeling van de sluis- en stuwbouw in Nederland tot 1940.
(Delft) Delftse Universitaire Pers / Rijksdienst voor de Monumentenzorg;
Bouwtechniek in Nederland 5
Asselborn, Eric;
Chiappero, Pierre-Jacques; Galvier, Jacques (2005) Mineralen
(Königswinter) Könemann, Tandem Verlag GmbH
ASVV [ed.] (2004) Verkeerstechniek.
Aanbevelingen voor verkeersvoorzieningen binnen de bebouwde kom (Ede) CROW
Bach, B.; Jong, T.M. de (2006) Traffic
and design of the urban fabric (Ede) CROW
Bach, Boudewijn (2006) Urban
design and traffic / Stedenbouw en verkeer (Ede) CROW
Bach, Boudewyn; Jong,
T.M. de; Jong, Marjolein de (2004) Stedebouwkundig ontwerpen voor verkeer
& stedelijke mobiliteit (Delft) Publicatiebureau Faculteit Bouwkunde
Bahrdt, Hans Paul
(1957) Die Moderne Gross-Stadt. (Tübingen)
Bakker, P. ;
Westrhenen, J. van (1973) De kaart, model van de werkelijkheid (xxx) xxx
Bal, D.; Beije, H.M.;
Fellinger, M.; Haveman, R.; Opstal, A.J.F.M. van; Zadelhoff, F.J. van (2001) Handboek
Natuurdoeltypen (Wageningen) Landbouw, natuurbeheer en visserij
Bal, D.; Beije, H.M.;
Hoogeveen, Y.R.; Jansen, S.R.J.; Reest, P.J. van der (1995) Handboek
natuurdoeltypen in Nederland, Bijlagen (Wageningen) Informatie en
kenniscentr.nat.beh.LNV
Bal, D.; Beije, H.M.;
Hoogeveen, Y.R.; Jansen, S.R.J.; Reest, P.J. van der (1995) Handboek
natuurdoeltypen in Nederland (Wageningen) Informatie en
kenniscentr.nat.beh.LNV
Barisi, I. (2004 ) Guide to
Villa d’Este Roma (...) De
Luca Ed. d’arte
Barkman, J.J.;
Stoutjesdijk, PH. (1987) Microklimaat, vegetatie en fauna (Wageningen)
Pudoc Wageningen
Barnes, Ch.W. (1988) Earth,
time, and life: an introduction to physical and historical geology (New
York)
Barton, Hugh; Tsourou, Catherine
(2000) Healthy Urban Planning (London) Spon Press
Bartram, R. (2003) Geography
and the Interpretation of Visual Imagery In: Clifford & Valentine; 149-161
Batenburg-Eddes, T.
van; Berg Jeths, A. van den; Veen, A.A. van der; Verheij, R.A.; Neeling, A.J.
de (2002) Slikken in Nederland; Regionale variaties in
geneesmiddelengebruik [Regional
variations in use of pharmaceuticals] (Bilthoven)
RIVM Rapport 270556005 pdf
[1481Kb] http://www.rivm.nl/bibliotheek/rapporten/270556005.html
Bateson, Gregory (1980) Mind
and nature - A Necessary Unity (Toronto) Bantam Books
Bateson, Gregory (1983, 1980,
1973) Steps to an Ecology of Mind (New York) Chandler Publishing;
Balantine Books
Batty, M. (2003) Using
Geographical Information Systems In: &, Clifford [ed.] Valentine;
409-425
Baum, Andrew; Epstein, Yakov M.
[eds.] (1978) Human response to Crowding (Hillsdale, New Jersey)
Lawrence Erlbaum Associates, Publishers
Beardsley, J. (1984-2006) Earthworks
and beyond - Contemporary art in the landscape (New York) Abbeville Press
Publ.
Begon, M.; Harper, J.L.;
Townsend, C.R. (1996) Ecology (Oxford) Blackwell Science
Beintema, Albert;
Moedt, Oene; Ellinger, Danny (1995) Ecologische atlas van de Nederlandse
Weidevogels m.m.v. SOVON (Haarlem) Schuyt & Co BV
Bekhuis, Johan;
Bijlsma, Rob; Dijk, Arend van; Hustings, Fred; Lensink, Rob; Saris, Frank
[eds.] (1988) Atlas van de Nederlandse Vogels (Arnhem) Sovon
Bense, M. (1954) Aesthetica
(Stuttgart) Deutsche Verlags-Anstalt
Berg, A.E. van den ;
Berg, M.M.H.E. van den (2001) Van buiten word je beter. Een essay over de
relatie tussen natuur en gezondheid. [The outside heals; an essay on the
relationship between nature and health] (Wageningen) Alterra, bijlage bij
het jaarboek 2001.
Berg, A.E. van den;
Berg, M.M.H.E. van den; Giesen, C.W.M. (2001) Van buiten wordt je beter. Een
essay over de relatie tussen natuur en gezondheid. (Wageningen) Alterra,
bijlage bij het jaarboek 2001
Betsky, A. (2002) Landscrapers
- building with the land London Thames & Hudson
Bijhouwer, J.T.P.
(1965) Een bodemkartering ten behoeve van de stedebouw in: De bodem van
Nederland - Toelichting bij de bodemkaart van Nederland schaal 1: 200.000
(j) Boor, Wageningen 1948: 97-102
Bink, F.A. (1992) Ecologische
atlas van de dagvlinders van Noordwest-Europa (Haarlem) Schuyt & Co
Uitgevers en Importeurs
Birkhoff, George D. (1933) Aesthetic
measure (Cambridge, Mass.) Harvard University Press
Bishop, A.C.; Wooley,
A.R.; Hamilton, W.R. (1978) Elseviers stenengids; stenen, mineralen,
fossielen (Amsterdam/Brussel) Elsevier
Blaeu, Joan (1652) Toonneel
der Steden van Holland - Westvriesland - Utrecht (Amsterdam)?
Blair, C.L.; Gutsell, B.V. (1974)
The american landscape - Map and air photo interpretation.
Bloemers, J.H.F.;
Kooijmans, L.P.; Sarfatij, H. (1981) Verleden land. (Amsterdam) Meulenhoff Informatief
Bloom, Arthur L. (1973) The
Surface of the Earth. (London) Prentice Hall International, Inc. / The Open
University Press; Foundations of Earth Science Series
Boekhorst, J. te; Deroose,
P.; Harsema, H.; Illés, V.; Jonge, N. de (1996) Het fenomeen delta-landschap
van Nico de Jonge/ The phenomenon delta-a Nico de Jonge landscape
(Wageningen) Uitgeverij Blauwdruk
Boersema, J.J. ; Copius
Peereboom, J.W. ; Groot, W.T. de (1991) Basisboek Milieukunde (Meppel /
Amsterdam) Boom
Bohemen, H.D. van (2004) Ecological
Engineering and Civil Engineering Works. A Practical Set of Ecological
Engineering Principles for Road Infrastructure and Coastal Management. (Delft)Thesis
Delft University of Technology/ Interfaculty Research Centre "The
Ecological City" Road and Hydraulic Engineering Institute of the
Directorate-General of Public Works and Watermanagement.
Bohemen, H.D.; Buizer,
D.A.G.; Littel, A. [eds.] (1986) Atlas van de Nederlandse amfibieën en
reptielen (Hoogwoud) KNNV Uitgeverij
Bohn, U.; Gollub, G.; Hettwer,
H.; Weber, H. [eds.] (2000) Map of the Natural Vegetation of Europe scale 1:
2.5 million (Bonn) Federal Agency for Nature Conservation; BN Bundesambt
für Naturschutz
Bohn, Udo (2001) Karte
der natürlichen Vegetation Europas. Map of the Natural Vegetation of Europe. (Bonn) Bundesambt fur Naturschutz
Bolhuis, P. van ;
Vrijlandt, P. (1993) Waterlijn - Ideeën voor de toekomst van de Stelling van
Amsterdam en de Nieuwe Hollandse Waterlinie (Wageningen)
Bont, G.W.Th.M. de;
Zwart, B.; KNMI (1985) De Wolken en het Weer (Zutphen) Uitgeverij Terra
Bosatlas (1996) De
Grote Bosatlas: voor Mavo/Havo/VWO. (Groningen) Wolters-Noordhof
Bosscher, F.F.A. (1980)
Bestemmingsplankaarten, codering, arcering en kleur - Samenvatting van het
nieuwe rapport van de werkgroep kleuren en tekens. (j) S&V: 604-607
Bouman, P.J. (1979) Hollands
welvaren In: Romein, J; Romein, A. [eds.] Delage landen bij de
zee (Amsterdam) Quirido's Uitgeverijen b.v.
Boven, Cees van; Freijser,
Victor; Vaillant, Christiaan (1997) Gids van de moderne architectuur in Den
Haag ('s-Gravenhage) Ulysses
Bovy, P.H.L.; Zijpp,
N.J. van der (2000) Transportation Modelling (Delft) Faculteit Civiele
Techniek en Geowetenschappen
Braams [ed.] (1982) Energie.
Een blik op de toekomst. (Utrecht) Het Spectrum
Braun-Blanquet, J.
(1964) Pflanzensoziologie (New York) Springer-verlag
Breems, W. den; Hoving,
S.; meeusen, C.; Methorst, R.; Michel, D.; Panebianco, D. (2000) Zoetermeer
NATUURLIJK! Een kleurige woonomgeving (Zoetermeer) Hogeschool Delft ,
Milieukunde
Bremer, P.; Smit, A.
(1995) Wilde planten in Oostelijk Flevoland (Zwolle / Lelystad)
Provincie Flevoland
Broekhuizen, S.;
Hoekstra, B.; Laar, V. van; Smeenk, C.; Thissen, J.B.M. [eds.] (1992) Atlas
van de Nederlandse zoogdieren (Utrecht) KNNV Uitgeverij; Natuurhistorische
Bibliotheek van de KNNV
Brown, L.; Kane, H.; Ayres, E.
(1993) Vital signs. The trends that are shaping our future (London)
Worldwatch Institute, Earthscan Publications Ltd
Bruin, D. de; Hamhuis,
D.; Nieuwenhuize, L. van; Overmars, W.; Sijmons, D.; Vera, F. (1987) Ooiveaar
De toekomst van het rivierengebied (Arnhem) Stichting Gelderse
Milieufederatie
Buchanan, Colin (1963) Traffic
in Towns. The specially shortened edition of the Buchanan report.
(Harmondsworth, Middlesex, England) Penguin Books; a Penguin special
Bucknell, J. (1967) Klimatologie
(j) Prisma-Compendia
Castex, J.; Panerai, J.-Ch.;
Depaule, Ph. [eds.] (1990) De
rationele stad. Van bouwblok tot wooneenheid. Met een nawoord van Henk Engel.
(Nijmegen) SUN; Teksten architect
CBS (1993) Standaard
Bedrijfsindeling (SBI), (Rijswijk) Centraal Bureau voor de Statistiek (CBS)
CBS (1994) 1899-1994.
Vijfennegentig jaren statistiek in tijdreeksen ('s-Gravenhage)
Sdu/uitgeverij / CBS publikaties
CBS (1994) Bodemstatistiek
1989 ('s-Gravenhage) Sdu-uitgeverij/ CBS publikaties
CBS (2003) Homepage;
http://www.cbs.nl/
CBS statistics (1978) Emission
registration 1974/1981
CBS, Centraal Bureau
voor de Statistiek (2001) Statistisch Jaarboek 2001 (Voorburg/Heerlen)
CBS
CBS; RIVM (2001) Milieucompendium
2001. Het Milieu in cijfers. (Alphen aan den Rijn) Kluwer;
http://arch.rivm.nl/environmentaldata/
Chadych, D.; Leborgne, D. (1999) Atlas
de Paris - Evolution d'un paysage urbain (Paris) Parigramma
Chinery, Michael (1988)
Nieuwe Insectengids (Baarn) Thieme
Cipolla, Carlo M. (1970) The
Economic History of World Population (Harmondsworth) Penguin Books Ltd
CityDisc (2001) Street
guide CDRom (Den Haag) CityDisk - Topografische Dienst
Clausman, P.H.M.A.;
Held, A.J. den (1984) Het vegetatieonderzoek van de provincie Zuid-Holland.
Algemeen rapport (Den Haag) Provinciale Planologische Dienst Zuid-Holland
Claval (1976) De
geschiedenis van de aardrijkskunde (Utrecht) Het Spectrum
Clifford, N. ; Valentine, G.
[eds.] (2003) Key methods in geography (London) SAGE Publ.
Cohen, Levi Ali [ed.]
(1872) Handboek der openbare gezondheidsregeling en der geneeskundige
politie met het oog op de behoeften en de wetgeving van Nederland
(Groningen) J.B. Wolters
Colenbrander, B.;
Broesi, R.; Veldhuis, W. (2005) Limes Atlas (Rotterdam) 010
Constandse, A.K. (1967)
De toekomst van het platteland In: Wegwijzers (Alphen aan de Rijn)
Uitgeverij Samson
Cooke; Doornkamp (1974) Geomorphology
in environmental management (Oxford) Clarendon press
Cosgrove, D. (2001) Apollo’s
eye - A cartographic genealogy of the earth in the western imagination (Baltimore/London)
Johns Hopkins Univ. Press
Creemers, M.R.; Atteveld, J.A.J.;
e.a. [eds.] (1983) Polytechnisch
zakboekje (Arnhem) Koninklijke PBNA bv / A. Huson
Dauvellier; Maarel, and
v.d. (1978) Globaal ecologische model Rijksplanologische Dienst
Deinema, J. [ed.]
(1996) Brussel en Wallonië (Antwerpen) Standaarduitgeverij
Denters, T. (1999) De
flora van het urbaan district (j) Gorteria 25-4: 65-76
Denters, Ton; Ruesink,
Rina; Vreeken, Bart (1994) Van Muurbloem tot Straatmadelief. Wilde planten
in en rond Amsterdam (Utrecht) KNNV uitgeverij
Dieckmann, U.; Law, R.;
Metz, J.A.J. (2000) The Geometry of Ecological Interactions: Simplifying
Spatial Complexity (Cambridge) Cambridge University Press
Dirkse, G.M. (1994) Bostypen
in Nederland (Utrecht) KNNV Uitgeverij; Wetenschappelijke Mededeling KNNV
Don, H.; Meadows,
Dennis; Meadows, L.; Randers, J. (1992) De grenzen voorbij (Utrecht)
Uitgeverij Het Spectrum
Donadieu, P. (1996) Paysages
de marais (Paris)
Doorn, Joseph van ;
Vught, Frans van (1978) Forecasting. Methoden en technieken voor
toekomstonderzoek (Assen / Amsterdam) Van Gorcum
Downs, R.M.; Stea, D. [eds.]
(1973) mage and environment - Cognitive mapping and spatial behavior (London)
Edward Arnold Publ.
Duijvenbooden, van
(1982) xxxx
Duuren, L. van (1997) Biobase
1997; Register biodiversiteit ('s-Gravenhage) CBS; CD-Rom
Duuren, L. van (1997) Biobase
1997; Register biodiversiteit CBS ('s-Gravenhage) CBS
Edelman, Cornelis
Hendrik (1950) Inleiding tot de bodemkunde van Nederland (Amsterdam)
Noord-Hollandsche Uitg. mij.
Ehrlich, Paul R.; Ehrlich, Anne
H. (1990) The Population Bomb (London) Hutchingson
Emery, F.E. [ed.] (1969) Systems
thinking (Hammondsworth) Penguin Books Ltd,
Escher (1962) Geologie
van Nederland [Geology of the Netherlands]
Eskens, E. (2000) Filosofische
reisgids voor Nederland en Vlaanderen (Amsterdam / Antwerpen) Uitgeverij
Contact
Eyck (1986) XXX
Eyck, A. E. v.; Parin, P.; al.,
et (1968) Ecology in Design / Kaleidoscope of the mind / Miracle of
Moderation / Image of Ourselves (Philadelphia) Graduate School of fine
arts, University of Pensylvania.
Faber, F.J. (1966) Zo
onstond Nederland (Den Haag) Servire
Faris; Dunham (1939) Mental
Disorders in Urban Areas (Chicago) University of Chicago Press
Feddes, Y.C.;
Halenbeek, F.L. (1988) Een scherpe grens - Ontwerpstudie naar de ruimtelijke
kwaliteit van verzwaarde rivierdijken , (Utrecht)...
Feynman, Richard P.; Leighton,
Robert B.; Sands, Matthew (1966,1965) The Feynman lectures on physics III
(Menlo Park, California) Addison-Wesley Publishing Company
Feynman, Richard P.; Leighton,
Robert B.; Sands, Matthew (1977,1963) The Feynman lectures on physics I
(Menlo Park, California) Addison-Wesley Publishing Company
Feynman, Richard P.; Leighton,
Robert B.; Sands, Matthew (1977,1964) The Feynman lectures on physics II
(Menlo Park, California) Addison-Wesley Publishing Company
Field, R. (2003) The Handling
and Presentation of Geographical Data In: &, Clifford [ed.] Valentine;
309-343
Fleming, J.; Honour, H.; Pevsner,
N. (1998) The Penguin Dictionary of architecture and landscape architecture
(London) Penguin
Fockema Andrea, S.J.;
Koeman, C. (1972) Kaarten en kaarttekenaars (Bussum) xxx
Frampton, K. (1995) Studies in
tectonic culture: the poetics of construction in nineteenth and twentieth
century architecture (Cambridge MA) MIT Press
Freedman, Jonathan L. (1975) Crowding
and behavior (San Francisco) W.H.Freeman and Company
Freedman, Jonathan L.
(1977) Psychologie en overbevolking (Utrecht / Antwerpen) Het Spectrum
Freijser, Victor; e.a.
(1997?) Het veranderend stadsbeeld van Den Haag. Plannen en processen in de
Haagse Stedebouw 1890-1990. (Zwolle) Waanders Uitgevers
Frieling, D.H. (2000) Delta
Design. Interpretations of and
reflections on national planning policy. Project and perspective for e
deltametropolis. (Delft) TUD Faculteit Bouwkunde
Fukuyama, Francis (1992) The
End of History and the Last Man (New York) Free Press
Furgeson-Lees, James;
Willis, Ian (1987) Tirions Vogelgids (Baarn) Tirion BV
Garms, Harry (1977) Dieren-
en Plantengids van Europa (Amsterdam / Brussel) Elsevier
Garretsen, H.F.L.;
Raat, H. (1989) Gezondheid in de vier grote steden. V65. ('s-Gravenhage)
SDU uitgeverij; Regeringsbeleid, Wetenschappelijke Raad voor het
Gent, B. v. (1999) Zoetermeer,
ontwikkeling van een nieuwe stad (Zoetermeer) Gemeente Zoetermeer
George, Pierre (1961) Précis
de géographie urbaine (Paris) Presses Universitaires de France
Geuze, A.; Feddes, F.
(2005) Polders! - Gedicht Nederland (Rotterdam) NAI
Gids, W.F. de (1986) Wind/temperatuur
statistiek MT-TNO
Gill, R.W. (2006) Perspective
- from basic to creative (London) Thames & Hudson
Gittenberger, E.;
Janssen, A.W. [eds.] (1998) De Nederlandse zoetwatermollusken; Recente en
fossiele weekdieren uit zoet en brak water (Leiden / Utrecht) Nationaal
Natuurhistorisch Museum Naturalis, KNNV Uitgeverij & EIS-Nederland;
Nederlandse Fauna 2
Gool, van ; e.a. (1986)
Poly-energie zakboekje (Arnhem) Koninklijke PBNA
Graaf, Jan de; Camp, D'Laine
[eds.] (1997) Europe: Coast Wise. An
anthology of reflections on architecture and tourism (Rotterdam) 010
publishers
Graafland, A.; Hauptmann, D.
[eds.] (2001) Cities in transition (Rotterdam) 010
Grime, J.P.; Hodgson, J.G.; Hunt,
R. (1988) Comparative Plant Ecology (London) Unwin Hyman
Groen; Gorree; Meijden;
Huele; Zelfde (1995) Florbase; een bestand van de Nederlandse flora periode
1975-1990 (Bilthoven) CML-rapport nr. 91, RIVM
Groenman, S.J. (1960) Theoretische
beschouwingen. Het discontinue wereldbeeld.
Mens en Maatschappij. 35: 401 - 411
Groningen;
Atlasproducties, Wolters - Noordhoff (2003) De Grote Bosatlas voor VMBO /
HAVO / VWO (Groningen (Groningen) Wolters - Noordhoff Atlasproducties
Groot, A.D. de (1970) Methodologie.
Grondslagen van onderzoek en denken in de gedragswetenschappen
('s-Gravenhage) Mouton & Co
Groot, R.S. de (1992) Functions
of Nature. Evaluation of nature in environmental planning, management and
decision making. Wolters-Noordhoff
Grotenhuis, R. te
(eindred. NIROV Den Haag) (1976) Planologische kengetallen (Alphen a/d
Rijn) Samsom Tjeenk Willink
Haaften, A. van (2001) Freehand
- sketching skills for students of architecture (Delft)
Haccou, H.; Tjallingii,
S.P.; Zonneveld, W. (1994) Econiveaus: een discussie over schaalniveaus en
strategieen voor duurzame ontwikkeling van stedelijke systemen.
(Wageningen) IBN-DLO Instituut voor Bos- en natuuronderzoek
Hagemeijer, W.; Blair,
M.J. [eds.] The Atlas of European Breeding
Birds (London) Poyser
Hails (1977) Applied
geomorphology (Amsterdam) Elsevier
Halder, Inge van;
Wynhoff, Irma; Swaay, Chris van (2000) Dagvlinders van Europa ETI,
Natuur en Techniek, Veen Magazines, Kosmos- Z&K Uitgevers; CD-Rom
Harrison, G.A.; Weiner, J.S.;
Tanner, J.M.; Barnicot, N.A. (1964) Human Biology (Oxford) The Clarendon
Press
Harrison, G.A.; Weiner,
J.S.; Tanner, J.M.; Barnicot, N.A. (1970) Biologie van de mens
(Utrecht/Antwerpen) Het Spectrum N.V.; Aula-boeken 443
Harrison, Helen Mayer;
Harrison, Newton (2001) Schiereiland Europa. De hooggelegen gebieden (Berlijn)
Reschke & Steffens
Harsema, H.; Bijhouwer,
R.; Cusveller, Sj.; Keulen, N. van; Luiten, E. [eds.] (1996) Landschapsarchitectuur
en stedebouw in Nederland 93-95 Landscape architecture and town planning in the
Netherlands 93 - 95 (Bussum) Thoth
Harsema, H.; Bijhouwer,
R.; Cusveller, Sj.; Keulen, N. van; Meyer, F. (2007) Landschapsarchitectuur
en stedebouw in Nederland 2003- 2007 (Wageningen) Blauwdruk
Harsema, H.; Cusveller,
Sj.; Bijhouwer, R.; Bolhuis, P. van; Keulen, N. van; Meyer, F. (2000) Landschapsarchitectuur
en stedebouw in Nederland 97-99
Landscape architecture and town planning in the Netherlands 97 - 99
(Bussum) Thoth
Harsema, H.; Cusveller,
Sj.; Bijhouwer, R.; Bolhuis, P. van; Keulen, N. van; Meyer, F. (2003) Landschapsarchitectuur
en stedebouw in Nederland 99-01 - Landscape architecture and town planning in
the Netherlands 99 - 01 (Bussum) Thoth
Hartman, W.; Hellinga,
H. [eds.] (1985) Algemeen Uitbreidingsplan Amsterdam 50 jaar (Amsterdam)
Amsterdamse Raad voor de Stedebouw
Haupt, Per ; Pont, Meta
Berghauser (2005) Spacemate©the spacial logic of urban density (Delft)
Imprint: DUP Science
Hazlehurst, F.H. (1980-1990) Gardens
of illusion - The genius of André Le Nostre Nashville (...)...
Heeling, Jan; Meyer,
Han; Westrik, John (2002) Het ontwerp van de stadsplattegrond
(Amsterdam) SUN; De kern van de stedebouw in het perspectief van de
eenentwintigste eeuw, Deel I.
Heijbroek, J.F.;
Schapelhouman, M. [eds.] (1989) Kunst in kaart - Decoratieve aspecten van de
cartografie (Utrecht) xxx
Held, J.J. van (1991) Beknopt
overzicht van de Nederlandse plantengemeenschappen (Utrecht) Stichting
Uitgeverij KNNV; Wetenschappelijke mededeling KNNV
Hendriks, L.W.J.L.
(1993) Begrippen rond bouwen en milieu (Rotterdam) SBR Stichting
Bouwresearch
Hermans, L.J.F.; Hoff, A.J.
[eds.] (1982) Energie. Een
blik op de toekomst. (Utrecht) Het Spectrum
Hettema, Tetman;
Hormeijer, Peter (1986) Nederland/Zeeland (Amsterdam) Euro-Book Productions
Hildebrandt, Stefan;
Tromba, Anthony (1989) Achitectuur in de natuur. De weg naar de optimale
vorm. (Maastricht/Brussel) Natuur&Techniek; Wetenschappelijke
bibliotheek. Deel 16.
Hoeven, C. v.d.; Louwe,
J. (1985) Amsterdam als stedelijk bouwwerk; een morfologische analyse
(Nijmegen) SUN
Hotzan, J. (1994) DTV-Atlas
Stadt. Von den ersten
Gründungen bis zur modernen Stadtplanung (München) Deutscher Taschenbuch Verlag GmbH&Co.
Houwaart, E.S. (1991) De
hygienisten. Artsen, staat & volksgezondheid in Nederland 1840-1890
(Groningen) Historische Uitgeverij Groningen
Huisman, P.; Cramer,
W.; Ee, G. van; Hooghart, J.C.; Salz, H.; Zuidema, F.C. [eds.] (1998) Water in the Netherlands (Delft) NHV, Netherlands
Hydrological Society NUGI 672; NHV-special; Euro 20
Israel, Jonathan I. (1995) The
Dutch Republic. Its Rise, Greatness and Fall, 1477-1806 (Oxford) Oxford University
Press
Jacobs, Jane (1961) Death and
Life of Great American Cities (New York) Random House
Jakubowski, Frans
(1936) Der ideologische Ueberbau in der materialistische
Geschichtsauffassung (Danzig)
Jansen, H.P.H. (1965) Middeleeuwse
geschiedenis der Nederlanden (Utrecht) Het Spectrum
Jansen; Heel, v. (1993)
Met zoeken en leren duurzaam op weg TU
(Delft )
Jellicoe, G.&S. (1987) The
landscape of man - Shaping the environment from prehistory to the present (London)
Jellicoe, G.A. (1996) The
studies of a Landscape Designer over 80 years (Woodbridge) Garden Art
Press; Studies in Landscape Design
Jong, H. de (1996) Handboek
Civiele Kunstwerken (losbladig 3 mappen) (Den Haag) TenHagen Stam
Jong, H. de (1996) Video
'Beweegbare stalen bruggen' Handboek
Civiele Kunstwerken (Den Haag) tenHagen&Stam bv. Afd. Klantenservice Lezersmarkt
Jong, M.T.T.M. de ; Kwa, Chunglin
(2000) Ecological theories and Dutch nature conservation (j)
Biodiversity an conservation 9: 1171-1186
Jong, Mechtild D. Th.
M. de (2002) Scheidslijnen in het denken over Natuurbeheer in Nederland. Een
genealogie van vier ecologische theorieen. (Deft)Thesis DUP Science
Jong, T. M. d. (2003)
program %Built-up.xls (Zoetermeer); http://team.bk.tudelft.nl/ http://team.bk.tudelft.nl/ > Publications
2006
Jong, T. M. d. (2003)
program Neighbourhood landuse.xls (Zoetermeer);
http://team.bk.tudelft.nl/Publications/2003/Neighbourhood%20landuse.xls
Jong, T. M. de (1978) 5
drawings by Jan Huffener
Jong, T.M. de (1978) Milieudifferentiatie;
Een Fundamenteel Onderzoek (Delft)Thesis Delft University of Technology
Faculty of Architecture
Jong, T.M. de (1985) Programma
NNAO scenario (Den Haag) Stichting Meso and Sociaal-geografisch instituut
UvA
Jong, T.M. de (1986) Configuratiekeuze
op buurt- en wijkniveau (Den Haag) MESO
Jong, T.M. de (1992) Kleine
methodologie voor ontwerpend onderzoek (Meppel) Boom;
www.bk.tudelft.nl/urbanism/TEAM
Jong, T.M. de (1995) Krantenknipsels
watersnoodramp 1995 (Rotterdam) NRC
Jong, T.M. de (1996) Een
geschiedenis van vrije ruimte In: Dienst, Rijksplanologische [ed.] Ruimte
als voorraad. Vijf essays. (Den Haag) VROM
Jong, T.M. de (2000) De
abiotische uitgangssituatie in de stad (j) De Levende Natuur 101-6;
http://team.bk.tudelft.nl/
Jong, T.M. de (2001) Ecologische
toetsing van drie visies op Almere Pampus. (Zoetermeer) Stichting MESO;
www.tudelft.nl/urbanism/team publications 2001
Jong, T.M. de (2001) Standaardverkaveling
11.exe; http://www.bk.tudelft.nl/urbanism/TEAM/ http://team.bk.tudelft.nl/ > publications 2003
Jong, T.M. de (2002) Verbal
models In: Jong, T.M. de; Voordt, D.J.H. van der [eds.] Ways to research and study architectural, urban and technical design (Delft) Faculteit Bouwkunde TUD
Jong, T.M. de (2003) Milieuwinst
en milieuverlies door bouwen In: Boersema, J.J.; Pulles, T.;
Straaten, J. van; Bertels, J. [ed.] De oogst van het milieu (Amsterdam)
Boom; 320-340
Jong, T.M. de (2003)
program FutureImpact.exe (Zoetermeer) MESO;
http://www.bk.tudelft.nl/urbanism/team , publications 2003
Jong, T.M. de (2003) program Trafficnoise.exe
(Zoetermeer) MESO; http://www.bk.tudelft.nl/urbanism/team , publications 2003
Jong, T.M. de (2006) Suppositions
of Imagination Boundaries of Design. (concept);
http://team.bk.tudelft.nl/Publications/2006/Suppositions.doc
Jong, T.M. de [ed.] (2004) Sun, wind, water, earth, life and living; legends for design.
(Delft) TUD Faculteit
Bouwkunde Publicatiebureau
Jong, T.M. de;
Achterberg, Jayand (1996) Het Metropolitane Debat. 25 Varianten voor 1mln
inwoners (Zoetermeer) Stichting MESO
Jong, T.M. de; Dieters,
M.; Boelen, A.J. (1996) Het Metropolitane Debat. Voorlopige Morfologische
Analyse van Twaalf Plannen voor de Randstad (Zoetermeer) Stichting Meso
Jong, T.M. de; Engel,
H. (2002) Typological research In: Jong, T.M. de; Voordt, D.J.H.
van der [eds.] Ways to research and study urban, architectural and technical design (Delft) DUP
Jong, T.M. de; Louwe,
J. (1972) 100 stellingen van Sharawagi. (Delft) Faculteit Bouwkunde; 100
stellingen van Sharawagi
Jong, T.M. de; Moens,
R.; Waals, J. van der (1996) Energie, water en mineralen Monografieen Milieuplanning SOM 25 (Delft)
TUDelft Faculteit Bouwkunde: 128
Jong, T.M. de; Paasman,
M. (1998) Het Metropolitane Debat. Een vocabulaire voor besluitvorming over
de kaart van Nederland (Zoetermeer) Stichting Milieu en stedelijke
ontwikkeling (MESO); Het Metropolitane Debat
Jong, T.M. de; Priemus,
H. (2002) Forecasting and Problem Spotting In: Jong, T.M. de;
Voordt, D.J.H. van der [eds.] Ways to research and study urban, architectural and technical design (Delft) DUP
Jong, T.M. de;
Ravesloot, C.M. (1995) Beeldkwaliteitsplan Stadsdeel 'De Baarsjes' Amsterdam
(Zoetermeer) assignment Stadsdeel De Baarsjes Amsterdam to MESO;
http://team.bk.tudelft.nl/ > Publications >
Jong, T.M. de; Voordt,
D.J.M. van der [eds.] (2002) Ways
to study and research urban, architectural and technical design (Delft) DUP
Science
Jong, T.M. de; Vos, J
[eds.] (1995) Kwartaalbericht
KNNV Zoetermeer 1-10
(Zoetermeer) KNNV Zoetermeer
Jong, T.M. de; Vos, J
[eds.] (1998) Kwartaalbericht KNNV Zoetermeer 11-20 (Zoetermeer) KNNV
Zoetermeer
Jong, T.M. de; Vos, J
[eds.] (2000) Kwartaalbericht
KNNV Zoetermeer 21-30
(Zoetermeer) KNNV Zoetermeer
Jong, T.M. de; Vos, J
[eds.] (2003) Kwartaalbericht
Natuurgroep Zoetermeer 31-40.
(Zoetermeer) Natuurgroep Zoetermeer
Jong, T.M. de; Vos, J.
(?) KNNV, Kwartaalbericht nr 19
Jong, Taeke M. de
(1988) Milieudifferentiatie (BK 119) (Delft) DUP Faculteit Bouwkunde;
Monografieën Milieuplanning/SOM
Jong, Taeke M. de
(2004) Grenzen van Stedelijkheid (Zoetermeer)
Joosten, J. H. J.;
Noorden, B. P. M. (1992) De Groote Peel: leren waarderen Een oefening in het
waarderen van natuurelementen ten behoeve van het natuurbehoud (j)
Natuurhistorisch maandblad 81(12): 203 e.v
Joustra, Douwe Jan;
Vries, Cees Anton de (2004) Het brilletje van Van Leeuwen. (Leeuwarden)
NIDO; Duurzame stedelijke vernieuwing.; www.nido.nu
Kant, Immanuel (1976) Kritik
der reinen Vernunft (Frankfurt am Main) Suhrkamp Verlag
Kegel, R. (1985) Hofmakerij,
een ruimtelijke beleving - Situatieve expressie van landschap in gebouwen en
buitenruimten In: Steenbergen, C.M. [ed.]; 135-191
Kegel, R. (1996) De
onderste laag boven - Compositorische kenmerken van Pendrecht en Nagele (Delft)
Kelle, A.; Sturm, H.
(1980) Prisma Plantengids (Utrecht/Antwerpen) Uitgeverij Het Spectrum
Kepes, G. (1965) Structure in
art and science (London); Vision + value
Kley (1969) xxxxx
Klijn, J.A. (1995) Hierarchical
concepts in landscape ecology and its underlying disciplines (Wageningen)
SC-DLO
Klok, R.H.J.; Brenders,
F. (1981) Reisboek voor Romeins Nederland en België (Haarlem/Antwerpen)
Fibula-Van Dishoeck/Standaarduitgeverij
KNMI, De Bilt (1976) Modellen
voor de berekening van de verspreiding van Luchtverontreiniging, inclusief
aanbevelingen voor de waarden van parameters in het Lange-Termijnmodel
('s-Gravenhage) Koninklijk Nederlands Meteorologisch Instituut
Kolasa, J. ; Pickett, S.T.A.
[eds.] (1991) Ecological Heterogeneity. Ecological Studies (New York)
Springer-Verlag
Koolenbrander, J.G.M.
(1995) Urgentie van bodemsanering: de handleiding ('s Gravenhage) SDU
Kostof, S. (1999) The city
shaped - Urban patterns and meanings through history (London) Thames and Hudson
Koten-Hertogs, M. van;
Beckers-de Bruyn, M.B.C.; Wolfson, D.J.; Cramer, J.M.; Opschoor, J.B. (1995) De
milieugebruiksruimte voorbij? (Rijswijk) RMNO
Koutamanis, A. (2002) Visualization
and architecture In: Jong, T.M. de; Voordt, D.J.M. van der [eds.] Ways to study and research urban, architectural and technical design (Delft) Delft University Press
Krebs, Charles J. (1994) Ecology
The Experimental Analysis of Distribution and Abundance (New York) Harper Collings
College Publishers
Kroonenberg, Salomon
(2006) De Menselijke Maat. De aarde over tienduizend jaar. (Amsterdam /
Antwerpen) Uitgeverij Atlas; www.uitgeverijatlas.nl
Kruedener, Arthur von
(1951) Ingenieurbiologie (Basel) Reinhardt
Krupp, Helmar (1995) European
Technology Policy and Global Schumpeter Dynamics: A Social Science Perspective
Technological Forecasting and Social Change 48, 7-26 (New York) Elsevier
Science Inc.
Krupp, Helmar (1996) Zukunftland
Japan. Globale Evolution und Eigendynamik (Darmstadt) Wissenschafliche
Buchgesellschaft
Kuipers, S.F. (1972) Bodemkunde
van de klei- , veen- , zand- en lössleemgronden (Culemborg) Tjeenk Willink;
Bodemkunde Hfdst. 11-14
Lachiver, M. (1964) Histoire
de Meulan et sa région (Paris)
Lambert, A.H. (1985) The
making of the Dutch Landscape, a historical Geography of the Netherlands (London)
Lame, F.P.J.; Bosman,
R. (1994) Protocol voor het oriënterend onderzoek: naar de aard en
concentratie van verontreinigende stoffen en de plaats van voorkomen van
bodemverontreiniging. ('s
Gravenhage) SDU
Laurie, M. (1976) An
introduction to landscape architecture (New York) American Elsevier
Lawrence, G.R.P. (1971) Cartographic
methods (xxx) xxx
Leeuwen, C.G. (1971) Ekologie
(Delft) Technische Universiteit Delft, faculteit Bouwkunde
Leeuwen, C.G. van (1964) The
open- and closed theory as a possible contribution to cybernetics (Leersum)
Rijksinstituut voor Natuurbeheer
Leeuwen, C.G. van (1965)
Het verband tussen natuurlijke en anthropogene landschapsvormen, bezien
vanuit de betrekkingen in grensmilieus (j) Gorteria 2: 93-105
Leeuwen, C.G. van
(1965) Over grenzen en grensmilieu's In: Jaarboek 1964 Kon. Nederlandse Botanische
Vereniging; 53-54
Leeuwen, C.G. van
(1966) A relation theoretical approach to pattern and process in vegetation
(j) Wentia 15: 25-46
Leeuwen, C.G. van
(1971) Ekologie. Cursus Natuurbehoud en Natuurbeheer. (Delft) TH-Delft,
Afd. Bouwkunde
Leeuwen, Ch.G. (1970) Onderzoek
aan structuur en dynamiek van vegetaties In: Kamer, J.C. van de
[ed.] Het Verstoorde Evenwicht (Utrecht) Oosthoek Uitgeversmaatschappij;
125-138
Leeuwen, Ch.G. (1987) De
grootvader van de relatietheorie (j) De levende Natuur 88e jaargang nr. 1.:
dec-15
Leeuwen, Chr. G. (1983)
Natuurtechnische maatstaven (1-2) (j) Tijdschrift Koninklijke
Nederlandse Heidemaatschappij 94: 20-23; 44-48
Leeuwen, Chr. G. van
(1973) Ekologie (Delft) TH-Delft, Afd. Bouwkunde, Vakgroep
Landschapskunde en Ekologie
Leeuwen, Chr.G. van
(1953 / 1954) Het blauwgrasland (j) Natuur & Landschap jrg. 7/8:
84-93
Leeuwen, Chr.G. van
(1955) Delfstof winning en natuurgebieden in Nederland (j) De Levende
Natuur 58: 217-220
Leeuwen, Chr.G. van
(1966) Het botanisch beheer van natuurreservaten op structuur-oecologische
grondslag Gorteria. 3-feb: 93
Leeuwen, Chr.G. van
(1967) Tussen observatie en conservatie In: Tien jaren RIVON. RIVON-verhandeling nr.4
1967 (Zeist) RIVON; 2-aug; 38-59
Leeuwen, Chr.G. van
(1973) Oecologie en Natuurtechniek (j) Natuur & Landschap 27: 57-67
Leeuwen, Chr.G. van
(1979-1980) Ekologie I en II. Beknopte syllabus (Delft) CvL/PKL
Leeuwen, Chr.G. van
(1981) From ecosystem to ecodevice In: Tjallingii, S.P.; Veer,
A.A. de [eds.] Perspectives in Landscape
Ecology; contributions to research, planning and management of our environment (Wageningen) Pudoc; 29-34
Leeuwen, Chr.G. van
(1984) Maatstaven voor natuurreservaten (1-3) (j) Tijdschrift
Koninklijke Nederlandse Heidemaatschappij 95: 179-186; 391-395; 419-123
Leeuwen, Chr.G. van;
Kraft, H. Doing (1959) Landschap en beplanting in Nederland (Wageningen) H. Veenman & Zonen
Legget, R.F. (1973) Cities and
Geology Scarborough (Ontario) McGraw-Hill Ryerson Ltd
Leonard, Jonathan
Norton (1974) De eerste boeren TIME-LIFE International (Nederland) B.V.
Leopold, L. B.; T. Maddock, Jr.
(1953) The hydraulic geometry of stream channels and some physiographic
implications.; U.S. Geological Survey Professional Paper 252.
Leupen, B.; Grafe,
Chr.; Körnig, N.; Lampe, M.; Zeeuw, P. de (1997) Design and analysis (Rotterdam)
010
Leupen, B.A.J. ; Grafe, C. (1997)
Design and Analysis (Rotterdam) 010 Publishers
Ligtelijn, V. (1999) Aldo
van Eyck; Werken (Bussum) Thoth
Lim, C.J. (2002) Realms of
impossibility: ground (London) Wiley-academy
Limpens, Herman; Mostert,
Kees; Bongers, Wim [eds.] (1997) Atlas van de Nederlandse vleermuizen;
Onderzoek naar verspreiding en ecologie (Utrecht) KNNV Uitgeverij;
Natuurhistorische Bibliotheek van de KNNV
LNV (1990) Natuurbeleidsplan;
Regeringsbeslissing (Den Haag) Ministerie van Landbouw, Natuurbeheer en
Visserij
LNV (2002) Structuurschema
Groene Ruimte 2 Samen werken aan groen Nederland (Den Haag) Ministerie van
Landbouw, Natuurbeheer en Visserij.
LNV, Min.v. (2000) Natuur
voor mensen - mensen voor natuur. Nota natuur, bos en landschap in de 21e eeuw
(Den Haag) Ministerie van Landbouw, Natuurbeheer en Visserij
Lobgeois, P.; Givry, J.
de (2000) Versailles - Les Grandes Eaux (Les Loges-en-Josas)
Londo, G. (1987) Natuurtuinen
en -parken (Zutphen) B.V. W.J. Thieme & Cie
Londo, G. (1997) Natuurontwikkeling
(Leiden) Backhuys Publishers; Bos en natuurbeheer in Nederland Deel 6
Londo, G. (1998) Spontane
ontwikkelingen op landschapsschaal en het belang van risicospreiding en
gradienten bij natuurontwikkeling. (j) De Levende Natuur(4)
Lovelock, James (1980) Gaia,
een nieuwe visie op de Aarde (Utrecht / Antwerpen) A.W. Bruna Uitgevers
B.V.; Kosmos New Age
Lovelock, Jim E. (1995) Gaia a
new look at life on earth (Oxford) Oxford University Press; Oxford
paperbacks
Luhmann, Niklas (1973, 1968)
Niklas Luhmann Zweckbegriff und System-rationalität. Über die Funktion von
Zwecken in sozialen Systemen. (Tübingen) Suhrkamp Taschenbuch Verlag; Suhrkamp Taschenbuch
Wissenschaft 12
Lynch (1981) A theory of good
city form (Cambridge Mass.) MIT Press
Lynch, K. (1974) Site planning
(Cambridge) MIT
Lysen, Erik (1980,
1977) Eindeloze energie. Alternatieven voor de samenleving (Utrecht) Het
Spectrum B.V.; Aula - Het Wetenschappelijke boek 600
Maarel, E. van de;
Dauvellier, P.L. (samenstellers) [eds.] (1978) Naar een globaal ecologisch
model voor de ruimtelijke ontwikkeling van Nederland, deel 2.
('s-Gravenhage) Ministerie van VROM; Studierapporten Rijksplanologische Dienst
Maarel, E. van der;
Dauvelier, P.L. (1978) Naar een Globaal Ecologisch Model voor de ruimtelijke
ontwikkeling van Nederland (Den Haag) Ministerie van Volkshuisvesting en
Ruimtelijke Ordening
Mann, R. (1973) Rivers in the
city (Newton) Abbot
Margulis, Lynn; Schwartz,
Karlene; Dolan, Michael (1994) The illustrated Five Kingdoms; A guide to the
diversity of life on earth (New York) Harper Collins College Publishers
Marijnissen, J.W.M.;
Mol, I. (1998) De Interactieve flora van Nederland en Vlaanderen; Alles over
de Nederlandse en Vlaamse wilde planten
Nova Zembla,VNU Interactieve Media BV
Marsh, W.M. (1983) Landscape
planning - environmental applications (New York) J. Wiley & Sons
McHarg, I.L. (1971) Design
with nature (Garden City) Doubleday & Co
McMahon, Thomas A.;
Bonner, John Tyler (1987) De Maat van het Leven. Hoe de natuur haar eigen
wetten gehoorzaamt. (Maastricht/Brussel) Natuur&Techniek;
Wetenschappelijke bibliotheek. Deel 8.
Meadows, Don. H.;
Meadows, Dennis L.; Randers, J. (1992) De grenzen voorbij (Utrecht)
Uitgeverij Het Spectrum / Aula
Meerendonk, Winfried W.
A. van (1998) Vogelwerkgroep Zoetermeer (j) Jong, T.M. de; Vos, J; KNNV,
Kwartaalbericht nr 19
Meertens, Roel (2000) Density? (Delft) DUT Faculty of Architecture
Meertens, Roel (2000) Dichtheidsstudie.
In: Stouten, Paul L.M. [ed.] Nieuwe stedelijke woonvormen (Delft)
DUP Satellite; 46-57; p.l.m.stouten@bk.tudelft.nl
Meijden, R. van der
(1999) Heukels' Interactieve Flora van Nederland Wolters-Noordhoff BV;
Biodiversity Center of ETI; Rijksherbarium; Natuur en Techniek; Kosmos-Z&K
Uitgevers; CD-Rom ISBN 90-215-3370-7 (Windows)
Meijden, R. van der
(2005) Heukels' Flora van Nederland (Groningen) Wolters-Noordhoff
Meijden, R. van der ;
Plate, C.L. ; Weeda, E.J. (1989) Atlas van de Nederlandse Flora. Deel 3.
Minder zeldzame en algemene soorten (Leiden/Voorburg/Heerlen)
Onderzoekinstituut Rijksherbarium/Hortus Botanicus Centraal bureau voor de
Statistiek
Meijden, R. van der
[ed.] (1996) Heukels' Flora van Nederland (Groningen) Wolters-Noordhoff
Melchers, Martin;
Daalder, Remco (1996) Sijsjes en Drijfsijsjes De vogels van Amsterdam
(Haarlem) Schuyt & Co
Mennema, J.;
Quene-Boterenbrood, A.J.; Plate, C.L.(red.) (1980) Atlas van de Nederlandse
flora. Deel 1. Uitgestorven en zeer zeldzame planten (Amsterdam) Uitgeverij
Kosmos
Metz, T.; Pflug, M.
(1997) Atlas van Nederland in 2005 - De nieuwe kaart (Rotterdam) NAI
http://www.nieuwekaart.nl/
Michels, Ulrich (1993) Sesam
Atlas van de Muziek. Middeleeuwen en Renaissance. Deel 1 (Baarn) Bosch
& Keuning; Systematisch deel; Historisch deel: Van Prehistorie tot
Middeleeuwen
Michelson, William (1970) Man
and his urban environment: a sociological approach (Menlo Park, California)
Addison-Wesley Publishing Company, Inc. Philippines
Mijksenaar, Paul;
Vervoerskartografie, Stichting [eds.] (1990) Maps. Kaarten en plattegronden
van bergtop tot oceaanbodem (Rotterdam) Stichting Kunstprojecten - III
Minnaert, Marcel Gilles
Jozef (1971) De natuurkunde van 't vrije veld. Deel 3. Rust en beweging
(Zutphen) Thieme & Cie
Minnaert, Marcel Gilles
Jozef (1974) De Natuurkunde van 't vrije veld. Deel I. Licht en kleur in het
landschap (Zutphen) Thieme & Cie
Minnaert, Marcel Gilles
Jozef (1975) De natuurkunde van 't vrije veld. Deel 2. Geluid, warmte, electriciteit (Zutphen) Thieme & Cie
Minnaert, Marcel Gilles Jozef
(1993) Light and color in the outdoors (New York, N.Y.,) Springer
Montesquieu, Charles de
Secondat baron de; Derathé, Robert (1973) De l'esprit des lois (Paris)
Garnier; Classiques Garnier
Morrison, Philip;
Morrison, Phylis; De_studio_van_Charles_and_Ray_Eames (1985) De machten van
tien (Maastricht/Brussel) Natuur en Techniek; Wetenschappelijke
Bibliotheek. Deel 1.
Morrison, Philip; Morrison,
Phylis; The_office_of_Charles_and_Ray_Eames (1982) The powers of ten (New
York) Scientific American Books, Inc.
Mosser, M.; Teyssot, G. (1991) The
history of garden design - The Western tradition from the Renaissance to the
present day (London)
Motloch, J.L. (2001) Introduction
to Landscape Design (New York) John Wiley & Sons Inc.
Myers, Norman [ed.]
(1985) Spectrum Atlas van de Aarde (Utrecht / Antwerpen) Het Spectrum
B.V.
NAI (2005) The flood
- De zondvloed 2nd International
Architecture Biennale Rotterdam (Rotterdam) NAI
Nauta, M.; Vellinga, E.
(1995) Atlas van Nederlandse paddestoelen (Rotterdam) A.A. Balkema
Nes, R. van; Zijpp, N. J. van der
(2000) Scale-factor 3 for hierarchical road networks: a natural phenomenon?
(Delft) Trail Research School Delft University of Technology
Newton, Isaac (1687) Philosophiae
naturalis principia mathematica (Internet)
http://members.tripod.com/~gravitee/; http://members.tripod.com/~gravitee/
Nie, Henk W. de [ed.]
(1996) Atlas van de Nederlandse zoetwatervissen (Doetinchem) Media
Publishing Int BV
Nijs, L. (1995) Verkeerslawaai
(Concept) Moduul BS (Delft)
Faculteit Bouwkunde, Vakgroep BT, sector Bouwfysica
NNAO (1986) Ontspannen
scenario (Den Haag) MESO
NNAO (1987) Nieuw
Nederland 2050 (Den Haag) SDU
NNAO, Stichting
Nederland Nu Als Ontwerp (1987) Nieuw Nederland 2050 deel I achtergronden
(Den Haag) SDU
NNAO, Stichting
Nederland Nu Als Ontwerp (1987) Nieuw Nederland 2050 deel II beeldverhalen
(Den Haag) SDU
Noordhuis, R. [ed.]
(2000) Biologische monitoring zoete Rijkswateren; Watersysteemrapportage
IJsselmeer en Markermeer (Lelystad) RIZA
Novelli, Italo [ed.] (1989) Atlante
di Venezia (Commune di Venezia) Marsilio Editori
Odum, E.P. (1971) Fundamentals
of ecology (Philadelphia/London/Toronto) W.B. Saunders Co.
Opschoor, J.B.;
Weterings, R. (1994) Environmental utilisation space: an introduction
(j) Milieu, Tijdschrift voor Milieukunde 9: 198 - 205
Ormeling, F.J.; Kraak,
M.J. (1999) Kartografie - visualisatie van ruimtelijke gegevens (Delft)
DUP
Ovenden, M. (2003/2006)
Metrokaarten van de wereld - Subway, underground, metro en U-bahn kaarten
van 200 steden (Arnhem) Terra Lannoo
Palmboom, F. (1990) Rotterdam:
the Dynamics of an Urban Landscape In: Vroom; Meeus [eds.]; 14-43
Pannekoek, A. J. [ed.]
(1956) Geological History of the Netherlands ('s-Gravenhage)
Staatdrukkerij- en Uitgeverijbedrijf
Pannekoek, A. J. [ed.]
(1973) Algemene Geologie (Groningen) Tjeenk Willink
Parsons, T. (1966) Evolutionary
and comparitive perspectives (Englewood Cliffs N.Y.)
Parsons, T.; Toby, J. (1977) The
evolution of societies (Englewood Cliffs; London) Prentice-Hall;
Prentice-Hall foundations of modern sociology series
Patri, T.; Streatfield, D.C.; Ingmire, T.J. (1970) Early warning
system - the Santa Cruz mountains regional pilot study (Berkeley) University of
California, Dept. of Landscape architecture
Pelletier, M. (1998) Couleurs
de la terre - Des mappemondes médiévales aux images satellitales (Paris)
Seuil/BNF
Perkins, Chr. (2003) Cartography
and Graphicacy In: &, Clifford [ed.] Valentine; 343-369
PERMETA_architecten; Pont, M.Y.
Berghauser; Haupt, P.A. (2002) Spacemate. FSI-GSI-OSR als instrument voor verdichting en verdunning (Amsterdam) Bureau Parkstad / TU-Delft, Faculteit
Bouwkunde
PERMETA-architecten,
Amsterdam; Pont, M.Y. Berghauser; Haupt, P.A.; Vegt, Jolai van der (2001) FSI-GSI-OSR
als instrument voor verdichting en verdunning (Amsterdam) Bureau Parkstad
Peters, J.A.V.F.M. [ed.] (2001) Bedrijven en milieuzonering (Den Haag) VNG
Uitgeverij; Milieu reeks 9; www.vnguitgeverij.nl
Philp, Richard B. (2001) Ecosystems
and Human Health. Toxicology and Environmental Hazerds (Boca Raton / London
/ New York / Washington, D.C.) Lewis Publishers
Piaget, J. ; Inhelder, B. (1947) La
representation de l'espace chez l'enfant (Paris) Presses universitaire de
France
Pianka, E.R. (1994) Evolutionary
ecology (New York) Harper Collins College Publisher
Pinon, P.; Boudec, B. Le (2004) Les
plans de Paris - Histoire d’une capitale (Paris) APUR
Poisson, G. (...) Sceaux -
domaine princier Paris, s.a. (...)...
Ponting, Clive (1992) Een
groene geschiedenis van de wereld (Amsterdam) Amber
Read, S.; Pinilla, C. (2006) Visualizing
the invisible: towards an urban space (Delft) TUDelft Fac. of Arch.
RECLUS (1989) Les villes
européennesand EREP-rapport, cited in Wolters-Noordhof (1996)
Reed, P. (2005) Groundswell -
Constructing the contemporary landscape (New York) MOMA
Reh, W. (1996) Arcadia
en Metropolis. Het landschapsexperiment van de verlichting, anatomie van het
picturale landschapsontwerp in de landschapsarchitectuur (Delft)Thesis
Publicatiebureau Faculteit Bouwkunde
Reh, Wouter;
Steenbergen, Clemens; Aten, Diederik (2005) Zee van Land. De droogmakerij
als atlas van de Hollandse Landschapsarchitectuur. (Wormer) Stichting
Uitgeverij Noord-Holland
Reuser, Bart; Schenk,
Marijn; architects, Next (1999) Het Gelaagde Land. Het aanzien van Nederland
in 2030 (Delft) TUD Faculteit Bouwkunde, De Architectonische Interventie,
Atelier Deltametropool.
Richardus, P. (1977) Kennis
van de kaart (Wageningen) LH
Richason, B.F. (1972) Atlas of
cultural features - A comparative study with topographic maps and aerial
photographs of man’s imprint on the land Northbrook Ill (xxx) Hubbard press
Riemsdijk, M.J. van
[ed.] (1999) Dilemma's in de bedrijfskundige wetenschap (Assen) Van
Gorcum
Rijkswaterstaat (1998) Delta's
of the World. 200th anniversary of Rijkswaterstaat (j) Land + Water 11
Rijkswaterstaat (1998) Summary
and Conclusions (SDD '98) In: Oudshoorn, Henk; Schultz, Bart; Urk,
Anne van [eds.] Proceedings International conference at the occasion of 200
year Directorate-General for Public Works and Water Management (Amsterdam)
Delft University Press
RIVM (1993) Nationale
Milieuverkenning 3. 1993-2015 (Alphen a/d Rijn) Samson H.D. Tjeenk Willink
RIVM (2000) Insights for the
third Global Environment Outlook from related global scenario anlayses
(Bilthoven); http://www.rivm.nl/bibliotheek/rapporten/402001017.pdf
RIVM (2001) Milieucompendum
RIVM CBS; http://arch.rivm.nl/environmentaldata/
RIVM (2003) Nuchter
omgaan met risico’s (Bilthoven) RIVM, Milieu- en Natuurplanbureau
RIVM, Rijksinstituut
voor Volksgezondheid en Mileu; DLO, Stichting Dienst Landbouwkundig Onderzoek
(2001) Natuurbalans 2001 (Alphen aan den Rijn) Kluwer
RIVM; Langeweg (1991) Zorgen
voor morgen, Nationale Milieuverkenning 1990-2010, deel 2 (Alphen a/d Rijn)
Samson H.D. Tjeenk Willink
Rodenacker, Wolf G.
(1970) Methodisches Konstruieren (Berlin / Heidelberg / New York)
Springer-Verlag; Konstruktionsbücher Band 27
Romein (1938, 1971) Erflaters
van onze beschaving (Amsterdam) Querido
Romera, A-M. [ed.] (1997) Trois
sičcles de cartographie en Ile-de-France - Volume 1 (Paris) IAURIF
Romera, A-M. [ed.] (1997) Trois
sičcles de cartographie en Ile-de-France - Volume 2 (Paris) IAURIF
Ross Ashby, W. (1957, 1956) An
Introduction to cybernetics (New York) Wiley
Rostaing, A. (2001) Les
jardins de Le Nôtre en Île-de-France (Paris)...
RPD (1966) Tweede
Nota over de ruimtelijke ordening (Den Haag) RijksPlanologische Dienst
RPD (1983) Structuurschets
Stedelijke gebieden (Den Haag) RijksPlanologische Dienst.
RPD (1988) Vierde
nota over de ruimtelijke ordening (Den Haag) RijksPlanologische Dienst;
Vino
Ruby, I.; Ruby, A. (2005) Groundscapes
- El reencuentro con el suelo en la arquitectura contemporánea - The
rediscovery of the ground in contemporary architecture (Barcelona) Ed. G.
Gili
Ruiter, Evert Ph.J. (2004) The
Great Canyon. Reclaiming land from urban traffic noise impact zones. (Zoetermeer) Peutz b.v.
Runhaar, J.; Groen,
C.L.C.; Meijden, R. van der; Stevers, R.A.M. (1987) Een nieuwe indeling in
ecologische groepen binnen de Nederlandse flora (j) Gorteria 13(11-dec):
277-359
Russell, Bertrand (1919) Introduction
to mathematical philosophy. (London and New York) Routledge
Sangster, B. (1987) Klinische
toxicologie (Wageningen) Pudoc; Toxicologische reeks 6
Savenije (2001) Stroming
7 Nummer 4 TU Delft; hsa@ihe.nl <mailto:hsa@ihe.nl>
Schaminee, J.H.J.;
Stortelder, A.H.F.; Weeda, E.D. (1996) De vegetatie van Nederland deel 3.
Graslanden, zomen en droge heiden (Leiden) Opulus press
Schaminee, J.H.J.;
Stortelder, A.H.F.; Westhoff, V. (1995) De vegetatie van Nederland deel 1
Grondslagen, methoden en toepassingen (Leiden) Opulus press
Schaminee, J.H.J.;
Weeda, E.J.; Westhoff, V (1998) De vegetatie van Nederland deel 4. Kust en
binnenlandse pioniersmilieus (Leiden) Opulus press
Schaminee, J.H.J;
Weeda, E.J.; Westhof, V (1995) De vegetatie van Nederland deel 2.
Plantengemeenschappen van wateren, moerassen en natte heiden (Leiden)
Opulus Press
Schaminee, Joop;
Jansen, Andre [eds.] (2001) Wegen naar Natuurdoeltypen 2 (Wageningen)
Expertisecentrum LNV, Alterra, KIWA, SOVON
Schans, R. van der
(1990/1991) Kaartgebruik (Wageningen) xxx
Schenk, D. (1990) Land
op zicht - Zicht op land - visies op de kaart van Nederland ('s Gravenhage)
SDU
Schimmel, H.J.W.;
Thalen, D.C.P.; Westhoff, V. (1985) Chris van Leeuwen, bouwmeester van het
natuurbeheer (j) De levende natuur 86 3: 66-73
Schlicher van Bath,
B.H. (1960) De agrarische geschiedenis van West-Europa (500 - 1850)
(Utrecht) Het Spectrum
Schut, E. (1994) In-situ
reinigingstechnieken voor vervuilde grond TU Delft Wetenschapswinkel
SDU (1994) Handboek
bodemsaneringstechnieken, Leidraad bodemsanering, leidraad bodembescherming
(’s Gravenhage) SDU
Segeren, W.A.;
Hengeveld, H. (1991) Bouwrijpmaken van terreinen (Delft) TU Delft
Civiele Techniek; Dictaat F17 CT
Sergeev (1973)... (...)...
Shelton, J.S. (1966) Geology
illustrated (San Francisco/London)...
Simonds, J.O. (1961) Landscape
architecture - The shaping of man's natural environment (New York)
McGraw-Hill
Simonds, J.O. (1997) Landscape
Architecture - A manual of site planning and design (New York) McGraw-Hill
Sitte, C. (1889) Der
Städtebau nach seine künstlerischen Grundsätzen
Sitte, Camillo (1991) De
stedebouw volgens zijn artistieke grondbeginselen (Rotterdam) Uitgeverij
010
Sloep, P.B. (1983) Patronen
in het denken over vegetaties Een kritische beschouwing over de relatietheorie (Groningen)
Regenboog
Speth, J.G. (1989) Can the
world be saved? (j) Ecological
economics 1: 289-302
Standaard; Elmar (1999)
Zo heet dat: Beeldwoordenboek (Antwerpen/Rijswijk) Standaard
Multimedia/Elmar multimedia
Standaardgidsen (1999) Parijs
(Antwerpen) Standaarduitgeverij; Standaardgidsen
Steegh, Arthur (1985) Monumentenatlas
van Nederland. 1100 historische nederzettingen in kaart (Zutphen) De
Walburg Pers
Steekelenburg, Marco van (2001) Self
sufficient world. De Gezonde Stad.
(Den Haag) VROM, RPD ontwerpatelier 2000; http://www.minvrom.nl
Steenbergen, C.; Reh, W. (1996) Architecture
landscape . The design experiment of the great european gardens and landscapes
(Bussum) Thoth
Steenbergen, C.; Zeeuw,
P. de (1995) Landschapsarchitectuur van de stad (Delft) TU-Delft BK
Publicatiebureau.
Steenbergen, C.M.
(1999) Architectuur en Landschap. De techniek van de rationele, formele en
picturale enscenering. (Delft) DUP
Steiner, F.R. (1991) The
living landscape - An ecological approach to landscape planning (New York)
McGraw-Hill
STIBOKA (1965, 1962) Bodem
van Nederland (Wageningen) Stichting Bodemkartering
Sticht.Wetensch.Atlas_v.Nederland
(1985) Atlas van Nederland. Deel 13. Geologie (Den Haag) SDU; Atlas van
Nederland
Sticht.Wetensch.Atlas_v.Nederland;
Piket, J.J.C.; Kalkhove, J.T.R.; Veer, dr. A.A. de; Vos, W. (1987) Atlas van
Nederland. Deel 16. Landschap (Den Haag) SDU; Atlas van Nederland
Stortelder, A.H.F.;
Schaminee, J.H.J.; Hommel, P.W.F.M. (1999) De vegetatie van Nederland deel
5. Ruigten, struwelen en bossen (Leiden) Opulus press
Stoutjesdijk
(1977)
Tax, M.H. (1989) Atlas
van de Nederlandse dagvlinders ('s-Gravenland /Wageningen) Vereniging tot
behoud van Natuurmonumenten in Nederland, Vlinderstichting
Tempel, Rita. van den;
Osieck, Eduard. R. (1994) Belangrijke Vogelgebieden in Nederland (Zeist)
Vogelbescherming Nederland
Thomson, D' Arcy Wenworth (1961) On
growth and form (Cambridge UK) Cambridge University Press; Bonner, J.T.; On
growth and form - abridged ed./Edited
Thornbury, W.D. (1969) Principles
of geomorphology J. Wiley & Sons Inc.; York/London, New
Thünen, Johann Heinrich
von (1921) Der isolierte Staat in Beziehung auf Landwirtschaft und
Nationalökonomie (Jena) Fischer; Sammlung Sozialwissenschaftlicher Meister
13
Tjallingii, S.P. (1996) Ecological
conditions - strategies and structures in environmental planning
(Wageningen)
Topografische Dienst
(2005) Topografische Atlas Nederland 1:50.000 (Den Haag) ANWB
Tufte, E.R. (1983/1997) The
visual display of quantitative information (Cheshire) xxx
Tummers, L.J.M.;
Tummers-Zuurmond, J.M. (1997) Het land in de stad. De stedebouw van de grote
agglomeratie De stedebouw van de
grote agglomeratie (Bussum) Thoth
Tzonis, Alexander ;
Lefaivre, Liane ; Bilodeau, Denis (1989) Klassieke architectuur, de poëtica
van de orde (Nijmegen) SUN; SUN-architectuur
U.S.-Geological-Survey
(1969)
UN (1992) Agenda 21
VN conferentie in zake milieu & ontwikkeling (Rio de Janeiro)
Uytenhaak, R.H.M.
(2005) Dichtheid en Ruimtelijke Kwaliteit. Onderzoek verricht binnen het
werkverband "MSc Architecture and Modernity". (Delft) TU-Delft,
faculteit Bouwkunde
V&W (1998) Vierde
Nota waterhuishouding Regeringsbeslissing, verkorte versie (Den Haag)
Ministerie van Verkeer & Waterstaat / Ando bv
V&W (2000) Anders
omgaan met water Waterbeleid in de 21e eeuw (Den Haag) Ministerie van
Verkeer en Waterstaat
V&W, M. v. (1998) Waterkader
Fourth National Policy Document on Water Management Government Decision. Abridged version. (The Hague) Ministerie V&W.
V&W, M. v. (1998) Waterkader
Vierde Nota waterhuishouding (Den Haag) Ministerie V&W.
V&W, M. v. (1998) Waterkader
Vierde Nota waterhuishouding. Verkorte versie (Den Haag)) Ministerie
V&W.
Vedel, H.; Lange, J.
(1974) Bomen en struiken in bos en veld (Baarn / Antwerpen) Moussault's
Uitgeverij Standaard Uitgeverij;
http://www.bk.tudelft.nl/urbanism/TEAM/Databases/BiobasePlanten07%20zonder.xls
Veer, J.T. van der
(1984) Landmeetkunde en kaartgebruik (Wageningen) xxx
Veer, Kees van der (?) Nederland/Waterland (Amsterdam) Eurobook productions
Ven, G.P. van de [ed.] (2004) Man-made lowlands - History of water management and land
reclamation in the Netherlands (Utrecht) Matrijs
Vera, Frans (1997) Metaforen
voor de wildernis. Eik hazelaar rund paard ('s-Gravenhage) Ministerie van
Landbouw, Natuurbeheer en Visserij
Verberk, M. M.;
Zielhuis, R. L. (1980) Giftige stoffen uit het beroep (Alphen aan den
Rijn) Stafleu; De Nederlandse bibliotheek der geneeskunde dl. 130
Verhulst, Frank C.
(2003) De ontwikkeling van het kind. (Assen) Koninklijke Van Gorcum
Vermeulen, P.E.J.
(1986) Experimenteel onderzoek ten behoeve van de modelbeschrijving van
drie-dimensionale ruwheidsovergangen MT-TNO
Vermeulen, P.E.J. ;
Hoogeveen; Leene (1983) Energie-opbrengsten van windturbines: een boek voor
berekeningen MT-TNO
Vermeulen, P.E.J. ; Jong,
T.M. de (1985) Wind vangen en wind weren. Een verkennende studie naar de
energetische consequenties van windafschermende maatregelen. (Delft) MT-TNO
Verschuren, J. (1993) Bodemsanering
van bedrijfsterreinen Praktijkboek voor bedrijf en beroep (Oosterhout) J.
Verschuren, Postbus 6038, 4900 HA Oosterhout
Vigny, A. (1995) Jacques Sgard
- Paysagiste & Urbaniste (Ličge) Mardaga
Vigny, A. (1998) Latitude Nord
- Nouveaux paysages urbains Arles/Versailles (...) Actes Sud/ENSP
Visscher, H.A. (1972) Het
Nederlandse Landschap. Een typologie ten behoeve van het milieubeheer (Utrecht)
Uitgeverij Het Spectrum B.V.
Visscher, J. (1949) Veenvorming
(Gorinchem) Noorduijn en Zoon N.V.; Noorduijn's wetenschappelijke reeks
Visser, G. Th. (1986) Winddrukverschillen
over woningen bij een viertal configuraties op wijkniveau MT-TNO
Visser, G. Th. (1987) Modelontwikkeling
voor de berekening van ventilatieverliezen in wijken bestaande uit identieke
bouwgroepverkavelingen MT-TNO
Visser, G.Th. (1987) Beoordeling
van de mogelijkheden voor theoretische modellering op wijkniveau aan de hand
van oriënterende windtunnelmetingen MT-TNO
Vogel; Günter;
Angermann; Hartmut; Steen, J.C. van der (1970) Sesam atlas bij de biologie
(Baarn) Bosch en Keuning
Vogler, Paul; Kuhn,
Erich [eds.] (1957) Medizin und Städtebau. Ein Handbuch fur gesundheitlichen
Stadtebau (Munchen, Berlin, Wien) Verlag von Urban & Schwarzenberg
Volksgezondheid en
Milieuhygiene, Ministerie van (1981) Berekening van wegverkeersgeluid
('s-Gravenhage) Staatsuitgeverij
VOMIL? (xxx) Omgaan
met risico's (xxx) xxx
Voorden, M. van der
(1979) Bezonning. Stedebouwfysica gc 49 (Delft) Technische Hogeschool
Delft, afdeling der Civiele Techniek; 5
Voorden, M. van der
(1990) Windhinder. Stedebouwfysica gc 49 (Delft) TU-Delft, Faculteit der
Civiele Techniek
Vos, J.G. (1990) Bloemrijke
linten door Zoetermeer. Het resultaat van 10 jaar maaien en afvoeren? (j)
Groen 90(2)
Vos, Johan (1993) Natuur
in Zoetermeer In: Jong, T.M. de; Vos, J. [eds.] Kwartaalbericht KNNV
Zoetermeer 1-10 (Zoetermeer) KNNV Zoetermeer; 2, 1993
Vries (2008) xxxx (xxxx) xxxx
Vries, J. de (1962) Woordenboek
der Noord- en Zuid-Nederlandse plaatsnamen (Utrecht/Antwerpen) Aula-boeken
VROM (1989) National
Environmental Policy Plan
VROM, Min.v. (1989) Nationaal
milieubeleidsplan 'kiezen of verliezen' (Den Haag) SDU uitgeverij
VROM, Min.v. (1990) Nationaal
milieubeleidsplan plus (Den Haag) SDU uitgeverij
VROM, Min.v. (2001) Een
Wereld en een Wil. Werken aan duurzaamheid.Nationaal Milieubeleidsplan 4 -
samenvatting (Den Haag) Ministerie van Volkshuisvesting, Ruimtelijke
Ordening en Milieubeheer
VROM, Min.v. (2001) Ruimte
maken, ruimte delen - Vijfde Nota over de Ruimtelijke Ordening 2000/2020
(Den Haag) SDU Uitgevers
VROM, Min.v. (2001) Samenvatting
Ruimte maken, ruimte delen. Vijfde Nota over de Ruimtelijke Ordening 2 000/2
020. (Den Haag) Ministerie van VROM.
VROM/LNV, Min.v. (1987)
Milieu-effect Rapportage. Effectvoorspelling van planten, dieren,
ecosystemen, 23 (Den Haag 1987) SDU
VROM/Rijksplanologische_Dienst
(2000) Ruimte maken, Ruimte delen, Vijfde nota over de Ruimtelijke Ordening
2000/2020
Vroom, M.J. [ed.]
(1992) Buitenruimten - ontwerpen van Nederlandse tuin- en
landschapsarchitecten in de periode na 1945O - Outdoor space - Environments
designed by Dutch Landscape Architects since 1945 (Amsterdam)...
Vroom, M.J.; Meeus,
J.H.A. [eds.] (1990) Learning from Rotterdam
- Investigating the process of urban park design (London/New York) Mansell
/ Nichols Publ.
Waal, A. de; Duijn, D.
v.; Janssen, A.; Wegbrans, S.; RWS/Q [eds.] (1995) Ruimtelijke Verkenningen
1995. Milieubalans 1995. Macro economische Verkenningen in kort bestek
('s-Gravenhage) Min. v. V&W, Directoraat-Generaal Rijkswaterstaat
Weeda, E.J.; Schaminée,
J.H.J.; Duuren, L. van (2000) Atlas van Plantengemeenschappen in Nederland.
Deel 1. Wateren, moerassen en natte heiden (Utrecht) KNNV Uitgeverij,
Alterra, CBS, LNV, KIWA, Directoraat-Generaal Rijkswaterstaat, VEWIN
Weeda, E.J.; Westra,
R.; Westra, Ch.; Westra, T. (1985) Nederlandse Oecologische Flora. Wilde
planten en hun relaties 1. (Hilversum Rijswijk) IVN VARA VEWIN
Weeda, E.J.; Westra,
R.; Westra, Ch.; Westra, T. (1987) Nederlandse Oecologische Flora. Wilde
planten en hun relaties 2. (Hilversum Rijswijk) IVN VARA VEWIN
Weeda, E.J.; Westra,
R.; Westra, Ch.; Westra, T. (1988) Nederlandse Oecologische Flora. Wilde
planten en hun relaties 3. (Hilversum Rijswijk) IVN VARA VEWIN
Weeda, E.J.; Westra,
R.; Westra, Ch.; Westra, T. (1991) Nederlandse Oecologische Flora, Wilde
planten en hun relaties 4 (Amsterdam) IVN
Weeda, E.J.; Westra,
R.; Westra, Ch.; Westra, T. (1994) Nederlandse Oecologische Flora. Wilde
planten en hun relaties 5. (Hilversum Rijswijk) IVN VARA VEWIN
Welsenes, Chr. van
(1975) Groninger land - Beeld en tegenbeeld (Groningen) Uitg. J.
Niemeijer
Wely, Peter van (1993) De
eerste Sint-Jacobsvlinder in Zoetermeer (j) Kwartaalbericht KNNV 2
Westhoff, V.; Bakker,
P. A.; al., et (1970) Wilde planten, flora en vegetatie in onze
natuurgebieden , deel 1, 2, en 3 Vereniging tot behoud van natuurmonumenten
Westhoff, V.; Held,
A.J. den (1975) Plantengemeenschappen in Nederland (Zutphen) B.V. W.J.
Thieme & Cie
Westra, C.; Tossijn, H.
(1980) Windwerkboek. Wat mogelijk is met windenergie
Wieringa, J.; Rijkoort,
P.J.; Bilt, Koninklijk Nederlands Meteorologisch Instituut. De (1983) Windklimaat
van Nederland (Den Haag) Staatsuitgeverij; Klimaat van Nederland 2
Wittgenstein (1919, 1959) Tractatus
logico-philosophicus (Oxford) Basil Blackwell
Wittgenstein, L. (1953) Philosophical
investigations (Oxford) Blackwell
Wittgenstein, Ludwig (1963) Tractatus
Logico-philosophicus (Frankfurt am Main) Suhrkamp Verlag
Wittgenstein, Ludwig;
Hermans, Willem Frederik (1986) Tractatus logico-philosophicus
(Amsterdam) Athenaeum-Polak & Van Gennep
Woestenburg (2006) Naar
een zelfreinigende groene stad in (j) Het kwartaaltijdschrift van
Wageningen Universiteit en Researchcentrum Nummer 2
Wolters-Noordhof (1996)
De Grote Bosatlas Eenenvijfstigste editie, deel 1 (Groningen)
Wolters-Noordhof, tweede oplage
Wolters-Noordhof [ed.]
(1981) De Grote Bosatlas 49e editie (Groningen) WN Atlas Productions
Wolters-Noordhof [ed.]
(2001) De Grote Bosatlas 2002/2003 Tweeënvijfstigste editie + CD-Rom
(Groningen) WN Atlas Productions
World commission environment and
development (1990) Our Common Future (Oxford/New York) Oxford University
press
World Commission on Environment
and development, U. (1987) Our common future (Oxford New York) Oxford
University Press
Woud, A. van der (1987)
Het lege land, de ruimtelijke orde van Nederland 1798-1848 (Amsterdam)
Olympus
Woud, A.v.d. (1998) Het
lege land. De Ruimtelijke Orde van Nederland 1798-1848
(Amsterdam/Antwerpen) Contact
xxx (1948) Verspreide
bijdragen tot de kennis van de bodem van Nederland (j) Boor en spade II,
Utrecht
xxx (1963-1977) Atlas
van Nederland - Atlas of the Netherlands (‘s-Gravenhage) Staatsuitgeverij
xxx (1970) Bodem en
planologie (j) S&V 51(1970)
xxx (1977) Probing the earth -
contemporary land projects (...)...
xxx (1979) Earthworks: Land
reclamation as sculpture (...)...
xxx (1991) "Koolmees
zwelgt in verzuurde bossen" (j) Bio Nieuws nr. 5
xxx (2006) Fieldwork -
Landscape architecture Europe (Basel) Birkhäuser
xxx [ed.] (1963-1977) Atlas
van Nederland - Atlas of the Netherlands (‘s Gravenhage) Staatsuitgeverij
xxx [ed.] (1980) Bestemmingsplankaarten
- Codering, arcering en kleur (xxx) xxx
xxx [ed.] (1987) Atlas
van Nederland in 20 delen (‘s Gravenhage) Staatsuitgeverij
xxx [ed.] (1987) Espace
Français - Vision et aménagement, XVIe-XIXe sičcle (Paris) xxx
Zanen, Ger van; Bremer,
Piet; Aa, Huub van der [eds.] (2000) Paddestoelen in Flevoland (Utrecht)
KNNV Uitgeverij
Zoest, Johan van (1998)
Biodiversiteit (Utrecht) KNNV-Uitgeverij
Zonneveld, J.I.S.
(1964-1971) Tussen de bergen en de zee - De wordingsgeschiedenis der lage
landen (Utrecht) Oosthoek
Zonneveld, J.I.S.
(1981) Vormen in het Landschap. Hoofdlijnen van de geomorfologie
(Utrecht / Antwerpen) Uitgeverij Het Spectrum; Aula - Geografie
%built-up surface............. 515, 517
%built-up
surface(quality(form, structure, function)) 517
%floor surface. 512, 513, 517, 520
1st National
Environmental Policy Plan 567,
570, 573
24 hour intensity....................... 272
24-hour average....................... 556
4th National Plan of
Environmental Policy 423,
575
4th National Plan of
Watermanagement Policy 423
5th National Plan of Spatial
Policy 418, 505, 575
A horizon.................................. 325
A value..................................... 587
Aalsmeer.................................. 518
aanbrug.................................... 259
Aanen(1990)............................ 437
aarvederkruid............................. 61
ABC model................................ 659
ABF.................................. 505, 506
abiotic....................................... 658
abiotic variation........................ 391
Abken
BV................................. 655
aboreal pre-adaptations........... 458
abrasion................................... 320
absorption................................ 590
abundance....................... 364, 387
abundance of organisms......... 371
abutment................................... 259
acacia (acacia............................ 98
acceleration............................. 12
accentuation(design
tools(planting)) 72
acceptable daily intake............. 576
accepted risk............................ 212
access crossings.................... 278
accessability.................... 626, 627
accessibility.............................. 633
accommodation........ 458, 459, 547
accord...................................... 629
accords............................ 370, 628
accords of dispersion.............. 469
accumulation(urban)................ 369
Achilles and the turtle....... 368, 667
achterdiep................................ 498
Achterhoek............................... 496
acid conditions......................... 386
acidity............................... 386, 561
acids......................................... 589
action space............................. 626
activities(interfunctional).......... 466
actors....................................... 476
adaptability(species)................ 389
adaptation................. 425, 458, 547
adhesion water........................ 578
adhesion(legend)..................... 632
adhesive force......................... 328
ADI............................................ 576
adiabatic................................... 156
adsorption........................ 588, 590
aeq............................... 12, 13, 710
aerodynamics........................... 111
aeroplanes(air(density)).......... 107
aerosols................... 555, 556, 561
aerosols, dust, soot................. 553
Afsluitdijk.. 209, 216, 217, 219, 220
after-school care centres........ 534
age range per continent........... 529
ageing....................................... 530
Agenda 21................................ 570
agenda(changed(design))....... 443
agenda(legend transition)........ 643
agglomerations................. 527, 528
agrarian firms........................... 542
agricultural
production(greenhouse-effect) 354
agricultural systems................. 485
agriculture........................ 461, 548
aim(scale)................................. 368
aim‑directed...................... 661, 663
air bubble.................................. 108
air density................................. 156
air dispersion(wind
velocity).... 110
air pollution............................... 558
Air Pollution Act........................ 590
air pollution(dispersion)............ 109
air pollution(models)................. 560
air pressure.............................. 106
air transport companies........... 545
air(density)....................... 106, 107
Akker(2001)......... 9, 198, 199, 202
alcohols.................................... 554
alder....................... 48, 64, 83, 376
alder and ash forests............... 378
alder(clay/loam).......................... 85
alder(coastal)............................. 84
alder(els).................................... 98
alder(nutrient-rich peat)............. 85
Alexander(1966)...................... 190
algae................. 354, 437, 454, 561
algae(blue)............................... 432
algae(yellow)........................... 432
algas........................................... 22
aliphatic compounds................. 588
Alleröd........................................ 57
allotment directions(wind)........ 144
allotment(courtyard)................. 151
allotment(wind)......................... 111
allotments......................... 265, 275
allotments(point,line)................. 151
allotments(point,line,corner,courtyard) 148
allotments(repeating)................ 149
allotments(wind)....................... 148
Almere...................... 433, 439, 527
Almere lake................................. 59
Almere Pampus................ 443, 509
alnion incanae.......................... 378
AlO4-tetrahedrons................... 333
alternating current...................... 21
Alterra...................................... 441
altitude lines.............................. 424
ambition.................................... 627
ambulances.............................. 263
amenities.......................... 521, 539
amenity park............................. 538
Amerongen(weir)..................... 208
amfibool.................................... 336
amino acids.............................. 554
ammonia................................... 555
ammoniac................................. 589
ammonium............................... 556
ampere..................................... 291
amphibians(atlas)................... 433
amphibole................................. 336
amphiboles............................... 336
amplitude.................................. 156
Amstelveen.............................. 504
Amsterdam 206, 209, 274, 277, 407, 444, 453, 476,
513, 515, 528, 664
Amsterdam harbour islands..... 508
Amsterdam Noord.................... 296
Amsterdam West...................... 517
Amsterdam(density)................. 512
amusement hall......................... 538
anaerobic decomposition......... 562
anchorage block....................... 259
and........................................... 623
Anderson(1984)....................... 625
Andrewartha (1961)................ 371
Vogel; Günter........................... 394
angiosperms..................... 356, 432
Angremond(1998).................... 479
animal husbandry..................... 486
animal kingdom......................... 352
animals(night)........................... 352
animals(size(habitat))............... 409
ankerblok.................................. 259
Ankum(2003) 203, 204, 230, 233, 253
Ankum, 2003 222, 223, 224, 225,
226, 227, 228, 229
annual meadow-grass............. 387
anonimity.................................. 466
anthropocentric........................ 549
anthropocentrism..................... 659
anthropogenesis...................... 458
anthropogenically added
dynamic 485
antimony................................... 589
antinode(sound)....................... 155
antipodal................................... 633
ants............................................ 47
Antwerp........................... 206, 493
ANWB....................................... 445
appartments............................. 631
apple............................... 83, 84, 88
approach ramp......................... 259
April............................................ 64
aquatic life................................ 433
aquifers.................................... 169
ARA ports................................ 206
arable land................................ 486
ARBO....................................... 569
arboretums............................... 538
arcades.................................... 649
arch bridge....................... 259, 260
arch(fixed, two-hinged,
three-hinged) 259
archeological finds................... 287
archeology............................... 319
ArchitectenCie.......................... 647
architectonic clarity.................. 629
architectural
plan(space(inside, outside)) 649
arctic circle................................. 35
arctic night.................................. 35
area capacity........................... 642
areal position............................ 364
areas of vegetation.................. 393
Arends(1994)........................... 230
Arends, 1994............................ 402
argex pellets............................... 87
Argus....................................... 249
Arnhem-Nijmegen..................... 638
aromatic compounds................ 588
arrangement............................... 18
arrowhead................................. 61
arsenic............................. 554, 589
arsenic eaters.......................... 425
art............................................. 660
art(emotions(diverse))............. 636
arthropoda................................ 431
articulation(design
tools(planting)) 71
artificial fertilisers..................... 494
Artificial fertilisers.................... 494
artificial(planting)........................ 68
artistic freedom........................ 628
artistic life style........................ 267
ash................................... 376, 554
ash(es)....................................... 98
Ashby(1960)............................ 665
ash–elm forest......................... 484
Asklepios.................................. 629
aspen....................................... 377
asphalt surfaces........................ 86
assess environmental effects. 551
associations............................. 392
associations(synecological).... 383
assumption............................... 659
assumptions(untraceable)....... 443
asthma...................................... 466
asymmetric street profile.......... 631
Atlanta...................................... 511
Atlantic heather........................ 372
Atlanticum............................. 58, 59
atmosphere(convection).......... 107
atmosphere(light, sombre)......... 88
atmosphere(planting)................. 68
atmospheres............................ 626
atmospheric cycle............ 316, 317
atmospheric influence................ 43
atmospheric refraction............... 42
atmosphers|cultures................. 627
attracting force......................... 470
attraction.................................. 471
attraction between
regions(functional charge) 474
attraction(mass,
specialisation) 474
auction...................................... 518
audible sound........................... 155
autecology........................ 371, 391
aut-ecology.............................. 458
autumn(colours)......................... 84
average.................................... 425
average maximum discharge... 211
average year maximal
discharges 211
average(reduction).................. 399
axial systems(design).............. 349
azalea......................................... 83
azalea(acid soils)....................... 85
azimuth............... 40, 42, 43, 44, 45
azimuth angle............................. 39
B horizon.................................. 325
B value..................................... 587
Baarsjes........................... 628, 629
Baas Becking........................... 391
Bach................. 278, 281, 284, 286
back gardens........................... 266
background.............................. 621
backside................................... 626
Bahrdt(1957)............................ 466
Bailey bridge..................... 259, 261
baileybrug................................. 259
Baileybrug................................ 261
Bal et al., 2001.................. 395, 396
Bal(1995).................................. 374
Bal(1995, 2001)........................ 447
Bal(2001).................................. 374
balance of use(energy)............. 33
balance(composition)............... 628
balconies.................................. 649
balconies(walled-in)................. 649
balk- of liggerbrug met meer
overspanningen 259
balkbrug............................ 259, 260
ballet theatre............................. 538
Baltic Sea......................... 220, 492
Baltic trade............................... 492
Barcelona......................... 278, 653
barrel.......................................... 13
barrier effect............................ 276
Barton(2000)............................ 426
basalt................................ 318, 335
bascule bridge.......................... 259
basculebrug..................... 259, 260
basic paradox of spatial
arrangement 401
Batenbur(Eddes)...................... 425
Bateson, 1980, 1983................ 395
bats(atlas)................................ 433
battery........................................ 34
Bazel........................................ 651
Beach banks............................ 497
beach nourishment................... 219
beam bridge...................... 259, 260
beam transmitters............. 295, 308
bearing capacity....................... 345
Beatrix...................................... 492
beech........................... 48, 83, 377
beech (beuk).............................. 98
beech forest............................. 484
beech woods........................... 436
beech(pavement raising)........... 87
beekdal..................................... 496
Beestenmarkt........................... 655
Begon, Harper et al. (1996)...... 371
Beidha...................................... 461
Beintema(1995)........................ 427
Bekhuis(1988).................. 427, 430
belt (‘boezem’) system of
Delfland................................ 226
belt canal.................................. 257
belt canals................................ 225
belt system............................... 226
Bense(1954).................... 368, 667
Benthem en Crouwel................ 653
benzene................... 554, 591, 592
Berg(2001)............................... 427
Bergse Maas............................ 209
beri-beri.................................... 434
berk.......................................... 376
Berlage............................. 277, 629
Berlin........................................ 501
Bern Convention....................... 364
berries........................................ 84
Best technical means’.............. 551
betulon pubescentis................. 378
Betuwe railway........................ 287
Betuwe(flooding)...................... 214
Betuwe(floods)........................ 210
Betuwelijn................................. 238
beurtvaart................................. 206
bicarbonate.............................. 386
bicycle lane(hedges)................ 101
Bierkens................................... 172
Biesbos.................................... 293
Biesbosch................................ 210
bifurcation ratio................ 190, 192
bifurcations(Rhine)........... 207, 209
Bijhouwer, J.T.P....................... 341
bike................................... 623, 626
Bink(1992)........................ 427, 430
bio restoration.......................... 591
Biobase............................ 361, 431
biodegradability........................ 590
biodiversity............... 352, 365, 570
biodiversity(genetic)................. 389
biodiversity(health)................... 365
biodiversity(infrastructure,
industial areas) 406
biodiversity(mankind)............... 666
biodiversity(means of
design).. 406
biodiversity(urban age,
seepage, drainage, water level, infrastructure(verges and slopes)) 406
biodiversity(urban, rural).......... 405
bio-industry.............................. 555
biological identity...................... 420
biological oxygen
consumption 556
biological soil purification.......... 590
biological weathering............... 320
biomass................................ 21, 23
biomass(energy
contribution(national)) 30
biomen.............................. 372, 393
bioreactor techniques...... 590, 591
biosphere................................. 391
biotic......................................... 658
biotic variation.......................... 391
biotope.............. 371, 382, 391, 393
biotope cities............................ 408
birch............................. 48, 84, 376
birch forest............................... 372
birch forests(acid peat
grounds) 378
birch forests(dehydrated
peat grounds) 378
birch(berk).................................. 98
birch(clay/loam).......................... 85
birch(nutrient-poor peat)............ 85
birch–common oak forest......... 484
Bird and Habitat Directive......... 436
birds......................... 353, 382, 389
birds(Dutch)............................. 431
birds(phosphate, nitrate).......... 437
Birkhoff (1933)......................... 368
Birkhoff(1933).......................... 667
biting stonecrop.......................... 63
black cherry............................. 377
black list.................................... 554
black poplar.............................. 376
black tern.................................. 436
Black-tailed Godwit.................. 431
Blaeu........................................ 274
blanket bog............................... 484
blanket bog formation............... 439
block distance.......................... 151
blocks....................................... 631
blocks(Eastern).......................... 46
blocks(Western)......................... 46
Bloemers(1981).......................... 60
Blom, P...................................... 340
blue algae......................... 432, 434
Blue Arrow............................... 438
blue legend............................... 251
blue list............................. 364, 365
blue print................................... 626
boerenhofsteden...................... 122
boerenwormkruid....................... 63
Boersema(1991)...................... 546
Boersema, Copius Peereboom
et al. (1991) 550
Boertange................................. 205
boezem..................................... 226
boezemkanalen........................ 225
Bohemen(1986)................ 427, 430
Bohemen, 2004........................ 403
Bohn(2001)...................... 372, 436
Boltzmann................................... 16
bomen....................................... 122
Bonn......................................... 476
boog(ingeklemde,
tweescharnier~, driescharnier) 259
boogbrug.......................... 259, 260
boogbrug met hooggelegen
rijvloer 259, 260
boogbrug met laaggelegen
rijvloer 259, 260
boogbrug met tussengelegen
rijvloer 259, 260
bookshops................................ 543
boomgaarden........................... 122
boomgaardgebieden................. 122
border(hedges)................ 102, 103
Boreal......................................... 58
boredom................... 368, 625, 628
bosanemoon............................... 64
bossen..................................... 123
boterbloem.................................. 65
bottom-up and horizontal
external contacts on the working floor 238
botulism.................................... 554
Bouman(1979).......................... 493
boundaries(drawing)............... 643
boundaries(sharp, vague)....... 398
boundaries(spaces)................. 394
boundary layer......................... 129
boundary layer thickness......... 130
boundary richness................... 396
bouwland......................... 122, 497
Boven(1997)............ 650, 652, 653
bovenkruising........................... 259
Bovy(2000).............................. 471
bowl......................................... 401
Boyle.......................................... 18
Braakman................................. 218
Brabant..................................... 496
brackish-water jellyfish............ 431
braided river............................. 195
braiding..................................... 196
branching(river)....................... 190
Brandaris.................................. 220
Brandes.................................... 651
brandnetel.................................. 66
brandstofcel............................... 20
Braun Blanquet........................ 396
Braun-Blanquet, 1964...... 395, 396
Brauwere.............................. 655
breaker’s yard.......................... 588
breakfast.................................... 46
breakwaters............................. 220
bream............................... 433, 434
bream colonisation................... 433
breast-feed.............................. 465
Breda........................................ 492
Breems( 2000)......................... 455
brem........................................... 64
brick houses............................. 220
brick yards in the river
area (flood plain) 220
bricks........................................ 220
bridge....................................... 232
bridges............................. 258, 259
Brielse Maas............................. 218
brink.......................................... 486
broekbos.................................. 496
Broekhuizen(1992)................... 427
brook................................ 247, 249
brooks...................... 169, 191, 247
broom......................................... 64
Brouwersdam.......................... 218
Brouwershavense Gat............ 218
brugdek.................................... 259
Bruges...................................... 492
Bruin................. 205,
207, 208, 210
Bruin et al., 1987...................... 401
Bruin et.al., 1987...................... 401
Brundtland........................ 367, 666
Brundtland Committee............... 570
brushwood....................... 436, 438
brushwood(ecological groups) 386
bryophyta................................. 355
BTEX......................................... 588
Buchanan................................. 277
Bucknell(1967)......................... 109
budget year.............................. 236
buffer zone.............................. 470
build outside the dykes............. 441
building..................................... 510
building companies................... 543
building complex....................... 510
building height........................... 519
building part.............................. 510
building segment....................... 510
building(height)........................... 45
building(prerequisite)................ 664
buildings(force(wind))............. 107
buildings(wind)......................... 111
built area per person................ 407
built area(>50%)....................... 518
built-up area............................. 512
built-up areas........................... 524
bulb field................................... 497
bulbs........................................... 83
bulrush....................................... 61
bundled concentration.............. 422
bundled deconcentration 369, 453, 468, 476, 642
bunkers(energy)........................ 33
Burgerweeshuis
(Amsterdam). 394
burning..................................... 485
bus................... 249, 263, 283, 623
bus station................................ 283
business................................... 626
business(Netherlands)............. 542
butterflies(Dutch)..................... 431
buy........................................... 627
buy........................................... 626
Buytenwegh............................. 364
BZV.................................. 554, 556
C horizon.................................. 325
C value..................................... 587
cabaret theatre......................... 538
cable and pipe tunnel............... 309
cable and pipe tunnels............. 308
cable networks........................ 296
cable stay anchorage.............. 259
cables................................. 88, 287
cables and pipes in streets...... 223
cables(planting).......................... 87
cadmium........................... 554, 589
café’s....................................... 545
calcium............................... 85, 389
Calthorpe.................................. 286
camping.................................... 538
camping grounds...................... 545
canal................. 247, 249, 257, 498
canalisation of the Lower
Rhine 208
canals(groundwater level)....... 223
cancer...................................... 466
cancer(stress)......................... 426
candela....................................... 48
canopy....................................... 92
canopy(road)............................. 95
cantilever bridge............... 259, 260
cantilever span......................... 259
cantileverbrug.......................... 259
capacity of the road................. 264
Capelle a/d IJssel...................... 340
capillary forces........................ 328
capillary fringe.......................... 327
capillary piezometric levels...... 328
capillary water................... 86, 578
capillary water zone................ 327
capillary zone........................... 328
capitals..................................... 630
capsella bursa-pastoris........... 387
captains of service.................. 476
car.................................... 263, 621
car exhaust gasses................. 555
car movements per hour.......... 269
car park(hedges)..................... 103
car parking............................... 263
car trips.................................... 269
car tunnels............................... 299
car widths................................ 262
carbon dioxide.... 22, 352, 354, 553
carbon monoxide.............. 553, 554
carbonated............................... 589
Carboniferous.......................... 354
carcinophobia........................... 426
care centres............................. 534
caressible................................. 440
car-free streets........................ 651
cargo........................................ 272
cargo transport(ship)............... 206
cargo vehicles/24 hour............ 272
Caribbean................................. 357
Carnot-engine............................. 19
carp.......................................... 434
carpentry.................................. 588
carpinion................................... 378
carpino-berberidion.................. 378
carrying capacity..................... 461
casae....................................... 489
cascade..................................... 14
casino or lottery....................... 538
Castex and Panerai.................. 274
castle........................................ 489
castles...................................... 639
casualties................................. 281
catalpa........................................ 84
catastrophes.................... 352, 366
catchment area........................ 169
catchment area A..................... 192
catchment areas...................... 169
category formation................... 444
cathedral effect(road)................ 95
cattle(groundwater level)......... 222
cattlefood(bream)..................... 434
causal relations........................ 547
causal thinking.......................... 660
causal thinking(recucing
diversity) 666
cause....................................... 109
cause(ceteris paribus)............. 660
cause(condition).............. 661, 669
Cavendish, 1798...................... 470
CBS.................................. 431, 523
CBS (1994)............................... 469
CBS Biobase............................ 361
CBS(1994)................................ 502
CBS(2001)................................ 523
CBS(2003)...................... 28, 31, 32
CBS’s Standard Company
Categorisation 444
CCNR........................................ 206
cd............................................... 48
CDA.......................................... 469
CEC........................................... 562
ceiling|shelter............................ 627
cell differentiation..................... 353
cell diversity............................. 353
cell walls.................................. 388
cell(membranes)............. 394, 424
cella.......................................... 630
Cenozoic.................. 316, 355, 357
center span.............................. 259
central green(wind)................. 141
central parking.......................... 276
central road.............................. 276
Central Slenk............................ 496
centralisation............................ 635
centre open.............................. 277
centre(periphery)..................... 634
centripetal force....................... 108
Cerdŕ........................................ 278
Cerda’s Barcelona.................... 653
ceteris non paribus.................. 662
ceteris paribus
presupposition. 661
CFK........................................... 556
CH4........................................... 555
chain of effects........................ 551
chalk......................................... 350
chamerion angustifolium........... 389
channel(width, depth,
current velocity) 185
chaos............................... 625, 628
chaos ecology.......................... 391
chaos equations....................... 398
chaos function................. 399, 464
chaotic behaviour............. 398, 399
characteristic details........ 625, 631
Charlemagne............................ 489
chemical energy......................... 34
chemical industry..................... 543
chemical lavendaries................ 588
chemical oxygen consumption. 556
chemical stability...................... 590
chemical weathering................ 320
chemistry(armamentarium)....... 424
chemists........................... 534, 543
cherry........................... 83, 88, 377
cherry(clay/loam)....................... 85
Chézy....................................... 201
chickweed.......................... 62, 389
children..................................... 425
childrens’ hospitals and
hospices 534
childrens’ independently
homes 534
Chinery(1988).......................... 388
chloride gases.......................... 555
chlorinated derivatives............. 590
chlorinated hydrocarbons........ 588
chlorofluoro-hydrocarbons...... 556
choice(forced)......................... 427
choices(design)....................... 367
cholesterol................................ 388
chordata................................... 433
christian democrats.................. 469
chrome..................................... 589
church...................................... 476
CIAM’s functional typology....... 637
cickweed.................................. 389
cinema...................................... 538
cinemas.................................... 537
Cipolla (1970)........................... 462
circumpolar................................. 38
circumstances(measure)......... 111
circumstances(succesively
added) 111
citrus cultivations..................... 555
city............................ 272, 624, 626
city highway..................... 247, 257
city highways................... 190, 191
city(Dutch(rareness)).............. 437
civil engineering........................ 319
civil engineering
constructions. 252
civil engineering offices........... 233
civil-engineering isolation
technique 592
civilisation damage................... 424
Cl 555
claims on Randstad.................. 422
claims(spatial(regional))........... 418
clairobscur................................. 47
clap bridge................................ 261
classes..................................... 392
classes of roughness(wind)... 122
classification(ecological).......... 392
Clausius...................................... 18
Clausman(1984)....................... 374
clay................... 326, 374, 577, 579
clay fractions........................... 326
clay granules.............................. 87
clay grounds............................ 247
clay marsh................................ 433
clay parts................................. 393
clay polders...................... 481, 482
clay(local inland movement)..... 220
clay(nature potential)............... 433
clay(use).................................. 333
clay/loam soils(trees)................. 84
clean soil statement.................. 579
clean soil target values............ 587
climate change... 23, 209, 211, 395
climatic changes....................... 360
climax....................................... 371
climax species(planting)............. 78
climax stage............................. 382
climax state.............................. 429
closed courtyards.................... 489
closed screen(trees)................. 96
closed water storage............... 344
cloud layer................................ 559
clouds....................................... 166
club-mosses............................. 355
CO............................................ 554
CO2............................................. 22
CO2 emissions.......................... 238
CO2(atmosphere)..................... 354
CO2-production........................... 30
coal mines................................ 489
coal(environmental costs).......... 30
coarse mode............................ 556
coast formation(mid-West)....... 379
coast formation(North)............. 379
coast forms.............................. 216
coast landscape....................... 312
coast line(central).................... 219
coast(natural potential)............ 436
coastal constructions............... 217
coastal defence....................... 216
coastal defence law................ 219
coastal defence systems......... 209
coastal engineering aspects.... 220
coastal research and model
investigations 216
coastal trees.............................. 84
coastline........................... 209, 217
coastline(closed, sandy).......... 209
coastline(erosion).................... 219
cobalt........................................ 589
Coenen.................................... 650
Coevorden................................ 205
cogeneration.............................. 13
cognition................................... 665
Cohen(1872)............................ 405
coherence(nearness,
infrastructure) 632
coherence(parts, whole)......... 632
cohesion(legend)..................... 632
cohesive force......................... 328
cohort....................................... 463
cold extensions........................ 649
collage...................................... 637
collective concepts.................. 644
Cologne.................................... 476
color......................................... 627
colour surfaces........................ 623
coltsfoot............................. 62, 326
combinating.............................. 445
combinations...................... 14, 418
combinations(regional)............. 475
combinatorial possibilities......... 508
combined sewage system....... 304
combined system of cable and
wire ducts 308
combined system of sewer
pipes and fibre optics cables 308
combustion............................... 554
combustion emissions...... 553, 554
combustion processes............ 556
comfort(outdoor)...................... 119
comfort(wind velocity)............. 110
comfrey...................................... 63
common oak............................... 65
common plantain....................... 400
common ragwort...................... 388
common reed.............................. 61
common whitlowgrass............... 62
communal trenches for cables
and pipes 309
communication(difference)...... 367
communication(diversity). 367, 666
communities.............................. 393
community care centres........... 534
community(species)................. 371
commuting................................ 531
compact cities.......................... 422
compact city..................... 469, 476
compact city/town.................... 642
compact town.......................... 370
compact(town)......................... 135
compacte Stad......................... 370
comparability(interdependent).. 440
comparability(internal).............. 440
comparability(regional
design). 506
comparable facts..................... 665
comparison............................... 658
compartmentalisation(islands).. 438
compass............................... 43, 45
compass card.......................... 114
compensation................... 421, 425
compete.................................... 626
competition............... 382, 388, 393
competition(interregional)......... 476
competition(light)........................ 48
competitors....................... 371, 389
complex models........................ 398
component(detail)..................... 630
components...................... 625, 628
components(composition)........ 631
components(focus).................. 631
composition.............................. 625
composition analysis................ 628
composition(balance(repetition,
diversity)) 628
composition(planting)................. 68
computer.................................. 623
computer network cables 300, 308
computerprogramming.............. 668
concentrated integration.......... 445
concentration 16, 370, 470, 625, 635
concentration(conurbation,
region) 408
concentration(probability).......... 15
concept............................ 621, 665
concept of context................... 625
concept(unforeseen
possibilities) 443
conception................................ 665
conceptual image..................... 629
conceptualization..................... 665
condition(semantic).................. 658
condition(wave-lengths).......... 662
conditional analysis.......... 573, 658
conditional assessments.......... 644
conditional comparisons........... 658
conditional evaluation............... 428
conditional functions................ 424
conditional links........................ 549
conditional operators................ 658
conditional range...................... 658
conditional sequence 111, 550, 661
conditional(causal)................... 661
conditionality............................. 546
conditionality(two
directions)... 111
conditionals.............................. 658
conditions................................. 546
conditions(administrative,
cultural, economical, technical, spatial) 663
conditions(architecture,
environmental planning) 442
conditions(ecological).............. 366
conditions(sunlight, moist, acidity) 386
conditions(time)........................ 662
configuration............................ 140
confusion................................. 368
confusion of scale................... 369
confuson of scale.................... 667
congestion................................ 272
conifers.................................... 432
connecting............................... 402
connection(separation)............ 399
connections(negative effect)... 403
connections(scale).................. 369
connections(separations)........ 393
Constandse (1967).................. 476
Constandse(1967)................... 436
Constandse, A.K. (1967)......... 482
constant(design
tools(planting)) 72
constellations............................. 38
consultancies........................... 545
contact zones.......................... 397
container trees........................... 94
containers................................ 299
context..................................... 627
context sensibility..................... 624
context sensitive effects......... 666
context(geographical,
historical) 647
contexts................................... 445
context-sensitive problems...... 400
continent................................... 393
continent(areas of
vegetation). 392
continental highway................. 247
continental networks................ 281
continental shelves.................. 165
continents(heating).................. 109
continuity.................................... 70
continuous beam...................... 259
contraception................... 465, 466
contradiction............................. 658
contradictions(scale)............... 445
contrapolar............................... 633
contrast.................................... 628
contrast(hedges)..................... 103
control.............................. 626, 627
conurbation...................... 369, 510
conurbation definition(CBS) 512, 527
conurbation density.................. 370
conurbation density10km......... 512
conurbations............ 407, 501, 502
conurbations(form(wind))........ 111
conurbations(high density)...... 422
convection losses(wind
velocity) 110
conversion(efficiencie).............. 19
conversion(energy)................... 19
convertibility............................. 590
conveyor pipelines................... 298
cooling systems....................... 556
cooling-water........................... 554
coordination...................... 382, 389
Copernicus................................. 38
copper...................................... 589
copper beeches......................... 88
copper-leaved trees................... 88
Corbulogracht............................. 60
cormorant................................. 438
Cormorants............................... 436
cornelian cherry......................... 64
corners............................. 268, 623
corners(inner).......................... 649
COROP areas................... 502, 508
corridors................................... 389
corridors(wet).......................... 205
cosine rules................................ 40
costs of risks........................... 563
costs preventing unnecessary
death 563
costs(safety)........................... 426
count of Holland....................... 491
country..................................... 624
country estates........................ 378
country road............................. 249
courtyard.................................. 649
courtyards................................ 654
courtyards’............................... 489
cover........................................ 626
coverage.................................. 387
cow parsley............................... 62
cowslip..................................... 389
crabs........................................ 431
crane bridge............................. 261
crawl spaces........................... 223
creativity........................... 658, 660
creativity centre....................... 538
crčches.................................... 534
creek bed................................. 497
creek relic................................. 497
Creemers(1983)....................... 158
criminality.................................. 466
crisis centres for women......... 534
crocus........................................ 83
crooked grids........................... 279
Crooswijk................................. 655
crop yields(open water
levels) 223
crops(groundwater level)........ 222
cross parking................... 263, 268
crossings 252, 253, 258, 265, 266, 271
cross-parking........................... 267
crossroads............................... 251
crowd pullers........................... 518
crowding.................................. 424
crown raising(tree).................... 99
crown(tree(dense, open))......... 88
crude oil...................................... 13
crust of the Earth..................... 334
crystals.................................... 334
cuckooflower............................. 64
culmination............................ 37, 43
cultural...................................... 658
cultural heritage................ 206, 555
cultural identity......................... 476
cultural life................................ 663
cultural-ecological study.......... 459
culture...................................... 659
culture(collective concepts)..... 644
culture(economy)..................... 644
cultures.................................... 626
culvert...................................... 232
culverts.................................... 258
cumulus clouds........................ 108
Curie......................................... 424
currant.................................. 83, 84
current intensity....................... 291
current(electric)......................... 21
curtain(design
tools(planting))... 71
curtis........................................ 489
cyanides................................... 589
cybernetic ecology........... 391, 458
cybernetics.............................. 399
cycle paths............................... 279
cycle
ride.................................. 249
cycle
route............................... 249
cycle shop................................ 544
cyclical
development(planting)... 73
cyclical planting.......................... 74
cyclist....................................... 263
cyclists............................. 265, 282
cyclone..................................... 108
cylinder....................................... 19
CZV.................................. 554, 556
D.J. Joustra, et al., 2004......... 395
daily rhythm.............................. 468
daisy........................................... 64
dam........................................... 401
Dam, M. van.............................. 502
damage..................................... 568
dance theatre........................... 538
dandelion.................................... 62
danger...................................... 627
dangerous................................ 623
darkness(atmospheric dust).... 357
Das, 1993................................. 234
data networks.......................... 288
data(accessible, reliable,
retrievable) 236
date............................................ 43
Dauvellier, P.............................. 342
daylight penetration........ 77, 88, 93
daylight
penetration(planting)..... 81
daylight(filtering(trees)).............. 89
dB............................................. 156
dB(A)................................ 158, 161
death rate................................. 463
December 22nd.......................... 37
decentralisation........................ 635
deciBell..................................... 160
decibells................................... 156
deciBells................................... 157
deck.................................. 259, 401
deck arch bridge.............. 259, 260
declination...................... 37, 40, 43
decomposition processes........ 555
deconcentrated
specialisation. 445
deconcentration....... 370, 470, 635
definition................................... 664
deglomeration........................... 502
degree of screening................... 68
Delfland.................................... 226
Delft.......... 123, 223, 235, 342, 359
Delft Hydraulics........................ 215
Delfzijl....................................... 220
Delta......................................... 205
Delta metropole................. 475, 476
Delta metropolis........................ 506
Delta project............................ 218
Delta works.............................. 494
delta(nature)............................. 437
Deltametropolis......................... 408
Deltawerken............................. 216
Deltawet................................... 217
Deltaworks............... 216, 219, 237
democracy............................... 475
demography............................. 463
Den Bosch................................ 205
Den Haag.................................. 307
Den Helder........................ 206, 220
denitrification............................ 562
densities(boundary-sensitive). 508
densities(diversity)................... 512
densities(national).................... 501
densities(population,
global)..... 499
density...................................... 499
density comparison.................. 520
density measures(urban)......... 507
density of homes...................... 502
density of investment............... 467
density(10km, conurbation)...... 512
density(300m neighbourhood). 513
density(30km, metropolis)........ 510
density(30m Urban island)....... 520
density(air)............................... 106
density(continentally gross)..... 499
density(continentally net)......... 499
density(ensemble house)......... 514
density(exclusive,
inclusive).... 191
density(frontal)......................... 151
density(gross and net)............. 500
density(gross house
neigbourhood) 514
density(increasing).................. 517
density(neighbourhood)........... 515
density(net house
neigbourhood) 514
density(road network)............. 525
density(scale).......................... 369
density(urban).......................... 408
density(ways).......................... 190
density100m(ensemble)........... 516
density1km(district).................. 513
Denters(1994).......... 407, 440, 664
Denters(1999).......................... 454
dentists..................................... 534
dependent variable................... 663
deposits.................................... 194
deposits(river).......................... 195
depressions............................. 560
deseases(population density).. 466
desert(brackish,
evaporation).. 400
deserts..................................... 167
design.............................. 547,
665
design decisions(tacitly
supposed)................................. 638
design measures...................... 262
design sketch........................... 430
design speed.................... 474, 479
design techniques(planting)....... 73
design tools(planting)................. 71
design transformation.............. 266
design transformations............ 266
design velocities....................... 264
design velocity......................... 272
design vocabulary.................... 638
design with nature approach... 220
design(diversity)...................... 367
design(generating study)......... 427
design(possible worlds).......... 660
design(urban, architectural)..... 549
design(vocabulary).................. 637
design(worthless areas)......... 443
designer....................................... 7
designer(intentions((past
experience, expectations)(use, perception))) 636
designers(possible
problems(uncertainty)) 426
designers’
imagination(ecology) 443
desintegration........................... 668
detail(component)..................... 630
detailing(morphological
reconstruction) 632
details............................... 625, 628
details(characteristic).............. 631
details(repeating)..................... 632
determinists.............................. 460
detour....................................... 278
detours..................................... 282
devaluation of house prices
by noise 272
dewatering............................... 344
dewatering level....................... 344
diatoma.................................... 432
Dieckmann(2000)............. 367, 455
diesel oil.................................... 588
difference................................. 664
difference(scale)..................... 399
different behaviour................... 627
differentiating........................... 399
differentiation'........................... 368
'differentiation'.......................... 668
differentiation(functional)......... 634
digestibility(salt, acid)............... 389
digging up................................. 485
digits(m2 area).......................... 510
dijkdorp..................................... 486
dike breaches........................... 209
dike strengthening............ 209, 238
dike structures......................... 209
diked land in open water.......... 324
dikes......................................... 206
dikes(elevation)........................ 209
dikes(height)............................. 214
dikes(wet)................................ 210
dilatation................................... 269
dilution of households.............. 502
dilution(household)................... 530
dinner......................................... 46
dinosaurs(extinction)............... 352
diploid....................................... 355
diploid life cycle........................ 355
diptera(Dutch).......................... 431
direct current.............................. 21
direction.................................... 624
direction(wind(probability))...... 115
direction(wind)......................... 112
direction-sensitive.................... 399
directly served inhabitants....... 271
Dirk II......................................... 490
Dirk III........................................ 490
Dirk V........................................ 491
Dirk VII...................................... 492
Dirkse(1994)............................. 436
dirty.......................................... 623
disaster(air pollution)................ 566
disasters(needed to make
progress) 216
discharge................................. 185
discharge distribution over
the various Rhine branches 209
discharge of a river.................. 195
discharge of a river(delay
after rainfall) 172
discharge of the Rhine............ 172
discharge pipes........................ 288
discharge Q(catchment area). 171
discharge Q(water depth H, Lobith) 171
discharges(river, maximum)..... 211
disco......................................... 624
discrimination(positive)............. 403
diseases(physicians)............... 426
disintegration(scale)................. 368
Disneyland................................ 475
disorder...................................... 14
distance meter............................ 45
distance to cars ahead............ 264
distances travelled................... 531
distribution.................................. 14
distribution and abundance
of organisms 371
distribution centres................... 299
distribution maps...................... 441
distribution substation.............. 292
distribution(particles).................. 15
distributive frequency
division(wind) 112
district....... 272, 369, 510, 624, 626
district configuration................. 140
district density1km.................... 513
district image............................ 631
district road...... 247, 249, 265, 273
district roads.................... 190, 272
district tare............................... 510
district ways............................ 190
district(lay-out(wind)).............. 111
district(polarisation).................. 634
disturbance.............................. 573
disturbing.................................. 399
ditch.................................. 247, 249
ditches...................... 221, 225, 258
ditches(distance)..................... 228
ditches(pattern)........................ 228
diversity.................... 420, 421, 628
diversity of species.................... 68
diversity(communication). 367, 666
diversity(legends).................... 470
diversity(locations)................... 191
diversity(risk)........................... 366
diversity(statistical reduction).. 427
dividing(morphological
reconstruction) 632
diving ducks............................. 434
division of functions................. 466
division of labour...................... 466
doctors’.................................... 534
Doesburg.......................... 205, 323
Dogon architecture................... 394
dogwood.................................. 376
Dollard.............................. 220, 324
domestic voltage...................... 298
domestic waste........................ 299
donk.......................................... 497
doom scenario.......................... 548
doorgaande ligger.................... 259
Doorn(1978)............................. 464
Dordrecht................. 273, 274, 492
dose-response diagram........... 563
dots distribution(real
measure) 509
dots overlap............................. 510
dots(gross).............................. 510
dots(Net).................................. 510
double-leaf
bascule bridge....... 260
downdraughts............................ 83
draaibrug.......................... 259, 260
drain pipes(distance).............. 228
drain systems........................... 424
drainage........................... 247, 344
drainage (profile
subdivisions and velocities) 199
drainage
directions(landscape) 188
drainage of reclaimed land....... 205
drainage pool............................ 249
drainage system............... 300, 343
drainage systems..... 190, 210, 303
drainage(building, roads,
paths, pipes, electric wires, parks, sports fields, playing fields) 344
drainage(large scale)............... 208
drainage(river)......................... 186
drainage(urban)....................... 454
drained by pumps..................... 221
drained lakes............................ 324
draining..................................... 485
draining an area(soil)............... 222
drains....................................... 258
drawing.................................... 626
drawing tube(sound)............... 155
drawing(difference)................. 663
drawing(preconditions)............ 660
dredge area.............................. 338
dredge spoil.............................. 338
dredgers(vegetation-unfriendly) 454
Drente......................................... 59
Driel.......................................... 207
Driel weir.................................. 208
Driemanspolder........................ 454
drinking water inlet................... 208
drinking water supplies............ 288
drinking water supply............... 219
droogmakerijen......................... 324
dry connections....... 247, 248, 479
dry periods............................... 208
dryas octopetala........................ 57
Dryas period......................... 57, 58
drying up of buildings(wind
velocity) 110
dual access.............................. 498
dual network strategy.............. 252
dubbele
basculebrug................ 260
ducks........................................ 436
ducts........................................ 287
dune areas............................... 288
dune birch forest...................... 484
dune county............................. 375
dune heath............................... 484
dune landscape........................ 497
dune oak forest........................ 484
dune
relics................................ 497
dune ridge................................ 497
dune valley
vegetation(calcium). 85
dune woods............................. 378
dune-grassland........................ 484
dunes 219, 288, 332, 372, 377, 481, 482, 489
dune-thicket.............................. 484
duration line of Rhine discharge 172
dust.................................. 553, 556
Dutch coastline......................... 217
Dutch Policy documents.......... 236
Dutch population....................... 529
Dutch trees............................... 376
Dutch water
management(history) 205
Duuren (1997).......................... 431
Duuren(1997)... 361, 431, 432, 438
Duurzaam Veilig....... 249, 265, 279
dwarswetering........................ 497
dwelling occupation................. 515
dwelling(occupance)............... 530
dwellings.................................. 266
dwellings(number, type).......... 532
dyke.......................................... 481
dyke occupation....................... 486
dykes................................ 330, 492
dykes(inner edge(nature
potential)) 433
dynamic character(planting)...... 73
dynamical ecology.................... 391
dynamics.................................. 399
eardrums.................................. 154
earth................................. 313, 393
Earth........................................... 10
earth quakes............................ 213
earth sciences................. 312, 314
earth(biomen)........................... 392
earth(nodding)............................ 37
earth(radius).............................. 35
earth(turning)............................. 38
Earth’s crust............................. 334
East Brabant(precipitation)....... 168
East from Greenwich................. 41
East gardens............................ 267
Eastern blocks............................ 46
eclipse........................................ 38
eclipse(sun)............................... 47
ecliptic surface........................... 35
eco parks................................. 308
ecocentric................................ 549
ecocentrism.............................. 659
eco-friendly building................. 304
ecological community............... 433
Ecological conditions.............. 404
ecological connection............... 420
Ecological connections........... 403
ecological disasters................. 666
ecological diversity................... 210
ecological footprint..................... 23
ecological
footprint(national(biomass)) 23
ecological
footprint(national(solar energy)) 23
ecological
footprint(national(wind))................................... 23
ecological groups............. 385, 393
ecological groups(progress, decline) 386
ecological infrastructure 389, 417, 454, 548
ecological potencies(technical measures) 385
ecological processes............... 486
ecological thinking(Dutch)...... 404
ecological tolerance. 366, 387, 666
ecological typology(scale)....... 372
ecological values going down.. 443
ecologies.................................. 391
ecology..................................... 549
ecology(time–space
connection) 644
ecology(urbanization).............. 664
economical conditions.............. 661
economical possibilities............ 661
economy(technical
infrastructure) 644
ecotope............................ 391, 393
Ede................................... 527, 655
edge green(wind).................... 141
edge profile(planting)........... 68, 70
edge space................................ 79
edge(design tools(planting))...... 71
Edge(hedges)........................... 103
edge(north-facing,
south-facing) 81
edges(hedges)......................... 103
edges(planting(profile)).............. 82
education.................................. 536
Edward III.................................. 492
Eemian interglacial.................... 358
Eemshaven............................... 209
effect analysis(double
counting) 573
effect prognoses..................... 566
effects(planting)......................... 67
efficiency(energy
conversion).. 19
effluent seepage...................... 330
Eh(redox potential)................... 561
EHS................... 374, 389, 441, 446
EHS doelsoort........................... 364
Eijck, Aldo van.......................... 393
Eindhoven................................. 426
elderly homes........................... 534
electric cables.......................... 298
electric power
stations(capacity) 31, 32
electric properties.................... 590
electricity distribution
network. 287
electricity grid............................. 21
electricity network.................... 291
electricity networks.................. 288
electricity production.................. 13
electricity(domestic)................... 21
electro-reclamation................... 592
elm........................................ 48, 95
elm lanes.................................. 378
elm(iep........................................ 98
elms...................................... 92, 99
elms(pavement raising).............. 87
elms(poplars)............................. 94
elongated lots........................... 497
elongated(town)....................... 135
elongating......................... 267, 268
elongation(networks)............... 252
els............................................. 376
elvers....................................... 432
emigration......................... 463, 464
emission ceilings...................... 570
emission factors....................... 550
emission limiting values............ 570
emission sources..................... 552
emission(dispersion)................ 550
emissions................................. 554
emissions(mixed)..................... 556
emissions(variation)................. 558
Emmen...................................... 527
empirical research(causal
thinking)................................. 660
empirical
research(generalisation) 400
empty cables............................ 300
empty pipes.............................. 308
empty shells............................. 300
empty spaces........................... 649
enclosed effects........................ 95
enclosed horizontally............... 654
enclosure................................. 249
Enclosure dike.......................... 216
endoplasmatic apparatus......... 424
energetic emissions......... 554, 558
energy................................ 12, 710
energy content........................... 13
energy conversion..................... 17
energy flows.............................. 32
energy profit(wind turbines).... 109
energy saving.......................... 424
energy slaves............................ 33
energy stocks(fossile fuels)...... 23
energy storage........................... 33
energy use(buildings(wind
velocity)) 109
energy use(global,national)........ 22
energy use(Netherlands)........... 28
energy(conversion)................... 19
energy(dimensions)................... 12
energy(flow diagram)................ 32
energy(runoff water).............. 165
enkele basculebrug.................. 260
enlarge............................. 621, 623
Enschede................. 406, 452, 454
ensemble.................. 510, 520, 653
ensemble density100m............. 516
ensembles................................ 631
ensembles(wind)..................... 111
entrance as a seat................... 394
entrance section...................... 630
entrances......................... 153, 651
entropy................................. 14, 18
entropy(increase)...................... 17
entropy(statistical definition)...... 16
entropy(thermodynamic
definition) 18
envelope curve........................ 464
environment...... 391, 546, 549,
659
environment(conditions for
life) 663
environmental accountancy..... 552
environmental charts................ 566
environmental costs................... 30
environmental ecology............. 458
environmental engineering....... 319
environmental hygiene............. 550
environmental impacts.............. 550
Environmental Management Law 552
environmental planning..... 549, 668
environmental policy................. 236
Environmental Policy................. 423
environmental policy plan......... 552
environmental policy plans....... 550
environmental problems........... 547
environmental
problems(solved by urban design) 426
environmental
problems(solving(conditions(restoring, creating))) 548
environmental quality
targets... 567
environmental quality(costs).... 568
environmental
quality(regional, special, general) 569
environmental science............. 391
environmental standards.......... 551
environmental strategies.......... 550
environmental tactics............... 550
environmental technical
design 549
environmental utility space....... 570
environmental-impact
statement 562
environmentally decisive
design 664
environmentally friendly........... 548
environmental-usage space..... 570
eons................................. 315, 316
EPEL......................................... 569
Epidauros................................. 629
epidemics................................. 462
epidemiological research.......... 426
epidemiological
research(cause<>effect) 403
epochs..................................... 315
equality............................. 664, 665
equality(difference).................. 398
equalizing................................. 399
equations.................................. 665
equator..................................... 108
eras.................................. 315, 316
EREP......................................... 479
erosion............. 320, 323, 461, 464
erosion of the sandy
coastline. 219
eruptions of vulcanoes............ 213
es..................................... 376, 496
escape routes.......................... 297
esdoorn.................................... 376
esdorp...................................... 486
Eskens, E. (2000)..................... 475
establishments......................... 541
esters....................................... 554
estuaries.................. 209, 218, 372
estuary..................................... 374
ethylbenzene............................ 591
etoilement................................... 54
Europe(vegetation(map))......... 436
European coasts...................... 477
European diversity and
rarity... 437
European nature map............... 493
eutrophe................................... 386
eutrophication........................... 454
evaluating(conditionally)........... 428
evaluation................................. 645
evaporation.............. 166, 169, 170
even(design tools(planting))...... 72
evergreen shrubs...................... 84
every time having its own
place 627
evolutionary
ecology(exceptions) 367
Excel........................................... 43
exceptional
occurrences(magnified(television)) 426
exceptions(average)................ 426
exclamations............................ 659
excommunicated...................... 466
exergy........................................ 14
exit frequency.......................... 479
exits.......................................... 473
exotic species............................ 82
expensiveness......................... 627
experiencial value.................... 634
experiencial value(shape)........ 634
experimental impact
assessment 111
exploitation scheme.................. 513
exploration................................ 627
Exploratory survey protocol 579, 581
exploratory survey(soil
contamination) 582
exponential formula.................. 129
exponential growth.................. 462
exposition................................. 562
exposure(length, frequency)... 569
exposure(stone, water)........... 647
express.................................... 249
extending 1 mole of gas............. 17
extensions................................ 649
externalised architectural
functions 649
extinct(species)....................... 352
extinction rate........................... 365
extinction(230 million years
ago) 355
extinction(230 years ago)........ 356
extinction(saurians)................. 357
extreme discharges................. 211
Eyck
(1955-1960...................... 394
Eyck(1968)............................... 427
Eyck,
1965............................... 394
Eyck, Aldo van......................... 394
Eyck, et al., 1968...................... 394
F(fluorine)................................. 555
façade relief............................. 656
façade(approaching)............... 629
façade(night, morning,
afternoon, evening) 657
façade(relief(horizontal,
vertical)) 649
façade(trees)............................. 88
façades.................... 519, 631, 649
facilities............................ 276, 539
Faculty of Architecture in
Delft.. 41
fall............................................... 33
falling water(energy)................. 33
fall-out...................................... 560
family dilution.................... 502, 530
fan cable stayed bridge... 259, 260
FARI.......................................... 520
farmland................................... 497
fast bus.................................... 249
fauna........................................ 354
Fe2O3....................................... 578
feather like connection............. 191
Feb............................................. 64
feldspar.................................... 336
feldspars.................................. 336
felsic rock................................. 335
fence........................................ 101
fenland communities................. 498
fenland community................... 498
FeO........................................... 578
ferns................................... 47, 355
ferriferous minerals.................. 320
ferry bridge.............................. 260
ferry terminals.......................... 220
fertilisation................................ 389
fertilisers(artificial)................... 494
fertilising................................... 485
fertility....................................... 464
feudal system........................... 492
Feynman(1977, 1963).................. 7
Feynman, Leighton et
al.,1977,1963) 470
field of vision............................ 624
fields......................................... 378
film theatre................................ 538
film theatres.............................. 537
filter(plantation).......................... 81
filtered light................................. 47
final use(energy)........................ 33
financial responsibility.............. 513
fine dust................................... 556
fine mode.................................. 556
fire brigade....................... 263, 294
first law of thermodynamics...... 13
fish(freshwater(atlas))............. 433
fishery firms............................. 542
fishing laws.............................. 434
fixation...................................... 624
fixation point............................. 625
fixed two-hinged
three-hinged arch 260
flageolet.................................... 156
Flanders................................... 492
flank in wind............................. 135
flea sedge................................ 396
Flevopolders(forests).............. 436
flexibility.................................... 636
floating bridge................... 259, 260
floating head............................. 400
floating homes.......................... 341
flood control............................. 209
flood control and safety........... 209
flood plain................................. 220
flood plain management............ 209
flood plains(ownership)........... 209
flood protection systems.......... 208
flooding............................. 342, 343
floods....................................... 208
floods 1953.............................. 216
floods by storm surges from
the sea 209
floods of 1953.......................... 209
floor space ratio....................... 269
floor surface............................ 502
floor(ground, top)..................... 649
floor(intermediate).................... 649
floor-space index............. 512, 513
floor-space ratio............... 512, 513
flora-counties........................... 393
Floris V..................................... 492
florists...................................... 543
Floron....................................... 454
FLORON Foundation................. 430
flow diagram(energy)................ 32
flower auction.......................... 518
flowering
periods(wetland,water) 61
flowering times(grass
land,forest) 65
flowering
times(pioneers,ruderals) 63
fluitekruid.................................... 62
flute.......................................... 156
fluvial area................................ 450
Fluvial landscape...................... 497
fluvial networks........................ 281
fly ash...................................... 554
focus................................ 625, 631
fog............................................ 561
foliage................................... 47,
48
Follow-up investigation protocol 579
food production........................ 324
food web(summit).................... 424
footpath.................................... 249
footpath(hedges)..................... 101
force........................................... 12
forest(ecological groups)......... 386
forest(typical(landscape))....... 377
forests........................................ 48
forests(tropical rain)................ 167
form parameters....................... 114
form quality............................... 517
form(legend)............................. 663
formal....................................... 626
formaldehyde........................... 555
formal-informal......................... 627
formalist position...................... 663
formation of the land by
rivers. 321
formation(landscapes)............. 392
formation(peat, river,
pleistocene sandy) 380
formations................................ 393
formula......................................... 7
forsythia..................................... 83
fortresses................................ 205
fortress-like extensions........... 651
fossile fuel(biomass(solar
power))................................... 22
fossile fuel(biomass).................. 21
fossile fuels.......................... 13, 30
foundations(wet)..................... 223
fox.................................... 437, 439
fracties..................................... 326
fragmentation........... 252, 503, 652
frame................................ 626, 637
frame(grain)............................. 430
frame(rareness)....................... 429
Fraunhofer Institut.................... 662
Freedman(1975)............... 424, 466
freedom of
choice(design(robustness)) 636
freedom of
choice(difference). 660
freedom of
choice(possibilities(variety)) 667
freedom of movement.......... 17, 18
freedom, equality and
brotherhood 469
freon......................................... 556
frequence................................. 154
frequency divisions.................. 114
fresh water.............................. 327
fresh water bubble(dunes)...... 219
fresh water(needed during
the dry season) 207
Friesian lake region.................. 438
Friesland........................... 388, 489
fringe layed out........................ 400
fringe(meadowland, forest)..... 400
front gardens........................... 266
front(polarisation(connection,
communication)) 633
frontside................................... 626
frost.......................................... 303
frost line................................... 344
frost-proof................................ 344
frozen ground.......................... 303
frustration................................. 467
FSI 269, 275, 509, 512, 513, 516, 519
Fukuyama(1992).............. 367, 667
Fukuyama-expectations........... 662
funcionalist position.................. 663
function(area capacity)............ 642
function(legend)....................... 663
function(probable, possible).... 642
function(structure(form))......... 663
function|time............................. 627
functional charge............. 249, 409
functional differentiation........... 634
functional profile....................... 523
functional quality...................... 517
functional value........................ 634
functional values(economy,
culture, administration) 634
funding(infrastructure)............. 236
fungi......................................... 432
Furgeso-Lees(1987)................ 430
future generations.................... 470
future value.............................. 634
futures(probable, possible,
desirable) 660
gadwall duck............................ 441
gadwall ducks.......................... 432
galleries.................................... 649
gametes.................................... 355
garages............................ 545, 588
garden...................................... 626
garden(front,back)..................... 45
garden(hedges)....................... 103
Garms(1977)............................ 356
Garretsen(1989)...................... 425
gas constant.............................. 17
gas network............................. 292
gas pressure............................ 293
gas(environmental costs).......... 30
gates........................................ 204
gauge points............................. 560
gauge(indicator)....................... 442
gauges(nature(present,
potential)) 442
gauging network...................... 560
gaussic plume model................ 560
Gay Lussac................................ 18
GDP.......................................... 511
gebundelde deconcentratie...... 370
Gelderland................................ 434
Gelderse Poort......................... 358
Gelderse Vallei......................... 332
gele kornoelje............................. 64
gele lis........................................ 61
gele plomp.................................. 61
Geleen–Sittard.......................... 527
gene banks............................... 389
genealogy of theories.............. 404
generalization(dangereous)..... 391
genesis of life........................... 353
genetic deterioration................. 389
genetic exchange..................... 389
genetic richness....................... 352
genius loci................................ 357
genius loci(biological)............... 361
genome..................................... 365
Gent (1999).............................. 256
geochronology......................... 315
geodesy................................... 319
geographical coordinates........... 43
geography................................ 319
geo-hydrologic isolation........... 592
geologic time scale................... 315
geological cycle................ 315, 316
geology..................... 312, 314, 319
geomorphological unit............... 393
geomorphological unit(flora
counties) 392
geomorphology................. 312, 319
George(1961)........................... 635
Gerberligger............................. 260
German economy..................... 206
germinating time........................ 364
gewoon herderstasje............... 387
gewoon varkensgras............... 387
GHG.................................. 329, 578
giant butterbur............................ 62
Gids(1986)............................... 118
Gijsbrecht van Amstel.............. 492
GIS............................................ 235
GIS system............................... 443
GIS-applications....................... 508
Gittenberger(1998)................... 430
GJ............................................... 13
glacials..................................... 358
glaciation.................................. 165
glaciers..................................... 194
GLG.................................. 329, 578
global warming......... 236, 238, 423
golden rain.................................. 84
Google Earth.................... 208, 221
Gooi(health).............................. 425
Gool(1986)................................. 20
gothic cathedral........................ 459
Gotthard tunnel......................... 297
Gouwzee................................. 432
gradient.................................... 396
gradient map............................ 397
Gradient map(1966)................. 397
Gradientenkaart RPD, 1966.... 397
gradients.................................. 397
gradients around farm and
town 485
grafitti....................................... 268
grain......................... 626, 637, 638
grain(frame)............................. 430
grain(rarenes).......................... 429
grain(rareness)........................ 429
granite.............................. 318, 335
grape.......................................... 47
graphic industry....................... 588
grass fields.............................. 436
grass land.................. 64, 107, 378
grass land(ecological
groups). 386
grass lands(poor).................... 387
grass snake............................. 433
grasses............................ 356, 357
grassland......................... 496, 497
grassland(groundwater level). 222
grasslands............................... 438
Grave....................................... 205
gravel......................... 87, 393, 577
grazers..................................... 400
grazing..................................... 485
grazing animals................ 382, 485
Great Bear.................................. 38
great titmouses......................... 389
greater burdock(river
county).. 375
greater plantain.................. 63, 366
grebe........................................ 437
green area................................ 275
green areas.............................. 474
Green Heart...... 408, 422, 470, 506
green lines................................ 279
green margin............................ 266
green monuments....................... 91
green network(water)............. 252
green river................................ 215
green seaweeds...................... 432
green surfaces........................ 521
green urban areas................... 418
green wall.................................. 92
greenery........................... 266, 649
greenhouse-effect................... 354
Greenwich................................. 41
Greiner..................................... 651
greppels................................... 225
Grevelingen...................... 210,
218
grey area.................................. 567
greylag goose.......................... 436
grid........................... 190, 191, 277
grid measure............................ 266
grid mesh.................................. 190
grid models(air pollution).......... 560
grid(square, triangular).............. 81
grienden................................... 378
Grime(1988)............................. 389
Grime. (1988)........................... 371
Groen et al. (1987)................... 387
Groen(1995)..................... 405, 430
Groene Hart.............................. 297
Groenman (1960)..................... 475
Grol........................................... 205
Grondmij................................... 493
grondsoorten............................ 326
grondwater.............................. 327
grondwaterstanden......... 329, 578
grondwaterstroming................. 578
grondwatertrappen.......... 329, 578
Groningen................................. 209
Grontmij.................................... 494
groot hoefblad............................ 62
Groot(1992).............................. 439
gross dots................................ 510
Grote Markt(Haarlem)............... 655
grote vuurvlinder...................... 388
grote weegbree................. 63, 387
ground.............................. 313, 577
ground criteria.......................... 344
ground descend....................... 423
ground ivy.................................. 64
ground level in Holland............. 209
ground pollution........................ 561
ground price............................. 516
ground prices........................... 275
ground statistics....................... 501
ground surface index............... 515
ground water
level(grasslands, crops) 222
ground water quality................ 324
groundsel................................... 62
groundwater...................... 85, 327
groundwater currents.............. 561
groundwater flows.. 169, 329, 578
groundwater level managed
artificially 222
groundwater levels.................. 222
groundwater protection........... 219
ground-water table.. 327, 337, 578
groundwater tables.......... 329, 578
groundwater zone........... 327, 328
groundwaterlevel..................... 223
group accommodations............ 538
growth...................................... 463
growth form(trees).................... 67
growyh..................................... 624
grubbers.................................. 400
GSI.................................... 515, 516
guide values............................. 567
guiding tower........................... 259
gulden sleutelbloem.......... 389, 390
Gumbel graph.......................... 213
Gumble graph........................... 213
gusts........................................ 112
gutter........................................ 401
GWe........................................... 34
gymnosperms................... 356, 432
gypsum..................................... 553
H+N+S...................... 409, 445, 506
H2S........................................... 555
H2SO4....................................... 555
Haagse Beemden..................... 341
Haarlem............................ 341, 497
Haarlemmermeer...................... 527
habitable land........................... 499
habitat............................... 371, 391
habitat(animals)........................ 409
Haccou(1994).......................... 392
Hachiro Gata Polder in
Japan. 228
haf county(sea clay, peat)....... 375
Hagemeijer(?)........................... 427
Hagestein(weir)....................... 208
Halder(2000)............................ 388
half-day crčches/nurseries..... 534
half-through arch bridge.. 259, 260
halogen............................. 554, 555
halogenated.............................. 589
halogenic hydrocarbons.. 555, 556
hamamelis................................... 83
Hamburg................................... 501
hamlet............................... 369, 510
hands....................................... 458
hangbrug.................................. 260
hanger...................................... 259
hangkabel................................. 259
Hannover.................................. 437
Hanseatic League.................... 492
Hanze cities.............................. 220
Hanze period............................ 220
haploid...................................... 355
Harbour Island.......................... 653
harbour island(IJburg).............. 647
harbour law outs...................... 220
hard.......................................... 626
hardened surfaces.................. 343
hardening................................. 485
hard-soft.................................. 627
Haringvliet......................... 210,
218
Haringvliet(sluices)................... 208
Harlingen.................................. 220
harmony(hedges)..................... 103
harp cable stayed bridge. 259, 260
harptuibrug....................... 259, 260
Harrison(1964). 458, 459, 460, 465
harvesting................................ 485
Haussmann.............................. 350
Haveneiland.............................. 653
Hawkstone Hall........................ 348
Hawkstone, Shropshire........... 349
hawthorn...................... 83, 84, 376
hazel................................... 64, 377
hazelaar..................................... 64
HCHO........................................ 555
head in wind............................. 135
health........................................ 570
health facilities.......................... 534
health objectives(urban
design) 426
health(biodiversity)................... 365
health(civilisation damage)....... 424
health(definition)....................... 365
health(scale)............................ 365
health(towns, income, life
style, soil conditions) 425
healthy city project................... 426
hear.......................................... 154
hearing..................................... 624
heart disease........................... 466
heat............................................ 34
heat
loss(radiation(atmosphere)) 107
heat pump................................... 19
heat pumps(energy
contribution(national)) 31
heathland reclamation.............. 496
heating........................................ 13
heavy metals............ 588, 589, 592
Hedel........................................ 205
hedge(height)........................... 102
hedges............................. 101, 378
hedges and thickets(limy
grounds) 378
hedges and
thickets(nutricous grounds) 378
hedges(deciduous).................. 104
hedges(evergreen).................. 104
hedges(pruning)....................... 104
Heerlen..................................... 527
hefbrug............................. 259, 260
heftoren.................................... 259
Heidemij............................ 493, 494
height belt................................. 364
height of buildings...................... 44
height of the land...................... 165
height(standard(wind))............ 112
Heijligers, W.............................. 420
Hekstra(1993).......................... 550
Held(1991)........................ 374, 383
Hellevoetsluis........................... 206
helophyte filters........................ 306
Hendriks(1993)................. 546, 663
HEPMEAP'............................... 556
herbivore grazing..................... 400
herbivores................................ 388
herb-robert................................. 65
herbs(shrubs(trees))................. 74
herdertasje................................. 62
heritage(cultural)...................... 206
Herk.......................................... 652
Hermans(1982).......................... 34
herring...................................... 492
hertz......................................... 154
Herzberger, H........................... 341
hesitate..................................... 626
heterogeneous......................... 628
Hettema and Hormeijer,
1986. 218
Heukels’ flora............................ 364
Heukels’ Flora... 352, 355, 356, 357
heuvelruggen........................... 330
hexachloro-benzene................ 555
hexachloro-butadiene.............. 555
hexachloro-cyclohexane......... 555
hexagonal grid.......................... 277
hexagonal patterns.................... 18
HF............................................. 555
hibiscus...................................... 84
hide-and-seek.................. 621, 627
high rise.................................... 519
high rise at the edge(wind)...... 141
high rise
buildings(ventilation).. 110
high rise on the edge(wind)..... 144
higher sandy soils.................... 449
highest average groundwater
level................................ 329
highschool................................ 624
high-speed rail.......................... 287
high-voltage.............................. 298
high-voltage cables
underground 292
high-voltage grids..................... 291
high-voltage transmission........ 287
high-voltage transmission
lines 291, 292, 554
highway................... 162, 247, 249
highways................. 190, 191, 272
highways(national, regional,
local, city) 190
Hildebrandt............................... 250
hill ridges.................................. 330
hinderance chart...................... 443
historic building projects........... 537
historic survey(soil
contamination) 579
HMGL................................ 329, 578
Hoekse en Kabeljauwse
Twisten 492
Hoeven and Louwe(1985)....... 632
holiday chalet........................... 538
holistic-vitalistic........................ 391
Holland.............................. 327, 491
Holland(hooiland)...................... 400
Hollandes IJssel barrier............ 218
Hollandse
Waterlinie................. 420
Hollerbroek............................... 492
holly.................................... 84, 377
Holocene.......... 359, 372, 373, 374
Holy.......................................... 342
holydays(dangerous)............... 426
home(nature(distance))........... 423
homes for the mentally
handicapped 534
homes for the those with
sensory handicaps 534
homes per year of
construction 533
homes(Netherlands)................. 532
homo erectus........................... 458
homo habilis.............................. 458
homo sapiens sapiens............. 458
homogenous............................. 628
homogenous mixture................ 453
Hondsbosse Zeewering.......... 219
hondsdraf................................... 64
honey-locust.............................. 84
Hoofdweg(Baarsjes)............... 631
Hooghoudt formula................... 229
hoogveen................................... 59
hooiland.................................... 400
Hook and Cod Disputes............ 492
Hook of Holland........................ 208
hop............................................. 65
hope......................................... 662
horizon(free)............................ 407
horizons(soil)........................... 325
horizontal groundwater flow... 578
horizontal
variation(planting)...... 68
hornbeam............................. 84, 98
horse chestnut... 83, 84, 89, 93, 95
horse chestnut (kastanje).......... 98
horse chestnut(clay/loam)......... 85
horsetails.................................. 355
horticultural gardens................ 538
horticulture....................... 354, 378
Hosper...................................... 445
Hosper(2001)........................... 421
hospitals................................... 534
hostels caring for vagrants
and homeless people 534
host-family care centres.......... 534
hotel with 1000 over-night
stays per year 538
hotels........................................ 545
Hotzan(1994)............................. 46
hour angle............................ 38, 43
hour average wind velocity..... 154
hour field.................................. 430
hour-field frequency................ 430
house............................... 623, 626
house from above.................... 624
houseboat parks...................... 341
household................................. 530
household
management(habitat) 460
household(electricity use).......... 20
household(occupants)............. 502
Houtribdijk......................... 436, 438
Houwaart(1991)............... 405, 452
HSL................................... 238, 297
Huber, H................................... 341
Huffener................................... 622
Huisman(1998)......................... 197
Huisman, Cramer et al.,
1998 169,
170, 227
human biodiversity................... 425
human capital approach........... 563
human centred approach......... 391
human dynamic........................ 382
humanity................................... 458
humus......................... 86, 577, 588
hunger...................................... 462
hunting...................................... 461
husbandry................................ 486
hut............................................ 623
hybrid systems......................... 249
hydrangea.................................. 84
hydrated calcium sulphate....... 553
hydrocarbon............................. 589
hydrocarbons................... 553, 555
Hydrofluoride............................ 555
hydrogen.................................... 34
hydrogen sulphide.................... 555
hydrogen(environmental
costs). 30
hydrolic radius.......................... 201
hydrological cycle.... 315, 316, 318
hydrological maps................... 235
hydrological measure points.... 234
hydrological unit....................... 393
hydrological
unit(communities). 392
hydrosphere............................. 318
hygienists................................. 452
hygienists(19th
century)........... 405
hymenoptera(Dutch)................ 431
Hz............................................. 154
iatrogeneous............................ 426
ice............................................. 165
ice age...................................... 437
ice ages.............................. 55, 358
ideal typical profiles.................. 379
idealistic position...................... 659
identifying plants...................... 361
identity...................... 420, 421, 627
identity of regions..................... 475
identity of towns...................... 470
identity(region,
conurbation, town, district, neighbourhood) 523
identity(time or place)............... 654
identity(town)........................... 477
igneous rock..................... 316, 335
IJ. 296
IJburg........................ 296, 324, 653
IJK............................. 207, 208, 209
ijle zone.................................... 475
IJmeer....................................... 432
IJmuiden.................................... 216
IJssel 197, 207, 208, 209, 323, 437
IJssel river................................ 207
IJsselkop -IJK............................ 207
IJsselmeer 209, 210, 216, 219, 432, 436, 437, 440
IJsselmeer polders................... 324
IJsselmeer region............. 434, 441
IJsselvallei................................ 332
ijsvlakte..................................... 122
IKC............................................ 447
illness rate................................ 562
image quality............................. 628
image quality plan..................... 453
image quality(variation)............ 636
image(conceptual).................... 629
image(district)........................... 631
image(neighbourhood)............. 631
image(urban(margin(built-up,
vacant))) 649
ImageJ...................................... 515
images(assembling)................. 637
imagination................................ 627
imagine(possible)..................... 660
immigrants................................ 530
immigration........................ 463, 464
immission.................................. 562
IMP Water................................. 569
impact(extremes)..................... 111
impacts(standard reference)... 111
improbable possibilities............. 547
in situ purification..................... 589
in water.................................... 303
in-beteens................................ 626
inbetween realm.............. 394, 626
inbetween-realms.................... 395
in-betweens to hesitate, to
decide 627
income...................................... 425
incomparable values................ 645
independent variable................ 663
Indicative Long-term Water
Programme 569
indicator species.............. 440, 443
indicator(gauge)....................... 442
indicators.................................. 387
indicators(climate,
environment) 54
indoor sports facility................. 538
industrial accidents.................. 555
industrial processes................. 555
industrial revolution 18, 31, 462, 466
industrial voltage...................... 298
industrial waste........................ 554
industrialization(awarenss
of problems) 237
industry.................................... 543
infiltration ability........................ 344
informal..................................... 626
informal use(planting)................. 82
information
emissions....... 554,
558
infrared light....................... 22, 107
infrasonic................................. 154
infrastructure........................... 521
infrastructure (funding)............ 236
infrastructure works(large,
logistics) 220
infrastructure(ecological)......... 417
infrastructure(major)................ 217
infrastructure(policy
papers, sectors involved) 237
infrastructure(separation,
connection) 632
inhabitants per hectare............ 515
Inhelder..................................... 621
initial abiotic situation(same)..... 440
initial interaction........................ 132
initial situation........................... 440
initiative..................................... 627
inner environments................... 466
inorganic emissions.................. 554
insecticide................................ 555
insects 353, 382, 388, 389, 426, 431
insects(Dutch).......................... 431
institutional aspect of
water management 210
insurance companies(fear)...... 426
insurance(children).................. 465
insurance(health)..................... 425
integrated reclaiming................ 342
integrated water management. 236
integration......................... 107, 668
integration(scale)..................... 368
intensity.................................... 518
intensity of use......................... 467
intensity(use)........................... 365
intensity-of-use gradient.......... 485
intention(tradition,
opportunity). 636
intercity train............................. 249
interdependent comparability... 440
interest..................................... 627
interference.............................. 251
interference(networks)............ 252
interfunctional activities.... 466, 467
interglacials.............................. 358
Interliner.................................... 249
internal boundary layer
thickness 130
internal comparability................ 440
internalised urban functions..... 649
International Central
Commision for Navigation on the Rhine 206
international functions.............. 477
international waters................. 238
interregional task division......... 474
intervention values................... 588
inundate indicated polders
preventively 214
inundation(critical periods)....... 206
inversion(weather).................. 559
investment................................ 641
inward-directed approach....... 549
irido-alnion................................ 378
irregular pattern.......................... 81
irreversible problems................ 550
islands(growing)...................... 219
islands(Wadden)...................... 220
isolating pollution...................... 589
isolation technique.................... 592
Israel(1995).............................. 493
Israel, J.I. (1995)....................... 475
ivy............................................... 84
ivy-leaved toadflax................... 386
J.. 13
Jacobs(1961)........................... 424
Jakarta...................................... 220
Jakubowski(1936).................... 635
Jan.............................................. 64
Jansen(1965)........................... 492
Jong.......................................... 622
Jong (1985).............................. 365
Jong and Engel(2002).............. 637
Jong and Priemus (2002)......... 462
Jong and Ravesloot (1995)...... 628
Jong and Voordt (2002)........... 367
Jong and Voordt, 2002..... 400, 404
Jong(1972)............................... 659
Jong(1978)............................... 633
Jong(1985)............................... 110
Jong(1986)............................... 140
Jong(1988)............................... 467
Jong(1992)....................... 549,
659
Jong(1993)............................... 571
Jong(1995)....................... 405, 453
Jong(1998)............................... 479
Jong(2000)............... 391, 406, 570
Jong(2001) 46, 106, 130, 421, 428, 442, 443, 520
Jong(2002) 354, 428, 462, 464, 658
Jong(2003)....................... 161, 188
Jong, M.D.T.M. de, 2002........... 404
Jong, M.D.T.M.d., 2002........... 404
Joosten(1992).......................... 439
Joustra, et al., 2004.................. 395
Julianakanaal locks................... 216
July....................................... 61, 65
June...................................... 61, 65
June 21st.................................... 37
juniper......................................... 84
k(adsorbtion)............................ 562
kadaster................................... 597
Kamerik..................................... 498
Kant(1976)........................... 7, 659
Karlsruhe.................................. 216
Kattendiep................................ 209
kattestaart................................ 388
Kelle(1980)... 61, 63, 373, 376, 377
kerb.......................................... 263
Kerf.......................................... 220
Keteldiep................................... 209
Kethel............................... 341, 342
key actors........................ 475, 476
key to symbols......................... 663
kg cargo/inhabitant/day............ 272
kg cargo/vehicle....................... 272
kilowatt*hour.............................. 13
Kinderdijk.................................. 226
kinds of clothes........................ 627
kinetic energy............................. 34
Kinkerbuurt............................... 515
kitch(emotions(prescribed))..... 636
Kjehldahl................................... 556
kjeldahl...................................... 554
klapbrug.................................... 261
kleifractie.................................. 326
klein hoefblad............................. 62
klein kruiskruid............................ 62
Kley, 1969................................ 228
Klijn(1995)................................ 392
Klok(1981).................................. 60
KNMI De Bilt(1979).................... 560
KNMI(1979)............................... 565
KNNV........................................ 454
knotgrass................................. 387
Kolasa(1991)............ 371, 392, 453
koolzaad..................................... 62
Kornwerderzand...................... 220
Koten-Hertogs(1995)............... 461
Koutamanis(2002).................... 667
kraagliggerbrug................ 259, 260
kraanbrug................................. 261
Krammerdam............................ 218
Krebs (1994)............................ 371
Kreekrakdam............................ 218
Krupp(1995)............................. 367
Krupp(1996)..................... 662, 667
kW.............................................. 13
kWa............................................ 12
kwel.......................................... 330
kwelwater................................ 330
kWh............................................ 13
kWhe.......................................... 13
kWhth......................................... 13
laagveen............................. 60, 483
Lachiver(1964)......................... 462
lady’s smock............................... 64
lagoon....................................... 209
lagoon county........................... 374
lake................................... 247, 249
lake bed(stabilisation)............... 433
land consolidation............. 494, 495
land reclamation............... 209, 221
land registry plans(cables
and pipes) 308
land use.................................... 501
land use in the Netherlands...... 524
land/water transitions.............. 439
landaanwinningswerken.......... 220
landfarming............................... 590
landhoofd................................. 259
landownership......................... 209
landscape......... 370, 393, 408, 642
landscape
changes(temperature) 360
landscape development........... 312
landscape parks............... 370, 642
landscape theatres.................. 639
landscape(cultural elements)... 206
landscapes(urban)................... 642
land-use statistics.................... 444
lane width................................. 272
lanes......................................... 264
large copper butterfy............... 388
Lascaux..................................... 57
lateral differences in wind
velocity 129
lateral moraines........................ 496
lateral wind effects.................. 136
latitudes...................................... 35
LAVIN....................................... 447
law of superposition................ 316
lawn......................................... 626
layered(design
tools(planting)).. 72
layers....................................... 316
layout of cables and pipes....... 307
LCA.......................................... 573
Le Marais.................................. 323
Le Nôtre.................................... 349
lead........................................... 589
leaf cover................................... 83
leaf mozaic................................. 47
learn......................................... 626
leather industry........................ 588
leaves(size(soil))....................... 84
Leeuwen.................................. 548
Leeuwen (1979-1980).............. 401
Leeuwen(1959)............... 378, 379
Leeuwen(1971)............... 485, 665
Leeuwen(1973)....................... 485
Leeuwen(gradientenkaart)....... 397
Leeuwen(references)............... 395
Leeuwen(variation).................. 398
Leeuwen, 1964........................ 395
Leeuwen, 1965........................ 396
Leeuwen, 1971........................ 395
Leeuwen, Chris van................. 394
Leeuwen, Chris van................. 393
Leeuwens van......................... 395
legend unit(type)...................... 637
legend units.............................. 632
legend units(mixing,
separating) 642
legend units(scale-segmented
approach) 642
legend(adhesion)..................... 632
legend(agenda)........................ 643
legend(cohesion)..................... 632
legend(efforts, existing,
planned) 503
legend(scale)........................... 638
legend(transition)..................... 643
legend(typology)...................... 637
legend(unconventional)............ 640
legend(vocabulary).................. 663
legends..................................... 626
legends(scale)......................... 372
legend-units infrastructure....... 641
legend-units landscaping......... 639
legend-units physics and
soil... 641
legend-units town and
traffic... 640
Leiden....................... 391, 491, 497
Leidscheveen........................... 123
Lek............................................ 208
Lely........................................... 216
Leonard(1977)......................... 461
Leopold............................. 188, 190
Leopold and Maddock.............. 185
Lepelaarsplassen............. 436, 441
lesser celandine......................... 64
leuning...................................... 259
liberals...................................... 469
licencing system....................... 552
lichens.............................. 320, 433
lids............................................ 402
life communities........................ 382
life community........................... 391
life forms(one-celled,
multiple-celled) 353
life span.................................... 364
life style.................................... 425
life(risk to die)........................... 426
life(sea, land)........................... 355
lifecycle.................................... 425
lift bridge........................... 259, 260
liggerbrug......................... 259, 260
light..................................... 48, 626
light permeability(tree)................ 48
light pollution............................... 83
light requirement(planting).......... 74
light vehicles............................. 272
light(city,artificial)....................... 48
light(water(silt))........................ 436
light|dark................................... 627
lighthouses............................... 220
lighting...................................... 649
lightning power........................... 49
lightrail...................................... 249
Ligtelijn,
1999.......................... 394
lijndorp...................................... 486
lijsterbes................................... 376
lilies................................... 356,
357
liliidae........................................ 357
Limburg............................. 373, 496
lime........................... 48, 92, 95, 98
lime (linde).................................. 98
lime tree...................................... 91
lime trees(pavement raising)...... 87
lime(summer).............................. 84
lime(winter)................................ 84
limes convergens.................... 396
limes divergens....................... 396
limiting condition chart.............. 443
limiting factor(minerals)............ 388
limiting value............................. 568
limiting values........................... 567
limits to growth......................... 464
Limpens(1997)................. 427, 430
line length................................. 285
line sources...................... 560, 561
linear-shaped legend
elements 503
liquid extraction........................ 591
lisdodde...................................... 61
litoral drift of the tide................. 209
liveliness................................... 518
liverworts................................. 355
living................................. 546,
626
living layer........................ 340, 593
living platforms......................... 340
lm 49
LMGL................................ 329, 578
LNV.................................. 437, 441
LNV(1990)................................ 389
LNV(2000)........................ 420, 575
LNV(2002)................ 374, 482, 483
load bearing capacity............... 344
loam.......................................... 577
Lobith................ 169, 171, 196, 210
lobsters.................................... 431
local average wind velocity..... 111
local choice of
location(wind).. 111
local highway................... 247, 249
local highways................. 190, 191
local train.................................. 249
location(choice(national))......... 115
location(choice(soil
pollution)).. 576
locations(building(national(wind))) 112
lock........................................... 232
locks......................... 206, 232, 253
locust tree................................ 377
locust tree / false acacia
(acacia) 98
Loerakker................................. 652
loess......................................... 326
loess region.............................. 488
logaritmic formula..................... 129
logic.......................................... 658
logic(formal)............................. 659
logical form............................... 659
logical operations..................... 621
logical reasoning...................... 658
logistic curve............................ 463
logistics(large
infrastructure works) 220
Londo (1997)............................ 366
Londo(1987)............................... 66
Londo(1998)............................. 352
London..................................... 501
longitudinal research................ 426
loose planting scheme................ 91
loosestrife................................ 388
lot 510
Lotke-Volterra.......................... 462
lounge(through)........................ 633
Lourijsen................................... 651
low rise at the edge(wind)....... 141
low rise
buildings(ventilation)... 110
low rise on the edge(wind)...... 144
Lower Rhine..................... 208, 209
lowest mean groundwater
level 329
lowland river............................ 194
lowland
system........................ 227
lowlands................................... 481
lowlands with drainage and
flood control problems 223
L-shape.................................... 268
Ludwig..................................... 492
Luhmann (1973)....................... 368
Luhmann(1973)........................ 668
lumen.......................................... 49
lux............................................... 49
lux meter..................................... 49
lx. 49
lycaena dispar.......................... 388
lye............................................. 589
Lyon......................................... 501
Lysen(1980)............................... 34
lythrum purple........................... 388
Maarel(1978)............................ 439
Maas, F..................................... 341
Maas, Thieme Meulenhoff)...... 170
Maaskant price......................... 219
Maastunnel............................... 296
Maasvlakte............................... 238
'Maasvlakte............................... 324
Maaswerken............................ 216
Mabelis(2000)........................... 442
MAC.......................................... 569
madeliefje................................... 64
mafic rock................................. 335
magma...................................... 333
magnetic properties.................. 590
magnolia..................................... 83
Main.......................................... 172
main ecological structure......... 446
main port................................... 439
main ports................................. 477
main road(hedges)................... 101
main street........................ 247, 249
Main-Danube canal................... 403
maintenance of public space... 513
maintenance
requirements(planting) 75
maintenance work(planting)....... 73
maisvelden............................... 122
Malschaert................................ 655
Malta Convention...................... 287
mammals........................... 353, 389
mammals(advance).................. 355
mammals(atlas)....................... 433
mammals(night animals)........... 352
mammals(saurians extinction).. 357
management theory.................. 400
management(culture)............... 644
manor....................................... 489
manrope................................... 259
mantouw.................................. 259
manure pollution....................... 550
manures(artificial).................... 486
manuring................................... 388
map cutting............................... 514
maple.......................................... 88
maple(esdoorn........................... 98
mapping the environment......... 443
maps................................. 319, 610
Marais....................................... 323
March......................................... 64
March 21st................................. 36
margin....................................... 264
margin(built-up area, vacant
area) 647
marginally growing specimens. 366
margins..................................... 262
margriet...................................... 63
Marijnissen(1998)..................... 357
marine-clay areas.................... 451
Markermeer 432, 434, 436, 437, 439
market....................................... 476
Markiezaatdam......................... 218
marram(dune county)............... 375
Mars........................................... 22
marsh....................................... 372
marsh fern–alder swamp......... 484
Marsh Fleawort........................ 431
marsh(clay).............................. 433
marsh(salt)............................... 433
marshland(draining)................. 226
mass migration......................... 466
mass(hedges).......................... 103
Mast Forest in Breda................ 492
matchmakers............................ 389
material..................................... 626
material storage........................ 299
materialistic position................. 659
mathematics................................. 7
mathematics(equality).............. 398
matricaria discoidea................. 387
Maurits...................................... 493
maximal acceptable level of
risks 567
may............................................. 61
May............................................. 65
McMahon(1983)....................... 155
McMahon(1987)....................... 155
meadow barley(Holocene)....... 374
meadow buttercup..................... 65
meadowland(prototypes)......... 400
meadows................................. 378
Meadows(1992)....................... 463
meander................................... 194
meandering............................... 196
meanders......................... 194, 323
means(scale)........................... 368
means‑directed................ 661, 663
measure................................... 111
measure(reference
situation(deviation)) 111
measures................................. 262
measures(condition)................ 111
measures(context
independent) 111
measures(possible)................. 138
Mecanoo................................... 650
mechanical emissions...... 554, 558
mechanical forms.................... 402
mechanical weathering............ 320
mechanisms............................. 402
median strip...................... 271, 278
medical day centres for
infants 534
medicine................................... 365
medicines(use)......................... 425
medieval town.......................... 476
medieval town(functional
differentiation) 634
medium voltage......................... 298
Meerendonk(1998)................... 430
Meerzicht.......................... 256, 454
meet.......................................... 626
meet|retire................................. 627
Mehrtens.................................. 653
meidoorn................................... 376
Meijden(1989)........................... 375
Meijden(1996)........... 352, 389, 392
Meijden(1999) 355, 357, 373, 375, 377, 387, 388, 390,
430
Melchers(1991)........................ 440
Melchers(1996)................ 430, 437
membranes(cell)..................... 394
Mennema(1980)....... 373, 427, 430
Mercator square....................... 277
Mercatorplein............ 629, 630, 655
mercury............................ 554, 589
meridian...................................... 41
merry-go-rounds...................... 621
mesh......................................... 250
mesh density............................ 479
mesh width............... 251, 269, 525
mesh width(local motorways). 473
mesh widths............................. 273
meshes..................................... 251
meshes..................................... 479
Mesolithicum............................... 58
Mesozoic.................. 316, 355, 356
metal and galvanic industry...... 588
metalloids.......................... 588, 589
metals....................... 588, 589, 592
metamorphic rock..................... 316
metamorphic rocks................... 318
meteoric collision(65
million years ago) 352
meteoric impact(65 million
years ago) 357
meteorology.............................. 317
methane.................................... 554
method(composition analysis).. 628
methylene chloride................... 591
metro................................ 249, 285
metro lines................................ 299
metro networks........................ 297
metropolis......................... 190, 510
metropolis density30km............... 510
Meuse............... 169, 208, 209, 219
Meuse works........................... 216
mica.......................................... 336
micas........................................ 336
Michels(1993)................... 155,
160
micro climate............................. 382
micro climate(wind).................. 111
Midden-Delfland........................ 342
middenoverspanning................ 259
Middle Stone Age....................... 58
migrations................................. 461
Milan......................................... 501
mi-lieu....................................... 401
milieugebruiksruimte................. 570
millet grass–beech................... 484
mind of technology................... 662
mineral gradient........................ 485
mineral oil.................................. 588
mineral
transporters(animals).. 424
mineralen.................................. 333
minerals............................ 333, 335
minimisation(energy
losses(wind velocity)) 110
ministries involved.................... 237
Ministry of VROM(1990)........... 571
Minnaert...................................... 47
Minnaert(1968)..................... 7, 154
mirroring................................... 266
mirroring transformations......... 268
mixed emissions....................... 554
mixed husbandry...................... 486
mixed sewerage system.......... 344
mixing....................................... 642
MJ......................................... 12, 13
MNP, 2004............................... 213
mobile telephone....................... 295
modality(designer,
empiricus).. 442
models(complex)...................... 398
module.............................. 269, 276
Moens............................. 9, 10, 191
moerasbos............................... 498
Moerdijk zone........................... 208
moisture in the air..................... 559
mole of gas................................. 16
molecule................................... 393
molengang............................... 227
molluscs................................... 434
momentum.................................. 12
money(scarcity, production).... 439
Monnikendam............................ 340
monocausal explanation........... 666
monocotyledons............... 356, 357
monocultures.............................. 23
monofunctional spaces............ 466
monotony.................................. 628
Mont Blanc tunnel..................... 297
montage.................................... 637
Montesquieu(1973).................. 635
Monuments and Historic
Buildings Act 287
mood(planting)............................ 68
Mook......................................... 205
moor......................................... 374
moor land.................................. 372
morphologically
reconstructed. 632
morphology of a river system.. 186
Morris Davis............................. 193
mortality rate............................. 562
Mosel........................................ 172
mosquito’s................................ 366
moss........................................... 47
mosses..................................... 433
mosses..................... 320, 352, 355
most practical means’............... 551
mother...................................... 621
motoric ability............................ 621
motoric deprivation................... 467
motorical polarity...................... 633
motorways............................... 525
moulting period......................... 438
movable.................................... 626
movable-non-movable.............. 627
moving vans............................. 263
mowing..................................... 485
mowing grasslands.................... 66
mowing policy............................ 66
mud flats................................... 482
mullein......................................... 84
multimodal
intersections(travel resistance) 475
multiple span beam bridge 259, 260
Mumbai..................................... 511
Munich...................................... 501
municipal costs......................... 275
municipal land development...... 265
municipalities(population)......... 526
museum.................................... 538
music........................................ 154
music and creative arts centre 538
music school............................ 538
mute swans..................... 432, 436
muurpeper.................................. 63
MVRDV(Dutch pavillion)........... 437
MWa........................................... 12
MWe........................................... 34
Myers(1985)............................. 372
Naardermeer............................ 439
NAP.................................. 209, 359
Napoleon.................................. 206
narcissus................................... 83
narrow streets(planting)............ 93
national choice of
location(wind) 111
national highway.............. 247, 249
national highways.................... 190
national networks..................... 280
National Plan of
Environmental Policy 423,
575
National Plan of Nature
Policy 420, 575
National Plan of Spatial
Policy 418, 575
national plan of
watermanagement policy 236
National Plan of
Watermanagement Policy 423,
575
national policy........................... 575
National Policy Document on
Spatial Planning 2, 1966 397
national policy documents........ 205
national rarity............................ 430
natte omtrek.............................. 201
natural area(types).................. 428
natural areas(dynamic)............ 221
natural gas................... 12, 13, 710
natural gas extraction.............. 292
natural landscape..................... 382
natural
vegetation(potential) 481, 484
natural world............................ 659
natural(concept(scale))........... 425
natural(planting)......................... 68
Naturalis Museum..................... 354
naturalness(planting)................. 70
nature............................... 491, 627
nature conservancy................. 447
nature conservation......... 459, 495
nature conservation plan......... 389
nature development.................. 459
nature in exile(hygiene)............ 426
Nature Policy............................ 420
nature target types................... 384
nature work-groups................. 433
nature(appreciation)................. 440
nature(clay).............................. 433
nature(concept)....................... 428
nature(mowning)...................... 455
nature(programme of
requirements) 636
nature(railway line).................. 454
nature(relief-rich
infrastructure) 454
nature(verges)......................... 454
nature(water
courses(urban(old)))................................ 454
nature(water level
management) 437
nature-target types.. 444, 447, 448
Natuurbeschermingswet.......... 364
natuurdoeltype......................... 420
Natuurmonumenten.................. 445
Nauta(1995)..................... 427, 430
nearness.................................. 632
Nederlands Normalisatie
Instituut 288
Nederlandse monumentenwet. 287
neigbourhood................... 510, 624
neighbour................................. 623
neighbourhood......... 272, 369, 623
neighbourhood density............. 515
neighbourhood density300m.... 513
neighbourhood facilities........... 269
neighbourhood image............... 631
neighbourhood islands............. 269
neighbourhood quarter............. 140
neighbourhood quarters........... 269
neighbourhood road................. 269
neighbourhood road’................ 265
neighbourhood roads 269, 272, 273
neighbourhood street............... 249
neighbourhood(allotment(wind)) 111
neighbourhood(polarisation).... 634
neighbourhood(wind)............... 140
NEN........................................... 395
NEN standard........................... 288
NEN standards. 292, 293, 294, 306
neolithic revolution.................... 461
neonlights................................. 624
Nes and Zijpp (2000)................ 190
Nes(2000)........................ 247,
479
nesting-boxes.......................... 403
net density................................ 251
net dots.................................... 510
net human density.................... 499
Netherlands Standardisation
Institute 288
Netherlands submerged........... 205
Netherlands(international
task) 481
network.................................... 478
network city............................. 476
network city(traffic
concept)... 474
network(green, water)............ 252
networks.................................. 287
networks for gas,
electricity and water 288
networks(alternating)............... 252
networks(dry, wet).................. 258
networks(elongation,
bundling) 252
networks(municipal
regulations) 300
New Amsterdam Level............. 359
New Map of the Netherlands
2000 504
New York................................. 510
Newton, 1687........................... 470
NGOs................................ 236, 238
NH3........................................... 555
nickel........................................ 589
Nie(1996).......................... 427, 430
Nienhuis(1993)......................... 550
Nieuwe Merwede..................... 209
Nieuwe Schans........................ 205
Nieuwe Waterweg........... 218, 287
Nieuwegein.............................. 504
night animals............................. 352
Nijmegen................................... 391
Nijs(1995)................................. 161
Nijs, L.(1995)............................ 161
nitrate....................... 437, 556, 589
nitrate cycle.............................. 462
nitrates..................................... 589
nitrification................................ 562
nitrogen...................... 22, 382, 556
nitrogen cycle........................... 486
nitrogen manure....................... 382
nitrogen oxide........................... 553
nitrogen oxides................. 554, 555
NMP.......................................... 571
NNAO(1987)............................. 495
NNAO(Ontspannen scenario).. 468
Noah......................................... 365
node(sound)............................. 155
nodes(patterns(tree,
feather)). 192
noise......................... 160, 626, 627
noise on façade....................... 272
noise(traffic, aviation).............. 161
nomenclature(plant species).... 352
nomenclature(scale(biology,
urbanism)) 392
nominal measure.............. 271, 393
nominal value............................ 369
non residential functions.......... 274
noon........................................... 46
Noord-Brabant............................ 83
Noordhuis(2000)...................... 441
Noordzeekanaal....................... 216
normal Amsterdam level........... 209
normal test population.............. 367
North -Brabant.......................... 496
North Brabant........................... 494
North gardens.................. 267, 268
North -Limburg.......................... 496
north pole................................... 35
North Sea................................. 219
North Sea Canal....................... 216
North-east polder..................... 498
Northern light rooms................. 267
note(music).............................. 154
Nôtre......................................... 349
Novelli(1989)............................ 648
NOx.................................. 554, 555
NRO2........................................ 476
NRO3........................................ 476
NRO5........ 477, 505, 506, 507, 526
N-S elongating.......................... 268
N-S mirroring............................ 267
number of houses per ha......... 514
nurse crop system......... 73, 74, 78
nurseries.................................. 534
nursery grown tree.................... 99
nursing homes.......................... 534
nutriciousness.......................... 386
oak.................................. 84, 88, 95
oak and ash forests(moisty).... 378
oak forest......................... 372, 484
oak forests(acid not poor
grounds)................................ 378
oak forests(acid poor
grounds) 378
oak(coastal)............................... 84
oak(eik)....................................... 98
oak(pavement raising)................ 87
oak, ash forests(dry
grounds). 378
oak-beach forest...................... 372
oak-beech forest...................... 482
oak–hornbeam.......................... 484
oaks(slow growing)................... 94
object and context.................... 621
object constancy...................... 621
objects...................................... 623
obstacle fright.......................... 264
occupance per dwelling........... 530
occupancy(dwelling)............... 533
occupants per household........ 502
ocean....................................... 165
octaves.................................... 154
Odum(1971)..................... 391, 392
oikos......................................... 444
oil pipelines............................... 287
oil platforms.............................. 296
oil(crude).................................... 13
oil(environmental costs)............. 30
oils............................................ 588
Old............................................ 650
Old Rhine.................................. 491
Oldenbarneveld........................ 493
oligotrophe................................ 386
olivine............................... 318, 334
OMA......................... 505, 506, 507
onderdoorgang......................... 259
one way traffic........................ 279
one-celled life forms................. 353
one-dimensional pollution
models 561
Ooievaar................................... 401
oorgatbrug................................ 261
Oosterschelde.. 210, 217, 218, 440
Oosterschelde barrier.............. 218
Oostvaarders
plassen............. 210
oostvaardersplassen............... 436
Oostvaardersplassen...... 436, 441
open area................................. 512
open areas(central,
peripheral) 417
open areas(function)............... 409
open space...................... 407, 519
open space(hedges)................ 103
open spaces(woodland)............ 74
open water............................... 438
open water storage................. 344
open-air sports facility............. 538
open-closed theory.................. 395
opening to a hamlet.................. 249
operational motoric
abilities...... 627
ophaalbrug............................... 260
opportunities............................. 391
opportunity-directed................. 468
Opschoor(1994)....................... 461
optical fibre networks.............. 288
options(left-over)..................... 443
orchard..................................... 497
orchards................................... 378
orchids..................................... 357
order..................................... 14, 18
order(chaos)............................ 109
orders....................................... 392
orders(synecological).............. 383
organic emissions.................... 554
organic matter.......................... 325
organic mercury....................... 554
organic phosphorus................. 554
organisation(temporal)............. 467
organohalogens....................... 590
oriels......................................... 649
orientation................................. 627
oriënterend onderzoek............. 579
original landscape.................... 382
orthogonal system.................... 250
orthopolar................................. 633
Osdorp..................................... 517
OSR.......................................... 518
other people............................. 627
Otto III........................................ 490
outdoor space(comfort)........... 109
outlet canals............................. 225
outside space(green, blue)...... 649
outside spaces......................... 654
outward boundaries................. 659
outward-directed approach..... 549
overall solution......................... 470
overflow system...................... 305
overflows................................. 305
overhanging(design
tools(planting)) 72
overhangs................................ 649
Overijssel................. 332, 388, 498
overloading............................... 628
overpass.................................. 259
overtones................................. 155
overtones(instrument).............. 159
overview.................................. 624
oxe-eye daisy............................ 63
oxidation process(fauna)......... 354
oxigen......................................... 22
oxygen............................. 354, 425
ozone....................................... 561
ozone layer.............................. 556
paardebloem............................... 62
paarse dovenetel....................... 62
Jong.......................................... 479
paint and dye industry.............. 588
pairing messengers.................. 426
Palaeozoic........................ 355, 356
Palenstein................................. 454
paleo-geographic maps............ 319
Paleozoic.................................. 316
Palladio’..................................... 629
Pampus-West........................... 433
PAN.......................................... 555
Pannerdensche Kop-PK........... 207
Papendrecht............. 272, 273, 274
paper instrument(height)............ 44
papillionaceous flowers........... 382
parabolic formula...................... 130
parabolic-shaped sand dune... 496
paradox.................................... 368
paradox of spatial
arrangement 401
paradoxical concepts............... 642
parallax............................. 621, 623
parallel........................................ 36
parallelogram(surface)............. 250
parapet..................................... 259
parasites.................................. 389
Parc de la Villette...................... 350
Parc de Sceaux at Paris........... 348
Parc de Sceaux in Paris........... 349
Parc des Buttes Chaumont....... 348
Parc des Buttes Chaumont in
Paris 350
parcel....................................... 510
parcellations(theoretical).......... 517
parent material.......................... 324
Parent material.......................... 324
Paris................................. 323, 501
parking.............................. 263, 275
parking areas............................. 87
parking lots................................. 47
parking places.......... 262, 266, 268
parking standard...................... 266
parks........................................ 626
Parma....................................... 493
Parsons(1966)......................... 635
Parsons(1977)......................... 635
particle size.............................. 326
particle size fractions............... 577
particle sizes of soil types....... 326
particle-size distribution........... 577
particulate matter...................... 556
partition(design
tools(planting)).. 71
partition(hedges)...................... 103
passableness........................... 344
passengers per day................. 285
passengers per hour............... 285
passengers per stop................ 285
path.................................. 247, 249
path around the back............... 266
path round the back................. 267
pattern on pattern..................... 399
pattern on process................... 399
patterns(tree, lattice)................ 190
paucicausal.............................. 666
pavement.... 88, 249, 264, 267, 626
pavements................................ 623
pavements(ants)........................ 47
paving(porous)........................... 86
paving(sinking areas)................. 87
paving-stones.......................... 263
Pavlov-reflex............................ 621
PCB................................... 555, 589
PCT........................................... 555
peak flows............................... 208
peak hours....................... 269, 272
peak loads.................................. 34
peak stress...................... 558, 569
peak times................................ 293
peat 58, 326, 374, 377, 483, 577, 588
peat areas................................ 205
peat bog................................... 498
peat bog area........................... 497
peat bogs................................. 498
peat counties............................ 388
peat deposits(subsiding).......... 208
peat exploitations..................... 482
peat extraction......................... 498
peat formation.................... 58, 433
peat formations.......................... 59
peat ground.............................. 579
peat layer................................. 222
peat polders............................. 225
peat soil.................................... 222
peat soils.................................... 87
peat stream.............................. 497
peat(drying).............................. 225
peat(formation)......................... 380
peat(use).................................. 333
pedestrian........................ 263, 281
pedestrian crossings............... 649
pedestrians.............................. 263
pedology........................... 327, 328
peekaboo.................................. 621
Peel..................................... 59, 439
Pekalska, 2005......................... 391
pendular water........................... 86
pentachloro-phenol.................. 555
people per dwelling.................. 469
perchloroethene....................... 591
perchloroethylene.................... 589
perennials............................. 67, 84
perifery/area ratio.................... 250
periods..................................... 315
peripheral open space............. 417
peripheral road......................... 276
periphery(centre)..................... 634
peristyllum................................ 630
permeability k of soil
types..... 229
permeability(soil)...................... 228
Permeta............................ 517, 518
Permian............................. 316, 354
peroxide-acyl-nitrate................ 555
perpendicular blocks................ 268
persicaria................................... 63
perspective(changing)............. 647
perspectives.................... 419, 445
perzikkruid.................................. 63
pest epidemic........................... 462
pest epidemics......................... 492
pesticide industry..................... 588
pesticides................................. 589
Peters(2001)............................ 569
petrographic microscope......... 319
petrol.................... 12, 13, 588, 591
petrol stations........... 545, 588, 592
pH..................................... 561, 562
Phanerozoic Eon...................... 316
phase
gas, liquid, solid......... 590
phenol....................................... 592
Philp (2001)...................... 366, 367
phosphate................................ 437
phosphates.............. 554, 555, 589
phosphorus.............................. 554
photo-chemical smog 555, 556, 560
photovoltaic cell........................ 664
phreatic level............ 327, 328, 578
physical conditions................... 546
physical determinists................ 460
physical weathering................. 320
physical-geographical region... 448
Piaget........................................ 621
Pianka(1994).... 352, 367, 371, 463
piano................................. 154, 156
pier........................................... 259
piezometric level....................... 328
pijler.......................................... 259
pijlkruid........................................ 61
pile heads................................. 338
pine forests...................... 482, 555
pineapple weed........................ 387
pine-spruce forest................... 372
pinksterbloem............................. 64
pioneer environment................. 454
pioneer species(planting)........... 78
pioneer vegetation.................... 382
pioneer(ecological groups)...... 386
pioneering plant.......................... 63
pioneering-plant.......................... 62
pipe........................................... 401
pipe drains................................ 225
pipes........................................... 88
pipes and cables outside
built-up areas 290
pistils........................................ 389
piston.......................................... 19
PK............................. 207, 208, 209
PKB........................................... 215
plaatliggerbrug.......................... 260
place(hedges).......................... 103
plan layers................................ 504
Plan Ooievaar........................... 401
Plan Ooievaar -1986................. 236
plane......................... 48, 89, 93, 98
plane tree................................... 67
plane trees(width)...................... 88
plane(plataan)............................ 98
planes(pavement raising)........... 87
planned
expenses(transparency, democratic decision making, political consistency) 236
planning horizon............... 237, 647
planning layer........................... 503
planning(spatial)....................... 467
planological index numbers...... 502
Planologische Kernbeslissing... 215
plans(perspective)................... 445
plant bed(dimensions)................ 76
plant beds(<6m wide)................ 79
plant communities..................... 441
plant identification(height
belt, areal position, use, germinating time, life span) 363
plant identification(height,
growth form, flowering time) 361
plant identification(Heukels’ flora(family, genus,
species)) 363
plant identification(leaf
form, flower colour) 361
plant identification(leaf
form, flower colour, sex, light, moist) 362
plant identification(name(scientific, english, dutch)) 361
plant identification(nutrients,acidity,salinity,dependency
ground water,root depth,water flow) 363
plant identification(occurrence in The Netherlands) 363
plant identification(occurrence in The Netherlands,
protection) 363
plant kingdom.................... 352, 430
plant kingdom(division)............. 356
plant material.............................. 74
plant taxonomy......................... 357
plantago maior.......................... 387
Plantago Major.......................... 400
plantain..................................... 387
plantation.......................... 626, 627
plantations................................ 639
planting distances...................... 94
planting distances(trees)........... 88
planting effects.......................... 68
planting elements........................ 67
planting forms............................. 75
planting scheme......................... 94
planting trees close
together...... 94
planting(cables).......................... 87
planting(climatological
conditions) 83
planting(physical
environment(urban)) 78
planting(soil)............................... 84
planting(visual effects).............. 67
planting(wind)............................ 93
plantpit........................................ 87
plants........................................ 389
plants(energy conversion)......... 21
plants(urban use)....................... 82
plastics..................................... 555
plate tectonics.......................... 315
platform.................................... 259
platforms.................................. 649
play........................................... 626
playground............................... 623
playgrounds(hedges)............... 102
playhouse................................. 538
playing tag................................ 621
Playstation................................ 623
Pleistocene............... 358, 372, 373
pleistocene(formation)............. 380
plot............................................ 510
plot division(shadow)................. 45
plot(regulation)........................... 46
plots(narrow,deep).................... 45
plots(private)............................ 513
plough....................................... 462
ploughing.................................. 485
plutonic rock............................. 334
PM(traffic contributions)......... 556
PM10.......................................... 556
poa annua................................ 387
pochards.................................. 436
pocket money........................... 623
poičsis...................................... 660
point sources................... 560, 561
pointillistic representation......... 418
poison....................................... 425
poison(resistance)................... 565
polar axis.............................. 35, 37
polar front................................. 559
polar ice caps........................... 318
Polaris......................................... 38
polarisation(open, closed)........ 633
polarisation(public,
private)...... 634
polarity(scale).......................... 633
polarity(sensoric, motoric)....... 633
polarity(structure).................... 633
polder....................................... 221
polder(site preparation)............ 338
polders..... 208, 224, 228, 324, 374
polders(different altitudes)....... 226
polders(history)....................... 222
Pole Star..................................... 38
police........................................ 263
policy document on spatial
planning around 1960 237
policy document on traffic
and transport 237
policy document(revisions
every 10 years) 237
policy documents..................... 236
Policy documents(political
consistency) 237
policy levels.............................. 237
policy paper on spatial
planning 237
policy paper on water
management 237
political consistency................. 237
political
programmes(concentration, deconcentration) 469
pollard willows......................... 378
pollarded willow(knotwilg)......... 98
pollen........................................ 389
pollen dating............................. 360
polluting.................................... 485
pollution(air(dispersion)).......... 120
pollution(awarenss of
problems) 237
polychlorobiphenyl................... 589
polychloro-biphenyles.............. 555
polychloro-therphenyles.......... 555
polycyclic aromatic
hydrocarbons 592
polygonum aviculare................ 387
polynomial................................. 529
polystyrene.............................. 340
pond......................................... 247
pontbrug................................... 260
Ponting (1992).......................... 461
ponton...................................... 259
pontonbrug....................... 259, 260
pontoon.................................... 259
poor grass lands...................... 387
poor soils.................................... 66
poplar........................... 48, 64, 376
poplar(coastal)........................... 84
poplar(populier).......................... 98
poplars..................................... 378
poplars(elms)............................. 94
poplars(growth)......................... 83
population................................. 391
population densitie(habitat)...... 459
population dynamics................. 462
population fluctuations............. 462
population(continental)............. 529
population(expectations).......... 465
population(isolation)................. 389
population(minimum)................. 389
population-density.................... 499
populations............................... 371
populier....................................... 64
porches.................................... 649
pores........................................ 327
portal bridge..................... 259, 260
possibilities for future
generations 470
possibilities for future
life......... 421
possibilities(economical
supply, choice(freedom)) 367
possibility(difference).............. 665
possibility(set of
conditions).... 669
possible.................................... 547
possible measures................... 138
possible(future)........................ 660
possible(imagination)................ 660
Postjes
neighbourhood(Baarsjes) 631
potential emissions........... 554, 558
potential energy.......................... 33
potential natural vegetation...... 484
potential of territory.................. 392
potential wind velocity.............. 112
power................................. 12, 710
power of attraction.................. 470
power station............................. 20
power stations(capacity)..... 31, 32
practical value.......................... 634
practitioners............................. 534
Prague...................................... 501
prawns..................................... 431
Pre-Boreal.................................. 58
precipitation 166, 168, 169, 170, 306, 423
precipitation(continental).......... 168
precipitation(global).................. 167
preconception.................. 658, 659
precondition.............................. 659
preconditions for life................ 659
predators.......................... 382, 462
predict...................................... 547
preparing of the site................. 312
prerequisite.............................. 659
preselection.............................. 424
presence.................................. 436
pressure differences(wind) 142, 148
presupposition.......................... 659
presuppositions (suppressed). 445
presuppositions(computerprogramming) 668
preventing informal
use(planting) 82
prey.......................................... 462
Prigogine................................... 109
Primary Ecological Structure.... 438
primary education..................... 536
primula veris............................. 389
priorities and criteria................. 236
priorities in the use of
time....... 468
priority substances.................. 568
privacy..................................... 266
private control.......................... 268
private space........................... 514
private surface......................... 516
privet.......................................... 84
probability................................... 15
probability distribution............... 213
probability of concentration........ 15
probable................................... 547
probable(future)....................... 660
problems(urban, architectural). 549
process emissions................... 553
process on pattern................... 399
process on process................. 399
procumbent pearlwort.............. 386
profile key................................. 271
profiles(ideal typical
formations) 379
prognoses(categorisation)....... 444
programme of
requirements(assigned, additional(intention of designer)) 636
projection|identification............. 627
projects.................................... 419
projects(consequences(small,
large)) 477
properties of soils.................... 324
property.................................... 510
proposals................................. 659
protection of plant species....... 364
Protocol for follow-up
investigation................................. 585
Protocol voor het nader onderzoek 579
Protocol voor het oriënterend onderzoek 579
prototypical plans
influenced by the ground 348
provincial highway................... 249
pruners..................................... 400
pruning....................................... 98
pruning hedges........................ 104
pruning methods......................... 89
prunus subhirtella
‘autumnalis’... 84
psychiatric disorders............... 466
psychiatric hospitals................ 534
pteridophyta............................. 355
public and private
sector(target) 236
public and private spaces........ 466
public disclosure...................... 236
public facilities.......................... 524
public green surface................ 516
public health facilities............... 534
public housing
policy(hygiene). 405
public paved surface............... 516
public pavement............... 265, 266
public sector(reform)............... 238
public space............................. 514
public space(light)...................... 48
public space(maintenance)...... 513
public transport(stops)............. 473
Public Works............................. 493
public works time schedule...... 299
pumping and drainage systems 210
pumping station........................ 338
pumping stations.............. 224, 225
pumps....................... 214, 221, 222
puppet theatre.......................... 538
purification techniques............. 589
purification works.................... 205
purple dead-nettle...................... 62
pyramid..................................... 519
pyroxeen.................................. 336
pyroxene.................................. 336
pyroxenes................................ 336
quadrangulation........................ 488
quality....................................... 367
quality standards(ground, water, air) 551
quality(%built-up surface)........ 517
quality(form, structure,
function) 517
quality(space, time).................. 439
quality(variation)....................... 667
quarter...................................... 369
quarter(neighbourhood)........... 140
quartz....................................... 336
Quaternary............................... 358
questions.................................. 659
R.W.D....................................... 344
race.................................. 247, 249
races................................ 225, 258
radial......................................... 277
radial lines................................ 282
radiation.............................. 48, 558
radio and television.................. 295
radius of awareness....... 621, 622
raft bridge................................. 261
ragged and soft(design
tools(planting)) 72
railway network....................... 494
railway network(density)......... 525
railway station.......................... 286
railways................................... 286
rainfall....................................... 210
rainwater.................................. 305
rainwater discharge................. 344
raise the level of the
ground.... 454
raising....................................... 485
raising with sand...................... 339
ramps....................................... 649
Randmeren....................... 434, 437
random walk............................. 188
Randstad.................................. 408
Randstadgroenstuctuur........... 420
rank size................................... 526
rape............................................ 62
rare plant species(urban,
national) 407
rareness........................... 368, 392
rareness and replaceability...... 494
rareness(artefacts)................. 429
rareness(grain)........................ 429
rarified zone............................. 475
rarified zones................... 474, 476
rarity......................................... 421
rarity resolution........................ 429
rarity resolution........................ 430
rarity(criterium)......................... 429
rarity(distance to the
nearest x examples) 429
rate of growth(planting)............. 74
rats........................................... 366
raw materials pipe lines........... 296
RE............................................. 584
real estate price(water’s
edge) 642
receding(design
tools(planting)) 72
recessed floors........................ 649
recesses(façade).................... 649
reclaimed land.......................... 205
reclamation....................... 208, 221
reclamation and drainage of
polders 226
RECLUS (1989)........................ 479
recognisability(species)........... 357
recognition 368, 625, 626, 627, 628, 665
recognition|suprise................... 627
recovery................................... 440
recreation(open space(size,
altitude)) 409
rectangular grid........................ 278
rectangular patterns................... 18
rectangularity........................... 250
recurrence time................ 212, 213
recurrence time(calculation)... 213
recurrence time(floods)........... 210
red legend................................ 251
red list....................................... 365
Red List.................................... 438
red oak..................................... 377
red shank................................... 63
red-listed birds......................... 438
red-listed species..................... 433
redox........................................ 562
redox potential.......................... 561
reduction into the average....... 400
reduction of diversity............... 665
reduction to the average.......... 399
reed marsh............................... 372
reed morass............................. 436
reed vegetation........................ 438
reference environment............. 458
reference images..................... 637
reference
situation(deviation).. 111
reference(choice).................... 111
reference(internal,
external).... 443
reference(nature(historical(climatic
change))) 443
references(change)................. 111
refinary....................................... 13
reflection(solar power).............. 22
reflexive judgements................ 368
refrigerator................................. 19
refuge hill.................................. 220
regional choice of
location(wind) 111
regional density........................ 370
regional highway.............. 247, 249
regional highways.... 190, 191, 272
regional networks.................... 280
regional policy.......................... 575
regional rarity........................... 430
regression(polynome).............. 151
regular pattern............................ 81
regulation......................... 401, 402
regulation theory.............. 398, 401
regulation(plot)........................... 46
regulators................................. 402
Reh........................................... 639
Rehbock laboratory.................. 216
Reichow................................... 281
relamations............................... 496
relation theory.......................... 398
relief......................................... 344
relief(frequency)...................... 656
remediation intervention
values 587
remediation techniques............ 589
removals................................... 532
repeating details....................... 632
repetition................................... 628
replaceability............................ 439
replacebility...................... 392, 421
representing existing areas..... 503
reproduction factor.................. 464
reproduction(water, vegetatively) 355
reproductive
organs(recognisability) 357
reptiles.............................. 353, 389
requirements for human
life(direct, indirect) 549
research(diminishing
returns).. 427
research(urban,
architectural). 549
residential area per
inhabitant.. 502
residential areas............... 263, 501
residential areas(industrial
areas) 569
residential courts........................ 82
residential parking.................... 276
residential paths............... 272, 275
residential street............... 263, 265
residential streets............. 264, 272
residential surface................... 514
residential walk........................ 249
residents per continent............ 529
resistance................................ 666
resistance(biological)............... 426
resistance(poison)................... 565
resolution.................................. 429
resolution(drawing).................. 637
resolution(frame, grain)............ 430
resonance................................ 159
respect from the public.............. 82
responsibility of the
designer... 547
responsibility(species)............. 365
restaurants............................... 545
retailers.................................... 543
retention................................... 214
retention basins........................ 214
retire......................................... 626
Reuzer(1999)........................... 479
reversible................................. 156
revolutions(natural history)...... 355
Rhine 169, 196, 206, 209, 211, 219, 479
Rhine axis................................. 476
Rhine branches........................ 209
Rhine canalisation.................... 207
Rhine river basin..................... 170
Rhine(catchment area, precipitation,
evaporation) 170
Rhine(discharge, variation)...... 171
Rhine(normal probabilities per discharge class) 212
Rhine(Old)........................ 483, 491
Rhine(potential vegetation structure and land use) 215
Rhine(Source)......................... 171
rhododendron....................... 83, 84
rhododendron(acid soils)........... 85
rhythm(design
tools(planting))... 72
richness in species(urban)...... 454
ride................................... 285, 627
ride a bike................................. 627
Riemsdijk and NOBO (1999)..... 367
Riemsdijk, 1999......................... 400
riet.............................................. 61
right angles............................... 250
Rijkswaterstaat................ 219, 238
Rijncommissie Koblenz............. 214
rijvloer....................................... 259
RIN............................................ 395
risc-cover for life(variety)........ 666
risk assessments..................... 587
risk calculation.......................... 426
risk coverage of
life(biodiversity) 352
risk coverage(diversity)........... 636
risk factors for tunnels............. 298
risk management...................... 558
risk of transported material...... 288
risk(accepted).......................... 212
risk(risk avoidance).................. 426
risk(species(extinction)).......... 365
risk-cover for
life(diversity)..... 366
risks.................................. 558, 567
risks of flooding........................ 173
risks of lowlands(water
storage) 236
risks of non-delivery.................. 34
river.......................... 247, 249, 273
river accompanying
vegetations 372
river county.............................. 375
river discharges....................... 208
river floods............................... 205
river forelands.......................... 378
river formation.......................... 323
river section(length)................. 192
river(drainage.exe).................. 188
river(formation)........................ 380
river(low land, cross section).. 215
river(morphology(transported
material)) 194
river(ownership)...................... 209
riverbed(widening)................... 214
rivers................ 169, 191, 321, 330
rivers(random walk)................. 190
rivers(regulated,
normalised, canalised) 205
RIVM................................. 573, 575
RIVM (2001)............................. 550
RIVM(2000)................................ 27
RIVM(2001).............. 374, 481, 483
RIZA......................................... 441
road.................................. 162, 249
road freight haulage
companies 545
road network(density)............. 525
road profiles............................. 266
road salting................................. 83
road system 1800.................... 206
road(district,neighbourhood,ensemble) 140
road(support base).................. 525
roads(district)........................... 190
roads(length)............................ 525
roadway................................... 263
roadways................................. 265
Robeco building in Rotterdam..... 83
robertskruid................................ 65
robustness............................... 442
robustness(flexibility, diversity) 636
rock.................................. 312, 313
rock salts.................................... 34
rock sequences....................... 316
rock textures............................ 319
rocks........................................ 335
rode kornoelje........................... 376
rode lijst.................................... 364
Rodenacker, 1970................... 402
Roermond................................. 205
Rokkeveen................................ 123
rolbrug...................................... 261
roll bridge.................................. 261
roller skates.............................. 623
Roman
sites................................ 60
Rome........................................ 348
Romein, J.M. (1938,1971)......... 475
roof of public space................... 47
room................................. 623, 626
Room for the river.................... 215
Room for the river’................... 216
Room for the Rivers
programme 209
room(polarisation(sensoric,
motoric)) 633
root ball....................................... 89
root ball(tree).............................. 86
rose............................................ 84
rosebay willowherb........... 63, 389
roses.................................... 67, 84
Ross Ashby (1957, 1956)........ 398
Ross Ashby, 1957, 1965......... 395
Rotterdam 206, 208, 296, 307, 308, 476, 505, 528
Rotterdam(Robeco building)....... 83
roughness................................ 107
roughness based
calculations(wind) 136
roughness classes.................. 112
roughness island.............. 129, 130
roughness(bed(river))............. 201
roughness(ground(standard)). 112
roughness(homogenuous
undirected) 140
roughness(wind)..................... 122
roundabout............................... 255
roundabouts..................... 255, 256
rowan....................................... 376
rowan(coastal).......................... 84
rowan(nutrient-rich peat)........... 85
RPD (1966)....................... 369, 370
RPD (1983)............................... 370
RPD(1983)........................ 476, 642
RPD(1988)................................ 476
RPD(1996)................................ 476
RPD, 1966................................. 397
rubion....................................... 378
ruderaal...................................... 62
ruderals............................ 371, 389
Ruhr area................................. 476
ruilverkaveling.......................... 494
rules......................................... 627
rum cherry................................ 377
rumex hydrolapathum............... 388
run.................................... 623, 626
run|compete.............................. 627
Runcorn.................................... 281
Runhaar(1987)......... 385, 387, 392
runoff....................................... 169
runoff coefficient..................... 306
runoff(catchment areas).......... 169
runoff(slope)............................ 188
rural.......................................... 418
rural
areas(arrangement(wind)) 111
rural estates............................. 639
Russell(1919)........................... 667
rust stains................................ 329
ruwe berk................................... 64
RWS......................................... 205
RWS, 1984....................... 235,
236
RWS, 1998............................... 223
S+N+S(2001)............................ 421
Saalian...................................... 358
safety....................................... 268
safety standards for floods...... 213
sagging..................................... 338
salers....................................... 544
salicion..................................... 378
saline plant communities........... 482
salinisation(irrigation)............... 401
salinity...................................... 386
salt............................................ 553
salt intrusion............................. 219
salt marsh................................. 433
salt proportion.......................... 386
salt spray particles........... 556, 557
salt vegetations........................ 372
salt water................................. 327
salt water intrusion.................. 208
salt(road).................................... 83
salt-marsh vegetation............... 484
salts of heavy metals............... 588
sambuco-berberidion............... 378
sanction possibilities................ 552
sanctuaries.............................. 438
sand................. 326, 393, 577, 623
sand delivery per 'axe'............. 340
sand fractions.......................... 326
sand supply.............................. 219
sand supply(North Sea beaches) 219
sand transport(North Sea)....... 219
sand(local inland movement).... 220
sand(use)................................. 333
sandy deposits......................... 205
sandy ground........................... 579
sandy grounds......................... 247
Sangster(1987)........................ 565
satellite connections................. 295
saturation of soil....................... 327
saturation(vapour)................... 166
Saurian Age..................... 355, 356
saurians................................... 357
saurians(extinction)................. 355
saw-wort................................. 400
SBI............................................ 444
scale articulation...................... 369
scale factor(traffic
calculation) 474
scale falsification..................... 642
scale paradox.......... 368, 453, 668
scale parameters..................... 114
scale range.............................. 369
scale sensitive concepts......... 368
scale(architecture,
politics, ecology) 443
scale(confusion)...................... 369
scale(levels of)........................ 399
scaup....................................... 436
scaup duck............................... 438
scenarios(energy supply).......... 27
Schaminee(1996)..................... 384
Schaminée(1998, 2001)... 441, 444
Schaminee, et al., 1995............ 395
Scheldt............................. 169, 217
Scheldt-Rhine canal................. 218
Schenk(1999)........................... 479
scherpe boterbloem................... 65
Schiedam.................................. 341
Schiermonnikoog...................... 527
schijfkamille.............................. 387
schipbrug................................. 260
Schiphol.................... 112, 238, 439
Schiphol tunnel......................... 297
schizophrenia........................... 466
Schlicher van Bath(1960)........ 462
school............................... 623, 626
schools..................................... 535
schoorbrug....................... 259, 260
Schoorl..................................... 220
schor........................................ 497
schuiven................................... 204
Schumpeter dynamics.............. 662
Schumpeter-economy.............. 367
science and art........................ 659
science(optimizing probable
effects) 668
scientific education.................. 536
scots pine................................. 377
screen(hedges)............... 101, 103
screening(degree)..................... 68
screening(design
tools(planting)) 71
screening(planting).................... 69
sculptural effect....................... 652
sea........................................... 247
sea and land winds.................. 560
sea bed polders....................... 324
sea buckthorn............................ 84
sea level rise............................ 208
sea trade.................................. 206
sea water................................. 327
sealevel rise and
subsidence expected until 2050 211
season fluctuations of
rivers(snow and ice in mountains) 170
seasonal maximum outside...... 436
seating shelter(hedges)........... 103
second law of thermodynamics 13, 399
secondary education............... 536
sediment................................... 194
sedimentary rock...................... 316
sedimentary rocks.................... 318
sedimentation........................... 323
sedimentation deposits............. 359
seed dispersion........................ 389
seed-bearing plants................. 355
seepage........... 210, 330, 332, 342
Seepage................................... 327
seepage areas......................... 331
seepage water......................... 330
seepage(phosphate, iron)........ 454
seepage(saltwater,
freshwater, brackish water) 330
seesaw.................................... 621
segmentation(façade(vertical,
horizontal)) 649
segmenting(morphological
reconstruction) 632
Seine........................................ 323
selection.................. 401, 424, 467
selection and regulation.......... 402
selector.................................... 467
selectors.................................. 401
selectors(................................. 401
self-sufficiency........................ 367
semantic conditional
sequence 661
semantic Venn diagram............ 659
semi-public spaces.................... 82
senses......................................... 7
sensoric deprivation................. 467
sensoric polarity....................... 633
separate sewage system........ 305
separating and connecting...... 402
separating flows....................... 404
separation................................ 399
separations in space and
time. 467
separations(connections)........ 393
September 23rd.......................... 36
Serratula Tinctoria.................... 400
service economy...................... 476
service vehicles....................... 263
service vehicles/24 hour
intensity 272
service visits/inhabitant............ 272
set-theory................................. 659
settlement of the ground.......... 338
settlements on sandy soils....... 489
sewage.................................... 303
sewage pressure pipelines..... 288
sewage system 299, 303, 304, 306
sewage systems..................... 294
sewage water......................... 294
sewage(autarkic systems)...... 304
sewer......................................... 88
sewer system.......................... 343
sewerage pipes....................... 288
Seyp, van de and van Dijk........ 655
shade(tree)................................ 75
shadow.......................... 43, 44, 45
shadow plan.............................. 48
shadow(trees)........................... 47
shadows(length)........................ 46
shelter|corners......................... 627
shepherd’s-purse....................... 62
shepherd's-purse..................... 387
ship bridge................................ 260
shipping traffic(locks).............. 232
shops............................... 544, 623
shortest path............................ 277
shrinking of the soil.................. 333
shrub bed(hedges).................. 103
shrub distance........................... 80
shrub planting............................. 76
shrub planting(occasional
trees) 76
shrubs........................................ 67
shrubs(sun-loving)..................... 76
shrubs(water)............................ 85
side façades............................ 268
side span.................................. 259
side-effects of activities.......... 550
sidewalks................. 263, 266, 267
sideways................................. 190
sieve analysis.......................... 443
silicate...................................... 589
siliceous sea weeds................ 432
silt............................. 393, 436, 577
silt fractions.............................. 326
siltfractie................................... 326
silver birch.................................. 64
single-family households.......... 530
single-leaf bascule bridge........ 260
single-person households........ 533
sinking areas.............................. 87
siphons..................................... 253
sit 626
site preparation........................ 337
site preparation(methods)........ 338
site preparation(polder)............ 338
site
preparation(purification).... 593
siting of plants............................ 82
sitosterol................................... 388
Sitte.................................. 255, 277
Sitte (1889)............................... 255
sitting area(hedges)................. 102
skateground............................. 623
skeletons(chalky)..................... 355
sketch....................... 430, 626, 637
sky dome.................................... 39
slagenlandschap...................... 497
slide.......................................... 623
slik............................................ 497
Sloedam.................................... 218
Sloep........................................ 400
Sloep, 1983.............................. 398
slope......................................... 257
slopes....................................... 261
slopes(road)............................. 257
sloten........................................ 225
slotted flags................................ 87
slowing down the cars............ 264
Slufter on the isle of Texel...... 221
slufters..................................... 221
sluice........................................ 232
sluices...................... 206, 221, 231
sluices(capacity)...................... 220
sluices(one way)............. 224, 225
sluices(open, closed............... 402
Sluis.......................................... 209
small ditch................................. 247
smeerwortel............................... 63
smog......................................... 560
sneeuwklokje............................. 64
Snep(2000).............................. 442
snow drop.................................. 64
snowdrop................................... 83
Snozzi.............................. 506, 507
SO2.................................. 554, 555
soap bubble.............................. 250
social control...................... 82, 466
social
differentiation(administration, culture, economy) 635
social diversity......................... 425
social life.................................. 663
social possibilities..................... 661
socialists.................................. 469
societal conditions.................... 546
soft........................................... 626
soil.................................... 313, 577
soil and ground......................... 577
soil complex.............................. 393
soil complex(ecological
groups) 392
soil contamination............. 324, 332
soil contamination(follow-up
investigation) 585
soil
contamination(protocols, methods) 576
soil formation............................ 325
soil fraction............................... 326
soil
fraction diagram................. 327
soil maps.................................. 377
soil mechanics.......................... 326
soil particles............................. 590
soil pollution.............................. 576
soil pollution (forms,
industry).. 588
soil profile................................. 393
Soil Protection Act.................... 576
Soil Protection Guidelines......... 579
soil quality................................. 576
soil recovery............................ 589
soil scienc................................ 312
soil science.............................. 324
soil slurry reactors................... 591
soil spray.................................. 386
soil structure............ 326, 382, 393
soil types.................................. 326
soil types and average
annual runoff 170
soil unit..................................... 393
soil unit(cooperation,
competition) 392
soil vapour................................ 579
soil vapour extraction............... 591
soil vapours.............................. 592
soil water......................... 327, 578
soil(draining an area)............... 222
soil(functions).......................... 577
soil(open, closed)....................... 86
soil(permeability)...................... 228
soil(spray, digged, treaded)..... 386
soil(vibration(heavy
traffic))...... 86
soils of The Netherlands............ 85
soils(plant diversity)................... 66
soils(properties, use,
management) 324
solar capacity............................. 36
solar cell..................................... 20
solar cells................................... 20
solar cells(costs)....................... 21
solar constant...................... 22, 35
solar energy(slow
development) 31
solar images............................... 47
solar power(global).................... 22
solar time.................................... 41
solitaires..................................... 83
solitary trees.............................. 91
solubility.................................... 590
solvents.................................... 588
Sonsbeek
paviljoen (Arnhem). 394
soot.......................................... 553
sound....................................... 154
sound(impression)................... 158
sound(intensity)....................... 156
sound(power).......................... 156
sound(spectrum)...................... 159
sound(travel speed)................. 155
sound(tube).............................. 155
soured forests......................... 389
South Flevoland........................ 438
South garden.............................. 47
South gardens.......................... 268
South Limburg(formation)......... 381
South-Limburg.......................... 496
southwest wind....................... 559
South-Western winds.............. 109
Space Mate.............................. 517
spaces(boundaries)................. 394
spaces(expanding(green))........ 88
spaces(shrinking(red,
brown)).. 88
space-time dilemma(size,
distance to residential area) 410
spacious effect........................ 277
span(bridge)............................. 260
sparrows................................. 366
spatial and temporal variation. 398
spatial
composition(streetscape) 88
Spatial Planning Key
Decision.. 215
spatial planning(first
policy document) 237
spatial
planning<>water management 237
spatial plans(water
management) 241
spatial policy............................. 418
spatial use................................ 501
specialisation function.............. 475
specialisation(regional).... 475, 477
specialised spaces.................. 470
specialising............................... 445
specialist species..................... 485
specialists........................ 388, 509
specialization............................ 367
species..................................... 365
species suppressed by other
species 77
species supressing other species 74
species(choive)......................... 94
species(determined
beforehand) 73
species(extinction)..................... 23
species(extinction)..................... 31
species(new(evoliotion))......... 352
species(planting)........................ 73
species(rare)........................... 368
species(threatened)......... 389, 430
species(urban presence)........ 407
species-specific environment.. 546
specific
cross-section(channel) 185
specific ecological groups....... 387
specimens(marginal)................ 366
speed(design).......................... 479
speed-specialised lines............ 474
speenkruid.................................. 64
sphagno-alnion......................... 378
spherical m2............................... 49
spherical radius.......................... 49
spiked water-milfoil.................... 61
spindle........................................ 84
SPKD........................................ 215
spoonbill................................... 439
spoonbills................................. 436
spores...................................... 355
sport and violence.................... 467
sports facility............................ 538
sprawl........................................ 18
sprawl(urban).......................... 369
spray cans............................... 556
spring(flowering)....................... 83
spruce........................................ 48
squares(façade margins)........ 655
squares(through-traffic).......... 654
sr 49
St. Elizabeth flood..................... 492
St. Petersburg.......................... 653
Stadtholders............................. 492
stage in the lifecycle................ 425
staghorn................................... 355
Standaardverkaveling.exe....... 265
standing whirl........................... 152
Staphorst.................................. 466
startbanen................................ 122
state of dispersion................... 369
static character(planting)........... 73
station stops............................. 473
stationers................................. 544
stations..................................... 286
Statistical Pocket Book............. 523
stature...................................... 624
steam engine...................... 31, 493
Stedenland perspective........... 477
Stedenland perspective (VROM
1998) 478
Steegh(1985)... 487, 488, 489, 491
Steekelenburg(2001)........ 367, 481
Steenbergen......................... 9, 639
Steenbergen(1995).................. 639
steering.................................... 399
stellaria media......................... 389
Stelling van Amsterdam.... 206, 420
steppe grasslands................... 400
stereoscopic vision.................. 458
Stevens method....................... 202
Sticht.Wetensch.Atlas_v.Nederland
(1985) 55
Sticht.Wetensch.Atlas_v.Nederland(1987) 484
stinging nettle............................. 66
stocks(energy)........................... 33
stollingsgesteente.................... 335
stop distance............................ 285
stops........................................ 277
storage
capacity(electricity(conversion)) 34
storage(concentration).............. 18
storeys..................................... 519
storm........................................ 107
storm systems.......................... 318
straatgras................................. 387
Strahler............................. 189, 190
straight and hard(design
tools(planting)) 72
strandwal................................. 497
strange people......................... 623
strata........................................ 316
strategies................................. 550
strategies for survival...... 389, 391
stratification.............................. 561
stratosphere............................. 559
strauszbridge........................... 260
stream.............................. 247, 496
stream valley............................ 496
streamlands.............................. 639
streekdorp................................ 497
street 162, 247, 249, 262, 263, 623, 626
street furniture......................... 649
street patterns.......................... 190
street profile............................. 299
street profile().......................... 631
street village............................. 489
street(image)............................ 629
street(polarisation)................... 634
streetcorners........................... 268
streetlamps................................. 48
streets...................................... 631
streets(planting(size))................ 93
streetscape................................ 88
stress tolerators....................... 371
stress-tolerators.............. 389, 390
stretch...................................... 250
stretching................................. 252
Strickler-Manning...................... 201
string(sound)............................ 156
structural quality....................... 517
structuralist position................. 663
structure................................... 399
structure ecology..................... 401
structure(divisions,
connections) 632
structure(form, function).......... 632
structure(legend)..................... 663
structure(nearness,
infrastructure) 632
structure(parts, whole)............ 632
structure(planting)...................... 68
Structure(planting)..................... 71
structure(polarity).................... 633
structure(separation,
connection) 401
Studio PRO............................... 652
studios...................................... 267
study proposal......................... 646
stuwen..................................... 204
stuwwal................................... 496
Stuyvesant, P........................... 475
Subatlanticum............................. 60
Sub-Boreal........................... 59, 60
subsidence expected until
2050 211
subsidence(west of the
Netherlands) 211
suburbs.................................... 425
succession............... 377, 382, 440
succession of visual effects..... 73
succession series.................... 441
succession(artificial).................. 78
succession(interrupted)........... 437
sulphate........................... 556,
589
sulphate reduction.................... 562
sulphates.................................. 589
sulphur dioxide......... 553, 554, 555
sulphuric acid................... 553, 555
summer temperatures.......... 50, 51
summer time............................... 43
summer(flowering)..................... 84
summertime.......................... 41, 42
sun..................... 35, 166, 626, 627
sun bows................................... 39
sun(energy
contribution(national)) 31
sunheight.................. 40, 42, 43, 44
sunlight....................................... 35
sunlight(foliage).......................... 81
sunrise..................... 37, 38, 43, 46
sunset...................... 37, 38, 43, 46
superposition............................ 251
supply channels....................... 191
support base............................ 539
supposition(tacit)...................... 658
suppression(species)................ 77
surface area(soil particle)........ 561
surface sources.............. 560, 561
surface temperatures................ 53
surface(light).............................. 49
surprise............ 368, 625, 626, 628
surrounding infrastructure....... 272
survival..................................... 371
survival journeys...................... 407
survival strategies.................... 393
survival value........................... 634
survival(chance)...................... 366
survival(tolerance)................... 366
suspended span...................... 259
suspender................................ 259
suspension bridge.................... 260
suspension cable..................... 259
sustainability............................. 367
sustainable development.. 570, 668
Susteren (2006)....................... 511
sweet chestnut.......................... 84
sweet vernal-grass................. 387
swell water.............................. 578
swimming bath......................... 538
swing bridge.................... 259, 260
swinging................................... 264
swings..................................... 621
sycamore............... 83, 84, 88, 376
sychronisation.......................... 382
symbiosis......................... 388, 393
symmetric street profile............ 631
synaesthesy............................ 621
Synbiosys................................ 441
synchronisation........................ 389
synecological classes.............. 383
synecological orders................ 383
synecological typology............. 374
synecology............... 371, 391, 441
synthetic judgements a
priori... 659
system characteristic functions 633
system dynamics ecology........ 391
Systemrationalität............. 368, 668
systems ecology...................... 458
T crossings.............................. 255
tactics....................................... 550
tailoring(morphological
reconstruction) 632
tanning industry........................ 588
tansy.......................................... 63
Tanthof..................................... 342
taps.......................................... 402
tare decreasing the density..... 521
tare space for urban
facilties... 512
tare surface..................... 499, 500
target species.......................... 442
target types.............................. 396
target value(emissions)............ 567
task division(interregional)....... 474
Tauern tunnel........................... 297
Tax(1989)......................... 427, 430
taxonomy.......................... 352, 357
taxonomy(plant)....................... 357
taxonomy(species).................. 444
T-crossings.............. 255, 256, 277
technical conditions.......... 547, 661
technical ecology..................... 549
Technical ecology................... 403
technique.................................. 458
technique(raw
materials(ecology)) 644
technological innovations......... 464
telephone network................... 294
telephone networks................. 288
temperature...................... 626, 627
temperature data(wind)........... 118
temperature increase............... 423
temperature(wind)................... 138
temperatures(continental).......... 50
temperatures(global).................. 50
temperatures(local).................... 53
temperatures(natonal)................ 51
temporal variation.................... 398
tension...................................... 628
tenures..................................... 489
Terlouw.................................... 210
terminal structures................... 220
terp................................... 220, 487
terp landscape......................... 497
terp villages.............................. 487
terps................................. 205, 489
terrace...................................... 626
territory(hedges)...................... 102
Terschelling.............................. 220
tetanus..................................... 554
textile cleaning service............. 588
textile industry.......................... 588
texture(planting)......................... 68
The Hague 206, 308, 454, 476, 528
The World commission
environment and development(1990) 367
theatre...................................... 538
theories(genealogy)................. 404
thermal soil purification............. 590
thermal stability......................... 590
thermodynamics....................... 399
thermodynamics(laws).............. 13
thiols......................................... 554
Third World(fertility).................. 466
tholos................................ 629, 630
Thomson(1961)............................ 7
thorny bushes............................ 82
three-dimensional pollution
models 561
threshold values............... 567, 568
through lounge......................... 633
throughway.............................. 249
thrust........................................ 259
Thünen(1921)........................... 485
ticket......................................... 623
tidal computations..................... 217
tidal creeks............................... 218
tidal differences....................... 209
tidal zone.................................. 208
tide............................................ 221
tide at sea................................. 205
tide(litoral drift)......................... 209
tiles........................................... 623
time..................................... 43, 468
time equalization......................... 42
time utilisation........................... 531
time zone.................................... 43
time(planting).............................. 73
time-segment approach............ 463
time-use.................................... 470
timezone..................................... 42
Timmermans(2000)................... 442
tin 589
tipping....................................... 589
Tivoli......................................... 348
Tjallingii (1996).......................... 366
Tjallingii, 1996................... 403, 404
TKA.......................... 445, 506, 507
TKA(2001)................................ 421
TLV........................................... 569
to escape adult movements..... 627
to learn..................................... 627
toadstools......................... 352, 432
tochten..................................... 225
Tokyo-Yokohama..................... 510
tolerance.................................. 366
tolerance to frustration............. 467
tolerance(classes)................... 387
tolerance(drawing).................. 637
toll system................................ 492
toluene.............................. 554, 591
tones(instrument)..................... 159
toolmaking................................. 458
tools.......................................... 458
topographic history.................... 55
topographic maps..................... 598
Topographic Survey................. 597
topographical maps.......... 247, 598
toren......................................... 259
tormentil...................................... 65
tow-barge canals..................... 493
tower........................................ 259
towing boats............................ 475
town................................. 369, 510
town edge design(wind).......... 136
town quarter............................ 510
town tare.................................. 510
town(form(wind)).................... 111
town(polarisation(sensoric,
motoric)) 634
townhall.................................... 476
towns(climate)......................... 452
toxicology................................. 565
trade(diversity)................. 367, 666
tradition-directed...................... 468
traffic........................................ 626
traffic and
transport(rail-road-water-pipeline-transmission-telecom) 237
traffic calming........................... 282
traffic lights.............................. 401
traffic load................................ 162
traffic models........................... 471
traffic safety(hedges).............. 101
traffic space............................. 262
traffic(noise(calculation))......... 161
trajectory models(air
pollution). 560
tram.......................................... 249
tram tunnels.............................. 299
tramway................................... 285
transbordeur............................ 260
transformers............................ 287
transitional zone....................... 131
transmission............................. 558
transparency of
infrastructure plans 238
transparency(planting)......... 68, 69
transparent wall of trees........... 92
transplanting trees............... 89, 94
transport system...................... 525
transport tunnels...................... 299
transport(ship)......................... 206
transportation(high
tech(urban capacity)) 423
transporter bridge............ 259, 260
travel costs.............................. 471
travel resistance...................... 471
travel resistance(distance,
commodities) 474
travel uitility function................. 471
travel utility function................. 479
travel utility(periodic
infrastructure) 473
travelling time............................ 471
travelling times.......................... 468
treading.................................... 485
Treaty of Utrecht...................... 492
tree........................................... 190
tree corridor............................... 88
tree distance........................ 80, 95
tree grille..................................... 87
tree layer.................................... 75
tree layer(occasional
shrubs).... 75
tree like connection.................. 191
tree pit........................................ 87
tree planting(shrub margin)........ 76
tree rhythm................................. 91
tree rows................................... 91
tree screen................................. 92
tree size..................................... 89
tree size(price ratio)................... 89
Tree Structure Plan
Amsterdam. 88
tree trunk(protected).................. 87
tree wall..................................... 92
tree(asymmetrical crown).......... 99
tree(crown raising heights)....... 99
tree(crown raising).................... 99
tree(planting distance)......... 96, 97
tree(size classes)...................... 88
trees................................... 67, 623
trees (oxygen)........................... 87
trees planted(period).................. 89
trees(climatic conditions)........... 67
trees(closed screen, wall)......... 96
trees(minimum distances).......... 89
trees(planting distances)........... 89
trees(row).................................. 97
trees(rows)................................ 89
trees(transplanted).................... 89
trees(water)............................... 85
trekvaart................................... 206
trench............................... 247, 249
trenches........... 221, 225, 247, 258
trenches(distance).................. 228
trendline.................................... 529
trias economica’....................... 635
trias politica.............................. 635
trias urbanica................... 476, 635
Triassic..................................... 316
trichloroethylene............... 589, 591
trichloro-phenol........................ 555
triglyphs.................................... 630
trodden land............................. 452
trolley........................................ 259
Tromba..................................... 250
tropical rain forest.................... 458
tropics........................................ 35
troposphere.............................. 559
trough arch bridge............ 259, 260
truncation orders...................... 189
truncing river systems............. 188
trussed arch............................. 259
tube(sound).............................. 155
tubifex...................................... 432
tufted duck............................... 436
tufted ducks............................. 436
tuiverankering........................... 259
tulip............................................. 83
Tummers(1997)................ 417, 503
Tummers, L............................... 341
tunnel........................................ 261
tunnels.............................. 287, 296
tunnels for rail transport........... 297
turbine principle........................ 277
turn distance............................ 271
turning circle............................. 263
Twente............................. 494, 496
twin phenomena....................... 395
twinphenomenon...................... 394
two-dimensional pollution
models 561
type.......................................... 637
type(collage)............................ 637
typology............................ 637, 653
typology(nature)....................... 444
tyria jacobaeae......................... 388
Tzonis(1989)............................ 630
Udo de Haes............................. 546
Uiterwaarden
Maas.................. 210
Uiterwaarden
Rijn..................... 210
uitkragende zijoverspanning.... 259
ulmion....................................... 378
ultrasonic.................................. 154
ultra-violet rays........................ 556
ultraviolet sunlight..................... 107
UN 1992.................................... 570
unbuilt/floor............................... 518
underground............................. 249
underground distribution
centres 299
underground infrastructure...... 308
underground installation........... 288
underground material storage.. 299
underpass................................ 259
under-reamed living
platforms.. 340
unhardened urban areas......... 343
uniformitarianism...................... 315
uniformity(planting)..................... 69
unions............................... 383, 392
unions(synecological).............. 383
unique....................................... 429
uniqueness............................... 428
uniqueness'.............................. 366
uniqueness(10 000km,
1000km, 100km) 428
unit............................................ 429
United States of The
Netherlands 475
Universiteit van
Utrecht(1987)... 56
University of Nijmegen.............. 395
University of Utrecht (1987)....... 58
unpredictability......................... 442
upright posture......................... 458
upright(design
tools(planting))... 72
uranium(environmental costs).... 30
urban areas(groundwater
level) 223
urban canal.............................. 249
urban centre............................. 418
urban crowd pullers................. 518
urban design(health objectives) 426
urban design(hygiene)............. 405
urban details(wind).................. 111
urban
differentiation(administration, culture, economy) 635
urban environment................... 526
urban functions........................ 627
urban growth........................... 422
urban highway......................... 249
urban highways....................... 272
urban intensity.......................... 518
urban island 266, 267, 269, 510, 520
urban island density30m.......... 520
urban landscapes.................... 642
urban outskirts......................... 418
urban sprawl.............. 18, 370, 408
urban units............................... 392
urbanisation.............................. 466
urbanisation
alternatives(use of time) 468
urbanisation(awarenss of
problems) 237
use and management of soils.. 324
use of time................................ 468
use(intensity)........................... 365
use(spatial).............................. 501
U-shape.................................... 268
utility companies....................... 534
Utrecht...... 223, 280, 476,
497, 528
Utrechtse Heuvelrug................ 332
Uytenhaak, R.H.M. (2005)........ 521
V&W......................................... 437
V&W (2000)............................. 236
V&W(1998)...................... 423, 575
V&W(2000).............. 423, 424, 575
V&W, 1998............................... 236
V&W, 2000............................... 236
vacant spaces......................... 649
vaccinio-quercion..................... 378
vacuum..................................... 106
vakwerkboog........................... 259
valbrug..................................... 261
valley forms.............................. 322
valuation chart.......................... 443
valuation
charts(suppositions). 444
valuation maps......................... 443
value of natural areas.............. 494
value(experiencial,
practical, functional, future, survival)) 634
value(shape, structure,
function) 634
value(term(short, medium,
long)) 634
values(incomparable)............... 645
values(partial, surplus)............ 443
valuing an ecosystem.............. 439
valuing(flora, fauna, scale)...... 428
valuing(rarity,
replaceability).... 439
valves....................................... 402
vandalism................................... 89
vans......................................... 263
vans of police........................... 263
vapour saturation..................... 166
variable(categorisation)........... 400
variation........................... 398, 664
variation(planting(horizontal,
vertical)) 68
variation(wanted(character,
scale)) 428
variety(risc-cover for life)........ 666
vascular disease...................... 466
vascular plants......................... 355
vault(road(trees))....................... 95
Vedel(1974)......................... 57, 58
Veerse Gat............................... 218
Veerse
Meer............................ 210
vegetation area(Middle European, West
European) 373
vegetation(Europe(map))......... 436
vehicles.................................... 263
vehicles/24 hour intensity........ 272
vehicles/hour intensity............. 272
veldspaat.................................. 336
velocity............................. 12,
264
velocity profile.......................... 130
velocity(wind(potential)).......... 112
velocity(wind(probability))....... 115
velocity(wind).......................... 109
Veluwe............. 332, 358, 437, 449
Veluwe(precipitation)............... 168
Veluwe-Arnhem-Nijmegen....... 638
Venice...................... 518, 647, 653
Venn diagram........................... 659
ventilation losses(wind)........... 118
ventilation(wind velocity)......... 110
Vera(1997)............................... 436
Vera, 1997................................ 400
Verberk(1980).......................... 565
Verheijen.................................. 354
Vermeulen and Jong(1985)...... 117
Vermeulen(1983).......... 113, 134
Vermeulen(1985)..................... 110
Vermeulen(1986)..... 110, 130, 134
vertebrates....................... 353, 433
VER-thema’s............................. 573
vertical relief in the
façade....... 651
vertical variation(planting).......... 68
veto chart................................. 444
viaduct...................... 259, 260, 401
vibration.................................... 154
vibration time............................ 154
viburnum..................................... 84
Vienna Congress 1815............ 206
Villa d'Este................................ 348
Villa d'Este at Tivoli................... 348
Villa d'Este in Tivoli................... 348
Villa Rotonda.................... 629, 630
village....... 369, 418, 510, 623, 626
village forms............................. 486
village road............................... 249
villas......................................... 488
VINEX districts(traffic
calculation)................................. 472
vinyl chloride............................ 554
viscose layer............................ 129
visibility..................... 625, 626, 627
Visscher(1972)................ 496, 497
Visser(1986).... 138, 140, 142, 143
Visser(1987)............................ 148
vista’s....................................... 639
Vlaardingen.............................. 342
Vlissingen................................. 218
vlotbrug.................................... 261
VNG.......................................... 569
VOC.......................................... 493
VOC vessels............................ 220
VOCs........................................ 576
Vogel(1970)............................... 54
vogelmuur................... 62, 389, 390
Vogler(1957)............................ 424
voice......................................... 156
voids................................. 519, 654
volatile organic compounds...... 576
volcanoes................................. 316
Volkerakdam............................. 218
Volksgezondheid en Milieuhygiene(1981) 161
volt............................................ 291
Voorburg - Leidschendam....... 123
Voorden(1979)........................... 40
Voorden(1990)......................... 152
Vos(1990).......................... 66, 455
Vos(1993)........................ 407, 664
Vries(1962).............................. 491
Vries(1981).............................. 475
vroegeling................................... 62
VROM(1989).................... 568, 570
VROM(1998)............................ 477
VROM(2000).................... 418, 575
VROM(2001)............ 419, 423, 575
VROM(2001, 2002).................. 478
VROM, 2001............................. 236
VROM/LNV(1987).................... 566
vulcanoes................................. 213
vulnerability charts................... 566
W 13
Wa........................................ 12, 13
waaiertuibrug................... 259, 260
Waal......................... 197, 208, 209
wad.......................................... 122
Wadden area............................ 428
Wadden Sea..................... 219, 220
Waddeneilanden....................... 220
Waddenzee........ 60, 209, 210, 217
wagen...................................... 259
Wageningen............................. 391
wake area................................ 152
walk.......................................... 627
walk.................................. 623, 626
walking............................. 263, 623
walking distance...................... 274
walking route............................ 249
wall........................................... 101
wall layer.................................. 129
wall vegetations....................... 386
wall(design tools(planting))........ 71
wall(trees).................................. 96
walled-in balconies.................. 649
walled-in zone.......................... 633
washing(soil contamination).... 589
waste disposal......................... 324
wastewater............................. 303
wastewater discharge system 299
wastewater production........... 306
wastewater purification........... 294
watch....................................... 626
watch, learn............................. 627
water.......................... 61, 165, 649
water (deep, shallow, bank,
swamp, bottom, salt, brackish, fresh, current, stagnating) 210
water as ally............................. 207
water as enemy........................ 207
water boards........................... 533
water collection........................ 497
water corridors........................ 205
water defence systems........... 205
water dock............................... 388
water flea................................. 434
water in the Netherlands(kinds) 210
water infrastructure
facilities(multi functional) 236
water level management.......... 437
water level regulators.............. 230
water levels(history)................ 222
water managemant tasks in
lowlands 234
water management
aspects(watertoets) 241
water management measures. 210
water management of major
waterways 206
water management policy(half
time) 205
water management tasks......... 233
water management(history)..... 205
water
management(institutional aspect) 210
water management(integrated) 236
water management(integrated,
sectors) 236
water
management<>spatial planning 237
water mint.................................. 65
water on the Earth................... 165
water pipes.............................. 293
water pollution.......................... 561
water production...................... 534
water retainability..................... 344
water storage reservoirs......... 293
water strategies(care,
store, drain 236
water supply............................ 234
water surface(claims in
zoning plans) 242
water table(planting).................. 86
water treatment plants............. 294
water(ecological groups)......... 386
water(fihing, drinking,
swimming) 569
water’s edge............................ 642
water’s edge villages............... 488
Waterboard Delfland................ 242
Waterboard Rijnland................. 242
watercourse.................... 247, 249
watercourse(hedges)...... 101, 103
watercycle(solar power)........... 22
waterlevel................................ 201
waterlevels.............................. 424
waterlogging control and
drainage of reclaimed land 205
Waterloo................................... 206
Waterman, 1992...................... 219
watermanagement................... 423
watermanagement policy......... 236
Watermanagement Policy......... 423
watermanagement(areas)....... 234
watermanagement(global
warming) 236
watermunt.................................. 65
waterparagraph....................... 241
waterschappen........................ 234
watersportclub......................... 538
water-table classes......... 329, 578
watertoets................................ 241
watertoets(contents)............... 241
watertoets(regional
elaborations) 242
waterway........................ 247, 249
waterways(urban).................. 454
waterzuring.............................. 388
watt.......................................... 291
watt*hour................................... 13
watt*jaar/jaar.............................. 12
wave length............................. 155
wavy hair-grass...................... 436
wavy hair-grass(pleistocene). 374
ways(density).......................... 190
ways(district)........................... 190
wear and tear............................ 82
weather............................ 316, 559
weather pattern....................... 559
weather patterns..................... 317
weather types.......................... 560
weathering............................... 320
weathering forces................... 325
wedges.................................... 402
Weeda(1985)........................... 389
Weeda(2000)........................... 427
weegbree................................. 400
weekly rhythm.......................... 468
weeping ash(treures)................ 98
weeping willow.......................... 48
weeping willow(treurwilg)......... 98
wegdorp................................... 497
Weichsel..................................... 57
Weichselian.............................. 358
Weilbull probability
distribution.. 114
Weir of Driel regulating Dutch water distribution 208
weirs........................ 204, 231, 253
Weirs directing water northwards and southwards 208
weirs in the Lower Rhine/Lek.. 207
Wely(1993)............................... 454
Western blocks.......................... 46
Westerschelde......................... 218
West-Friesland......................... 497
Westhoff.......................... 391, 395
Westhoff(1969)................ 374, 392
Westhoff(1970)........................ 548
Westhoff(1975)........................ 383
Westhoff, et al., 1975....... 395, 396
Westhoffs synecology............. 396
Westland.................................. 219
Westra(1980)........................... 115
Wet Bodembescherming.......... 576
wet connections.............. 247, 248
wet cross section.................... 201
Wet op de
Luchtverontreiniging 590
wet wood................................. 497
wetand....................................... 61
weteringen............................... 225
wetland(ecological groups)..... 386
wetness........................... 626, 627
Wh.............................................. 13
wheels..................................... 402
whirls....................................... 152
white willow(schietwilg)............ 98
whitebeam.......................... 84, 376
WHO......................................... 426
wholesalers............................. 544
wide-angle lens........................ 629
wiel........................................... 497
Wieringa(1983)......................... 112
Wieringen................................. 220
Wieringermeer.......................... 220
Wieringermeer
polder............. 228
Wieringerwerf.......................... 220
wijk........................................... 498
wild honeysuckle....................... 65
wild parsnip.............................. 361
wilde kamperfoelie..................... 65
Wilderbaan....................... 488, 489
wilderness................................ 400
wilg........................................... 376
wilgenroosje..................... 389, 390
wilgeroosje................................. 63
Willem I...................................... 492
Willem II..................................... 492
Willem III............................ 475, 492
Willemstad................................ 205
Willerich.................................... 488
Willerrode......................... 488, 489
willow................................. 83, 376
willow and poplar forests........ 378
willow(coastal).......................... 84
willow(wilg)............................... 98
Wils........................................... 652
wind......................................... 154
wind direction........................... 112
wind effects(water system).... 210
wind force................................ 106
wind loads................................ 109
wind potential............................. 29
wind shelter(local)................... 128
wind stations............................ 112
wind statistics.......................... 111
wind turbine(power(wind
velocity)) 110
wind turbine(power)................ 115
wind turbine(profit).................. 115
wind turbines(efficiency)........... 28
wind turbines(energy profit).... 109
wind turbines(enery
profit(rule of thumb)) 116
wind
velocities(distribution)..... 112
wind velocity............................ 106
wind velocity(average(calculation)) 113
wind
velocity(height,lateral)..... 129
wind(allotment directions)........ 144
wind(central green)................. 141
wind(direction(tree shape))....... 83
wind(district road trees).......... 147
wind(district road).................... 146
wind(dwelling density)............. 151
wind(edge green).................... 141
wind(edge of town)................. 126
wind(energy
contribution(national)) 31
wind(energy harversting).......... 28
wind(forests)........................... 126
wind(green areas)................... 126
wind(high rise at the edge)...... 141
wind(highway)......................... 126
wind(low rise at the edge)....... 141
wind(new urban area lose or
adjacent) 124, 125
wind(open green area)............ 147
wind(permeable walls)............ 153
wind(planting)............................ 93
wind(railways)......................... 126
wind(shrubs)........................... 153
wind(solar power)..................... 22
wind(temperature)................... 138
wind(trees)...................... 146, 150
wind(velocity(average(hour))) 112
wind(velocity(average(year))) 112
wind(velocity(frequences))..... 115
wind(velocity).......................... 109
wind(wall(permeable))............. 153
Wind-borne sand dunes........... 496
windmills(row).......................... 227
windmills(rows)....................... 226
window side............................ 633
window(design
tools(planting)). 72
window-frames....................... 656
windows|doors........................ 627
windtunnel
experiment(roughness island) 131
windvelocity(height)................. 130
winning(energy)......................... 33
winter (flowering)...................... 84
winter temperatures............. 50, 51
wipperchicken.......................... 623
with multiple-celled life
forms... 353
Wittgenstein.............................. 659
Wittgenstein(1919)................... 659
Wittgenstein(1953)................... 659
WLO......................................... 442
Wolman............................. 188, 190
Wolocas................................... 472
Wolters-Noordhof(1981).......... 495
Wolters-Noordhof(1996).......... 479
Wolters-Noordhof(2001).. 167, 168
Wolters-Noordhof(2001))..... 50, 51
Wolters-Noordhof, 2001.......... 169
wood........................................ 497
wood anenome.......................... 64
wood/forest............................... 64
wooded morass....................... 437
wooden pile heads................... 338
wooden piles............................ 303
woodland planting................ 74, 83
woodland planting schemes...... 73
woodland planting(>6m
wide).... 79
woodland profile........................ 74
woodland(open spaces)............ 74
woodrush–beech forest.......... 484
woods...................................... 436
Work Group for Urban
Ecology(WLO) 442
work groups(bird, butterfly,
plant, toadstool, reptile, mammal, bat) 440
World commission environment
and development(1990) 666
World commission environment
and development(1990) 570
World Health Organization........ 365
World War I............................... 205
World War II.............................. 237
Worldbank................................ 219
world-wide rarity..................... 430
worms...................................... 432
Woud(1998)............................. 493
wreath seaweed............. 432, 433
Wright effect............................ 649
Ws.............................................. 13
Würm.................................. 57, 437
WWII......................................... 220
xylene....................................... 591
yacht harbour........................... 538
yard.................................. 623, 626
year average potential wind
velocity 112
yearly rhythm........................... 468
yellow algae............................. 432
yellow corydalis....................... 386
yellow flag.................................. 61
yellow iris................................... 61
yellow water-lily......................... 61
yew............................................ 83
youth and group
accommodations 538
Zaanstad.................................. 527
zandfractie............................... 326
Zandkreekdam.......................... 218
Zanen(2000)............................ 436
zebra mussel............................ 434
zebra mussels.......................... 436
Zeeland............................ 327, 438
Zeeland waters........................ 438
Zeeuws Vlaanderen................ 209
zeil- en surfschool................... 538
Zevenkamp............................... 307
zijoverspanning........................ 259
Zijpp(2000)....................... 471, 479
zinc........................................... 589
Zodiac........................................ 38
Zoest........................................ 444
Zoest (1998)............................ 365
Zoest(1998)............................. 352
Zoest(2001)............................. 442
Zoetermeer 123, 364, 405, 407, 452, 454, 527, 570,
664
Zoetermeer(1969).................... 255
Zoetermeer(nature policy)....... 453
Zoetermeer(rarity policy)......... 430
Zoetermeer(wild plant
species) 361
zomereik..................................... 65
zoning...................................... 401
Zonneveld(1981) 188, 189, 190, 195, 196
zoo........................................... 538
Zuiderzee........................... 60, 216
Zuiderzee area........................... 59
Zuiderzee works...................... 216
Zuiderzee(flooding 1916)......... 216
Zuiderzeewerken............. 216, 217
zuyder sea herring................... 431
Zwart(2000)............................. 442
zwarte els.................................. 64
zwarte populier........................ 376
Zweckbegriff................... 368, 668
zweefbrug....................... 259, 260
zwevend brugdeel................... 259
Zwin......................................... 218
DCp(10).................................... 142
DCp(z)...................................... 148
Di 130
r. 142
The Belgian standard TAW in Fig. 381 means ‘above average sea level at ebb-tide on
Ostende, 2.426m higher than NAP, the Dutch standard for measuring heights.
Huub Savenije (2001) Stroming 7
Nummer 4 TU Delft, hsa@ihe.nl
B. van Gent (1999), p. 2/30
Odum,
E. P. (1971). Fundamentals of ecology. Philadelphia, W.B. Saunders Company.
VNG, Vereniging van Nederlandse Gemeenten (2007)
Bedrijven en milieuzonering. (Den Haag) SDU Uitgevers bv.
[1] How does the SI system of units define energy and power?
[6] In what units are energy and power expressed?
[8] What is the energy content of 1 m3 natural gas (aeq)?
[9] What is the energy content of 1 litre petrol?
[10] Give three expressions for the power of one watt during
a year.
[11] Give three examples for the power of one watt during a year.
[13] Give three examples of a power of
100W in every day life.
[14] Why is electric energy more expensive than the same energy from
gas?
[15] What is the relation between entropy and efficiency?
[16] Which conversions are combined in
an electric power station and which efficiencies are involved?
[17] How long could we maintain current energy use by fossile fuels?
[18] Name 3 drawbacks of the use of uranium for energy supply, explain
every drawback with three elements.
[19] Where hides the danger of misuse of nuclear energy using a fast
breeder reactor?
[20] What is nuclear fusion. What are the dangers of nuclear fusion?
[21] Which proportion of Dutch energy use is electric?
[22] What is the best alternative for future energy production?
[23] What is the largest flow of commercial energy through The
Netherlands?
[24] For which applications is
energy storage of decisive importance?
[25] Which kind of energy storage is
most efficient. Why don’t we use it?
[26] When and at what time a building of 50m casts a shadow of 100m in
North-Eastern direction in The Netherlands?
[30] What is the name of the age 75 000 B.C?
[31] Where could you find daisies (madeliefjes) and from which month do
they flower in the Netherlands?
[32] Which plants in The Netherlands start to flower in February as
pioneering plants, in grassland and in forests?
[33] Why are flowering periods important
for nature management? What types of biotope have an early flowering period and
what types have a late one? What types of biotope have a limited flowering
period late in the summer? To what extent can the daily variations in growing
circumstances play a role in nature management?
[34] What is a key characteristic of plants in a built environment?
[35] What is 'screening' effect of plants?
[36] What is 'structure' in plantation?
[37] What can be the effect in time of planting schemes?
[38] What are restrictions in the choice of plant material?
[39] What is the primary factor that influences the planting of trees
next to buildings?
[40] What are the climatic conditions for use of plantation?
[41] Which kinds of plantation are coloured or flowering in spring?
[42] Which kinds of plantation are coloured or flowering in summer?
[43] Which kinds of plantation are coloured or flowering in autumn?
[44] Which kinds of plantation are coloured or flowering in winter?
[45] Which are the physical conditions for use of plantation apart from
the climatic ones?
[46] Which kinds of plantation are applicable in coastal areas?
[47] Which kinds of plantation are applicable on clay/loam soils?
[48] Which kinds of plantantion are applicable on peat soils?
[49] Which kinds of trees are applicable on wet soils?
[50] Which water table is the best situation for trees?
[51] In ‘sinking’ areas (peat soils) in the West of the Netherlands the paving
has to be raised every so often, even up to 30 or more centimetres at a time.
As a result, many trees receive too little oxygen and die. Which kinds of trees will die?
[52] How is space in streets organised to enable tree planting?
[53] Which size classes are distinguished concerning trees?
[54] What is the minimum distance between the buildings and the centre
of the stem of a size class 1 tree?
[55] What visual effects can be used in tree planting in urban space?
[56] In what ways can planting distances influence the urban
environment?
[57] How can hedges be used in creating urban space?
[58] What is 1 bar air pressure?
[59] What is the mass of 1m3 of air on sealevel?
[60] Which relation exists between wind force and velocity?
[61] Why could you not multiply a locally measured wind force by the
surface of a building to get the total force?
[62] In what order of magnitude air density decreases by altitude?
[63] How many turningpoints the air temperature counts in the atmosphere
from ground level until 500km altitude?
[64] Why do cumulus clouds mainly have a flat bottom?
[65] Which length has the equator?
[66] Why is the atmosphere thicker at the equator than at the poles?
[67] What are 'trade winds'?
[68] How much energy non airtight houses in a moderate climate winter
could loose by 5m/sec increase of average wind velocity?
[69] At which wind velocity a normal wind turbine has its maximum energy
production?
[70] In what range the year average potential wind velocity varies in
the Netherlands?
[71] What is an 'hour average wind velocity'?
[72] What is a 'year average wind velocity'?
[73] How can wind velocity statistics be reliably simulated?
[74] How is the energy in wind related to its velocity?
[75] What is best to decrease energy losses from buildings: sheltering
form the coldest (NE) winds or from the most frequently appearing (SW) wind
directions?
[76] From which wind direction a city in the Netherlands could best be sheltered
to decrease comfort complaints about wind?
[77] What is the best place concerning all aspects of wind: Schiphol or Eindhoven?
[78] What is the standard class of roughness supposed in wind data?
[79] Which roughness class has obstacles of 10m < H < 15m: bottom
regularly and fully covered by rather large obstacles with mutual distance not
larger than 2x their height: regular forests, low rise buildings in villages,
suburbs?
[80] How much could a windvelocity of 7m/sec on 20m altitude be reduced
by 1km urban area?
[81] How much could a windvelocity of 5m/sec on 20m altitude be
increased by a profile of 500m highway and railway?
[82] If there
were no differences in temperature or ground level and water was equally
dispersed over the Earth, how deep the ocean would be?
[83] Why is snow and ice in mountains important?
[84] As a very rough approximation, how much is the m3/sec of
discharge per km2 catchment area?
[85] What is the ‘duration line’ of a river?
[86] How changes velocity downstream?
[87] Why are street patterns and artificial drainage systems in flat
lands not like a tree but like a lattice?
[88] How large are the differences in sea water levels caused by tides
in The Netherlands?
[89] Which Dutch weirs are closed successively to store enough fresh
water in the IJssellake during warm and dry periods?
[90] How is salt water intrusion near Rotterdam reduced?
[91] What is the hydrological effect of climate change in The
Netherlands?
[92] Which four major systems of coast development can be distinguished
in The Netherlands?
[93] Within which period a severe rainfall with critical intensity must
be pumped out completely in Dutch populated and industrialised areas?
[94] The discharge of the river Rhine
at Lobith in February 1995 was 12 000m3/sec. What is normal?
[95] Which general subsidence faces The West of the Netherlands
until 2050?
[96] The Parliament of The Netherlands decided in 1960 to accept the
risk of a disastrous flooding of rivers once in how many years?
[97] What is a Gumble graph?
[98] Give some norms for water storage in urban areas.
[99] Suppose the hierarchy of roads would follow a semi logarithmic
sequence of meshwidths. Which nominal meshwidths (exit intervals) and widths
(form facade to facade) would then approximately fit best residential streets,
main streets, district roads, urban, local, regional and national highways on a
Dutch topographic map?
[100] If a network with square meshes has a density of 2 km/km2,
what is then the mesh width?
[101] What is a normal network density of neighbourhood streets?
[102] The most efficient enclosure is made by surrounding the enclosed
area with a minimum length of road. Which pattern of continuous network, fits
that requirement best?
[103] Why is an orthogonal network
pattern so often applied in an urban road network?
[104] If a rectangular network with square meshes is elongated into
different widths and lengths keeping the same density (road investment), what
happens to length of enclosing roads and the surface of the enclosed area?
[105] If a rectangular network with square meshes is elongated into
different widths and lengths keeping the same density (road investment), which
ratio of width and length is then the limit?
[106] If a rectangular network with square meshes is elongated into
different widths and lengths keeping the same density (road investment), what
happens to number of crossings per km2?
[107] Which effect has superposition of a higher order over the lower
order in a road network, on the density of the lower order?
[108] Which kind of interference of two networks delivers the least
crossings?
[109] Which kind of crossings give the least conflict points?
[110] What is the maximum span of a suspension bridge?
[111] What is the maximum span of a arch bridge in steel?
[112] What is the maximum span of a beam bridge in steel?
[113] What is the maximum span of a swing bridge?
[114] Suppose there is a highway on + 0.1 metre. If you want to make a
tunnel for cyclists, what length of
slopes you will need then on both sides?
[115] What is the average width of a car?
[116] What is the average width of a car parking place?
[117] Which width does a pedestrian need at least in a street profile?
[118] Which width does a cyclist need at least in a street profile?
[119] Which width does a car need at least in a street profile?
[120] Which width does a bus need at least in a street profile?
[121] Which width requires a normal residential street profile between
the facades at average?
[122] At which speed a lane has its higest capacity for cars?
[123] What is the equivalent per day of 1000 cars per hour?
[124] What is the maximum capacity for cars of a lane?
[125] If three houses in one block are surrounded by roads, what is then
the proportion of public pavement to the area between the centre lines of
surrounding roads?
[126] What is a normal proportion of public pavement to the area between
the centre lines of roads surrounding a residential building block with
entrances at all sides?
[127] Which width requires a normal neighbourhood road profile between
the facades at average?
[128] Suppose a residential building block surrounded by roads contains
some 75 inhabitants going out 4 times a day of which 3 by car. Suppose in 1/3
of the car trips the driver is accompanied by a passenger. How many car
movements per hour will the residential street count?
[129] If there are 1000 inhabitants in a neighbourhood how many car
movements will there be per hour on a neighbourhood road?
[130] How much pavement surface you can save if approximately 200
inhabitants are willing to walk one minute longer into their parking space
instead of parking in front of their home?
[131] How could you save pavement surface if approximately 2000
inhabitants are willing to walk ten minutes into their parking space instead of
parking in front of their home?
[132] How could you save neighbourhood pavement surface in a grid of
1x1km district roads filled in with a grid of 300x300 m neighbourhood roads?
[133] How was the principle named by Berlage not making X-crossings on
central squares, giving access roads along the square a focal point on larger
buildings located at T-crossing?
[134] Which traffic expert proposed a hexagonal grid in 1963?
[135] How does a regular grid of district roads and neighbour streets
solve some problems arising if you look at an isolated neighbourhood only?
[136] What were the measures of urban islands Cerdŕ (1867) designed for Barcelona?
[137] How many urban islands contains a neigbourhood Cerdŕ (1867)
designed for Barcelona?
[138] What was the width from façade to façade of residential,
neighbourhood and district roads Cerdŕ (1867) designed for Barcelona?
[139] What are the advantages of a rectangular grid concerning its
flexibility?
[140] Why did towns change from a spider into a fly in the regional web?
[141] 'Care for the pedestrian is the core of urban design.' In which
Dutch publication this statement is supported most extensively?
[142] What causes deviations in a rectangular town grid?
[143] In what sense the lay-out strategy of public transport lines by
busses changed at the beginning of the twentieth century?
[144] What are the km radius served area; km stop distance; km/h
velocity; km average ride; minutes per ride; stops per ride; passengers per
hour; passengers per stop of bus, tram, fast tram, (semi)metro or NS-sprinter?
[145] What is a light rail?
[146] If 14% of the inhabitants is expected to use metro if available,
what density you need for anexploitable metro line?
[152] What is plate tectonics?
[153] What is uniformitarianism?
[154] What is geochronology?
[155] What
happened between Triassic and Permian?
[156] What is the
duration of eons?
[157] What is the
Phanerozoic Eon?
[158] How is the Phanerozoic subdivided?
[160] What is the
geological cycle and on which insights the concept is
based?
[161] What is meteorology?
[162] Which major
forms of ingenious rock can be found at the surface of the Earth?
[163] What are
sedimentary rocks?
[164] What are metamorphic rocks?
[165] Which kinds
of instruments are used by geologists?
[166] What is geomorphology?
[167] Which are
the key concepts of geomorphology?
[168] Which are
the main processe studied by geomorphology?
[169] What is the
difference between weathering and erosion?
[170] Which kinds
of weathering could be distinguished?
[172] Give some examples of chemical weathering.
[173] Give some examples of biological weathering.
[174] What are
the basic activities concerning topography and form of
the land starting a
design project?
[175] Which are
the determining factors in the formation of rivers?
[176] Give some
reasons to study river forms in a design project.
[177] Which kind
of polders you can distinguish?
[178] What is soil
science?
[179] Why is soil
science important?
[180] How deep
does soil science go?
[181] What is
parent material?
[182] Summarise five soil forming factors.
[183] Wich
organic factors could have influenced the properties of
the soi?
[184] Wich
topographic factors could have influenced the properties of the soil?
[185] Name four phases of soil formation.
[186] Which soil
horizons you can distinguish?
[187] What is the
physical structure of sand, clay and peat?
[188] How could
you identify the particle size of soil?
[189] Which zones
of soil saturation by water can be distinguished?
[190] What is the
difference between soil water and ground water?
[191] At what specific places in the western part of Holland, the influence of seawater is
apparent and why is that?
[192] Hoe could
you easily determine the depth of the groundater zone?
[193] Why is sand
more easily drained than clay?
[194] What is a groundwater table and why is it important?
[195] What is seepage and at which places does it take place in Holland?
[196] Which characteristics of soil determine their use?
What is the main difference of using sand, clay and peat?
[197] What is the
cause of the magnetic field of the Earth?
[198] Why is the
composition of the Earth’s crust different from that of the Earth as a whole?
[199] Why is the
composition of the Earth’s crust different according to its depth?
[200] Why are the
minerals near the surface of the Earth mainly oxides?
[201] What is the
difference between minerals and rocks?
[202] What is the
difference between mafic and felsic rock?
[203] What is the most important mineral in igneous rock?
[204] What are two different approaches in preparing a site for
development?
[205] Which site
preparation methods can be distiguished?
[206] What is the number of kown species on Earth?
[207] Who called biodiversity 'a risk cover for life'?
[208] What is botanical taxonomy?
[209] What class of life forms counts the highest number of species in
the Netherlands?
[210] What were the first organisms producing oxygen from carbon dioxide?
[211] When established life a foothold beyond the sea by which mosses and
liverworts (Bryophyta) brought a green colour to the wet parts of the land?
[212] What is the evolutionary advantage of vascular plants?
[213] From which period we recognise ice ages (glacials) and warmer
interglacials in the soil of the Netherlands?
[214] How is the last ice age named?
[215] In which period the higher parts of the Netherlands were formed?
[216] To which depth Holocene deposits under Delft reach?
[217] Where in
the Netherlands
is the sedimentation deposited since the last Ice Age the thickest? How thick
is it there? How thick is it under Delft?
From what period of time after the last Ice Age have human beings been present
in the Netherlands?
Did human beings live in the Netherlands
before the last Ice Age?
[218] A year counts 8760 hours. How many hours per m2 do
people spend in shops, how many in home and garden?
[219] What is a curve of ecological tolerance?
[220] Who was Brundtland?
[221] What is 'sustainable develoment' in terms of the UN World
commission environment and development (1990)?
[222] What are reflexive judgements and what kind of problems do they
raise?
[223] What does the term 'scale paradox' emphasise?
[224] What is a 'nominal value'?
[225] How could you articulate a state of dispersion by scale?
[226] By whom ecology is defined as 'the scientific study of the
distribution and abundance of organisms'?
[227] What is the difference between autecology and synecology?
[228] What kind of ecology is elaborated by Grime, Hodgson et al. (1988)?
[230] What
are the average global life conditions of a desert, maquis, grassland, moderate
decideous forests?
[231] What are the average global life conditions of the Netherlands?
[232] Welke Europese floragebieden zijn in Nederland
vertegenwoordigd?
[233] Which vegetation areas are destinguished in the Netherlands?
[234] At which altitude approximately Holocene and Pleistocene are
separated in the Netherlands?
[235] How many nature target types Bal, Beije et al. distinguished in
2001?
[236] Welke drie geologische eenheden
onderscheidt men in Nederland?
[237] For which parts of the Netherlands respectively barley,
wavy hair-grass, marram, greater burdock are typical?
[238] Which trees are general in the Netherlands?
[239] Which trees are specific for holocene and river grounds in the Netherlands?
[240] Which trees are specific for pleistocene and dunes in the Netherlands?
[241] Noem vier plantengeografische districten
die in Nederland worden onderscheiden. Noem uit elk district twee
kenmerkende bomen of planten.
[242] Where are Holoceneous willow and poplar forests (salicion) often
found?
[243] Where are Holoceneous alder and ash forests with densely shrubs
(alnion incanae) often found?
[244] Where are Holoceneous oak, ash (somtimes elm or maple, ulmion)
forests often found?
[245] Where are holoceneous Hedges and thickets (sambuco-berberidion)
often found?
[246] Where are pleistoceneous hedges and thickets (hawthorn, sloe,
roses, blackberries, rubion) often found?
[247] Where are pleistoceneous oak, ash (sometimes maple or beech,
carpinion) forests mostly found?
[248] Where are pleistocenious oak (seldom birch or beech) forests or
coppice wood mostly found?
[249] Where are pleistoceneous oak (sometimes birch or beech,
violeto-quercion) forests or coppice wood mostly found?
[250] Where are pleistoceneous oak (sometimes birch or beech,
vaccinio-quercion) forests or coppice wood mostly found?
[251] Where are rarefied birch peat forests (betulon pubescentis) mostly
found?
[252] Where are Birch (sometimes alder) peat forests (sphagno-alnion)
with shrubs of alder buckthorn, willows,
bog myrthle sometimes found?
[253] Where are Alder or willow (mostly coppice wood) peat forests
(irido-alnion) mostly found?
[254] Waardoor draagt hetzelfde biotooptype niet
altijd dezelfde levensgemeenschap? Noem twee klassen uit de klassificatie volgens Den Held (1989).
[255] Noem drie ecologische groepen die
achteruitgaan.
[256] Waarom is de indeling naar biotooptypen
van Runhaar, Groen, Van der Meijden en Stevers niet op oorzakelijke
differentiatiefactoren zoals bodemtype en waterhuishouding gebaseerd?
[257] Wat zijn de voordelen van een zekere
hiërarchie in de typologie?
[258] Wat
betekenen in de Heukels' Flora bij een soort achtereenvolgens de volgende
toevoegingen: W18sa, V11, H27, G23, P21, P28, H42, H47, G47kr, P41, P42, P43,
P40mu, H61, H63, P63ro.
[259] Runhaar c.s. (1987) houden als criterium
voor de indeling van soorten in biotooptypen en ecologische groepen aan. Welk criterium voor de
indeling van soorten in biotooptypen houden Runhaar c.s. aan en waarom?
[260] Geef
een voorbeeld van de causale samenhang tussen voedselarmoede en soortenrijkdom
[261] Op
welke schaalniveaus en waarom is de herkenning van planten en dieren onderling
en door elkaar van belang? Welke factoren spelen daarbij een rol? In welke fase
van de voortplanting is deze herkenning belangrijk en welke fase volgt daarna?
Welke betekenis heeft dit voor de planning van ecologische infrastruktuur?
[262] Welke
overlevingsstrategieën onderscheidt Grime (1988)?
[263] Geef
5 verschillen tussen pionierstadium en climaxstadium volgens Odum (1971).
[264] Wat
betekenen de strategieeën volgens Grime voor de eisen die de plant aan de bodem
stelt? Naar welke categorie gaat de belangstelling van de natuurbescherming in
het bijzonder uit?
[265] What is systems ecology?
[266] Give an indication in order of size of 6 claims on the surface of
the Deltametropolis.
[267] How could you define an urban centre, an urban outskirt, a green
urban area, a village and a rural living environment morphologically?
[268] Which 3 three robust connections counts Deltametropolis in the
National Plan of Nature Policy [LNV, 2 000a #810]
[269] How does the National Plan of Nature
Policy control the biological
identity of areas?
[270] Why is global biological diversity a basic criterion for ecological
evaluation and how could you make it locally operational?
[271] The 4th National Plan of Watermanagement Policy [V&W, 1998c #829], and
its last successor ‘Anders omgaan met water’[V&W, 2 000b #832] mark a
change from accent, just as the 4th National Plan of Environmental Policy [VROM, 2 001a #839] compared
with its predecessors. Which change of accent is that?
[272] Which future problems in watermanagement and proposed solutions
have a great impact on landuse in the Netherlands? Which solutions are
proposed in the 4th National Plan of Watermanagement Policy [V&W, 1998c #829], and
its last successor ‘Anders omgaan met water’[V&W, 2 000b #832]?
[273] Which kind of ecology is human ecology?
[274] When
lived homo habilis and which change of habitat accompanied its appearance?
[275] How
old is the genus 'homo' and which capacity determines that distinction from
other species?
[276] Noem 3 menselijke eigenschappen die wel
worden toegeschreven aan het leven in een boom-milieu voorafgaand aan Homo
Habilis.
[277] Schets enkele ergonomisch en
architektonisch relevante kenmerken van het bosmilieu.
[278] In
which biomen the highest human population densities are found? In which biomen
the majority of people live?
[279] In which biomens most types of ancient economic household
management are found?
[280] Welke relatie bestaat tussen huishouding
en dichtheid?
[281] In
what nominal radius 100 efficient ancient hunters and farmers could survive
respectively?
[282] Which
consequences the transition from gathering and hunting to agriculture have had?
[283] What
is the neolithic revolution?
[284] How
could the slowing down of world population growth around the beginning of the
Christian era be explained?
[285] Around the beginning of the Christian era European population
slowed down. By which mediaeval
development a renewed growth was
caused?
[286] To
which ecological model war and illness, such as the pest epidemic around 1300
A.D., could be compared?
[287] By
which economic factor in the past milennium decrease of population was often
preceded?
[288] Where death rates vary per generation, there is also a variation in
birth rates. How to contain these variations within one model?
[289] What
is a logistic curve?
[290] Concerning
limited availability of raw materials the growth of a technology or a
population slow down after a period of exponential growth. However, a new
technology can restore the growth of a population into exponential growth. How
is the overall curve called?
[291] Which
shapes the curve of a mathematical chaos function could produce?
[292] Wich
population maxima for the Netherlands
have been predicted by the CBS between 2002 and 2006?
[293] In which societies cases of birth control by infanticide, abortion
and restricting coitus are confirmed?
[294] By which development the biggest mass migration ever was caused?
[295] Name
some societal consequences of the industrial revolution.
[296] Which
relation is found between increasing population density and differentiation of
functions?
[297] Name
some physical consequences of living in high densities.
[298] In
which dimensions intensity of use can be measured?
[299] Which
planning methods are available to avoid displacement and waiting?
[300] Why
is intensity of use important for spatial planning?
[301] Why
plays intensity of use seldom a role in spatial planning?
[302] Which urban space was the most intensily used
in 1983?
[303] How much time urban inhabitants are since long prepared to accept
for travelling twice a day between their homes and their work?
[304] Which
remarkable developments in the Dutch landscapes could be mentioned in the
periods of
1000 - 1100
1675 - 1800
1850 - 1960
1960
– 2000 A.D.
[305] Which
ecologically relevant human activities can be distinguished on the lowest level
of scale and what are its ecological effects?
[306] How
agriculture in the Netherlands
until 1900 A.D. has increased the number of species?
[307] Give
a schematic overview of the ecological influence of traditional and modern
agriculture.
[308] How
many m2 agricultural, natural and urban space the Netherlands counts per inhabitant?
[309] Which proportion of the urban area (industry and recreational areas
excluded) is residential in the Netherlands?
[310] What
is 'residential area' according to the CBS?
[311] How
does the residential area vary in different parts of the Netherlands?
[312] Why
the use of Planological Index Numbers for the amount of space needed for
facilities should be put into perspective?
[313] By
which factor you can derive the number of dwellings from population density?
[314] How
did the average number of occupants per household in the Netherlands
develop after the Second World War?
[315] Geef de namen van relatief bebouwde en
onbebouwde gebieden in een semi-logaritmische morfologische reeks tussen 30km
en 10m.
[316] Geef de namen van ontsluitingswegen in een
semi-logaritmisch-morfologische reeks tussen 30m en 10km.
[317] Geef de namen van waterlopen in een
semi-logaritmische reeks tussen 30m en 100km.
[318] Hoe kun je in een gestyleerd regionaal
plan de planlaag onderscheiden van de reeds bestaande gebieden? Geef een
voorbeeld van functionele inkleuring van legenda-eenheden voor bebouwd en
onbebouwd gebied in een gestyleerd regionaal plan.
[319] How could the current definition of environment as ‘physical
surroundings of society’ be changed to be part of a family of technically
useful definitions?
[320] How could accomodation and adaptation be opposed?
[321] In which mode operate design, empirical research, policy and art
respecitively?
[322] Which kinds of sources, emissions, transmissions and suffering
objects can be distinguished?
[323] Which kinds of environmental standards can be distinguished?
[324] How could emissions of an area be estimated?
[325] Which compounds contains the largest amount of combustion and which
process emissions?
[326] Give 3 examples of hydrocarbons and their impacts.
[327] In which measures standards for complex mixtures are given?
[328] Which kind of emission is most predictable, distance-sensitive and
controllable within
the framework of spatial planning?
[329] What contains transmission?
[330] What is ‘troposphere’?
[331] Warm air rises until the surroundings become warmer, but, in
retaining its own heat content, rising air also cools off due to expansion. How
much °C per 100 m it cools off?
[332] In which weather circumstances air pollution accumulates?
[333] What is an inversion? When does it occur and why? How does an
inversion dissolve? In which circumstances it remains?
[334] Why is the underside clouds mainly flat?
[335] Why do the temperate climates often have turbulent wheathers?
[336] Which air streams meet in temperate climates?
[337] Which turning direction do whirling air movements have in the
Northern hemisphere and why?
[338] How changes the wind direction in coastal areas after a sunny day
and why?
[339] Welke beperking geldt voor de het voorspellen
van verspreiding van luchtvervuiling in stedelijk gebied?
[340] Welke drie soorten verspreidingsmodellen
bestaan er?
[341] Met welke 3 maten kan concentratie van
luchtverontreiniging gemeten worden?
[342] Welke ontwikkeling heeft de
transmissieberekening in water te zien gegeven vanaf 1960?
[343] Waarom gebruikt men bij de berekening van
grondwaterstromen niet altijd driedimensionale modellen?
[344] Wanneer kan men ook met tweedimensionale
modellen volstaan?
[345] Noem 5 bronnen voor een snelle orientatie
omtrent de eventuele risico's van verbreiding van bodemverontreiniging. Waar moet
men op letten?
[346] Wat betekent pH, Eh, k en CEC? Wat is in dit
verband het verschil tussen zand en veen?
[347] Geef 3 benaderingen die ooit zijn toegepast om
de prijs van een mensenleven te ramen. Is een van deze benaderingen naar Uw inzicht
redelijk? Zo niet, hoeveel geld moet er dan naar Uw inzicht aan het herstel van
het milieu worden uitgegeven wanneer U daarmee een mensenleven zou kunnen
redden? Wie moet dat bedrag betalen wanneer de schuldigen niet kunnen worden
aangewezen?
[348] Which are
the three approaches ever used to estimate the price of a human life? Is one of
these approaches reasonable in your view? If not, how much money must then, in
your view, be spent on the environment, to save one human life? If the guilty
parties cannot be identified, who should then pay that amount?
[349] What is a dose-response relation?
What does LD50 mean?
[350] Hoe zou men een dosis‑ effectrelatie
voor materialen kunnen vaststellen?
[351] Hoe kent men de dosis‑ effectrelatie van
een groot aantal stoffen bij mensen?
[352] Welke organen spelen een rol bij de opname en
verwerking van vergiftigingen?
[353] Hoeveel % sterfte kan men ongeveer voorkomen
door een reduktie in de luchtverontreiniging van ca. 10%?
[354] Why is the
pollution prevention insufficient for retaining plant and animal species?
[355] Which individual chance of dying per annum caused by the totality
of environmental risks to human beings is accepted by Dutch government; what is
the maximal acceptable level for each single activity or substance?
[356] What is an environmental target value (streefwaarde) in the Netherlands?
[357] What is an environmental threshold value (drempelwaarde) in the Netherlands?
[358] What is an environmental limiting value (grenswaarde) in the Netherlands?
[359] What is an environmental guide value (richtwaarde) in the Netherlands?
[360] What is an environmental quality target (milieukwaliteitsdoelstelling) in the Netherlands?
[361] What is an environmental quality requirement (milieukwaliteitseis) in the Netherlands?
[362] How could an economic optimum of
environmental quality be determinded?
[363] How does the strictness of
environmental standards mainly vary with he area they apply?
[364] Wat betekent EPEL, MAC, TLV?
[365] Waarin schieten de bestaande
milieudoelstellingen van het NMP tekort ten opzichte van ‘sustainable
development’ bij verdubbeling van de bevolking?
[366] Welke direkte bijdragen aan de
milieugebruiksruimte kunnen aan het bouwen worden toegewezen?
[367] Hoe kan men de eigen milieutaak van het bouwen
in termen van milieugebruiksruimte formuleren?
[368] In hoeverre kan men de in het NMP+ opgesomde
bijdragen van de doelgroep 'Bouw' ook aan andere doelgroepen toerekenen?
[369] Which environmental problems the NMP1 distinguished as global?
[370] Which environmental problems the NMP1 distinguished as continental?
[371] Which environmental problems the NMP1 distinguished as fluvial?
[372] Which environmental problems the NMP1 distinguished as regional?
[373] Which environmental problems the NMP1 distinguished as local?
[374] Which policy outlines the NMP1 used as an agenda to the discussions
with target groups?
[375] Hoe zou men verschillende milieuthema's en
-doelstellingen onderling kunnen wegen?
[376] Noem 5 'ver-thema's' uit het milieubeleid
sinds het NMP.
[377] Welk thema is stilzwijgend verondersteld bij
elk milieuthema sinds het NMP?
[378] What is a groundwater table and why is it important?
[379] What information must be incorporated into the “follow-up
investigation” report?
[380] What are the causes of soil pollution in industrial sites?
[381] What is a reference value?
[382] What is a target value?
[383] What is an intervention value?
[384] Name at least 5 operational activities that can cause soil
pollution.
[385] Which remediation methods have been identified?
[386] Name 3 purification techniques.
[387] When should contaminated soil tipping be considered?
[388] When is contaminated soil storage preferred?
[389] List 3 disadvantages of in-situ soil purification.
[390] List 3 advantages of in-situ soil purification.
[391] When is contamination isolated?
[392] What is the focus of soil remediation?
[393] What is structure and why can it be
developed separately as a design category between form and function, and how
can one recognise structure in the drawing?
[394] Give an
example of polarity between ‘open’ and ‘closed’ on five different levels of
scale. Are they positioned perpendicular to each other or equidistant? Are they
motoric or sensoric?
[395] What is ‘function’ in the technical–ecological
sense?
[396] Give the main division of urban
functions according to the concepts of George, Parsons and Jakubowski.
[397] On which variable should one be
able to classify intentions?
[398] What alternative is there for freedom
of choice by introducing flexibility into the design?
[399] What is the fundamental problem
that comes to the fore when we want to make a ‘programme of requirements’ for nature and what is De
Jong’s suggested way out?
[400] Which suppositions hides a legend using the CIAM typology of living, working,
recreating and travelling for a district sketch (R=1km, r=100m)?
[401] Give a meaning to each cell in Fig. 1103 in words or in small illustrations.
Make – whether on location or not – a design sketch in the five colours in
which all transitions occur, each in at least four directions of the compass.
Make a detailed design sketch of at least three transitions. Then characterise
each area by means of its boundaries.
Pagina: 29
[T.M.1]Op basis van de energiestatistieken van het CBS
voor 2000 is dit Sankey diagram gemaakt, dat de herkomst en bestemming van
energiestromen in Nederland aangeeft. De verschillende
energiedragers (aardgas, ruwe olie, olieproducten, kolen, kernenergie,
duurzaam, elektriciteit, warmte en afval) zijn alle in PJ’s, maar in
verschillende kleuren weergegeven. Herkomst van energiedragers is winning dan
wel import, of een conversie vanuit andere energiedragers (raffinaderijen,
elektriciteitscentrales en WKK). Energieverliezen bij conversie zijn ook in het
Sankey diagram verwerkt. Dat is vooral goed te zien bij
elektriciteitscentrales: de ingaande stroom gas, kolen, kernergie en afval is
groter dan de uitgaande stroom elektriciteit. Bestemming van energiedragers is
export of het verbruikssaldo van één van de eindverbruikerssectoren (diensten,
huishoudens, landbouw, industrie of transport). De dikte van de lijnen wordt
bepaald door de omvang van de energiestromen. Hiermee is in één oogopslag te
zien wat de onderliggende verhoudingen zijn. Opvallend is de omvangrijke
doorvoer van olie en olieproducten. Ook is het belang van de
raffinaderijensector in Nederland
te zien. De daar geproduceerde olieproducten worden slechts beperkt in eigen
land gebruikt, ze zijn vooral voor de export bestemd. In het binnenlands
verbruik speelt aardgas een belangrijke rol.
Page: 62
[B5] Bouwkundestudenten zijn niet geďnteresseerd in de
op blz. 45 t/m 51 genoemde plantensoorten.
Page: 73
[B6] Blz. 59, 60 Section )???
Pagina: 164
[T.M.7]kan uitgebreider
[T.M.de8]P.M. zones voor uitzwaailengte bij
breuk.
Pagina: 468
[T.M. de9]ZIj komen voor
in beekdalen, vochtige laagten in dekzandgebieden en oude duinlandschappen,
laaggelegen rivier- en zeekleigronden, niet regelmatig overstroomd buitendijks
rivierlandschap, bemeste en iets ontwaterde veengronden.
Pagina: 468
[T.M. de10]stroomruggronden
in het rivierkleigebied, kreekrug- en kwelderwalgronden in het zeekleigebied
grensstroken tussen droge, zandige heuvels en vochtige dalen.
Pagina: 468
[T.M. de11]Vooral in de
kalkrijke jonge duinen, ook in Zuid Limburg en hier en daar langs de rivieren,
waar de grond kalrijk is.
Pagina: 468
[T.M. de12]op
voedselrijke, maar niet uitgesproken kalkrijke gronden in het rivieren gebied
op de leem- en losgronden in Limburg. Vroeger werden ze ook veel gevonden in de oudere zeekleigebieden
zoals op Walcheren.
Pagina: 468
[T.M. de13]in Oost
Nederland, Zuid Limburg, Achterhoek, Twente, plaatselijk in het Nijmeegs
heuvelland, Veluwezoom, Drente en Noord Brabant.
Pagina: 468
[T.M. de15]Bovenste deel
van hellingen in Zuid-Limburg, grensstrook tussen Ulmoin en Vaccinio-Quercion
in geaccidenteerde zandgebieden, hoogste gedeelte van de oude strandwallen, op
dunnen zankdgebieden, hoogste gedeelte van de oude strandwallen, op dunnen
lagen dekzand op keileem, verlaten en beboste oude bouwlanden op zandgrond enz.
Pagina: 468
[T.M. de16]Vlakke plateaus
in Zuid Limburg, het grootste gedeelte van de pleistocne znadgebieden in Oost
en Zuid Nederland, plaatselijk in het jonge en oude duinlandschap.
Pagina: 468
[T.M. de17]iets ontwaterde
veenterreinen in Oost en West Nederland. Zeer zeldzaam.
Pagina: 469
[T.M. de18]Laagste
gedeelten met slecht waterafvoer in de pleistocene zandgebieden, voedselrijkere
delen van de veengebieden in Noord en Zuid Holland, Noord-West Overijssel en
Friesland.





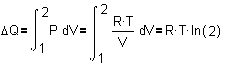
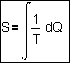
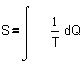

































































 -200000
-200000
































































































































































































































































































































































































































































































































































































































































































































































































































 feldspars
feldspars
 quarts
SiO2
quarts
SiO2 plagioklases
plagioklases pyroxenes
-SiO3
pyroxenes
-SiO3 olivine
-SiO4
olivine
-SiO4





































































































































































































































































































































































































































































































































































